-
采用“3S”集成技术进行森林蓄积量定量估测,国内外已有学者做过大量研究和试验。现有研究成果多采用TM,SPOT5,ALOS和资源-3号等卫星影像数据,并结合少量地面样地调查因子信息,建立以样地为单位的估测模型,进行区域森林蓄积量定量估测。多在估测模型解算方法、主要影响因子筛选、估测精度影响因素、建模样地抽样等方面进行研讨[1-6]。伴随中国高分系列卫星的发射和应用,如何利用国产高分卫星影像进行森林资源监测,已成为林业遥感学者关注的热点。因GF-1卫星搭载了4台16 m分辨率的多光谱相机,成像幅宽可达800 km,单台相机的幅宽为200 km,单台相机一景16 m分辨率的影像,其覆盖范围将达到40 000 km2,超过30 m分辨率的TM卫星影像。若能利用GF-1卫星影像,结合地面样地调查资料进行森林蓄积量估测,将极大提高监测效率,对促进国产高分卫星影像的应用、减轻野外调查劳动强度和降低调查成本均有重要意义。k-近邻(k-nearest neighbor, k-NN)作为一种非参数化统计方法,不受建模变量间复共线性影响,且对异常样地有一定抵抗作用,不仅可用于分类,也可用于森林蓄积量估测,在芬兰、瑞典等北欧国家已将该方法应用于小面积单元的森林蓄积量估测[7-8],国内也开展了一定探索[9]。本研究采用黑龙江省某林业局一类样地调查资料、试验区GF-1号16 m分辨率的多光谱影像、数字高程模型(DEM)和土地利用类型图,分别采用k-NN算法、最小二乘估计和稳健估计,建立以样地大小为单位的森林蓄积量估测模型,通过分析各种模型的估测精度及GF-1遥感信息对建模的影响,讨论利用GF-1影像和k-NN算法实现县/林业局级尺度森林蓄积量估测的可行性。
-
研究区地理坐标范围为50°04′59.3″~51°12′44.9″N,123°45′40.4″~126°04′0.6″E,在试验区主要优势树种中,针叶树种有兴安落叶松Larix gmelinii和樟子松Pinus sylvestris var. mongolica,阔叶树种有白桦Betula platyphylla,山杨Populus davidiana,蒙古栎Quercus mongolica等。全局经营面积为966 110 hm2,其中林地面积为944 948.6 hm2,占经营面积的97.81%。在林地中,有林地面积为623 870 hm2,占经营面积的64.58%[10]。
在建模所用数据中,样地资料为最近一期森林资源连续清查固定样地数据,调查时间为2010年。样地为0.06 hm2的长方形样地,坐标采集点位于样地中心。落入试验区的样地总数为153个,其中有林地样地为87个。
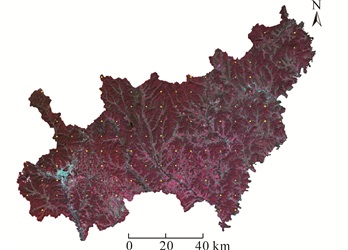
遥感影像采用GF-1号16 m多光谱数据,成像时间为2013年9月7日。依据中国卫星资源应用中心公布的定标系数及波谱响应函数对数据进行了辐射定标和大气校正处理。使用研究区1:50 000等高线数据生成的数字高程(DEM)模型对影像进行了正射校正,参考试验区融合后分辨率为2.5 m的ZY-3影像,采集控制点对高分影像进行几何精校正。几何精校正误差在1个像元以内,几何精校正后影像像元分辨率为16 m。将样地叠加在校正后的影像上,所得结果如图 1所示。
DEM模型采用覆盖研究区1:50 000等高线数据生成的栅格DEM模型,用于获取研究区的坡度、坡向和海拔等信息,并作为可能影响蓄积量估测的地形因子。以覆盖研究区林地“一张图”成果数据,生成覆盖研究区的土地利用类型图,作为森林蓄积量估测的输入数据。该“一张图”数据是根据2012年前后ZY-3多光谱与全色波段融合数据进行人工判读区划所得结果,如图 2所示。地类包括:有林地、疏林地、灌木林地等[11],为定性数据。在建模分析时,需进行定量化处理[12]。在本研究中,将有林地和疏林地划归为林地,将其余地类划归为非林地,即定量化处理后的地类仅包括林地和非林地。
-
将样地分布图层叠加在高分遥感影像上,提取样地范围各波段的灰度值,根据波段灰度值生成归一化植被指数、差值植被指数等若干比值波段,与样地地类、坡度、坡向、海拔、郁闭度等调查因子,作为可能影响蓄积量估测的自变量因子[2]。在设置的可能影响蓄积估测的自变量中,可能有的因子对蓄积量估测影响较大,有的影响较小或没有影响,且影响因子间可能存在多重相关性,为优选对蓄积量估测起主要作用的因子,采用平均残差平方和准则筛选影响蓄积量估测的主要变量[2, 13-14]。为克服多重相关性对蓄积量估测的影响,将研究k-NN方法估测蓄积量,并与传统最小二乘估计和稳健估计进行对比分析[2, 15-21]。以样地调查数据和最优建模变量筛选结果,使用上述方法分别建立森林蓄积量估测模型;将遥感影像分割为样地大小的对象,提取对应的遥感信息,代入模型,计算得到监测区域每样地单元的蓄积量,最后积分得到监测区域总的蓄积量。设研究区域样地总数为n,影响蓄积量估测的主要因子个数为m,则n个样地m个因子对应的观测阵X可表示为:
$$X=\left( \begin{matrix} {{x}_{11}}&{{x}_{12}}&\cdots &{{x}_{1m}} \\ {{x}_{21}}&{{x}_{22}}&\cdots &{{x}_{2m}} \\ \vdots &\vdots &\cdots &\cdots \\ {{x}_{n1}}&{{x}_{n2}}&\cdots &{{x}_{nm}} \\ \end{matrix} \right)。$$ (1) -
k-NN法的基本思想是在多维特征空间中找到与未知点距离最近的k个已知点q1,q2,…,qk,并根据这k个点的值来判定未知点的值,这k个点就是未知点的k-近邻。需将监测区域遥感影像分割为若干样地大小的单元。设其中任意一单元为p,其特征向量可表示为(xp1,xp2,…,xpm),则p到任一样地qi间的欧式距离dpqi可表示为:
$${{d}_{pqi}}=\sqrt{\sum\limits_{j=1}^{m}{{{\left( {{X}_{pj}}-{{X}_{qij}} \right)}^{2}}}。}$$ (2) 按式(2)计算p到全部n块样地的距离,将计算结果按从小到大的顺序进行排列,选取前k个样地,作为p的k-近邻。设k个近邻样地的蓄积分别为yq1,yq2,…,yqk,则该单元p的蓄积量yp可用下式计算:
$${{y}_{p}}=\frac{\sum\limits_{i=1}^{k}{{{y}_{qi}}}}{k}。$$ (3) 实际上,因目标对象p受其附近各个近邻样地的影响是不同的,通常认为距离越近的近邻与p相似性越高,对其影响也就越大。为减少k-NN估计的偏差,对各近邻按距离远近进行加权,距离越近权重越大,距离越远则权重越小。各近邻样地权重计算方法为:
$${{w}_{{{q}_{i}}p}}=\frac{\frac{1}{d_{{{q}_{i}}p}^{t}}}{\sum\limits_{i=}^{k}{\frac{1}{d_{{{q}_{i}}p}^{t}}}}。$$ (4) 式(4)中:t为距离分解因子,t值越大,估计结果受距离近的样地影响越大。一般取t=2。加权改进后的目标样地单元的蓄积量计算表达式为:
$${{y}_{p}}=\sum\limits_{i=1}^{k}{{{w}_{{{q}_{i}}p}}{{y}_{pi}}}=\frac{\sum\limits_{i=1}^{k}{\frac{1}{d_{{{q}_{i}}p}^{2}}{{y}_{{{q}_{i}}}}}}{\sum\limits_{i=1}^{k}{\frac{1}{d_{{{q}_{i}}p}^{2}}}}。$$ (5) 式(5)中:yp为预测点p的蓄积量,yqi为近邻点qi的蓄积量。
使用k-NN法估测森林蓄积量,不需要各样地蓄积量满足Gauss-Markov线性假设[6-7],不受自变量间不存在多重共线性影响的限制[2, 6-7],因每个样地单元蓄积使用k个近邻样地蓄积进行估算,模型对异常样地也具有一定的抵抗能力。
-
设监测区域调查样地的蓄积量y和m个主要影响因子间存在下列线性关系:
$$y={{\beta }_{0}}+{{\beta }_{1}}{{x}_{1}}+{{\beta }_{2}}{{x}_{2}}+\cdots +{{\beta }_{\text{m}}}{{x}_{\text{m}}}+{{e}_{\text{Y}}}。$$ (6) 对监测区域的n个用于蓄积量估测的建模样地,式(6)的矩阵表达式为:
$$Y=X\beta +{{e}_{Y}}。$$ (7) 式(7)中:Y=(y1, y2, …, yn),β=(β0, β1, …, βm),X为:
$$X=\left( \begin{matrix} 1&{{x}_{11}}&\cdots &{{x}_{1m}} \\ 1&{{x}_{21}}&\cdots &{{x}_{2m}} \\ \vdots &\vdots &\cdots &\vdots \\ 1&{{x}_{1}}&\cdots &{{x}_{m}} \\ \end{matrix} \right)。$$ eY=(ey1,ey2,…,eyn),当n个样地的蓄积量观测误差向量eY满足Gauss-Markov假设时[2],式(7)中待定参数β的最小二乘解为:
$$\hat{\beta }={{\left( {X}'X \right)}^{-1}}{X}'Y。$$ 根据上式可得监测区域森林蓄积量估测的经验回归方程为:
$$\hat{y}={{\hat{\beta }}_{0}}+{{\hat{\beta }}_{1}}{{X}_{1}}+{{\hat{\beta }}_{2}}{{X}_{2}}+\cdots +{{\hat{\beta }}_{m}}{{X}_{m}}。$$ (8) -
在监测区域用于建立估测模型的n个样地中,因森林类型、生长状况和树种的差异,可能出现有的样地蓄积量很大,有的却很小,在进行残差分析时,这些样地可能被作为异常样地删除,但实际上却属于正常情况。若采用最小二乘估计建模,最小二乘法就会起一种调和作用,以牺牲平均蓄积量样地的拟合程度为代价,使蓄积量异常的样地的“异常程度”降低,掩盖事实真相,导致蓄积量估测模型预报精度降低,为此,可以考虑使用稳健估计。将式(7)的模型表示为误差方程形式:
$${{e}_{Y}}=X\beta-Y。$$ (9) 稳健估计要求:$\sum\limits_{i=1}^{n}{\rho \left( {{e}_{i}} \right)=}\sum\limits_{i=1}^{n}{\rho }$$\left( {{\beta }_{0}}+{{X}_{i1}}{{\beta }_{1}}+{{X}_{i2}}{{\beta }_{2}}+\cdots {{X}_{im}}{{\beta }_{m}}-{{y}_{i}} \right)$为最小,即用误差的绝对最小值作为稳健估计的极值函数,以便减弱异常样地的影响。可按以下迭代法求解稳健估计模型中待定参数的最优解:① 根据式(9),组成法方程X′Xβ=X′Y,计算待定参数的估值β和残差eY;② 计算加权函数阵Wn×n;③ 组成方程X′WXβ=X′WY,计算待定参数的估值和残差;④ 再次计算加权函数阵Wn×n。重复上述步骤,直至连续2次迭代权函数之差小于阈值为止,最后求得即为森林蓄积量稳健估计方程的系数。权函数阵表达式为:
$${{W}_{n\times n}}=\left( \begin{matrix} \frac{1}{1+\left| {{e}_{{{y}_{1}}}} \right|}&0&\cdots &0 \\ 0&\frac{1}{1+\left| {{e}_{{{y}_{2}}}} \right|}&\cdots &0 \\ \vdots &\vdots &\cdots &\vdots \\ 0&0&\cdots &\frac{1}{1+\left| {{e}_{{{y}_{n}}}} \right|} \\ \end{matrix} \right)。$$ -
提取试验区域样地对应GF-1遥感影像各波段的灰度值,构造比值波段[22],考虑监测区域样地调查因子,设置可能影响蓄积估测的自变量:海拔(h),阴坡(SC),阳坡(SS),坡度(Si),郁闭度(P),b,g,r,nir,$\frac{b-g}{b+g}, \frac{b-r}{b+r}, \frac{b-{{n}_{ir}}}{b+{{n}_{ir}}}$,$\frac{g-r}{g+r}, \frac{r-{{n}_{ir}}}{r+{{n}_{ir}}}, \frac{r-{{n}_{ir}}}{r+{{n}_{ir}}}$,$\frac{b+gr}{b+g+r}, \frac{b+g-{{n}_{ir}}}{b+g+{{n}_{Eir}}}, \frac{r+g-{{n}_{\text{ir}}}}{r+g+{{n}_{\text{ir}}}}, \frac{b\cdot g\cdot r}{b+g+r}$。其中,b,g,r和nir分别表示样地对应的GF-1号16 m多光谱影像的蓝、绿、红及近红外波段的灰度值。
采用平均残差平方和准则,筛选对蓄积量估测起主要作用的影响因子:海拔(h),阴坡(SC),阳坡(SS),坡度(Si),郁闭度(P),b,g,r,$\frac{b-r}{b+r}, \frac{b+g-r}{b+g+r}, \frac{b+g-{{n}_{\text{ir}}}}{b+g+{{n}_{\text{ir}}}}, \frac{b\cdot g\cdot r}{b+g+r}$。在影响蓄积量估测的主要因子中,高分遥感信息占有很大比重。如何有效挖掘遥感信息,对蓄积量估测精度和效率均有重要意义。
利用筛选所得影响蓄积量估测的主要因子建模,当采用k-NN方法时,因监测区域样地较少,采用交叉验证方法进行精度评价。设样地总数为n,每次从n个样地中不重复地抽取1个样地i,其蓄积量实测值为yi,利用剩余的n-1个样地按照k-NN法估测样地i的蓄积量yi′。这样不断抽取,直至全部样地都仅被抽中1次。则相对均方根误差E′RMS可表示为:
$${{{E}'}_{\text{RMS}}}=\frac{\sqrt{\frac{\sum\limits_{i=1}^{n}{{{\left( {{{{y}'}}_{i}}-{{y}_{i}} \right)}^{2}}}}{n}}}{{\bar{Y}}}。$$ (10) 式(10)中:Y是yi的平均值。
按照上述方法,利用样地数据分别计算k取5~10时的均方根误差(m3·hm-2),所得结果如图 3所示。
对k取不同值时ERMS计算结果进行分析,认为k取9时具有较好的结果精度。采用最小二乘估计所得模型为:
$$\begin{align} &\hat{Y}=16.2255+0.0123h-0.0714{{S}_{\text{C}}}+0.6519{{S}_{\text{S}}}+0.1053{{S}_{\text{i}}} \\ &+0.0030P+0.1021b+0.1719g+0.3639r-0.0457\frac{b-r}{b+r} \\ &-0.1203\frac{b+g-r}{b+g+r}+0.0241\frac{b+g-{{n}_{\text{ir}}}}{b+g+{{n}_{\text{ir}}}}+0.1691\frac{b\cdot g\cdot r}{b+g+r}。 \\ \end{align}$$ 采用稳健估计所得模型为:
$$\begin{align} &\hat{Y}=16.2255+0.01105h-0.3112{{S}_{\text{C}}}+0.4067{{S}_{\text{C}}}+0.0928{{S}_{\text{i}}} \\ &+0.0034P+0.2130b+0.2133g+0.4068r-0.0562\frac{b-r}{b+r} \\ &-0.1381\frac{b+g-r}{b+g+r}+0.0217\frac{b+g-{{n}_{\text{ir}}}}{b+g+{{n}_{\text{ir}}}}+0.0345\frac{b\cdot g\cdot r}{b+g+r}。 \\ \end{align}$$ 按上述模型,将试验区的GF-1遥感影像分割成样地大小的单元。根据GF-1遥感影像和DEM模型计算方程中各样地大小单元对应自变量的值,并代入估测模型,得到样地大小单元蓄积量的估值(图 4)。

图 4 根据一类样地估测试验区蓄积量的分布
Figure 4. The stock volume maps by different estimation methods based on sample plots
利用估测结果统计研究区域总体森林蓄积量,并与研究区2012年森林资源二类调查蓄积量统计结果进行比较,可得如表 1所示3种建模方法的精度结果。由表 1中数据可得,k-NN方法估测精度最高,稳健估计略优于最小二乘估计。
表 1 3种估测方法估测结果精度比较
Table 1. The comparation of the precision of three estimation methods
蓄积量估测方法 蓄积量/m3 相对精度/% 二类调查 39 595 184 100.0 最小二乘估计 40 817 098 96.9 稳健估计 40 762 574 97.1 k-NN法 40 651 710 97.3 -
在建立蓄积量估测模型时,高分遥感影像原始波段和比值波段对蓄积量估测均有较大影响。在利用高分遥感影像进行蓄积量定量估测时,应充分挖掘遥感信息,以提高森林蓄积量估测的精度和效率。
在本研究讨论的研究区域中,采用平均残差平方和准则,经过大量仿真计算发现,GF-1的b,r,nir,$\frac{b-r}{b+r}, \frac{b+g-r}{b+g+r}, \frac{b\cdot g\cdot r}{b+g+r}$等遥感信息对蓄积量估测均有较大影响,并且随参选因子的变化,最终筛选结果会有一定差别。
k-NN方法作为一种非参数化方法,不需要参与建模样地的蓄积量满足Gauss-Markov假设,且不受自变量间不存在多重共线性的限制,由于每个样地单元蓄积量使用k个近邻样地蓄积进行估算,模型对样地异常值具有一定的抵抗能力。相比传统多元回归估测模型,能有效提高估测精度,可广泛应用于森林资源监测遥感定量估测。
Forest stock volume estimation based on the k-NN method and GF remote sensing data
-
摘要: 综合利用黑龙江省某林业局的一类样地调查资料、GF-1号卫星影像、数字高程(DEM)模型以及土地利用类型图,采用k-近邻(k-nearest neighbor,k-NN)法进行森林蓄积量估测研究,分析k-NN方法及GF-1卫星数据在森林资源调查与监测中的应用效果。为对比k-NN方法的估测精度,对相同试验数据也进行了最小二乘估计和稳健估计建模。采用GF-1号16 m分辨率的多光谱数据,在林业局级尺度上分别应用这3种方法进行森林蓄积量建模估测,生成了监测区域森林蓄积量分布图并统计得到监测区域总的蓄积量值。将3种方法估测结果与二类调查实测结果进行比较,k-NN方法估测精度达到97.3%,略优于传统的最小二乘估计和稳健估计建模估测精度。因k-NN方法不受Gauss-Markov假设限制,且能有效克服建模变量间的复共线性问题,研究成果可用于县/林业局级尺度的森林蓄积量估测,且国产GF-1卫星影像能有效应用于森林资源监测。Abstract: To analyze application results of the k-nearest neighbor (k-NN) method and GaoFen-1 (GF-1) satellite data in forest resources investigation and monitoring, sample plot data of national continuous forest inventory, GF-1 satellite images, digital elevation model (DEM), and land utilization type pictures from a Forestry Bureau in Heilongjiang Province were used. To compare estimation accuracy of the k-NN method, least squares regression and robust regression were used based on the same test data. By using GF-1 satellite images of 16 m resolution wide field view (WFV) Multi-spectral data, models based on k-NN, least squares regression, and robust regression, models were built with a map showing stock volume distribution. Results comparing the estimated stock volume and the survey value showed that the overall accuracy for the forestry bureau scale was over 90% with performance of the k-NN method being 0.4% higher than the least squares regression and 0.2% higher than robust regression methods. Because the k-NN method was neither limited by the Gauss-Markov hypothesis nor the effects of the Multi-collinearity between the modeling variables, the research results could be used for county or Forestry Bureau scale forest stock volume estimations, and domestic GF-1 satellite images could be effectively applied to forest resource monitoring.
-
Key words:
- forest management /
- k-NN method /
- stock volume estimation /
- least squares regression /
- robust regression
-
表 1 3种估测方法估测结果精度比较
Table 1. The comparation of the precision of three estimation methods
蓄积量估测方法 蓄积量/m3 相对精度/% 二类调查 39 595 184 100.0 最小二乘估计 40 817 098 96.9 稳健估计 40 762 574 97.1 k-NN法 40 651 710 97.3 -
[1] 赵宪文, 李崇贵.基于"3S"的森林资源定量估测--原理、方法、应用及软件实现[M].北京:中国科学技术出版社, 2001. [2] 李崇贵, 赵宪文, 李春干.森林蓄积量遥感估测理论与实现[M].北京:中国科学技术出版社, 2006. [3] 杨永恬. 基于多源遥感数据的森林蓄积量估测方法研究[D]. 北京: 中国林业科学研究院, 2010. YANG Yongtian. Study on Estimating Methods of Forest Stem Volume Base on Multi-source Remote Sensing Image[D]. Beijing:Chinese Academy of Forestry, 2010. [4] 余坤勇, 刘健, 亓兴兰, 等.基于RS技术闽江流域生态公益林林分蓄积量的动态监测[J].福建农林大学学报 (自然科学版), 2007, 36(5):481-485. YU Kunyong, LIU Jian, QI Xinglan, et al. Dynamical monitoring on the ecological forest stand volume in Minjiang watershed based on RS technology[J]. J Fujian Agric For Univ Nat Sci Ed, 2007, 36(5):481-485. [5] FAZAKAS Z, NILSON M, OLSSON H. Regional forest biomass and wood volume estimation using satellite data and ancillary data[J]. Agric For Meteorl, 1999, 98(1):417-425. [6] de GROEVE T, LOWELL K. Improving local forest volume estimates by fusion of multi-temporal forest type maps[J].Environ Model Software, 2000, 15(4):373-385. [7] LABRECQUE S, FOURNIER R A, LUTHER J E, et al. A comparison of four methods to map biomass from Landsat-TM and inventory data in western New foundland[J]. For Ecol Manage, 2006, 226(1/3):129-144. [8] KATILA M. Empirical errors of small area estimates from the multi-source national forest inventory in eastern Finland[J]. Silv Fenn, 2006, 40(4):729-742. [9] 陈尔学, 李增元, 武红敢, 等.基于k-NN和Landsat数据的小面积统计单元森林蓄积估测方法[J].林业科学研究, 2008, 21(6):745-750. CHEN Erxue, LI Zengyuan, WU Honggan, et al. Forest volume estimation method for small areas based on k-NN and landsat data[J]. For Res, 2008, 21(6):745-750. [10] 刘景贵.基于森林资源现状的加格达奇林业局林业发展对策探讨[J].林业科技情报, 2014(3):12-15. LIU Jinggui. Discussion on the strategy for the forest resource situation of Jiagedaqi forest bureau[J]. For Sci Technol Inf, 2014(3):12-15. [11] 国家林业局. 国家森林资源连续清查技术规定[S]. 北京: 国家林业局, 2004. [12] 李崇贵, 蔡体久.森林郁闭度对蓄积量估测的影响规律[J].东北林业大学学报, 2006, 34(1):15-17. LI Chonggui, CAI Tijiu. Effect of forest canopy density on stock volume estimation[J]. J Northeast For Univ, 2006, 34(1):15-17. [13] 何晓群.多元统计分析[M].北京:中国人民大学出版社, 2015. [14] 何晓群, 刘文卿.应用回归分析[M].北京:中国人民大学出版社, 2015. [15] 戚玉娇, 李凤日.基于KNN方法的大兴安岭地区森林地上碳储量遥感估算[J].林业科学, 2015, 51(5):46-55. QI Yujiao, LI Fengri. Remote sensing estimation of aboveground forest carbon storage in Daxing'an Mountains based on KNN method[J]. Sci Silv Sin, 2015, 51(5):46-55. [16] 许东, 代力民, 邵国凡, 等.基于RS、GIS及k-近邻法的森林蓄积量估测[J].辽宁工程技术大学学报 (自然科学版), 2008, 27(2):46-55. XU Dong, DAI Limin, SHAO Guofan, et al. Stand volume estimation based on RS, GIS and k-nearest neighbor methods[J]. J Liaoning Tech Univ Nat Sci, 2008, 27(2):46-55. [17] BAFFETTA F, CORNOA P, FATTONRINI L. A matching procedure to improve k-NN estimation of forest attribute maps[J]. For Ecol Manage, 2012, 272(3):35-50. [18] 姚宜斌, 陶本藻, 施闯.稳健回归分析及其应用研究[J].大地测量与地球动力学, 2002, 22(2):16-19. YAO Yibin, TAO Benzao, SHI Chuang. Research on robust regression analysis and its application[J]. J Geodesy Geodynam For Univ, 2002, 22(2):16-19. [19] 包鑫. 稳健回归技术及其在光谱分析中的应用[D]. 杭州: 浙江大学, 2010. BAO Xin. Robust Regression and Its Application in Spectral Analysis[D]. Hangzhou:Zhejiang University, 2010. [20] 郭颖. 森林地上生物量的非参数化遥感估测方法优化[D]. 北京: 中国林业科学研究院, 2011. GUO Ying. Optimum Non-parametric Method for Forest above Ground Biomass Estimation Based on Remote Sensing Data[D]. Beijing:Chinese Academy of Forestry, 2011. [21] 梁长秀, 冯仲科, 郎南军, 等.森林资源调查数据的稳健估计及分析[J].北京林业大学学报, 2001, 23(6):10-12. LIANG Changxiu, FENG Zhongke, LANG Nanjun, et al. Robust estimation and analysis of investigation data in forest resource[J]. J Beijing For Univ, 2001, 23(6):10-12. [22] 高阳. 森林蓄积量估测遥感影像比值波段和纹理信息选择及研究[D]. 西安: 西安科技大学, 2014. GAO Yang. Research on the Ratio Band of Remote Sensing Image in Forest Stock Volume and Choice of Texture Infomation[D]. Xi'an: Xi'an University of Science and Technology, 2014. 向安民等: 基于k-NN方法和GF遥感影像的森林蓄积量估测 -

-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2017.03.004







 下载:
下载: