-
高光谱图像具有光谱分辨率高、图谱合一、波段多且连续、信息量丰富等优点[1]，但这一系列优点提高了数据维数，增加了数据运算量，给高光谱图像遥感地物分类等实际应用带来困难，严重影响了高光谱遥感技术的推广。因此，要从高光谱图像中获得更加精准的信息，需在处理之前进行波段降维。这样不仅有利于降低数据的空间维数，减少数据处理工作量，也有利于人工图像解译和后续的分类处理[2]。对高光谱数据进行波段降维处理时一般考虑3个方面的因素：波段信息量的多少、波段间相关性的强弱以及目标地物的光谱响应特征[3]。常见的波段降维方法主要分为2种：基于特征变换的方法和基于原始信息的波段选择方法。基于特征变换的方法是依据某一原则，运用一定的数学运算法则，将原始高维特征空间的多个特征值映射到低维空间。近年来，ROWEIS等[4]提出了局部线性嵌入的流行学习方法，白杨等[5]提出了改进的核二维主成分分析方法，杜博等[6]提出新的判别流行学习方法。这些方法都是以严格的数学理论为支撑，但是由于改变了高光谱数据的原有特性，导致原始波段物理信息损坏甚至丢失，存在一定的局限性。基于原始信息的波段选择方法是依据某个准则从原始波段中选择部分最具代表性的波段，常用的有自适应波段选择[7]、波段指数[8]、最佳指数因子[9]等。秦方普等[10]提出了基于谱聚类与类间可分性因子的高光谱波段选择方法，CHEPUSHTANOVA等[11]提出了基于稀疏支持向量机的波段降维方法，宋欠欠等[12]探讨了关于随机森林的变量捕获方法及其在高维数据变量筛选中的应用，GEORGE等[13]用Wilks’ Lambda的方法对EO-1Hyperion数据选择特征波段。由于这些方法直接从原始光谱空间中选择波段，未经过变换处理，保持了图像的原有特性[14]，因此，成为高光谱遥感降维处理的重要研究方向。波段选择还存在另外2个关键的问题：如何选择合适的波段数量以及如何评价不同降维方法的优劣性。关于波段数量选择的研究，2004年，CHANG等[15]提出一种衡量波段数目的指标“虚拟维度”，并且得到了广泛的应用；在评价波段选择方法优劣的研究方面，也出现了一些判定标准，如欧氏距离、信息熵、光谱角匹配、光谱信息散度等[7]。基于以上成果，本研究比较分析了Wilks’ Lambda（WL）, 随机森林（random forest，RF）和自适应波段选择（adaptive band selection，ABS）这3种基于原始信息的波段降维方法；同时提出一种基于曲线误差指数的评价方法，旨在找到3种方法中最有效的降维方法以及检验基于曲线误差指数的方法是否具有可行性。
-
实验数据采用的是由AISA Eagle传感器获取的位于浙江省衢州市开化县（29°13′N，118°05′E）的机载高光谱影像。开化县是全国重点的生态功能保护区，属于中亚热带常绿阔叶林带。研究区有大量的植被覆盖，且植被种类繁多，主要植被类型为常绿阔叶林、针叶林和毛竹Phyllostachys edulis林等。机载高光谱数据覆盖了398.55~994.44 nm光谱区间的64个波段，每个波段对应的波长如表 1所示。野外样地数据的获取时间为2014年12月，结合谷歌地球（Google Earth），最终确定14个10 m × 10 m的小样本：包括2个阔叶林，3个针叶林，2个毛竹林，2个农田，2个不透水地表，2个裸地，1个水体，平均分布在研究区范围内。
表 1 不同波段对应中心波长位置
Table 1. Different bands corresponding to the wavelength center position
波段 中心波长位置/nm 1 398.55 2 407.39 3 416.27 4 425.18 5 434.13 6 443.10 7 452.11 8 461.14 9 470.21 10 479.30 11 488.43 12 497.58 13 506.76 14 515.96 15 525.19 16 534.44 17 543.72 18 553.02 19 562.35 20 571.70 21 581.07 22 590.46 23 599.86 24 609.29 25 618.74 26 628.21 27 637.69 28 647.19 29 656.70 30 666.24 31 675.78 32 685.34 33 694.91 34 704.50 35 714.09 36 723.70 37 733.32 38 742.95 39 752.58 40 762.23 41 771.88 42 781.54 43 791.21 44 800.88 45 810.56 46 820.24 47 829.92 48 839.61 49 849.30 50 858.99 51 868.68 52 878.38 53 888.07 54 897.76 55 907.45 56 917.13 57 926.81 58 936.49 59 946.16 60 955.83 61 965.49 62 975.15 63 984.80 64 994.44 -
Wilks’ Lambda（WL）是逐步判别分析法中的一种方法，它基于多变量的方差分析。计算时，首先确定分类系统，然后把每个变量建立于分类样本之上，在分类总体中检验类均值是否一致。最后，对研究的对象总体，假设总体服从正态分布，将样本量为n的样本按大小顺序排列编秩，然后由确定的显著性水平α，以及样本量为n时所对应的系数αi，根据式（1）计算出统计量W。最后根据W的大小选择出合适的波段。Wilks’ Lambda计算公式如下[16]：
$$\left\{ {\begin{array}{*{20}{l}} {W = \frac{{{S_{{\text{SE}}}}}}{{{S_{{\text{ET}}}}}}} \\ {{S_{{\text{SE}}}} = \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^p {{{\left( {{x_{ij}} - {{\bar x}_i}} \right)}^2}} } } \\ {{S_{{\text{ET}}}} = \sum\limits_{i = 1}^r {\sum\limits_{j = 1}^p {{{\left( {{x_{ij}} - \bar x} \right)}^2}} } } \end{array}} \right.。$$ (1) 式（1）中: xij（i=1，…，r, j=1，…，p）, SSE为样本离差矩阵中的组内平方和，SST为总平方和（即组间平方和与组内平方和的总和）。W值在0到1之间变化，值越接近0则说明组间差别越大，反之，值接近于1说明组间差别越小[13]。因此，用Wilks’ Lambda方法进行降维选择波段是基于不同类别的类内差异。
-
随机森林法（RF）是一种现代回归和分类技术，同时也是一种组合式的自学习技术，能够有效地处理高维变量问题[17]。它以装袋算法（bagging）为理论基础。装袋算法是在样本中随机抽样，生成多个树模型，然后以多数投票的方式来预测结果。随机森林法比装袋算法更进一步，不仅对样本随机抽样，而且对变量（波段）随机抽样。最后可以计算出每个变量（波段）的重要性，且计算速度快。随机森林法计算波段重要性的主要步骤[17-18]为：① 将样本随机分为训练样本和测试样本（如7:3），生成分类树组成随机森林；② 以波段xi（i∈1，2，…，m）为例，将检测样本中xi的所有值随机打乱，然后根据步骤① 中建立好的随机森林模型对每个样本所属类别进行预测，计算波段xi去掉前后检测样本预测错误率的大小；③ 对于所有的树，计算波段xi去掉前后的检测样本预测错误率的大小，将平均值作为变量重要性的评分；④ 计算出每个变量的重要性R。
-
自适应波段选择法（ABS）[7]主要考虑每个波段自身信息量的大小以及波段之间相关性的大小。计算公式为：
$$I = \frac{{{\sigma _i}}}{{\left( {{R_{i - 1,i}} + {R_{i,i + 1}}} \right)/2}}。$$ (2) 式（2）中：I为自适应指数，σi为第i个波段的标准差，Ri-1, i为第i-1波段与第i波段之间的相关系数，Ri, i+1为第i波段与第i+1波段之间的相关系数。从式（2）可以看出，I值的计算是用波段的标准差除以某一波段与前后2个波段之间相关系数的平均值。由于波段的标准差代表了波段信息量的丰富程度，相关系数代表了波段的独立性，因此相除运算可以找出信息量大且独立性好的波段。对于最终波段的选择，首先将自适应指数I从大到小排序，然后根据后续处理的需要选择合适的波段数量或者设定阈值选择最终的波段。
-
评价一个波段降维方法的优劣时，不仅要考虑降维后的波段所包含信息量的多少，还要考虑所选择出的波段对目标地物光谱响应曲线趋势是否改变。基于此思想，本研究提出基于曲线误差的评价方法。曲线误差主要对波段选择前后同一目标地物光谱响应曲线的匹配度进行检验，即以选择的波段为基础，在相邻2个波段之间以一个波段为内插距离进行线性内插，直到整个波谱段内插完毕，然后计算各波段内插值与原始值之间差值，见式（3）。
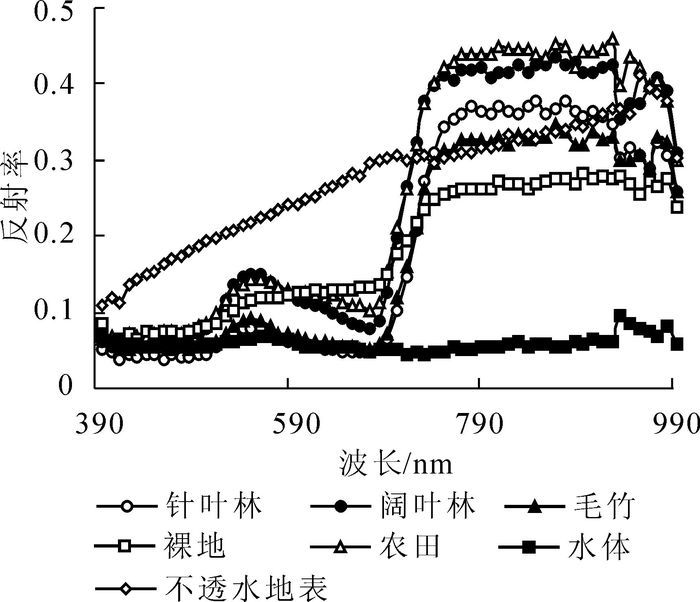
$$\sigma = \sqrt {\frac{1}{{n - 1}}\sum\limits_{n = 1}^n {D_n^2} } 。$$ (3) 式（3）中：σ为曲线误差，n为波段数，D为内插值与原始值的差值。观察图 1可以发现：水体的曲线相对平稳, 不透水地表的曲线呈上升趋势，裸地的曲线在675~742 nm之间有小幅度波动，而针叶林、阔叶林、毛竹林和农田这类绿色植物的曲线最为复杂，含有2个波峰和1个波谷。综合考虑不同地物的光谱曲线发现，6个位置（425，506，553，675，742，965 nm附近）的光谱非常重要，因此，要想把不同地物的光谱曲线完整地表现出来，至少需要6个波段。将上述3种方法计算的W值、R值、I值，从大到小分别进行排列。以排在前面的6个波段开始，1次增加1个波段，计算原始曲线与内插曲线之间的整体误差。这样，每个波段数量都会得到1个整体误差值σ。根据σ的趋势，将σ趋于平稳时所对应的波段数量确定为最佳波段数量，从而得出每种降维方法的最佳波段。由于整体曲线误差值的趋势反映的是不同降维方法选择的波段对曲线拟合程度的强弱，以及是否选择了反射率突变的一些重要波段位置，因此选择6个波段时的初始误差值α6与误差的平稳值α平稳之间的差最能反映降维方法的优劣。α6-α平稳越小，则说明降维方法越好，反之，则越差。
图 1 不同地物的波谱曲线
Figure 1. Spectral curves of different features
-
本研究分类采用的是支持向量机（support vector machine, SVM）分类器。支持向量机是CORTES等[19]提出的。该分类器是针对小样本训练区分类设计的，根据有限的样本信息在模型的复杂性（对特定训练样本的学习精度）和学习能力（无错误识别任意样本的能力）之间寻求最佳状态，以获得最好的推广能力[20]。支持向量机对高维数据的分类尤其方便，相较与最大似然法等传统分类方法有很大的提高。在使用SVM分类器分类时，为了方法的可重复性，本研究尽量选择遥感图像处理软件（the environment for visualizing images，ENVI）中默认的参数，惩罚参数、分类概率阈值与金字塔等级分别为100，0，0。选择的函数为径向基核函数，设置的伽玛核函数参数为输入图像波段数的倒数（0.016）。
将Wilks’ Lambda法、随机森林法与自适应波段选择法这3种方法选择的波段重新组合为新的图像，并使用同样的训练样本与验证样本分别进行分类验证。
-
表 2为不同波段的W，R，I值计算结果（W值中的空白值是在计算过程中被剔掉而没有参与分析的波段）。根据计算结果，选择W值比较小的前6个波段，R值和I值比较大的前6个波段开始，计算不同波段数量下内插曲线与原始曲线之间的整体误差值σ。结果如图 2所示。
表 2 3种降维方法的波段计算结果
Table 2. Index calculation result of three dimension reduction methods
波段 W R I 1 0.124 23.8 583.0 2 0.349 48.4 525.5 3 0.087 77.9 473.7 4 0.034 72.1 473.1 5 35.6 476.6 6 0.161 29.3 481.4 7 0.077 34.0 500.6 8 15.6 495.7 9 0.105 9.2 507.4 10 0.279 15.3 490.8 11 7.4 501.0 12 0.200 5.4 521.4 13 0.075 14.2 553.6 14 0.109 28.2 616.6 15 0.083 14.0 722.4 16 0.067 35.0 803.1 17 0.245 43.1 849.7 18 0.081 46.1 872.5 19 0.461 15.8 860.7 20 0.114 9.4 812.2 21 0.065 27.0 762.7 22 0.079 22.7 742.5 23 17.5 719.7 24 0.073 24.8 708.2 25 0.137 19.3 686.7 26 49.9 681.0 27 42.3 674.2 28 0.144 53.4 651.0 29 61.5 641.1 30 37.6 632.9 31 0.065 44.7 634.0 32 34.9 689.3 33 0.066 29.0 858.4 34 0.085 21.7 1 209.1 35 0.044 117.0 1 550.3 36 0.102 2 251.0 1 971.4 37 0.070 1 256.3 2 344.0 38 0.119 38.2 2584.1 39 10.0 2 743.3 40 0.099 41.0 2 831.4 41 0.220 3.0 2 854.2 42 0.068 8.0 2 853.1 43 7.7 2 872.1 44 0.130 79.2 2 862.6 45 0.976 6.6 2 899.7 46 0.093 40.2 2 915.2 47 4.1 2 920.5 48 39.0 2 908.9 49 0.096 2.2 2 937.6 50 0.172 36.1 2 923.0 51 0.301 5.5 2 963.6 52 30.5 2 936.7 53 41.5 2 915.5 54 0.647 39.7 2 945.4 55 0.039 39.2 2 962.6 56 58.3 2 943.2 57 0.152 8.7 2 968.4 58 0.071 7.0 2 801.5 59 0.090 84.9 2 806.1 60 0.186 413.1 2 820.4 61 823.0 2 794.8 62 244.7 2 854.0 63 0.415 832.2 2 775.3 64 194.5 2 217.9 
图 2 3种方法不同波段数量的曲线误差结果
Figure 2. Curve error results of different band numbers in three methods
曲线误差是从地物的光谱特征出发，评价波段选择前后同一地物光谱曲线的相似度。若在波峰波谷等曲线突变点选有波段，则曲线误差较小，反之较大。分析图 2可以发现，Wilks’ Lambda法在选择10个波段之后，曲线的误差趋向于平稳，随着波段数的增加误差值没有明显的变化，说明10个波段都在植被曲线的重要位置（即波谷或波峰），可以将植被的光谱曲线完整地表示出来；随机森林法在选择13个波段的时候趋向于平稳，但之后仍有轻微下降的趋势，平稳度低于Wilks’ Lambda法选择10个波段之后的平稳度；自适应波段选择法的曲线误差值则一直在下降，只在选择20个波段时有1个小的平稳值，说明随着波段的增加曲线发生很大的变化，即所选择的波段没有选在关键的波长位置，不具有代表性。从曲线误差的趋势出发，我们可以得出结论：Wilks’ Lambda法选择的最佳波段数量为10个波段，随机森林法为13个波段，自适应波段选择法为20个波段（表 3）。
表 3 3种降维方法波段选择结果
Table 3. Band selection results of three dimension reduction methods
Wilks’ Lambda法（10个） 随机森林法（13个） 自适应波段选择法(20个） 4 (425.18)/16 (534.44)/21 (581.07)/31 (675.78)/33 (694.91)/35 (714.09)/37 (733.32)/42 (781.54)/ 55 (907.45)/58 (936.49) 3 (416.27)/4 (425.18)/29 (656.70)/35 (714.09)/36 (723.70)/37 (733.32)/44 (800.88)/59 (946.16)/ 60(922.83)/61 (965.49)/62 (975.15)/63 (984.80)/B64 (994.44) 40 (762.23)/41 (771.88)/42 (781.54)/43 (791.21)/44 (800.88)/45 (810.56)/46 (820.24)/47 (829.92)/ 48 (839.61) /49 (849.30) /50 (858.99) /51 (868.68) /52 (878.38)/53 (888.07)/54 (897.76)/55 (907.45)/ 56 (917.13) /57(926.81) /60(955.83) /62(975.15) 说明：括号外的数字为波段号，如4为第4波段；括号内的数字为波长，如425.18为波长425.18 nm。 从表 3选择的结果也可以看出，Wilks’ Lambda法选择的波段在整个光谱范围内分布比较均匀，随机森林法选择的波段较多的分布在红光以及近红外波段附近，而自适应波段选择法选择的波段都集中在40波段之后，即选择的都为近红外范围的波段。
对于绿色植被（如阔叶林、针叶林、毛竹林和农田等）的反射曲线，在0.54 μm（17波段）附近有1个小的反射峰，主要反映植被叶绿素吸收带的强弱。从图 4可以看出：用Wilks’ Lambda法方法选择的波段包含了小反射峰波段（第17波段附近的波段），而随机森林法选择的波段直接从第3波段和第4波段跨越到第29波段，忽略了小反射峰。红边峰值及红边位置是监测植被叶绿素、生理活动以及生物量等最常用的因素，是植被光谱最明显的标志。分析图 3的原始波段曲线可发现，植被的红边范围为675~762 nm（31~40波段），因此，31~40波段之间的选择十分重要。Wilks’ Lambda法选择的波段在此范围内都有分布，与原始曲线保持一致；随机森林法选择的波段拉长了红边的范围；自适应波段选择法选择的波段集中在40波段之后，直接忽略了小反射峰和红边的位置，没有将植被的光谱特征表现出来。
图 3 波段选择结果对不同地类的光谱响应曲线
Figure 3. Spectral response curve of different feature in different methods
图 4 不同方法的曲线误差平稳值与6个波段的曲线误差差值
Figure 4. Curve error difference between selecting six bands and when the curve becomes smooth in different methods
由于不透水地表的光谱曲线以及裸地的曲线并没有存在很明显的波谷与波峰，因此不同的方法选择的波段并没有很大的区别，但是由于自适应波段选择法所选择的波段集中在近红波段，仍然不能表现地物的光谱响应曲线。
-
内插计算时，默认将原始波段的第1个波段到所选择波段的第1个波段之间、所选择波段的最后一个波段到原始波段的最后一个波段之间的内插曲线值均设置为0（首尾位置不存在内插值）。由于近红外波段的反射率明显高于可见光波段，因此每种降维方法的最终曲线误差值与选择的波段的起始位置相关。若选择的波段集中在近红外波段，则误差值整体偏低，选择的波段集中在可见光波段，则误差值整体偏高。因此，不同降维方法之间的整体误差值不存在比较意义，而应重点关注整体曲线误差值的趋势，α6-α平稳才能评价不同降维方法的优劣。
图 4显示：α6-α平稳值Wilks’ Lambda法最小，其次为随机森林法，最大为自适应波段选择法。因此我们可以得出结论：Wilks’ Lambda法可以选择出数量最少且最具有代表性的波段。Wilks’ Lambda法与随机森林法都是监督分类的降维方法，在降维的时候不仅考虑波段本身的信息量，并且也考虑到了类内类间的差距。自适应波段选择法是基于波段的标准差与波段间的相关性来计算的，由于高光谱图像波段之间的相关性本来就高，2个波段之间的相关系数只有微小的差别，而每个波段的标准差却差别很大，特别是近红外区域，每个波段都具有很高的标准差。这样自适应指数的大小就由波段的标准差决定，最后选择的波段多集中在近红外波段的范围内，因此存在的误差较大。
-
从图 5的分类结果可以看出，自适应波段选择法选择的波段分类结果与原始波段、Wilks’ Lambda法选择的波段、随机森林法选择的波段的分类结果有很明显的不同，其中最大的区别在于不透水地表和植被的大面积混淆。主要是因为自适应波段选择法选择的波段主要集中在近红外波段，而植被与不透水地表光谱特征的最大的差异在可见光波段，自适应波段选择法忽略了可见光部分，最终导致植被与不透水地表混分现象严重。
图 5 不同降维方法的分类结果
Figure 5. Results of different dimension reduction methods
从总体分类精度来看（表 4），自适应波段选择法选择的20个波段具有最小的总体分类精度49.94%，虽然选择的波段数量多，但是由于选择的波段都不具有代表性且比较集中，分类效率明显低于随机森林法与Wilks’ Lambda法。随机森林法与Wilks’ Lambda法选择的波段总体分类精度和原始波段的总体分类精度相差不大，但Wilks’ Lambda法的精度（80.56%）高于随机森林法（79.11%）。
表 4 不同降维方法分类结果的混淆矩阵
Table 4. Confusion matrix of classification results in different dimension reduction methods
不同方法 类别 阔叶林 针叶林 毛竹林 农田 不透水地表 裸地 水 总计 用户精度/% 阔叶林 191 89 14 27 0 0 0 321 59.5 针叶林 3 305 165 0 3 0 0 476 64.1 毛竹林 0 3 19 0 0 0 0 22 86.4 农田 6 3 2 173 8 20 0 212 81.6 原始波段 不透水地表 0 0 0 0 184 0 2 186 98.9 裸地 0 0 0 0 1 180 0 181 99.5 水体 0 0 0 0 4 0 198 202 98.0 总计 200 400 200 200 200 200 200 总体精度/% 80.56 生产者精度/% 95.5 76.3 9.5 86.5 92.0 90.0 99.0 Kappa系数 0.77 阔叶林 189 81 9 27 0 0 0 306 61.8 针叶林 3 315 180 0 3 0 0 501 62.9 毛竹林 0 1 10 0 0 0 0 11 90.9 农田 8 3 1 173 9 17 0 211 82.0 Wilks ’ Lambda法 不透水地表 0 0 0 0 181 0 1 182 99.5 裸地 0 0 0 0 2 183 0 185 98.9 水体 0 0 0 0 5 0 199 204 97.6 总计 200 400 200 200 200 200 200 总体精度/% 80.56 生产精度/% 94.5 78.8 5.0 86.5 90.5 91.5 99.5 Kappa系数 0.77 阔叶林 173 72 16 26 0 0 0 287 60.3 针叶林 5 318 161 0 0 0 9 493 64.5 毛竹林 0 3 22 0 0 1 0 26 84.6 农田 22 7 1 174 8 13 0 225 77.3 随机森林法 不透水地表 0 0 0 0 167 0 7 174 96.0 裸地 0 0 0 0 19 186 0 205 90.7 水体 0 0 0 0 6 0 184 190 96.8 总计 200 400 200 200 200 200 200 总体精度/% 79.11 生产精度/% 86.5 79.5 11.0 87.0 83.5 93.0 92.0 Kappa系数 0.76 阔叶林 129 44 7 26 2 0 0 208 62.0 针叶林 5 141 144 80 55 101 62 588 24.0 毛竹林 0 0 0 0 0 0 0 0 0 农田 59 92 30 93 17 1 0 292 31.9 自适应波段选择法 不透水地表 7 99 17 1 101 0 1 226 44.7 裸地 0 0 2 0 20 98 0 120 81.7 水体 0 24 0 0 5 0 137 166 82.5 总计 200 400 200 200 200 200 200 总体精度/% 49.94 生产精度/% 64.5 35.3 0 46.5 50.5 49.0 68.5 Kappa系数 0.41 比较每种降维方法中所有地类的生产者精度和用户精度，植被都普遍偏低，其中毛竹林最低，与其他树种之间混分现象严重。前面的分析中提到，自适应波段选择法和随机森林法在绿光波段的小波峰以及红边附近选择的波段不合理，影响不同树种之间的分类精度，使树种之间存在错分混分的现象。
-
本研究采用Wilks’ Lambda法、随机森林法、自适应波段选择法等3种降维方法分别对高光谱图像进行降维处理，并提出一种基于曲线误差指数的高光谱降维方法评价指标。通过比较分析发现，Wilks’ Lambda法选择的波段能够完整地将植被的光谱信息表示出来，是最佳的波段降维方法。
本研究在分类精度评价的基础上，验证了基于曲线误差指数这种评价指标的可行性。结果表明：分类精度与基于曲线误差指数的评价方法得出的结果一致，都得出对于本研究区，Wilks’ Lambda法是最佳的波段降维方法，即曲线误差指数作为评价不同降维方法优劣性的指标是可行的。曲线可以反映地物的光谱特征，基于曲线的误差计算不仅可以体现所选波段的波长位置是否合适，同时通过曲线误差的趋势也可以确定合适的波段数量。基于曲线误差指数的评价方法完全符合了评价降维方法时要考虑所选择出的波段对目标地物光谱响应曲线保持不变的思想，方法操作简单，物理意义明确，易于理解和分析，可以准确地在众多降维方法中选择最合适的波段降维方法。
A comparative study of dimension reduction methods for airborne hyperspectral images
-
摘要: 高光谱数据波段多、波段之间相关性强，导致信息冗余严重，增加了数据处理的工作量，有效准确地在众多波段中选择具有代表性的波段尤为重要。首先用Wilks' Lambda（WL），随机森林（random forest，RF）与自适应波段选择（adaptive band selection，ABS）这3种方法对高光谱数据进行降维处理。然后提出了基于曲线误差指数的评价方法，用此指数的趋势来确定每种降维方法所要选择的合适波段数量，同时用指数的大小评价不同降维方法的优劣，并用分类方法对评价结果加以验证。结果显示：Wilks' Lambda最终选择的波段数为10个，α6-α平稳值（选择6个波段时的曲线误差值与曲线误差平稳值之间的差值）为0.05；随机森林最终选择的波段数为13个，α6-α平稳值为0.06；自适应波段选择方法最终选择的波段数为20个，α6-α平稳为0.14。Wilks' Lambda的总体分类精度为80.56%，Kappa系数为0.77；随机森林的总体分类精度为79.11%，Kappa系数为0.76；自适应波段选择方法的总体分类精度为49.94%，Kappa系数为0.41。得出以下结论：① 基于曲线误差指数的方法得出Wilks' Lambda有最小的α6-α平稳值，是最佳的波段降维方法；分类结果显示：Wilks' Lambda有最大的总体分类精度与Kappa系数，是最佳的波段降维方法。② 基于曲线误差指数的评价方法与基于分类结果的误差一致，说明此方法具有可行性。Abstract: Hyperspectral datasets have been widely used in monitoring analyses of vegetation due to their abundant spectral information; however, their spectral resolution greatly increases information redundancy causing more data processing work. To find an efficient method for selecting the most representative bands to reduce redundancy before using them, three traditional dimension reduction methods, namely Wilks' Lambda (WL), random forest (RF), and adaptive band selection (ABS), were used to select optimal bands among the 64 bands. Then, a new evaluation method based on a curve error index was proposed to determine the appropriate number of bands through analysis trend of the index values and to select the best dimension reduction method. Lastly, classification results were used to demonstrate the validity of this method. Results indicated that WL selected 10 bands and the α6-αsmooth value (the curve error difference between selecting six bands and when the curve becomes stable) was 0.05. The RF method selected 13 bands and its corresponding α6-αsmooth value was 0.06. The ABS method selected 20 bands and its α6-αsmooth value was 0.14. The overall accuracy of WL based band selection was 80.56% with a Kappa coefficient of 0.77; RF was 79.11% with a Kappa coefficient of 0.76; and ABS had an overall accuracy of 49.94% and a Kappa coefficient of 0.41. Thus, (1) with the curve error index method WL presented the smallest α6-αsmooth value and had the highest overall classification accuracy, suggesting WL was the optimal method for dimensional reduction, and (2) the two evaluation methods had the same results, illustrating the curve was feasible.
-
Key words:
- forest management /
- hyperspectral imagery /
- curve error index /
- Wilks' Lambda /
- random forest /
- adaptive band selection
-
图 2 3种方法不同波段数量的曲线误差结果
Figure 2 Curve error results of different band numbers in three methods
图 3 波段选择结果对不同地类的光谱响应曲线
Figure 3 Spectral response curve of different feature in different methods
图 4 不同方法的曲线误差平稳值与6个波段的曲线误差差值
Figure 4 Curve error difference between selecting six bands and when the curve becomes smooth in different methods
表 1 不同波段对应中心波长位置
Table 1. Different bands corresponding to the wavelength center position
波段 中心波长位置/nm 1 398.55 2 407.39 3 416.27 4 425.18 5 434.13 6 443.10 7 452.11 8 461.14 9 470.21 10 479.30 11 488.43 12 497.58 13 506.76 14 515.96 15 525.19 16 534.44 17 543.72 18 553.02 19 562.35 20 571.70 21 581.07 22 590.46 23 599.86 24 609.29 25 618.74 26 628.21 27 637.69 28 647.19 29 656.70 30 666.24 31 675.78 32 685.34 33 694.91 34 704.50 35 714.09 36 723.70 37 733.32 38 742.95 39 752.58 40 762.23 41 771.88 42 781.54 43 791.21 44 800.88 45 810.56 46 820.24 47 829.92 48 839.61 49 849.30 50 858.99 51 868.68 52 878.38 53 888.07 54 897.76 55 907.45 56 917.13 57 926.81 58 936.49 59 946.16 60 955.83 61 965.49 62 975.15 63 984.80 64 994.44 
下载: 导出CSV
表 2 3种降维方法的波段计算结果
Table 2. Index calculation result of three dimension reduction methods
波段 W R I 1 0.124 23.8 583.0 2 0.349 48.4 525.5 3 0.087 77.9 473.7 4 0.034 72.1 473.1 5 35.6 476.6 6 0.161 29.3 481.4 7 0.077 34.0 500.6 8 15.6 495.7 9 0.105 9.2 507.4 10 0.279 15.3 490.8 11 7.4 501.0 12 0.200 5.4 521.4 13 0.075 14.2 553.6 14 0.109 28.2 616.6 15 0.083 14.0 722.4 16 0.067 35.0 803.1 17 0.245 43.1 849.7 18 0.081 46.1 872.5 19 0.461 15.8 860.7 20 0.114 9.4 812.2 21 0.065 27.0 762.7 22 0.079 22.7 742.5 23 17.5 719.7 24 0.073 24.8 708.2 25 0.137 19.3 686.7 26 49.9 681.0 27 42.3 674.2 28 0.144 53.4 651.0 29 61.5 641.1 30 37.6 632.9 31 0.065 44.7 634.0 32 34.9 689.3 33 0.066 29.0 858.4 34 0.085 21.7 1 209.1 35 0.044 117.0 1 550.3 36 0.102 2 251.0 1 971.4 37 0.070 1 256.3 2 344.0 38 0.119 38.2 2584.1 39 10.0 2 743.3 40 0.099 41.0 2 831.4 41 0.220 3.0 2 854.2 42 0.068 8.0 2 853.1 43 7.7 2 872.1 44 0.130 79.2 2 862.6 45 0.976 6.6 2 899.7 46 0.093 40.2 2 915.2 47 4.1 2 920.5 48 39.0 2 908.9 49 0.096 2.2 2 937.6 50 0.172 36.1 2 923.0 51 0.301 5.5 2 963.6 52 30.5 2 936.7 53 41.5 2 915.5 54 0.647 39.7 2 945.4 55 0.039 39.2 2 962.6 56 58.3 2 943.2 57 0.152 8.7 2 968.4 58 0.071 7.0 2 801.5 59 0.090 84.9 2 806.1 60 0.186 413.1 2 820.4 61 823.0 2 794.8 62 244.7 2 854.0 63 0.415 832.2 2 775.3 64 194.5 2 217.9
下载: 导出CSV
表 3 3种降维方法波段选择结果
Table 3. Band selection results of three dimension reduction methods
Wilks’ Lambda法（10个） 随机森林法（13个） 自适应波段选择法(20个） 4 (425.18)/16 (534.44)/21 (581.07)/31 (675.78)/33 (694.91)/35 (714.09)/37 (733.32)/42 (781.54)/ 55 (907.45)/58 (936.49) 3 (416.27)/4 (425.18)/29 (656.70)/35 (714.09)/36 (723.70)/37 (733.32)/44 (800.88)/59 (946.16)/ 60(922.83)/61 (965.49)/62 (975.15)/63 (984.80)/B64 (994.44) 40 (762.23)/41 (771.88)/42 (781.54)/43 (791.21)/44 (800.88)/45 (810.56)/46 (820.24)/47 (829.92)/ 48 (839.61) /49 (849.30) /50 (858.99) /51 (868.68) /52 (878.38)/53 (888.07)/54 (897.76)/55 (907.45)/ 56 (917.13) /57(926.81) /60(955.83) /62(975.15) 说明：括号外的数字为波段号，如4为第4波段；括号内的数字为波长，如425.18为波长425.18 nm。
下载: 导出CSV
表 4 不同降维方法分类结果的混淆矩阵
Table 4. Confusion matrix of classification results in different dimension reduction methods
不同方法 类别 阔叶林 针叶林 毛竹林 农田 不透水地表 裸地 水 总计 用户精度/% 阔叶林 191 89 14 27 0 0 0 321 59.5 针叶林 3 305 165 0 3 0 0 476 64.1 毛竹林 0 3 19 0 0 0 0 22 86.4 农田 6 3 2 173 8 20 0 212 81.6 原始波段 不透水地表 0 0 0 0 184 0 2 186 98.9 裸地 0 0 0 0 1 180 0 181 99.5 水体 0 0 0 0 4 0 198 202 98.0 总计 200 400 200 200 200 200 200 总体精度/% 80.56 生产者精度/% 95.5 76.3 9.5 86.5 92.0 90.0 99.0 Kappa系数 0.77 阔叶林 189 81 9 27 0 0 0 306 61.8 针叶林 3 315 180 0 3 0 0 501 62.9 毛竹林 0 1 10 0 0 0 0 11 90.9 农田 8 3 1 173 9 17 0 211 82.0 Wilks ’ Lambda法 不透水地表 0 0 0 0 181 0 1 182 99.5 裸地 0 0 0 0 2 183 0 185 98.9 水体 0 0 0 0 5 0 199 204 97.6 总计 200 400 200 200 200 200 200 总体精度/% 80.56 生产精度/% 94.5 78.8 5.0 86.5 90.5 91.5 99.5 Kappa系数 0.77 阔叶林 173 72 16 26 0 0 0 287 60.3 针叶林 5 318 161 0 0 0 9 493 64.5 毛竹林 0 3 22 0 0 1 0 26 84.6 农田 22 7 1 174 8 13 0 225 77.3 随机森林法 不透水地表 0 0 0 0 167 0 7 174 96.0 裸地 0 0 0 0 19 186 0 205 90.7 水体 0 0 0 0 6 0 184 190 96.8 总计 200 400 200 200 200 200 200 总体精度/% 79.11 生产精度/% 86.5 79.5 11.0 87.0 83.5 93.0 92.0 Kappa系数 0.76 阔叶林 129 44 7 26 2 0 0 208 62.0 针叶林 5 141 144 80 55 101 62 588 24.0 毛竹林 0 0 0 0 0 0 0 0 0 农田 59 92 30 93 17 1 0 292 31.9 自适应波段选择法 不透水地表 7 99 17 1 101 0 1 226 44.7 裸地 0 0 2 0 20 98 0 120 81.7 水体 0 24 0 0 5 0 137 166 82.5 总计 200 400 200 200 200 200 200 总体精度/% 49.94 生产精度/% 64.5 35.3 0 46.5 50.5 49.0 68.5 Kappa系数 0.41
下载: 导出CSV
-
[1] CHANG C I. Hyperspectral Imaging: Signal Processing Algorithm Design and Analysis [M]. Baltimore: University of Maryland, 2009. [2] 耿修瑞. 高光谱遥感图像目标探测与分类技术研究[D]. 北京: 中国科学院, 2005. GENG Xiurui. Target Detection and Classification for Hyperspectral Imagery [D]. Beijing: Chinese Academy of Sciences, 2005. [3] BAJWA S G, BAICSY P, GROVES P, et al. Hyperspectral image data mining for band selection in agricultural applications [J]. Transac Am Soc Agric Eng, 2004, 47(3): 895-907. [4] ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding [J]. Science, 2000, 290(5500): 2323-2326. [5] 白杨, 赵银娣, 韩天庆.一种改进的K2DPCA高光谱遥感图像降维方法[J].测绘科学, 2014, 39(7): 126-130. BAI Yang, ZHAO Yindi, HAN Tianqing. Hyperspectral remote sensing dimensional reduction based on improved kernel two-dimension principal component analysis [J]. Sci Surv Map, 2014, 39(7): 126-130. [6] 杜博, 张乐飞, 张良培, 等.高光谱图像降维的判别流形学习方法[J].光子学报, 2013, 42(3): 320-325. DU Bo, ZHANG Lefei, ZHANG Liangpei, et al. Discriminant manifold learning approach for hyperspectral image dimension reduction [J]. Acta Photonica Sin, 2013, 42(3): 320-325. [7] 刘春红, 赵春晖, 张凌雁.一种新的高光谱遥感图像降维方法[J].中国图象图形学报, 2005, 10(2): 218-222. LIU Chunhong, ZHAO Chunhui, ZHANG Lingyan. A new method of hyperspectral remote sensing image dimensional reduction [J]. J Image Graph, 2005, 10(2): 218-222. [8] 姜小光, 唐伶俐, 王长耀, 等.高光谱数据的光谱信息特点及面向对象的特征参数选择:以北京顺义区为例[J].遥感技术与应用, 2002, 17(2): 59-65. JIANG Xiaoguang, TANG Lingli, WANG Changyao, et al. Spectral characteristics and feature selection of hyperspectral remote sensing data: taking shunyi region of Beijing as a study area [J]. Remote Sens Technol Appl, 2002, 17(2): 59-65. [9] CHAVEZ B P S, BERLIN G L, SOWERS L B. Statistical method for selection Landsat MSS ratios [J]. J Appl Photogr Eng, 1984, 8(1): 23-30. [10] 秦方普, 张爱武, 王书民, 等.基于谱聚类与类间可分性因子的高光谱波段选择[J].光谱学与光谱分析, 2015, 35(5): 1357-1364. QIN Fangpu, ZHANG Aiwu, WANG Shumin, et al. Hyperspectral band selection based on spectral clustering and inter-class separability factor [J]. Spectrosc Spectr Anal, 2015, 35(5): 1357-1364. [11] CHEPUSHTANOVA S, GITTINS C, KIRBY M. Band selection in hyperspectral imagery using sparse support vector machines [C]//Proceedings of the SPIE, 2014, 9800: 90881F-15. [12] 宋欠欠, 李轶群, 侯艳, 等.随机森林的变量捕获方法在高维数据变量筛选中的应用[J].中国卫生统计, 2015, 32(1): 49-53. SONG Qianqian, LI Yiqun, HOU Yan, et al. The application of a random forest-based variable hunting method to variable selection in high-dimensional data [J]. Chin J Health Stat, 2015, 32(1): 49-53. [13] GEORGE R, PADALIA H, KUSHWAHA S P S. Forest tree species discrimination in western Himalaya using EO-1 Hyperion [J]. Int J Appl Earth Observ Geoinform, 2014, 28(5): 140-149. [14] 卓莉, 郑璟, 王芳, 等.基于GA-SVM封装算法的高光谱数据特征选择[J].地理研究, 2008, 27(3): 493-501, 726. ZHUO Li, ZHENG Jing, WANG Fang, et al. A genetic algorithm based wrapper feature selection method for classification of hyper spectral data using support vector maching [J]. Geogr Res, 2008, 27(3): 493-501, 726. [15] CHANG Cheinl, DU Qian. Estimation of number of spectrally distinct signal sources in hyperspectral imagery [J]. IEEE Trans Geosci Remote Sens, 2004, 42(3): 608-619. [16] GREEN P E, CARROLL J D. Analyzing Multivariate Data [M]. Hinsdale: Dryden Press, 1978. [17] BREIMAN L. Random forest [J]. Mach Learn, 2001, 45(1): 5-32. [18] WU Xiaoyan, WU Zhenyu, LI Kang. Identification of differential gene expression for microarray data using recursive random forest [J]. Chin Med J, 2008, 121(24): 2492-2496. [19] CORTES C, VAPNIK V N. Support vector networks [J]. Mach Learn, 1995, 20(2): 273-297. [20] VAPNIK V N. 统计学习理论的本质[M]. 张学工, 译. 北京: 清华大学出版社, 2000. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2017.05.001
点击查看大图
图(5) / 表(4)
计量
- 文章访问数: 3228
- HTML全文浏览量: 743
- PDF下载量: 681
- 被引次数: 0
