Spatial continuity for DBH in dominant populations of an evergreen broadleaved forest in National Nature Reserve of Mount Tianmu, China

浙江省天目山国家级自然保护区位于浙江省西北部临安市境内的西天目山，距省会杭州94 km，30°18′30″~30°24′55″N，119°23′47″~119°28′27″E。区内年平均气温为8.8~14.8 ℃^[9]；≥10 ℃积温2 500~5 100 ℃；年降水量1 390~1 870 mm，相对湿度76%~81%。自然保护区受海洋暖湿气候影响较深，具有中亚热带向北亚热带过渡特征，森林植被十分茂盛。由于区内地势较为陡峭，海拔上升快，气候差异大，植被的分布有着明显的垂直界限，自山麓到山顶垂直带谱为：海拔870 m以下为常绿阔叶林；870~1 100 m为常绿、落叶阔叶混交林；1 100~1 380 m为落叶阔叶林；1 380~1 506 m为落叶矮林。其中，常绿阔叶林是自然保护区内重点保护植被类型。

选择保存较完好的常绿阔叶林设置样地，样地大小为100 m×100 m（图 1）。用相邻格子调查方法，把样地划分为100个10 ｍ×10 ｍ的调查单元。在每个调查单元内，对胸径大于或等于5 cm的木本植物进行每木调查，记录树木种类，测定每株树木的胸径、树高、活枝下高、冠幅等因子，采用激光对中全站仪（徕卡TCR702Xrange）测定每株树木坐标（x，y，z）。

Figure 1.  3D map of the plot

优势树种按优势度分析法确定^[10]。其方法是首先计算群落乔木层每个树种的相对胸高断面积，并作为优势度，按优势度从大到小排序。然后，通过下式确定优势树种数：

式（1）中：x_i为排序在前的上位种（T）的相对胸高断面积，x为优势树种所占的理想百分比，x_j为上位种以外的剩余种（U）的相对胸高断面积，N为总种数。如果群落只有1个优势树种，则优势树种的理想百分比为100.0%。如果有2个优势树种，则它们的理想百分比为50.0%，如果有3个优势树种，则理想百分比为33.3%，依次类推，分别计算d值。当d为最小值时的上位种数为群落乔木层优势树种数。

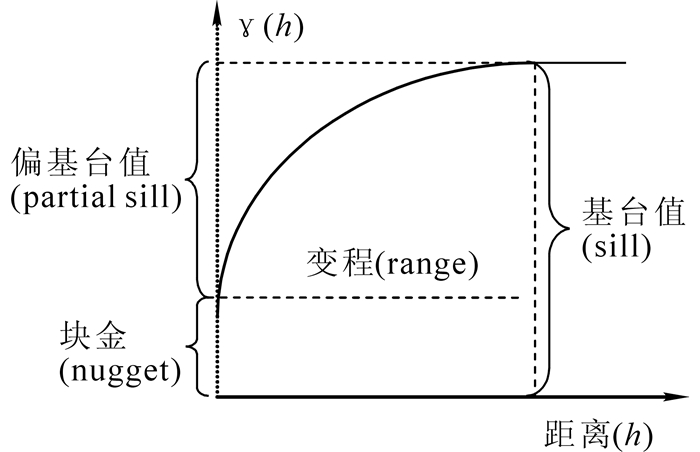
地统计学的核心是半变异函数。半变异函数分析是通过测定区域化变量分隔等距离的样点间的差异来研究变量的空间相关性和空间结构。分隔距离h的2点x₀和x的区域化变量Z（_xi）和Z（x_i+h）之间的变异，可用增量值Z（x_i）-Z（x+h）平方的数学期望（即区域化变量增量的方差）表示：

式（2）中：γ（h）称为半变异函数。半变异函数既是距离h函数，又是方向a的函数。半变异函数曲线图（semivariogram）是半变异函数值γ（h）对距离h的函数的图形，它有3个特征参数：基台值（sill），变程（range）和块金值（nugget），可作为各个方向的平均值，也可作为某一特定方向的值。基台值表示变量在研究系统中最大的变异程度，包括空间结构方差（c）和块金方差（c₀）。空间结构方差表示非随机的结构原因形成的变异，块金方差则反映的是由实验误差和小于最小取样尺度所引起的随机变异。变程表示研究变量在空间上自相关的范围。对于观测的数据系列Z（x_i）（其中i＝1，2，3，…，n），样本半变异函数值可由下式计算：

式（3）中：γ（h）是相隔距离为h的半变异函数曲线图的估计值，N（h）为被h分割的数据对（x_i，x_i+h）的总数即是相隔距离为h的所有点的配对数，Z（x_i）和Z（x_i+h）分别为在点x和（x_i+h）处样本的测量值，h为样点间距离（图 2）。当用变异函数定量描述整个区域时，需给变异曲线配制相应的数学模型。本研究拟合了有基台值的3个模型：球状模型、指数模型和高斯模型（表 1）。Journel等^[11]推荐遵循间距和最远配对样品之间的距离。间距距离4 m保证有1个足够的间距配对数。最大搜索距离使用相应样地宽的一半，即50 m^[12]。地统计学计算分析使用的是GS+软件。

Figure 2.  A typical Simivariogram

根据调查结果进行统计，样地内胸径5 cm以上的乔木共计1 603株，72个种。计算群落乔木层各树种的相对胸高断面积，并按降序排列，根据式（1）确定优势树种。结果显示：群落有13个优势树种（表 2）。13个优势树种的株数和胸高断面积分别占样地的78.66%和81.13%，表明这些树种在森林群落乔木层中占明显的优势。其中细叶青冈Cyclobalanopsis myrsinaefolia（A），杉木Cunninghamia lanceolata（B），短尾柯Lithocarpus brevicaudatus（C），青冈Cyclobalanopsis glauca（E）和豹皮樟Litsea coreana（M）是常绿树种，占样地总株树的61.01%。细叶青冈（A），短尾柯（C）和青冈（E）三者的株树占了总株树的52.71%，胸高断面积占了总样地胸高断面积的34.04%。

不同方向上的半变异函数往往会表现出不同的性质，这种不同方向上的差异称为各向异性^[13]，反之称为各向同性。各向同性是各向异性的特例。对本次调查的数据进行方向差异性检验时发现树木胸径的空间相关性仅仅与2点间的距离有关，即具有各向同性，因此不考虑方向效应，用各向同性变异函数进行分析。在各优势树种中，蓝果树（H）和金钱松（L）的株数太少，达不到最低配对数，不符合地统计分析要求，不予计算。黄檀（K）函数变程大于50 m，超出了最大搜索距离，在空间分布的函数假设中，认为超出最大距离的树是没有意义的，也不予计算。地统计模型的拟合，首要考虑决定系数r²的大小，然后考虑变程和块金值的大小，从而确定最佳模型。结果如表 3。

从表 3可见：豹皮樟（M）块金值为0，半变异函数值具有纯金块效应，即在该样地空间尺度上不存在空间相关性。杉木（B），枫香（D），白栎（F），黄连木（G），天目木姜子（I）和榉树（J）的结构比大于0.75，空间相关性较强；细叶青冈（A），短尾柯（C），青冈（E）结构比都在0.55以上，具有中度的空间相关性。短尾柯（C），青冈（E）和细叶青冈（A）的变程较大，空间连续性范围分别为35.70 m，45.55 m和11.10 m，其余优势树种的变程都在7.50 m以内。样地整体结构比为0.70，具有中度的空间相关性，平均空间连续性范围为5.70 m。

天目山国家级自然保护区常绿阔叶林的优势树种中，以细叶青冈、杉木、短尾柯和枫香为主，形成多优势种结构特征，林分胸径特征具有较高的空间相关性，但林分整体的空间连续性范围较小，仅在6 m以内，这也体现了常绿阔叶林的结构复杂性。汤孟平等^[14]采用Ripley’s K（d）函数分析优势种群空间分布格局和种间关联关系，认为天目山常绿阔叶林群落的优势种均呈显著聚集分布，多数优势种间有较强的种间关联性。这与本研究的结果是一致的。本研究仅对树木胸径这一属性特征，分析其空间连续性，林分其他因子，包括土壤性质、竞争等的空间连续性有待进一步研究。地统计分析是研究林分特征的有力工具，有必要在林业领域开发出具有林业特色的实用空间统计软件，使空间统计学理论、方法、程序系统一体化^[15]，以促进空间统计分析在林业领域的广泛应用。