-
尺度的合理选择对研究区土地利用景观变化和生态效应的分析具有科学的指导意义，也是目前景观生态学和地理学研究的热点问题之一。尺度的选择是进行生态学研究的基础，通常由空间粒度和幅度来描述。空间粒度是指景观中可以辨别的最小单元，所代表的特征长度、面积和体积，在空间数据和图像资料中通常对应于最大分辨率和像元的大小[1]。进行生态学研究的位置不同，粒度的划分方法、划分范围、步长的选择等均不相同[2-4]；数据源大多采用遥感影像人工解译法获得的解译图或土地利用现状图等[5-7]，研究区域多集中于城市热岛[8-10]、典型区域[11]、生态脆弱区[12-13]、流域或交通沿线等[14-18]。地形和地貌的差异会造成景观指数不同的粒度响应，只有当测量尺度、研究对象及本质特征与研究区符合时，景观指数才能将研究区的景观格局特征显示和反映出来[2]。因此，适宜空间粒度的选择，是反映景观格局状况和景观生态研究的关键。县域不仅是行政区划的重要单元，更是连接城市与乡村的重要节点。目前，景观指数粒度效应多以大尺度区域为研究对象，如孟楠等[19]研究发现：中国澳门城市生态系统格局分析的最佳粒度为25 m，张玲玲等[20]研究得出：沂蒙山区景观指数最佳粒度为35 m，马胜等[13]研究表明：黄土高原生态脆弱区景观生态风险分析的最佳粒度为120 m。而对县域尺度等中小区域的案例研究较少。鉴于此，本研究分析了安徽省宿松县不同景观指数在类型和景观水平下的粒度效应，以探讨长江中下游县域景观的粒度效应问题，对揭示县域景观生态规律具有一定的指导意义。
HTML
-
宿松县(29°47′~30°26′N，115°52′~116°35′E)位于安徽省西南方向，是长江中下游北岸的顶端。全县东西宽约67 km，南北长约72 km，总面积达2 394 km2。东北接壤太湖县，西边紧邻湖北省的蕲春县和黄梅县，东南角连接望江县，南边隔江相望于江西省的湖口县和彭泽县，是皖、鄂、赣三省的交界处，也是八县结合部。宿松县地势高低起伏明显，呈阶梯形式自西北向东南方向地势逐渐降低，属北亚热带湿润季风气候，四季分明，季风性明显，光照充足，雨水多，平均无霜期为255 d，植物生长期长。
-
以宿松县研究区2017年的地理国情普查成果为依据，结合研究目标，参考GB/T 21010−2017《土地利用现状分类》，根据土地实际用途以及地物意义，将地理国情普查数据中的地表覆盖分类重新划分为耕地、园地、林地、草地、建筑用地(房屋建筑区、构筑物、人工堆掘地)、交通用地(道路)、水域、未利用地(荒漠与裸露地表)等8个土地利用类型[21]。通过ArcGIS对划分后的土地斑块类型进行分类合并处理。
-
研究区范围以及景观格局的不同，粒度范围及步长的选择也大小不一，通常大步长会掩盖小步长的变化规律，小步长则可重演大步长的尺度变化规律[22]。因此，本研究以筛选合并的景观类型专题图为基础，参考前人粒度范围及步长的划分案例[8-12]，结合研究区实际概况，运用ArcToolbox中的Feature to Raster工具和重采样工具，将源数据转化为20~150 m以10 m为步长的14个数据，150~500以50 m为步长的7个数据，共21幅不同景观类型栅格图。
-
本研究根据实际需要从景观面积、形状复杂程度、聚集和散布状况、优势度、多样性等方面选取对粒度变化敏感且能较全面反映整个景观格局特征的景观指数。其中：在类型水平上选取斑块类型面积、斑块密度、斑块形状指数、平均分维数、最大斑块面积比例、斑块数量、斑块类型面积比例、平均斑块面积、有效网格大小；在景观水平上，面积边缘指标选取了景观总面积、景观总周长、边缘密度、周长面积分维数，密度大小及差异指标选取了斑块密度、斑块数量、平均斑块面积，形状指标选取了平均形状指数、平均分维数、景观形状指数。聚散性指标选取了散布与并列指数、景观聚合度、景观聚集度、景观凝聚度。多样性指标选取了斑块丰富度、Simpson多样性指数、Simpson均匀度指数[13-15, 23-25]。
-
利用Fragstats 4.2软件计算景观格局指数，并在Origin 2018下绘制不同空间粒度下的景观指数曲线，最后建立景观格局指数与粒度之间的函数关系，用拟合度(R2)检验其相关性，R2最大为1，R2越接近于1，表明回归直线对景观指数曲线的拟合程度越高，反之，回归直线对景观指数曲线拟合程度越差。然后利用拐点法和景观面积损失评价法[26]，确定研究区土地利用景观最佳适宜粒度。景观面积损失评价模型为：
式(1)中：P表示区域景观面积损失值；Li表示i类景观面积损失相对值；Ai表示i类景观类型粒度变化后景观面积；Abi表示第i类景观粒度变化前的景观面积；n表示景观类型的总数目。
1.1. 研究区概况
1.2. 方法
1.2.1. 数据来源及预处理
1.2.2. 粒度推绎
1.2.3. 土地利用景观格局指数筛选
1.2.4. 最佳景观粒度效应分析
-
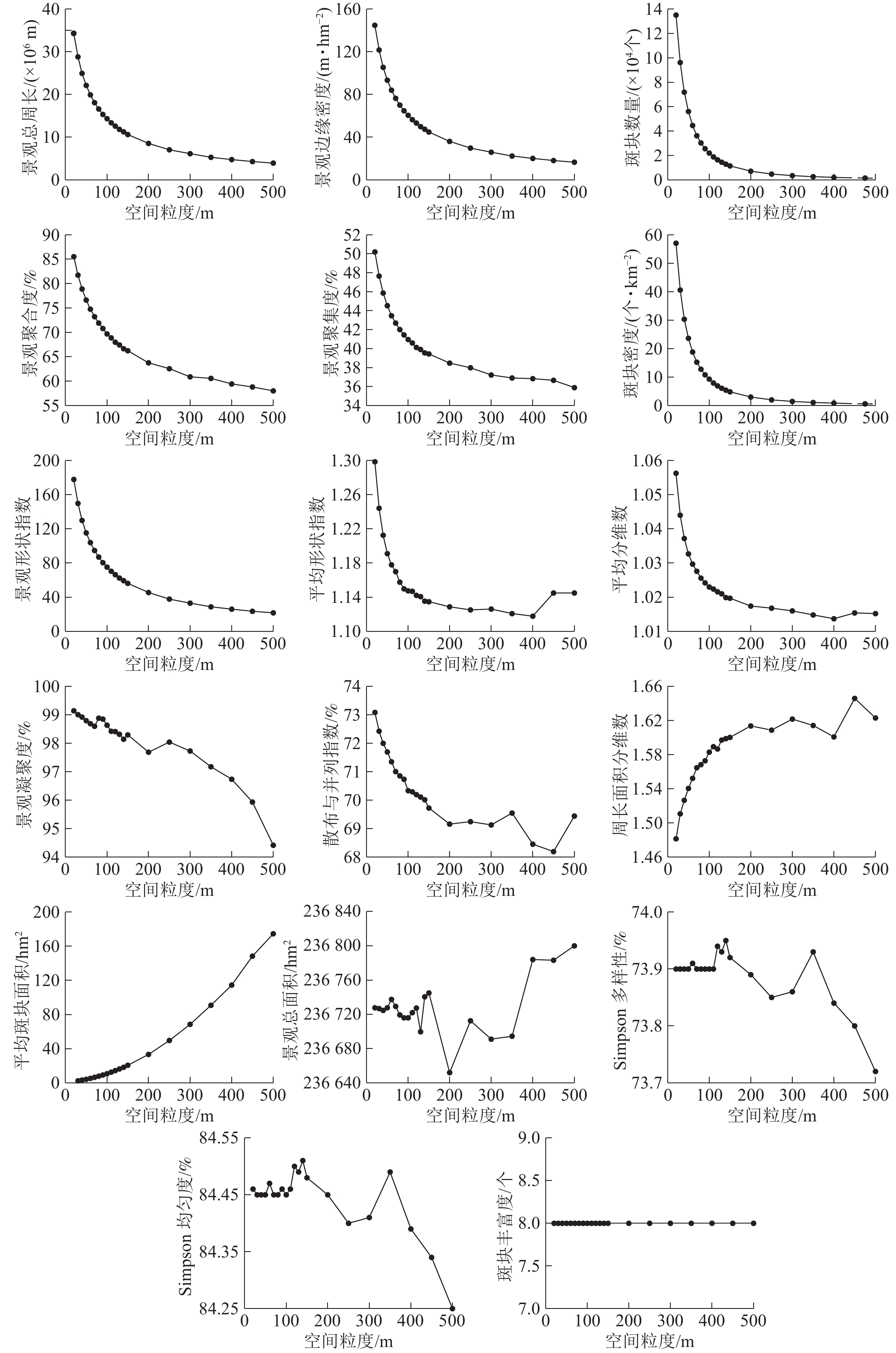
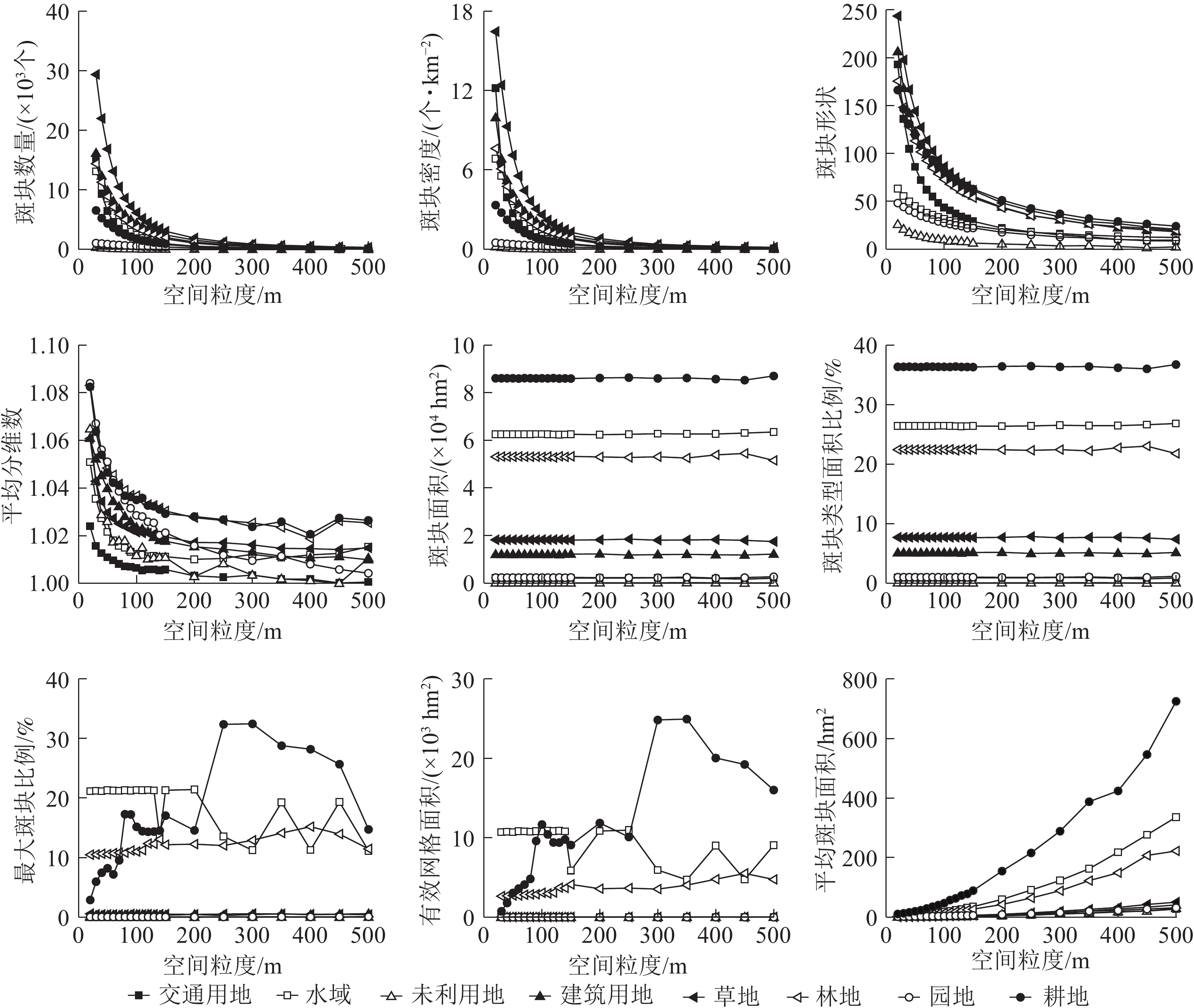
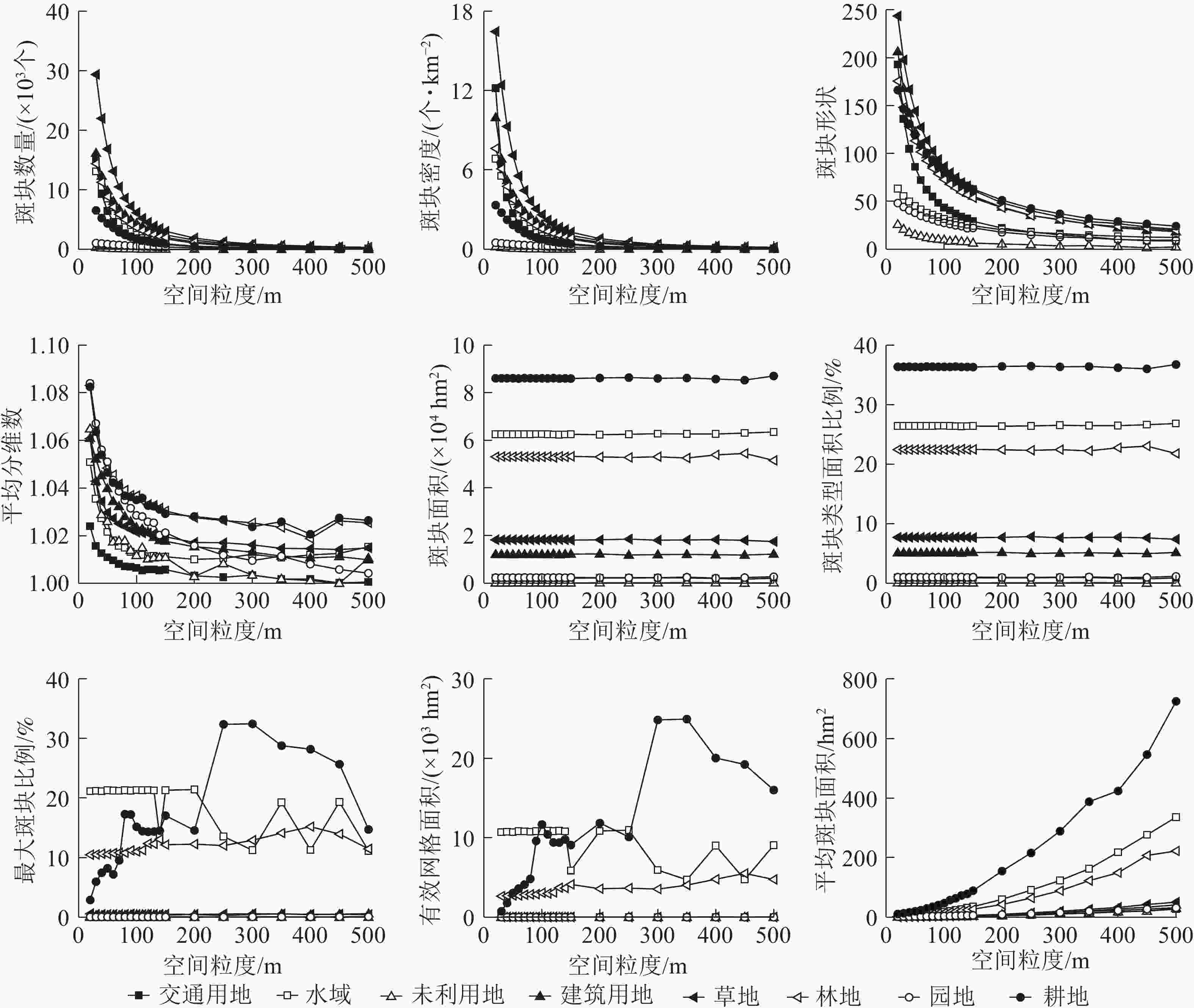
类型水平下宿松县的景观指数随着粒度的变粗呈不同的变化趋势(图1)。根据各种土地利用类型景观指数对粒度变化的响应差异，可以将宿松县类型水平指数分为以下4种类型。
Figure 1. Grain sizes change of landscape indices under type level
指数类型1包括斑块密度、斑块形状指数、斑块个数和平均分维数，呈逐渐减小的趋势，“L”型变化，与粒度的变化具有明显的响应关系。随着粒度的变粗，斑块个数、斑块密度、斑块形状指数下降幅度均比较剧烈，明显拐点为70 m，表明粒度的增加造成景观破碎度明显下降，景观异质性减小。其中草地、交通用地的斑块个数、斑块密度下降的最为剧烈，未利用地、园地变化幅度相对较小，这与研究区中草地分布较分散，交通用地相互交错、复杂分散，未利用地、园地面积较少，且分布较集中有关。水域、园地、未利用地景观形状指数变化不明显，与研究区中水域集中分布，耕地、水域、林地逐渐融合周围景观类型造成小斑块逐渐消失，斑块形状趋于单一有关。平均分维数明显的拐点为60 m，未利用地、园地、耕地、林地的下降的幅度较显著，建筑用地和园地降幅较大，未利用地变化趋势较复杂，与未利用地的斑块数目最少及呈聚集状态分布有关。
指数类型2包括斑块类型面积和斑块类型面积比例指数，无明显变化趋势，与粒度的变化具有明显的响应关系。随着粒度的增大，景观指数值均基本保持不变，粒度＞350 m后，林地的斑块类型面积和斑块类型面积比例上下波动，但变化较小，整体基本不变。研究区中土地利用类型的面积比例从大到小依次为耕地、水域、林地、草地、建筑用地、园地、交通用地、未利用地。
指数类型3包括最大斑块面积和有效网格大小指数，呈现“无规则”变化趋势，与粒度变化不具有明显的响应关系。林地、交通用地、未利用地、园地的景观指数变化幅度很小，且无明显拐点；草地明显拐点为70 m，在20~70 m内呈单调下降趋势，降幅明显；水域明显拐点为130 m，＞130 m后发生剧烈的浮动变化；建筑用地和耕地明显拐点为100 m，整体呈剧烈的不规则变化，但100~130 m呈轻微的波动变化，这与耕地、建筑用地分布较分散，130 m后景观异质性发生了变化有关；其他土地利用类型粒度效应响应不明显，这与自身斑块类型面积少且破碎度较大有关。
指数类型4包括平均斑块面积指数，呈现“J”上升趋势，与粒度的变化具有明显的响应关系。在不同的粒度范围内呈现出不同程度的增加趋势，转折点为150 m，20~70 m幅度增加很小；70~150 m幅度增加较大，但相对来说变化不大，＞150 m各土地利用类型的平均斑块面积指数急剧增大。这说明粒度的增大会引起大斑块夺取周围小斑块造成各土地类型的破碎度逐渐降低。
-
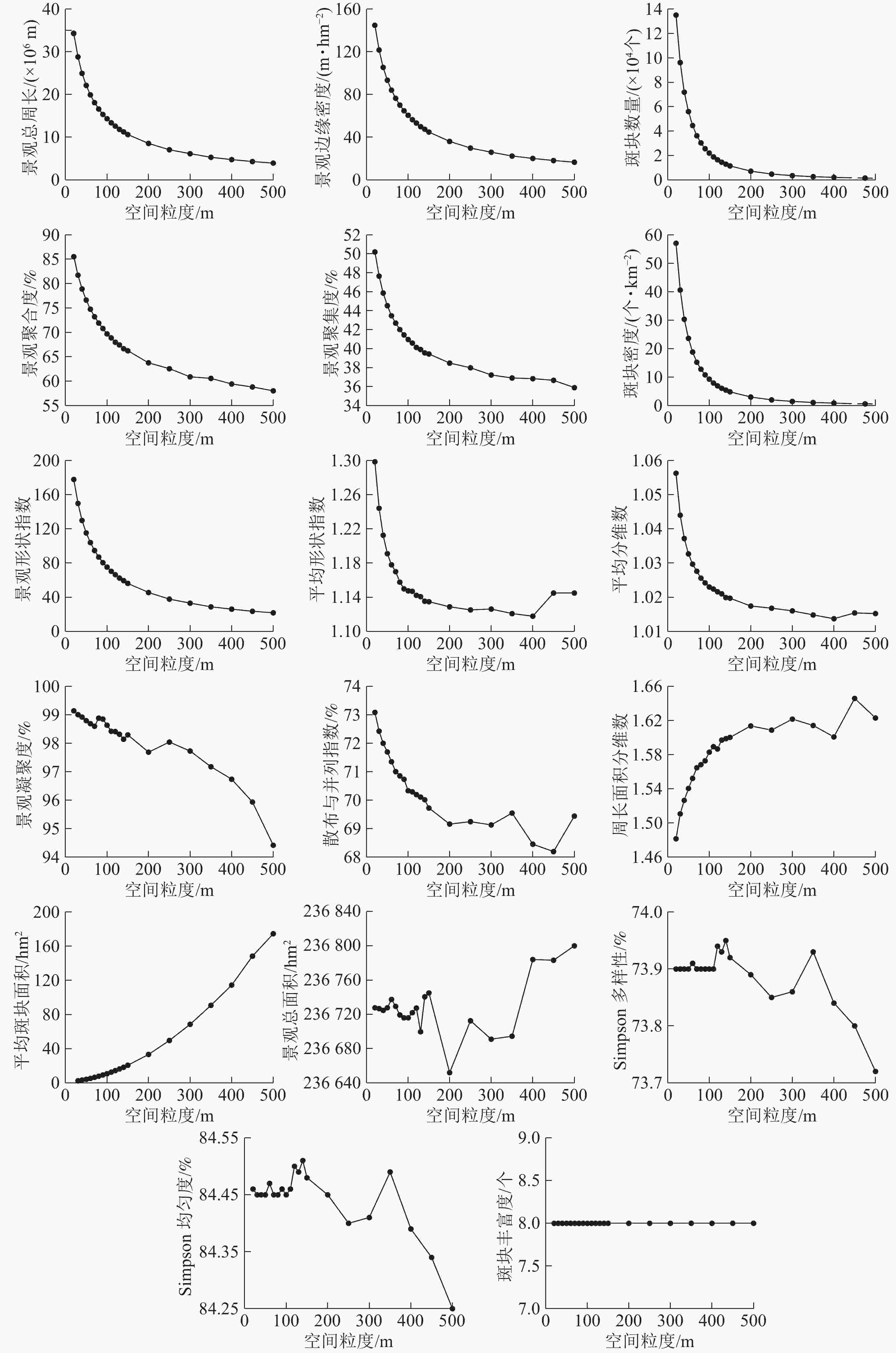
分别对不同的景观指数进行拟合，选取拟合程度最高的函数作为该景观指数的拟合函数(表1)。从图2可以看出：景观水平下的景观指数随着粒度的增大具有明显的响应关系。
指标(y) 景观指数(x) 函数类型 拟合函数 拟合度(R2) 预测强度 面积边缘 景观总面积 二次多项式 $y = 12 \times \mathop {10}\nolimits^{ - 4} \mathop x\nolimits^2 - 0.474\;7x + 236\;751$ 0.570 较低 边缘密度 幂函数 $y = 1\;434.2\mathop x\nolimits^{ - 0.702} $ 0.988 极高 周长面积分维数 对数 $ y = 0.042\; 7 \ln\! x + 1.376\; 2 $ 0.903 高 景观总周长 幂函数 $y = 3 \times \mathop {10}\nolimits^8 \mathop x\nolimits^{ - 0.702} $ 0.988 极高 密度大小及差异 斑块密度 幂函数 $y = 8\;089.4\mathop x\nolimits^{ - 1.503} $ 0.986 极高 斑块数量 幂函数 $y = 2 \times \mathop {10}\nolimits^7 \mathop x\nolimits^{ - 1.503} $ 0.986 极高 平均斑块面积 二次多项式 $y = 6 \times \mathop {10}\nolimits^{ - 4} \mathop x\nolimits^2 + 0.039\;2x + 0.686$ 0.999 极高 形状 平均形状指数 二次多项式 $y = 2 \times \mathop {10}\nolimits^{ - 6} \mathop x\nolimits^2 - 0.001x + 1.248\;1$ 0.752 一般 平均分维数 幂函数 $y = 1.078\;1\mathop x\nolimits^{ - 0.011} $ 0.856 一般 景观形状指数 幂函数 $y = 1\;634.4\mathop x\nolimits^{ - 0.681} $ 0.989 极高 聚散性 散布与并列指数 幂函数 $y = 77.157\mathop x\nolimits^{ - 0.019} $ 0.927 高 景观聚合度 幂函数 $y = 123.05\mathop x\nolimits^{ - 0.122} $ 0.997 极高 景观聚集度 幂函数 $y = 65.514\mathop x\nolimits^{ - 0.099} $ 0.975 极高 景观凝聚度 二次多项式 $y = - \mathop {10}\nolimits^{ - 5} \mathop x\nolimits^2 - 0.000\;5x + 98.848$ 0.944 高 多样性 斑块丰富度 常数 $y = 8$ 1.000 极高 Simpson多样性 二次多项式 $y = - \mathop {10}\nolimits^{ - 8} \mathop x\nolimits^2 + 4 \times \mathop {10}\nolimits^{ - 6} x + 0.738\;8$ 0.770 一般 Simpson均匀度 二次多项式 $y = - 2 \times \mathop {10}\nolimits^{ - 8} \mathop x\nolimits^2 + \mathop {5 \times 10}\nolimits^{ - 6} x + 0.844\;3$ 0.771 一般 Table 1. Fitting function of landscape horizontal landscape index
Figure 2. Grain sizes change of landscape indices under landscape level
指数类型1包括景观总周长、斑块数量、景观形状指数、景观聚集度、景观聚合度、边缘密度和斑块密度，总体呈“L”型单调下降变化趋势，景观指数拟合度高，可预测性强。斑块数量、斑块密度、景观总周长、景观形状指数的粒度响应曲线变化规律相似，明显拐点为70 m，70~200 m景观指数值下降幅度较小，＞200 m后景观指数值逐渐趋于稳定状态。据此可知随着粒度的增大整个景观内的小斑块逐渐被优势斑块融合，景观破碎化程度降低，整体景观形状趋于单一，小的斑块被融合，不同土地利用类型的分散程度逐渐增大。
指数类型2包括散布与并列指数、平均分维数、平均形状指数和景观凝聚度，总体呈单调下降后出现不同程度的波动变化，但整体依然呈下降趋势，其中：散布与并列指数、景观凝聚度拟合度高可预测性强，平均分维数、平均形状指数拟合度一般。景观凝聚度随着粒度的增大而下降，整体变化范围不大，值接近于100 m说明整个景观的连通性比较好，＞300 m后呈单调下降趋势，且降幅增大，表明景观的连通性降低且程度增加。散布与并列指数曲线明显拐点为70 m，70~300 m为适宜粒度域，＞300 m呈不同程度的波动变化，并且波动程度逐渐加剧但总体呈下降趋势，表明粒度的增大导致斑块类型周围的小斑块被优势斑块融合，邻接的斑块类型逐渐降低，景观的形状越来越简单。平均分维数、平均形状指数的适宜粒度为70~400 m，＞400 m呈现波动变化的趋势，表明随着粒度的增大斑块形状逐渐变得规则。
指数类型3包括周长面积分维数和平均斑块面积，总体呈上升趋势，景观指数拟合度高可预测性强。周长面积分维数的明显拐点为70 m，适宜粒度为70~200 m，＞200 m呈波动变化且变化强度逐渐增强；粒度＞200 m后平均斑块面积指数呈急剧增长趋势，表明在200 m下景观格局发生了剧烈的变化，且对平均斑块面积指数影响较大。据此可知：随着粒度的增大，斑块间相互融合引起斑块周长不断的减小，周长面积分维数值增大，整体景观内的斑块形状复杂性增大。
指数类型4包括景观总面积、斑块丰富度、Simpson多样性和Simpson均匀度，整体呈无变化或复杂变化趋势，拟合度整体一般。Simpson多样性和Simpson均匀度指数变化幅度很小；＞110 m后变化程度增强，但是变化依然很小，表明随着粒度的增大斑块之间会不断进行分割和融合；＞110 m后Simpson多样性和Simpson均匀度指数的变化强度加剧且总体景观值呈降低趋势，说明随着粒度的增大景观的破碎化程度逐渐降低，斑块类型在景观中的均衡化趋势分布逐渐降低。斑块丰富度在所选的粒度范围内一直未变，说明在所选的粒度范围内，随着粒度的增大整个景观的空间组分未消失。
-
对同一县域景观进行景观格局分析，空间粒度的选取直接影响结果的科学性和合理性，因此，适宜粒度的选取对研究县域的景观格局具有重要意义。景观指数曲线转折点附近景观特征会发生较大的变化，在适宜粒度域内选取最佳的景观分析粒度，以保证空间的边界信息损失值降到最小。适宜粒度域内的景观指数变化相对平稳，没有剧烈的波动变化，景观格局特征保持相对稳定状态[27]。根据景观指数的粒度效应曲线所对应不同转折点，将第1个变化相对稳定的区域作为适宜粒度区域，过大的粒度会造成交通用地、园地、未利用地等比较分散，且会让较小的斑块丢失边界空间信息，造成空间内部的景观特征发生改变，粒度越小越接近真实的景观特征。在类型水平下主体景观类型耕地景观指数的适宜粒度域为100~130 m，林地适宜粒度域为100~110 m，水域适宜粒度域为20~130 m。据此可知：类型水下景观指数的适宜粒度域为100~130 m。景观水平下指数类型4在粒度为110 m后开始出现逐渐增强的变化，因此，景观水平下的适宜粒度域为100~130 m。
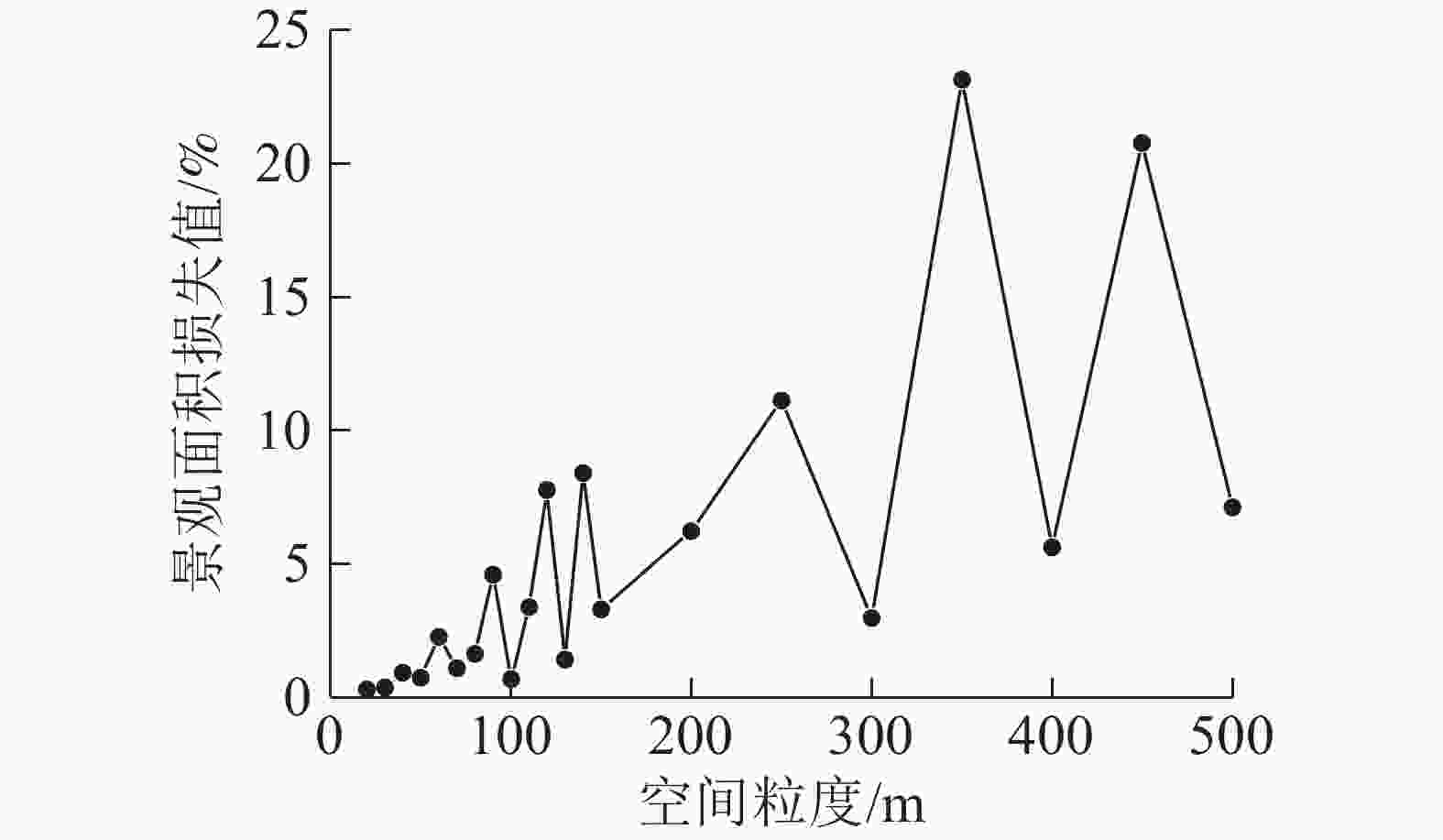
根据不同水平下对应的景观指数粒度效应曲线的拐点分布，以及适宜粒度域，表明宿松县内部景观格局的最佳适宜粒度为100~110 m。从图3可见：在粒度为100~110 m内，景观面积损失值由0.7%上升到3.4%，呈现出逐渐增高的趋势。综合可知：宿松县县域水平下适宜的景观粒度为100 m。
Figure 3. Grain sizes change of landscape area loss value
2.1. 类型水平下粒度效应分析
2.2. 景观水平下粒度效应分析
2.3. 最佳空间粒度的选取
-
数据源、研究对象、粒度变化方式、空间数据聚合方式、景观类型的不同均会造成景观结构组成的不同空间特征[11]。目前，大尺度区域的粒度效应研究[2-3, 9, 14]，数据源多采用人工解译的遥感数据，存在人工目视解译误差大、地物类别判定等问题，而本研究采用的地理国情数据源是高分辨率的影像，具有精度高、要素全、尺度精细等优点[5]。本研究区位于大别山南麓，位于长江中下游北岸，西北向东南依次地跨大别山山脉、丘陵岗地和平原、湖畈区，自然条件的差异形成了资源的多样性，林地、耕地、水域为研究区的主体类型。不同地貌下相同景观指数的拐点不同，如在景观水平下，施英俊等[25]研究发现：森林景观地貌下景观指数拐点为120 m，翟俊等[15]研究认为：青海湖流域地貌下的景观指数拐点集中于60和90 m，张韧璎[9]研究认为：天水市景观指数拐点集中于10、15和35 km，任梅等[11]研究表明：喀斯特山地城市安顺市的景观指数拐点集中于20和100 m，本研究表明：宿松县景观指数曲线的拐点主要集中于70和110 m，说明不同研究区地貌、土地类型的分布特征对确定区景观格局分析的粒度有较大影响。丁雪姣等[24]认为：安徽省省域尺度下的合适粒度为100~125 m，但并未确定粒度值，且选择粒度步长为25 m。本研究选择粒度步长为10和50 m，确定宿松县最佳粒度为100 m，这为研究整个安徽省的景观格局提供了一定的参考，也表明了粒度划分粗细的重要性。在景观水平下大部分景观指数均可用幂函数来对景观指数进行拟合，且拟合程度高，这与翟俊等[15]的研究结果类似，表明随着粒度的增大，部分景观指数粒度效应可预测性强。为减少粒度效应引起的误差，需要根据研究区特有的地形、地貌景观组成成分、面积大小来选择合适的粒度区间及景观指数。
-
本研究表明：在类型水平上，宿松县耕地景观指数的适宜粒度域为100~130 m，林地适宜粒度域为100~110 m，水域适宜粒度域为20~130 m。研究区草地、耕地、建筑用地分布比较分散，交通用地相互交错，复杂分散，未利用地、园地面积较少且分布比较集中。在景观水平上，景观指数的粒度效应曲线呈现4种不同的变化趋势，且大部分景观指数粒度效应可用拟合函数来进行预测，包括幂函数、对数函数、二次多项式、常数函数4种，主要函数类型为幂函数，且幂函数拟合程度高(R2＞0.92)。随着粒度的变化，景观指数的粒度响应也各不同，综合不同水平下各个景观指数的拐点信息确定了宿松县景观格局的最佳粒度域为100~110 m，结合景观面积损失模型，确定宿松县景观格局分析的最佳粒度为100 m。
DownLoad: