Study on the factors affecting breast-height basal area increment of evergreen broad-leaved forest in Mount Tianmu

天目山国家级自然保护区位于浙江省杭州市临安区西北部(30°18′30″~30°24′55″N， 119°24′11″~119°28′21″E)，距杭州市中心94 km，总面积为4 284 hm²。该保护区属中亚热带向北亚热带过渡气候，受海洋暖湿气流影响，季风盛行，气候温和。年平均气温为 8.8~14.8 ℃，最冷月平均气温为−2.6~3.4 ℃，最热月平均气温为19.9~28.1 ℃。雨水充沛，年降水量为1 390~1 870 mm。森林类型多样，主要有常绿阔叶林、常绿落叶阔叶混交林、落叶阔叶林、落叶矮林、针叶林和毛竹Phyllostachys edulis林等^[16]。

2005年，在研究区内选择代表性地段，设置100 m×100 m的常绿阔叶林固定样地，样地中心地理坐标为： 30°19′40″N， 119°26′12″E，并用相邻格子调查法将样地划分成10 m×10 m的网格单元。对网格单元进行每木检尺，记录树种、胸径、树高、活枝下高、冠幅等，并以样地西南角为原点，采用激光对中全站仪(徕卡TCR702)测定每株林木的坐标及海拔。2020年对该样地进行复查。本研究采用2005和2020年2期调查数据，从中筛选出2期均存活且胸径≥5 cm的活立木共计733株。其中，常绿阔叶优势树种有细叶青冈Cyclobalanopsis gracilis、短尾柯Lithocarpus brevicaudatus、青冈C. glauca、小叶青冈C. myrsinifolia、豹皮樟Litsea coreana等，占全部活立木的51.99%。

林木的生长量指一定间隔期内林木各种调查因子的变化量，分为总生长量、定期生长量、连年生长量、定期平均生长量和总平均生长量等^[17]。本研究采用2005—2020年15 a间林木胸高断面积的定期生长量。计算公式为：

式(1)中：B_AI为林木胸高断面积生长量(cm²)；$D_{t_1} $和$D_{t_2} $分别为林木在t₁和t₂时的胸径(cm)。

单木生长模型主要有潜在生长量修正法、回归分析法和生长分析法^[18]。本研究采用回归分析法，建立林木胸高断面积生长量对数与林木大小、竞争和立地等因子之间的回归方程^[5−8]：

式(2)中：B_AI为胸高断面积生长量；$f(x_1) $为林木大小因子的函数；$f(x_2) $为林木竞争因子的函数；$f(x_3) $为林木立地因子的函数；a为常数项；b、c、d为方程参数。

林木大小是影响林木断面积生长量的最重要因子^[6]。林木胸径是反映林木大小的最直观因子，也是预测林木生长最重要的因子之一^[19]。林木胸径平方能够很好地表述林木生长趋势，即林木在幼龄时生长速度较快，成熟时生长达到顶峰，随后生长速度开始逐渐下降^[2]。此外，用胸径对数进行建模分析也较常见^[5−6]。冠幅直接影响林木进行生理活动的能力^[20]，因此在林木生长模型中常作为反映林木大小的变量。如 MONSERUD等^[6]发现：冠长率能解释奥地利针叶树种和阔叶树种断面积生长量14%~47%的变异。本研究选取林木的胸径平方、胸径对数和冠幅来代表林木大小。这里，冠幅用冠幅半径表示，计算公式为：

式(3)中：C_r为林木冠幅半径(m)；L₁、L₂分别为林木东西、南北冠幅半径(m)。因此，林木大小因子的函数表达式为：

式(4)中：D为林木胸径； b₁、b₂、b₃为方程参数。

林木竞争限制林木生长^[21]。本研究选取Hegyi竞争指数^[22]及其对数形式来表示林木竞争因子的大小。其中，竞争木的选择采用汤孟平等^[23]提出的基于Voronoi图的方法。Hegyi竞争指数的计算公式为：

式(5)中： I_C为对象木i的竞争指数；D_i、D_j分别为对象木i和竞争木j的胸径(cm)；L_ij为对象木i与竞争木j之间的距离(m)；n_i为对象木i所在竞争单元的竞争木株数。因此，林木竞争因子的函数表达式为：

式(6)中： c₁、c₂为方程的参数。

地形是影响林木生长的重要因素。如COOMES等^[24]在研究新西兰的森林时，发现随着海拔的升高，林木生长率有下降的趋势；STAGE 等^[25]发现：坡度、坡向、海拔的交互作用影响森林的物种组成和森林的生产力；BARIBAULT等^[26]发现：森林地形的差异会导致林木间的生长有很大的不同。根据前人构建的生长模型^[5−6]，选取海拔、坡度和坡向作为模型的立地因子。其中，采用坡向指数(A_s)来代表坡向。坡向指数的计算公式为^[27−28]：

式(5)中：A_s为坡向指数；θ为坡向值(0°~360°)。因此，立地因子的函数表达式为：

式(8)中：A_l为林木所处的海拔；S_l为林木所处的坡度；d₁、d₂、d₃分别为方程参数。将式(4)、式(6)、式(8)代入式(2)得到最终的林木胸高断面积生长模型：

在 Excel 2019 中对数据进行预处理。基于林木的三维坐标，利用ArcMap 10.7插值分析提取坡度、方位角数据；基于 ArcMap 10.7 和 Python 语言编程计算每株林木的竞争指数；在 SPSS 26中采用Kolmogorov-Smirnov检验法对各因子进行正态性分析，并利用Spearman相关系数进行相关性分析；利用SPSSAU采用Kruskal-Wallis检验法(K-W)和Nemenyi法分析不同胸径大小、竞争条件下林木胸高断面积生长量的差异性，采用岭回归方法建立单木生长模型。

在常绿阔叶林样地内，计算活立木在2005年时的胸径、冠幅、海拔、坡度、坡向指数、竞争指数及2005—2020年间胸高断面积生长量的均值、标准差(表1)。对各变量进行Kolmogorov-Smirnov检验，发现所有变量的显著性都小于0.05，均不符合正态分布，故用Spearman 相关系数进行相关性分析(表2)。结果表明：胸高断面积生长量与胸径、冠幅均呈现极显著正相关(P＜0.01)，与竞争指数呈现极显著负相关(P＜0.01)，与地形因子的相关系数均不显著。说明天目山常绿阔叶林的林木胸径、冠幅对林木胸高断面积的生长起到正向作用，竞争对林木胸高断面积生长起到负向作用，地形因子对林木胸高断面积生长的影响小。胸径和冠幅均与竞争指数极显著负相关(P＜0.01)，说明竞争抑制林木胸径和冠幅的生长。冠幅与海拔极显著正相关(P＜0.01)，说明海拔影响林木冠幅的生长。坡向指数与冠幅显著负相关(P＜0.05)，说明坡向影响林木冠幅的生长。

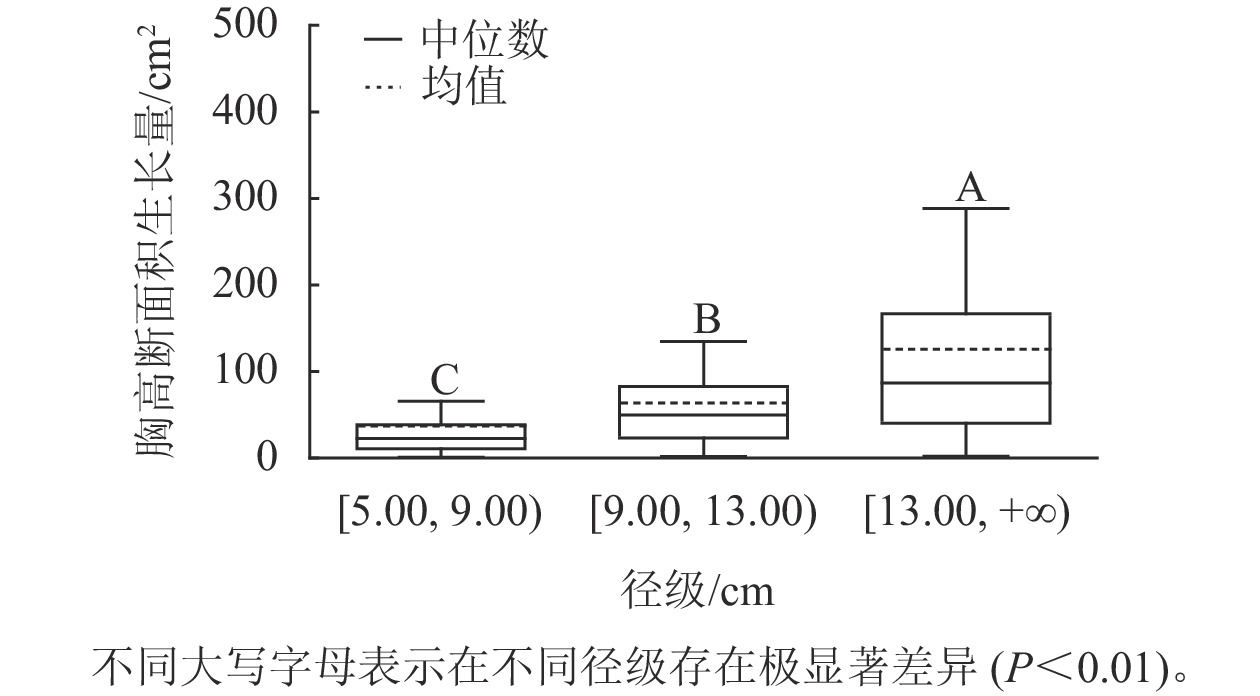
样地林木胸径均值为13.15 cm，胸径最小值为5.00 cm，最大值为50.30 cm。根据林木胸径均值和分布范围，将其分为3个径级：[5.00, 9.00)、[9.00, 13.00)、[13.00, +∞)，分别表示为Ⅰ_径级、Ⅱ_径级、Ⅲ_径级。对不同径级林木的胸高断面积生长量进行Kruskal-Wallis非参数检验。结果显示：Ⅰ_径级、Ⅱ_径级和Ⅲ_径级的胸高断面积生长量中位数分别为22.50、49.68和86.71 cm²，K-W检验的统计量(H)=185.84，P＜0.01，存在极显著差异，表明胸高断面积生长量随着林木胸径的增加而增加。用Nemenyi法进一步证明(图1)：Ⅰ_径级、Ⅱ_径级、Ⅲ_径级林木的胸高断面积生长量两两之间差异极显著(P＜0.01)。说明林木胸径大小是导致胸高断面积生长量差异的主要因子之一。

Figure 1.  Breast-height basal area increment for different diameter classes　　　　　　　　

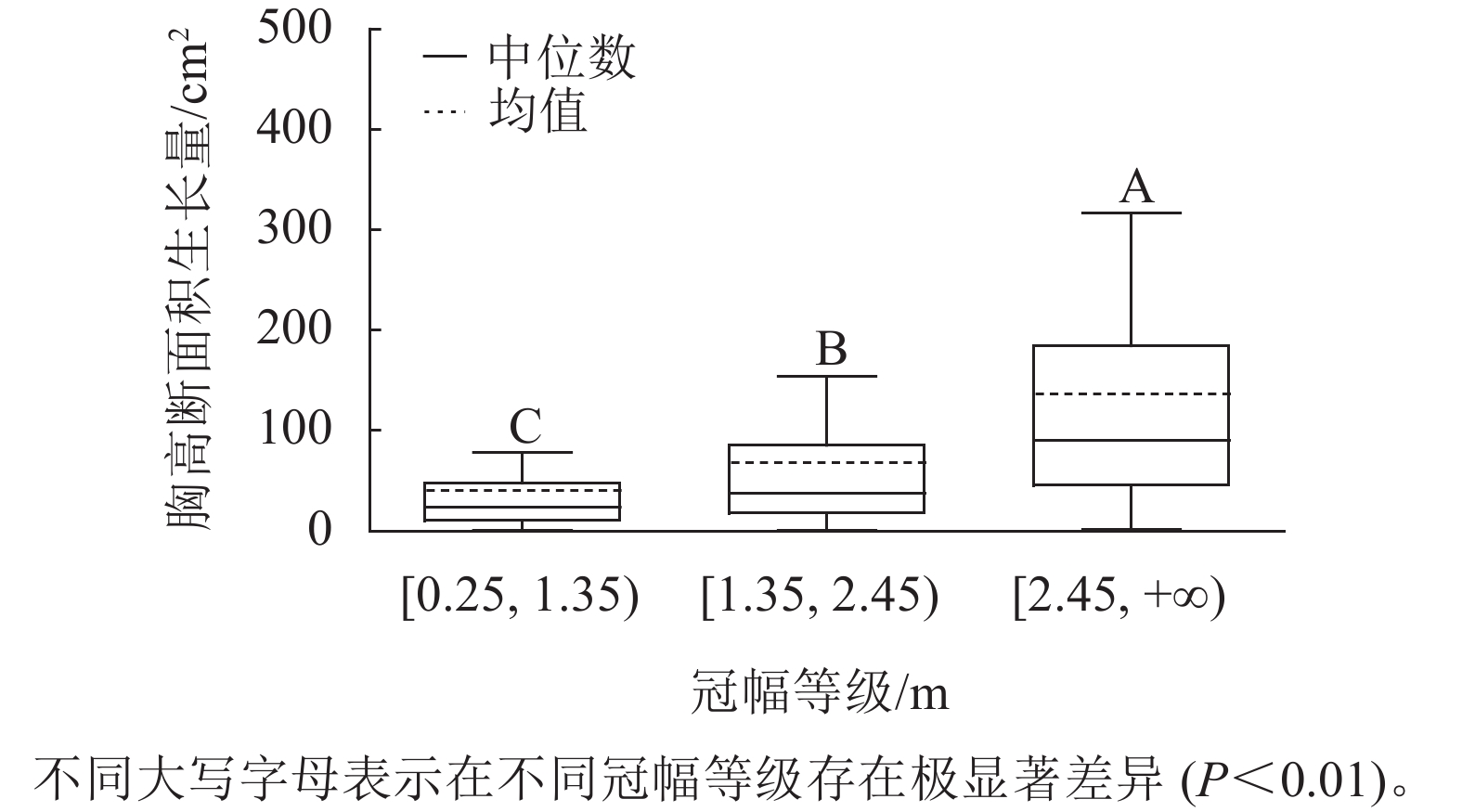
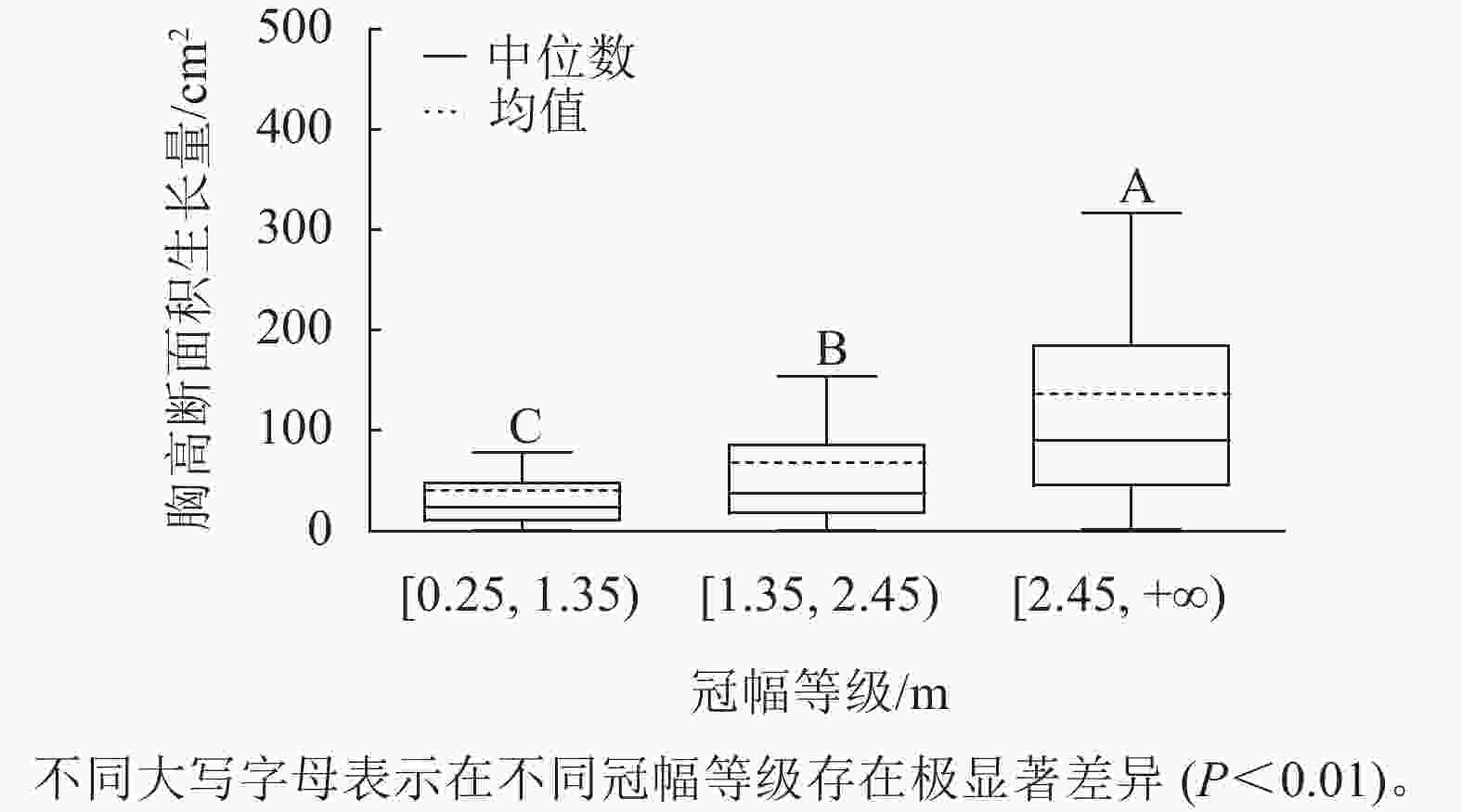
样地林木冠幅均值为1.86 m，冠幅最小值为0.25 m，最大值为6.11 m。根据林木冠幅均值和分布范围，将其分为3个等级：[0.25, 1.35)、[1.35, 2.45)、[2.45, +∞)，分别表示为Ⅰ_冠幅、Ⅱ_冠幅、Ⅲ_冠幅。对不同冠幅等级林木的胸高断面积生长量进行Kruskal-Wallis非参数检验。结果显示：Ⅰ_冠幅、Ⅱ_冠幅和Ⅲ_冠幅林木的胸高断面积生长量的中位数分别为24.03、37.37和90.65 cm²，H=96.627，P=0.000＜0.01，存在极显著差异，林木胸高断面积生长量随着林木冠幅的增加而增加。用Nemenyi法进一步证明(图2)：Ⅰ_冠幅与Ⅱ_冠幅、Ⅲ_冠幅林木的胸高断面积生长量两两之间差异极显著(P＜0.01)。说明，林木冠幅大小是导致胸高断面积生长量差异的主要因素之一。

Figure 2.  Breast-height basal area increment for different crown classes

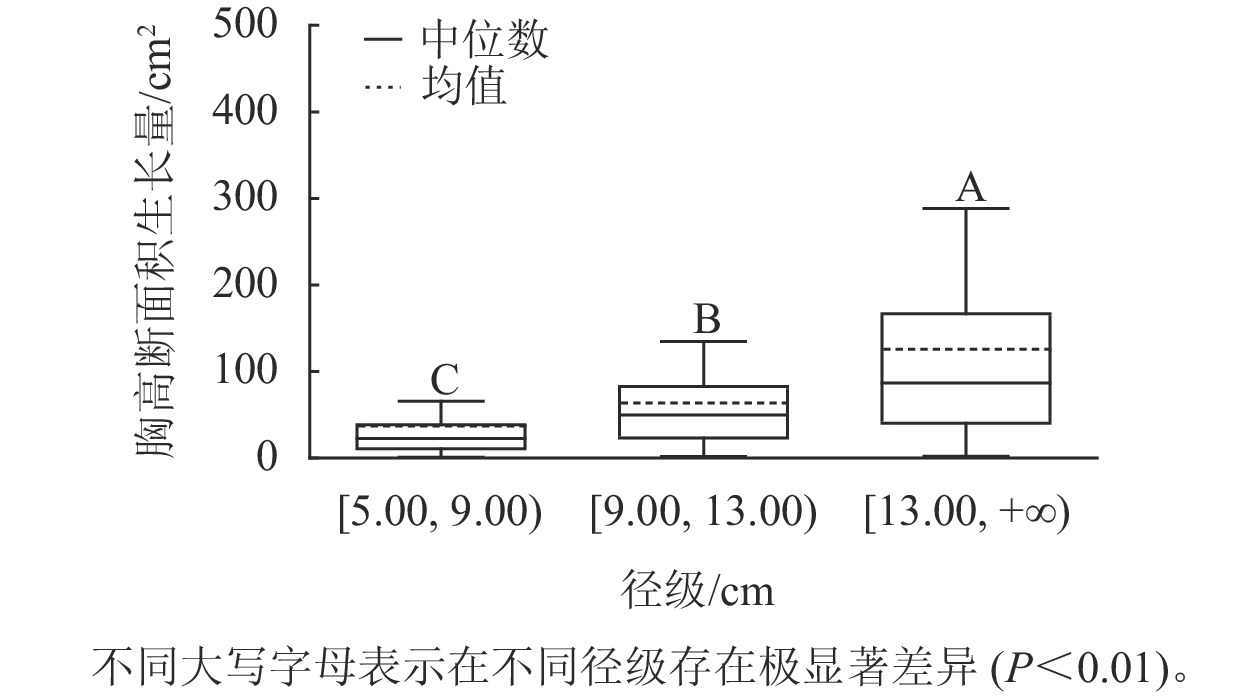
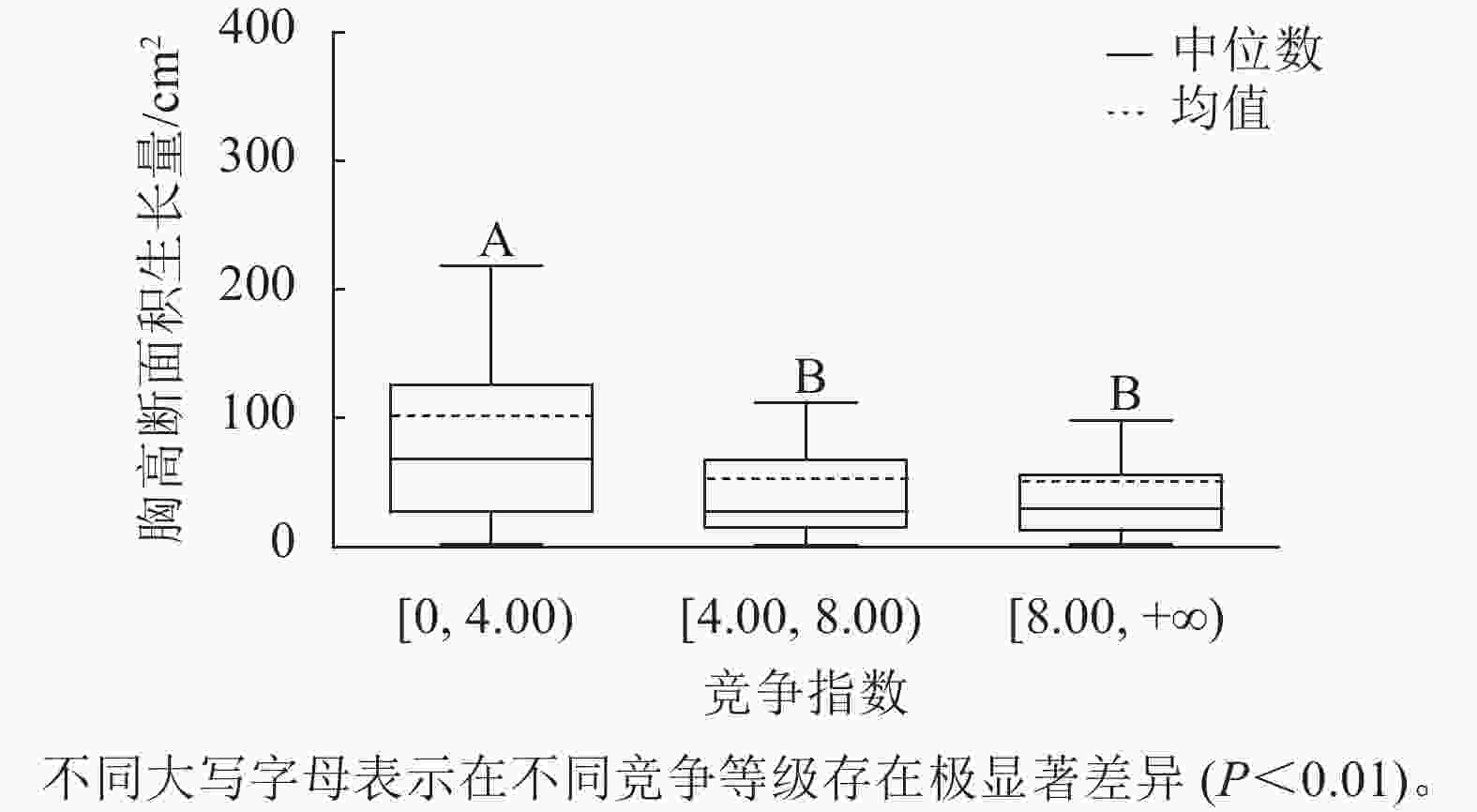
样地林木竞争指数均值为8.44，竞争指数最小值为0.47，最大值为217.79。根据林木竞争指数均值和分布范围，将其分为3个等级：[0, 4.00)、[4.00, 8.00)、[8.00, +∞)，分别用Ⅰ_竞争、Ⅱ_竞争和Ⅲ_竞争表示，对应3个竞争强度等级：低度、中度、强度。不同等级的竞争指数代表林木受到的竞争压力大小不同，数值越大，竞争压力越大。对不同竞争强度等级林木的胸高断面积生长量进行K-W非参数检验。结果显示：Ⅰ_竞争、Ⅱ_竞争和Ⅲ_竞争林木的胸高断面积生长量的中位数分别为67.90、27.14和29.90 cm²，H=67.434，P＜0.01，存在极显著差异；不同竞争强度等级的林木的胸高断面积生长量不同，低度竞争强度的林木胸高断面积生长量最大。用Nemenyi法进一步证明(图3)：低度竞争与中度竞争、强度竞争林木的胸高断面积生长量呈现极显著差异(P＜0.01)。低度竞争林木的胸高断面积生长量中位数最大，说明林木受到的竞争压力越小，有利于提高林木胸高断面积生长量。

Figure 3.  Breast-height basal area increment for different competition classes

因为冠幅、竞争指数与胸径相关系数的绝对值均大于0.6，所以进行最小二乘回归时存在共线性问题。因此，本研究为探究胸径和竞争指数对胸高断面积生长量的影响，以式(9)为基础模型，林木胸高断面积生长量对数为因变量，冠幅、海拔、坡度和坡向指数为控制变量，分别以胸径平方、胸径对数、竞争指数和竞争指数对数的不同组合为自变量进行岭回归，得到基于单株林木的单木生长模型(表3)；对2005年调查的林木胸径按2 cm为组距进行径阶整化，对林木大小因子、竞争因子和立地因子计算其每一径阶的平均值，以每一径阶内林木胸高断面积生长量对数的平均值为因变量，冠幅、海拔、坡度和坡向指数等因子的平均值为控制变量，分别以每一径阶内胸径平方、胸径对数、竞争指数和竞争指数对数的平均值的不同组合为自变量进行岭回归，得到基于径阶平均值的单木生长模型(表4)。其中2类岭回归模型的K值采用SPSSAU给予的推荐值。

在基于单株林木的单木生长模型中(表3)，比较模型2和模型3、模型8和模型10、模型9和模型11，发现含有胸径对数的模型比含有胸径平方的模型拟合精度高；比较模型1~模型4，发现含有胸径因子的模型拟合精度优于不含胸径的模型；比较模型1、模型5、模型6和模型7，有无竞争指数对模型的拟合精度影响小；比较模型1~模型11，发现模型中常数项、胸径对数、胸径平方、冠幅和竞争指数对数的回归系数均极显著(P＜0.01)，说明胸径、冠幅和竞争指数对数是单木生长模型中的重要因子；比较模型1~模型11的R²及调整后的R²，模型1是基于单株林木的单木生长模型中的最优模型，该模型中的常数项、胸径对数、胸径平方、冠幅、竞争指数对数和坡度等回归系数显著(P＜0.05)。

在基于径阶平均值的单木生长模型中(表4)，比较模型13和模型14、模型19和模型21、模型20和模型22，发现含有胸径对数的模型比含有胸径平方的模型拟合精度高；比较模型12~模型15，发现含有胸径因子的模型拟合精度优于不含胸径因子的模型；比较模型12、模型16、模型17和模型18，有无竞争指数对模型的拟合精度影响小；比较模型12~模型22，发现模型中胸径对数和胸径平方的回归系数均显著(P＜0.05)，说明胸径是基于径阶平均值的单木生长模型中的重要因子；比较模型12~模型22的R²及调整后的R²，得出模型13是基于径阶平均值单木生长模型中的最优模型，该模型中胸径对数的回归系数极显著(P＜0.01)。

比较表3和表4中的模型，发现2类生长模型中胸径因子的回归系数均显著，且含有胸径因子的模型拟合精度均优于不含胸径因子的模型；基于径阶平均值的单木生长模型拟合精度高于基于单株林木的单木生长模型。

通过对胸径与胸高断面积生长量进行Spearman相关分析和Kruskal-Wallis检验，发现胸径与胸高断面积生长量呈正相关，且胸高断面积生长量随着胸径的增大而增大。该结论与多数学者的研究一致，如CHI等^[29]在研究中国神农架常绿落叶阔叶混交林的林木大小、相邻木和立地条件对林木生长的影响时发现，林木的生长量与初始胸径大小具有显著的相关关系 ，并且随着初始胸径的增大而增大。FIEN等^[30]对美国缅因州中部的异龄林单木生长和死亡的影响因子进行了研究，认为树种的胸高断面积与胸径均呈显著正相关。有研究表明：林木生长通常会先随胸径的增大而增加，在达到一定阶段后又会随胸径的增大而减小^[31]。但也有研究指出：不同的森林类型，林木生长与胸径的关系有较大差异^[32]。

竞争与胸高断面积生长量的Spearman相关分析表明：竞争与胸高断面积生长量呈现负相关关系，低度竞争强度有助于林木生长。这个结论与前人的研究结果基本一致，de GROOTE等^[33]研究了比利时北部森林竞争对夏栎Quercus robur、欧洲山毛榉Fagus sylvatica和红槲栎Q. rubra生长的影响，指出竞争与断面积生长量呈负相关。窦啸文等^[34]在研究天目山针阔混交林竞争对生长的影响时，证实林木胸高断面积生长量与Hegyi竞争指数服从对数函数关系，且胸高断面积生长量与竞争指数显著负相关。

分析地形因子与胸高断面积生长量的相关性发现：海拔、坡向、坡度等地形因子与胸高断面积生长量的相关性较小。POMPA-GARCÍA等^[35]研究了地形对墨西哥针叶树生长的影响，指出林木基部断面积生长量随海拔的变化有显著差异，海拔1 001~1 500 m的地区林木基部断面积生长量较高。本研究所选取的林木在同一固定样地内，海拔范围为575~677 m，地形变化不大，因此对林木生长影响较小。

本研究中竞争指数的回归系数并非都在单木生长模型达显著水平，这可能与竞争指数的选择有关。有研究表明：在选择与距离有关的竞争指数时，包含树冠因子的竞争指数优于胸径大小比值的竞争指数^[31]。而本研究中冠幅因子的回归系数均在单木生长模型达到显著水平，这也验证了这一观点。但是，也有学者认为采用与距离无关的竞争指数的生长模型的拟合精度优于采用与距离相关的竞争指数的生长模型^[36]。针对常绿阔叶林的生长模型，与距离无关的竞争指数是否优于与距离有关的竞争指数值得探讨。

林木生长还受光照、温度、 水和土壤等因子的影响^[37−41]，本研究未考虑这些因素。近些年来，有学者构建了不同树种的生长混合效应模型，发现混合效应模型的拟合精度明显优于一般模型^[42−45]。因此，在进一步研究中，可构建多因子的混合效应模型，综合分析影响林木胸高断面积生长量的因素。

通过对浙江天目山国家级自然保护区内的常绿阔叶林的林木胸高断面积生长量的影响因子进行分析，得出以下主要结论：①胸径、冠幅和竞争指数与胸高断面积生长量的相关性高，地形因子与胸高断面积生长量的相关性低。②不同径级、冠幅等级和竞争指数等级的胸高断面积生长量差异性显著。③基于径阶平均值的单木生长模型拟合精度高于基于单株林木的单木生长模型，且胸径和冠幅的回归系数均显著。④影响常绿阔叶林胸高断面积生长量的主要因子是林木胸径、冠幅和竞争指数，海拔、坡度等地形因子对胸高断面积生长量的影响不大。