-
根冠比(root shoot ratio，RSR)是指林木地下部分与地上部分生物量的比值，是研究森林生物量存储方式和分配策略的基础，也是森林生态系统物质循环的重要组成部分[1]。根冠比受气候和林分因子的影响，主要包括林分起源、林分类型、林龄、气温、水分的影响[2-5]。根冠比与林分和气候因子的关系大多数以线性或者非线性的方程解释。如LUO等[4]建立了不同林分类型根冠比与年平均气温和年平均降水量的方程，郭炳桥等[5]建立了中国天然林根冠比与年平均气温、林分密度和林龄的方程，SANQUETTA等[6]建立了松树根冠比与生物量转换因子的方程。这些研究都是分析各因子对根冠比影响的直接作用，忽视了对根冠比的间接作用，特别是根冠比与气候和林分因子的关联研究未见报道。杉木Cunninghamia lanceolata是中国重要用材树种。根据第8次全国森林资源调查，杉木人工林面积和蓄积居人工乔木林首位，很多学者对杉木人工林生物量和根冠比进行了大量的研究。由于森林生物量的测定费事费力，因此，收集前人关于生物量和根冠比的测定数据，分析生物量和根冠比在不同森林类型、气候因子、林分结构因子等的变化特征成为重要的途径[4-5, 7-10]。本研究通过收集杉木人工林根冠比数据，分别建立根冠比与降水量、气温、林分密度和林龄的方程，同时，利用结构方程建立根冠比与气温、降水量、林龄和林分密度的关联模型，阐述气候和林分因子对根冠比的影响，以期为杉木人工林生态系统的物质分配与林分可持续经营提供理论依据。
-
基于Science direct，Springer Link，中国知网数据库，维普中文期刊等数据库，搜索“杉木”“杉木生物量”“杉木根冠比”“杉木生产力”等关键词，收集相关文献。在收集文献的基础上进行删选和整理。首先，去除杉木天然林相关文献。其次，统计各个文献数据，统计中仅仅输入杉木人工林根冠比的测定为标准木解析计算得到的数据，不输入其他方法测定的根冠比数据。数据包含试验地坐标、地上部分生物量、地下部分生物量、根冠比、年平均气温、年平均降水量、林龄、胸径、树高、林分密度等信息。接着，去除林龄小于3 a的杉木人工林数据。对于含有地上部分生物量和地下部分生物量，没有根冠比的数据行，利用地下部分生物量与地上部分生物量的比值计算根冠比；对于缺失年平均气温和年平均降水量的数据，通过中国气象科学数据共享网(http://cdc.cma.gov.cn/home.do)，利用缺失数据的经纬度坐标，获取该样地的年平均气温和年平均降水量。还对于杉木人工林根冠比异常值进行判断取舍。
基于上述收集和统计步骤，本研究最终收集了134篇文献608条杉木人工林根冠比数据。数据试验地的分布如表 1所示。杉木人工林根冠比数据的基本信息包含了福建、广东、广西、湖南、湖北、贵州、四川、重庆、江西、江苏和安徽11个省(直辖市)。数据的年平均气温为13.7~21.5 ℃，年平均降水量为1 100~2 100 mm，林龄为4~68 a，林分密度为400~7 000株·hm-2。
表 1 杉木人工林根冠比数据的基本信息
Table 1. Basic information of root-shoot ratio (RSR) data in Cunninghamia lanceolata plantation
区域 地上部分生物量/(t·hm-2) 地下部分生物量/(t·hm-2) 根冠比 均值 范围 均值 范围 均值 范围 福建 120.365 7.428~445.750 25.000 1.000~78.580 0.246 0.141~0.565 广东 88.471 38.372~131.654 21.523 11.142~34.330 0.352 0.268~0.461 广西 110.778 13.370~271.860 22.667 3.120~17.620 0.212 0.102~0.414 湖南 83.363 18.225~274.910 15.340 3.365~53.660 0.243 0.156~0.578 湖北 140.659 72.807~294.890 23.045 13.130~45.860 0.216 0.172~0.315 贵州 50.893 1.471~338.060 8.710 0.258~58.390 0.147 0.063~0.143 四川 45.732 0.567~306.482 11.542 0.356~57.622 0.211 0.131~0.522 重庆 57.833 1.857~276.548 8.751 1.256~46.782 0.168 0.112~0.467 江西 94.786 7.344~270.249 16.508 2.707~51.534 0.192 0.104~0.379 江苏 54.010 11.047~98.853 16.415 5.500~21.600 0.359 0.282~0.500 安黴 87.004 41.650~146.890 17.688 7.470~32.290 0.196 0.179~0.220 -
利用一次和二次多项式方程，分别拟合根冠比与年平均气温、年平均降水量、林分密度、林龄的关系，找出最优方程。其表达式分别为：RSR=a+bxi+ei；RSR=a+bxi+cxi2+ei。其中：RSR为杉木人工林根冠比，xi分别表示年平均气温、年平均降水量、林分密度或林龄，xi2分别表示年平均气温、年平均降水量、林分密度或林龄的平方，a，b和c为方程参数，ei为误差项。使用决定系数(R2)对拟合效果进行评价。R2的计算方法为$ {R^2} = 1 - \sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}/} \sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\bar y}_i}} \right)}^2}} $。其中：yi为实际测定的RSR值，yi为RSR的平均值，$ {{{\hat y}_i}} $为方程预测的RSR估计值，n为样本数。
-
线性方程可以分析年平均气温、年平均降水量、林分密度和林龄对根冠比的直接影响、预估杉木人工林的根冠比。但是，无法分析各因子与根冠比的间接作用。结构方程(structural equation model，SEM)是基于变量的相关或者协方差矩阵来阐释各变量之间关联特征的统计方法。该方法假定一组隐变量之间存在因果关系，隐变量通常是某几个显变量中的线性组合[11-12]。它通过结构模型中的通径系数，在统计检验所假设的基础上证实所假设的模型是否合适，进一步证实假设隐变量之间的关系的合理性，最后，分析各变量之间的关联特征。结构方程模型的一般表达式为：
$$ \eta = \beta \eta + \mathit{\Gamma }\xi + \zeta ; $$ (1) $$ x = {\mathit{\Lambda }_X}\xi + \delta ; $$ (2) $$ y = {\mathit{\Lambda }_Y}\eta + \varepsilon 。 $$ (3) 式(1)为结构方程中的结构模型，表示隐变量与显变量之间的关系。其中，η是隐变量向量，β是隐变量η的系数矩阵，也是隐变量间的通径系数矩阵；ξ是显变量向量；Г是显变量ξ的系数矩阵，也是显变量对相应内生潜变量的通径系数矩阵；ζ为残差向量。式(2)和式(3)为结构方程模型中的测量模型。测量模型一般由2个方程组成，分别表示显变量向量ξ和观测变量x之间，以及隐变量向量η和内生的观测变量y之间的联系。其中，ΛX为观测变量x在显变量向量ξ上的因子载荷矩阵，δ为式(2)的误差向量；ΛY为观测变量y在隐变量向量η上的因子载荷矩阵，ε为式(3)的误差向量。
数据统计分析和绘图使用R和Excel软件[13]，应用R中的lavaan包建立结构方程，解析杉木人工林根冠比与年平均气温、年平均降水量、林分密度和林龄之间的关联特征。
-
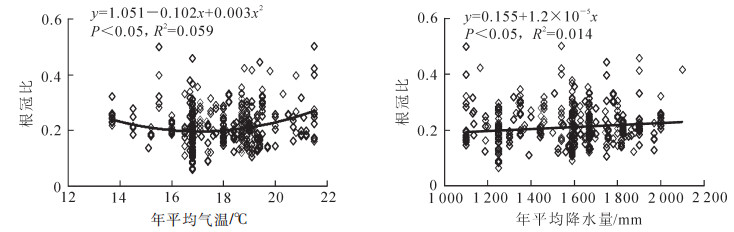
以根冠比为因变量，以年平均气温和年平均降水量2个气候因子为自变量，分别进行拟合。结果如图 1所示：根冠比与年平均气温的最优方程为二次多项式，其方程表达式为y=1.051-0.102x+0.003x2(P＜0.05)，决定系数为0.059；根冠比与年平均降水量的最优方程为一元线性，其方程表达式为y=0.155+1.2×10-5x(P＜0.05)，决定系数为0.014。基于年平均气温和年平均降水量，根据拟合方程就可以估算杉木人工林的根冠比。
图 1 年平均气温、年平均降水量与杉木人工林根冠比的拟合图
Figure 1. Fitted result between mean annual precipitation, mean annualair temperature and RSR in Cunninghamia lanceolata plantation
-
利用根冠比分别与林分密度和林龄建立拟合方程，结果如图 2所示：根冠比与林分密度和林龄的最优拟合方程为一元线性，根冠比与林分密度的方程为y=0.179+3.1×10-5x(P＜0.05)，决定系数为0.115；根冠比与林龄的方程为y=0.289-0.002x(P＜0.05)，决定系数为0.188。2个方程呈现相反的趋势，即根冠比随着林分密度的增加而增加，随着林龄的增加而减少。利用林分密度和林龄也可以估算杉木人工林的根冠比。
图 2 林分密度、林龄与杉木人工林根冠比的拟合图
Figure 2. The fitted result between stand density, stand age and RSR in Cunninghamia lanceolata plantations
-
利用结构方程建立杉木人工林根冠比与年平均气温、年平均降水量、林分密度和林龄的关联图(图 3)显示：年平均气温、年平均降水量、林分密度、林龄对根冠比都有直接影响，它们对根冠比的直接通径系数分别为0.515(P＜0.01)，0.548(P＜0.01)，-0.462(P＜0.01)和0.201(P＜0.01)。由此可知：年平均降水量和林龄不仅直接影响杉木林净生产力，还通过影响年平均气温和林分密度间接影响林分净生产力。结果如表 2所示：年平均降水量和林龄的间接通径系数分别为-0.308(P＜0.01)和-0.082(P＜0.05)。年平均降水量和林龄的总通径系数分别为0.207(P＜0.05)和-0.360(P＜0.05)。结构方程结果显示：影响杉木人工林根冠比变化因素的69%来自年平均气温、年平均降水量、林分密度和林龄。
图 3 杉木人工林根冠比与年平均气温、年平均降水量、林分密度、林龄的关联模型图
Figure 3. Cor-relationship models between mean annual precipitation, mean annual air temperature, stand density, stand age and RSR in Cunninghamia lanceolata plantations
表 2 杉木人工林根冠比与年平均气温、年平均降水量、林分密度、林龄的通径系数
Table 2. Total, direct and indirect path coefficient of mean annualair temperature, mean annual precipitation, stand density, stand age on RSR of Cunninghamia lanceolata plantations
隐变量 显变量 直接系数 标准差 间接系数 标准差 总系数 标准差 根冠比 年平均气温/℃ 0.515 0.155 -0.308 0.118 0.207 0.166 年平均降水量/mm 0.548 0.156 0.548 0.156 林龄/a -0.462 0.141 0.082 0.066 -0.360 0.202 林分密度/(株·hm-2) 0.201 0.140 0.201 0.140 -
多数研究基于林分类型(天然林和人工林、针叶林和阔叶林)分析根冠比与气候和林分因子的关系，本研究在建立杉木人工林根冠比与平均气温、年平均降水量、林分密度和林龄线性方程基础上，分析各因子对根冠比的影响。很多研究建立了人工林生物量拟合方程[14-18]，但是根冠比的方程较少。本研究建立的根冠比与年平均气温的方程为y=1.051-0.102x+0.003x2(P＜0.05)，这与MOKANY等[1]、WANG等[3]和LUO等[4]的结果相似，与郭炳桥等[5]、REICH等[8]、CAIRNS等[18]的研究结果不同，这种趋势性的表现可能和林分类型相关。根冠比与年平均降水量的方程为y=0.155+1.2×10-5x(P＜0.05)，表明杉木人工林根冠比随年平均降水量的增加而增加。MOKANY等[1]、郭炳桥等[5]、ZERIHUN等[19]结果表明根冠比与降水量呈负相关，但是LUO等[4]研究表明：在年平均降水量多的地区不相关，降水量少的地方呈负相关。因此，气候因子与根冠比的关系受林分类型的影响，杉木人工林根冠比随年平均气温和年平均降水量的增加而增加。
-
杉木人工林根冠比与林分密度和林龄也建立了线性方程，根冠比随林分密度的增加而增加，这与MOKANY等[1]、WANG等[3]、郭炳桥等[5]研究结果一致。这说明密度会造成个体之间的竞争，导致杉木将较多的生物量分配到地下。根冠比随林龄的增加而减少，这与LUO等[4]、郭炳桥等[5]、LIM等[20]、PERI等[21]的结果相似，但是也有研究认为根冠比与林龄没有显著相关[22]，这可能是林龄通过林分密度或者其他因子间接作用于根冠比。
-
单独建立根冠比与年平均气温、年平均降水量、林分密度、林龄的线性方程，可以分析各因子的直接作用，但是忽略了因子之间的间接影响[23-25]。结构方程不仅可以解释各因子之间对根冠比的直接作用，也可以分析各因子间的相互作用及间接作用[26]。KANG等[27]利用结构方程分析了生物量与气候和土壤因子的关联特征；LAMB等[25]利用结构方程阐述了氮沉降与土壤理化性质的关联特征；黄兴召等[28]利用结构方程解析了杉木生产力与气候和林分因子的关联特征。这些研究表明：结构方程可以很好地分析因子的直接和间接作用。
利用结构方程，阐述气候和林分因子与根冠比关联特征。结果表明影响杉木人工林根冠比变化因素的69%来自年平均气温、年平均降水量、林分密度和林龄，因此，还存在其他重要因子影响杉木人工林根冠比。气候因子对生物量及分配的影响是长期的。土壤的理化性质、立地条件也是影响生物量分配的重要因素[29-30]。土壤的呼气作用、养分的利用效率也是影响根冠比的重要因素[2, 31-33]。
Relationship between environmental and stand factors and root-shoot ratio in Cunninghamia lanceolata plantation
-
摘要: 根冠比是研究森林生物量存储方式和分配策略的基础，是森林生态系统物质循环的重要组成部分。通过收集筛选134篇文献608条杉木Cunninghmia lanceolata人工林根冠比（RSR）的数据，分别建立根冠比与年平均气温、年平均降水量、林分密度和林龄的最优方程。根冠比随年平均气温、年平均降水量和林分密度的增加而增加，随林龄的增加而减小。同时，利用结构方程，阐述气候和林分因子与根冠比关联特征。结果表明：年平均气温、年平均降水量、林分密度和林龄对根冠比的直接通径系数分别为0.515（P < 0.01），0.548（P < 0.01），-0.462（P < 0.01）和0.201（P < 0.01）。年平均降水量和林龄还通过影响年平均气温和林分密度间接影响根冠比，其间接通径系数分别为-0.308（P < 0.01）和-0.082（P < 0.05）。影响杉木人工林根冠比变化因素的69%来自气候和林分因子。Abstract: Root-shoot ratio(RSR)is the basis for biomass distribution, and plays an important roles in material circulation of forest ecosystem. By collecting 608 data from 134 published literatures on RSR measurements of Cunninghamia lanceolata plantation, we used linear function to build the relationship between RSR and mean annual temperature, mean annual precipitation, stand density and stand age, respectively. The RSR increased with mean annual temperature, mean annual precipitation and stand density, decreased with stand age. Thus, we also used structural equation model to analysis the relationship between RSR and mean annual temperature, mean annual precipitation, stand density and stand age. The results showed that mean annual temperature, mean annual precipitation, stand density and stand age effect on RSR, which direct path coefficient were 0.515 (P < 0.01), 0.548 (P < 0.01), -0.462 (P < 0.01) and 0.201 (P < 0.01), respectively. The mean annual precipitation and stand age had also indirect effect on RSR, and indirect path coefficient were -0.308 (P < 0.01) and -0.082 (P < 0.05) in our structural equation model. The structural equation model analyses also indicated that mean annual temperature, mean annual precipitation, stand density and stand age explained 69% of the variation in RSR of C. lanceolata plantation.
-
图 1 年平均气温、年平均降水量与杉木人工林根冠比的拟合图
Figure 1 Fitted result between mean annual precipitation, mean annualair temperature and RSR in Cunninghamia lanceolata plantation
图 2 林分密度、林龄与杉木人工林根冠比的拟合图
Figure 2 The fitted result between stand density, stand age and RSR in Cunninghamia lanceolata plantations
图 3 杉木人工林根冠比与年平均气温、年平均降水量、林分密度、林龄的关联模型图
Figure 3 Cor-relationship models between mean annual precipitation, mean annual air temperature, stand density, stand age and RSR in Cunninghamia lanceolata plantations
表 1 杉木人工林根冠比数据的基本信息
Table 1. Basic information of root-shoot ratio (RSR) data in Cunninghamia lanceolata plantation
区域 地上部分生物量/(t·hm-2) 地下部分生物量/(t·hm-2) 根冠比 均值 范围 均值 范围 均值 范围 福建 120.365 7.428~445.750 25.000 1.000~78.580 0.246 0.141~0.565 广东 88.471 38.372~131.654 21.523 11.142~34.330 0.352 0.268~0.461 广西 110.778 13.370~271.860 22.667 3.120~17.620 0.212 0.102~0.414 湖南 83.363 18.225~274.910 15.340 3.365~53.660 0.243 0.156~0.578 湖北 140.659 72.807~294.890 23.045 13.130~45.860 0.216 0.172~0.315 贵州 50.893 1.471~338.060 8.710 0.258~58.390 0.147 0.063~0.143 四川 45.732 0.567~306.482 11.542 0.356~57.622 0.211 0.131~0.522 重庆 57.833 1.857~276.548 8.751 1.256~46.782 0.168 0.112~0.467 江西 94.786 7.344~270.249 16.508 2.707~51.534 0.192 0.104~0.379 江苏 54.010 11.047~98.853 16.415 5.500~21.600 0.359 0.282~0.500 安黴 87.004 41.650~146.890 17.688 7.470~32.290 0.196 0.179~0.220 
下载: 导出CSV
表 2 杉木人工林根冠比与年平均气温、年平均降水量、林分密度、林龄的通径系数
Table 2. Total, direct and indirect path coefficient of mean annualair temperature, mean annual precipitation, stand density, stand age on RSR of Cunninghamia lanceolata plantations
隐变量 显变量 直接系数 标准差 间接系数 标准差 总系数 标准差 根冠比 年平均气温/℃ 0.515 0.155 -0.308 0.118 0.207 0.166 年平均降水量/mm 0.548 0.156 0.548 0.156 林龄/a -0.462 0.141 0.082 0.066 -0.360 0.202 林分密度/(株·hm-2) 0.201 0.140 0.201 0.140
下载: 导出CSV
-
[1] MOKANY K, RAISON R J, PROKUSHKIN A S. Critical analysis of root:shoot ratios in terrestrial biomes[J]. Global Change Biol, 2006, 12(1):84-96. [2] LITTON C M, RYAN M G, TINKER D B, et al. Belowground and aboveground biomass in young postfire lodgepole pine[J]. Can J For Res, 2003, 33(2):351-363. [3] WANG Xiangping, FANG Jingyun, ZHU Biao. Forest biomass and root-shoot allocation in northeast China[J]. For Ecol Manage, 2008, 255(12):4007-4020. [4] LUO Yunjian, WANG Xiaoke, ZHANG Xiaoquan, et al. Root:shoot ratios across China's forests:forest type and climatic effects[J]. For Ecol Manage, 2012, 269(1):19-25. [5] 郭炳桥, 钟全林, 马玉珠, 等.林分和气候因子对中国天然林根冠比的影响[J].应用与环境生物学报, 2016, 22(2):326-331. GUO Bingqiao, ZHONG Quanlin, MA Yuzhu, et al. The effect of stand and climatic factors on the root-shoot allocation in Chinese natural forest[J]. Chin J Appl Environ Biol, 2016, 22(2):326-331. [6] SANQUETTA C R, CORTE A P, da SILVA F. Biomass expansion factor and root-to-shoot ratio for Pinus in Brazil[J]. Carbon Balance Manage, 2011, 6(1):6. doi:10.1186/1750-0680-6-6. [7] 侯振宏, 张小全, 徐德应, 等.杉木人工林生物量和生产力研究[J].中国农学通报, 2009, 25(5):97-103. HOU Zhenhong, ZHANG Xiaoquan, XU Deying, et al. Study on biomass and productivity of Chinese fir plantation[J]. Chin Agric Sci Bull, 2009, 25(5):97-103. [8] REICH P B, LUO Yunjian, BRADFORD J B, et al. Temperature drives global patterns in forest biomass distribution in leaves, stems, and roots[J]. Proc Nat Acad Sci USA, 2014, 111(38):13721-13726. [9] 左舒翟, 任引, 王效科, 等.中国杉木林生物量估算参数及其影响因素[J].林业科学, 2014, 50(11):1-12. ZUO Shuyao, REN Yin, WANG Xiaoke, et al. Biomass estimation factors and their determinants of Cunninghamia lanceolata forests in China[J]. Sci Silv Sin, 2014, 50(11):1-12. [10] POORTER H, JAGODZINSKI A M, RUIZ-PEINADO, et al. How does biomass distribution change with size and differ among species? An analysis for 1200 plant species from five continents[J]. New Phytol, 2015, 208(3):736-749. [11] WOODRUFF R, GARDIAL S F. Know Your Customer:New Approaches to Understanding Customer Value and Satisfaction[M]. Massaehusetts:Blackwell Business, 1996. [12] 侯杰泰, 成子娟.结构方程模型的应用及分析策略[J].心理学探新, 1999, 19(1):54-59. HAU Kittai, CHENG Zijuan Application and analytical strategies of structural equation modelling[J]. Explor Psychol, 1999, 19(1):54-59. [13] R Core Team. R: a language and environment for statistical computing, version 3. 1. 2. Lavaan, China: R Foundation for Statistical Computing[CP]. 2015-11-07. https://cran.r-project.org/web/packages/lavaan/index.html. [14] 符利勇, 曾伟生, 唐守正.利用混合模型分析地域对国内马尾松生物量的影响[J].生态学报, 2011, 31(19):5797-5808. FU Liyong, ZENG Weisheng, TANG Shouzheng. Analysis the effect of region impacting on the biomass of domestic masson pine using mixed model[J]. Acta Ecol Sin, 2001, 31(19):5797-5808. [15] ZAPATA-CUARTAS M, SIERRA C A, ALLEMAN L. Probability distribution of allometric coefficients and Bayesian estimation of aboveground tree biomass[J]. For Ecol Manage, 2012, 277(4):173-179. [16] ZHANG Xiongqing, DUAN Aiguo, ZHANG Jianguo. Tree biomass estimation of Chinese fir (Cunninghamia lanceolata) basedon Bayesian method[J]. PLoS One, 2013, 8(11):e79868. doi:10.1371/journal.pone. 0079868. [17] 黄兴召, 陈东升, 孙晓梅, 等.基于异速参数概率分布的立木地上生物量估算[J].林业科学, 2014, 50(6):34-41. HUANG Xingzhao, CHEN Dongsheng, SUN Xiaomei, et al. Estimation of above-ground tree biomass based on probability distribution of allometric parameters[J]. Sci Silv Sin, 2014, 50(6):34-41. [18] CAIRNS M A, BROWN S, HELMER E H, et al. Root biomass allocation in the world's upland forests[J]. Oecologia, 1997, 111(1):1-11. [19] ZERIHUN A, MONTAGU K D, HOFFMANN M B, et al. Patterns of below-and aboveground biomass in Eucalyptus populnea woodland com munities of northeast Australia along a rainfall gradient[J]. Ecosystems, 2006, 9(4):501-515. [20] LIM H, LEE K H, PARK I H. Biomass expansion factors and allometric equations in an age sequence for Japanese cedar (Cryptomeria japonica) in southern Korea[J]. J For Res, 2013, 18(4):316-322. [21] PERI P L, GARGAGLIONE V, PASTUR G M. Dynamics of above-and below-ground biomass and nutrient accumulation in an age sequence of Nothofagus antarctica forest of Southern Patagonia[J]. For Ecol Manage, 2006, 233(1):85-99. [22] 汪金松, 范秀华, 范娟, 等.林木竞争对臭冷杉生物量分配的影响[J].林业科学, 2012, 48(4):14-20. WANG Jinsong, FAN Xiuhua, FAN Juan, et al. Effects of tree competition on the biomass partitioning of Abies nephrolepis[J]. Sci Silv Sin, 2012, 48(4):14-20 [23] HARRELL F E Jr, LEE K L, MARK D B. Multivariable prognostic models:issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors[J]. Stat Med, 1996, 15(4):361-387. [24] COUPLAND R T. Grassland Ecosystems of the World:Analysis of Grasslands and Their Uses:International Biological Programme Synthesis Series[M]. Cambridge:Cambridge University Press, 1979:41-45. [25] LAMB E G, MENGERSEN K L, STEWART K J, et al. Spatially explicit structural equation modeling[J]. Ecology, 2014, 95(9):2434-2442. [26] PAAP R. What are the advantages of MCMC based inference in latent variable models?[J]. Stat Neerl, 2002, 56(1):2-22. [27] KANG Muyi, DAI Cheng, JI Wenyao, et al. Biomass and its allocation in relation to temperature, precipitation, and soil nutrients in Inner Mongolia Grasslands, China[J]. PLoS One, 2013, 8(7):e69561. doi:10.1371/journal.pone. 0069561. [28] 黄兴召, 许崇华, 徐俊, 等.利用结构方程解析杉木林生产力与环境因子及林分因子的关系[J].生态学报, 2017, 37(7):2274-2281. HUANG Xingzhao, XU Chonghua, XU Jun, et al. Structural equation model analysis of the relationship between environmental and stand factors and net primary productivity in Cunninghamia lanceolata forests[J]. Acta Ecol Sin, 2017, 37(7):2274-2281. [29] BROWN S. Measuring carbon in forests:current status and future challenges[J]. Environ Pollut, 2002, 116(3):363-372. [30] POORTER H, SACK L. Pitfalls and possibilities in the analysis of biomass allocation patterns in plants[J]. Front Plant Sci, 2012, 3:259. doi:10.3389/fpls. 2012. 00259. [31] ENQUIST B J, NIKLAS K J. Global allocation rules for patterns of biomass partitioning in seed plants[J]. Science, 2002, 295(5559):1517-1520. [32] READ J, STOKES A. Plant biomechanics in an ecological context[J]. Am J Bot, 2006, 93(10):1546-1565. [33] BARRIO-ANTA M, BALBOA-MURIAS M, CASTEDO-DORADO F, et al. An ecoregional model for estimating volume, biomass and carbon pools in maritime pine stands in Galicia (northwestern Spain)[J]. For Ecol Manage, 2006, 223(1/3):24-34. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2018.04.009
点击查看大图
图(3) / 表(2)
计量
- 文章访问数: 2578
- HTML全文浏览量: 624
- PDF下载量: 616
- 被引次数: 0
