-
足尺人造板是指人造板生产和销售中最常见的幅面为2.44 m × 1.22 m标准尺寸的成品人造板。在足尺人造板的力学性能指标中，弹性模量（MOE）是最有代表性的指标之一，因为它与静曲强度（MOR）等其他主要力学性能指标间存在着统计上的线性关系[1]。目前，足尺人造板弹性模量的测定方法是根据国家标准从板材不同部位截取数个小试件在力学试验机上进行弯曲实验，再根据小试件的平均值评价足尺板材的弹性模量。这种方法属于有损检测，成本高，检测效率低，只适于产品的抽检，只能在实验室环境中进行。如何找到一种快速、无损检测足尺人造板弹性模量的方法是人造板行业亟须解决的一个问题。20世纪80年代以来，国外的研究人员利用声发射、应力波和模态测试等技术对足尺人造板等大幅面人造板弹性模量的无损测定进行了许多研究[2-9]。相比之下国内相关研究较少，高燕秋等[10]通过在大尺寸人造板几何中心加载静载荷，测量其挠度进而计算弹性模量；周海宾等[11]采用了一种悬臂扭弯振动法测定板材的弹性模量和剪切模量，但这些研究成果因可操作性差等原因均未能在生产实际中广泛应用。本研究提出一种基于薄板横向自由振动原理的足尺人造板弹性模量动态测定方法，即通过测量在2节线处支承下足尺人造板自由振动时的第1阶固有频率和其质量来测定其弹性模量，力图为足尺人造板弹性模量的快速、无损测定，提供一种可选择的方法。
-
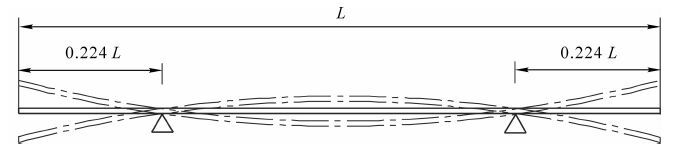
如图 1所示：将被测足尺人造板在其长度方向的22.4%及77.6%等2个节线处支承，即形成“自由-自由”支承。通过试验模态和计算模态分析确定了足尺人造板在这种支承下自由振动的第1阶模态都是沿长度方向的1阶弯曲振动[12-13]，因此，足尺人造板弹性模量的计算方法可通过薄板横向自由振动理论得到。
图 1 足尺人造板“自由-自由”支承自由振动的1阶振型
Figure 1. First vibration mode of full-size wood composite panels supported in “free-free” condition
本研究将此弹性模量称为足尺人造板的动态弹性模量，可通过式（1）来计算[14]。
$${E_d} = \frac{{48{\pi ^2}m{l^3}\left( {1 - {v_x}{v_y}} \right)}}{{500.6b{h^3}}}.$$ (1) 式（1）中：Ed为足尺人造板的动态弹性模量（Pa），f为板的1阶弯曲振动固有频率（Hz），m为板的质量（kg），l，b和h分别为板的长度（m），宽度（m）和厚度（m），vx和vy为板的泊松比。借鉴文献[14]，1-vxvy的值取为0.99。由于板的几何尺寸（l，b，h）已知，所以在测得板材第1阶振动固有频率f和其质量m的情况下，就可以计算出被测板材的弹性模量。这就是振动方式测定足尺人造板弹性模量的理论基础。
-
共有206张足尺人造板被用作试验材料。其中，刨花板有5种厚度，胶合板有9种厚度，被测板材数量及尺寸等参数如表 1所示。为便于试验操作和记录结果，对试验用板材进行了编号，PB代表刨花板，PW代表胶合板，字母后面紧跟的数字代表板材公称厚度；板材的长度×宽度均为2 440 mm × 1 220 mm，不标出。
表 1 被测板材参数
Table 1. Full-size panels’ parameters
板材编号 材料 数量/张 板材平均尺寸/(厚×宽×长，mm) 平均密度/(g·cm-3) 平均含水率/% PB9 刨花板 12 8.97×1 223.00×2 442.30 0.66 4.50 PB12 刨花板 14 12.15×1 222.90×2 441.90 0.70 4.10 PB16 刨花板 25 16.04×1 223.10×2 441.00 0.70 4.30 PB18 刨花板 25 18.03×1 220.20×2 437.00 0.66 5.70 PB25 刨花板 10 25.05×1 220.90×2 440.70 0.68 6.80 PW5 胶合板 7 4.98×1 218.60×2 439.40 0.51 9.00 PW6 胶合板 6 6.00×1 220.00×2 440.00 0.59 10.20 PW7 胶合板 8 6.52×1 218.90×2 437.90 0.53 9.50 PW9 胶合板 23 9.35×1 219.20×2 438.40 0.51 9.40 PW12 胶合板 8 11.59×1 223.00×2 439.40 0.54 9.00 PW15 胶合板 20 14.47×1 220.80×2 439.40 0.51 10.50 PW18 胶合板 24 17.28×1 220.80×2 438.80 0.52 8.60 PW20 胶合板 8 19.46×1 218.00×2 439.40 0.51 9.00 PW25 胶合板 16 24.36×1 219.20×2 439.50 0.53 9.80 -
图 2是自行研制的足尺人造板力学性能检测试验装置示意图[15]。其中，力传感器用于测量足尺人造板的质量；激光传感器用于检测足尺人造板中部振动位移信号；支撑机构是整个试验装置的结构基础，主要用来规范板材放置位置，并为力传感器和激光传感器提供安装位置。试验装置软件用LabVIEW软件编写，实现力信号和激光振动信号的采集、处理、弹性模量计算和结果存储。
图 2 足尺人造板力学性能检测试验装置示意图
Figure 2. Schematic diagram of laboratory testing apparatus for measuring mechanical performance of full-size wood composite panels
试验过程中，首先，将待测板材摆放在试验装置上，将位置调好，确保板材是在全长的22.4%位置以及77.6%位置被线支承；计算机开始执行测试软件，采集力传感器信号，测得被测板材的质量。然后，用双手在远离力传感器的一端向下按压板材，使其自由振动，此时，激光传感器将检测出的板材振动信号通过数据采集卡传到计算机中，经测试软件处理得到板材的第1阶振动固有频率[16]。最后，通过测试软件中根据式（1）编制的计算模块计算出板材的动态弹性模量（Ed）。
-
为了验证上述所提出的振动测定方法的可行性，需要对比所测得的足尺人造板动态弹性模量（Ed）与传统小试件弯曲方法测得的静态弹性模量（Eb）间的相关性。在前面试验完成后，将检测过的每块板材沿长度方向按国家标准[17]裁出6块小试件（胶合板小试件裁制方法参照刨花板标准）；再按国家标准GB/T 17657-2013[18]规定的方法进行小试件3点弯曲试验。每块足尺人造板的静态弹性模量（Ed）为其6块小试件弹性模量的均值。
-
刨花板和胶合板总体测量结果如表 2和表 3所示。可以看到：动态弹性模量（Ed）比静态弹性模量（Ed）略大，两者比值为1.03~1.22。以所有足尺人造板为研究对象，足尺人造板Ed比Ed高11.63%，其中，刨花板Ed比Ed高7.88%，胶合板Ed比Ed高13.11%。即胶合板与刨花板相比，其Ed与Ed相差更大。
表 2 刨花板弹性模量2种测定方法测量结果
Table 2. Results of MOE tested of particleboard in the two methods
板材编号 弹性模量代号 弹性模量/Pa 平均弹性模量之比(Ed/Eb) 平均 标准偏差 变异系数/% PB9 Ed 2 903.09 175.06 6.03 1.08 Eb 2 696.42 127.81 4.74 PB12 Ed 3 670.95 280.66 7.65 1.04 Eb 3 537.74 297.16 8.40 PB16 Ed 3 631.94 141.47 3.90 1.06 Eb 3 415.47 116.85 3.42 PB18 Ed 2 338.77 164.23 7.02 1.12 Eb 2 083.80 187.93 9.02 PB25 Ed 3 022.87 422.67 13.98 1.12 Eb 2 697.27 433.03 16.05 表 3 胶合板弹性模量2种测定方法测量结果
Table 3. Results of MOE tested of plywood in the two methods
板材编号 弹性模量代号 弹性模量/Pa 平均弹性模量之比(Ed/Eb) 平均 标准偏差 变异系数/% PW5 Ed 3754.08 612.87 16.33 1.22 Eb 3066.90 249.97 8.15 PW6 Ed 7259.83 663.87 9.14 1.19 Eb 6096.83 543.53 8.91 PW7 Ed 3377.30 467.37 13.84 1.19 Eb 2836.41 319.78 11.27 PW9 Ed 4178.87 1177.09 28.17 1.11 Eb 3748.21 988.81 26.38 PW12 Ed 5128.97 1014.52 19.78 1.11 Eb 4630.52 388.28 8.39 PW15 Ed 3391.24 678.72 20.01 1.06 Eb 3208.55 493.82 15.39 PW18 Ed 4997.50 727.79 14.56 1.14 Eb 4372.35 476.21 10.89 PW20 Ed 4482.71 259.21 5.78 1.03 Ed 4342.56 244.23 5.62 PW25 Ed 4790.10 346.15 7.23 1.12 Eb 4263.15 450.38 10.56 从表 2和表 3所列的变异系数可以看出：每种厚度的刨花板和胶合板，2种测量方法得到的Ed和Ed都有一定的变动量，说明同一批次足尺人造板的力学性能不是固定不变的。与刨花板相比，胶合板的弹性模量变异性更大一些。这可能主要是由于胶合板由单板构成，单板力学性能变异性较大所致。
-
测得的2种材质的足尺人造板动态弹性模量（Ed）与静态弹性模量（Ed）的总体关系如图 3所示。图 4和图 5分别为刨花板和胶合板的Ed与Ed之间的关系。可以看到：无论是将2种板材的测定结果放在一起，还是单独分析，足尺人造板Ed与Ed间都存在着显著的线性关系。其中，足尺人造板试件总体数据的Ed与Ed之间的相关系数达到了0.94；刨花板的Ed与Ed之间的相关系数为0.96，胶合板的Ed与Ed之间的相关系数为0.91，都在0.90以上。
图 3 足尺人造板动态弹性模量（Ed）与静态弹性模量（Eb）总体数据间的关系
Figure 3. Relationship between full-size wood composite panels’ dynamic MOE Ed and static MOE Eb
图 4 刨花板2种测定方法测量结果间的关系
Figure 4. Relationship between the results of MOE tested of particleboard in the two methods
图 5 胶合板2种测定方法测量结果间的关系
Figure 5. Relationship between the results of MOE tested of plywood in the two methods
利用R语言建模[19]采用一元线性回归分析方法对这些试验数据进行回归分析，并进行方差分析和t检验，得到的回归方程及其相关参数，如表 4所示。通过这些回归方程，可以实现Ed 与Ed 之间的相互转换，也即在振动方式测定足尺人造板弹性模量之后，可以通过这些回归方程推算出其传统测量方法的测量数值。因而，基于薄板横向自由振动理论的足尺人造板弹性模量振动测定是可行的。
表 4 足尺人造板动态弹性模量(Ed)与静态弹性模量(Eb)回归方程及相关参数
Table 4. Correlation equations and related parameters between full-size wood composite panels5 dynamic MOE Ed and static MOE Eb
板材编号 板材数 y=ax+b 相关系数r F值 显著性 a b PB 86 1.01 -266.18 0.96 1 092.00 *** PW 120 0.73 718.94 0.91 601.30 *** PB和PW 206 0.79 455.97 0.94 1 669.00 *** 说明:***0.001差异显著。 -
振动方式测得的足尺人造板动态弹性模量（Ed）比传统方法测得的静态弹性模量（Ed ）略大，两者比值为1.03~1.22。足尺人造板Ed与Ed 间存在着良好的线性关系，刨花板和胶合板的Ed与Ed 之间的相关系数分别为0.96和0.91，2种板材总体数据的Ed与Ed 之间的相关系数达到了0.94，且均在0.001水平上显著相关。基于薄板横向自由振动理论的足尺人造板弹性模量振动测定是可行的。
Measuring modulus of elasticity of full-size wood composite panels using vibration method
-
摘要: 为了无损检测足尺人造板的弹性模量，提出一种基于薄板横向自由振动原理的测定方法。利用自行开发的足尺人造板力学性能检测试验装置，以206张足尺人造板为试验对象，包括86张刨花板和120张胶合板，进行了测定试验。同时，从每张板材上裁制6块小试件，通过传统的小试件3点弯曲检测法来获得静态弹性模量，并将2种检测方法的结果进行对比。结果表明：以所有足尺人造板为研究对象，足尺人造板动态弹性模量比其静态弹性模量稍大，两者比值为1.03~1.22；2种检测方法获得的足尺人造板弹性模量值间的相关系数为0.94（P<0.001），证明基于薄板横向自由振动原理的足尺人造板弹性模量振动方式测定是可行的。图5表4参19Abstract: In order to detect the modulus of elasticity of full-size wood composite panels non-destructively, this research presents a test method based on the transverse free vibration of thin plate. A laboratory testing apparatus for measuring mechanical performance of full-size panels was built. Two hundred and six pieces of full-size wood composite panels including eighty-six pieces of particleboard panels and one hundred and twenty pieces of plywood panels were tested. Following free vibration testing, six small specimens were cut from each panel and traditional static mid-point bending test was then performed on each specimen to obtain static MOE. Then, the test results of two methods were compared. The results indicated that:all the full-size wood composite panels as the research object, the dynamic MOE of full-size panels by vibration method was slightly higher than their static MOE and their ratio were in the range of 1.03-1.22; a highly significant correlation relationship (P<0.001) was found between dynamic MOE and static MOE of full-size panels,which proved that determination of modulus of elasticity of full-size wood composite panels based on the transverse free vibration of thin plate was feasible.[Ch, 5 fig. 4 tab. 19 ref.]
-
图 1 足尺人造板“自由-自由”支承自由振动的1阶振型
Figure 1 First vibration mode of full-size wood composite panels supported in “free-free” condition
图 2 足尺人造板力学性能检测试验装置示意图
Figure 2 Schematic diagram of laboratory testing apparatus for measuring mechanical performance of full-size wood composite panels
图 3 足尺人造板动态弹性模量（Ed）与静态弹性模量（Eb）总体数据间的关系
Figure 3 Relationship between full-size wood composite panels’ dynamic MOE Ed and static MOE Eb
图 4 刨花板2种测定方法测量结果间的关系
Figure 4 Relationship between the results of MOE tested of particleboard in the two methods
图 5 胶合板2种测定方法测量结果间的关系
Figure 5 Relationship between the results of MOE tested of plywood in the two methods
表 1 被测板材参数
Table 1. Full-size panels’ parameters
板材编号 材料 数量/张 板材平均尺寸/(厚×宽×长，mm) 平均密度/(g·cm-3) 平均含水率/% PB9 刨花板 12 8.97×1 223.00×2 442.30 0.66 4.50 PB12 刨花板 14 12.15×1 222.90×2 441.90 0.70 4.10 PB16 刨花板 25 16.04×1 223.10×2 441.00 0.70 4.30 PB18 刨花板 25 18.03×1 220.20×2 437.00 0.66 5.70 PB25 刨花板 10 25.05×1 220.90×2 440.70 0.68 6.80 PW5 胶合板 7 4.98×1 218.60×2 439.40 0.51 9.00 PW6 胶合板 6 6.00×1 220.00×2 440.00 0.59 10.20 PW7 胶合板 8 6.52×1 218.90×2 437.90 0.53 9.50 PW9 胶合板 23 9.35×1 219.20×2 438.40 0.51 9.40 PW12 胶合板 8 11.59×1 223.00×2 439.40 0.54 9.00 PW15 胶合板 20 14.47×1 220.80×2 439.40 0.51 10.50 PW18 胶合板 24 17.28×1 220.80×2 438.80 0.52 8.60 PW20 胶合板 8 19.46×1 218.00×2 439.40 0.51 9.00 PW25 胶合板 16 24.36×1 219.20×2 439.50 0.53 9.80 
下载: 导出CSV
表 2 刨花板弹性模量2种测定方法测量结果
Table 2. Results of MOE tested of particleboard in the two methods
板材编号 弹性模量代号 弹性模量/Pa 平均弹性模量之比(Ed/Eb) 平均 标准偏差 变异系数/% PB9 Ed 2 903.09 175.06 6.03 1.08 Eb 2 696.42 127.81 4.74 PB12 Ed 3 670.95 280.66 7.65 1.04 Eb 3 537.74 297.16 8.40 PB16 Ed 3 631.94 141.47 3.90 1.06 Eb 3 415.47 116.85 3.42 PB18 Ed 2 338.77 164.23 7.02 1.12 Eb 2 083.80 187.93 9.02 PB25 Ed 3 022.87 422.67 13.98 1.12 Eb 2 697.27 433.03 16.05
下载: 导出CSV
表 3 胶合板弹性模量2种测定方法测量结果
Table 3. Results of MOE tested of plywood in the two methods
板材编号 弹性模量代号 弹性模量/Pa 平均弹性模量之比(Ed/Eb) 平均 标准偏差 变异系数/% PW5 Ed 3754.08 612.87 16.33 1.22 Eb 3066.90 249.97 8.15 PW6 Ed 7259.83 663.87 9.14 1.19 Eb 6096.83 543.53 8.91 PW7 Ed 3377.30 467.37 13.84 1.19 Eb 2836.41 319.78 11.27 PW9 Ed 4178.87 1177.09 28.17 1.11 Eb 3748.21 988.81 26.38 PW12 Ed 5128.97 1014.52 19.78 1.11 Eb 4630.52 388.28 8.39 PW15 Ed 3391.24 678.72 20.01 1.06 Eb 3208.55 493.82 15.39 PW18 Ed 4997.50 727.79 14.56 1.14 Eb 4372.35 476.21 10.89 PW20 Ed 4482.71 259.21 5.78 1.03 Ed 4342.56 244.23 5.62 PW25 Ed 4790.10 346.15 7.23 1.12 Eb 4263.15 450.38 10.56
下载: 导出CSV
表 4 足尺人造板动态弹性模量(Ed)与静态弹性模量(Eb)回归方程及相关参数
Table 4. Correlation equations and related parameters between full-size wood composite panels5 dynamic MOE Ed and static MOE Eb
板材编号 板材数 y=ax+b 相关系数r F值 显著性 a b PB 86 1.01 -266.18 0.96 1 092.00 *** PW 120 0.73 718.94 0.91 601.30 *** PB和PW 206 0.79 455.97 0.94 1 669.00 *** 说明:***0.001差异显著。
下载: 导出CSV
-
[1] DÜNDAR T, AS N, AKKILIÇH. The prediction of mechanical properties of wood-based composites with vibration NDE method[J]. J Fac For Istanbul Univ, 2008, 58(2):43-59. [2] COPPENS H. Quality control of particleboards by means of their oscillation behavior[C]//Proceedings of FESYP Technical Conference. Munich:European Federation of Associations of Particleboard Manufactures, 1988:143-165. [3] McNATT J D, WELLWOOD R W, BACH L. Relationships between small-specimens and large panel bending tests on structural wood-based panels[J]. For Prod J, 1990, 40(9):10-16. [4] SHYAMASUNDER K, ASWATHANARAYANA B S, NAIDU M V. Nondestructive evaluation of modulus of elasticity and modulus of rigidity of plywood by sonic methods[C]//PELLERIN R F, MCDONALD K A. Proceedings of the 9th International Symposium on Nondestructive Testing of Wood. Madison:Forest Products Society, 1994:113-116. [5] SHI Bozhong, CAI Zhiyong. Nondestructive evaluation of full-sized particleboard panels using the vibration technique[C]//PELLERIN R F, MCDONALD K A. Proceedings of the 9th International Symposium on Nondestructive Testing of Wood. Madison:Forest Products Society, 1994:117-122. [6] LARSSON D. Stiffness characterization of wood based panels by modal testing[C]//SANDOZ J L, PELLERIN R F, MCDONALD K A. Proceedings of the 10th International Symposium on Nondestructive Testing of Wood. Lausanne:IBOIS-Chair of Timber Construction of the Swiss Federal Institute of Technology, 1996:237-246. [7] LAU P W, TARDIF Y. Evaluation of Moduli of Elasticity and Rigidity of Panel Products by Torsional-Bending Vibration[R]. Edmonton:Canadian Forest Service, 1996. [8] SCHULTE M, FRÜHWALD A, BRÖKER F W. Non-destructive testing of panel products by vibration technique[C]//SANDOZ J L, PELLERIN R F, McDONALD K A. Proceedings of the 10th International Symposium on Nondestructive Testing of Wood. Lausanne:IBOIS-Chair of Timber Construction of the Swiss Federal Institute of Technology, 1996:259-268. [9] MIRBOLOUK P, ROOHNIA M. Evaluation of dynamic modulus of elasticity of medium density fiberboard panel from longitudinal vibration tests on specimens[J]. BioResources, 2015, 10(1):613-621. [10] 高燕秋,王兆伍,张齐生. TMJ-A人造板弹性模量无损检测显示机的误差因素分析[J]. 木材工业,2002,16(5):24-26. GAO Yanqiu, WANG Zhaowu, ZHANG Qisheng. Analysis of measuring error on TMJ-a nondestructive testing equipment for structural board[J]. China Wood Ind, 2002, 16(5):24-26. [11] 周海宾,任海青,费本华,等. 木质复合板弯曲、剪切弹性模量动态测试[J]. 建筑材料学报,2007,10(5):561-565. ZHOU Haibin, REN Haiqing, FEI Benhua, et al. Dynamical test on flexural and shear modulus of composite wood panels[J]. J Build Mater, 2007, 10(5):561-565. [12] ZHOU Lujing, ZHANG Houjiang, GUAN Cheng, et al. Analysis of vibration modal testing for the full-size artificial board[J]. J Mult, 2014, 9(6):816-821. [13] 管成,周卢婧,张厚江. 足尺中密度纤维板振动模态分析[J]. 西北林学院学报,2015,30(3):228-233. GUAN Cheng, ZHOU Lujing, ZHANG Houjiang. Analysis of the vibration modal of the full-sized medium density fiberboard[J]. J Northwest For Univ, 2015, 30(3):228-233. [14] ZHOU Jianhui, CHUI Y H. Influence of boundary conditions on measurement of elastic constants of engineered wood-based panels using modal testing[C]//ROSS R J, GONÇALVES R. Proceedings of the 19th International Symposium on Nondestructive Testing of Wood. Rio de Janeiro:Forest Products Society, 2015:321-332. [15] 张厚江,周卢婧,吴江. 足尺人造板弹性模量和动态粘弹性无损检测装置与检测方法:CN103439251A[P]. 2013-12-11. ZHANG Houjiang, ZHOU Lujing, WU Jiang. Nondestructive full-scale artificial board elasticity modulus and dynamic viscoelasticity testing device and method:CN103439251A[P]. 2013-12-11. [16] 管成,张厚江,周卢婧,等. 足尺人造板动态粘弹性检测[J]. 南京林业大学学报:自然科学版,2015,39(6):131-136. GUAN Cheng, ZHANG Houjiang, ZHOU Lujing, et al. Detection on dynamic viscoelasticity of full-size wood composite panels[J]. J Nanjing For Univ Nat Sci Ed, 2015, 39(6):131-136. [17] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会. GB/T 4897.1-2003刨花板第1部分:对所有板型的共同要求[S]. 北京:中国标准出版社,2003. [18] 中华人民共和国国家质量监督检验检疫总局,中国国家标准化管理委员会. GB/T 17657-2013人造板及饰面人造板理化性能试验方法[S]. 北京:中国标准出版社,2014. [19] 王斌会. 多元统计分析及R语言建模[M]. 广州:暨南大学出版社,2014:62-77. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2016.06.020
点击查看大图
计量
- 文章访问数: 2565
- HTML全文浏览量: 520
- PDF下载量: 401
- 被引次数: 0
