-
森林作为独有的陆地生态系统，发挥着无可替代的作用与功能[1]。森林具有运动和变化的特征，随着时间的推移，树种组成会发生明显的变化，从而引起整个森林组分的变化，这一现象称为森林演替[2]。森林演替中森林组分的变化除了与木材的供应有关外，还与生产力、碳固存、动植物生境等有关，因此，对森林演替进行预测，在森林生态系统管理中尤为重要[3]。
长期以来生态学一直在深入探究和预测森林演替[4−5]。研究者使用高度参数化的模型从模拟叶片的光合作用、蒸腾作用等方面来解释森林动态演替进程[6−7]。较多研究通过单木生长、光照、温度、养分、水分、更替及死亡的林窗模型描述森林演替过程[2, 8−9]。较大空间尺度有林分级混合模型、景观级模型等，随着模拟单位尺度的变大，林分水平、样地水平的模型也得到更多的认识，并且伴随着空间分辨率和时间间隔的增加，可以使用相对较少的参数模拟森林动态[10]。此外，也有马尔科夫链的概率转移理论考虑了外部扰动、空间异质性等因素描述森林转移的过程[11]。
以单木为基本单元来描述森林是最为标准的，但不适用于大面积区域，此类模型往往伴随着大量反映局部地块特征的参数，能够很好地模拟试验区的森林动态变化，但是过度复杂的模型如果没有大量的工作准备，对新的应用环境并不友好[2, 12−13]。森林资源连续清查结果表明：因受松材线虫Bursaphelenchus xylophilus病的危害，台州市松类资源大幅减少，受经济因素影响，杉类资源也在减少，同时阔叶类资源在大幅增加。但通过建立数学模型定量描述并预测这种变化的研究鲜见报道。现有模型过于依赖细节和大量变量，并不适用于大区域树种结构变化情况的模拟[12−13]。鉴于此，本研究对台州市森林树种结构变化的特殊情况及其变化缺乏适用模型的情况进行了研究，以期为台州市森林树种结构调整提供科学依据。
-
台州市(28°01′~29°20′N，120°17′~121°56′E)位于浙江省中部沿海，总面积约10 050 km2。该区属中亚热带季风气候，年均日照时数为1 800~2 037 h，全年降水日数为132~171 d，年均降水量为1 632 mm。夏、秋季受台风影响比较大。地带性植被为中亚热带常绿阔叶林，主要的阔叶乔木树种有壳斗科Fagaceae的甜槠Castanopsis eyrei、山茶科Theaceae的木荷Schima superba等，针叶树种主要有马尾松Pinus massoniana、杉木Cunninghamia lanceolata等。主要森林类型有常绿阔叶林、落叶阔叶林、针阔混交林、常绿落叶阔叶混交林、竹林等[14]，森林覆盖率为67.0%。
-
选用台州市6期(1994、1999、2004、2009、2014和2019年)森林资源连续清查固定样地和固定样木的资料作为研究数据，各期固定样地总数(含非林地、无林地等非乔木林样地)分别为379、390、388、388、388和388个。1994和1999年2期样地数和后面各期相比略有差异，是因为前3期每期有1/3的样地进行了移动。移动部分样地的目的是为了检验固定样地是否受到特殊对待，即样地内部和外部是否具有相同的经营措施，结果表明没有特殊对待的情况发生，即样地固定后对总体的代表性不会改变。固定样地为800 m2的正方形。森林资源连续清查体系是基于概率抽样理论的机械抽样，每5 a复测1次，是森林资源调查中最具权威性的数据，对于森林的动态变化分析及预测十分有利[15]，同时也便于更有效地传播和利用现有数据进行可持续的森林生态系统经营和管理[16]。本研究的对象是乔木树种，所以只选择其中的乔木林样地，根据地类选择样地不改变其随机性和代表性。由于经济林比较特殊，所以本研究不包括乔木经济林。
由于树种众多，对每一树种进行模拟是不现实的，因此需要将具有共同特性的树种聚集为组进行模拟[17]。将样木分为3个树种组：①松类包括马尾松、黑松P. thunbergii、黄山松P. taiwanensis、湿地松P. elliottii等，其中马尾松占绝对多数；②杉类包括杉木、柳杉Cryptomeria fortunei、水杉Metasequoia glyptostroboides、池杉Taxodium ascendens、红豆杉Taxus wallichiana var. chinensis等，其中杉木占绝对多数；③阔叶类包括栎属Quercus、栲属Castanopsis、枫香Liquidambar、木荷、樟科Lauraceae等植物。
将乔木林样地按优势树种组(样地中蓄积比例最大的树种组)统计，乔木林样木胸径最大值、均值、中位数和标准差等见表1。其中，最小值均为森林资源连续清查规定的5.0 cm，故没列出。
表 1 乔木林各期树种组的胸径统计
Table 1. DBH statistics of tree species groups in different stages of arbor forest
年份 树种组 样地数/个 胸径/cm 最大值 均值 中位数 标准差 1994 松类 110 29.8 9.5 8.5 3.78 杉类 22 24.0 8.7 8.2 3.03 阔叶类 7 36.2 8.8 7.5 3.88 1999 松类 103 32.8 9.7 8.9 3.84 杉类 42 28.5 8.6 7.8 3.16 阔叶类 10 39.3 8.6 7.2 3.75 2004 松类 105 31.3 10.3 9.4 4.20 杉类 54 34.6 9.4 8.5 3.57 阔叶类 24 40.5 7.8 6.8 3.08 2009 松类 81 33.2 10.9 9.8 4.62 杉类 46 39.7 10.0 9.1 3.95 阔叶类 54 39.6 8.1 7.0 3.32 2014 松类 61 34.2 11.8 10.5 5.33 杉类 42 44.0 10.6 9.6 4.47 阔叶类 82 44.4 8.7 7.5 3.81 2019 松类 41 37.6 12.7 10.4 6.18 杉类 47 48.7 11.3 9.8 5.06 阔叶类 95 45.9 9.2 7.5 4.18 -
将所有乔木林样地上的样木合在一起，统计3个树种组的总样木数和总材积及其比例。材积数据来自森林资源连续清查数据库，是根据一元材积表计算的。这些数据将用于建立自约束模型。统计各树种组的进界木和采枯木株数(受松材线虫病危害的林木在死亡后及时得到清理，所以调查时根据伐根难以区分采伐木和枯损木，所以本研究将两者合在一起，简称采枯木)，用于解释模型的预测结果。
-
设y1、y2和y3分别为松类、杉类和阔叶类树种组的株数比例或材积比例，t为年份，可得：
$$ \left\{\begin{array}{l}{y}_{1}={(1+{\lambda }_{1}{{\rm{e}}}^{{\gamma }_{1}/t}+{\lambda }_{2}{{\rm{e}}}^{{\gamma }_{2}/t})}^{-1}\\ {y}_{2}={[(1/{\lambda }_{1}){{\rm{e}}}^{-{\gamma }_{1}/t}+1+({\lambda }_{2}/{\lambda }_{1}){{\rm{e}}}^{({\gamma }_{2}-{\gamma }_{1})/t}]}^{-1}\\ {y}_{3}={[(1/{\lambda }_{2}){{\rm{e}}}^{-{\gamma }_{2}/t}+({\lambda }_{1}/{\lambda }_{2}){{\rm{e}}}^{({\gamma }_{1}-{\gamma }_{2})/t}+1]}^{-1}\end{array} 。\right. $$ (1) 式(1)中：λ1、λ2、γ1和γ2为模型参数。由于变量和参数自动满足0＜y1，y2，y3＜1，y1+y2+y3=1，λ1，λ2＞0，γ1，γ2＜0，所以本研究将式(1)命名为非线性方程组自约束树种结构模型。式(1)推导过程繁复，本研究略去推导过程的介绍。年份t的起点可以自由设定，本研究为了方便取起点，即1994年时的t取5，1999年时的t取10等，当然也可以取实际数1994、1999等。y1，y2，y3存在理论极限值y1∞，y2∞，y3∞(极限的点估计)，根据式(1)可得：
$$ \left\{ {\begin{array}{*{20}{c}} {{y_{1\infty }} = \mathop {\lim }\limits_{t \to \infty } {y_1} = 1/{{(1 + {\lambda _1} + {\lambda _2})}^{ - 1}}} \\ {{y_{2\infty }} = \mathop {\lim }\limits_{t \to \infty } {y_2} = {\lambda _1}{{(1 + {\lambda _1} + {\lambda _2})}^{ - 1}}} \\ {{y_{3\infty }} = \mathop {\lim }\limits_{t \to \infty } {y_3} = {\lambda _2}{{(1 + {\lambda _1} + {\lambda _2})}^{ - 1}}} \end{array}} \right. 。 $$ (2) -
极限作为今后的发展趋势，具有重要意义。设
$ {y_\infty } = {({y_{1\infty }},{y_{2\infty }},{y_{3\infty }})^{\text{T}}} $ 为极限的点估计，各极限点估计的方差D为：$$ \left\{ {\begin{array}{*{20}{l}} {D({y_{1\infty }}) = (\sigma _{_{{\lambda _1}}}^2 + \sigma _{_{{\lambda _2}}}^2 + 2{\sigma _{{\lambda _1}{\lambda _2}}})/{{(1 + {\lambda _1} + {\lambda _2})}^4}} \\ {D({y_{2\infty }}) = [{{(1 + {\lambda _2})}^2}\sigma _{_{{\lambda _1}}}^2 + \lambda _1^2\sigma _{_{{\lambda _2}}}^2 - 2{\lambda _1}(1 + {\lambda _2}){\sigma _{{\lambda _1}{\lambda _2}}}]/{{(1 + {\lambda _1} + {\lambda _2})}^4}{\text{ }}} \\ {D({y_{3\infty }}) = [\lambda _2^2\sigma _{_{{\lambda _1}}}^2 + {{(1 + {\lambda _1})}^2}\sigma _{_{{\lambda _2}}}^2 - 2{\lambda _2}(1 + {\lambda _1}){\sigma _{{\lambda _1}{\lambda _2}}}]/{{(1 + {\lambda _1} + {\lambda _2})}^4}{\text{ }}} \end{array}} \right. 。 $$ (3) 式(3)中：
$ \sigma _{_{{\lambda _1}}}^2 $ 、$ \sigma _{_{{\lambda _2}}}^2 $ 、$ {\sigma _{{\lambda _1}{\lambda _2}}} $ 分别为参数λ1、λ2的方差和它们之间的协方差。式(1)有4个独立参数，而用于估计参数的数据只有6组，自由度只有2，所以只能采用小样本t分布方法。同时由于比例数不可能小于0、大于1，所以应该采用截尾t分布。设自由度为k的t分布概率密度函数为
$ p(t,k) $ ，则截尾t分布概率密度函数pa(t, k)为：$$ {p}_{{\rm{a}}}(t,k)=p(t,k)/\tau \text{ }\text{，}\text{ }\tau ={\displaystyle {\int }_{0}^{1}p(t,k){\rm{d}}t} 。 $$ (4) 用式(4)进行区间估计，具体操作利用Excel的对应函数实现。设α为显著性水平，
$ {t_{\rm{l}}}{(k)_{\alpha /2}} $ 、$ {t_{\rm{r}}}{(k)_{\alpha /2}} $ 满足以下条件：$$ \int_0^{{t_{\rm{l}}}{{(k)}_{\alpha /2}}} {{p_{{\rm{a}}}}(t,k){\rm{d}}t = } \alpha /2 \text{，} \int_{1 - {t_{\rm{r}}}{{(k)}_{\alpha /2}}}^1 {{p_{{\rm{a}}}}(t,k){\rm{d}}t = } \alpha /2 。 $$ (5) 则极限真值
$ {Y_\infty } $ 的1−α双侧区间估计为：$$ [{y_\infty } - {t_{\rm{l}}}{(k)_{\alpha /2}}\sqrt {D({y_\infty })} ,{y_\infty } + {t_{\rm{r}}}{(k)_{\alpha /2}}\sqrt {D({y_\infty })} ] = ({y_\infty } - {\Delta _{{\rm{l}} \cdot \alpha /2}},{y_\infty } + {\Delta _{{\rm{r}} \cdot \alpha /2}}) 。 $$ (6) 若
$ {t_{\rm{l}}}{(k)_\alpha } $ 、$ {t_{\rm{r}}}{(k)_\alpha } $ 满足以下条件：$$ \int_0^{{t_{\rm{l}}}{{(k)}_\alpha }} {{p_{{\rm{a}}}}(t,k){\rm{d}}t = } \alpha \text{，} \int_{1 - {t_{\rm{r}}}{{(k)}_\alpha }}^1 {{p_{{\rm{a}}}}(t,k){\rm{d}}t = } \alpha 。 $$ (7) 则极限真值
$ {Y_\infty } ＞ {t_{\rm{l}}}{(k)_\alpha }\sqrt {D({y_\infty })} = {\Delta _{{\rm{l}} \cdot \alpha }} $ 的概率为1−α，同理，$ {Y_\infty } ＜ 1 - {t_{\rm{r}}}{(k)_\alpha }\sqrt {D({y_\infty })} = 1 - {\Delta _{{\rm{r}} \cdot \alpha }} $ 的概率为1−α。 -
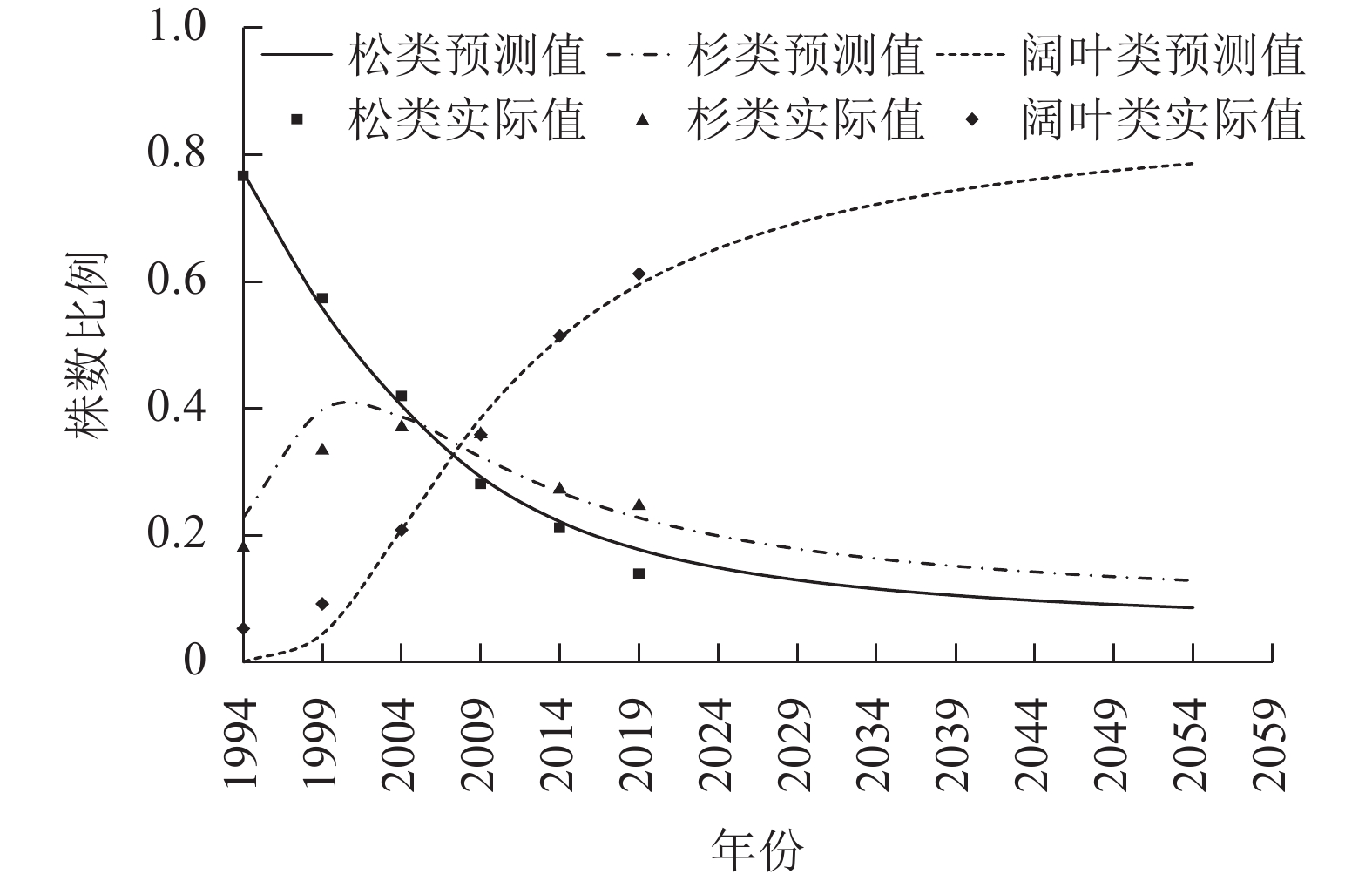
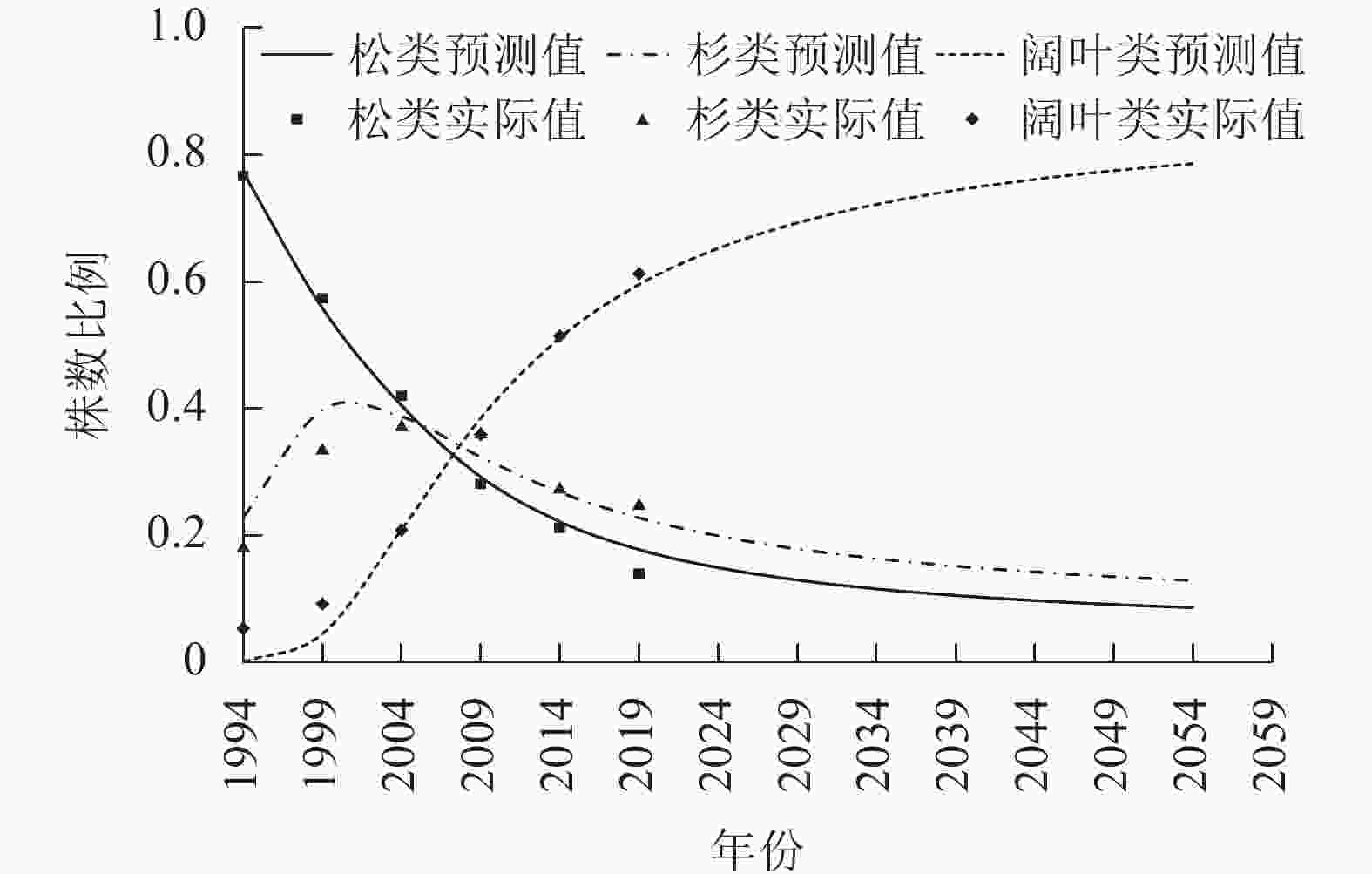
从表2和表3可以看出：株数比例和材积比例表现出了相同的规律，松类比例持续下降，阔叶类比例持续上升，杉类比例呈先上升后下降的变化趋势。
表 2 各树种组样木株数及其比例
Table 2. Numbers of total sample trees and their proportions by species group
年份 各树种组样木株数/株 各树种组样木株数比例 松类 杉类 阔叶类 合计 松类 杉类 阔叶类 合计 1994 6 418 1 926 460 8 804 0.729 0.219 0.052 1.000 1999 6 409 3 758 1 023 11 190 0.573 0.336 0.091 1.000 2004 7 270 6 462 3 606 17 338 0.419 0.373 0.208 1.000 2009 5 420 6 990 6 918 19 328 0.280 0.362 0.358 1.000 2014 4 251 5 539 10 328 20 118 0.211 0.275 0.514 1.000 2019 3 119 5 557 13 664 22 340 0.139 0.249 0.612 1.000 表 3 各树种组样木材积及其比例
Table 3. Volumes of total sample trees and their proportions by species group
年份 各树种组样木材积/m3 各树种组样木材积比例 松类 杉类 阔叶类 合计 松类 杉类 阔叶类 合计 1994 214.9 44.9 13.9 273.7 0.785 0.164 0.051 1.000 1999 223.0 82.5 30.5 336.0 0.664 0.245 0.091 1.000 2004 300.7 187.0 77.2 564.9 0.532 0.331 0.137 1.000 2009 268.5 193.3 161.5 623.3 0.431 0.310 0.259 1.000 2014 270.0 242.7 296.6 809.3 0.334 0.300 0.366 1.000 2019 250.8 303.1 466.5 1 020.4 0.246 0.297 0.457 1.000 -
从表4可见：松类和杉类的进界木株数在下降，阔叶类的进界木株数在上升，且总量远大于松类和杉类之和。5 a进界率和5 a采枯率分别为监测周期内发生的进界木总株数和采枯木总株数与初期的活立木总株数的比值。从表5可见：松类平均单株材积单调上升，杉类早期有波动，后期也是明显上升，阔叶类则是先下降后上升，树种组的总平均值也整体呈上升趋势。
表 4 各树种组的样地进界木和采枯木株数变化
Table 4. Numbers of ingrowth trees and numbers of felled and dead trees by species groups
时段 进界木株数/株 采枯木株数/株 5 a进界率/% 5 a采枯率/% 松类 杉类 阔叶类 合计 松类 杉类 阔叶类 合计 松类 杉类 阔叶类 松类 杉类 阔叶类 1994—1999 1 683 2 141 833 4 657 1 916 456 92 2 464 26.22 111.16 181.09 29.85 23.68 20.00 1999—2004 2 321 2 397 2 894 7 612 1 466 432 84 1 982 36.21 63.78 282.89 22.87 11.50 8.21 2004—2009 912 901 4 255 6 068 2 656 1 537 511 4 704 12.54 13.94 118.00 36.53 23.79 14.17 2009—2014 600 933 5 133 6 666 1 755 813 895 3 463 11.07 13.35 74.20 32.38 11.63 12.94 2014—2019 420 788 4 946 6 154 1 519 702 1 196 3 417 9.88 14.23 47.89 35.73 12.67 11.58 表 5 各树种组的平均单株材积变化
Table 5. Change of mean single tree volumes by species groups
年份 平均单株材积/m3 平均单株材积比值 松类 杉类 阔叶类 总平均 阔叶类/松类 阔叶类/杉类 杉类/松类 1994 0.033 5 0.023 3 0.030 2 0.031 1 0.901 1.295 0.696 1999 0.034 8 0.021 9 0.029 8 0.030 0 0.857 1.359 0.631 2004 0.041 4 0.028 9 0.021 4 0.032 6 0.518 0.740 0.700 2009 0.049 5 0.027 7 0.023 3 0.032 2 0.471 0.844 0.558 2014 0.063 5 0.043 8 0.028 7 0.040 2 0.452 0.655 0.690 2019 0.080 4 0.054 6 0.034 1 0.045 7 0.425 0.626 0.678 -
基于表2和表3数据，利用Stata 15.1拟合自约束模型，结果见表6、图1和图2。从图1和图2可知2019年之后40 a株数和材积的预测情况，株数比例模型和材积比例模型的
$ {\sigma _{{\lambda _1}{\lambda _2}}} $ 分别为0.239 4和0.051 9。表 6 自约束模型的拟合结果
Table 6. Fitting results of self-constrained models
建模数据 λ1 λ2 γ1 γ2 极限 决定系数 极限名 极限值/% R2 数值 株数比例 参数 1.718 0 21.745 8 −8.780 3 −56.058 8 $ {y_{1\infty }} $ 4.09 R1 2 0.996 7 标准差 0.168 4 4.833 8 0.896 5 4.617 1 $ {y_{2\infty }} $ 7.02 R2 2 0.989 3 P 0.00 0.00 0.00 0.00 $ {y_{3\infty }} $ 88.89 R3 2 0.992 9 材积比例 参数 1.185 8 7.743 6 −9.080 6 −49.356 3 $ {y_{1\infty }} $ 10.09 R1 2 0.996 4 标准差 0.123 0 1.983 6 1.131 2 5.678 8 $ {y_{2\infty }} $ 11.94 R2 2 0.987 0 P 0.00 0.00 0.00 0.00 $ {y_{3\infty }} $ 77.99 R3 2 0.986 1 说明：λ1、λ2、γ1、γ2为模型参数。 
图 1 各树种组的株数比例模型预测图
Figure 1. Graph of predicted percentages of the numbers of trees by species group
图 2 各树种组的材积比例模型预测图
Figure 2. Graph of predicted percentages of the volumes of trees by species group
-
从表7可见：区间估计的可靠性均为95%，即α统一取0.05。各t值均为自由度为2的标准化截尾t分布取值。双侧分布区间估计给出95%分布的下限和上限，例如松类极限值在1.50%~7.63%的概率为95%。单侧分布区间估计下限表示极限值大于这个下限的概率为95%，例如松类株数比例的极限值大于2.10%的概率为95%。同理单侧分布上限表示极限值小于这个上限的概率为95%，例如松类株数比例的极限值小于6.50%的概率为95%。
表 7 区间估计结果
Table 7. Results of interval estimation
模型 极限
名极限
值/%$ \sqrt {{D({y_\infty })}} $ τ 双侧分布
tl(2)α/2双侧分布
tr(2)α/2$ {\Delta _{{\rm{l}} \cdot \alpha /2}} $ $ {\Delta _{{\rm{r}} \cdot \alpha /2}} $ 双侧
分布
下限/%双侧
分布
上限/%单侧
分布
tl(2)α单侧
分布
下限/%单侧
分布
tr(2)α单侧
分布
上限/%株数
比例
模型$ {y_{1\infty }} $ 4.09 0.008 2 0.981 1 0.0150 0.0763 0.025 9 0.035 5 1.50 7.63 0.0210 2.10 0.0650 6.50 $ {y_{2\infty }} $ 7.02 0.013 5 0.982 5 0.0267 0.1286 0.043 5 0.058 4 2.67 12.86 0.0371 3.71 0.1099 10.99 $ {y_{3\infty }} $ 88.89 0.021 0 0.982 8 0.7983 0.9571 0.090 6 0.068 2 79.83 95.71 0.8272 82.72 0.9407 94.07 材积
比例
模型$ {y_{1\infty }} $ 10.07 0.020 4 0.980 4 0.0364 0.1890 0.064 3 0.088 3 3.64 18.90 0.0513 5.13 0.1609 16.09 $ {y_{2\infty }} $ 11.94 0.024 0 0.980 5 0.0435 0.2231 0.076 0 0.103 6 4.35 22.31 0.0612 6.12 0.1901 19.01 $ {y_{3\infty }} $ 77.99 0.043 0 0.980 5 0.5990 0.9176 0.180 9 0.137 7 59.90 91.76 0.6552 65.52 0.8851 88.51 -
本研究表明：松类的株数比例和材积比例均在持续单调下降，杉类均是先上升后下降，阔叶类均在快速单调增长。自约束模型很好地拟合了1994—2019年25 a间台州市乔木林3大树种组的株数比例和材积比例的变化情况。
松类、杉类、阔叶类株数比例的极限点估计分别为4.09%、7.02%、88.89%，材积比例为10.07%、11.94%、77.99%。按95%的可靠性，松类、杉类、阔叶类株数比例极限分布双侧区间估计分别为1.50%~7.63%、2.67%~12.86%、79.83%~95.71%，材积比例分别为3.64%~18.90%、4.35%~22.31%、59.90%~91.76%。单侧区间估计表明：松类、杉类、阔叶类株数比例极限分别大于2.10%、3.71%、82.72%，分别小于6.50%、10.99%、94.07%，材积比例分别大于5.13%、6.12%、65.52%，分别小于16.09%、19.01%、88.51%的可能性为95%。可见，阔叶树将占绝对优势，松类的比例将会是最低的，但永远不会消失，将以低比例一直存在，这与已有研究结论相似[18]，杉类的比例比松类略高，也将以低比例一直存在。
本研究还表明：松类的单株材积在单调上升，尤其近些年上升速度更快。杉类整体也在上升，且也是近年上升更快。阔叶类是先下降后上升，但上升速度比松类和杉类低，尤其和松类相比低更多。阔叶类与松类单株材积的比值，从1994年的0.901下降到2019年的0.425，阔叶类与杉木的比值从1994年的1.295下降到2019年的0.626，中间有波动。单株材积的变化规律导致了松类和杉类的株数极限比例分别小于各自的材积比例，而阔叶类正好相反，株数比例大于材积比例。
平均材积的变化差异主要原因在于进界木株数的差异。本研究表明：从1999—2004年这个复查期开始，松类的进界木株数持续大幅减少，进界率也在下降，造成松类小径阶林木的占比减少，导致松类的平均单株材积上升，杉类也有类似的情况，而阔叶类进界木持续增加，导致其平均单株材积增长缓慢。
-
本研究表明：以松类为优势的样地数从2004年的105个下降到2019年的41个，减少了60%；株数占比和材积占比分别从1994年的0.729和0.785单调下降至2019年的0.140和0.246，下降速度很快。松类资源下降的主要原因是松材线虫病的危害[19]。2019年，浙江省新增松材线虫病发生面积为29.88万hm2，新增病枯死松树达413.74万株[20]。从本研究可以看出，松类的采枯率高出阔叶类很多。随着疫情的加重和疫区的扩大，正常的商业采伐和抚育采伐比例越来越小，而因疫情死亡的比例越来越高。因为松类树种易受疫情危害，所以松类人工造林急剧下降。由于林分整体密度在增加，整体竞争逐步加剧，马尾松等阳性树种在正常的自然演替中处于相对劣势地位，这也导致了随着演替的进程马尾松枯死现象的增多[21−24]。
杉类树种的株数比例及材积比例在1994至2004年间增加，其后缓慢减少。杉木优势的样地数由1994年的22个增加至2004年的54个，而同时期的松类样地数变化并不大，说明这个时期台州市造林以杉类为首选。此后样地数略有下降。杉类中杉木占绝大部分，近年由于经济效益的下降，杉木造林不多。但杉木具有萌芽的特性，样地数减少的速度比松类低，进界率近年也比松类略高，但比阔叶类低很多。杉类由于不受松材线虫病的危害，采枯率比松类低很多，但略高于阔叶类。
阔叶类占优势的样地数从1994年的7个增加到2019年的95个，株数比例和材积比例分别从1994年的0.052和0.051上升到2019年的0.612和0.457。进界木株数绝对值从1994年的833株上升到2019年的4 946株，阔叶类进界率是松类的4.8倍以上，对比杉类，除了1994—1999是1.6倍外，其余是3.3倍以上。而最近3个监测期的采枯率低于松类的2/5。阔叶林资源的增加主要有以下几个方面：①为了公益林建设，大面积的封山育林和林种结构调整，使得阔叶幼林和部分灌木林发展成为阔叶林；②随着近自然经营的兴起，出现了大量的“针改阔”，通过针叶树采伐或死亡后补植阔叶树种或促进阔叶树幼树生长的形式调整林分的树种组成[25]；③随着人们对森林生态系统认识的提高，以及对病虫害的考虑，有意识地增加了造林时对阔叶树种的选择[26]；④松材线虫病危害导致了松林资源的损失，但同时为阔叶林资源的发展提供了空间；⑤随着演替的不断进行，密度增大，马尾松等阳性先锋树种的竞争力下降，并逐渐被淘汰，阔叶树种的优势逐渐扩大，随之达到树种结构的平衡并趋于稳定[21−24]。
一般来说常绿阔叶林是中亚热带的顶级森林群落，具有最好的生态功能，但适量的松类和杉类树种有利于生物多样性的保持和生态功能的优化。在控制松材线虫病的前提下，松类是很好的景观树种和用材树种，杉类也是很好的用材树种，尤其是大径材培育的优先选择树种。本研究表明：松类和杉类的比例虽然在下降，但始终会以一定的比例存在而不会消亡。
虽然3个树种组的变化各异，但3个树种组的总株数和总材积均在稳定增长。乔木林的总样地数从2004年开始基本稳定，但总株数和总材积却在持续增长，说明林分的相对密度在持续增大。需引起重视的是阔叶类采枯木在快速增加，这其中采伐木的比例不大，主要是由于密度过大导致枯死增加，这说明需要适当加强阔叶林的抚育。
-
本研究是一个区域的乔木林树种结构变化规律，需要大量的数据支撑。由于2个原因没有将数据分为建模和检验2个部分：一是乔木林样地不足200个，如果分成2个部分则会造成建模和检验的数据都不够充分，得不到可靠的结果；二是6期数据的乔木林样地并不是固定不变的，前3期每期样地都有1/3移动，后面虽然不再移动，但样地的地类有变化，有的从乔木林变为其他地类，有的从其他地类变成乔木林，乔木林样地不固定，乔木林总样地数也在变化，这给数据建模和检验造成了麻烦。所以本研究采用基于建模结果进行可靠性理论分析的方法。
式(1)具有4个独立参数，而建模数据只有6组，自由度只有2，所以本研究采用自由度为2的小样本t分布方法进行极限分布的区间估计。由于比例数据不可能小于0、大于1，所以又进行了截尾调整，即采用了截尾t分布模型。松类的株数比例极限分布95%的可能性在1.50%~7.63%，大于2.10%的可能性为95%，是具有实际参考价值的。
-
非线性方程组自约束树种结构模型适用于大区域树种组结构的模拟和预测。它反映区域的整体变化情况，但不能反映局部细节。25 a间台州市乔木林资源总量在持续增加，但呈现“针减阔增”的现象：①受松材线虫病危害以及自然演替中的不利因素影响松类比例持续降低；②受市场因素影响，杉类的比例在1999—2004年间达到最大值后开始下降，但幅度比松类小；③阔叶类的比例呈现持续、稳定增加趋势，将占绝对优势。松类和杉类的比例虽然在下降，但最终会稳定在一定的比例而不会消亡。这表明台州市森林生态系统正朝着以阔叶树种为主、结构更合理的植被群落方向正向演替。
Simulation and prediction of tree species composition change of forests in Taizhou City
-
摘要:
目的 阐明浙江省台州市乔木林1994—2019年25 a间3个树种组(松类、杉类和阔叶类)之间的结构变化规律以及未来可能的变化趋势，为今后森林结构调控提供依据。 方法 基于6期台州市森林资源连续清查固定样地数据，建立非线性方程组自约束树种结构模型，模拟25 a来3个树种组的株数比例和材积比例变化规律，并预测其变化趋势。 结果 ①台州市松类受松材线虫Bursaphelenchus xylophilus病以及自然演替中的不利因素影响其比例持续降低，杉类的比例在1999—2004年达到最大值后缓慢下降，阔叶类比例呈现持续快速稳定增加的趋势；②经预测，松类、杉类和阔叶类各树种组林木株数占乔木林总株数的比例将分别从2019年的14.00%、24.90%和61.20%趋向于极限4.09%、7.02%和88.89%，占乔木林总材积的比例将从2019年的24.60%、29.70%和45.70%趋向于极限10.07%、11.94%和77.99%。 结论 整体上，台州市过去25 a间乔木林资源总量持续增加，树种结构“针减阔增”，朝着结构更合理的顶级植被群落方向演替。松类和杉类的比例虽然在下降，但最终会稳定在一定的比例而不会消亡。本研究提出的非线性方程组自约束树种结构模型对乔木林的株数比例和材积比例模拟具有较好的适应性，对变化趋势的预测具有较好的合理性。图2表7参26 -
关键词:
- 森林资源连续清查 /
- 树种结构变化 /
- 非线性方程组自约束树种结构模型 /
- 预测
Abstract:Objective This study, with an exploration of the composition changes among three tree species groups of pine, fir and broadleaf within 25 years between 1994 and 2019 in Taizhou City, Zhejiang Province, is aimed to investigate the possible future change trends so as to provide theoretic basis for future forest composition regulation. Method Based on six batches of continuous forest inventory data collected in Taizhou City, a self-constrained model with nonlinear equations was developed to simulate the proportion of numbers of trees and proportion of stem volume of three species over 25 years, and predict their future trends. Result (1) As a result of Bursaphelenchus xylophilus and natural succession, the proportion of pine species in Taizhou suffered a decrease, that of fir species reached a maximum between 1999 and 2004 and then decreased slowly whereas that of broadleaf species enjoyed a continuous and steady increase; (2) The proportions of trees of the pine, fir and broadleaf groups accounting for the total numbers will change from 14.00%, 24.90% and 61.20% in 2019 to 4.09%, 7.02% and 88.89% eventually, whereas the proportions of the three groups in terms of volumes will change from 24.60%, 29.70% and 45.70% in 2019 to 10.07%, 11.94% and 77.99% eventually. Conclusion The total amount of forest resources in Taizhou increased in the past 25 years and, with a structural change of tree species featured as “an increase in broadleaf and a decrease in coniferous forests”, it’s gradually developing into a top vegetation community. Although the proportion of pine and fir trees decreases continuously, it will eventually stabilize at a certain proportion instead of going extinct. Also, the proposed self-constrained model of nonlinear equations demonstrated good performance in the simulation of tree number proportion and volume proportion of forests. [Ch, 2 fig. 7 tab. 26 ref.] -
图 1 各树种组的株数比例模型预测图
Figure 1 Graph of predicted percentages of the numbers of trees by species group
图 2 各树种组的材积比例模型预测图
Figure 2 Graph of predicted percentages of the volumes of trees by species group
表 1 乔木林各期树种组的胸径统计
Table 1. DBH statistics of tree species groups in different stages of arbor forest
年份 树种组 样地数/个 胸径/cm 最大值 均值 中位数 标准差 1994 松类 110 29.8 9.5 8.5 3.78 杉类 22 24.0 8.7 8.2 3.03 阔叶类 7 36.2 8.8 7.5 3.88 1999 松类 103 32.8 9.7 8.9 3.84 杉类 42 28.5 8.6 7.8 3.16 阔叶类 10 39.3 8.6 7.2 3.75 2004 松类 105 31.3 10.3 9.4 4.20 杉类 54 34.6 9.4 8.5 3.57 阔叶类 24 40.5 7.8 6.8 3.08 2009 松类 81 33.2 10.9 9.8 4.62 杉类 46 39.7 10.0 9.1 3.95 阔叶类 54 39.6 8.1 7.0 3.32 2014 松类 61 34.2 11.8 10.5 5.33 杉类 42 44.0 10.6 9.6 4.47 阔叶类 82 44.4 8.7 7.5 3.81 2019 松类 41 37.6 12.7 10.4 6.18 杉类 47 48.7 11.3 9.8 5.06 阔叶类 95 45.9 9.2 7.5 4.18 
下载: 导出CSV
表 2 各树种组样木株数及其比例
Table 2. Numbers of total sample trees and their proportions by species group
年份 各树种组样木株数/株 各树种组样木株数比例 松类 杉类 阔叶类 合计 松类 杉类 阔叶类 合计 1994 6 418 1 926 460 8 804 0.729 0.219 0.052 1.000 1999 6 409 3 758 1 023 11 190 0.573 0.336 0.091 1.000 2004 7 270 6 462 3 606 17 338 0.419 0.373 0.208 1.000 2009 5 420 6 990 6 918 19 328 0.280 0.362 0.358 1.000 2014 4 251 5 539 10 328 20 118 0.211 0.275 0.514 1.000 2019 3 119 5 557 13 664 22 340 0.139 0.249 0.612 1.000
下载: 导出CSV
表 3 各树种组样木材积及其比例
Table 3. Volumes of total sample trees and their proportions by species group
年份 各树种组样木材积/m3 各树种组样木材积比例 松类 杉类 阔叶类 合计 松类 杉类 阔叶类 合计 1994 214.9 44.9 13.9 273.7 0.785 0.164 0.051 1.000 1999 223.0 82.5 30.5 336.0 0.664 0.245 0.091 1.000 2004 300.7 187.0 77.2 564.9 0.532 0.331 0.137 1.000 2009 268.5 193.3 161.5 623.3 0.431 0.310 0.259 1.000 2014 270.0 242.7 296.6 809.3 0.334 0.300 0.366 1.000 2019 250.8 303.1 466.5 1 020.4 0.246 0.297 0.457 1.000
下载: 导出CSV
表 4 各树种组的样地进界木和采枯木株数变化
Table 4. Numbers of ingrowth trees and numbers of felled and dead trees by species groups
时段 进界木株数/株 采枯木株数/株 5 a进界率/% 5 a采枯率/% 松类 杉类 阔叶类 合计 松类 杉类 阔叶类 合计 松类 杉类 阔叶类 松类 杉类 阔叶类 1994—1999 1 683 2 141 833 4 657 1 916 456 92 2 464 26.22 111.16 181.09 29.85 23.68 20.00 1999—2004 2 321 2 397 2 894 7 612 1 466 432 84 1 982 36.21 63.78 282.89 22.87 11.50 8.21 2004—2009 912 901 4 255 6 068 2 656 1 537 511 4 704 12.54 13.94 118.00 36.53 23.79 14.17 2009—2014 600 933 5 133 6 666 1 755 813 895 3 463 11.07 13.35 74.20 32.38 11.63 12.94 2014—2019 420 788 4 946 6 154 1 519 702 1 196 3 417 9.88 14.23 47.89 35.73 12.67 11.58
下载: 导出CSV
表 5 各树种组的平均单株材积变化
Table 5. Change of mean single tree volumes by species groups
年份 平均单株材积/m3 平均单株材积比值 松类 杉类 阔叶类 总平均 阔叶类/松类 阔叶类/杉类 杉类/松类 1994 0.033 5 0.023 3 0.030 2 0.031 1 0.901 1.295 0.696 1999 0.034 8 0.021 9 0.029 8 0.030 0 0.857 1.359 0.631 2004 0.041 4 0.028 9 0.021 4 0.032 6 0.518 0.740 0.700 2009 0.049 5 0.027 7 0.023 3 0.032 2 0.471 0.844 0.558 2014 0.063 5 0.043 8 0.028 7 0.040 2 0.452 0.655 0.690 2019 0.080 4 0.054 6 0.034 1 0.045 7 0.425 0.626 0.678
下载: 导出CSV
表 6 自约束模型的拟合结果
Table 6. Fitting results of self-constrained models
建模数据 λ1 λ2 γ1 γ2 极限 决定系数 极限名 极限值/% R2 数值 株数比例 参数 1.718 0 21.745 8 −8.780 3 −56.058 8 $ {y_{1\infty }} $ 4.09 R1 2 0.996 7 标准差 0.168 4 4.833 8 0.896 5 4.617 1 $ {y_{2\infty }} $ 7.02 R2 2 0.989 3 P 0.00 0.00 0.00 0.00 $ {y_{3\infty }} $ 88.89 R3 2 0.992 9 材积比例 参数 1.185 8 7.743 6 −9.080 6 −49.356 3 $ {y_{1\infty }} $ 10.09 R1 2 0.996 4 标准差 0.123 0 1.983 6 1.131 2 5.678 8 $ {y_{2\infty }} $ 11.94 R2 2 0.987 0 P 0.00 0.00 0.00 0.00 $ {y_{3\infty }} $ 77.99 R3 2 0.986 1 说明：λ1、λ2、γ1、γ2为模型参数。
下载: 导出CSV
表 7 区间估计结果
Table 7. Results of interval estimation
模型 极限
名极限
值/%$ \sqrt {{D({y_\infty })}} $ τ 双侧分布
tl(2)α/2双侧分布
tr(2)α/2$ {\Delta _{{\rm{l}} \cdot \alpha /2}} $ $ {\Delta _{{\rm{r}} \cdot \alpha /2}} $ 双侧
分布
下限/%双侧
分布
上限/%单侧
分布
tl(2)α单侧
分布
下限/%单侧
分布
tr(2)α单侧
分布
上限/%株数
比例
模型$ {y_{1\infty }} $ 4.09 0.008 2 0.981 1 0.0150 0.0763 0.025 9 0.035 5 1.50 7.63 0.0210 2.10 0.0650 6.50 $ {y_{2\infty }} $ 7.02 0.013 5 0.982 5 0.0267 0.1286 0.043 5 0.058 4 2.67 12.86 0.0371 3.71 0.1099 10.99 $ {y_{3\infty }} $ 88.89 0.021 0 0.982 8 0.7983 0.9571 0.090 6 0.068 2 79.83 95.71 0.8272 82.72 0.9407 94.07 材积
比例
模型$ {y_{1\infty }} $ 10.07 0.020 4 0.980 4 0.0364 0.1890 0.064 3 0.088 3 3.64 18.90 0.0513 5.13 0.1609 16.09 $ {y_{2\infty }} $ 11.94 0.024 0 0.980 5 0.0435 0.2231 0.076 0 0.103 6 4.35 22.31 0.0612 6.12 0.1901 19.01 $ {y_{3\infty }} $ 77.99 0.043 0 0.980 5 0.5990 0.9176 0.180 9 0.137 7 59.90 91.76 0.6552 65.52 0.8851 88.51
下载: 导出CSV
-
[1] ZELLER L, LIANG Jingjing, PRETZSCH H. Tree species richness enhances stand productivity while stand structure can have opposite effects, based on forest inventory data from Germany and the United States of America [J]. Forest Ecosystems, 2018, 5(1): 36 − 52. [2] 薛建辉. 森林生态学[M]. 修订版. 北京: 中国林业出版社, 2006: 165 − 169. XUE Jianhui. Forest Ecology [M]. Revised ed. Beijing: China Forestry Publishing House, 2006: 165 − 169. [3] TAYLOR A R, CHEN H Y H, van DAMME L. A review of forest succession models and their suitability for forest management planning [J]. Forest Science, 2009, 55(1): 23 − 36. [4] Jr SHUGART H H, CROW T R, HETT J M. Forest succession models: a rationale and methodology for modeling forest succession over large regions [J]. Forest Science, 1973, 19(3): 203 − 212. [5] PACALA S W, CANHAM C D, SAPONARA J, et al. Forest models defined by field measurements: estimation, error analysis and dynamics [J]. Ecological Society of America, 1996, 66(1): 1 − 43. [6] MEDLYN B E, BERBIGIER P, CLEMENT R, et al. Carbon balance of coniferous forests growing in contrasting climates: model-based analysis [J]. Agricultural and Forest Meteorology, 2005, 131(1/2): 97 − 124. [7] IBROM A, JARVIS P G, CLEMENT R, et al. A comparative analysis of simulated and observed photosynthetic CO2 uptake in two coniferous forest canopies [J]. Tree Physiology, 2006, 26(7): 845 − 864. [8] 桑卫国, 李景文. 小兴安岭南坡红松林动态模拟[J]. 生态学报, 1998, 18(1): 38 − 47. SANG Weiguo, LI Jingwen. Dynamics modeling of korean pine forest in southern lesser Xingan mountains of China [J]. Acta Ecologica Sinica, 1998, 18(1): 38 − 47. [9] SHUGART H H. A Theory of Forest Dynamics: the Ecological Implications of Forest Succession Models [M]. Berlin: Springer-Verlag, 1984. [10] MLADENOFF D J. LANDIS and forest landscape models [J]. Ecological Modelling, 2004, 180(1): 7 − 19. [11] YEMSHANOV D, PERERA A H. A spatially explicit stochastic model to simulate boreal forest cover transitions: general structure and properties [J]. Ecological Modelling, 2002, 150(1/2): 189 − 209. [12] VANCLAY J K. Modeling Forest Growth and Yield: Appli-cations to Mixed Tropical Forests [M]. Wallingford: CAB International, 1994. [13] KORZUKHIN M D, TER-MIKAELIAN M, WAGNER R G. Process versus empirical models: which approach forforest ecosystem management? [J]. Canadian Journal of Forest Research, 1996, 26(5): 879 − 887. [14] 王冬米, 邱智敏, 陈征海, 等. 台州市乡土木本植物资源调查与特征分析[J]. 浙江林业科技, 2017, 37(6): 51 − 56. WANG Dongmi, QIU Zhimin, CHEN Zhenghai, et al. Native woody plant resources and their characteristics in Taizhou [J]. Journal of Zhejiang Forestry Science and Technology, 2017, 37(6): 51 − 56. [15] 陶吉兴, 张国江, 季碧勇. 森林资源一类清查与二类调查数据控制与融合研究[J]. 浙江林业科技, 2016, 36(6): 8 − 14. TAO Jixing, ZHANG Guojiang, JI Biyong. Research on data control and fusion of continuous forest inventory and forest management inventory [J]. Journal of Zhejiang Forestry Science and Technology, 2016, 36(6): 8 − 14. [16] ZELLER L, PRETZSCH H. Effect of forest structure on stand productivity in central European forests depends on developmental stage and tree species diversity [J]. Forest Ecology and Management, 2019, 434: 193 − 204. [17] KAZMIERCZAK M, WIEGAND T, HUTH A. A neutral vs. non-neutral parametrizations of a physiological forest gap model [J]. Ecological Modelling, 2014, 288: 94 − 102. [18] 戴冬, 彭楚才, 黄鑫, 等. 鄂中地区马尾松人工林群落演替特征研究[J]. 林业科学研究, 2019, 32(6): 48 − 55. DAI Dong, PENG Chucai, HUANG Xin, et al. Community succession characteristics of Pinus massoniana plantation in central Hubei Province [J]. Forest Research, 2019, 32(6): 48 − 55. [19] 李兰英, 高岚, 温亚利, 等. 松材线虫病对浙江省环境影响经济评价[J]. 林业经济, 2009(8): 68 − 73. LI Lanying, GAO Lan, WEN Yali, et al. Environmental impact eco-assessment of pine wood nematode in Zhejiang Province [J]. Forestry Economics, 2009(8): 68 − 73. [20] 潘佳亮, 姚翰文, 董瀛谦, 等. 2019年全国松材线虫病疫情分析[J]. 中国森林病虫, 2021, 40(1): 32 − 37. PAN Jialiang, YAO Hanwen, DONG Yingqian, et al. Analysis of the epidemic situation of pine wilt disease in China in 2019 [J]. Forest Pest and Disease, 2021, 40(1): 32 − 37. [21] 彭少麟. 鼎湖山人工马尾松第1代与自然更新代生长动态比较[J]. 应用生态学报, 1995, 6(1): 11 − 13. PENG Shaolin. Comparison of the growth dynamics of the 1st generation and the natural renewal generation of artificial Pinus massoniana in Dinghu Mountain [J]. Chinese Journal of Applied Ecology, 1995, 6(1): 11 − 13. [22] 丁圣彦, 宋永昌. 浙江天童常绿阔叶林演替系列优势种光合生理生态的比较[J]. 生态学报, 1999, 19(3): 318 − 323. DING Shengyan, SONG Yongchang. The comparation of photosynthesis physi-ecology of evergreen broad-leaved forest of Tianton National Forest Park in Zhejiang Province, China [J]. Acta Ecologica Sinica, 1999, 19(3): 318 − 323. [23] 汪殿蓓, 暨淑仪, 陈飞鹏, 等. 深圳南山区天然森林群落多样性及演替现状[J]. 生态学报, 2003, 23(7): 1415 − 1422. WANG Dianpei, JI Shuyi, CHEN Feipeng, et al. A study on the species diversity and succession situation of natural forest communities in Nanshan District, Shenzhen City [J]. Acta Ecologica Sinica, 2003, 23(7): 1415 − 1422. [24] COELHO P A, SANTOS P F, de PAIVA PAULA E, et al. Tree succession across a seasonally dry tropical forest and forest-savanna ecotone in northern Minas Gerais, Brazil [J]. Journal of Plant Ecology, 2016, 10(5): 859 − 868. [25] 李婷婷, 陆元昌, 庞丽峰, 等. 杉木人工林近自然经营的初步效果[J]. 林业科学, 2014, 50(5): 90 − 100. LI Tingting, LU Yuanchang, PANG Lifeng, et al. Initial effect of close-to-nature management of Chinese fir plantation [J]. Scientia Silvae Sinicae, 2014, 50(5): 90 − 100. [26] 詹学齐. 马尾松公益林林冠下套种阔叶树后林分生态功能评价研究[J]. 福建师范大学学报(自然科学版), 2018, 34(3): 71 − 77. ZHAN Xueqi. Evaluation of ecological benefits for Pinus massoniana stand interplanting hardwood tree species after twenty years [J]. Journal of Fujian Normal University (Natural Sciences Edition), 2018, 34(3): 71 − 77. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20220341
点击查看大图
图(2) / 表(7)
计量
- 文章访问数: 368
- HTML全文浏览量: 58
- PDF下载量: 33
- 被引次数: 0
