-
空间异质性（spatial heterogeneity）普遍存在于景观的各个尺度上[1]。由于森林生态系统中环境因素（地形、地貌、光照、水分和土壤养分等）分布的不均匀性，以及长期存在于种群间和个体间的竞争排斥作用，使得植被个体、种群和群落在不同尺度上呈现出空间异质性[2]。地统计方法是分析空间异质性的有效方法。NICOTRA等[3]采用地统计方法研究哥斯达黎加东北部热带雨林受空间自相关控制的有效光与森林更新之间的关系。ABBOTT等[4]研究了土壤微生物的空间异质性与植被竞争之间的关系。曾春阳等[2]为评价江西枫树山林场杉木Cunninghamia lanceolata林的立地质量，利用地统计方法分析杉木立地指数的空间分布。杜华强等[5]利用半方差函数模型分析了天目山常绿阔叶林土壤有机质、全氮、有效氮、有效磷和速效钾的空间异质性。在环境因素一定的条件下，竞争是产生植被个体属性差异的重要因素[6]，但是长期以来，植物竞争研究侧重于分析植物种内和种间竞争关系[7-11]，较少关注植物竞争的空间异质性。毛竹Phyllostachys edulis是中国数量最多，分布面积最大，用途最广泛，价值最高的经济竹种[12]。毛竹具有速生的特点，导致毛竹林内个体的竞争十分激烈。毛竹林依赖多年生竹鞭发笋进行更新，形成异龄纯林结构特征，更加剧了毛竹林种内的竞争。近年来，对毛竹的竞争开展了大量研究，包括毛竹之间的竞争关系[13]、毛竹与生物量的竞争关系[14]、毛竹种群向常绿阔叶林的扩张[15]以及改进竞争指数[16]。但是，这些研究较少关注毛竹竞争依赖距离尺度的空间异质性及其动态特征。为此，本研究利用2009-2015年浙江天目山国家级自然保护区长期未受人为干预的毛竹林固定样地调查数据，以基于Voronoi图的Hegyi竞争指数、半方差函数拟合、各向异性与空间自相关分析、经验贝叶斯克里金插值等空间分析技术，定量地研究毛竹林竞争空间格局特征及其动态变化，确定毛竹竞争变程距离尺度，揭示毛竹竞争空间格局变异与地形因子的关系，为毛竹林经营中调控竞争关系提供理论依据。
HTML
-
浙江天目山国家级自然保护区位于浙江省西北部杭州市临安区境内的西天目山（119°23′47″~119°28′55″N），总面积为1 050 hm2，主峰海拔为1 506 m。年平均气温为8.8~14.8 ℃，年降水量为1 390.0~ 1 870.0 mm，相对湿度为76%~81%。该自然保护区受海洋暖湿气候影响，森林植被丰茂，植被分布呈垂直带状分布。毛竹林主要分布在海拔350~900 m的地区，区内的毛竹林很少有人为干扰，毛竹生长状况接近自然状态[17]。
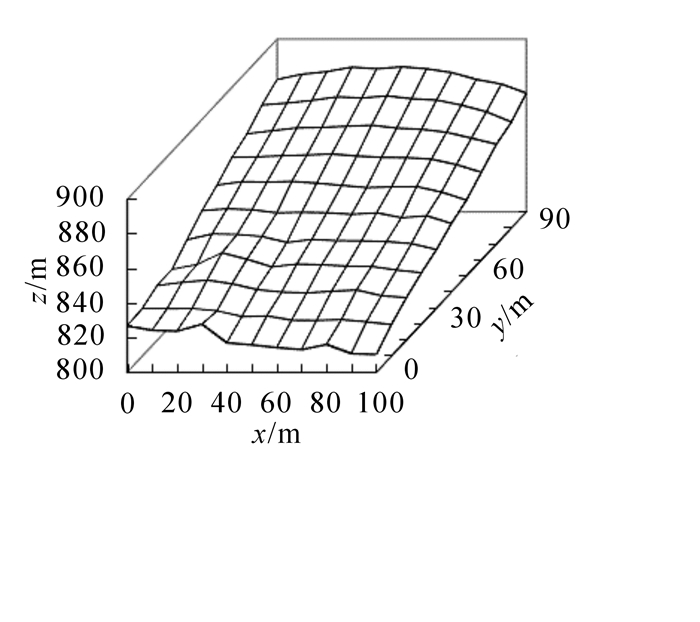
2009年7月，在浙江天目山国家级自然保护区内，选择毛竹林典型地段，建立了1块大小为100 m × 100 m的固定样地，样地中心海拔为840 m，主坡向南偏东30°，最高处海拔为886 m，最低处海拔为810 m，高差为76 m，平均坡度为37°（图 1）。利用南方全站仪NTS355设定样地的坐标轴，采用相邻网格法将整个样地划分为100个10 m × 10 m的样方。用全站仪测定样地内每株毛竹的基部三维坐标（x，y，z）。每木调查测定毛竹胸径、竹高、年龄、枝下高、冠幅、弯曲状态等因子。2010-2015年，每年4月对毛竹林固定样地内新笋进行地径调查，7月对样地进行复查，记录各年毛竹更新情况。2009, 2011，2013和2015年为小年，2010，2012和2014年为大年。
Figure 1. 3D map of the 1 hm2 plot
-
为了避免样地界外毛竹可能是样地内毛竹的最近邻竹的情况，对样地进行边缘校正。采用八邻域平移式边缘校正，使样地内所有毛竹作为对象竹和竞争竹处理，进行竞争指数计算。
-
用Voronoi图确定由对象竹与竞争竹组成的竞争单元[10]。根据Voronoi图特征，每个Voronoi多边形内仅包含1株毛竹。对象竹所在的Voronoi多边形的相邻Voronoi多边形内的毛竹就是竞争竹。可以看出，对象竹的竞争竹株数与相邻Voronoi多边形的个数相等（图 2）。
Figure 2. Competition unit based on Voronoi diagram
毛竹竞争关系分析选择常用的Hegyi竞争指数，计算公式详见参考文献[7]。
-
半方差函数（semivariogram）是研究区域化变量空间异质性的常用地统计学方法，其计算要求数据符合正态分布[18]，若不符合正态分布则进行博克斯-考克斯（Box-Cox）转换，使其呈正态分布后进行半方差函数计算。半方差函数计算公式为：
式（1）中：γ（$\hat{h} $）为半方差γ（h）的估计值；h为样本间距；N（h）是间距为h的样本对；Z（xi）和Z（xi+h）是区域化变量Z（x）在点xi和xi+h上的值。
根据半方差函数理论模型的参数块金值C0，变程A和基台值C0+C，可以推知空间格局的类型及评估变量的随机性和结构性所占的成分，测定空间依赖范围。空间结构比C/（C0+C）反映了空间变异程度，可划分为3个级别：微弱（＜25%），中等（25%~75%），强烈（＞75%）[2]。
微地形对毛竹个体分布有直接影响[19]，所以毛竹在不同方向上的竞争空间格局可能存在各向异性。绘制各年毛竹竞争指数空间变异半方差图，若不同方向所得最大变程不同，则说明研究对象具有各向异性特征[20]，选择拥有最大变程A0方向作为半方差模型优势方向。
本研究的半方差函数理论模型数据处理采用GS+软件完成。
-
通过空间自相关分析可确定变量是否在空间上相关及相关程度如何。Moran’s I指数是用于全局衡量位置接近性和属性相似的数量指标，能够很好地表现总体空间趋势，对空间自相关进行全局评估。其详细计算公式参见文献[21]。Moran’s I指数的取值在-1和1之间：小于0表示负相关，等于0表示不相关，大于0表示正相关。
为直观了解各年毛竹竞争空间格局动态特征，采用经验贝叶斯克里金插值法绘制竞争指数空间分布格局图。本研究按子集大小500，重叠系数1以及1 000次模拟参数设定在Arc GIS 10.2软件进行经验贝叶斯克里金插值，对生成的竞争指数空间分布格局图进行栅格化处理，并用栅格计算器将当年竞争指数插值栅格图减上年竞争指数插值栅格图得到年度毛竹竞争指数增量栅格数据，增量为正加剧竞争，增量为负缓和竞争，再进行竞争格局变化统计分析，获得竞争加剧面积与竞争缓和面积，判断各年度竞争变化趋势。
2.1. 边缘校正
2.2. 竞争单元确定与竞争指数计算
2.3. 半方差函数和空间异质性
2.4. 竞争指数空间自相关和经验贝叶斯克里金插值
-
从表 1可以看出：2009-2015年，天目山毛竹林竞争指数为1.203~18.442，平均值为6.415。各年竞争指数变异系数为35.62%~40.80%，平均变异系数为38.69%。表明毛竹竞争指数具有中等程度的空间离散。
年份 株数/株 竞争指数 偏度 P值 P*值 平均值 最小值 最大值 变异系数/% 2009 5 406 6.579 1.203 14.599 35.62 1.071 0.000 0.564 2010 6 238 6.569 1.203 17.582 38.09 1.305 0.000 0.682 2011 5 906 6.279 1.488 17.479 37.13 1.350 0.000 0.441 2012 5 964 6.355 1.522 17.737 39.40 1.406 0.000 0.488 2013 5 690 6.212 1.587 17.701 39.02 1.411 0.000 0.161 2014 6 032 6.432 1.618 18.442 40.80 1.453 0.000 0.100 2015 5 942 6.477 1.333 18.426 40.69 1.404 0.000 0.127 平均 6.415 1.422 17.440 38.69 说明：P是转换前竞争指数的正态检验概率值，P*是经正态转换后竞争指数的正态检验概率值 Table 1. Statistical summary of competition index in each year
经过数据正态性检验，各年竞争指数分布均正偏，不符合正态分布要求。为此，对竞争指数进行统一λ参数的正态转换，经检验各年竞争指数符合正态分布要求。
-
根据各年毛竹点坐标和竞争指数，进行竞争指数空间自相关Moran’s I指数计算并作显著性检验（表 2）。从表 2可见：各年毛竹竞争指数空间分布均呈现全局一般正向自相关（P＜0.001）。Moran’s I值为0.197 5~0.251 7，说明毛竹竞争指数呈现竞争聚集分布，即竞争强度相近的竹子相邻分布。
年份 I值 P值 2009 0.218 0 < 0.001 2010 0.197 5 < 0.001 2011 0.251 7 < 0.001 2012 0.220 7 < 0.001 2013 0.226 5 < 0.001 2014 0.220 7 < 0.001 2015 0.2140 < 0.001 Table 2. Spatial autocorrelation of competition index of bamboo in each year
为了直观分析毛竹竞争指数呈现空间聚集分布特征，对经正态转化的竞争指数通过经验贝叶斯克里金插值法，绘制出各年毛竹林竞争指数插值图（图 3）。由图 3可见：样地内毛竹竞争格局总体上呈现上部竞争强度大、下部竞争强度小的特征。根据样地的海拔高度（810~886 m），划分为3个海拔范围：下部（810~835 m），中部（835~860 m），上部（860~886 m），对不同海拔范围的毛竹胸径进行分区统计分析（表 3）。结合图 3和表 3可见：随着坡位海拔上升，毛竹平均胸径减小而变异系数增大。毛竹竞争强度随海拔上升逐渐增强且竞争强度相近的毛竹从点状分布格局逐渐形成以水平带状、垂直复杂斑块状分布格局，符合毛竹竞争指数空间异质性与竞争聚集分布特征。样地下部毛竹株数少，对象竹与竞争竹的竞争距离大，平均胸径大且变异系数小，缓和了竞争，呈现弱竞争聚集格局；样地上部毛竹株数多，对象竹与竞争竹的竞争距离小，胸径随海拔上升而平均胸径变小，但变异系数增大，加剧了竞争压力，呈现强竞争聚集格局。
Figure 3. Spatial distribution pattern of competition index by Empirical Bayesian Kriging
海拔范围 胸径均值/cm 最小值/cm 最大值/cm 变异系数/% 株数/株 上部 10.40 3.3 19.3 18.29 2 932 中部 10.87 1.2 17.0 15.21 3 979 下部 11.34 3.1 22.0 14.22 2 521 说明：株数包含各年死亡毛竹 Table 3. Statistical summary of diameter at breast height of bamboo in altitude
-
采用半方差函数对天目山毛竹各年竞争指数进行拟合，分析竞争指数的空间异质性。根据决定系数R2确定最优理论模型（表 4）。结果表明：各年毛竹竞争指数可用指数模型进行描述，各模型决定系数R2为0.971~0.979。结构比为81.78%~89.79%，均在75%以上，表明毛竹竞争指数空间变异强烈，引起空间变异的主要因素是结构性因素。各年毛竹竞争指数各向异性优势方位角为88°，即东西方向是维持毛竹稳定竞争关系的方向。各年毛竹竞争指数半方差模型变程存在与大小年相反的长短交替现象，最大值为4.581 m（2011年），最小值为4.059 m（2014年），平均为4.306 m。根据毛竹竞争空间变异特征，以4.306 m作为毛竹的竞争单元半径及调控毛竹竞争关系的距离尺度比较合适。
年份 模型 块金值 基台值 结构比/% 变程/m 各向异性/(°) 决定系数 2009 指数模型 0.007 2 0.055 8 88.71 4.467 90 0.971 2010 指数模型 0.012 7 0.057 0 81.78 4.068 86 0.977 2011 指数模型 0.007 0 0.054 5 88.62 4.581 90 0.976 2012 指数模型 0.010 8 0.060 0 84.75 4.170 86 0.976 2013 指数模型 0.006 7 0.058 9 89.79 4.474 91 0.979 2014 指数模型 0.0102 0.062 9 86.05 4.059 89 0.977 2015 指数模型 0.0109 0.064 9 85.62 4.322 86 0.974 平均 4.306 88 Table 4. Parameters of semivariogram model of competition index of bamboo in each year
绘制各年毛竹竞争指数空间异质性与海拔高度变化各向异性半方差图，可进一步分析毛竹竞争指数与地形的关系（图 4）。从图 4可见：竞争指数与海拔高度的各向异性主方向一致，呈现出各年毛竹竞争指数在东西方向上半方差变异较小，而在南北方向上随海拔高度变异较大的带状分布特征。毛竹竞争指数空间变异受以海拔为主导因子的微地形影响而存在各向异性。
Figure 4. Variogram maps of competition index of bamboo and plot topography
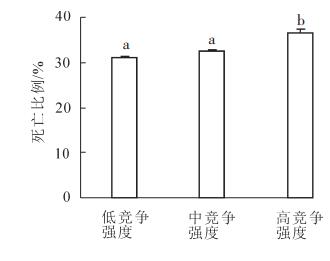
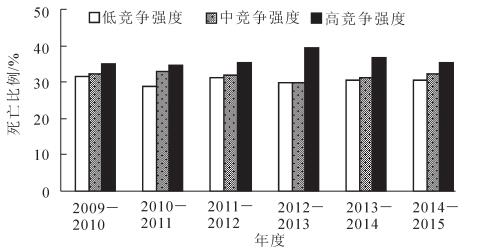
由图 4看出：2013年毛竹竞争有趋于匀质的特征。为分析其原因，采用自然断裂法把竞争指数IC划分为低（IC＜1.290 1），中（1.290 1≤IC＜1.596 9），高（IC≥1.596 9）3个竞争强度等级，对不同竞争强度等级下各年毛竹死亡株数进行方差分析（图 5和图 6）。方差分析表明：高竞争强度毛竹死亡比例与其他竞争强度的毛竹死亡比例存在显著差异（P＜0.05），而低竞争强度与中竞争强度毛竹死亡比例差异不显著（图 5）；2012-2013和2013-2014年度，高竞争强度下毛竹死亡比例明显大于其他竞争强度的死亡比例，竞争指数空间变异趋于各向同性，而其他年度不同竞争强度等级毛竹死亡比例呈阶梯状排列，竞争指数空间变异保持各向异性（图 6）。
Figure 5. Difference of proportion of death under different competitive intensities
Figure 6. Statistical summary of proportion of death under different competitive intensities
-
分析毛竹竞争空间格局的动态变化，可以掌握毛竹竞争关系的发展趋势。对图 3各年毛竹竞争指数插值分布图进行栅格化处理，再用栅格计算器获取年度毛竹竞争指数增量栅格数据，并进行竞争格局变化统计分析（表 5）。从表 5可见：从小年到大年时，毛竹竞争加剧；大年到小年时，毛竹竞争缓和。特别地，2009-2010年毛竹林竞争加剧面积及2010-2011年竞争缓和面积明显大于其余各年，这是因为2008年末和2011年初2次大雪使得毛竹林密度有较大减少，且2009年和2011年是毛竹林小年，林内少有新竹生长，所以从小年到大年的2009-2010年竞争加剧面积和大年到小年的2010-2011年竞争缓和面积明显大于其余各年。此外，毛竹平均竞争指数增量为正，且平均竞争加剧面积大于竞争缓和面积，毛竹竞争强度总体趋向加剧。
年度 平均竞争指数变化量 竞争加剧面积/
m2竞争缓和面积/
m22009-2010 0.072 0 8 415.26 1 584.74 2010-2011 -0.035 4 2 712.97 7 287.03 2011-2012 0.012 4 5 424.52 4 575.48 2012-2013 -0.022 9 3 462.48 6 537.52 2013-2014 0.025 5 6 191.17 3 808.83 2014-2015 -0.004 5 4 685.20 5 314.80 平均趋势 0.007 8 5 148.60 4 851.40 说明：总体竞争均值是经正态转换之后的竞争指数 Table 5. Statistical summary of changed pixel of raster data through the years
3.1. 竞争指数统计分析
3.2. 竞争指数空间自相关分析
3.3. 竞争指数空间异质性分析
3.4. 竞争指数空间格局动态变化特征
-
本研究以浙江天目山毛竹为研究对象，采用半方差函数拟合、空间自相关与各向异性分析、经验贝叶斯克里金插值等空间分析技术，分析了天目山毛竹竞争指数空间格局及其动态变化特征，为提高毛竹经营管理水平提供科学依据。
研究结果表明：更新和自然干扰是毛竹竞争强度变化的主要因素。毛竹生长从小年到大年，竞争加剧，从大年到小年，竞争缓和，其竞争变程存在与大小年相反的长短交替现象；毛竹林生境的异质性对其竞争指数空间变异存在影响，而极端气候等的自然干扰促使毛竹竞争空间变异趋于各向同性。受毛竹繁殖方式的影响，毛竹各年竞争指数空间分布存在一般正相关且呈聚集分布，竞争强度相近的竹子相邻分布。以往研究认为：干扰通过对林内光照、水分、土壤和微地形产生影响，改变了干扰生境的异质性，从而影响植被竞争关系[22-23]。本研究中，2011年研究区遭受的雪灾在短时间内造成了大量毛竹死亡，降低了林分整体的竞争强度，但并未改变毛竹林内部不同竞争强度的关系，因此维持了毛竹竞争指数空间变异的异质性。而2013年，研究区遭遇的极端干旱气候对毛竹林内水分等条件产生了影响，加剧毛竹个体间对水分的竞争，高竞争强度下的毛竹更易死亡[24-25]，而该年是毛竹更新小年，使得原本主要受地形影响呈现各向异性的竞争指数空间变异趋于各向同性，降低了毛竹林竞争关系的异质性。当林内恢复正常水分等条件时，毛竹竞争指数的空间变异再次呈现各向异性。表明，不同的自然干扰对毛竹竞争关系的影响是不同的。
地理信息系统（GIS）有强大的空间分析功能[26]，利用空间插值方法可以直观展示毛竹林竞争指数空间分布状况。在经营管理中，对竞争强度大的地方进行砍竹，对竞争强度弱的地方留笋养竹，优化调控毛竹林空间结构[27]，达到提高毛竹林产量的目的。
周隽等[6]发现天然次生林中林木竞争指数变程为12.400 m，远大于树木的间距。本研究的毛竹竞争指数变程为4.306 m，小于乔木的竞争指数变程。这是因为毛竹以地下竹鞭发笋繁殖，地上散生的竹子通过地下庞大而复杂的鞭根系统相连，其竞争关系不仅存在于地上部分，地下部分对毛竹竞争也有影响。
本研究在100 m × 100 m的范围内对毛竹竞争空间格局的异质性进行了分析。采用地统计学方法分析时，研究尺度的变化对研究结果存在影响。因此，在不同的尺度上对毛竹的竞争异质性特征有待进一步研究。
DownLoad: