Biomass allocation characteristics and a compatible model for Phoebe bournei in a natural secondary forest

安福县（27°04′~27°36′N，114°00′~114°47′E）位于江西省中部偏西。地形以山地、丘陵为主，三面环山；地势西北高，东南低；海拔300~1000 m。土壤类型主要为红壤、山地黄壤等。成土母岩类型主要为千枚岩、花岗岩、板岩等。属亚热带季风温润性气候区，年平均气温为17.7 ℃，最热月为7月，平均气温28.9 ℃，最冷月1月，平均气温5.9 ℃。年均降水量1 553.0 mm，平均降雨日166.0 d，降水明显集中在春季和初夏，平均日照时数1 649.0 h，山区日照偏少，年无霜期279.0 d，适宜林木生长。全县森林覆盖率达70.5%，被誉为“樟乡安福”，森林资源丰富。森林植被类型有阔叶林、针阔混交林、针叶林、竹林等，主要树种有马尾松Pinus massoniana，杉木Cunninghamia lanceolata，樟树Cinnamomum camphora，木荷Schima superba，枫香Liquidambar formosana，拟赤杨Alniphyllum fortunei和毛竹Phyllostachys edulis等^[9]。灌木草本主要以檵木Loropetalum chinense，杜茎山Maesa japonica，铁芒萁Dicranopterias linearis和庐山楼梯草Elatostema stewardii等为主^[6]。

通过森林资源二类调查数据及在当地林业部门获取的信息，在对安福县闽楠天然次生林分布地进行踏查的基础上，选择人为干扰程度轻且有代表性的地块设置标准地，面积为400 m²（20 m × 20 m）或600 m²（20 m × 30 m），共计16块标准地。记录标准地所有乔木树种、胸径、树高等因子，同时，选择闽楠对象木，对其生物量及周围的竞争木进行调查。

由于闽楠为Ⅱ级重点保护植物，对象木的采伐受到严格限制，因此对闽楠研究过程中未按常规要求采伐大量对象木。根据标准地每木检尺数据，选取1~2株与标准地林分平均胸径及平均树高相接近且生长正常、无病虫害的林木作为平均标准木用于生物量研究。总共选取了17株闽楠，其胸径为12.3~32.1 cm，树高为12.7~23.4 m。采用整株收获法，为准确获取树冠生物量，按树冠长度平均分为上层和下层，记录各层枝条数量，并在各层分别取1~2根与该层平均枝基径与平均枝长相近且生长正常的标准枝，17株解析木共获取35根标准枝，在标准枝基部测量直径，剖离枝条，测量枝条长度和宽幅，并分不同层次（上层、下层），不同枝级（一级枝、次级枝）和不同种类（枝、叶）称取鲜质量。将各层标准枝的树枝和叶各取500 g左右的样品，准确称取鲜质量并带回。称取树干解析后的所有圆盘和分段后的树干鲜质量。挖掘根系时尽可能将根系全部挖出，对根系称量前清除干净泥土等附着物。将所有的样品带回实验室烘干、称量，计算各类样品含水率进而计算单木各器官和全株干质量。

生物量模型中的自变量通常选择实际易测量且与各器官生物量相关性较强的林木因子，且不宜选择过多自变量。目前研究学者多采用胸径（D），树高（H）或D²H，DH等作为模型自变量。本研究参考相关文献[10]并通过各分项生物量与林木因子之间的相关关系分析，将D，H和D²H及反映树冠长度及其所占空间大小的因子冠幅（W_C）和树冠体积（V_C）作为待选自变量。由于林木竞争值（I_C）对生物量分配的影响也相对较大，为提高模型的预估效果，也将I_C作为模型的一个待选自变量。

选取与各组分生物量相关性显著的因子作为模型的自变量，采用非线性方程建立各组分生物量独立模型。为消除异方差性，将方程进行对数转换，利用最小二乘法估计回归系数^[11]。

参照唐守正等^[12]提出的思路，本研究以总生物量为基础，采用3级控制的方法对生物量进行相容性模型的建立。表达式详见参考文献[12]。生物量数据通常表现出异方差性，即误差的方差随观测值是变化的，因此需选择权函数消除异方差。相容性模型构建中，采用了对数转换的方法消除独立模型生物量的异方差，而由于相容性生物量模型方程式较复杂，采用对数转换比较复杂，因此本研究采用非线性加权法，根据独立模型的残差方差来确定权函数，即地上、地下、树冠、树枝、树叶和树干生物量独立拟合方程的方差建立的一元回归方程（W=1/D^x，其中D为样木胸径），方程参数是通过对各独立模型的方差进行拟合而得，在采用ForStat 2.1软件求解参数时，采取每一个方程两边乘以权重变量的方法进行处理^[13]。

为分析天然林中闽楠所受周围林木的竞争压力，采用研究林木种群竞争关系及单木生长模型常用的与距离有关的竞争指数Hegyi指数^[14]。惠刚盈等^[15]研究表明：以参照数及其相邻最近4株树组成的最小空间结构单元更能恰当地进行林分空间结构分析。因此，在用邻近木法确定对象木周围的竞争木时，取离对象木最近的4株树来计算，测量竞争木胸径、树高、冠幅及其到相应对象木的距离。

模型构建中，需要有一套指标来进行检验与评价。常用的模型评价指标有决定系数（R²），均方根误差（E_RMS），剩余标准差（E_SE），赤池信息准则（C_AI），总相对误差（E_TR），平均系统误差（E_MS），平均百分标准误差（E_MPS）和预估精度（P），具体定义及表达式见文献[12, 16]。

运用SPSS 19.0的简单相关分析法分析各组分生物量与林木特征因子的相关关系，采用单因素方差分析法分析不同直径枝条或胸径下各组分生物量大小及其占比的差异。运用Forsat 2.1软件的非线性度量误差法建立相容性生物量模型。运用Excel进行数据处理分析。运用Origin 7.5进行相关图表绘制。

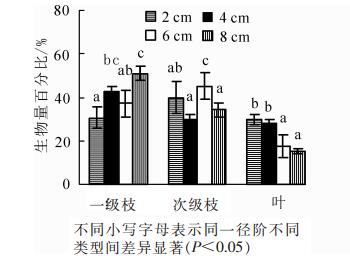
枝条生物量为0.343~16.474 kg·枝^－1，其中一级枝生物量为0.087~9.308 kg·枝^－1，次级枝生物量为0.110~5.299 kg·枝^－1，叶生物量为0.096~2.373 kg·枝^－1。由图 1可知：叶生物量占枝条生物量的比值随枝径阶的增加而不断减少，而一级枝和次级枝生物量占比随枝径阶增加呈波动变化，其中，径阶为4和8 cm时一级枝生物量占比最大，而径阶为2和6 cm时次级枝生物量占比最大。单因素方差分析表明：不同枝径阶的一级枝、次级枝和叶生物量分配比均差异显著（P＜0.05）。

Figure 1.  Biomass allocation ratios of branch and leaf at different branch diameters levels

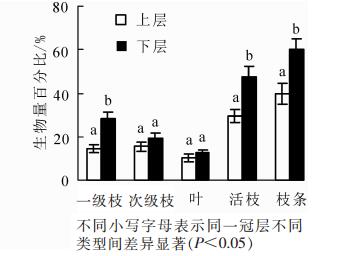
树冠生物量为23.40~185.71 kg·枝^－1。由表 1可知：整体上来看，树冠一级枝和叶总生物量均随胸径的增加而不断增加，次级枝生物量则随胸径的增加呈先减后增的变化趋势；同一径阶各部分生物量表现为一级枝＞次级枝＞叶。不同径阶的一级枝、次级枝和叶生物量占整株生物量的比值差异显著（P＜0.05），但进一步分析表明，当除去径阶为30 cm的各部分生物量，其余不同胸径间的一级枝生物量以及树冠总生物量之间均差异不显著（P＞0.05）。树冠的垂直分配特征如图 2所示。下层一级枝和次级枝之和（活枝）明显大于上层。方差分析表明：位于树冠上层一级枝、次级枝及叶生物量之和（枝条）显著低于下层枝条生物量（P＜0.05）；位于树冠上层的活枝生物量显著低于下层生物量（P＜0.05），其中一级枝生物量显著低于下层（P＜0.05），而次级枝和叶生物量无显著差异（P＞0.05）。

Figure 2.  Biomass allocation ratio of each component at different crown levels

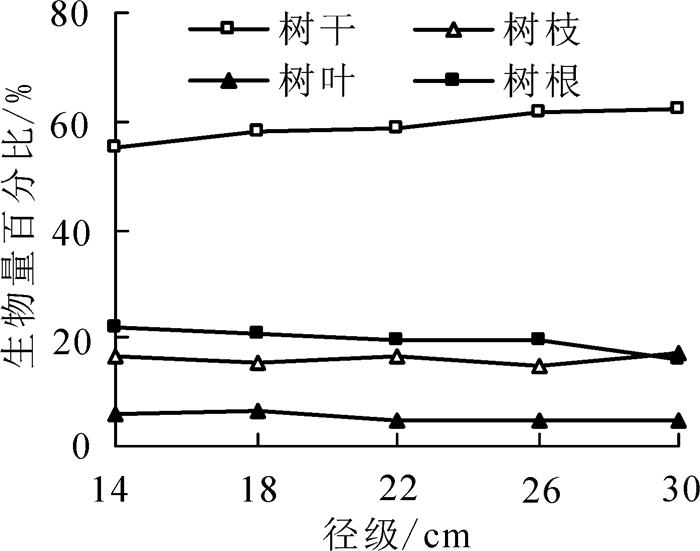
单木生物量为110.92~725.93 kg·株^－1，各器官生物量占整株生物量的比值表现为：0.59（树干）＞0.19（树根）＞0.16（树枝）＞0.06（树叶）。由表 2可知：各器官生物量均随胸径的增加而增加，不同胸径大小的各器官生物量差异显著（P＜0.05）。由图 3可知：随着胸径的增大，树枝和树叶生物量占比表现为波动变化，树干生物量占比呈现逐渐增大的趋势，树根生物量占比则表现为下降趋势。不同胸径级的树根生物量占比差异显著（P＜0.05），其余各器官生物量占比均差异不显著（P＞0.05）。

Figure 3.  Biomass allocation ratio of each tree organ at different DBH levels

由表 3可知：各器官生物量与林木特征因子之间存在显著相关，其中树干生物量与林木年龄、冠长呈显著相关（P＜0.05），与树高极显著相关（P＜0.01），树根生物量与树高显著相关（P＜0.05），树干、树枝、树叶、树根生物量与胸径、冠幅和树冠体积均呈极显著相关（P＜0.01）。树干生物量与胸径有较强相关性，树枝和树冠生物量则与冠幅和树冠体积相关性较大。

将选取的D，H，D²H，W_C，V_C和I_C逐步代入到回归方程进行参数拟合，最后根据调整的决定系数（R²），E_SE，C_AI及模型复杂程度等选择较优的独立基础模型。由于各种因子组成的回归方程形式较多，本研究仅列出各组分拟合效果较好的前3个模型。较优模型F值检验结果均表现为极显著（P＜0.001），独立基础模型最终形式、参数估计值及拟合优度见表 4。由表 4可知：树冠、树枝和树叶生物量模型R²较小，其余各项生物量模型的R²均达93.0%以上，其中树干生物量模型的R²达96.3%，树叶生物量模型最低，最优R²为71.9%。绝大部分基于D的独立模型R²都较高；模型在有D的基础上逐步加入D²H，I_C，W_C变量后，R²均有一定程度的提高。在模型中引入I_C因子能在一定程度上提高各分项生物量的预估效果，而W_C仅对树冠生物量预估有一定影响。除了自变量本身与生物量相关性从而影响模型R²大小外，自变量个数的增加也会导致模型R²增大，因此利用调整决定系数（R_Adj²）值来评价模型的优劣。综合考虑R_Adj²较大者、E_SE较小者以及C_AI较小者为最优模型，最终模型形式及评价指标见表 5。由表 5可知：模型对闽楠全株及各项生物量估计的E_TR均在10%以内，E_MS在5%以内。所有模型的E_MPS在30%以内，其中树冠、树枝、树叶的E_MPS较大。除树叶、树枝、树冠生物量预估精度较小以外，其余各项生物量预估精度均大于90%，其中模型对树干生物量预估精度达93%。综上，最终所选模型对生物量拟合效果相对较好，可作为相容性模型的基础模型。

利用上述最优独立基础模型基于非线性度量误差法构建相容性联立方程组。一级控制：

其中：${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} _1} $为总生物量估计值，$ \tilde{W}_{2}$和$\tilde{W}_{3} $为联合估计后的地上部分生物量和树根生物量估计值。令$ {a_{\rm{3}}}{\rm{ / }}{a_{\rm{2}}}{\rm{ = }}{r_0}, \quad {b_3} - {b_2} = {r_1}, \quad {c_3} - {c_2} = {r_2}, \quad {d_2} = {r_3};\quad {r_0}, \quad {r_1}, \quad {r_2}, \quad {r_3}$为联合估计参数，其初值为地上部分和树根生物量独立模型的参数估计值。二级控制：

其中：${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} }_2} $为地上部分生物量估计值，$\tilde{W}_{4} $和$ \tilde{W}_{7}$为联合估计后的树干和树冠生物量估计值。令$a_{7} / a_{4}=r_{0} $，$ {b_7} - {b_4} = {r_1}, \quad {c_7} - {c_4} = {r_2}, \quad {d_7} - {d_4} = {r_3}, \quad {e_7} - {e_4} = {r_4}。\quad {r_0}, \quad {r_1}, \quad {r_2}, \quad {r_3}$和r₄为联合估计参数，其初值为树干和树冠生物量独立模型的参数估计值。三级控制：

其中：${{\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over W} }_7} $为树冠生物量估计值，$ \tilde{W}_{5}$和$ \tilde{W}_{6}$为联合估计后的树枝和树叶生物量的估计值。令$ a_{6} / a_{5}=r_{0}, b_{6}-$ $b_{5}=r_{1}, \quad d_{6}=r_{3}, \quad-e_{5}=r_{4 } 。\quad r_{0}, \quad r_{1}, \quad r_{2}, \quad r_{3} $和r₄为联合估计参数，其初值为树枝和树叶生物量独立模型的参数估计值。进行模型参数估计值求解时要在方程两边同时乘以各分项的权重函数（表 5）。参数拟合结果及评价指标见表 6。由表 6可知，各项拟和的决定系数R²较高，除树枝、树叶生物量仅为85.2%和81.5%外，其他各项生物量的R²均大于90%。除树叶生物量外，其他各项生物量的E_TR和E_MS值均在±10%内，地上、树干和树根生物量预估精度P值也均达90%以上，树冠、树叶和树枝生物量P值相对较低，但也大于70%，模型具有一定的预估性。

枝叶生长不仅受年龄、林分密度、气候环境等的影响^[17-19]，而且还受其在树冠垂直分布的影响，因为不同的空间分布会影响枝叶对光照的吸收和有机物质的积累^[20]。卢军等^[21]对帽儿山天然次生林主要阔叶树种叶量分布模拟研究表明：天然次生林阔叶树种的叶量在树冠上部所占比例很小，在树冠中部及中下部叶量所占比例较大，几乎集中了整个树冠60%~70%的叶量。本研究发现：树冠下层活枝生物量显著高于上层，而下层树叶生物量略大于上层，但表现并不显著。这可能是因为天然次生林中尽管树冠上层光照充足，但本身枝条较小，着生的叶量也因此较少，而树冠下层枝条虽大，但获得的光照较少，且易受周围林木的遮挡，导致着生的叶量也不是很多，从而上下层树叶生物量差异不显著。玉宝等^[22]对兴安落叶松Larix gmelinii天然林单株树冠生物量分配研究表明：树枝生物量分配比高于树叶，并因其相对直径大小的不同而不同。本研究也得出相似的结论，且研究发现叶生物量占比随枝径的增大而逐渐减少，一级枝和次级枝生物量占比则呈波动变化。究其原因可能是树冠下层的枝条多为已经生长的直径较大的活枝，但位于树冠下层的枝条因受遮蔽等影响使得获取的光照资源较少，从而导致着生在枝条上的阔叶量相对减少，而光照的缺乏对一级枝和次级枝自身物质积累影响不大。活枝分配比呈波动变化的原因可能与环境因素或树种生态学特征有关^[23]，如林木一定条件下的自然整枝。

植物的个体生理生态学特征、林内环境、立地空间是影响植物器官生物量积累及分配差异的重要原因^[24]。相关研究表明：通常植株地上部分生物量占植株总生物量的79.0%，而地下生物量约占21.0%^[25]，这与本研究得出的次生林中闽楠地下生物量占全株生物量的19.0%有差异。同时，董点等^[26]研究表明：紫椴Tilia amurensis树根生物量占全株生物量的24.2%，刘坤等^[10]发现银杏Gingo biloba根生物量占全株生物量的26.0%，造成这种差异的原因可能是因为树种间本身特性及立地环境的不同导致，如闽楠适合生长在土层深厚、肥沃、排水良好的土壤，多分布在峡谷、山洼和河流两岸的台地等，而这些地方往往光照不足，因此树体相对减少树根有机质积累，增加树干及树冠等有机质积累以获取更多的光照资源，加速生长。王宁等^[27]对山杨Populus davidiana生物量分配研究表明：各器官生物量分配比从小到大依次为树叶、树枝、树根、树干，本研究结果与之相一致。植物生物量分配特征与胸径、年龄等因子密切相关，如余碧云等^[28]对栓皮栎Quercus variabilis生物量研究表明：树干生物量分配比随胸径的增加呈先减小后逐渐增大的趋势，而枝叶生物量分配比则随胸径的增加呈先增后减再增的变化趋势。本研究表明：叶生物量占比随胸径增大呈先增后减，树干生物量占比表现为先减后增的波动变化，而树根生物量占比则逐渐减小。一方面可能是由于幼林时期植株相对较小，枝叶及根部具有充足的营养资源及生长空间进行物质积累，而随着幼苗的逐渐生长，生长空间不断减小，周围林木的遮蔽影响树冠的生长，树枝生物量减小；为获得林木上层充足资源，林木开始积累主干生物量而削弱对树根生物量的积累。另一方面，闽楠在一定阶段的自然整枝以及林内的环境变化也会影响枝叶生物量占比。这也表明，前期闽楠幼苗主要靠树根生长获取营养资源，随着径级增加，逐渐转为主干有机质的积累，这有利于形成大径材。

不少研究学者对林木生物量模型进行研究。如程堂仁等^[29]为准确预估小陇山林区的森林生物量以及碳汇能力，通过标准木资料建立了锐齿槲栎Quercus aliena等8种树种的各器官生物量回归方程。魏海燕等^[30]采用幂函数回归模型对甜槠Castanopsis eyrei单木生物量数据进行拟合，得到各器官生物量最优模型，除树枝、树叶生物量预估精度较差外，其余各器官生物量预估精度均达90%以上。本研究建立的相容性模型系统对闽楠全株、树根、地上部分、树冠、树干、树枝、树叶生物量的拟合精度分别为91.8%，90.2%，91.0%，85.1%，91.6%，86.8%和71.0%，除叶生物量外，其余各分项生物量预估精度值均大于85%，总相对误差均在3%以下，能较准确地预估研究区次生林中闽楠全株及各部分生物量。树冠、树枝和树叶的模型预估精度较差，可能是树叶本身受环境影响因素较大等原因造成的。树叶是光合作用的最重要场所，对周围光照条件敏感，因此异质性较大^[31]，另一方面也可能是次生林中阔叶树树枝易分叉，尽管在枝条数据获取时考虑到分叉的枝条，但在实际取样时还是会出现抽样误差，同时模型指标的选取及评价标准也可能是导致树叶等生物量预估精度较低。

相容性模型主要是协调各分量间的关系，使其预估值等于总体和相应的分项。相关研究对独立模型和相容性模型的生物量预估效果评价表明：这2种方法对总量和各分量的预估精度没有很大差异^[11]。本研究也得出类似的结论。为更全面地分析林分因子对生物量的影响，本研究在构建生物量模型时引入除胸径、树高之外的冠幅和竞争因子，结果表明：引入与生物量相关性较强的因子能在一定程度上提高模型的拟合优度（R²）以及估测精度。由于研究区域立地条件差异不大，因此在构建生物量模型时未考虑随机效应和区域差异。同时采伐解析木受到限制，本研究生物量样本数据相对较少，特别是小径阶的样本，这将会影响所建立的模型精度，有待补充这部分数据并做深入研究。