Layout and optimal design of watchtowers in forest regions

原则上林区中的制高点都可被选建瞭望塔，可采用顶点法提取林区内有限个通视效果较好的山顶点作为覆盖选址模型的备选点。步骤包括：①以ArcGIS作为分析工具，利用1∶10 000等高线矢量图制作出数字高程模型(DEM)。②焦点统计每个窗口内的最大高程，获取最大值栅格矩阵。③将最大值栅格矩阵与原有栅格DEM差值运算，标注结果为0的栅格即为顶点，形成瞭望塔布局分析的备选点集P。为提高顶点提取精度，防止漏提与多提，本研究采用11×11的栅格窗口提取林场中的顶点(DEM分辨率为5 m，最大高程阈值为20 m)^[14-15]。如图1所示，共得到38个后备选点P={p₀，p₁，…，p₃₇}。

Figure 1.  P distribution map of alternative set in W Forest Farm

最大监测面积模型(Max-MAM)可表述为从备选点集P中选择n个点，使得n个点构成监测网络的监测(可视)面积最大。设选择n个点建成的监测网为$ {\overline{P}}_{n} $={p₁，p₂，$\cdots $，p_n}。其中，p_n为第n个备选点选建的瞭望塔；S_n(p₁，p₂，$\cdots $，p_n)为$ {\overline{P}}_{n} $的监测面积。则最大监测面积模型为：

由式(1)可得$ {\overline{{P}}}_{{n}}^* $={$ {p}_{1}^{*} $，$ {p}_{2}^{*} $，$\cdots $，$ {p}_{n}^{*} $}即为最优布局，此时n值为根据约束(如投资)或监测网预设目标确定的待建瞭望塔数；$ {p}_{i}^{*} $为第i次选建时的最优瞭望塔；$ {{S}}_{{n}}^* $为$ {\overline{P}}_{n} $的最大监测面积。

Greedy算法结合GIS视域分析工具可实现Max-MAM的快速近似求解。记P_i={$ {p}^{i}_{j} $，j=1，$\cdots $，i，$ {p}^{i}_{j} $∈P}为第i次迭代时备选点集；$ {\overline{P}}_{i} $={$ {{p}^{i}_{j}}^{*} $，j=1，…，N−i，$ {{p}^{i}_{j}}^{*} $∈P}为第i次迭代时已选瞭望塔集，满足式(2)关系，其中0≤i≤n≤N。

根据上述定义，Greedy算法第i次迭代选择的最优备选点$ {{p}_{i}^{i}}^{*} $可表示为：

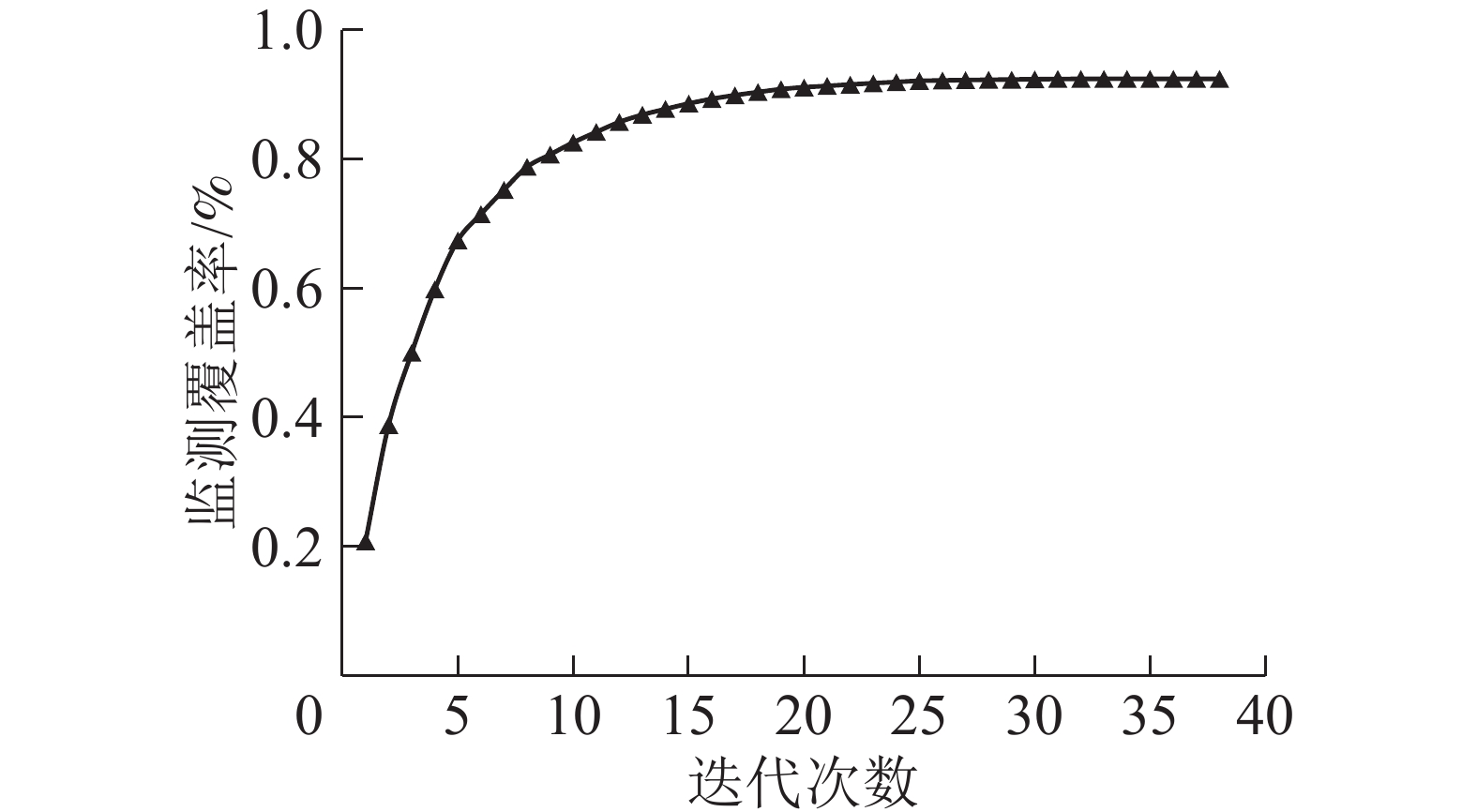
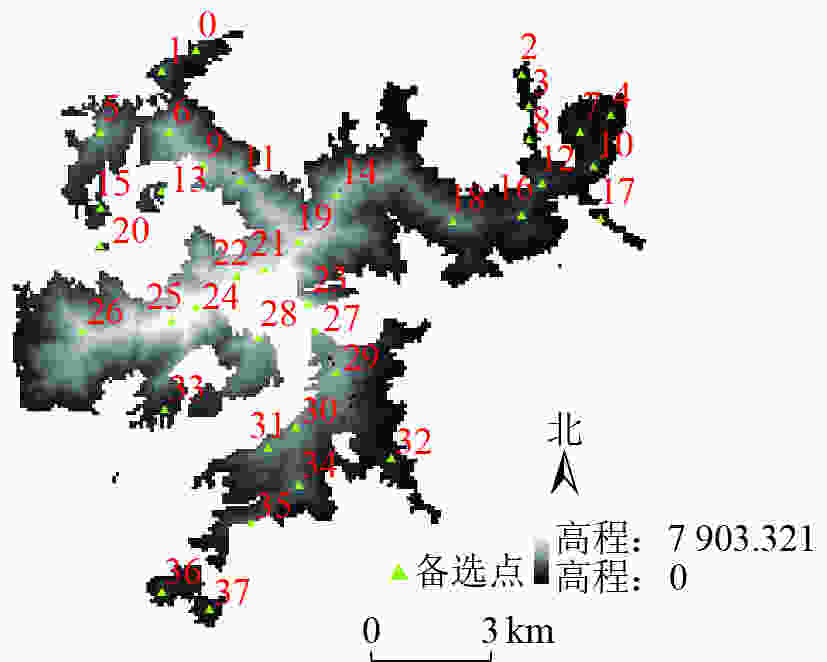
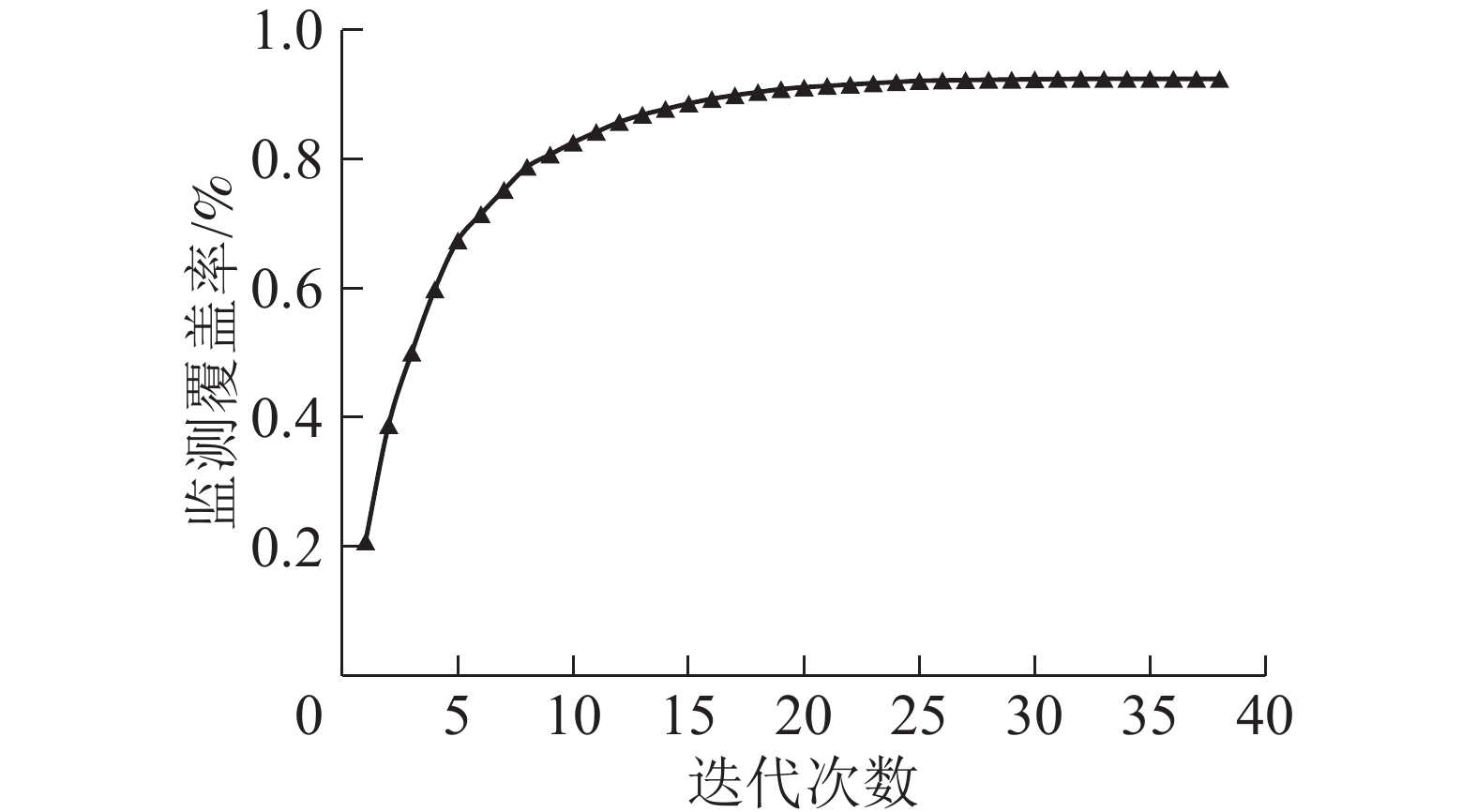
式(3)中，$ {S}_{i} $(p₁，p₂，…，p_i)是监测网$ {\overline{P}}_{i} $的监测面积(可视域面积)，由GIS视域分析工具统计$ {\overline{P}}_{i} $可视域栅格数$ \left|{V}_{\rm{i}}\right| $得到。结合ArcPy中的visibility_3d函数运行上述Greedy算法迭代计算可得最大监测面积$ {S}_{i}^{*} $($ {{p}_{1}^{i}}^{*} $，$ {{p}_{2}^{i}}^{*} $，…，$ {{p}_{i}^{i}}^{*} $)。Greedy算法应用于W林场38个瞭望塔备选点，监测覆盖率随迭代次数变化如图2所示。

Figure 2.  Monitoring coverage change

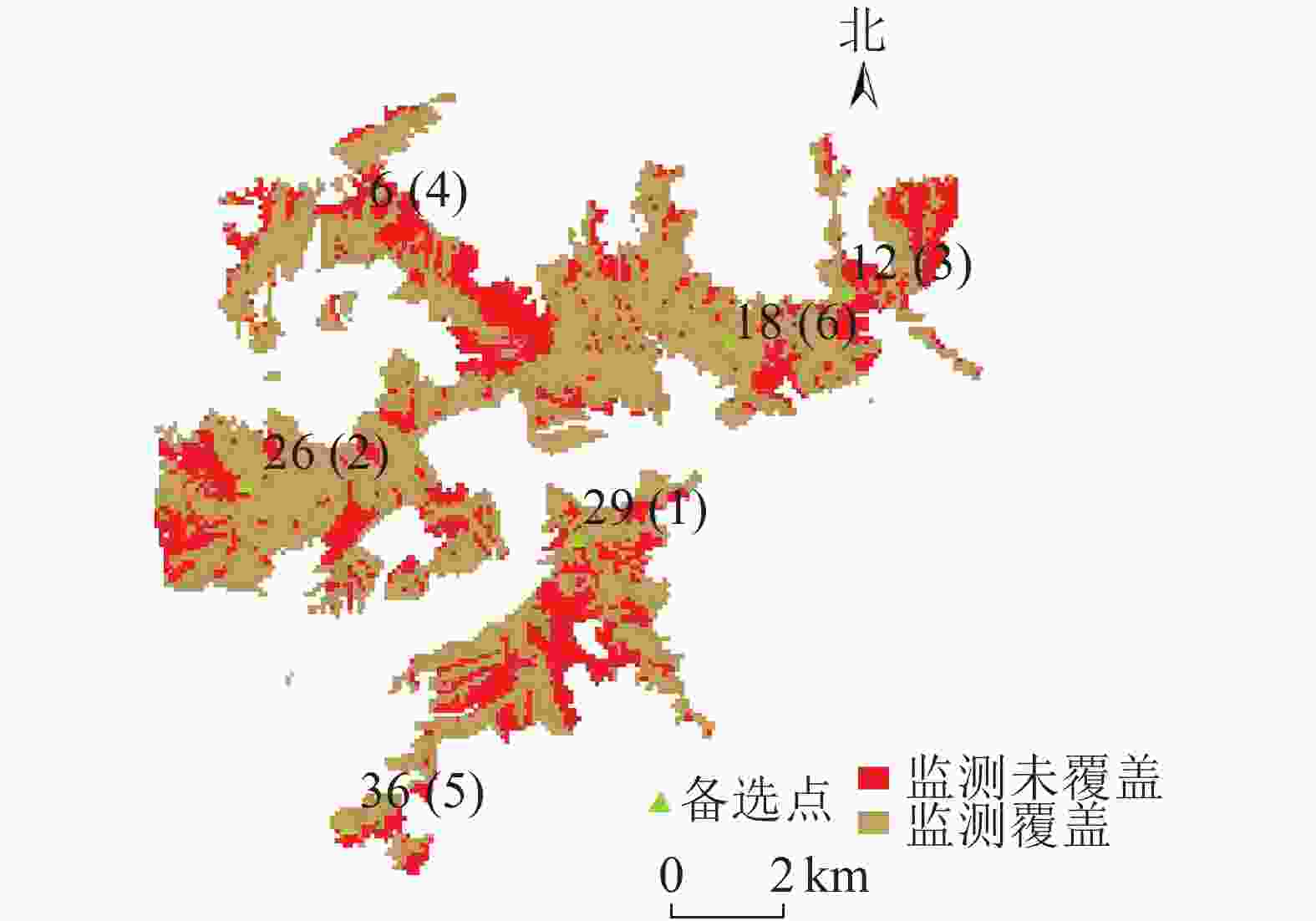
表1列出了Greedy算法前6次迭代得到的瞭望塔优化布局方案，当i=5时，优化布局方案$ {\overline{{P}}}_{{6}} $={$ {{p}}_1^* $，…，$ {{p}}_{{6}}^* $} ＝{a₆，a₂₉，a₃₆，a₁₂，a₂₆，a₁₈}，结合图1可知，$ {\overline{{P}}}_{{6}} $的监测覆盖率达71.47%，近似实现了设计最少的瞭望塔数目及空间布局、以获得最大监测覆盖面积的整体优化目标。

为进一步提升瞭望塔网络建设过程的阶段性效益，建立DMACTSM模型，通过动态计算布局方案中各瞭望塔的综合属性值，对$ {\overline{P}}_{n} $中各瞭望塔的建设时序进行优化分析。设$ {u}_{i}^{k} $为第k次迭代计算瞭望塔$ {p}_{i}^{k} $的综合属性值，则第k次迭代得到优先建设的瞭望塔$ {{p}_{i}^{k}}^{*} $满足如下最大化问题：

式(4)中：$ {{p}_{i}^{k}}^* $，$ {p}_{i}^{k} $∈$ {\overline{P}}_{n} $ (k=0，1，$\cdots $，n−2)，则监测网$ {\overline{P}}_{n} $的最优建设时序为$ {{p}_{i}^{0}}^{*} $、$ {{p}_{i}^{1}}^{*} $、$\cdots $、$ {{p}_{i}^{n-1}}^{*} $。MACTSM对建设时序的优化包括3步。

新建塔要求交通便利，地势平坦，尽量依附已有建筑建设^[7]。表2给出了MACTSM的4个属性，增长监测面积、交通情况、坡度与依附建筑情况。记p_i的增长监测面积为y_i1，指加入$ {p}_{i} $后$ {\overline{P}}_{i-1} $增加的监测面积，即p_i对监测网$ {\overline{P}}_{i} $的单独监测面积^[8]。 y_i1是正向属性，反映新增瞭望塔对监测网总监测面积的贡献，随监测网变化而变化，满足$ {y}_{i1}{=}\left(\left|{{\rm{V}}}_{{i}}\right|{=}\left|{{\rm{V}}}_{{i}{-}{1}}\right|\right){×}{s} $，其中，$ \left|{V}_{i}\right| $是监测网$ {\overline{P}}_{i} $可视域栅格数，s是单位栅格面积。设交通情况指瞭望塔所处位置距离道路的远近，即瞭望塔到最近道路的垂线长度(m)，对林区防火公路图进行近邻分析求得。坡度指林区地面的陡峭程度(°)，对DEM进行坡度分析求得。依附建筑情况指瞭望塔与已有建筑的贴近程度，即瞭望塔距最近已有建筑的直线距离(m)，对林区含风景点的建筑设施图进行近邻分析求得。该决策矩阵可记为Y=(y_ij)_n×4，其中，j为属性编号，y_i=(y_i1，$\cdots $，y_i4)为瞭望塔$ {p}_{i}^{*} $的属性向量，i=1，2，$\cdots $，n。

根据式(5)对正向属性y_i1消除量纲，对反向属性y_i2、y_i3、y_i4进行极差标准化，再进行归一化，得到决策矩阵Z=(Z_ij)_n×4。

对归一化矩阵Z采用熵权法确定权重。熵权法不依赖于专家经验，可通过数据间差异客观确定属性权重^[16]。根据式(6)分3步进行确权：先计算各属性熵值e_j；然后计算各属性差异系数g_j；最后计算各属性权重ω_j。

若各属性已有主观权重时，则可采用式(7)修正。建设前期注重增长监测面积可以将y_i1权值提高，当y_i1权值为1，表示不关心其他属性，排序结果与Greedy算法一致。

根据式(8)对各属性线性加权，得瞭望塔p_i综合属性值。

以林场优化布局方案$ {\overline{P}}_{6} $=$ \{{p}_{1}^*，\dots ，{p}_{6}^*\} $={a₆，a₂₉，a₃₆，a₁₂，a₂₆，a₁₈}为例。当k=0时，对林区DEM数据、防火公路图、建筑设施(含风景点)图等数据进行领域分析计算，6个瞭望塔4个属性的初始决策矩阵Z⁰。

计算可知：6个瞭望塔的综合属性值向量u⁰=(0.67，0.76，0.35，0.50，0.30，0.29)。$ {{u}}_2^{{0}} $=max{$ {{u}}_{{i}}^{{0}} $}=0.76，$ {{p}}_2^* $(即$ {{a}}_{{29}} $瞭望塔)率先被加入建设序列。

同理，当k=1时，对余下5个瞭望塔重新计算增长监测面积属性值，得到归一化决策矩阵Z¹，计算可知：第2个被加入建设序列的瞭望塔为$ {{a}}_{{26}} $；依此类推，DMACTSM迭代5次，得到各阶段被优先建立的瞭望塔及最终建设时序优化结果，如表3所示。

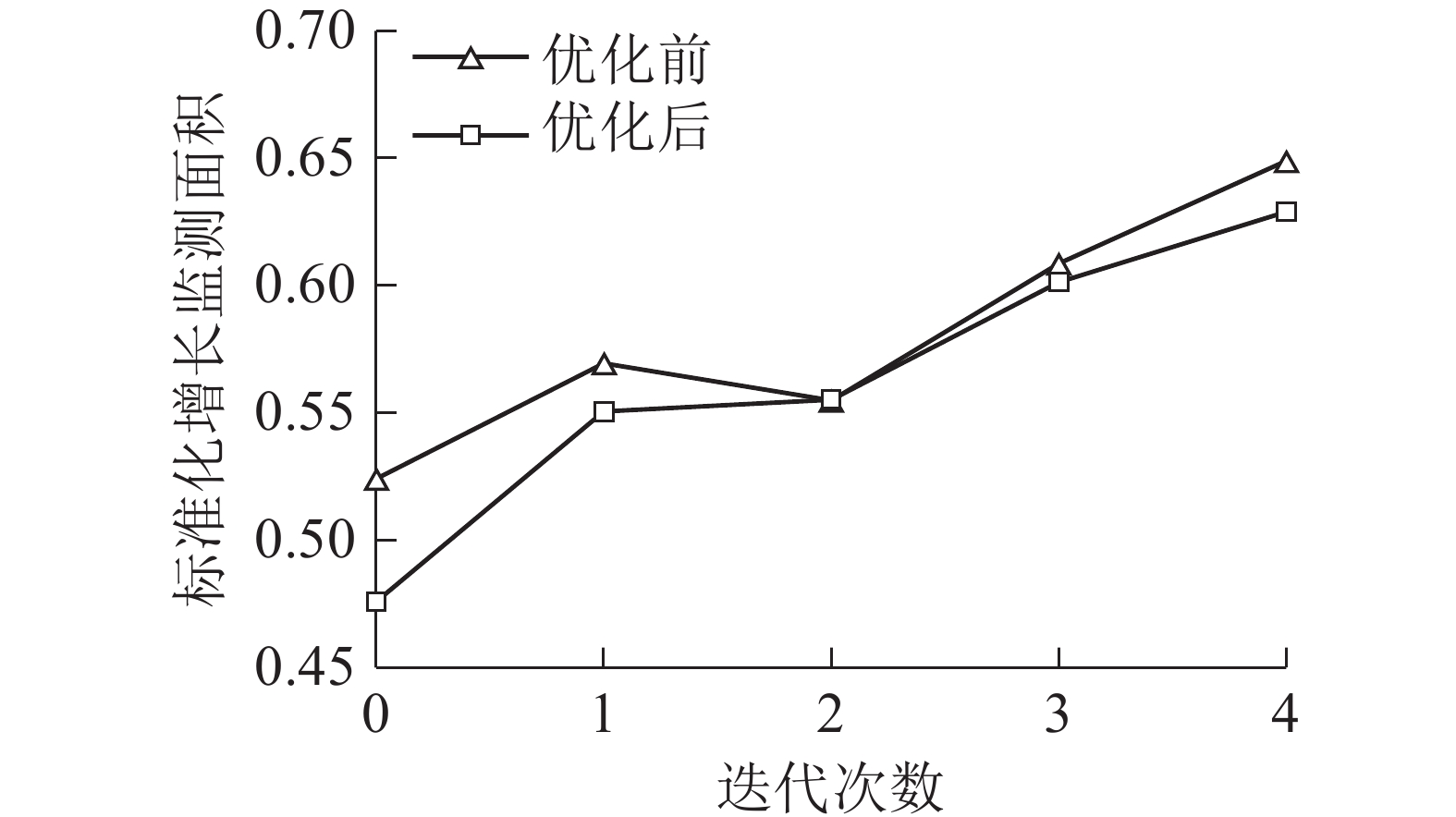
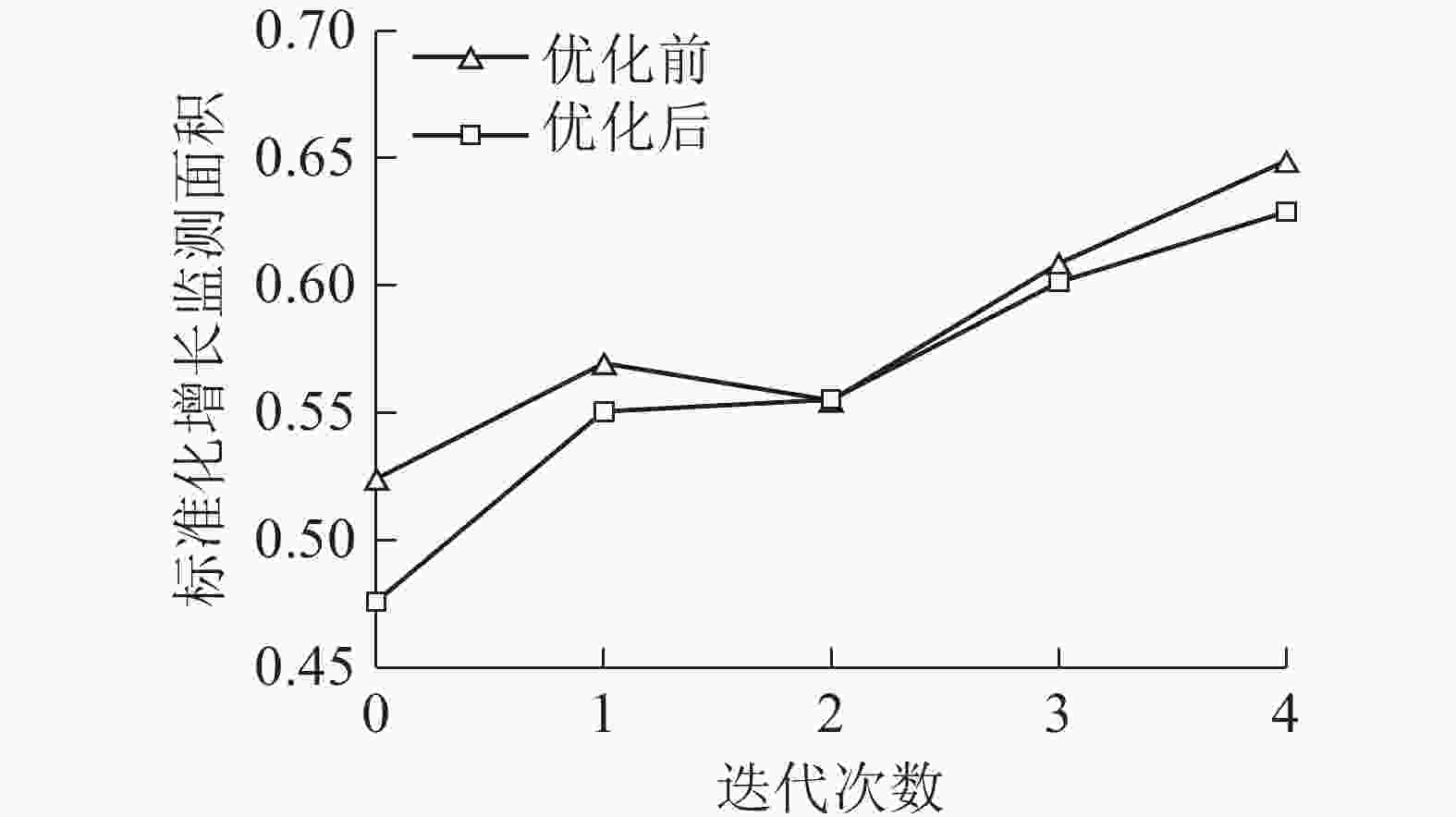
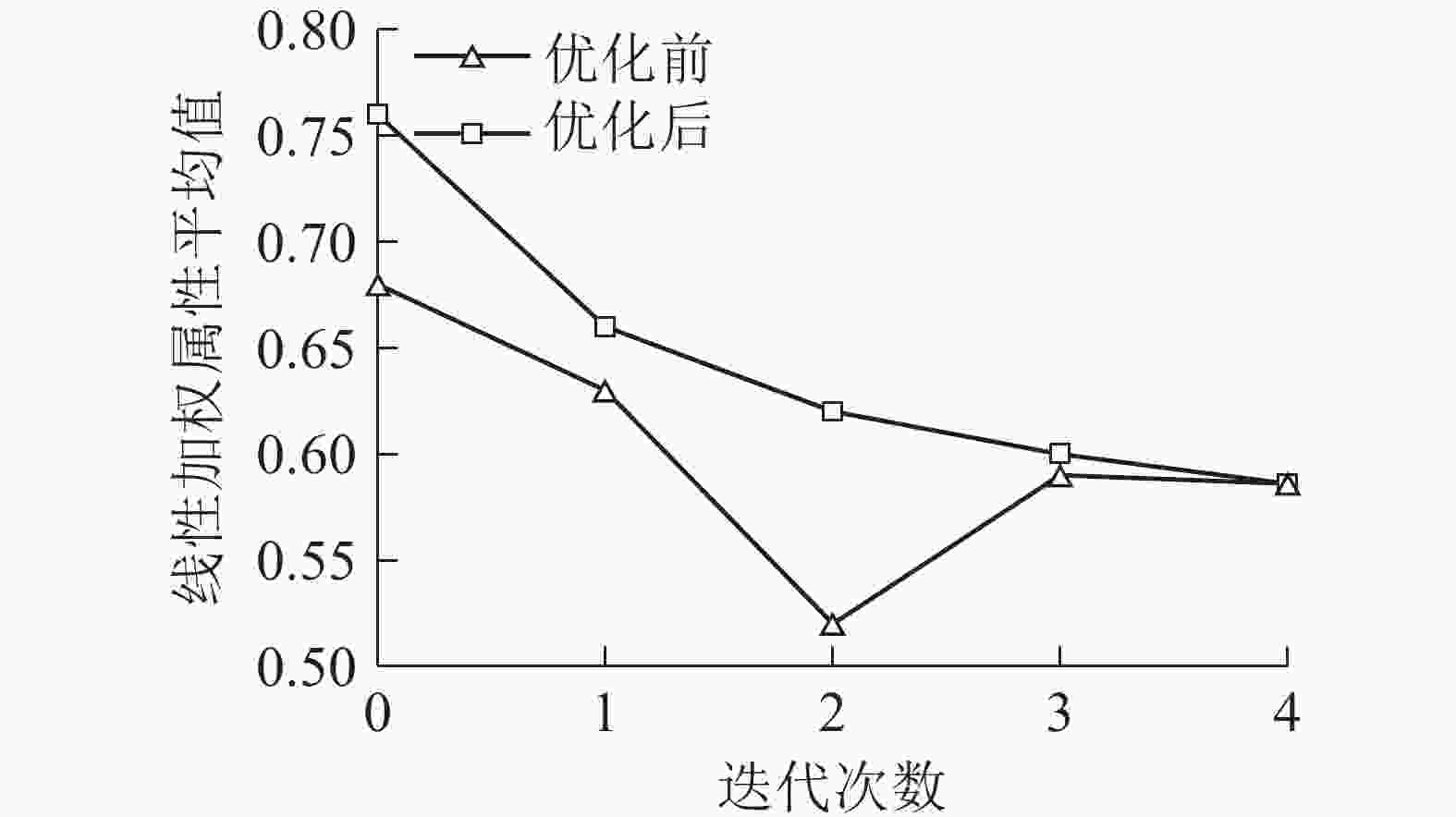
林场瞭望塔网络优化布局及建设时序效果，如图3所示。对比图4、图5可得：监测覆盖面积增长最快的建设时序为a₆、a₂₉、a₃₆、a₁₂、a₂₆、a₁₈，DMACTSM调整后建设时序为a₂₉、a₂₆、a₁₂、a₆、a₃₆、a₁₈，不仅保证瞭望塔网络总体效益最优，也实现了各阶段建设效益的优化，说明DMACTSM对瞭望塔建设过程优化有实际意义。

Figure 3.  Optimal design of watchtower network in W (optimal layout and construction sequence)

Figure 4.  Comparison of standardized growth monitoring area before and after optimization

Figure 5.  Comparison of comprehensive attribute values before and after optimization

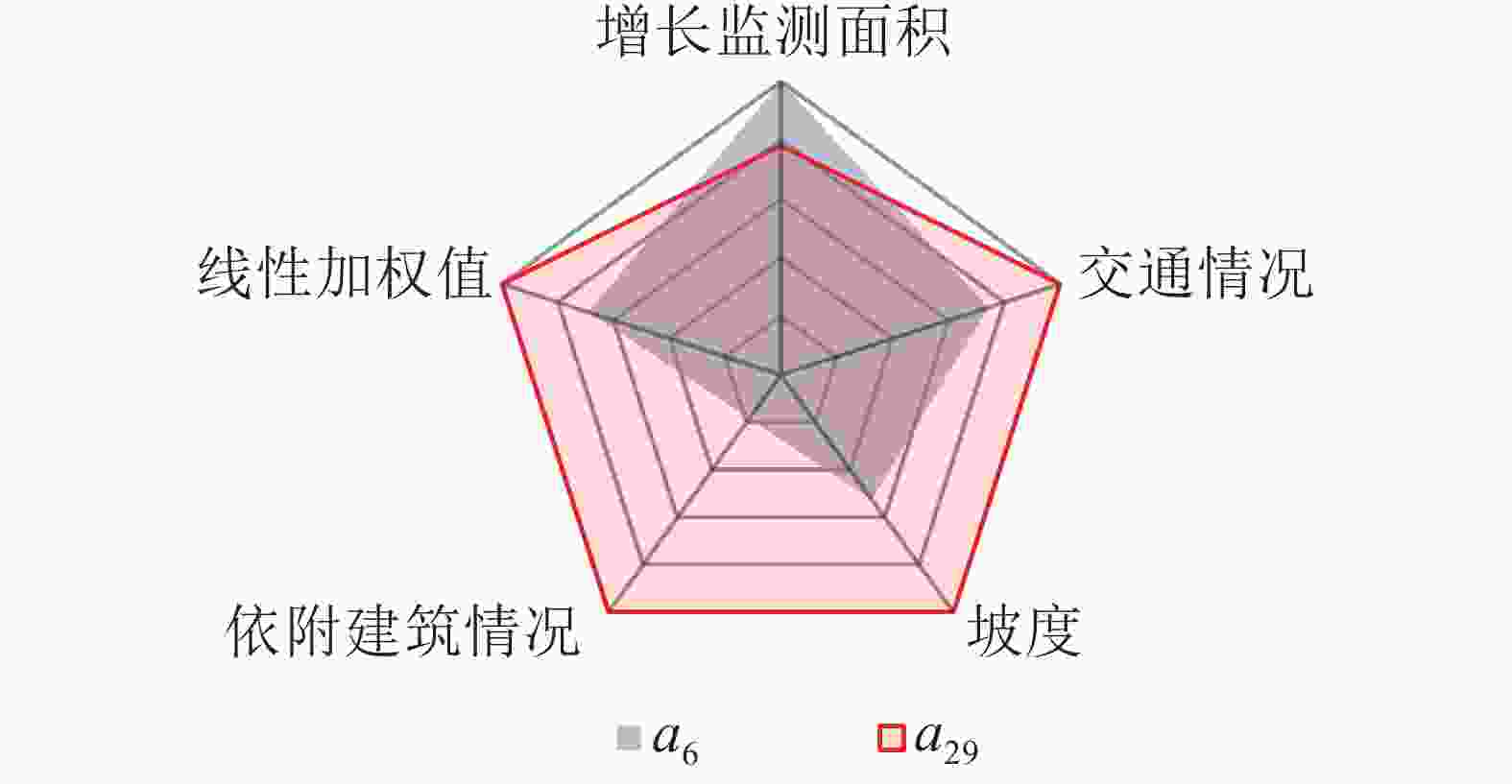
雷达图可对比优化前后首建瞭望塔的效益(图6)。首建$ {{a}}_{{6}} $增长监测面积最大，在其他成本属性和综合值上均不如率先建立$ {{a}}_{{29}} $。

Figure 6.  Radar map for comparison of comprehensive attribute values of a₆ and a₂₉

林区瞭望塔网络建设具有明显的空间性、阶段性和动态性。本研究结合林场实际，将林区瞭望塔网络建设规划问题转换为瞭望塔布局与时序优化问题，建立了最大监测面积模型(Max-MAM)和动态多属性建设时序模型(DMACTSM)，并利用GIS工具设计实现了求解模型的方法。计算和实际验证表明：Max-MAM及Greedy算法可得到满意的优化布局方案；DMACTSM兼顾收益与多个成本属性，在瞭望塔建设时序的综合优化中兼顾了瞭望塔建设的整体与阶段效益的优化，且计算方法实用可行，为林区瞭望塔网络建设规划提供科学依据。

研究发现：顶点法提取备选点集是优化的基础，其关键是确定提取窗口的尺寸^[15]。本研究采用11×11栅格大小的窗口提取备选点集，窗口尺寸可通过试验计算进一步优化提高顶点提取的效度。监测覆盖率最大与瞭望塔数最小问题互为对偶，当预设约束不是瞭望塔数n，而是监测覆盖率时，求解Max-MAM同样可得近似最优方案。本研究选取了面积较小的林场作为方法研究实验区，所提出的时空优化设计方法与研究对象的面积大小无关。在实践中，对于面积大的林区，甚至是1个县、1个州市的林区，更能体现时空优化设计带来的经济效益。