-
林分结构决定其功能。林分结构指标是描述森林质量和制定经营决策的重要基础，是对更新、生长、竞争、自然稀疏等林分发育过程和人类经营活动的综合反映。林分结构分为非空间结构和空间结构，两者之间最重要的区别是非空间结构不依赖林木的空间坐标，而空间结构与林木的空间位置有关，可以为森林可持续经营提供精确信息[1]。林分空间结构指数是定量描述林分空间结构特征的指标[2]。描述空间结构特征的竞争指数、混交度、聚集指数、大小比数和角尺度等指数，可反映森林中树种的混交状况、林木个体间的竞争关系和林木的空间分布形式等。地形通过对热量、水分、光照等的再分配，间接影响林分的生长发育，是影响林分因子空间分布的关键因素[3]。近年来，国内外有关地形因子与林分非空间结构的关系研究报道很多。TRAN等[4]在研究微地形对林分结构和树木多样性的影响中发现：海拔在450 m以下和450 m以上的林分非空间结构指数和物种多样性指数具有显著差异。汤孟平等[5]研究了不同地形条件下常绿阔叶林群落物种多样性与胸高断面积的差异，表明坡度过大过小都会导致物种多样性和胸高断面积的下降。范叶青等[6]认为：坡度和海拔对毛竹Phyllostachys edulis平均胸径具有显著影响；而杨帆等[7]研究发现：海拔对毛竹立竹度的影响极为显著，但对林分平均胸径无显著影响。于顺龙[8]研究指出：坡向对林分平均胸径和优势木高具有显著影响。可见，地形位置(山谷、山脊)的差异影响着植物群落的组成和结构[9]。关于林分空间结构的研究多集中于分析林分空间结构的优化和评价[10-13]、不同森林类型的空间结构特征[14-16]、林分空间结构与物种多样性的关系[3, 17]以及干扰对林分空间结构的影响[18-20]，而关于地形因子与林分空间结构之间的关系研究甚少。本研究以浙江省天目山常绿阔叶林为研究对象，设置大型固定样地，采用相邻格子调查方法进行样地调查，基于数字高程模型(DEM)提取网格单元的地形因子，采用基于Voronoi图的空间结构指数，分析天目山常绿阔叶林空间结构与地形因子的关系，为常绿阔叶林可持续经营提供科学依据。
HTML
-
浙江省天目山国家级自然保护区坐落于浙江省杭州市临安区西北部，与杭州市中心相距94 km，占地面积为4 284 hm2，位于30°18′30″~30°24′49″N，119°24′11″~119°28′23″E。海拔300~1 556 m。年平均气温8.8~14.8 ℃，最热月平均气温 19.9~28.1 ℃，最冷月平均气温2.6~3.4 ℃，平均最低气温−20.2~−13.1 ℃，平均最高气温29.1~38.2 ℃。无霜期209~235 d，雨水充沛，年雨日为159.2~183.1 d，年降水量达1 390~1 870 mm，积雪期较长，比区外多10~30 d，形成浙江西北部的多雨中心。天目山土壤随着海拔升高由亚热带红壤向湿润的温带型棕黄壤过渡，海拔600 m以下为红壤，海拔600~1 200 m为黄壤，海拔1 200 m以上为棕黄壤。森林类型多样，包括常绿阔叶林、落叶阔叶混交林、落叶矮林、针阔混交林、竹林等。
-
2005年，在天目山国家级自然保护区常绿阔叶林内选择有代表性的地段设置大小为100 m×100 m的固定样地，用相邻格子调查方法将固定样地分为100个10 m×10 m的网格，按从下到上、从左到右顺序对网格编号，用每个网格的左下角行列号作为网格编号。以每个网格为调查单元，对样地内胸径大于5 cm的林木进行每木检尺，记录树木种类，测定每株树木的胸径、树高、活枝下高、冠幅等因子，采用激光对中全站仪(徕卡TCR702Xrange)测定每株树木坐标(x，y，z)。从2005年开始，隔5 a对固定样地进行1次复查。本研究利用2015年的复查数据进行分析。样地内的树种共86种，总株数1 869株，常绿阔叶优势种有细叶青冈、青冈、短尾柯、豹皮樟、小叶青冈等(表1)。
树种 株数 株数比例/% 细叶青冈Cyclobalanopsis gracilis 464 24.83 青冈C. glauca 187 10.01 短尾柯Lithocarpus brevicaudatus 163 8.72 豹皮樟Litsea coreana 100 5.35 小叶青冈C. myrsinifolia 82 4.39 连蕊茶Camellia fraterna 55 2.94 大叶冬青Ilex latifolia 28 1.50 浙江樟Cinnamomum chekiangense 19 1.02 主要优势树种合计 1 098 58.75 全部树种合计 1 869 100.00 Table 1. Main dominant species in the sample plot
-
空间结构单元 (spatial structural unit)是分析林分空间结构的基本单位，由对象木和相邻木构成。本研究采用汤孟平等[21]提出的基于Voronoi图确定空间结构单元的方法，以对象木所在多边形的相邻多边形内的林木作为相邻木。为了消除边缘效应，对样地采用8领域法进行边缘矫正。如图1所示(仅列出部分)。
Figure 1. Diagram of competition unit and marginal correction
-
混交度(mingling，M)用来描述林分内树种的空间隔离程度，被定义为对象木的相邻木中和对象木不是同种株数所占的比例[22]。本研究运用汤孟平等[23]提出的树种多样性混交度。计算公式：
式(1)~(2)中：Mi为对象木i的混交度；n为相邻木株数；ni为对象木i的竞争单元中相邻木j之间的树种不同的个数；vij为离散变量，当相邻木j与对象木的树种不同时，vij=1，否则，vij=0；N为林分内林木株数；M为林分混交度。若M=0，属于0度混交；若M=0.25，属于弱度混交；若M=0.50，属于中度混交；若M=0.75，属于强度混交；若M=1.00，属于极强度混交。
-
竞争指数(competition index，IC)用来描述林分内林木之间的竞争关系。采用基于Voronoi图的Hegyi竞争指数[21]。计算公式：
式(3)~(4)中：ICi为对象木i的竞争指数；Lij为对象木与相邻木之间的距离；di为对象木的胸径；dj为相邻木的胸径；ni为对象木i所在竞争单元的相邻木株数；N为对象木株数；IC为林分竞争指数。
汤孟平等[21]根据竞争指数的变动范围对竞争强度进行分级。本研究采用此方法，根据竞争指数的差异和100个网格单元的竞争指数从大到小排序将竞争强度为3级：若IC≤8，属于弱度竞争；若8＜IC≤16，属于中度竞争；若IC＞16，属于强度竞争。
-
聚集指数(aggregation index，R)用来描林木在空间位置上的分布状况，定义为最近邻单株距离的平均值与随机分布的期望平均距离之比[24]：
式(5)中：R为聚集指数，N为样地内林木株数，F为样地面积，ri为对象木到其最近邻木的距离。若R＜1，则空间分布趋于聚集分布；若R=1，则空间分布趋于随机分布；若R＞1，则空间分布趋于均匀分布。
-
汤孟平等[5]利用数字高程模型(DEM)，提取每个网格单元的坡度和坡向等地形信息，分析不同地形条件下常绿阔叶林群落物种多样性与胸高断面积的差异。本研究借鉴此方法，根据激光对中全站仪(徕卡TCR702Xrange)测定固定样地网格线交点处的坐标(x，y，z)，计算网格单元的坡度和坡向[5, 25]。海拔高度为网格线4个交点高程的平均值。计算公式为：
其中：Si, j为坡度(°)，Ai, j为坡向角(°)，Ei, j为海拔(m)，Ri, j为地表粗糙度(m)；∆x和∆y为网格的投影边长(m)，Zi,j为网格线交点的高程(m)；i为网格线行号，i=0、1、2、
$\cdots $ 、10；j为网格线列号，j=0、1、2、$\cdots $ 、10。根据样地内各网格单元的坡向、坡度、地表粗糙度、海拔的分布范围，将样地的坡向等级划分为阳坡和半阳坡；坡度等级划分为Ⅰ级坡(20°~30°)、Ⅱ级坡(30°~40°)、Ⅲ级坡(40°以上)；地表粗糙度划分为Ⅰ级粗糙度(0~0.5 m)、Ⅱ级粗糙度(0.5~1.0 m)、Ⅲ级粗糙度(1.0 m以上)[5]；将海拔划分为低海拔(590~620 m)、中海拔(620~650 m)、高海拔(650~680 m)。
-
在Excel 2013中对数据进行预处理，基于ArcMap 10.2和Python语言编程计算每个网格单元(10 m×10 m)的林分空间结构指数，在SPSS 20.0软件中采用单因素方差分析与多因素方差分析评价天目山常绿阔叶林在不同地形条件下森林空间结构特征的差异性。空间结构指数在不同地形因子组合中的差异性分析通过SPSS 20.0语言编程完成，采用最小显著性差异法(LSD)检验是否具有显著性。
2.1. 样地设置
2.2. 林分空间结构分析方法
2.2.1. 空间结构单元
2.2.2. 混交度
2.2.3. 竞争指数
2.2.4. 聚集指数
2.3. 地形因子
2.4. 统计分析
-
林分空间结构指标的统计描述：样地的单位面积株数为1 869株·hm−2，平均胸径为9.86 cm，平均树高为5.73 m；林分树种多样性混交度为0.53，说明林分的树种隔离程度属于中度混交；林分的聚集指数为0.68，说明林分的林木分布格局属于聚集分布；林分的平均竞争指数14.04，说明林分中林木的竞争状况为中等竞争。
-
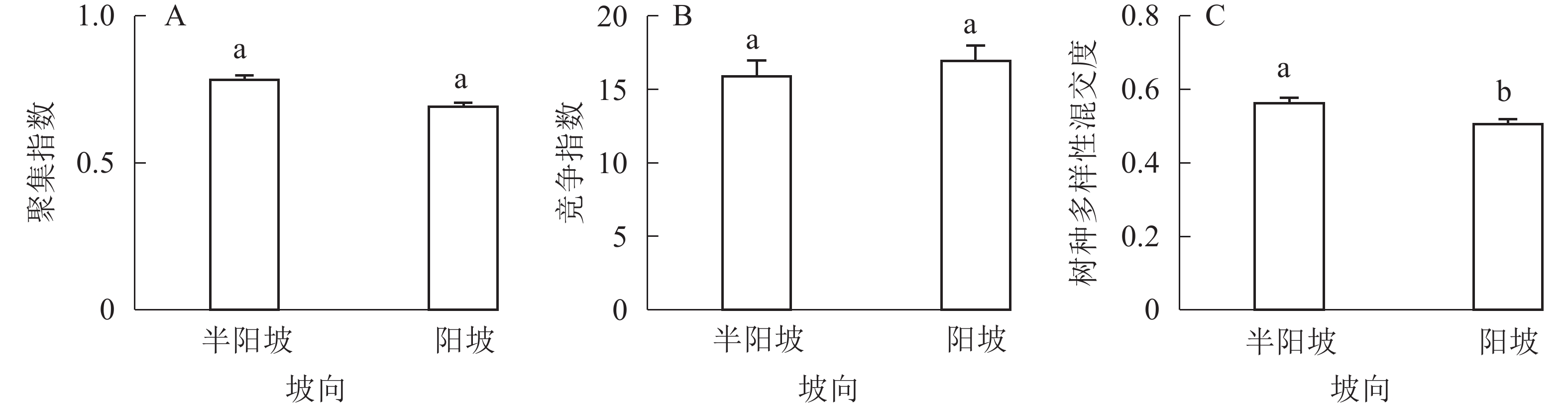
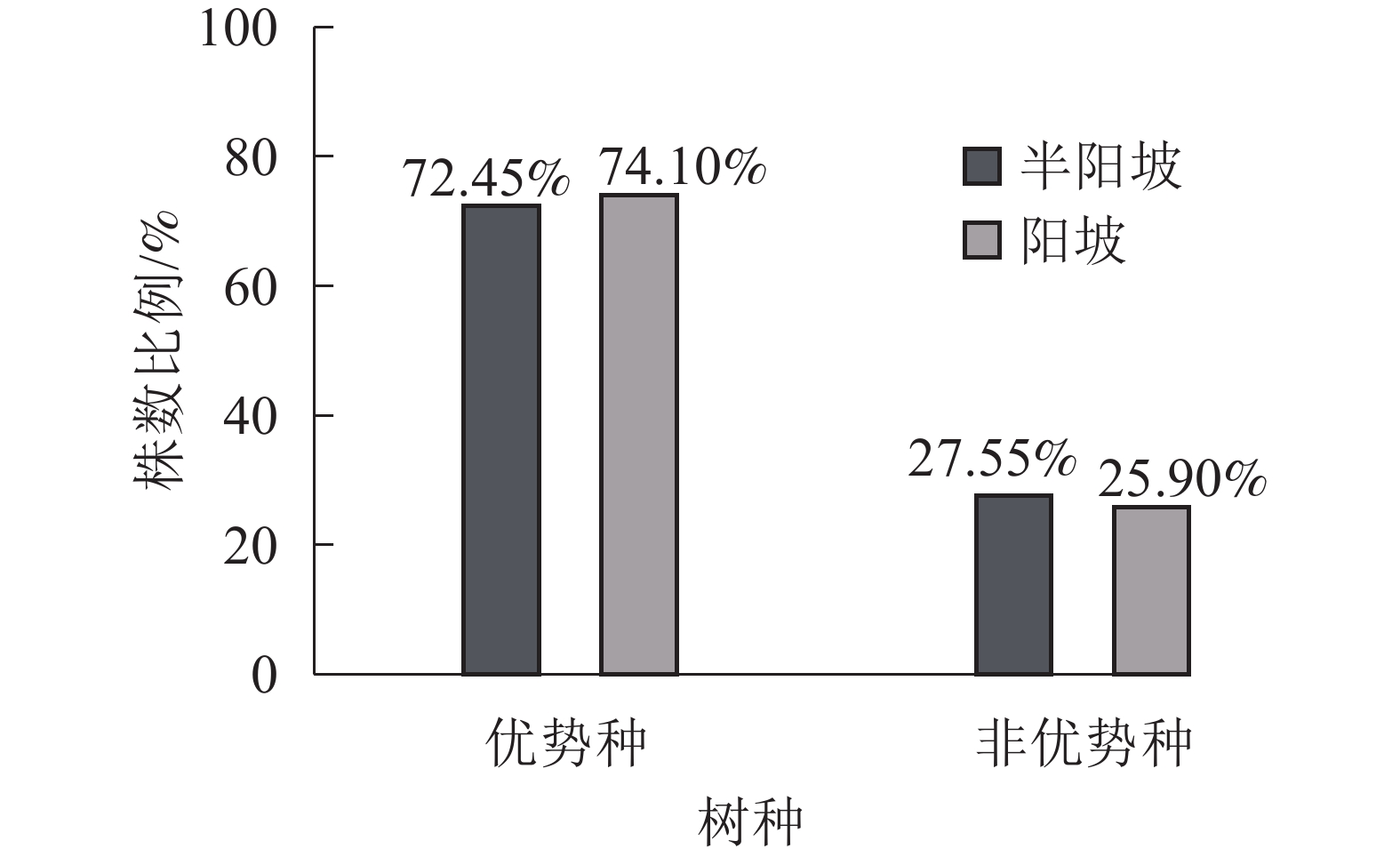
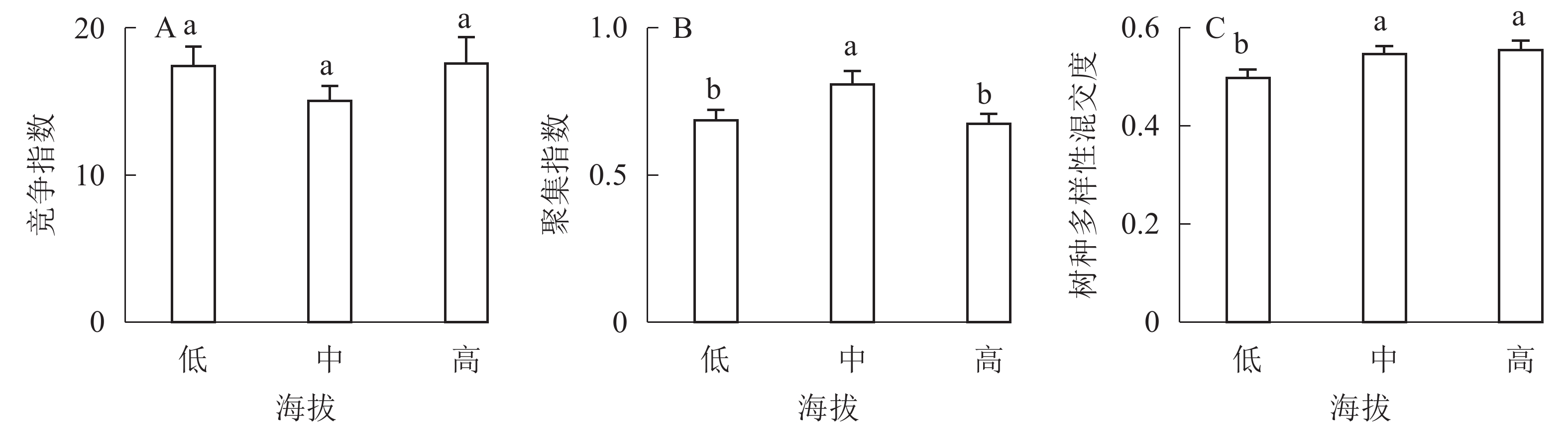
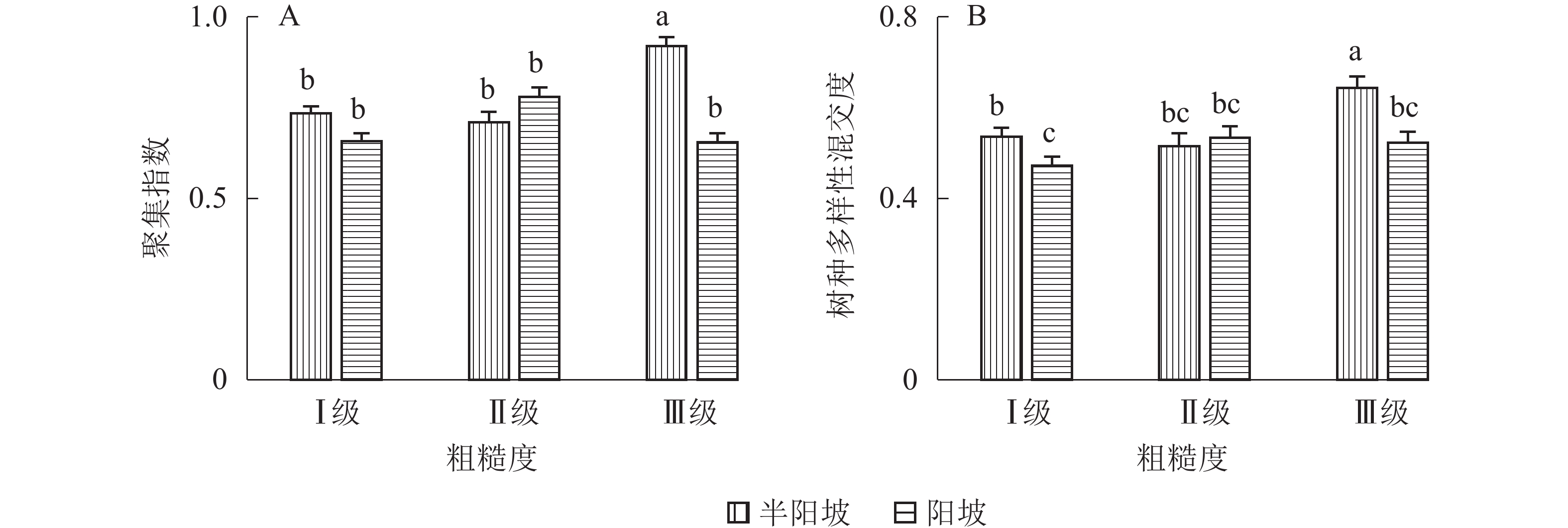
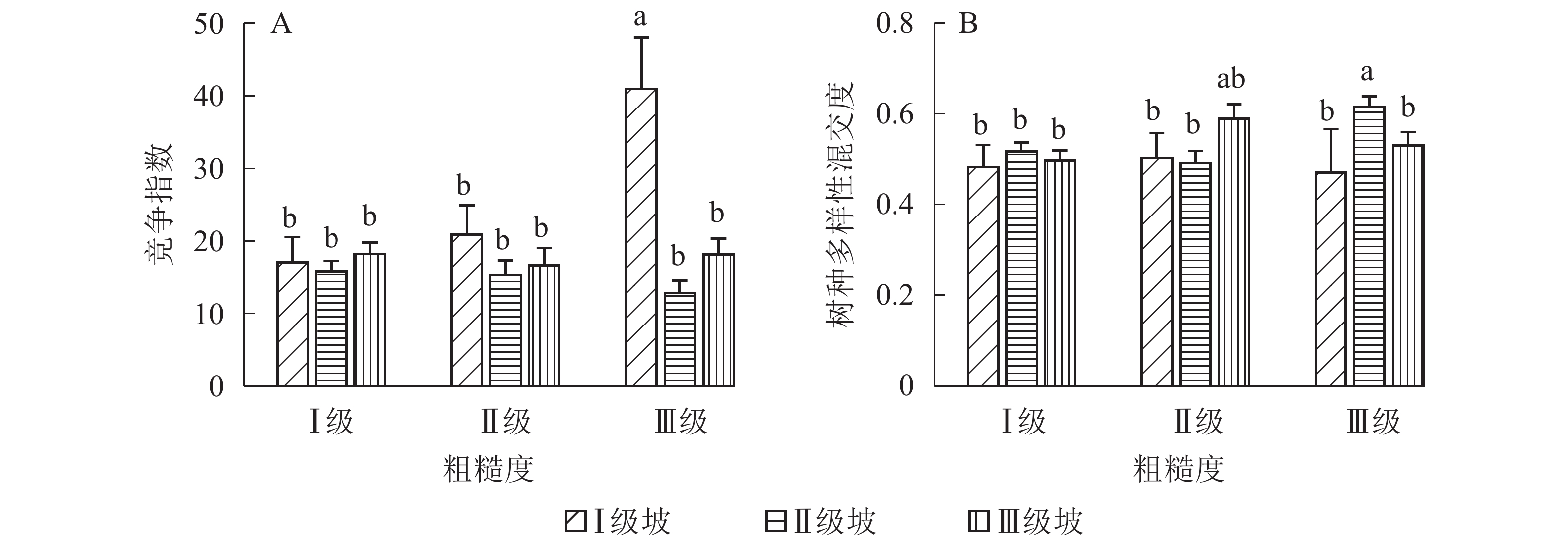
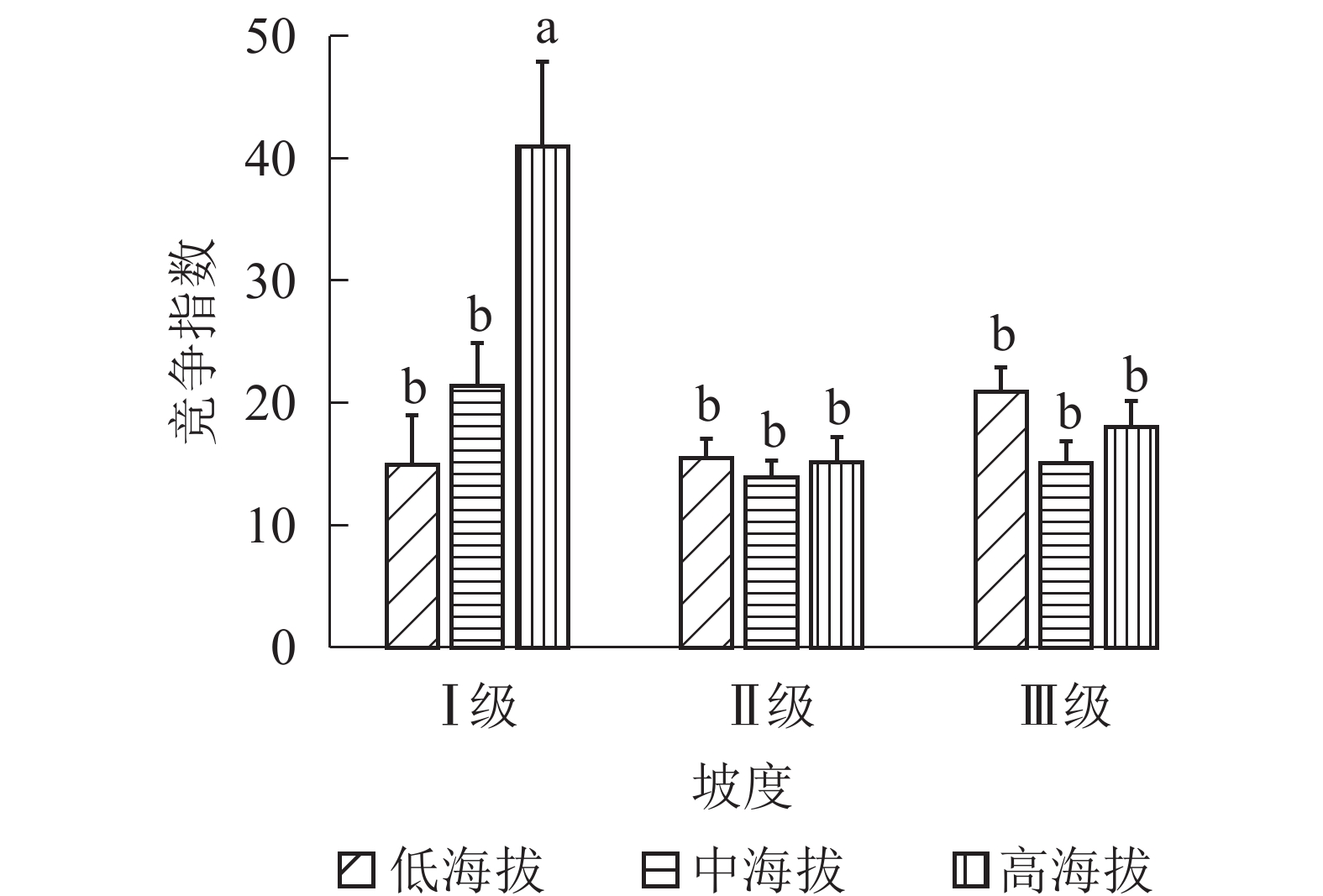
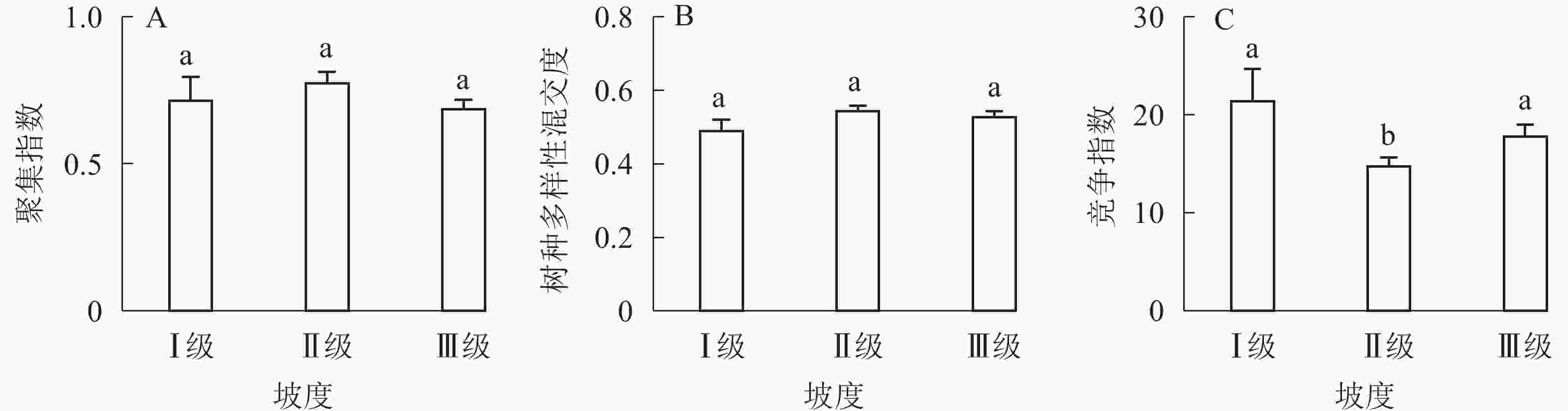
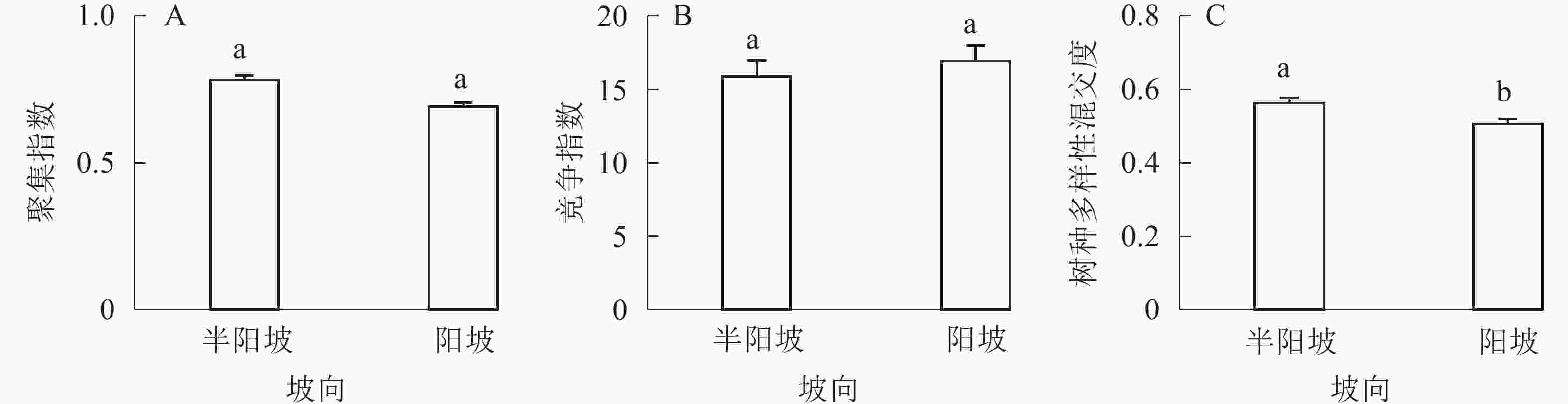
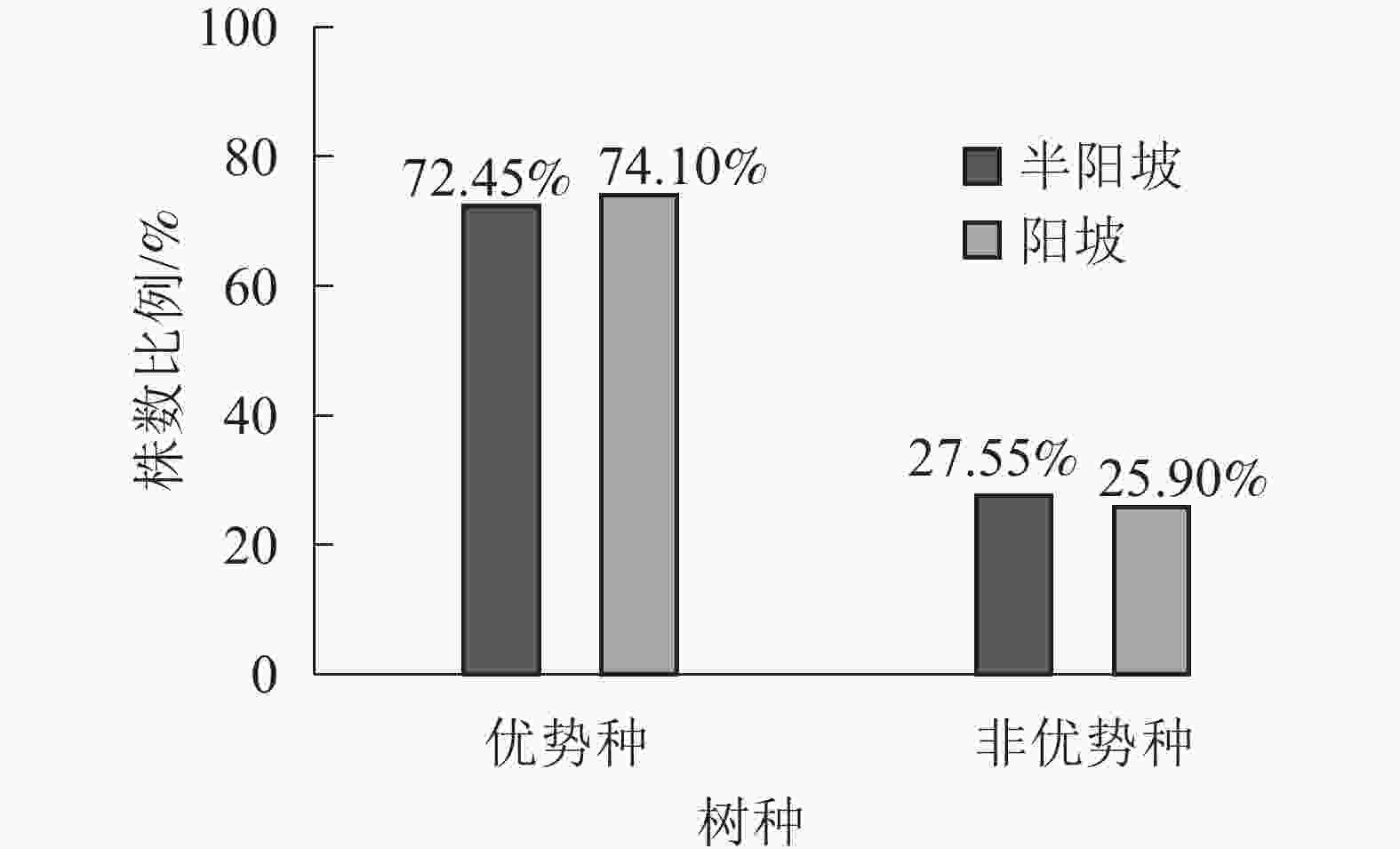
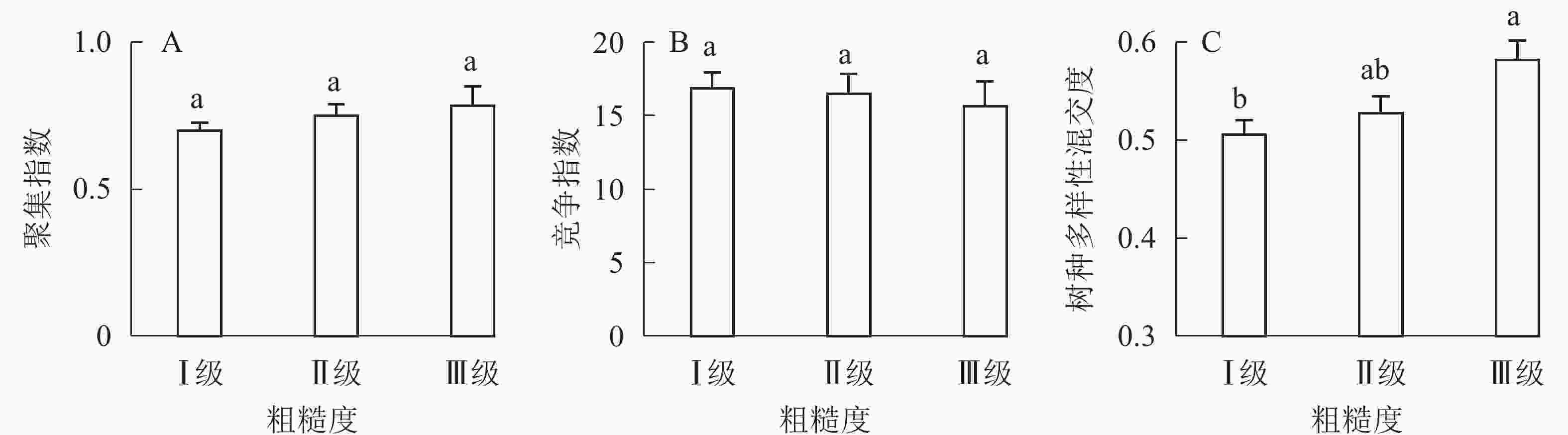
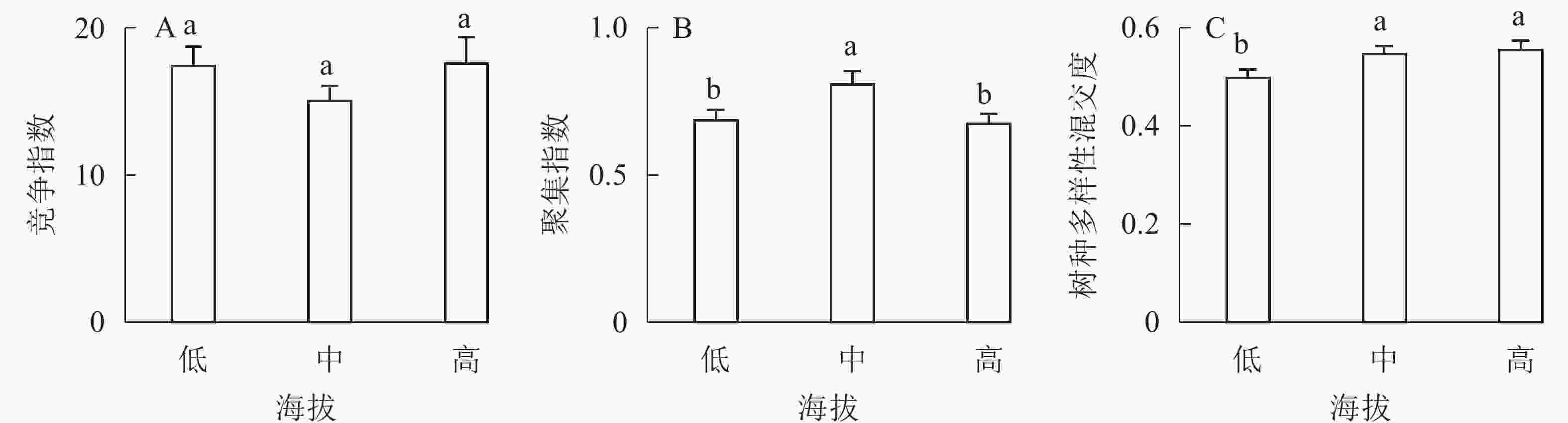
①坡度因子对林分空间结构的影响。由图2可知：坡度对聚集指数和树种多样性混交度影响均不显著(图2A和图2B)，对竞争指数具有显著影响(图2C)。Ⅱ级坡的竞争指数与Ⅰ级坡、Ⅲ级坡存在显著差异(P＜0.05)，而Ⅰ级坡与Ⅲ级坡无显著差异。随着坡度的增大，竞争指数呈先减小后增大的趋势，说明坡度过大或过小，都会导致林木受到来自侧方挤压和上方遮盖程度加剧。②坡向因子对林分空间结构的影响。由图3可知：半阳坡的聚集指数和竞争指数与阳坡不存在显著差异(图3A和图3B)。半阳坡的树种多样性混交度与阳坡存在显著差异(P＜0.05)，并且半阳坡的树种多样性混交度显著高于阳坡(图3C)，说明半阳坡的树种隔离程度高于阳坡，同种个体聚集生长的情况相对较少。相对而言，优势树种多分布于阳坡，非优势树种多分布于半阳坡(图4)，表明阳坡中有利于优势种株数的生长，而半阳坡有利于非优势种株数的生长。可见，半阳坡的树种多样性混交度高于阳坡与树种在坡向中的分布具有密切的关系。③粗糙度对林分空间结构的影响。图5表明：粗糙度对聚集指数和竞争指数的影响不显著(图5A和图5B)，对树种多样性混交度的影响存在显著差异(图5C)。Ⅰ级粗糙度的树种多样性混交度与Ⅲ级粗糙度存在显著差异(P＜0.05)，而Ⅱ级粗糙度与Ⅰ级粗糙度、Ⅲ级粗糙度无显著差异，且树种多样性混交度随着粗糙度的增大而增大，说明地表的起伏程度越大，林分内同种个体聚集生长的情况较少。④海拔因子对林分空间结构的影响。由图6可知：海拔对竞争指数的影响不大(图6A)，但对聚集指数和树种多样性混交度具有不同程度的影响(图6B和图6C)。其中，中海拔区域的聚集指数显著高于低海拔和高海拔区域(P＜0.05)，而低海拔和高海拔区域无显著差异；随着海拔的升高，聚集指数呈先增大后减小的趋势，而树种多样性混交度呈增大的趋势，说明在样地内海拔过高或过低，都会导致林分内林木的空间分布格局相对更聚集；同时，随着样地内海拔的升高，林内同种个体聚集生长的情况减小。
Figure 2. Influence of slope factor on forest spatial structure
Figure 3. Influence of aspect factor on forest spatial structure
Figure 4. Proportion of the number of tree species in different aspect
Figure 5. Influence of roughness on forest spatial structure
Figure 6. Influence of altitude factor on forest spatial structure
-
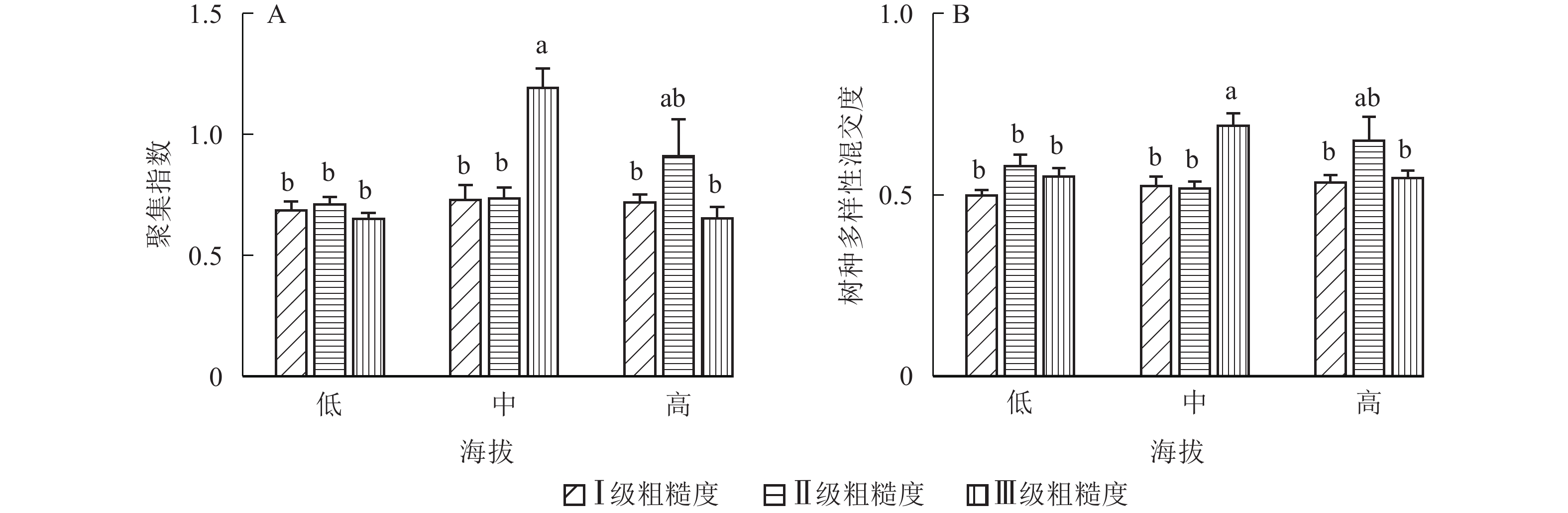
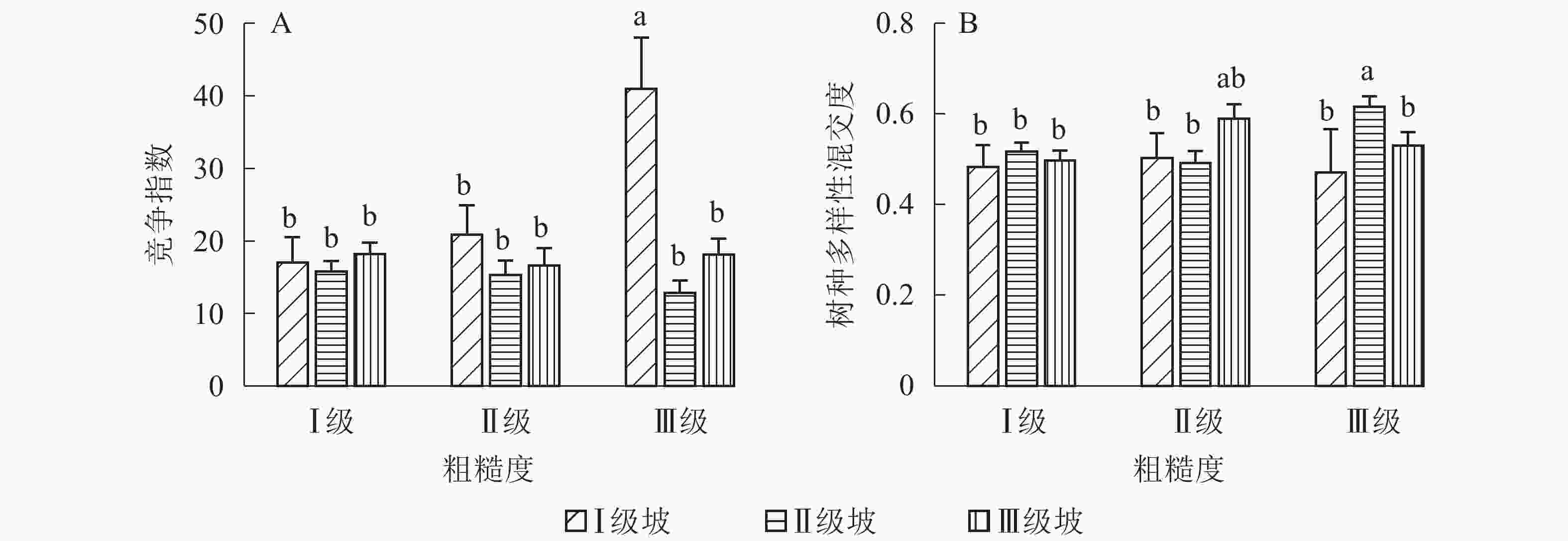
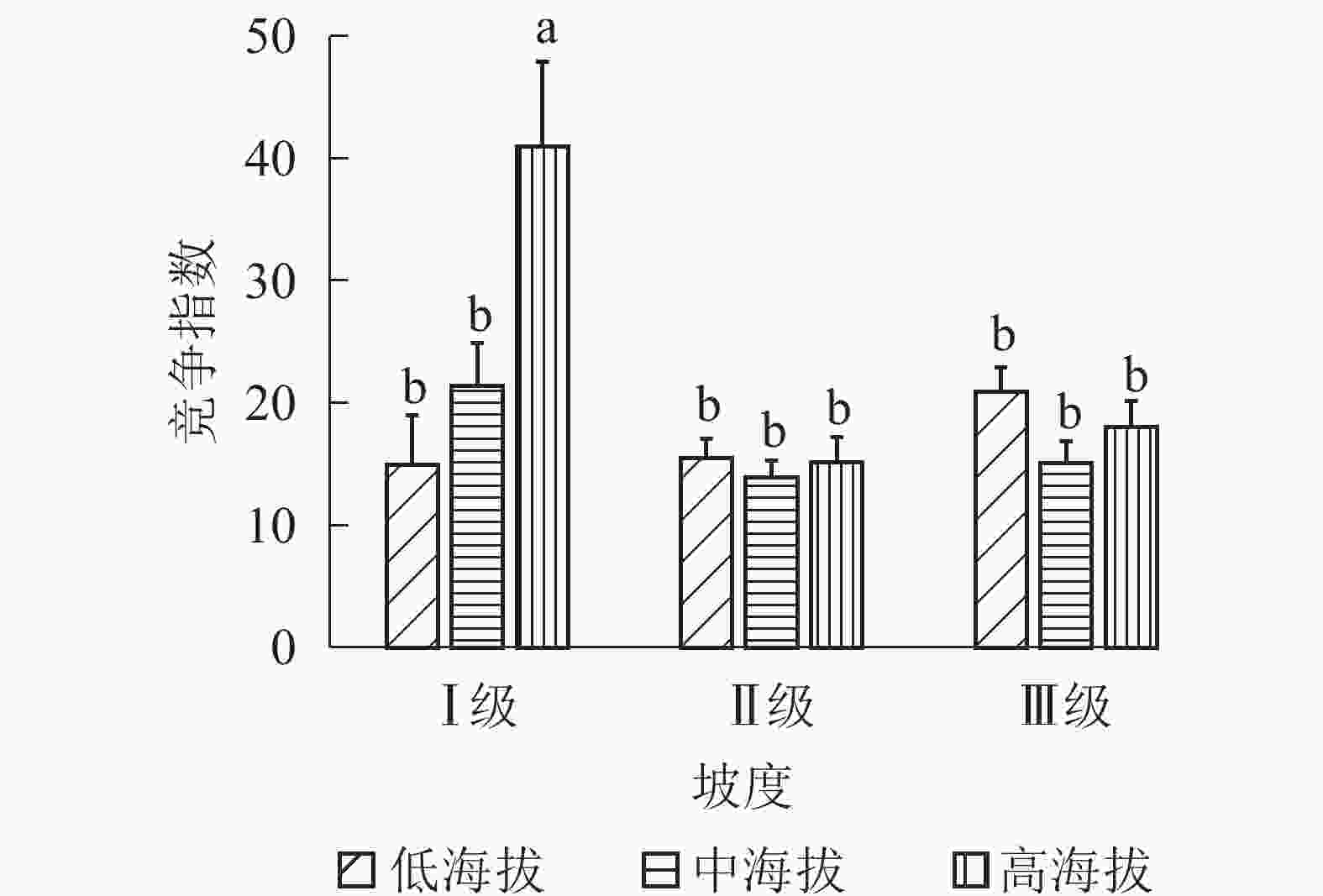
地形因子的组合与林分空间结构指数的多因素方差分析表明(表2)：在坡向与粗糙度、海拔与粗糙度的组合中，聚集指数均存在显著差异(P＜0.05)；在坡度与海拔、坡度与粗糙度的组合中，竞争指数均存在显著差异(P＜0.05)；在坡度和粗糙度、坡向与粗糙度、海拔与粗糙度的组合中，树种多样性混交度存在显著差异(P＜0.05)；其他地形因子两两组合对空间结构指数均不存在显著差异。①粗糙度与海拔因子组合。进一步分析粗糙度与海拔因子组合对聚集指数、树种多样性混交度的影响。由图7可知：在中海拔区域，Ⅲ级粗糙度的聚集指数、树种多样性混交度均显著高于Ⅰ级粗糙度、Ⅱ级粗糙度(P＜0.05)；在Ⅲ级粗糙度中，高海拔与中海拔的聚集指数、树种多样性混交度均存在显著差异(P＜0.05)，中海拔区域的聚集指数显著高于高海拔区域。说明在样地内的中海拔区域，Ⅲ级粗糙度中的林木空间分布格局更均匀，树种隔离程度更高。②粗糙度与坡向因子组合。由图8A可知：在Ⅲ级粗糙度中，半阳坡的聚集指数显著高于阳坡(P＜0.05)；在半阳坡中，Ⅲ级粗糙度的聚集指数显著高于Ⅰ级粗糙度、Ⅱ级粗糙度(P＜0.05)。由图8B可知：在半阳坡中，Ⅲ级粗糙度的树种多样性混交度显著高于Ⅰ级粗糙度、Ⅱ级粗糙度(P＜0.05)；在Ⅰ级粗糙度、Ⅲ级粗糙度中，半阳坡的树种多样性混交度显著高于阳坡(P＜0.05)。可见，在半阳坡中，Ⅲ级粗糙度中的林木空间分布格局更均匀，Ⅲ级粗糙度中的树种隔离程度更高。③粗糙度与坡度因子组合。粗糙度与坡度因子组合对竞争指数、树种多样性混交度的影响见图9。由图9A可知：在Ⅰ级坡中，Ⅲ级粗糙度的竞争指数显著高于Ⅰ级粗糙度、Ⅱ级粗糙度(P＜0.05)；在Ⅲ级粗糙度中，Ⅰ级坡的竞争指数显著高于Ⅱ级坡、Ⅲ级坡(P＜0.05)。说明在Ⅰ级坡中，Ⅲ级粗糙度的林木受到来自侧方挤压和上方遮盖程度更强。由图9B可知，在Ⅱ级坡中，Ⅲ级粗糙度的树种多样性混交度显著高于Ⅰ级粗糙度、Ⅱ级粗糙度(P＜0.05)；在Ⅲ级粗糙度中，Ⅱ级坡的树种多样性混交度显著高于Ⅰ级坡、Ⅲ级坡(P＜0.05)。说明在Ⅱ级坡中，Ⅲ级粗糙度的树种隔离程度较高，同种个体聚集生长的情况降低。④海拔与坡度因子组合。由海拔与坡度因子组合对竞争指数的影响可知(图10)：在高海拔区域，Ⅰ级坡中的竞争指数显著高于Ⅱ级坡、Ⅲ级坡(P＜0.05)；在Ⅰ级坡中，高海拔区域的竞争指数显著高于Ⅱ级坡、Ⅲ级坡(P＜0.05)。说明在样地内的高海拔区域，Ⅰ级坡中的林木竞争情况更激烈。
组合因子 空间结构指数 显著性 组合因子 空间结构指数 显著性 坡度×坡向 聚集指数 0.054 坡向×海拔 聚集指数 0.755 竞争指数 0.764 竞争指数 0.618 树种多样性混交度 0.856 树种多样性混交度 0.262 坡度×海拔 聚集指数 0.867 坡向×粗糙度 聚集指数 0.042 竞争指数 0.017 竞争指数 0.274 树种多样性混交度 0.461 树种多样性混交度 0.025 坡度×粗糙度 聚集指数 0.233 海拔×粗糙度 聚集指数 0.000 竞争指数 0.032 竞争指数 0.062 树种多样性混交度 0.026 树种多样性混交度 0.001 Table 2. Statistical table of multivariate analysis of variance
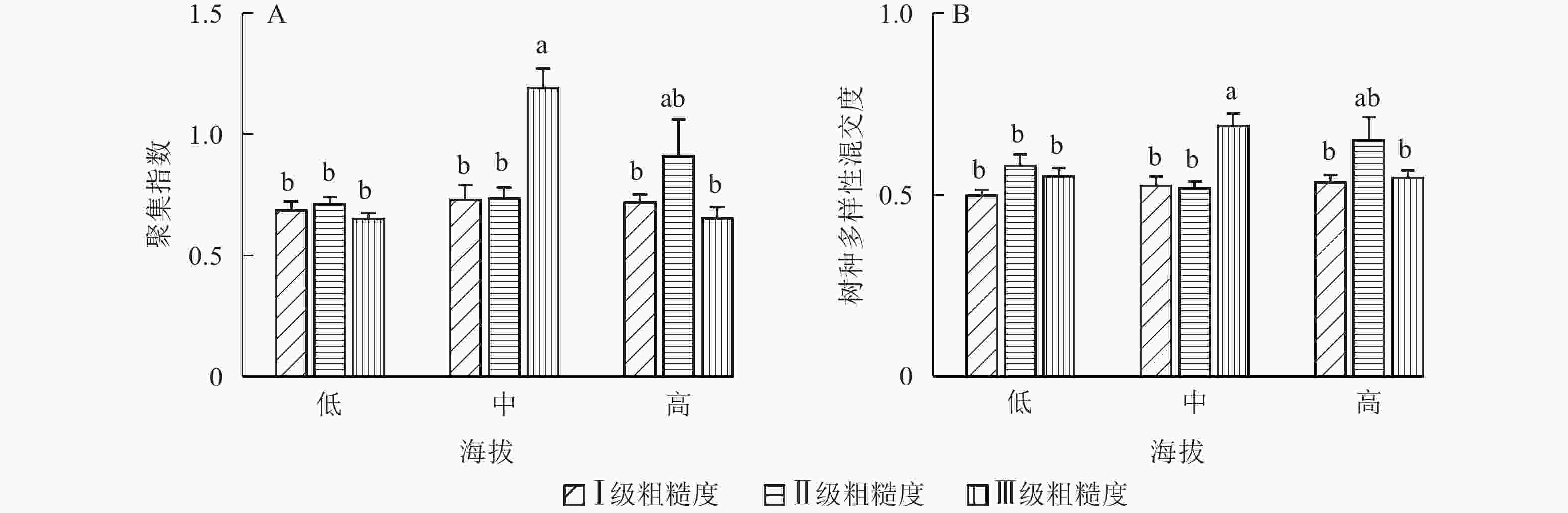
Figure 7. Influence of combination of roughness and altitude factors on aggregation index and tree species diversity mingling
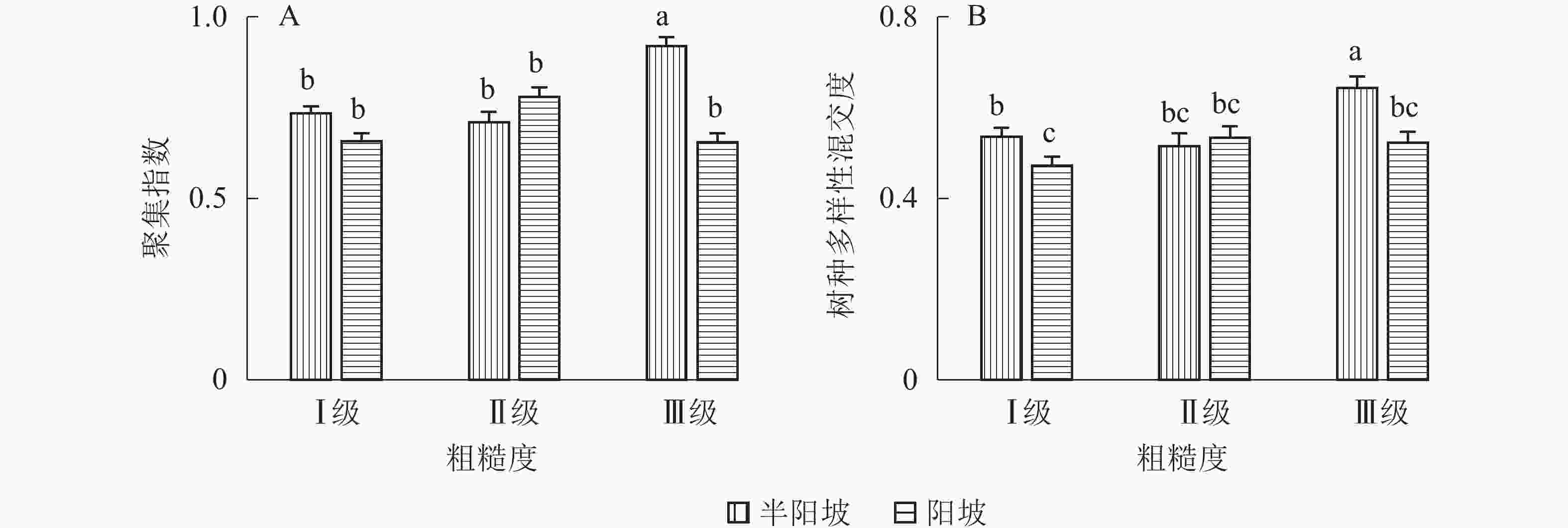
Figure 8. Influence of combination of roughness and aspect factors on aggregation index and tree species diversity mingling
Figure 9. Influence of combination of roughness and slope factors on competition index and tree species diversity mingling
Figure 10. Influence of combination of altitude and slope factors on competition index
3.1. 林分空间结构特征
3.2. 地形因子对林分空间结构的影响
3.2.1. 单一地形因子对林分空间结构的影响
3.2.2. 地形因子的组合对林分空间结构的影响
-
本研究表明：在常绿阔叶林群落中，不同的地形因子对其空间结构特征有着不同程度的影响。从单一地形因子来看，坡度主要影响竞争指数，坡度过大或过小，都会导致竞争指数增大，使林木受到来自侧方挤压和上方遮盖程度加剧；坡向和粗糙度对树种多样性混交度存在显著影响，半阳坡的树种隔离程度显著高于阳坡，而粗糙度越大树种隔离程度越高；海拔主要影响树种多样性混交度和聚集指数，样地内海拔过高或过低，都会引起聚集指数降低，使林分内林木的空间分布格局相对更聚集，而样地内海拔越高，林分的树种隔离程度越高。从地形因子组合来看，坡度与粗糙度的组合对竞争指数和树种多样性混交度具有显著影响，在Ⅲ级粗糙度中，Ⅰ级坡的竞争指数最大，而Ⅱ级坡的树种多样性混交度最高；坡度与海拔的组合对竞争指数的影响显著，在样地内的高海拔区域，Ⅰ级坡的林木竞争程度加剧；海拔与粗糙度的组合主要影响聚集指数和树种多样性混交度，在样地内的中海拔区域，Ⅲ级粗糙度的林木空间分布格局更均匀，树种隔离程度更高；坡向与粗糙度的组合对聚集指数和树种多样性混交度存在显著影响，在半阳坡中，Ⅲ级粗糙度的林木空间分布格局更均匀，Ⅰ级粗糙度、Ⅲ级粗糙度的树种隔离程度较高。因此，在森林经营过程中，不可忽视地形因子对林分空间结构的作用。在一定地形条件下，合理调控常绿阔叶林的空间结构是促进树木生长的重要经营策略。
-
地形因子通过影响林分所处的水、热和养分环境，在一定程度上决定林分的空间结构特征[26-27]。树种多样性混交度从半阳坡到阳坡呈下降趋势，这与孙洪刚等[28]研究结果一致。阳坡优势种的株数比例分布多于半阳坡，但非优势树种的株数比例分布少于半阳坡，原因是阳坡光照充足，有利于优势种的生长，且细叶青冈、青冈等优势种群兼有萌生和实生的繁殖更新方式[27]，使同种个体聚集生长的情况增加；半阳坡相对凉爽湿润，促进非优势种的生长，而青冈、短尾柯、豹皮樟等部分优势树种占比减小，使同种个体聚集生长的情况减小。在样地范围内随海拔升高，树种隔离程度增强。这与王志鸣等[29]研究结果一致，可能是随着海拔升高，种内竞争增强，自疏作用加剧，同种个体间的聚集情况降低，从而使林木个体间的树种隔离程度增强。在常绿阔叶林群落中，坡度过大或过小都会导致林木间的竞争加剧。这与汤孟平等[5]研究坡度对物种多样性和胸高断面积的影响变化趋势相反，说明竞争指数随着坡度的变化与林内的物种多样性和胸高断面积息息相关。因此，在未来的研究中可以此为切入点，研究不同坡度等级下林木竞争状况与物种多样性和胸高断面积之间的关系。样地粗糙度越大，地表起伏程度就越高，易形成多样的微环境，从而促进不同树木生长。纵观不同空间结构指数对地形因子的响应可知，聚集指数与树种多样性混交度对同一地形因子的变化趋势是相似的，而竞争指数对同一地形因子的变化趋势与聚集指数与树种多样性混交度对地形因子的响应是相反的，说明不同空间结构指数之间存在一定的联系。
本研究不仅分析了单个地形因子对空间结构指数的影响，同时也具体分析了空间结构在不同地形因子组合中的差异性，从而更深入地揭示林分空间结构与地形因子之间的关系。但从实际情况来看，除地形因子外，林分空间结构还受土壤有机质[26]、不同的经营方法[18, 30]与树种组成[31]等指标的影响。因此，对影响林分空间结构的各个指标进行综合的分析是全面掌握和了解地形因子在林分空间结构中所起作用的关键。
DownLoad: