下载:
-
尺度的合理选择对研究区土地利用景观变化和生态效应的分析具有科学的指导意义，也是目前景观生态学和地理学研究的热点问题之一。尺度的选择是进行生态学研究的基础，通常由空间粒度和幅度来描述。空间粒度是指景观中可以辨别的最小单元，所代表的特征长度、面积和体积，在空间数据和图像资料中通常对应于最大分辨率和像元的大小[1]。进行生态学研究的位置不同，粒度的划分方法、划分范围、步长的选择等均不相同[2-4]；数据源大多采用遥感影像人工解译法获得的解译图或土地利用现状图等[5-7]，研究区域多集中于城市热岛[8-10]、典型区域[11]、生态脆弱区[12-13]、流域或交通沿线等[14-18]。地形和地貌的差异会造成景观指数不同的粒度响应，只有当测量尺度、研究对象及本质特征与研究区符合时，景观指数才能将研究区的景观格局特征显示和反映出来[2]。因此，适宜空间粒度的选择，是反映景观格局状况和景观生态研究的关键。县域不仅是行政区划的重要单元，更是连接城市与乡村的重要节点。目前，景观指数粒度效应多以大尺度区域为研究对象，如孟楠等[19]研究发现：中国澳门城市生态系统格局分析的最佳粒度为25 m，张玲玲等[20]研究得出：沂蒙山区景观指数最佳粒度为35 m，马胜等[13]研究表明：黄土高原生态脆弱区景观生态风险分析的最佳粒度为120 m。而对县域尺度等中小区域的案例研究较少。鉴于此，本研究分析了安徽省宿松县不同景观指数在类型和景观水平下的粒度效应，以探讨长江中下游县域景观的粒度效应问题，对揭示县域景观生态规律具有一定的指导意义。
-
宿松县(29°47′~30°26′N，115°52′~116°35′E)位于安徽省西南方向，是长江中下游北岸的顶端。全县东西宽约67 km，南北长约72 km，总面积达2 394 km2。东北接壤太湖县，西边紧邻湖北省的蕲春县和黄梅县，东南角连接望江县，南边隔江相望于江西省的湖口县和彭泽县，是皖、鄂、赣三省的交界处，也是八县结合部。宿松县地势高低起伏明显，呈阶梯形式自西北向东南方向地势逐渐降低，属北亚热带湿润季风气候，四季分明，季风性明显，光照充足，雨水多，平均无霜期为255 d，植物生长期长。
-
以宿松县研究区2017年的地理国情普查成果为依据，结合研究目标，参考GB/T 21010−2017《土地利用现状分类》，根据土地实际用途以及地物意义，将地理国情普查数据中的地表覆盖分类重新划分为耕地、园地、林地、草地、建筑用地(房屋建筑区、构筑物、人工堆掘地)、交通用地(道路)、水域、未利用地(荒漠与裸露地表)等8个土地利用类型[21]。通过ArcGIS对划分后的土地斑块类型进行分类合并处理。
-
研究区范围以及景观格局的不同，粒度范围及步长的选择也大小不一，通常大步长会掩盖小步长的变化规律，小步长则可重演大步长的尺度变化规律[22]。因此，本研究以筛选合并的景观类型专题图为基础，参考前人粒度范围及步长的划分案例[8-12]，结合研究区实际概况，运用ArcToolbox中的Feature to Raster工具和重采样工具，将源数据转化为20~150 m以10 m为步长的14个数据，150~500以50 m为步长的7个数据，共21幅不同景观类型栅格图。
-
本研究根据实际需要从景观面积、形状复杂程度、聚集和散布状况、优势度、多样性等方面选取对粒度变化敏感且能较全面反映整个景观格局特征的景观指数。其中：在类型水平上选取斑块类型面积、斑块密度、斑块形状指数、平均分维数、最大斑块面积比例、斑块数量、斑块类型面积比例、平均斑块面积、有效网格大小；在景观水平上，面积边缘指标选取了景观总面积、景观总周长、边缘密度、周长面积分维数，密度大小及差异指标选取了斑块密度、斑块数量、平均斑块面积，形状指标选取了平均形状指数、平均分维数、景观形状指数。聚散性指标选取了散布与并列指数、景观聚合度、景观聚集度、景观凝聚度。多样性指标选取了斑块丰富度、Simpson多样性指数、Simpson均匀度指数[13-15, 23-25]。
-
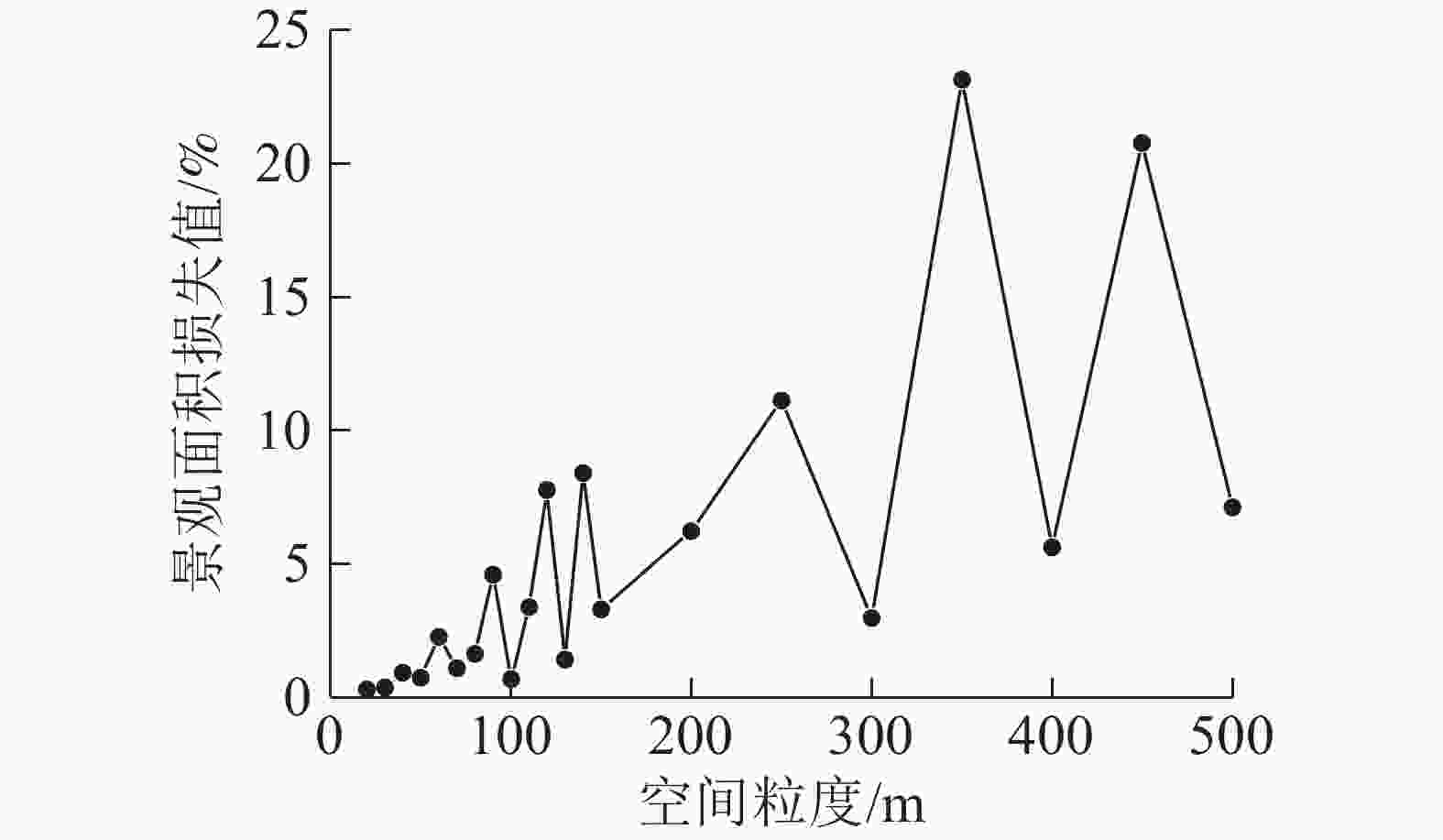
利用Fragstats 4.2软件计算景观格局指数，并在Origin 2018下绘制不同空间粒度下的景观指数曲线，最后建立景观格局指数与粒度之间的函数关系，用拟合度(R2)检验其相关性，R2最大为1，R2越接近于1，表明回归直线对景观指数曲线的拟合程度越高，反之，回归直线对景观指数曲线拟合程度越差。然后利用拐点法和景观面积损失评价法[26]，确定研究区土地利用景观最佳适宜粒度。景观面积损失评价模型为：
$$ P = \sqrt {\dfrac{{\sum\limits_{i = 1}^n {\mathop L\nolimits_i^2 } }}{n}} \text{；} \mathop L\nolimits_i = \dfrac{{\mathop A\nolimits_i - \mathop A\nolimits_{{\rm{b}}i} }}{{\mathop A\nolimits_{{\rm{b}}i} }} \times 100\% \text{。} $$ (1) 式(1)中：P表示区域景观面积损失值；Li表示i类景观面积损失相对值；Ai表示i类景观类型粒度变化后景观面积；Abi表示第i类景观粒度变化前的景观面积；n表示景观类型的总数目。
-
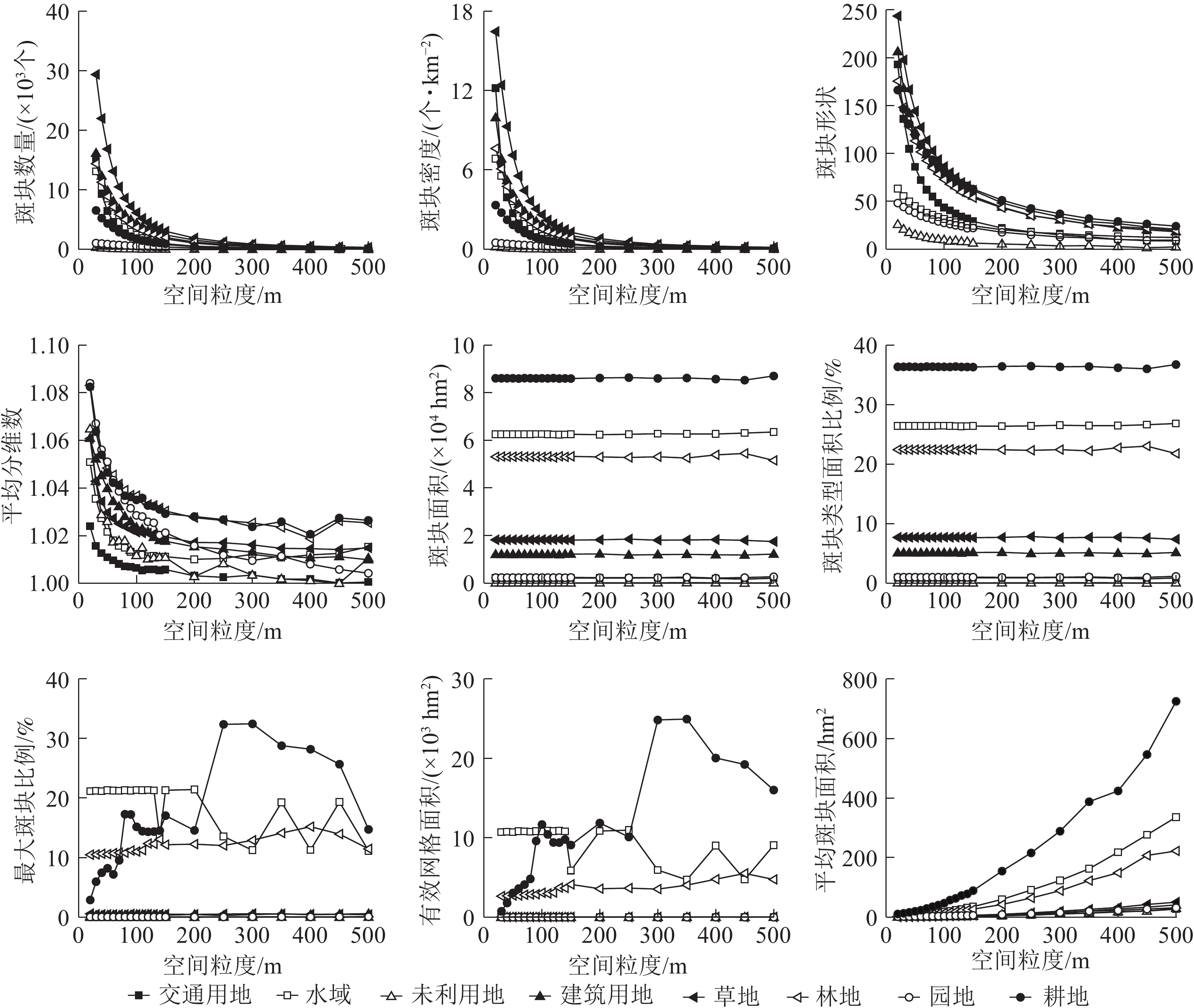
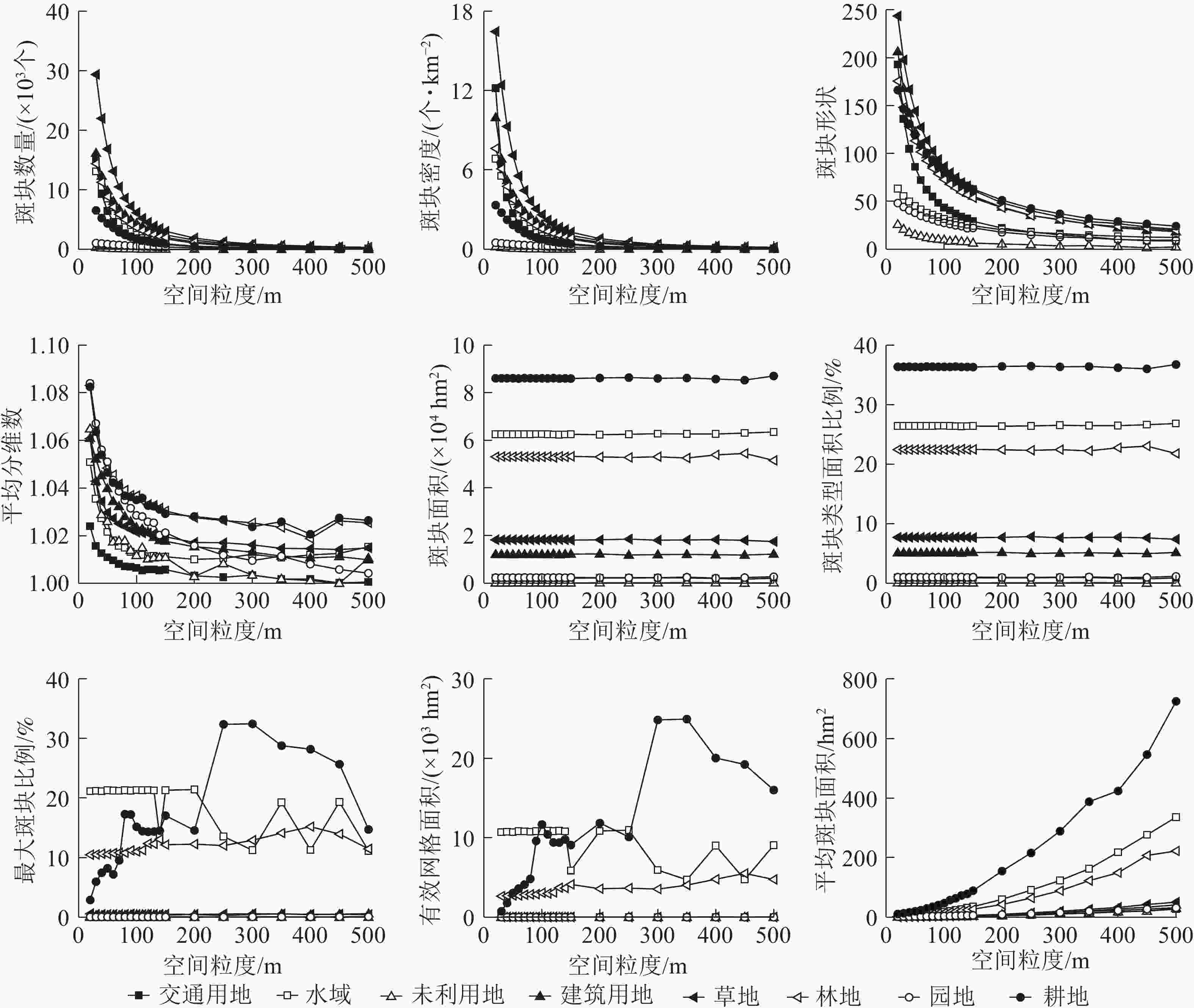
类型水平下宿松县的景观指数随着粒度的变粗呈不同的变化趋势(图1)。根据各种土地利用类型景观指数对粒度变化的响应差异，可以将宿松县类型水平指数分为以下4种类型。
图 1 类型水平下景观指数的粒度变化
Figure 1. Grain sizes change of landscape indices under type level
指数类型1包括斑块密度、斑块形状指数、斑块个数和平均分维数，呈逐渐减小的趋势，“L”型变化，与粒度的变化具有明显的响应关系。随着粒度的变粗，斑块个数、斑块密度、斑块形状指数下降幅度均比较剧烈，明显拐点为70 m，表明粒度的增加造成景观破碎度明显下降，景观异质性减小。其中草地、交通用地的斑块个数、斑块密度下降的最为剧烈，未利用地、园地变化幅度相对较小，这与研究区中草地分布较分散，交通用地相互交错、复杂分散，未利用地、园地面积较少，且分布较集中有关。水域、园地、未利用地景观形状指数变化不明显，与研究区中水域集中分布，耕地、水域、林地逐渐融合周围景观类型造成小斑块逐渐消失，斑块形状趋于单一有关。平均分维数明显的拐点为60 m，未利用地、园地、耕地、林地的下降的幅度较显著，建筑用地和园地降幅较大，未利用地变化趋势较复杂，与未利用地的斑块数目最少及呈聚集状态分布有关。
指数类型2包括斑块类型面积和斑块类型面积比例指数，无明显变化趋势，与粒度的变化具有明显的响应关系。随着粒度的增大，景观指数值均基本保持不变，粒度＞350 m后，林地的斑块类型面积和斑块类型面积比例上下波动，但变化较小，整体基本不变。研究区中土地利用类型的面积比例从大到小依次为耕地、水域、林地、草地、建筑用地、园地、交通用地、未利用地。
指数类型3包括最大斑块面积和有效网格大小指数，呈现“无规则”变化趋势，与粒度变化不具有明显的响应关系。林地、交通用地、未利用地、园地的景观指数变化幅度很小，且无明显拐点；草地明显拐点为70 m，在20~70 m内呈单调下降趋势，降幅明显；水域明显拐点为130 m，＞130 m后发生剧烈的浮动变化；建筑用地和耕地明显拐点为100 m，整体呈剧烈的不规则变化，但100~130 m呈轻微的波动变化，这与耕地、建筑用地分布较分散，130 m后景观异质性发生了变化有关；其他土地利用类型粒度效应响应不明显，这与自身斑块类型面积少且破碎度较大有关。
指数类型4包括平均斑块面积指数，呈现“J”上升趋势，与粒度的变化具有明显的响应关系。在不同的粒度范围内呈现出不同程度的增加趋势，转折点为150 m，20~70 m幅度增加很小；70~150 m幅度增加较大，但相对来说变化不大，＞150 m各土地利用类型的平均斑块面积指数急剧增大。这说明粒度的增大会引起大斑块夺取周围小斑块造成各土地类型的破碎度逐渐降低。
-
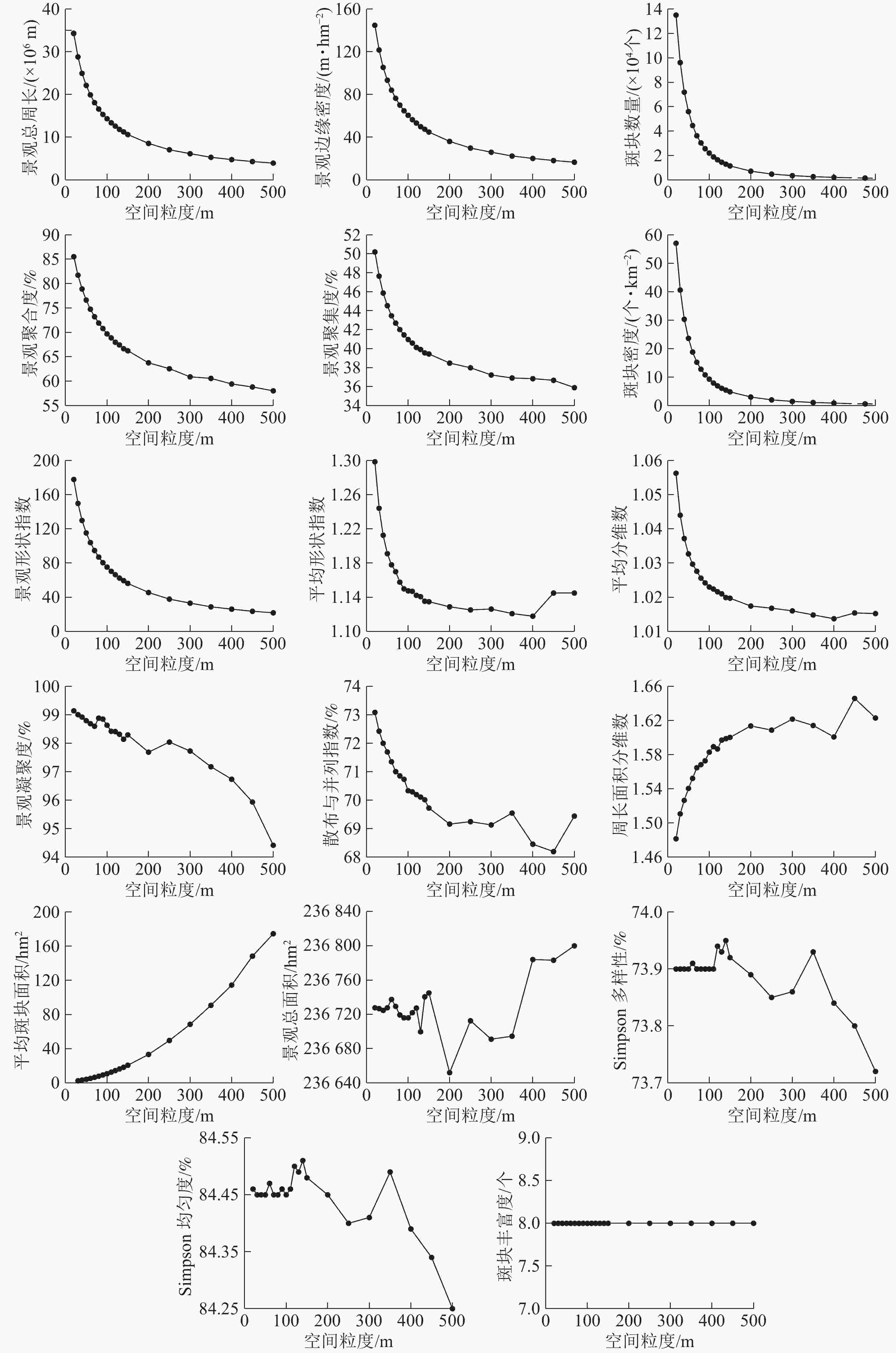
分别对不同的景观指数进行拟合，选取拟合程度最高的函数作为该景观指数的拟合函数(表1)。从图2可以看出：景观水平下的景观指数随着粒度的增大具有明显的响应关系。
表 1 景观水平下景观指数的拟合函数
Table 1. Fitting function of landscape horizontal landscape index
指标(y) 景观指数(x) 函数类型 拟合函数 拟合度(R2) 预测强度 面积边缘 景观总面积 二次多项式 $y = 12 \times \mathop {10}\nolimits^{ - 4} \mathop x\nolimits^2 - 0.474\;7x + 236\;751$ 0.570 较低 边缘密度 幂函数 $y = 1\;434.2\mathop x\nolimits^{ - 0.702} $ 0.988 极高 周长面积分维数 对数 $ y = 0.042\; 7 \ln\! x + 1.376\; 2 $ 0.903 高 景观总周长 幂函数 $y = 3 \times \mathop {10}\nolimits^8 \mathop x\nolimits^{ - 0.702} $ 0.988 极高 密度大小及差异 斑块密度 幂函数 $y = 8\;089.4\mathop x\nolimits^{ - 1.503} $ 0.986 极高 斑块数量 幂函数 $y = 2 \times \mathop {10}\nolimits^7 \mathop x\nolimits^{ - 1.503} $ 0.986 极高 平均斑块面积 二次多项式 $y = 6 \times \mathop {10}\nolimits^{ - 4} \mathop x\nolimits^2 + 0.039\;2x + 0.686$ 0.999 极高 形状 平均形状指数 二次多项式 $y = 2 \times \mathop {10}\nolimits^{ - 6} \mathop x\nolimits^2 - 0.001x + 1.248\;1$ 0.752 一般 平均分维数 幂函数 $y = 1.078\;1\mathop x\nolimits^{ - 0.011} $ 0.856 一般 景观形状指数 幂函数 $y = 1\;634.4\mathop x\nolimits^{ - 0.681} $ 0.989 极高 聚散性 散布与并列指数 幂函数 $y = 77.157\mathop x\nolimits^{ - 0.019} $ 0.927 高 景观聚合度 幂函数 $y = 123.05\mathop x\nolimits^{ - 0.122} $ 0.997 极高 景观聚集度 幂函数 $y = 65.514\mathop x\nolimits^{ - 0.099} $ 0.975 极高 景观凝聚度 二次多项式 $y = - \mathop {10}\nolimits^{ - 5} \mathop x\nolimits^2 - 0.000\;5x + 98.848$ 0.944 高 多样性 斑块丰富度 常数 $y = 8$ 1.000 极高 Simpson多样性 二次多项式 $y = - \mathop {10}\nolimits^{ - 8} \mathop x\nolimits^2 + 4 \times \mathop {10}\nolimits^{ - 6} x + 0.738\;8$ 0.770 一般 Simpson均匀度 二次多项式 $y = - 2 \times \mathop {10}\nolimits^{ - 8} \mathop x\nolimits^2 + \mathop {5 \times 10}\nolimits^{ - 6} x + 0.844\;3$ 0.771 一般 
图 2 景观水平下景观指数的粒度变化
Figure 2. Grain sizes change of landscape indices under landscape level
指数类型1包括景观总周长、斑块数量、景观形状指数、景观聚集度、景观聚合度、边缘密度和斑块密度，总体呈“L”型单调下降变化趋势，景观指数拟合度高，可预测性强。斑块数量、斑块密度、景观总周长、景观形状指数的粒度响应曲线变化规律相似，明显拐点为70 m，70~200 m景观指数值下降幅度较小，＞200 m后景观指数值逐渐趋于稳定状态。据此可知随着粒度的增大整个景观内的小斑块逐渐被优势斑块融合，景观破碎化程度降低，整体景观形状趋于单一，小的斑块被融合，不同土地利用类型的分散程度逐渐增大。
指数类型2包括散布与并列指数、平均分维数、平均形状指数和景观凝聚度，总体呈单调下降后出现不同程度的波动变化，但整体依然呈下降趋势，其中：散布与并列指数、景观凝聚度拟合度高可预测性强，平均分维数、平均形状指数拟合度一般。景观凝聚度随着粒度的增大而下降，整体变化范围不大，值接近于100 m说明整个景观的连通性比较好，＞300 m后呈单调下降趋势，且降幅增大，表明景观的连通性降低且程度增加。散布与并列指数曲线明显拐点为70 m，70~300 m为适宜粒度域，＞300 m呈不同程度的波动变化，并且波动程度逐渐加剧但总体呈下降趋势，表明粒度的增大导致斑块类型周围的小斑块被优势斑块融合，邻接的斑块类型逐渐降低，景观的形状越来越简单。平均分维数、平均形状指数的适宜粒度为70~400 m，＞400 m呈现波动变化的趋势，表明随着粒度的增大斑块形状逐渐变得规则。
指数类型3包括周长面积分维数和平均斑块面积，总体呈上升趋势，景观指数拟合度高可预测性强。周长面积分维数的明显拐点为70 m，适宜粒度为70~200 m，＞200 m呈波动变化且变化强度逐渐增强；粒度＞200 m后平均斑块面积指数呈急剧增长趋势，表明在200 m下景观格局发生了剧烈的变化，且对平均斑块面积指数影响较大。据此可知：随着粒度的增大，斑块间相互融合引起斑块周长不断的减小，周长面积分维数值增大，整体景观内的斑块形状复杂性增大。
指数类型4包括景观总面积、斑块丰富度、Simpson多样性和Simpson均匀度，整体呈无变化或复杂变化趋势，拟合度整体一般。Simpson多样性和Simpson均匀度指数变化幅度很小；＞110 m后变化程度增强，但是变化依然很小，表明随着粒度的增大斑块之间会不断进行分割和融合；＞110 m后Simpson多样性和Simpson均匀度指数的变化强度加剧且总体景观值呈降低趋势，说明随着粒度的增大景观的破碎化程度逐渐降低，斑块类型在景观中的均衡化趋势分布逐渐降低。斑块丰富度在所选的粒度范围内一直未变，说明在所选的粒度范围内，随着粒度的增大整个景观的空间组分未消失。
-
对同一县域景观进行景观格局分析，空间粒度的选取直接影响结果的科学性和合理性，因此，适宜粒度的选取对研究县域的景观格局具有重要意义。景观指数曲线转折点附近景观特征会发生较大的变化，在适宜粒度域内选取最佳的景观分析粒度，以保证空间的边界信息损失值降到最小。适宜粒度域内的景观指数变化相对平稳，没有剧烈的波动变化，景观格局特征保持相对稳定状态[27]。根据景观指数的粒度效应曲线所对应不同转折点，将第1个变化相对稳定的区域作为适宜粒度区域，过大的粒度会造成交通用地、园地、未利用地等比较分散，且会让较小的斑块丢失边界空间信息，造成空间内部的景观特征发生改变，粒度越小越接近真实的景观特征。在类型水平下主体景观类型耕地景观指数的适宜粒度域为100~130 m，林地适宜粒度域为100~110 m，水域适宜粒度域为20~130 m。据此可知：类型水下景观指数的适宜粒度域为100~130 m。景观水平下指数类型4在粒度为110 m后开始出现逐渐增强的变化，因此，景观水平下的适宜粒度域为100~130 m。
根据不同水平下对应的景观指数粒度效应曲线的拐点分布，以及适宜粒度域，表明宿松县内部景观格局的最佳适宜粒度为100~110 m。从图3可见：在粒度为100~110 m内，景观面积损失值由0.7%上升到3.4%，呈现出逐渐增高的趋势。综合可知：宿松县县域水平下适宜的景观粒度为100 m。
图 3 景观面积损失值的粒度变化
Figure 3. Grain sizes change of landscape area loss value
-
数据源、研究对象、粒度变化方式、空间数据聚合方式、景观类型的不同均会造成景观结构组成的不同空间特征[11]。目前，大尺度区域的粒度效应研究[2-3, 9, 14]，数据源多采用人工解译的遥感数据，存在人工目视解译误差大、地物类别判定等问题，而本研究采用的地理国情数据源是高分辨率的影像，具有精度高、要素全、尺度精细等优点[5]。本研究区位于大别山南麓，位于长江中下游北岸，西北向东南依次地跨大别山山脉、丘陵岗地和平原、湖畈区，自然条件的差异形成了资源的多样性，林地、耕地、水域为研究区的主体类型。不同地貌下相同景观指数的拐点不同，如在景观水平下，施英俊等[25]研究发现：森林景观地貌下景观指数拐点为120 m，翟俊等[15]研究认为：青海湖流域地貌下的景观指数拐点集中于60和90 m，张韧璎[9]研究认为：天水市景观指数拐点集中于10、15和35 km，任梅等[11]研究表明：喀斯特山地城市安顺市的景观指数拐点集中于20和100 m，本研究表明：宿松县景观指数曲线的拐点主要集中于70和110 m，说明不同研究区地貌、土地类型的分布特征对确定区景观格局分析的粒度有较大影响。丁雪姣等[24]认为：安徽省省域尺度下的合适粒度为100~125 m，但并未确定粒度值，且选择粒度步长为25 m。本研究选择粒度步长为10和50 m，确定宿松县最佳粒度为100 m，这为研究整个安徽省的景观格局提供了一定的参考，也表明了粒度划分粗细的重要性。在景观水平下大部分景观指数均可用幂函数来对景观指数进行拟合，且拟合程度高，这与翟俊等[15]的研究结果类似，表明随着粒度的增大，部分景观指数粒度效应可预测性强。为减少粒度效应引起的误差，需要根据研究区特有的地形、地貌景观组成成分、面积大小来选择合适的粒度区间及景观指数。
-
本研究表明：在类型水平上，宿松县耕地景观指数的适宜粒度域为100~130 m，林地适宜粒度域为100~110 m，水域适宜粒度域为20~130 m。研究区草地、耕地、建筑用地分布比较分散，交通用地相互交错，复杂分散，未利用地、园地面积较少且分布比较集中。在景观水平上，景观指数的粒度效应曲线呈现4种不同的变化趋势，且大部分景观指数粒度效应可用拟合函数来进行预测，包括幂函数、对数函数、二次多项式、常数函数4种，主要函数类型为幂函数，且幂函数拟合程度高(R2＞0.92)。随着粒度的变化，景观指数的粒度响应也各不同，综合不同水平下各个景观指数的拐点信息确定了宿松县景观格局的最佳粒度域为100~110 m，结合景观面积损失模型，确定宿松县景观格局分析的最佳粒度为100 m。
Granularity effect of landscape index at the county scale
-
摘要:
目的 尺度的合理确定是景观格局和生态研究过程的关键。研究县域尺度下景观指数的粒度效应，并计算景观指数的适宜粒度范围对分析景观格局变化具有重要意义。 方法 以2017年安徽省宿松县的景观分布图为数据源，从类型和景观水平分析了各个景观指数在20~500 m粒度范围内的粒度效应，并选取适宜的粒度范围；通过拟合函数揭示不同景观格局指数随粒度增大的变化特征；结合景观面积损失精度评价模型确定宿松县景观格局变化的最适宜空间粒度值。 结果 景观指数具有一定的空间粒度效应性，其中大部分景观指数的可预测性强，但景观总面积、平均面积分维数、平均形状指数、Simpson多样性、Simpson均匀度指数对空间粒度响应不敏感；景观指数的粒度效应曲线可分为单调递减、单调递增、无变化、复杂变化4种类型；景观指数的拐点主要集中在70和200 m；在景观水平下景观指数粒度效应曲线拟合后的函数主要为幂函数，且拟合程度高。 结论 宿松县景观格局变化的适宜粒度为100~110 m，最佳粒度为100 m。图3表1参27 Abstract:Objective Reasonable scale determination is the key to the research of landscape pattern and ecology and has become one of the research focuses in landscape ecology and geography. Hence, the present research is focused on the granularity effect of landscape index at the county scale and appropriate granularity range of landscape index which is of great significance to the analysis of landscape pattern changes. Method First, with the landscape distribution map of Susong County, Anhui Province in 2017 was used as the data, an analysis was conducted of the granularity effect of each landscape index in the granularity range of 20−500 m from the two levels of type and landscape with the appropriate granularity range selected. Then, the fitting function was used to reveal the variation features of different landscape pattern indexes with the increase of granularity. Lastly, the optimal spatial granularity value of landscape pattern changes in Susong County was determined by the results of the precision evaluation model of landscape area loss. Result (1) The landscape indexes had a certain spatial granularity effect and most of them were highly predictable; (2) Landscape total area index, average area fractal dimension, average shape index, Simpson diversity index and Simpson evenness index demonstrated low response sensitivity to spatial granularity; (3) There were four different types of granularity effect curves of the landscape index: monotonically decreasing, monotonically increasing, no change, and complex change and their inflection points were mainly occurred at 70 and 200 m; (4) Power function was the main function upon the favorable fitting of the landscape index granularity effect curve. Conclusion The suitable grain size range landscape pattern change was 100−110 m in Susong County, Anhui Province, and the optimal grain size value was 100 m. [Ch, 3 fig. 1 tab. 27 ref.] -
Key words:
- landscape ecology /
- landscape index /
- granularity effect /
- geographical conditions /
- patches /
- Susong County
-
山核桃Carya cathayensis为落叶乔木，是含油率极高的胡桃科Juglandaceae高档干果，其果实为世界四大名优坚果之一[1-2]。因其口味独特、营养价值高而受到人们的广泛喜爱。浙江省杭州市临安区是中国山核桃主产区之一，种植历史悠久[3]。近几十年来，临安山核桃产业迅猛发展，现有种植面积已达5.3万 hm2，已成为当地林农重要的经济来源[4]。山核桃在临安广泛种植，但由于各镇林地有着不同的土壤特征，导致经济效益存在较大差异，即使在同一乡镇，产量大小年份的情况也依然存在[5]。这些问题在一定程度上限制了山核桃产业的发展。国内对于山核桃生长规律、规范施肥、产量提升等方面多有研究。杨慧思等[6]发现：山核桃产地土壤中大量及微量元素的空间分布特征与变异规律有着对应关系；张红桔等[7]揭示了山核桃产区主要养分因子和产量的关系以及空间分布特征；丁立忠等[8]研究结果指出：近10 a临安7 个山核桃主产镇的林地土壤有机碳含量总体呈升高趋势，而土壤碱解氮、有效磷和速效钾含量下降明显，养分现状不容乐观。但是有关水解酶活性与土壤肥力的关系，以及在山核桃产区空间上的分布特点还没有详细的报道和深入研究。水解酶与土壤中营养物质循环、能量转化以及环境质量等密切相关，并参与了土壤环境中重要的生物化学过程[9]。水解酶活性的空间分布特点可以灵敏地反映不同区域土壤中物质循环的速率，这种速率极大程度影响着林地土壤生态系统的功能。同时，水解酶活性能表征土壤养分转化的潜力，度量土壤污染程度和生产力，是人们评价土壤质量和土壤健康的重要经验指标之一[10]，因此，对土壤水解酶活性空间分布特点的研究十分重要。
本研究分析山核桃林土壤水解酶活性的空间分布特点，并通过地统计方法揭示土壤养分与水解酶的空间异质性及其影响因子，为林农掌握土壤肥力特性及养分转化潜力，合理经营山核桃林提供理论依据和技术支撑，对山核桃产业可持续发展具有重要的指导意义。
1. 材料与方法
1.1 研究区概况与样品采集
研究区位于浙江省杭州市临安区(31°14′N，119°42′E)，是中国山核桃的核心产区，属亚热带季风气候，年平均气温为16.0 ℃，极端最高和最低气温分别为41.7和−13.3 ℃。山核桃产区土壤以红壤土类分布最广，多发育于泥岩、页岩、砂岩、凝灰岩、花岗岩、流纹岩以及第四世纪红土[11]。山核桃是该地重要的经济树种，主要分布在海拔50~1100 m的丘陵和山地。林农一般在每年5月上旬和9月上旬将氮肥、复合肥与微肥配合施用。
样地按1 km×1 km网格在全市范围内布设，与临安区森林资源分布图相叠加，有山核桃分布的网格点即为山核桃林样地。根据均匀分布原则，2019年7—8月在山核桃分布较集中的岛石、龙岗、清凉峰、昌化、河桥、湍口、太阳等7个镇，共选取259个样地。在选定的区域内，采集0~20 cm的5个样点土壤样品后，混合，并在样地中心以全球定位系统(GPS)定位，记录经纬度。土壤样品带回实验室，去除石块、植物残体等异物，用木棒碾碎后过2 mm筛。将土壤样品分成2份，一份置于4 ℃冰箱保存，尽快测定土壤酶活性；另一份摊开后在室内自然风干，用于测定土壤养分指标和pH。
1.2 样品测定方法
测定涉及与土壤碳、氮、磷循环的α-葡萄糖苷酶(AG)、β-葡萄糖苷酶(BG)、纤维二糖水解酶(CBH)、木糖苷酶(XYL)、亮氨酸氨基肽酶(LAP)、N-乙酰-β-氨基葡萄糖苷酶(NAG)、酸性磷酸酶(PHOS)等7种土壤水解酶。土壤酶活性测定参照SAIYA-CORK等[12]的荧光微孔板检测技术。具体操作为：称取2 g鲜土于离心管中，加入30 mL提前配置好的pH为5.0的醋酸铵缓冲液，在25 ℃ 180 r·min−1摇床上震荡30 min，再用70 mL醋酸铵缓冲液冲洗至烧杯中，用磁力搅拌器搅拌1 min，用排枪取200 μL土壤悬液于96孔板中，并立即加入50 μL反应底物，放入25 ℃培养箱中避光培养3 h，取出后迅速加入15 μL 0.5 mol·L−1的氢氧化钠结束反应，用多功能酶标仪检测吸光值并计算土壤酶活性。土壤养分指标和pH参照鲁如坤[13]方法测定：土壤pH采用土水比(质量比)为1.0∶2.5的悬浊液，微电极法测定；土壤有机质采用浓硫酸-重铬酸钾外加热法测定；土壤碱解氮采用碱解扩散法测定；土壤有效磷采用盐酸-氟化铵(HCl-NH4F)浸提，钼锑抗比色法测定；土壤速效钾采用醋酸铵浸提，火焰光度计测定。
1.3 数据处理
1.3.1 空间自相关水平
水解酶活性的空间分布特征采用地统计分析方法。半方差变异函数是研究区域化变量模型，其公式为:
$$ y=\frac{1}{2 N} \sum_{i=1}^{N}[Z(x_i)-Z(x_i+h)]^{2} 。 $$ 其中：y表示间隔距离为h点的半方差值，h为空间间隔点的距离，即步长；N为样点观测数值成对的数目；Z(xi+h)和Z(xi)为样点测定值[14]。常用的半方差变异函数模型有球状(Spherical)、高斯(Gaussian)、指数(Exponential)[15]模型。模型中，C0代表块金值，C+C0代表基台值，当块基比C0/(C+C0)＜25%时，表明变量具有强烈的空间自相关，即主要受到结构性变异的影响；当C0/(C+C0)为25%~75%时，变量属于中等程度空间自相关；当C0/(C+C0)＞75%的，变量空间自相关程度较弱，即主要受随机因素影响[16-17]。
采用全局莫兰指数(Ig)来体现研究区域土壤水解酶的空间自相关水平。使用GeoDa软件对样点构建空间权重矩阵，可以根据局部莫兰指数(IL)绘制局部空间自相关聚类图[18]，采用Canoco 5.0对酶活性高、低聚集样点间总体差异采用999次的蒙特卡罗排列检验（Monte Carlo permutation test，999 permutations，full model），然后找出土壤酶活性关系密切的环境因子进行冗余分析(RDA)。
$$ {I_{\rm{g}}} = {\frac{{N\displaystyle \sum\limits_{i = 1}^N {{W_{ij}}({Z_i} - \overline Z )({Z_j} - \overline Z )} }}{{\displaystyle \sum\limits_{i = 1}^N {\displaystyle \sum\limits_{j = 1}^N {{W_{ij}}{{({Z_i} - \overline Z )}^2}} } }}_{}} ; $$ $$ {I_{\rm{L}}} = \frac{{{Z_i} - \overline Z }}{{{\sigma ^2}}}\sum\limits_{i = 1}^N {[{W_{ij}}({Z_i} - \overline Z )]} 。 $$ 其中：
$\overline Z$ 为变量Z的平均值；Zi、Zj分别是变量Z在空间i、j处的数值(i≠j)；σ2是变量Z的方差；Wij是Zi与Zj之间的空间权重函数，在选定尺度内时赋予权重值为1，超过尺度时权重值为0。当Ig＞0，表示目标样点与邻近样点有空间结构上的相似性，存在空间集聚区；当Ig＜0，表示空间区域异常[19]。1.3.2 土壤肥力分值
用SPSS 22.0对土壤水解酶活性与土壤性质数据进行描述性统计分析，计算变异系数，Pearson相关性分析设置显著水平为0.05。在Excel 2007中进行数据的对数转化。采用因子分析中的主成分分析法(PCA)和系统聚类分析，对山核桃林地土壤肥力情况进行评价[20]。通过因子分析确定参评土壤指标主成分特征值和特征向量，选取特征值较高的关键主成分，计算各主成分得分，再利用得分公式求出各样点土壤肥力分值(IIF)[21]，采用类平均法对分值进行系统聚类。肥力分值计算采用肥力指数和法。公式为：
$$ I_{\rm{IF}} = \frac{{{x_1}}}{{\displaystyle \sum\limits_{i = 1}^m {{x_i}} }}{F_1} + \frac{{{x_2}}}{{\displaystyle \sum\limits_{i = 1}^m {{x_i}} }}{F_2} + \frac{{{x_3}}}{{\displaystyle \sum\limits_{i = 1}^m {{x_i}} }}{F_3}+ \cdots + \frac{{{x_n}}}{{\displaystyle \sum\limits_{i = 1}^m {{x_i}} }}{F_n} 。 $$ 可简化为：IIF=λ1F1+λ2F2+λ3F3
$+\cdots+ $ λnFn。其中：Fi表示单个主成分得分；λi表示对应主成分解释的总变异。2. 结果与讨论
2.1 土壤性质描述性统计分析
土壤pH平均为5.76，最小为4.50，说明山核桃林地土壤主要为酸性土壤，且酸化较为严重。土壤有机质为5.41~98.08 g·kg−1，平均为37.39 g·kg−1；土壤有效磷为0.52~22.43 mg·g−1；土壤速效钾为22.06~466.07 mg·g−1；土壤碱解氮为28.62~192.53 mg·g−1。研究区域土壤变异系数从大到小依次为有效磷、速效钾、有机质、碱解氮、pH。土壤酶活性变异系数从大到小依次为CBH、XYL、AG、NAG、LAP、BG、PHOS，其中CBH、XYL为高度变异，AG、NAG、LAP、BG、PHOS为中等变异(表1)。根据ZHANG等[22]对变异系数的划分，当变异系数＜10%时为弱变异，在10%~90%时为中等变异，＞90%时则为高度变异。研究区域有效磷质量分数变异系数＞90%，具有明显的变异性，为高度变异。这可能是由于山核桃产区地势起伏较大，在雨水冲刷后有效磷极易流失，且林农施用磷肥量不均匀，土壤利用率较低，常年累积造成。土壤pH变异系数为10.28%，变异较小，与张红桔等[7]研究结果基本一致，说明山核桃林地土壤总体pH比较接近。
表 1 土壤性质描述性统计分析Table 1 Descriptive statistics of soil properties项目 有机质/
(g·kg−1)有效磷/
(mg·kg−1)速效钾/
(mg·kg−1)碱解氮/
(mg·kg−1)pH AG/
(mol·g−1·h−1)最小值 5.41 0.52 22.06 28.62 4.50 0.12 最大值 98.08 22.43 466.07 192.53 7.48 1.67 平均值 37.39 4.23 113.77 132.40 5.76 0.35 标准差 15.38 3.90 72.58 43.47 0.59 0.30 变异系数/% 41.15 92.20 63.80 32.83 10.28 88.12 项目 BG/
(mol·g−1·h−1)CBH/
(mol·g−1·h−1)XYL/
(mol·g−1·h−1)LAP/
(mol·g−1·h−1)NAG/
(mol·g−1·h−1)PHOS/
(mol·g−1·h−1)最小值 4.58 0.04 0.17 0.10 0.15 18.31 最大值 192.62 63.06 62.91 32.95 93.60 1042.63 平均值 47.06 8.14 7.44 4.44 17.75 160.43 标准差 31.50 8.09 6.91 3.62 15.27 89.10 变异系数/% 66.95 99.48 92.98 81.54 86.07 55.54 2.2 土壤水解酶活性与土壤肥力指标及pH相关性分析
土壤有机质和碱解氮与7种水解酶均呈极显著正相关(P＜0.01)；有效磷与BG 、NAG呈极显著正相关，与CBH呈显著正相关(P＜0.05)；pH与CBH呈极显著正相关(P＜0.01)，与BG呈显著正相关(P＜0.05)，与PHOS、XYL呈极显著负相关(P＜0.01)；速效钾与7种水解酶均没有表现出明显的相关性(表2)。土壤酶主要来源于土壤微生物、土壤动物和植物根系的分泌，土壤养分质量分数可以直接影响土壤动植物长势、微生物的活性与分布，整合了土壤理化条件的信息[23]，因此土壤水解酶活性与土壤养分因子密切相关，水解酶活性也通常被作为土壤质量的生物活性指标[24]。对土壤水解酶活性与土壤肥力指标及pH的相关性分析发现：土壤有机质和碱解氮与7种酶存在极显著正相关(P＜0.01)。土壤有机质是评价土壤肥力的重要指标，土壤有机质的形成与分解都与酶的作用有关[25]。水解酶可以吸附在土壤有机质上，以酶-腐殖质复合物的形式从土壤中提取出来，并仍可保留有活性。土壤碱解氮主要集中在土壤表层，其含量受人为施肥的影响较大[26]。山核桃林农为提高产量大量撒施氮肥。氮素供应的增加可以使植物细胞原生质合成加快，细胞数量增多，有了更多的水解酶产出渠道。此外，土壤微生物也会通过分泌多种水解酶固定氮素[27]。PHOS与有效磷质量分数和pH之间存在显著正相关和极显著负相关。由于PHOS会参加土壤磷的矿化作用过程，使土壤有机态磷转化为植物可吸收的无机态磷，有效磷质量分数增加。pH是控制土壤中磷有效性和PHOS活性的关键因子，在山核桃林地土壤酸化的环境下，pH小幅降低可能有利于植物对有效磷的吸收，PHOS参与矿化作用的活性增强[28]。
表 2 土壤水解酶与养分因子及pH相关性分析表Table 2 Correlation coefficients of soil hydrolase activities and soil nutrient factors and pH水解酶 有机质 有效磷 速效钾 碱解氮 pH AG 0.355** 0.061 0.060 0.419** 0.102 BG 0.406** 0.172** 0.066 0.354** 0.147* CBH 0.356** 0.158* 0.060 0.275** 0.196** XYL 0.302** 0.088 −0.090 0.278** −0.283** LAP 0.170** 0.042 −0.015 0.230** −0.028 NAG 0.431** 0.267** 0.114 0.357** 0.109 PHOS 0.272** 0.123* 0.007 0.346** −0.286** 说明：*P＜0.05, **P＜0.01 2.3 不同土壤水解酶活性空间变异特征及聚集效应
7种土壤水解酶活性在山核桃林地表现出不同的空间异质性(表3)。在GS+ 9.0中进行方差变异函数拟合，分别选用最优模型。不同水解酶拟合模型的差异，表示相应的酶在土壤中的空间变化规律不同。本研究中，AG、BG、CBH、LAP、NAG、XYL活性具有中等空间自相关性，活性均呈现斑块状分布；不同水解酶活性区域分布呈现差异性，块基比分别为55%、42%、56%、49%、66%、47%、78%，说明它们的变异情况主要受到人为因素和结构性因素共同影响。PHOS块基比为78%，具有较弱的空间自相关，其活性空间分布主要受随机因素如施肥方式和耕作强度的影响[29]。本研究中, 虽然各酶活性的空间自相关性存在差异，但变程均大于最小采样距离，因此，本研究所选择的采样距离能够反映土壤水解酶活性在研究区域最小尺度下的空间变异特征。从土壤水解酶活性的空间分布情况来看(图1)：活性较高的区域位于临安区西北方向的岛石镇。该镇有中国“山核桃第一镇”的美称，这可能与当地特色生态化经营方式有关，如：林下种植茶Camellia sinensis、黑麦草Lolium perenne、油菜Brassica napus等适生植物，丰富林下土壤生态结构的同时起到涵养水肥、改良酸性土质的作用；林间饲养家禽吃掉害虫、消灭虫卵，产生的鸡粪也可作为有机肥为山核桃树生长提供养分。这些特色经营方式都为植物根系发育、土壤微生物的快速新陈代谢提供了有利的条件，从而提高了相关水解酶参与复杂生化反应的活性。
表 3 土壤水解酶活性半方差函数理论模型及其相关参数Table 3 Theoretical model of semi-variance function of soil hydrolase activities and its related parameters水解酶 函数模型 块金值(C0) 基台值(C+C0) 块基比[C0/(C+C0)] 变程 决定系数 AG 球状模型 0.050 0.090 0.55 9.63 0.46 BG 指数模型 136.800 324.400 0.42 8.76 0.65 CBH 指数模型 0.140 0.250 0.56 1.60 0.43 XYL 高斯模型 0.080 0.170 0.47 2.12 0.37 LAP 高斯模型 10.970 21.960 0.49 11.20 0.73 NAG 高斯模型 197.150 294.260 0.66 27.30 0.45 PHOS 球状模型 0.032 0.041 0.78 14.60 0.54 根据全局莫兰指数，AG、BG、CBH、XYL、LAP、NAG、PHOS等7种水解酶活性在空间分布上都存在相关性(Ig＞0)，且存在高低值聚集区域。在本研究中，7种水解酶活性在高低值聚类上呈现出了相似的特点，岛石镇为水解酶活性高值聚集(high-high)区域，部分水解酶(如AG)在太阳镇北部也有高值聚集的现象；低值聚集(low-low)区域多位于清凉峰以及河桥、龙岗、昌化三镇交界处附近(图2)。在冗余分析结果中，高低值聚集区域样点的水解酶活性在第1轴有明显的分离，第1轴和第2轴分别有82.92%和14.42%的贡献度(图3)。结果显示：碱解氮、有机质、pH与水解酶活性有极显著正相关(P＜0.01)。水解酶活性高低值聚类结果和土壤肥力分值高低值聚类情况相似，说明土壤水解酶活性大小和周围可利用的营养物质关系十分密切。由于山核桃林地土壤常年受到不同程度的人为经营干扰，造成这种现象的原因多为当地经营方式的不同，如氮肥、有机肥的投入是增加土壤肥力较为直接的方式，因此各区域出现高低值聚集的现象可以一定程度反映当地肥力水平以及施肥情况。岛石镇高值聚集，一方面可能是由于岛石镇山核桃林氮肥、有机肥常年投入量高于清凉峰等区域，同时岛石镇明确规定当地所有山核桃林地禁用除草剂，防止除草剂的不合理使用破坏产区生态平衡，影响山核桃产量。另一方面，岛石镇相对其他镇海拔较高，大部分产区山高树茂，年降水量充沛，林下、林间生态系统的结构与功能较为完整，因此土壤微生物活动旺盛，作物根系发达，从而成为水解酶活性的高值聚集区。而清凉峰以及河桥、龙岗、昌化交界处的冒尖山、石柱山、云台山、鸡哺山等区域地势极为陡峭，当地山核桃林水土流失现象严重，养分较为贫乏，相对其他区域处于较低的水平，水解酶活性受到影响，产生低值聚集。杭瑞高速经过清凉峰镇与龙岗镇南部，该区域交通便利，人类活动造成了一定程度的干扰。当地存在铅锌矿、钨钼矿以及铜矿等正在开发的金属矿[30]。采矿活动产生的粉尘、废水和尾矿渣可能会对土壤水解酶活性和分布造成一定影响[31]。
图 3 高低聚类点冗余分析结果Figure 3 Redundancy analysis of high-high and low-low clustering points2.4 土壤肥力状况
据浙江省地方标准，山核桃林地土壤样地中碱解氮、有效磷、速效钾、有机质位于丰富等级的样地分别占64%、56%、23%、45%，绝大部分样点各养分指标等级处于中等以上(表4)，能够满足山核桃的生长发育需求，但是由于各区域土壤中养分比例以及酸碱度的不同，综合肥力状况也有所差异。在主成分分析结果中，IIF均值为91.67，变幅为35.29~277.05，变异系数为42.73%。第1主成分解释了48.39%的总变异，第2主成分解释了26.50%的总变异，第3主成分解释了17.12%的总变异(表5)。采用类平均法对土壤肥力分值(IIF)进行系统聚类，将259个样本分为4类，即第Ⅰ类IIF≥146.83，第Ⅱ类87.11≤IIF＜146.83，第Ⅲ类59.72≤IIF＜87.11，第Ⅳ类IIF＜59.72，分别对应土壤肥力高、较高、中、低4个等级。结果显示：IIF变异系数为42.73%，属于中等变异，但其中有174个样本处于中低水平，肥力相对较差。从采样区域土壤肥力分值所占比例来看，山核桃林地有58.7%的样地土壤肥力低于平均水平，有32.7%的样地土壤肥力为Ⅰ和Ⅱ等级，大部分样地土壤肥力处于Ⅲ、Ⅳ等级，说明大部分山核桃林地土壤肥力还有提高的空间。从使用IIF绘制的空间分布图来看，岛石镇山核桃林地土壤肥力在所有山核桃产区中最高，该区域的土壤管理方法值得借鉴。沈一凡等[32]研究了近10 a山核桃林地主要分布区域的土壤养分变化情况，发现林地土壤酸化的现象一直在加重，肥力也有不断下降的趋势。这是由于大多数山核桃林农缺乏相关技术指导和对立地环境的认知，长期施用以氮素为主的化学肥料造成的。而且从20世纪80年代开始，山核桃林地不断扩张，但大多数新兴产区酸化严重，土壤宜肥、宜种性较差。针对这一现象，还需要增施有机肥，并施用一定量的石灰，逐渐改善各地土壤酸化的情况，规范林地生草管理和生态化采收技术，以稳步提升山核桃林地的土壤肥力。
表 4 山核桃土壤肥力指标丰缺等级及各等级占比Table 4 Level of soil fertility indexs and the proportion of each level项目 碱解氮 有效磷 速效钾 有机质 质量分数/(mg·kg−1) 占比/% 质量分数/(mg·kg−1) 占比/% 质量分数/(mg·kg−1) 占比/% 质量分数/(g·kg−1) 占比/% 缺乏 ＜80 6 ＜5 12 ＜80 34 ＜10 7 中等 80~120 30 5~10 32 80~110 43 10~40 48 丰富 ＞120 64 ＞10 56 ＞110 23 ＞40 45 说明：土壤肥力指标丰缺等级参考浙江省地方标准 DB33/T 2205—2019《山核桃分区施肥技术规范》 表 5 主成分贡献率与各因子得分Table 5 Principal component contribution rates and each factor score因子 主成分得分 第1主成分(48.39%) 第2主成分(26.50%) 第3主成分(17.12%) 有机质 0.144 0.268 0.225 有效磷 0.071 0.451 0.116 速效钾 0.027 0.481 0.046 碱解氮 0.061 0.040 0.652 AG 0.160 −0.058 0.039 BG 0.205 0.017 −0.299 CB 0.182 0.064 −0.393 XYL 0.177 −0.240 0.042 LAP 0.122 −0.238 0.345 NAG 0.179 0.111 −0.130 PHOS 0.184 −0.219 0.100 3. 结论
研究区山核桃林土壤水解酶活性均具有较好的空间变异结构和空间分布格局，结构性变异占总变异的比例较小。研究区山核桃林土壤受到人为因素的干扰较多，人为施肥与经营强度是影响其空间格局形成的最直接因素。土壤水解酶活性空间分布和养分分布联系密切，在养分质量分数较高的区域有高值聚集的现象，低值聚集区域多位于清凉峰等区域。特色的生态经营方式可以使土壤水解酶活性处于相对较高的水平，从而提高山核桃的宜种性。
研究区山核桃林土壤酸化较为普遍，平均pH为5.76，严重限制了山核桃的生长。岛石镇、太阳镇北部土壤肥力得分较高。从总体来看，大部分区域土壤各肥力指标等级处于中等以上，但有过半土壤综合肥力未达到平均水平。产区内部各镇土壤肥力也有着明显差异，大部分区域土壤肥力还有待提高；土壤水解酶活性变异系数较高，且与有机质、碱解氮、pH、有效磷等肥力因子有较强的相关性。
-
图 2 景观水平下景观指数的粒度变化
Figure 2 Grain sizes change of landscape indices under landscape level
表 1 景观水平下景观指数的拟合函数
Table 1. Fitting function of landscape horizontal landscape index
指标(y) 景观指数(x) 函数类型 拟合函数 拟合度(R2) 预测强度 面积边缘 景观总面积 二次多项式 $y = 12 \times \mathop {10}\nolimits^{ - 4} \mathop x\nolimits^2 - 0.474\;7x + 236\;751$ 0.570 较低 边缘密度 幂函数 $y = 1\;434.2\mathop x\nolimits^{ - 0.702} $ 0.988 极高 周长面积分维数 对数 $ y = 0.042\; 7 \ln\! x + 1.376\; 2 $ 0.903 高 景观总周长 幂函数 $y = 3 \times \mathop {10}\nolimits^8 \mathop x\nolimits^{ - 0.702} $ 0.988 极高 密度大小及差异 斑块密度 幂函数 $y = 8\;089.4\mathop x\nolimits^{ - 1.503} $ 0.986 极高 斑块数量 幂函数 $y = 2 \times \mathop {10}\nolimits^7 \mathop x\nolimits^{ - 1.503} $ 0.986 极高 平均斑块面积 二次多项式 $y = 6 \times \mathop {10}\nolimits^{ - 4} \mathop x\nolimits^2 + 0.039\;2x + 0.686$ 0.999 极高 形状 平均形状指数 二次多项式 $y = 2 \times \mathop {10}\nolimits^{ - 6} \mathop x\nolimits^2 - 0.001x + 1.248\;1$ 0.752 一般 平均分维数 幂函数 $y = 1.078\;1\mathop x\nolimits^{ - 0.011} $ 0.856 一般 景观形状指数 幂函数 $y = 1\;634.4\mathop x\nolimits^{ - 0.681} $ 0.989 极高 聚散性 散布与并列指数 幂函数 $y = 77.157\mathop x\nolimits^{ - 0.019} $ 0.927 高 景观聚合度 幂函数 $y = 123.05\mathop x\nolimits^{ - 0.122} $ 0.997 极高 景观聚集度 幂函数 $y = 65.514\mathop x\nolimits^{ - 0.099} $ 0.975 极高 景观凝聚度 二次多项式 $y = - \mathop {10}\nolimits^{ - 5} \mathop x\nolimits^2 - 0.000\;5x + 98.848$ 0.944 高 多样性 斑块丰富度 常数 $y = 8$ 1.000 极高 Simpson多样性 二次多项式 $y = - \mathop {10}\nolimits^{ - 8} \mathop x\nolimits^2 + 4 \times \mathop {10}\nolimits^{ - 6} x + 0.738\;8$ 0.770 一般 Simpson均匀度 二次多项式 $y = - 2 \times \mathop {10}\nolimits^{ - 8} \mathop x\nolimits^2 + \mathop {5 \times 10}\nolimits^{ - 6} x + 0.844\;3$ 0.771 一般 
下载: 导出CSV
-
[1] 邬建国. 景观生态学——格局、过程、尺度与等级[M]. 北京: 高等教育出版社, 2007: 106−115. [2] 陈永林, 谢炳庚, 李晓青. 长沙市土地利用格局变化的空间粒度效应[J]. 地理科学, 2016, 36(4): 564 − 570. CHEN Yonglin, XIE Binggeng, LI Xiaoqing. Spatial grain size effect on land use pattern changes in Changsha City [J]. Sci Geogr Sin, 2016, 36(4): 564 − 570. [3] 殷小彤. 西北地区农村居民点景观格局指数的尺度效应及其最佳粒度选择分析:以西安市为例[J]. 中国农业资源与区划, 2016, 37(12): 149 − 154. YIN Xiaotong. Analysis of the scale effect on landscape spatial pattern of rural residential area: taking Xi’an City as an example [J]. Chin J Agric Resour Reg Plann, 2016, 37(12): 149 − 154. [4] 郭琳, 宋戈, 张远景, 等. 基于最佳分析粒度的巴彦县土地利用景观空间格局分析[J]. 资源科学, 2013, 35(10): 2052 − 2060. GUO Lin, SONG Ge, ZHANG Yuanjing, et al. Land-use spatial analysis for Bayan County based on optimal grain size [J]. Resour Sci, 2013, 35(10): 2052 − 2060. [5] 王彦军, 杨月. 基于地理国情普查成果的城市景观格局分析[J]. 现代测绘, 2018, 41(2): 27 − 30. WANG Yanjun, YANG Yue. Analysis on landscape pattern of city based on the survey of geographical conditions [J]. Modern Surv Mapp, 2018, 41(2): 27 − 30. [6] 刘玉卿, 张华兵, 张云峰. 盐城海岸带生态系统服务价值时空分异[J]. 浙江农林大学学报, 2019, 36(4): 774 − 782. LIU Yuqing, ZHANG Huabing, ZHANG Yunfeng. Spatio-temporal variation of ecosystem services value in Yancheng coastal zone [J]. J Zhejiang A&F Univ, 2019, 36(4): 774 − 782. [7] 周媛. 多元目标导向下的成都中心城区绿地生态网络构建[J]. 浙江农林大学学报, 2019, 36(2): 359 − 365. ZHOU Yuan. Developing urban greenspace ecological network in Chengdu City center based on multiple objectives [J]. J Zhejiang A&F Univ, 2019, 36(2): 359 − 365. [8] 冀亚哲, 张小林, 吴江国, 等. 聚落景观格局的空间粒度转换响应及其机理分析:以江苏省镇江地区为例[J]. 长江流域资源与环境, 2013, 22(3): 322 − 330. JI Yazhe, ZHANG Xiaolin, WU Jiangguo, et al. Analysis of mechanism of the settlements landscape change during transforming data with several spatial granularities [J]. Resour Environ Yangtze Basin, 2013, 22(3): 322 − 330. [9] 张韧璎. 天水市土地利用景观格局动态及空间幅度效应研究[D]. 兰州: 甘肃农业大学, 2018. ZHANG Renying. Study on Dynamics of Landscape Pattern and Spatial Extent Effect in Tianshui[D]. Lanzhou: Gansu Agricultural University, 2018. [10] 乔伟峰, 吴江国, 王亚华. 多尺度粒度变化对区域土地利用景观格局的影响:以镇江市为例[J]. 南京师大学报(自然科学版), 2015, 38(3): 120 − 126. QIAO Weifeng, WU Jiangguo, WANG Yahua. Effect of multi-scale granularity change to regional land use landscape pattern: a case study of Zhenjiang [J]. J Nanjing Norm Univ Nat Sci Ed, 2015, 38(3): 120 − 126. [11] 任梅, 王志杰, 王志泰, 等. 黔中喀斯特山地城市景观格局指数粒度效应——以安顺市为例[J]. 生态学杂志, 2018, 37(10): 3137 − 3145. REN Mei, WANG Zhijie, WANG Zhitai, et al. Grain size effect of karst mountainous urban landscape pattern indices in the central Guizhou: a case study of Anshun City [J]. Chin J Ecol, 2018, 37(10): 3137 − 3145. [12] 刘德林, 方炫, 李壁成. 黄土高原小流域尺度土地利用景观格局指数的粒度效应[J]. 水土保持通报, 2013, 33(4): 206 − 210. LIU Delin, FANG Xuan, LI Bicheng. Effects of grain change on landscape metrics of landuse in small watershed on Loess Plateau [J]. Bull Soil Water Conserv, 2013, 33(4): 206 − 210. [13] 马胜, 梁小英, 刘迪, 等. 生态脆弱区多尺度景观生态风险评价:以陕西省米脂县高渠乡为例[J]. 生态学杂志, 2018, 37(10): 3171 − 3178. MA Sheng, LIANG Xiaoying, LIU Di, et al. Multi-scale landscape ecological risk assessment in ecologically fragile regions: a case study in Gaoqu Town in Mizhi County, Shaanxi Province [J]. Chin J Ecol, 2018, 37(10): 3171 − 3178. [14] 孟瑶瑶, 薛丽芳. 南四湖流域土地利用及其景观格局变化分析[J]. 水土保持研究, 2017, 24(3): 246 − 252. MENG Yaoyao, XUE Lifang. Analysis on landscape pattern change and land use in Nansi Lake Basin [J]. Res Soil Water Conserv, 2017, 24(3): 246 − 252. [15] 翟俊, 侯鹏, 赵志平, 等. 青海湖流域景观格局空间粒度效应分析[J]. 国土资源遥感, 2018, 30(3): 159 − 166. ZHAI Jun, HOU Peng, ZHAO Zhiping, et al. An analysis of landscape pattern spatial grain size effects in Qinghai Lake watershed [J]. Remote Sensing Land Resour, 2018, 30(3): 159 − 166. [16] 孔维静, 王一涵, 潘雪莲, 等. 辽宁太子河上游沿岸景观格局的幅度效应[J]. 山地学报, 2013, 31(3): 287 − 293. KONG Weijing, WANG Yihan, PAN Xuelian, et al. Extent effect of landscape pattern along upper reaches of Taizi River, Liaoning, China [J]. J Mt Sci, 2013, 31(3): 287 − 293. [17] 易海杰, 张丽, 罗维, 等. 1990−2013年洋河流域土地利用景观格局的粒度效应[J]. 中国农学通报, 2018, 34(19): 83 − 95. YI Haijie, ZHANG Li, LUO Wei, et al. Spatial grain size effect on land use pattern changes within the Yanghe Watershed in 1990−2013 [J]. Chin Agric Sci Bull, 2018, 34(19): 83 − 95. [18] 王德智, 邱彭华, 方源敏. 丽香铁路建设对沿线景观格局影响的尺度效应及其生态风险[J]. 应用生态学报, 2015, 26(8): 2493 − 2503. WANG Dezhi, QIU Penghua, FANG Yuanmin. Scale effect of Li-Xiang Railway construction impact on landscape pattern and its ecological risk [J]. Chin J Appl Ecol, 2015, 26(8): 2493 − 2503. [19] 孟楠, 韩宝龙, 王海洋, 等. 澳门城市生态系统格局变化研究[J]. 生态学报, 2018, 38(18): 6442 − 6451. MENG Nan, HAN Baolong, WANG Haiyang, et al. Study on the evolution of urban ecosystem patterns in Macao [J]. Acta Ecol Sin, 2018, 38(18): 6442 − 6451. [20] 张玲玲, 史云飞, 刘玉华. 空间粒度变化对沂蒙山区景观格局指数的影响[J]. 生态学杂志, 2013, 32(2): 459 − 464. ZHANG Lingling, SHI Yunfei, LIU Yuhua. Effects of spatial grain change on the landscape pattern indices in Yimeng Mountain area of Shandong Province, East China [J]. Chin J Ecol, 2013, 32(2): 459 − 464. [21] 杨晓红, 张双双, 汪鑫. 基于地理国情数据的土地利用景观格局分析[J]. 地理空间信息, 2019, 17(10): 32 − 36, 40, 10. YANG Xiaohong, ZHANG Shuangshuang, WANG Xin. Land use landscape pattern analysis based on geographical conditions data [J]. Geospat Inf, 2019, 17(10): 32 − 36, 40, 10. [22] 邱海军, 曹明明. 土地利用景观格局指数的粒度效应:以黄龙县为例[J]. 地域研究与开发, 2011, 30(1): 126 − 129. QIU Haijun, CAO Mingming. The effects of grain change on land use landscape pattern indices: a case study of Huanglong County [J]. Areal Res Dev, 2011, 30(1): 126 − 129. [23] 张皓玮, 李欣, 殷如梦, 等. 旅游城镇化地区土地利用景观格局指数的粒度效应:以扬州市广陵区为例[J]. 南京师大学报(自然科学版), 2018, 41(3): 122 − 130. ZHANG Haowei, LI Xin, YIN Rumeng, et al. Grain size effect of urbanization tourist areas of land use landscape pattern index: a case study of Guangling District of Yangzhou [J]. J Nanjing Norm Univ Nat Sci Ed, 2018, 41(3): 122 − 130. [24] 丁雪姣, 沈强, 聂超甲, 等. 省域尺度下不同时序景观指数集与粒度效应分析[J]. 中国农业资源与区划, 2019, 40(3): 111 − 120. DING Xuejiao, SHEN Qiang, NIE Chaojia, et al. Analysis of landscape indice set and grain effect of different time series at provincial scale [J]. Chin J Agric Resour Reg Plann, 2019, 40(3): 111 − 120. [25] 施英俊, 高健, 雷亚君, 等. 阿尔泰山森林景观特征及其适宜粒度分析[J]. 西部林业科学, 2019, 48(1): 63 − 69. SHI Yingjun, GAO Jian, LEI Yajun, et al. Landscape characteristics and suitability analysis of the Altai Mountains [J]. J West China For Sci, 2019, 48(1): 63 − 69. [26] WU Jianguo, HOBBS R. Key issues and research priorities in landscape ecology: an idiosyncratic synthesis [J]. Landscape Ecol, 2002, 17(4): 355 − 365. [27] 黄晶晶, 于银霞, 于东升, 等. 利用景观指数定量化评估历史土壤图制图精度[J]. 土壤学报, 2019, 56(1): 44 − 54. HUANG Jingjing, YU Yinxia, YU Dongsheng, et al. Quantitative evaluation of mapping precision of historical soil maps with landscape indices [J]. Acat Pedol Sin, 2019, 56(1): 44 − 54. 期刊类型引用(7)
1. 戴梦婷，杨士杰，张艳梅，秦华，彭丽媛. 6株不同来源外生菌根真菌的生物量、养分吸收能力及酶活性. 福建农林大学学报(自然科学版). 2025(01): 135-144 . 
百度学术2. 饶盈，王江铭，朱先富，夏国华. 不同海拔的大别山山核桃林地土壤性质和叶片营养元素分析. 安徽农业大学学报. 2024(01): 96-101 . 百度学术3. 徐雅雯，吴文丰，王其竹，王代全，徐朝煜，陈万胜，徐永杰. 基于地统计分析的核桃园土壤养分空间特征研究. 果树学报. 2024(05): 968-979 . 百度学术4. 张艳梅，郑梦杰，杨士杰，吴权杰，黄坚钦，彭丽媛，秦华. 山核桃根际解磷及水解复杂有机物细菌的分离. 微生物学报. 2024(10): 3809-3824 . 百度学术5. 潘昱伶，璩向宁，李琴，王磊，王筱平，谭鹏，崔庚，安雨，佟守正. 黄河宁夏段典型滩涂湿地土壤理化因子空间分布特征及其对微地形的响应. 生态环境学报. 2023(04): 668-677 . 百度学术6. 姚熠涵，代英超，王卫国，朱先富，陈涛梅，周鑫洋，夏国华. 大别山山核桃林地土壤养分特征及肥力评价. 林业科学研究. 2023(05): 180-188 . 百度学术7. 刘丽丽，任涛. 核桃嫁接繁殖苗木技术. 中国林副特产. 2022(06): 55-56 . 百度学术其他类型引用(2)
-
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20190477
点击查看大图
计量
- 文章访问数: 2154
- HTML全文浏览量: 631
- PDF下载量: 136
- 被引次数: 9
