-
樟子松Pinus sylvestris var. mongolica主要天然分布区为中国黑龙江大兴安岭海拔400~900 m山地及海拉尔以西、以南一带沙丘地区，于20世纪50年代被成功地引种到辽宁省阜新市彰武县章古台（科尔沁沙地东南前缘）。樟子松喜光、抗旱、耐寒、耐瘠薄、干形优良、生长迅速、根系发达，迅速成为中国北方地区重要的造林树种。作为中国最早引种成功樟子松的地区，辽宁省章古台现已发展成为樟子松国家良种基地，每年生产数以亿株优良的樟子松苗木和优良种子供应中国北方19省（自治区、直辖市）造林和用种。引种的同时，学者们先后开展了樟子松对引种地环境的适应性、引种地栽植密度、种源选择、林分自然稀疏规律、人工林群落稳定性、引种地樟子松提早衰退原因、幼苗生理生态、人工林土壤营养等方面的科学研究[1-9]，取得了显著的成就。经过60多年的生长，引种的第1代沙地樟子松人工林逐渐退出了历史舞台，为了给推广地区沙地樟子松林的营建以及下一代人工林的更新及经营管理提供理论依据，有必要对第1代沙地樟子松的生长过程进行总结。林木或林分生长受立地、气候等多种因子的影响[10-13]，通过测定树高或胸径因子，计算材积大小，利用生长函数能够揭示立地或气候等影响因子对林分高（或林木高）或胸径的影响规律[11, 14-16]。诸多函数中，Richards模型由于具有广泛的适应性、合理的解析性和良好的拟合性而应用广泛[17-22]，同时樟子松生长曲线为“S”或反“J”型[22]，而Richards函数是单调递增函数，存在1个拐点，具备“S”或反“J”型。因此，本研究选择不同立地条件下30 a以上的第1代沙地樟子松人工林标准地进行每木调查，每块标准地选出1株平均木做解析木，获取平均木的树高、胸径、材积数据，建立Richards模型并检验，然后运用建立的模型计算沙地樟子松生长过程中的特征值，利用特征值分析第1代沙地樟子松的生长过程。
-
试验地位于辽宁省固沙造林研究所章古台试验基地（42°43′~43°20′N，122°22′~123°22′E），该区地处科尔沁沙地东南前缘，年平均降水量1959－1965年为512.2 mm，1983－1987年为499.7 mm，2005－2015为518.24 mm，年平均蒸发量为1 762 mm，年平均气温为6.2 ℃，≥10 ℃年积温平均为2 890 ℃，无霜期平均为154 d，土壤主要为生草固定风沙土和流动风沙土，流动风沙土的物理性沙粒占94.7%，物理性黏粒占5.3%，养分含量比较低，有机质质量分数为0.6~1.6 g·kg－1，全氮质量分数为0.17~0.38 g·kg－1，磷（P2O5）质量分数为0.12~0.27 g·kg－1。代表性植物主要有蒺藜梗Agriophyllum squarrosum，小黄柳Salix gordejevii，差巴戈蒿Artemisia halodendron，拂子茅Calamagrostis epigeios，山杏Armeniaca sibirica，榆树Ulmus pumila等。由于树干解析对于研究较大年龄树木生长具有巨大优势，所以于2014年9月选择了30年生以上的不同立地的樟子松标准地11块进行每木调查，每块样地的平均木作为解析木，共计11株解析木。各解析木伐根处取0号圆盘，0.5 m处取1号圆盘，1.3 m处取2号圆盘，1.5 m处取3号圆盘，以后隔1 m取1个圆盘。量测直径时，2 a为1个龄阶，东西和南北2个方向上同一龄阶的平均值即为该龄阶的直径，各龄阶的树高用内插法按比例计算得到，各龄阶的材积按伐倒木区分求积法计算得到。解析木信息如表 1。
表 1 沙地樟子松解析木信息
Table 1. Stem analysis information of Mongolian pine
立地 年龄/a 数量/株 树高/m 胸径/cm 沙丘顶部 30~35 1 9.0 14.94 40 1 11.6 19.10 平坦沙地 35 1 13.2 22.75 34 1 12.4 20.55 丘间低地 40~50 2 14.2~15.5 19.90~20.65 沙丘中部 30~40 1 9.8 18.00 30~40 2 9.9~10.3 14.40~16.80 50~60 2 13.0~13.3 20.90~22.80 -
通过解析木资料得到各龄阶树高、胸径、材积生长量值，计算11株解析木各龄阶对应的树高、胸径、材积生长量的平均值，通过SPSS 20的非线性回归方法求出模型各参数值和决定系数，然后运用模型计算沙地樟子松的各特征值并进行分析。
-
Richards模型是基于Bertalanffy生长理论扩展而来，生物生长的实质是同化与异化综合作用的结果，由于树木生长的不可逆性，其同化作用效果必定大于或等于异化作用效果，同时由于树木生长的阻滞性，树木同化作用效果一般与其大小的m次幂呈正比，即m＜1，树木异化作用的效果一般与其大小成线性递增关系。因此，树木的生长能够表达为：
$$ \frac{{{\rm{d}}y}}{{{\rm{d}}t}} = \alpha {y^m}-\beta y。 $$ (1) 式（1）中：y为树木总生长量，包括树高（m），胸径（cm）和材积（m3），t为树木年龄（a），α，β，m是参数，实际上，树木的瞬间生长量经常用期间生长量代替。对应的生长方程为：
$$ \left\{ \begin{array}{l} y = A{\left( {1-\gamma {{\rm{e}}^{-kt}}} \right)^{\frac{1}{{1-m}}}}\\ A = {\left( {\frac{\alpha }{\beta }} \right)^{\frac{1}{{1 - m}}}}\\ k = \beta \left( {1 - m} \right)\\ \gamma = {{\rm{e}}^{k{t_0}}} \end{array} \right.。 $$ (2) 式（2）中：A是当t→∞的一条渐近线，k是和生长率相关的参数，m是形状参数，t0为y=0时的年龄，如果t0=0，那么γ=1。对于树木来说，树高和材积生长满足t=0时，y=0的初始条件，同时满足y=0时，t0=0；胸径生长满足t=t0（生长至1.3 m所需的年龄），y=0。令1/（1－m）=c，得到树高和材积生长方程为式（3），胸径生长方程为式（4）。
$$ y = A{\left( {1-{{\rm{e}}^{-kt}}} \right)^c}; $$ (3) $$ y = A{\left( {1-{{\rm{e}}^{-k\left( {t-{t_0}} \right)}}} \right)^c}。 $$ (4) -
连年生长量Zt是说明树木在某一年的实际生长速度，即连年生长量是树木年龄t的函数，其生长函数为：
$$ {Z_t} = \frac{{{\rm{d}}y\left( t \right)}}{{{\rm{d}}t}}。 $$ (5) 式（5）是对式（3）和式（4）取一阶导数得到。即树高和材积连年生长量方程为：
$$ {Z_t} = \frac{{{\rm{d}}y\left( t \right)}}{{{\rm{d}}t}} = Akc{\left( {1-{{\rm{e}}^{-kt}}} \right)^{c-1}}{{\rm{e}}^{ - kt}}。 $$ (6) 胸径的连年生长量方程为：
$$ {Z_t} = \frac{{{\rm{d}}y\left( t \right)}}{{{\rm{d}}t}} = Akc{\left( {1-{{\rm{e}}^{-k\left( {t-{t_0}} \right)}}} \right)^{c - 1}}{{\rm{e}}^{ - k\left( {t - {t_0}} \right)}}。 $$ (7) 对连年生长量式（6）和式（7）取一阶导数，并令导数值为0，可以得到连年生长量达到极大值时的年龄tZmax和极大值Zmax。即对于树高和材积连年生长量有：
令$ \frac{{{\rm{d}}Z\left( t \right)}}{{{\rm{d}}t}} = \frac{{{{\rm{d}}^2}y\left( t \right)}}{{{\rm{d}}{t^2}}} = {\left( {kc} \right)^2}y\left( t \right)[1-{\left( {\frac{A}{{y\left( t \right)}}} \right)^{\frac{1}{c}}}][1-\left( {\frac{{c-1}}{c}} \right){\left( {\frac{A}{{y\left( t \right)}}} \right)^{\frac{1}{c}}}] = 0$。
得到：
$$ {t_{{Z{\max }}}} = \frac{{\ln c}}{k}; $$ (8) $$ {Z_{\max }} = Ak{\left( {\frac{{c-1}}{c}} \right)^{c-1}}。 $$ (9) 同理，胸径连年生长量为：
$$ {t_{Z{\rm{max}} }} = {t_0} + \frac{{\ln c}}{k}。 $$ (10) 将式（10）代入式（7）得到胸径连年生长量极大值Zmax。
-
平均生长量函数θ（t）是说明树木在某一时刻t的平均生长速度，即总平均生长量是树木年龄t的函数。其方程为：
$$ \theta \left( t \right) = \frac{{y\left( t \right)}}{t}\frac{A}{t}{\left( {1-{{\rm{e}}^{-kt}}} \right)^c}。 $$ (11) 对式（11）求一阶导数，并令一阶导数值为0，可得到平均生长量达到极大值时的年龄tθmax和极大值θmax。即树高和材积平均生长量为：
$$ \frac{{{\rm{d}}\theta \left( t \right)}}{{{\rm{d}}t}} = \frac{A}{t}{\left( {1- {{\rm{e}}^{- kt}}} \right)^{c- 1}}\left[{ck{{\rm{e}}^{-kt}}-\frac{1}{t}\left( {1-{{\rm{e}}^{ - kt}}} \right)} \right] = 0。 $$ (12) 式（12）运用迭代法在MATLAB上运算求解，得到tθmax，代入式（11）求出θmax。同理求出胸径的平均生长量达到极大值时的年龄tθmax和极大值θmax。
-
检验一：利用解析木资料得到模型参数后，计算残差$ \left( {{R_{\rm{e}}}} \right) = {y_j}-{\hat y_j} $，检验残差值是否满足正态分布。
检验二：计算决定系数R2值，R2=SSR/SSJ。SSR为回归平方和，SSJ为总平方和。R2越大，说明模型拟合越好。
-
通过综合不同立地条件的解析木数据，得到生长模型参数估计值和决定系数值（表 2），检验结果显示残差值满足正态分布。因此，所建Richards模型可以用来拟合沙地樟子松的生长，拟合结果见图 1。将所得到的模型参数代入式（3），令y=1.3 m，求出时间t，t即为树木长到1.3 m时所需要的时间t0=6.6 a。将所得到的模型参数代入式（8）式（9）式（10）并求解得到树高、胸径、材积连年生长量最大值及达到最大值的时间，用模型参数及迭代法解式（12）得到树高、胸径、材积平均生长量最大值及达到最大值的年龄，将这些沙地樟子松生长的特征值一并列入表 3。同时将树高、胸径、材积的连年生长量与平均生长量曲线绘制成图 2。
表 2 樟子松生长模型参数表
Table 2. Parameter estimates of Richards model on Mongolian pine
测树因子 A k C $ Sig \cdot {y_j}-{\hat y_j} $ 决定系数R2 树高 14.179 0.084 2.803 0.088 0.994 胸径 19.379 0.075 1.712 0.200 0.998 材积 0.296 0.062 5.926 0.139 0.996 
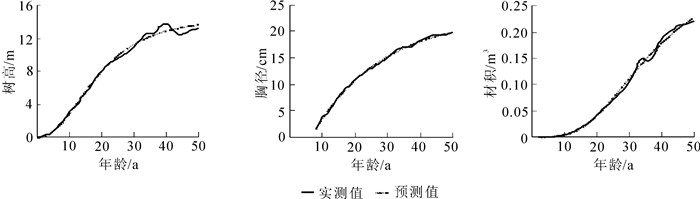
图 1 沙地樟子松树高、胸径、材积生长量观测值与模型预测值曲线
Figure 1. Measurement and predictive value of increment for H, DBH and V of mongolian pine on sandy land
表 3 樟子松树高、胸径、材积生长的特征值表
Table 3. Height(H), diameter at breast height(DBH) and volume(V) growth eigen values on Mongolian pine
测树因子 tZmax Zmax tθmax θmax 树高 12.3 0.54 21.4 0.39 胸径 13.8 0.77 26.0 0.47 材积 28.7 0.007 4 46.8 0.004 5 
图 2 沙地樟子松人工林树高、胸径、材积连年生长量、平均生长量
Figure 2. Annual and average increment for H, DBH and V of mongolian pine in sandy land
-
一般认为，树高生长随年龄的增加而增加，到一定时期后，其生长率逐渐下降[23]。引种地与原产地气候因子的差异，会导致树木因适应气候变化而发生响应[24]。沙地樟子松从内蒙古红花尔基引种到科尔沁沙地的章古台后，树高生长从6.0 a后便进入旺盛生长期，连年生长量逐年加大。在12.3 a时连年生长量达最大，为0.54 m·a－1；而且这种旺盛的生长一直持续（图 1，表 3），到21.4 a时，即图 2中连年生长量和平均生长量的交点，沙地樟子松平均生长量达最高峰，为0.39 m·a－1；21.0 a后，树木的平均生长量开始下降，树高的旺盛生长期结束，前后经历15.0 a的时间。这一结果和其他学者早期的研究结果相符合[22, 25]，实测和预测表明：到40.0 a后，沙地樟子松人工林的连年高生长量降低到0.20 m以下，这与学者早期预测的结果有明显出入[26]。
-
胸径是表征树木生长的另一个重要指标。图 1表明：樟子松引种到章古台后，经过6.6 a就开始了胸径生长；第10.0年开始，胸径便进入旺盛生长阶段；到第14.0年连年生长量达最大，为0.77 cm·a－1；到第26.0年时平均生长量达最大，为0.47 cm·a－1（表 3）。和树高相比，胸径进入旺盛生长的年龄晚4.0 a，达到连年生长量最大的年龄比树高晚2.0 a，达到平均生长量最大值的年龄比树高要晚5.0 a。实测和预测值表明：44.0 a后，胸径的连年生长量下降到0.2 cm·a－1以下。
-
材积是反映树木生长的一个综合指标，随树高、胸径的增加而增加[27]。引种到章古台沙地的樟子松材积生长在12.0 a之前生长缓慢，随着树高和胸径的加快生长，12.0 a之后材积开始加快生长（图 1），在第29.0年其连年生长量达最高值（0.007 4 m3·a－1），而平均生长量达最大时的年龄为47.0 a，平均最大生长量达0.004 5 m3·a－1（表 3）。在测树学上，材积连年生长量曲线和平均生长量曲线的交点（即平均生长量最大值点）有重要的意义，该点是树木达到数量成熟的时间点，因此，引种到章古台的沙地樟子松数量成熟年龄为47.0 a。数量成熟后，树木的材积连年生长量便开始显著下降。实测值表明，第48.0年的连年生长量值只有0.002 4 m3·a－1，第50.0年下降到0.002 0 m3·a－1。相较于树高和胸径，材积旺盛生长的年龄比较晚，持续的时间比较长，但不论是达到连年生长量最大值时的年龄还是达到平均生长量最大值时的年龄均晚于树高和胸径。
-
选择引种地不同立地条件下30 a以上的樟子松人工固沙林为标准地，以标准地的平均木做解析木，求解Richards模型的参数并检验模型的拟合性，运用建立的Richards模型求解沙地樟子松的各种特征值，揭示沙地樟子松在引种地生长过程。结论如下：①建立的关于树高、胸径、材积生长的Richards模型拟合性好，决定系数分别达0.994，0.998，0.996，残差（Re）符合正态分布，且显著性均大于0.05，3个参数分别为树高：14.179，0.084，2.803；胸径：19.379，0.075，1.712；材积：0.296，0.062，5.926。②樟子松引种到章古台后，树高在第12.3年连年生长量达最大，为0.54 m·a－1，21.4 a平均生长量达到最高峰，最大值为0.39 m·a－1；经过6.6 a就开始了胸径生长，第14.0年连年生长量达最大，为0.77 cm·a－1，第26.0年时平均生长量达最大，为0.47 cm·a－1；材积在12.0 a之前生长缓慢，第29.0年其连年生长量达最高值，为0.007 4 m3·a－1，平均生长量达最大时的年龄为47.0 a，最大达0.004 5 m3·a－1，引种到章古台的沙地樟子松数量成熟年龄为47.0 a。
由于章古台和原产地的气候因子有较大差别[5, 23, 26]，樟子松自引种到章古台后，和原产地比较，引种地的降水量、气温、蒸发量、无霜期等均增加，生长季变长。樟子松为了适应新的生长环境，不得不调整自身原有的生长节律，树高、胸径、材积旺盛生长开始的时间提前[22, 26]，但持续的时间缩短。数量成熟年龄在原产地为102.0 a[23]，而在引种地，数量成熟年龄仅为47.0 a，比朱教君等[23]研究的43.0 a略长，和姜凤岐等[28]预测的46.0 a大致一致。因此，樟子松引种到章古台后，其生长进程加快，生命周期缩短，成熟期提前。这种变化与其说是生长环境导致的“早衰”，不如说是樟子松引种到新的地区后，为适应新的生长环境而做出的自身调整的结果。有必要及时发现树木本身的这种改变，调整经营管理措施，为树木更好地生长创造条件。
Growth of Mongolian pine in Zhanggutai of Liaoning Province
-
摘要: 樟子松Pinus sylvestris var.mongolica引种至沙地，经过60多年的生长已经到了生命周期的末期。及时总结第1代沙地樟子松的生长过程，可以更好地为沙地樟子松的推广、更新、经营管理提供理论依据。选择引种地辽宁章古台不同立地条件下30 a以上樟子松人工林标准地（11块）的平均木作为解析木（11株），求解Richards模型的参数并检验模型的拟合性，运用建立的Richards模型求解沙地樟子松的各种特征值，从而揭示沙地樟子松的生长进程。结果表明：①樟子松的生长能够用Richards模型很好地模拟，残差符合正态分布，显著性均大于0.05。模型的参数值分别为树高：14.179，0.084，2.803；胸径：19.379，0.075，1.712；材积：0.296，0.062，5.926。②引种到章古台沙地的第1代樟子松，树高在第12.3年连年生长量达到最大值0.54 m·a-1，第21.4年平均生长量达到最大值0.39 m·a-1；胸径平均在6.6 a后开始生长，第14.0年连年生长量达到最大值0.77 cm·a-1，第26.0年时平均生长量达到最大值0.47 cm·a-1；材积生长在12.0 a之前生长缓慢，第29.0年其连年生长量达到最高值0.007 4 m3·a-1，平均生长量在第47.0年达到最大（即林木数量成熟年龄），最大平均生长量达0.004 5 m3·a-1。樟子松引种到章古台后，生长进程加快，生命周期缩短，成熟期提前。Abstract: The aim is to summarize the growth process for first generation Mongolian pine (Pinus sylvestris var.mongolica) on sandy land, where its life cycle ends after about 60 years, and to provide a theoretical basis for promotion, regeneration, and management of a Mongolian pine plantation. 11 trees were selected for analysis, chosen from standard plots of 11 Mongolian pine plantation stands (> 30 a) with different site conditions in Zhanggutai of Liaoning Province. Then parameters for Richards model were solved and the goodness-of-fit was tested. To reveal the growth process of Mongolian pine, eigenvalues of Mongolian pine trees were used in Richards Equation. Results of height, diameter at breast height (DBH), and volume of Mongolian pine were simulated by Richards model with the parameter estimated values of 14.179, 0.084, and 2.803 for height; 19.379, 0.075, and 1.712 for DBH; and 0.296, 0.062, and 5.926 for volume. For tree height growth of first generation Mongolian pine introduced to Zhanggutai, the relative growth rate reached its maximum of 0.54 m·a-1 at year 12.3, and the average growth rate achieved its peak at year 21.4 with 0.39 m·a-1. Growth of DBH for trees started at year 6.6 with the relative growth rate reaching its maximum of 0.77 cm·a-1 at year 14.0 and the average growth rate achieving its peak at year 26.0 with 0.47 cm·a-1. Volume growth was very slow before age 12.0 with the relative growth rate reaching its maximum of 0.007 4 m3·a-1 at 29.0 years, the average growth rate achieving its peak at year 47.0 with 0.004 5 m3·a-1. The quantitative maturity age, when the maximum of average growth rate of volume appears, was 47.0 years of Mongolian pine in Zhanggutai. We drew a conclusion that the maximum of relative growth rate of height, DBH and volume of Mongolian pine appear at the age of 12.3 a, 14.0 a and 29.0 a, respectively. The maximum of average growth rate of height, DBH and volume appear at the age of 21.4, 26.0 and 47.0 years, respectively. The quantitative maturity appears in the 47th year after planting.
-
Key words:
- forest measuration /
- Richards model /
- sandy land /
- Pinus sylvestris var.mongolica /
- tree height /
- diameter at breast height /
- volume /
- growth process
-
图 1 沙地樟子松树高、胸径、材积生长量观测值与模型预测值曲线
Figure 1 Measurement and predictive value of increment for H, DBH and V of mongolian pine on sandy land
图 2 沙地樟子松人工林树高、胸径、材积连年生长量、平均生长量
Figure 2 Annual and average increment for H, DBH and V of mongolian pine in sandy land
表 1 沙地樟子松解析木信息
Table 1. Stem analysis information of Mongolian pine
立地 年龄/a 数量/株 树高/m 胸径/cm 沙丘顶部 30~35 1 9.0 14.94 40 1 11.6 19.10 平坦沙地 35 1 13.2 22.75 34 1 12.4 20.55 丘间低地 40~50 2 14.2~15.5 19.90~20.65 沙丘中部 30~40 1 9.8 18.00 30~40 2 9.9~10.3 14.40~16.80 50~60 2 13.0~13.3 20.90~22.80 
下载: 导出CSV
表 2 樟子松生长模型参数表
Table 2. Parameter estimates of Richards model on Mongolian pine
测树因子 A k C $ Sig \cdot {y_j}-{\hat y_j} $ 决定系数R2 树高 14.179 0.084 2.803 0.088 0.994 胸径 19.379 0.075 1.712 0.200 0.998 材积 0.296 0.062 5.926 0.139 0.996
下载: 导出CSV
表 3 樟子松树高、胸径、材积生长的特征值表
Table 3. Height(H), diameter at breast height(DBH) and volume(V) growth eigen values on Mongolian pine
测树因子 tZmax Zmax tθmax θmax 树高 12.3 0.54 21.4 0.39 胸径 13.8 0.77 26.0 0.47 材积 28.7 0.007 4 46.8 0.004 5
下载: 导出CSV
-
[1] 李蒙蒙, 丁国栋, 高广磊, 等.樟子松(Pinus sylvestris var.mongolica)在中国北方10省(区)引种的适宜性[J].中国沙漠, 2016, 36(4):1021-1028. LI Mengmeng, DING Guodong, GAO Guanglei, et al. Introduction suitability of Pinus sylvestris var.mongolica in 10 northern provinces of China[J]. J Des Res, 2016, 36(4):1021-1028. [2] 移小勇, 赵哈林, 崔建垣, 等.科尔沁沙地不同密度(小面积)樟子松人工林生长状况[J].生态学报, 2006, 26(4):1200-1206. YI Xiaoyong, ZHAO Halin, CUI Jianyuan, et al. Growth of small area Pinus sylvestris var.mongolica artificial forest under different densities in Horqin sandy land, north of China[J]. Acta Ecol Sin, 2006, 26(4):1200-1206. [3] 曾德慧, 姜凤岐, 范志平, 等.沙地樟子松人工林自然稀疏规律[J].生态学报, 2000, 20(2):235-242. ZENG Dehui, JIANG Fengqi, FAN Zhiping, et al. Self-thinning of even-aged pure plantations of Pinus sylvestris var.mongolica on sandy soil[J]. Acta Ecol Sin, 2000, 20(2):235-242. [4] 曾德慧, 姜凤岐, 范志平, 等.樟子松人工固沙林稳定性的研究[J].应用生态学报, 1996, 7(4):337-343. ZENG Dehui, JIANG Fengqi, FAN Zhiping, et al. Stability of Mongolian pine plantations on sandy land[J]. Chin J Appl Ecol, 1996, 7(4):337-343. [5] 焦树仁.辽宁省章古台樟子松固沙林提早衰弱的原因与防治措施[J].林业科学, 2001, 37(2):131-138. JIAO Shuren. Report on the causes of the early decline of Pinus sylvestris var.mongolica shelterbelt and its preventative and control measures in Zhanggutai of Liaoning Province[J]. Sci Silv Sin, 2001, 37(2):131-138. [6] 朱教君, 康宏樟, 李智辉, 等.水分胁迫对不同年龄沙地樟子松幼苗存活与光合特性影响[J].生态学报, 2005, 25(10):2527-2533. ZHU Jiaojun, KANG Hongzhang, LI Zhihui, et al. Impact of water stress on survival and photosynthesis of Mongolian pine seedlings on sandy land[J]. Acta Ecol Sin, 2005, 25(10):2527-2533. [7] 康宏樟, 朱教君, 许美玲.科尔沁沙地樟子松人工林幼树水分生理生态特性[J].干旱区研究, 2007, 24(1):15-22. KANG Hongzhang, ZHU Jiaojun, XU Meiling. Study on water physiological properties of the artificially-planned saplings of Pinus sylvestris var.mongolica in the Horqin sand land[J]. Arid Zone Res, 2007, 24(1):15-22. [8] 陈伏生, 曾德慧, 范志平, 等.章古台沙地樟子松人工林土壤有效氮的研究[J].北京林业大学学报, 2005, 27(3):6-11. CHEN Fusheng, ZENG Dehui, FAN Zhiping, et al. Available nitrogen in forest soil of Pinus sylvestris var.mongolica plantations in Zhanggutai sandy lands[J]. J Beijing For Univ, 2005, 27(3):6-11. [9] 陈伏生, 曾德慧, 范志平, 等.沙地不同树种人工林土壤氮素矿化过程及其有效性[J].生态学报, 2006, 26(2):341-348. CHEN Fusheng, ZENG Dehui, FAN Zhiping, et al. Comparative nitrogen mineralization and its availability in certain woody plantations in Keerqin sand lands, China[J]. Acta Ecol Sin, 2006, 26(2):341-348. [10] ALLEN C D, MACALADY A K, CHENCHOUNI H, et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests[J]. For Ecol Manage, 2010, 259(4):660-684. [11] CARNWATH G C, PETERSON D W, NELSON C R. Effect of crown class and habitat type on climate-growth relationships of ponderosa pine and Douglas-fir[J]. For Ecol Manage, 2012, 285(1):44-52. [12] DAS A. The effect of size and competition on tree growth rate in old-growth coniferous forests[J]. Can J For Res, 2012, 42(11):1983-1995. [13] FORD K R, BRECKHEIMER I K, FRANKLIN J F, et al. Competition alters tree growth responses to climate at individual and stand scales[J]. Can J For Res, 2017, 47(1):53-62. [14] ALLEN M G Ⅱ, BURKHART H E. Comparison of alternative data sources for modeling site index in loblolly pine plantations[J]. Can J For Res, 2015, 45(8):1026-1033. [15] GARCÍA O, BURKHART H E, AMATEIS R L. A biologically-consistent stand growth model for loblolly pine in the Piedmont physiographic region, USA[J]. For Ecol Manage, 2011, 262(11):2035-2041. [16] 姜立春, 杜书立.基于非线性混合模型的东北兴安落叶松树高和直径生长模拟[J].林业科学研究, 2012, 25(1):11-16. JIANG Lichun, DU Shuli. Height and diameter growth modeling of dahurian larch based on nonlinear mixed model in northeastern China[J]. For Res, 2012, 25(1):11-16. [17] 段爱国, 张建国, 童书振. 6种生长方程在杉木人工林林分直径结构上的应用[J].林业科学研究, 2003, 16(4):423-429. DUAN Aiguo, ZHANG Jianguo, TONG Shuzhen. Application of six growth equations on stands diameter structure of Chinese fir plantations[J]. For Res, 2003, 16(4):423-429. [18] 孙晓梅, 张守攻, 孔凡斌, 等.日本落叶松家系对树高生长模型参数的影响[J].林业科学, 2005, 41(1):78-84. SUN Xiaomei, ZHANG Shougong, KONG Fanbin, et al. Analyzing parameters of height-age models for open-pollinated Japanese larch families[J]. Sci Silv Sin, 2005, 41(1):78-84. [19] 张雄清, 张建国, 段爱国.基于贝叶斯法估计杉木人工林树高生长模型[J].林业科学, 2014, 50(3):69-75. ZHANG Xiongqing, ZHANG Jianguo, DUAN Aiguo. Tree-height growth model for Chinese fir plantation based on Bayesian method[J]. Sci Silv Sin, 2014, 50(3):69-75. [20] 姚丹丹, 雷相东, 张则路.基于贝叶斯法的长白落叶松林分优势高生长模型研究[J].北京林业大学学报, 2015, 37(3):94-100. YAO Dandan, LEI Xiangdong, ZHANG Zelu. Bayesian parameter estimation of dominant height growth model for Changbai larch (Larix olgensis Henry) plantations[J]. J Beijing For Univ, 2015, 37(3):94-100. [21] TOMEÉJ, TOMÉM, BARREIRO S, et al. Age-independent difference equations for modeling tree and stand growth[J]. Can J For Res, 2006, 36(7):1621-1630. [22] ZHU Jiaojun, FAN Zhiping, ZENG Dehui, et al. Comparison of stand structure and growth between plantation and natural forests of Pinus sylvestiris var. mongolica on sandy land[J]. J For Res, 2003, 14(2):103-111. [23] 朱教君, 曾德慧, 康宏樟, 等.沙地樟子松人工林衰退机制[M].北京:中国林业出版社, 2005:41-47. [24] 孙毓, 王丽丽, 陈津, 等.中国落叶松属树木年轮生长特性及其对气候变化的响应[J].中国科学:地球科学, 2010, 40(5):645-653. SUN Yu, WANG Lili, CHEN Jin, et al. Growth characteristics and response to climate change of Larix Miller tree-ring in China[J]. Sci Chin Earth Sci, 2010, 40(5):645-653. [25] 焦树仁.干旱对章古台沙地樟子松人工林生长的影响[J].林业科学, 1986, 22(4):419-425. JIAO Shuren. The influence of aridity on the growth of Mongolian pine plantation in Zhanggutai sand land, Liaoning Province[J]. Sci Silv Sin, 1986, 22(4):419-425. [26] 焦树仁.章古台固沙林生态系统的结构与功能[M].沈阳:辽宁科学技术出版社, 1989:39-43. [27] FABBIO G, FRATTEGIANI M. Height estimation in stem analysis using second differences[J]. For Sci, 1994, 40(2):329-340. [28] 姜凤岐, 曾德慧, 范志平, 等.沙地樟子松林单木生长的研究[J].应用生态学报, 1996, 7(增刊1):1-5. JIANG Fengqi, ZENG Dehui, FAN Zhiping, et al. Simulation of individual tree growth of Mongolian pine forest in sandy land[J]. Chin J Appl Ecol, 1996, 7(suppl 1):1-5. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2018.02.017
点击查看大图
图(2) / 表(3)
计量
- 文章访问数: 2883
- HTML全文浏览量: 574
- PDF下载量: 492
- 被引次数: 0
