-
近年来,树木三维可视化建模成为虚拟植物研究领域的热点课题之一,在数字植物园建设、虚拟景观规划设计、三维游戏开发和影视动画设计等诸多领域都有着广阔的应用前景。树木包含的器官较多,其结构较为精细且无规则性,尤其是枝干和树叶,具有复杂的几何拓扑结构。这使得计算机对其进行建模会比较困难,所以如何快速、精准建立具有高真实感的树模型是主要需要解决的问题[1]。目前,植物三维建模的方法主要分为3种:基于图形的方法、基于图像的方法和基于专业软件的方法。3种建模方法各有优劣,基于图形方法的模型比较注重植物生理的形态结构,主要包括基于分形理论的迭代函数系统(iterated function system)和L系统(L-system),还有粒子系统(partial system)和随机过程生长法等,建立模型效率较高且构建方式较为灵活,但是难以对形态结构特别复杂的植物进行三维建模。图像方法则是针对图形方法的不足提出的,它是根据输入计算机的一幅或多幅2维图像来完成对植物形体的三维重建,但其建模过程较为复杂,生成的模型形态结构固定,缺乏灵活性。另外,由于易受室外环境的影响,如遮挡或季节因素导致图像数据的缺失而难实现可视化建模[2-3]。基于软件建模的方法,目前比较流行的软件有SpeedTree,Xfrog,3dsMax以及Maya等[4-7],虽然生成的模型真实感是所有方法里最好的,并且能实现具有复杂形态结构的植物体的建模,但是该建模方法要求用户具备较扎实的植物生理学知识。综合比较上述方法,出于能够快速、高仿真、可交互建立具有真实植物空间结构信息的三维树木模型的目的,本研究针对现有建模方法的缺陷和不足,利用基于改进的分形迭代函数系统的建模方法,设计并实现了单树建模软件系统,通过提取特征参数和变量控制系数来控制树体模型生成,所建立的模型能较好地反应树木生理生态结构,还克服了建模流程复杂、模型真实感弱、交互性差等缺点。
-
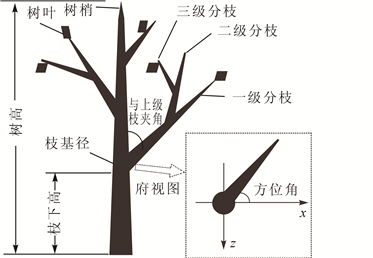
本研究涉及的树体三维可视化建模仅考虑地上部分。树体地上部分的器官主要可分为枝干、树叶、花朵、果实。枝干的形态结构复杂多变,根据生长层次的不同可将枝干按层级划分[8]:主干、一级分枝、二级分支枝和三级分枝……。决定分枝形态和空间格局的因素又可分为:分枝长度、分枝基径、分枝着枝角(与上级枝干的夹角)、分枝方位角(沿上级枝干旋转的角度)、弯曲度等。
一般来讲,园林植物外部形态可以由树枝的分枝模式来区分。分枝模式主要分为两大类:主(单)轴分枝和合轴分枝。主轴分枝主要表现为其主茎上的顶芽不断向上生长形成明显的主干,主茎上的腋芽形成侧枝,侧枝上再生成各级分枝,但它们的生长均不超过主茎,形态结构抽象图如图 1所示。合轴分枝则主要表现为茎的顶芽发育到一定时候停滞或死亡,由其下方腋芽取而代之形成强壮的侧枝,一段时间后生长优势又转向下一级分枝,因此没有明显的主干,形成了多个弯曲的主轴,整个树冠呈开张状态[5]。
-
在模型构建中,本研究将可视化建模过程拆分成3个部分:树体的枝干建模、叶片建模以及模型和场景渲染。将建模过程分步处理,不仅可以简化整个建模的流程,还可以提高模型的重用性,方便在植物模型生成后进行局部调整[10]。这使得建模系统具有很好的交互性,用户只需通过调节几个部位对应的属性值,就可以根据自己的需要设计生成相应的树枝形态和树叶形态。
-
将树枝分级处理,每一级树枝可以理解成由不同的枝段构成,而每一个枝段又可以理解为由若干个不同的枝段元连接构成——枝段元是构成枝干模型的最小单位。在自然界里植物枝干的形状几乎都近似圆台形,因此,有研究者用圆台模型模拟三维分形树的树木枝段元[9]。但是经实验发现,如果直接简单调用OpenGL图形库里的圆台而不做处理,那么就会导致树枝弯曲时枝段元拼接处出现缺口(图 2)。经实验发现:用多边形棱台进行枝干模拟可以较好地处理枝段元的拼接问题,所以本研究采用正六边形棱台近似模拟枝干。实验结果显示枝干模型的平滑性较好且未出现连接缺口。其原理是先通过定义点的初始位置和终点位置,然后根据定义的位置绘制2个正六边形,最后把2个正六边形的12个顶点相互进行连接[11]。因此,该方法很好地解决了枝干连接的问题,同时也提高了模型的渲染效率。枝段元由4个参数来进行控制,分别是:Radius,Length,Angle,Twist。其中Radius表示枝段元的底面半径,Length表示枝段元的高度,而Angle表示枝段元上底面、下底面中心连线绕z轴(Open-GL三维坐标系)的夹角,Twist表示枝段元上底面、下底面中心连线绕x轴的角度,两者共同作用来控制枝干生长方向,效果如图 3(A)所示。基于以上枝段元属性控制,若干个枝段元通过偏转、弯曲、连接就可以组成一条枝段,如图 3(B)所示,而枝段又受SideAngle即侧枝着枝角度属性控制。
-
由于树枝与树枝之间存在相似的生理特征和结构特征,也就是自相似性,而分形方法恰好能够较好地描述这一特征,那么可以将三维树木的枝干生成过程看成是一个分形迭代过程。将当前树枝段元的参数数据经过一定的算术运算后所得的结果作为次级枝段元的参数数据,然后再进行递归调用得到再下一级枝段元的参数。按这种算术关系多次迭代后再将枝段元首尾连接即可实现一根一定长度的由粗变细且具有弯曲度的枝条[12]。利用这种递归调用思想最终可生成具有自相似结构的三维分形树木。用Radius′,Length′,Angle′,Twist′分别表示次级枝段元的属性,可以得到如下关系式:
$$ \left\{ \begin{array}{l} {\rm{Radius' = Radius}} \times {\rm{RadScale}}\\ {\rm{Length' = Length}} \times {\rm{LenScale}}\\ {\rm{Angle' = Angle + }}{{\rm{C}}_{\rm{1}}}\\ {\rm{Twist' = Twist + }}{{\rm{C}}_{\rm{2}}}\\ {\rm{SideAngle' = SideAngle}} \end{array} \right.。 $$ (1) 关系式(1)中:LenScale表示枝段元长度控制系数,RadScale表示枝段元半径控制系数,C1和C2分别表示一个固定常数。然而基于以上建模方法,其生成的枝干模型是规则的、有序的,这与实际自然界的树枝生长形态不符,因为受自然环境的影响,虽然整体上具有自相拟性,但每个分支在粗细长度、弯曲程度、着枝角度和方位角度等方面都是有所差异的。为了更好地还原真实情况,在迭代生成枝干的过程中加入了随机干扰因子,由关系式(1)可得关系式(2):
$$ \left\{ \begin{array}{l} {\rm{Radius' = Radius}} \times {\rm{RadScale}}\\ {\rm{Length' = Length}} \times {\rm{LenScale}} \times {\rm{random(n)}}\\ {\rm{Angle' = Angle + (}}{{\rm{C}}_{\rm{1}}} \times {\rm{rando}}{{\rm{m}}_{\rm{1}}}{\rm{(n))}}\\ {\rm{Twist' = Twist + (}}{{\rm{C}}_2} \times {\rm{rando}}{{\rm{m}}_{\rm{2}}}{\rm{(n))}}\\ {\rm{SideAngle' = SideAngle}} \times {\rm{rando}}{{\rm{m}}_{\rm{3}}}{\rm{(n)}} \end{array} \right.。 $$ (2) -
由于1株树的叶子数量比较庞大,并且树叶的边缘信息和叶脉纹路差异巨大,若对每一片叶子进行几何建模不仅会增加计算量,同时也会比较耗时,所以本研究采用通用的方法——纹理映射。该方法只需利用OpenGL先设置一个多边形模板作为树叶的模板,然后将树叶纹理(树叶图片)映射到模板上,最后加以渲染就可以得到较为真实的树叶模型。通过设置树叶(多边形模板)属性参数,如叶片大小(LeafSize),叶片着枝角(LeafAngle),叶片方位角(LeafTwist)等就可获得形态各异的树叶,从而改变树模型的局部形态。
-
第1步:先设定起始枝段元参数,如枝段元的长度(Length),底面半径(Radius),夹角(Angle),旋转角(Twist),长度控制系数(LenScale),半径控制系数(RadScale)以及树枝干深度系数(TreeDepth),也就是递归算法深度,即递归调用的次数。第2步:根据第1步设定的参数绘制起始枝段元模型,并贴上纹理。第3步:上一步的长度和半径乘以控制系数(LenScale和RadScale)得到本次应绘制的枝段元的长度和半径,贴上纹理,并缓存此次结果作为下次执行递归函数时需调用的参数,同时树枝干深度系数(TreeDepth)减小1个单位。第4步:判断TreeDepth是否等于0,若TreeDepth为0,则停止绘制枝段元,转而开始绘制树叶,设置叶子的数量、大小以及旋转角和夹角等属性参数,添加纹理并生成树叶。若TreeDepth>0,则以当前段元长度(Length),半径(Radius),夹角(Angle)和旋转角(Twist)作为参数进入递归函数,继续绘制枝段元。第5步:重复第3步到第4步操作,直到树的枝干深度系数达到生成树叶的递归系数值,程序运行结束跳转生成1株完整的三维分形树。
-
//初始值设置
floatAngle=15.0f;//枝段元偏移角度
floatLateralAngle=10.0f;//侧枝段元偏移角度
floatScaleLen=0.85f;//长度衰减系数
floatScaleRad=0.75f;//半径衰减系数
floatTwist=65.0f;//侧枝旋转角度(方位角)
floatSideAngle=60.0f;//侧枝与上级枝的分叉角度
floatSideScaleDepth=0.80f;//侧枝深度控制系数
floatSideScaleSize=0.90f;//侧枝粗细长度衰减系数
//枝干段元迭代函数
voidBuildBranch(intCount, GLfloatLeafSize)
{
if(Count)
{
if(Next)
{
Next->SetAngle(Angle * random2);
Next->SetTwist(Twist + Twist * random1(1, 3));
Next->SetLength(ScaleLen*Length); //长度衰减系数×长度
Next->SetRadius(ScaleRad*Radius); //半径衰减系数×半径
Next->BuildBranch(Count-1, LeafSize);
}
}
if(Count>=1)
{//建侧枝
SideBranch=newCBranch;
ASSERT(SideBranch);
if(SideBranch)
{
SideBranch->LeafScale=LeafSize/CSegment::SideScale;
SideBranch->Base=this;
SideBranch->Rebuild(max(1.0f, min(Count, Count*SideScaleDepth)));
}
}
else
{//建树叶
Leaves=newCLeaf;
Leaves[0].Angle=LeafAngle;
Leaves[0].Scale=LeafSize;
Leaves[0].Twist=Twist+(Twist+180);
}
}
-
为了实现基于OpenGL的交互式树木三维可视化建模系统,本研究选用Visual Studio 2010作为开发工具,用Visual C++语言编程实现,通过配置OpenGL运行环境,运用OpenGL提供的图形图像技术以及基于改进的分形迭代算法绘制虚拟三维树木,实现通用性高、真实感强且人机交互性良好的虚拟三维树木模型的自动化生成系统。运行硬件环境具体为:Windows 10 64位操作系统,8G内存,Inter Core i5-4200h处理器,NVIDIAGeForceGTX 950M显卡。
-
根据1.2节模型构建内容可知,若知道枝段元底面半径就可以依据三角函数定理得到正六边形下底面每个顶点在三维坐标系中的位置,由枝段元的高度和半径衰减系数又能得到上底面六边形顶点坐标,也就是次级枝段元下底面六边形各顶点坐标。利用OpenGL图形绘制技术就能绘制出六边形棱台用以表示枝段元。表 1列出了六边形底面各点在三维坐标系的具体取值,图 4是六边形各坐标点的位置及对应纹理贴图的示意图。
表 1 各坐标点取值
Table 1. Value of each point
坐标点 坐标值 次级坐标点 次级坐标值 Q1 (R·cos$ \frac{\pi }{3}$,0,R·sin$ \frac{\pi }{3}$) Q1′ (R′·cos$ \frac{\pi }{3}$,L,R′·sin$ \frac{\pi }{3}$) Q2 (-R·cos$ \frac{\pi }{3}$,0,R·sin$ \frac{\pi }{3}$) Q2′ (-R′·cos$ \frac{\pi }{3}$,L,R′·sin$ \frac{\pi }{3}$) Q3 (-R,0,0) Q3′ (-R′,L,0) Q4 (-R·cos$ \frac{\pi }{3}$,0,-R·sin$ \frac{\pi }{3}$) Q4′ (-R′·cos$ \frac{\pi }{3}$,L,-R′·sin$ \frac{\pi }{3}$) Q5 (R·cos$ \frac{\pi }{3}$,0,-R·sin$ \frac{\pi }{3}$) Q5′ (R′·cos$ \frac{\pi }{3}$,L,-R′·sin$ \frac{\pi }{3}$) Q6 (R,0,0) Q6′ (R′,L,0) 由于枝段存在弯折和偏转的特征,坐标点位置就要根据夹角和旋转角加以变更,具体变更公式见关系式(3)。各坐标点位置确定后即可通过OpenGL的纹理贴图函数glNormal3f,glTexCoord2f,glVertex3f加以贴图渲染,基于以上操作即可得到带纹理效果的枝干,具体效果如图 5。
$$ \left\{ \begin{array}{l} {{\rm{X}}_{\rm{i}}}^\prime {\rm{ = (Zi^{*}CosTwist + }}{{\rm{X}}_{\rm{i}}}{\rm{^{*}SinTwist)^{*}SinTwist + ((-}}{{\rm{Z}}_{\rm{i}}}{\rm{^{*}SinTwist + }}{{\rm{X}}_{\rm{i}}}{\rm{^{*}CosTwist)^{*} }}\\ \;\;\;\;\;\;\;{\rm{CosAngle-Length^{*}SinAngle)^{*}CosTwist}}\\ {{\rm{Y}}_{\rm{i}}}^\prime {\rm{ = (-}}{{\rm{Z}}_{\rm{i}}}{\rm{^{*}SinTwist + }}{{\rm{X}}_{\rm{i}}}{\rm{^{*}CosTwist)^{*}SinAngle + Length^{*}CosAngle}}\\ {{\rm{Z}}_{\rm{i}}}^\prime {\rm{ = (}}{{\rm{Z}}_{\rm{i}}}{\rm{^{*}CosTwist + }}{{\rm{X}}_{\rm{i}}}{\rm{^{*}SinTwist)^{*}CosTwist - (( - }}{{\rm{Z}}_{\rm{i}}}{\rm{^{*}SinTwist + }}{{\rm{X}}_{\rm{i}}}{\rm{^{*}CosTwist)^{*}}}\\ \;\;\;\;\;\;\;{\rm{CosAngle - Length^{*}SinAngle)^{*}SinTwist}} \end{array} \right.。 $$ (3) -
本研究用图片贴图的方法模拟树叶,素材取自自然界真实树叶的照片,格式选择24位图的bmp格式。为了提高树叶的真实感,需要将除叶片以外的图像像素全部消除或隐藏,所以这里采用了BMP透明处理技术,其方法原理是获取一张像素为2n×2n,格式为bmp的位图,将图片中所有需要透明处理的地方的Alpha值设置为0.0,不需要透明处理的地方的Alpha值设置为1.0,然后设置Alpha的测试通过条件为:“大于0则通过”。如一张背景为黑色的树叶照片,将像素为黑色的Alpha值设为0.0,除黑色以外的Alpha值设为1.0,绘制树叶纹理时使用OpenGL图库自带的glEnable(GL_ALPHA_TEST)和glAlphaFunc(GL_GREATER, 0)函数就可以使树叶完整的显示出来,从图 6可以看到经BMP透明技术处理后的树叶模型效果。
-
为了增加树木绘制的真实感,本研究还增加了光照和阴影效果。在OpenGL里光照模型是由光源、材质和光照环境决定的,通过设置光源位置(LightPosition),环境光(LightAmbient)和反射光(LightDiffuse)等属性值,共同作用来模拟现实光照效果。基于光照就可以绘制阴影效果,目前比较流行的阴影模拟方法是采用Shadow Maping算法,其生成阴影的原理为:shadow map将场景渲染2次,第1次是从灯光的角度(把相机放到灯光位置)渲染场景,然后存储渲染的深度信息到一张纹理上。第2次再从观察者的角度来渲染,在第2次渲染时才渲染阴影,对于每个图元的深度信息和第1次从灯光角度渲染的深度信息比较,如果当前深度值大于第1次渲染的深度值,则说明有物体在当前片元和灯光之间,那么当前片元在阴影区[13]。
-
为了增加树体建模的灵活性,本研究将树木模型参数做了可视化处理,即把涉及到树木形态结构的参数整合到一个参数控制面板上,这些参数总共包括了14项:树枝干深度系数(TreeDepth),枝干段元夹角(Angle),侧枝段元夹角(LateralAngle),沿上级枝的旋转角(Twist),与上级枝的夹角(SideAngle),枝干长度衰减系数(LenScale),枝干半径衰减系数(RadScale),侧枝深度衰减系数(SideScaleDepth),侧枝尺寸系数(SideScaleSize),树叶大小(LeafSize),树叶偏转角(LeafAngle),树影长度(TreeShadowLen),枝影密度(BranchShadowDen)和叶影密度(LeafShadowDen)。当改变其中一项参数后,树体的形态变化将实时显示在视图区。另外,还增加了贴图更换功能,当点击更换按钮后可通过选择文件夹里已有的贴图文件来更换模型外部特征,进一步增加了建模的灵活性。通过控制键盘前后左右按键和鼠标左右键实现上下左右旋转功能和前进后退功能,有利于更细致的观察。
-
树干建模的参数主要受枝干深度系数、枝干段元夹角、侧枝段元夹角、沿上级枝的旋转角、与上级枝的夹角、枝干长度衰减系数、枝干半径衰减系数、侧枝深度衰减系数、侧枝尺寸衰减系数等9项参数控制,参数不同生成的树木形态结构就不同,由此可以生成形态各异的三维树木。为了适应树木模型的多变性,添加了树皮更换功能。点击控制面板上的“树皮更改”按钮后(图 7A)弹出树皮选择窗口(如图 7B),选择所需树皮贴图,点击确认按键后即可生成用户所需的树皮样式。树皮更改后的树木模型如图 7C。
-
根据1.1节树木形态结构分析可知,单轴树会有一根明显的主干,围绕主干生成侧枝,主干和侧枝的长度、半径自底向上呈现缩减趋势,所以需设置长度和半径缩减系数。为了模拟现实中弯曲状态,通过设置枝段元夹角等参数即可实现,主要参数如表 2所示,效果如图 8所示,稍微调节其中一个参数就可改变相应树形态。但是需注意的是TreeDepth和SideScaleDepth的属性值不能同时设置到最大值,若设置过大,会引起枝干数量呈指数型增长,从而瞬间增加计算机显卡的计算量并占用大量内存而造成卡顿。
表 2 单轴树参数参考表
Table 2. The parameter graph of a monoaxial tree
参数 参数值 取值范围 SetTreeDepth 23 1~25 SetAngle 10 0~90 SetLateralAngle 15 0~90 SetTwist 73 0~180 SetSideAngle 50 0~180 SetLenScale 0.95 0~1 SetRadScale 0.82 0~1 SetSideScaleDepth 0.75 0~1 SetSideScaleSize 0.83 0~1 -
合轴树没有明显的主枝干,具有茂密的侧枝,整个植物冠状呈张开形态,所以只需根据上表的参数加以调整,利用分形迭代算法即可实现合轴树的效果,主要参数如表 3所示,效果如图 9所示。同样,这里只需调节其中一个参数就可改变相应树形态,TreeDepth和SideScaleDepth属性值不能同时设置到最大值。
表 3 合轴树参数参考表
Table 3. The parameter graph of a multiway tree
参数 参数值 取值范围 SetTreeDepth 21 1~25 SetAngle 13 0~90 SetLateralAngle 10 0~90 SetTwist 79 0~180 SetSideAngle 34 0~180 SetLenScale 0.92 0~1 SetRadScale 0.73 0~1 SetSideScaleDepth 0.86 0~1 SetSideScaleSize 1 0~1 -
对于构建好的枝干模型,根据树叶建模和可视化模拟,添加树叶后使得树木进一步增加了真实感,为了进一步增加建模的灵活性,本研究将树叶的大小和角度属性进行了交互式的设计,通过调节控制面板对应属性值即可自动调整树叶在枝干上的分布特征。另外,为了适应树模型的多变性,也添加了树叶更换功能,同树皮更改一样,点击控制面板上的“树叶更改”按钮后(图 10A)弹出树叶选择窗口(如图 10B),选择所需树叶贴图点击确认按键后即可生成用户所需的树叶样式。树叶更改后的树木模型如图 10C。
-
树的影子主要通过树影长度、枝影密度、叶影密度3项属性值加以控制。用户可以通过对以上属性参数调节来获得所需的阴影效果,数值越大树影长度越长,枝干和树叶影子越明显;数值越小树影长度越短,枝干和树叶影子越稀薄(图 11);当数值为0时无阴影效果。
-
本研究在分形理论的基础上,利用改进的树木生成算法以及通过Visual Studio和OpenGL图形技术相结合的方法,实现了可视化效果良好的交互式三维树木建模系统。本研究提出的建模方法不是针对单一树种进行建模的,而是通过调整控制面板的属性参数和变量或者自定义贴图的方式来构建形态样式各异的三维树木模型的。实验结果表明:本研究提出的方法是有效可行的,相比于基于单图、多图建模或基于激光点云等图像建模方法出现的模型真实感低,交互性差,构建效率不高的缺点,本方法生成的树体模型不仅形态结构和外部特征具有很高的灵活性且操作方法简单易上手,在保证实时性绘制的前提下,能够达到真实性的要求。当然本研究的三维树木建模方法也存在不足,对于形态结构较为复杂的树木无法精确建模,且对于植物器官细节的特征变量还不能进行有效提取,真实感也还有待提高。生成算法也还需进一步优化,进一步提升计算速度,从而建立一个通用性更强、建模效率更高、人机交互性更好的自动化三维树木建模系统。
Research on interactively 3D tree modeling and visualization based on OpenGL
-
摘要: 通过讨论树体枝干几何建模的理论和方法,重点围绕树木交互式建模技术和三维可视化实现进行了研究探讨。实现过程主要分为3步:首先,对真实树木枝干的几何形态结构进行分析,利用分析结果构建枝干模型生成方法,用六边形棱柱近似模拟树干和枝段,再用六边形棱台作为枝段元经过连续偏转、连接的方法模拟枝干弯曲的形态。其次,基于枝干生成方法,利用分形迭代思想实现整株树体的建模。为提高仿真度,通过加入干扰因子使最终生成的树体枝干模型不过于规则。最后,为实现模型的可视化,选用OpenGL图形技术和Visual C++作为模型可视化工具和开发工具,通过对所建立的模型进行数学描述以及场景渲染和特征参数提取,建立一个支持交互的三维树木建模系统。Abstract: To discuss the theory and methodology of geometrical modeling for a tree and research on interactive modeling and 3D visualization technology, a three-step realization process was established. Results of model development were as follows:Firstly, the geometric structure of real branches was analyzed to construct a generation method for the branch model, and a hexagonal prism was proposed to represent the trunk or branch. The curved shape was realized by using segment elements through continuous deflection and connection. Secondly, based on the generation method for a branch, the whole tree was constructed by a fractal iterative method. To improve the degree of simulation, interference factors were added to make the final stem model not too regular. Finally, the OpenGL graphics technology and Visual C++ were chosen as visualization and development tools. Thus, the modeling system of 3D trees supporting interaction was constructed by a mathematical description of the tree model, a rendering of the scene and a extracting of the feature parameters.
-
Key words:
- forest mensuration /
- tree modeling /
- 3D visualization /
- fractal iterative method /
- OpenGL /
- interactive design
-
表 1 各坐标点取值
Table 1. Value of each point
坐标点 坐标值 次级坐标点 次级坐标值 Q1 (R·cos$ \frac{\pi }{3}$,0,R·sin$ \frac{\pi }{3}$) Q1′ (R′·cos$ \frac{\pi }{3}$,L,R′·sin$ \frac{\pi }{3}$) Q2 (-R·cos$ \frac{\pi }{3}$,0,R·sin$ \frac{\pi }{3}$) Q2′ (-R′·cos$ \frac{\pi }{3}$,L,R′·sin$ \frac{\pi }{3}$) Q3 (-R,0,0) Q3′ (-R′,L,0) Q4 (-R·cos$ \frac{\pi }{3}$,0,-R·sin$ \frac{\pi }{3}$) Q4′ (-R′·cos$ \frac{\pi }{3}$,L,-R′·sin$ \frac{\pi }{3}$) Q5 (R·cos$ \frac{\pi }{3}$,0,-R·sin$ \frac{\pi }{3}$) Q5′ (R′·cos$ \frac{\pi }{3}$,L,-R′·sin$ \frac{\pi }{3}$) Q6 (R,0,0) Q6′ (R′,L,0) 表 2 单轴树参数参考表
Table 2. The parameter graph of a monoaxial tree
参数 参数值 取值范围 SetTreeDepth 23 1~25 SetAngle 10 0~90 SetLateralAngle 15 0~90 SetTwist 73 0~180 SetSideAngle 50 0~180 SetLenScale 0.95 0~1 SetRadScale 0.82 0~1 SetSideScaleDepth 0.75 0~1 SetSideScaleSize 0.83 0~1 表 3 合轴树参数参考表
Table 3. The parameter graph of a multiway tree
参数 参数值 取值范围 SetTreeDepth 21 1~25 SetAngle 13 0~90 SetLateralAngle 10 0~90 SetTwist 79 0~180 SetSideAngle 34 0~180 SetLenScale 0.92 0~1 SetRadScale 0.73 0~1 SetSideScaleDepth 0.86 0~1 SetSideScaleSize 1 0~1 -
[1] 徐旭东, 王菁.基于Opengl的虚拟吊兰建模与可视化研究[J].计算机工程与设计, 2013, 34(12):4304-4309. XU Xudong, WANG Jing. Research of virtual chlorophytum modeling and visualization based on OpenGL[J]. Comput Eng Des, 2013, 34(12):4304-4309. [2] 胡春华, 李萍萍.树木三维可视化建模技术研究述评[J].南京林业大学学报(自然科学版), 2015, 39(6):148-154. HU Chunhua, LI Pingping. A survey of 3D visualization modeling technologies for trees[J]. J Nanjing For Univ Nat Sci Ed, 2015, 39(6):148-154. [3] 谭云兰, 贾金原, 张晨, 等. 3D树木建模技术研究进展[J].中国图象图形学报, 2013, 18(11):1520-1528. TAN Yunlan, JIA Jinyuan, ZHANG Chen, et al. Survey on virtual 3D tree modeling technologies[J]. J Image Graphics, 2013, 18(11):1520-1528. [4] 夏红梅, 张欣景, 胡训强.基于SpeedTree工具的三维真实感树木建模研究[J].舰船电子工程, 2015, 35(1):99-101. XIA Hongmei, ZHANG Xinjing, HU Xunqiang. Modeling of realistic 3D tree based on SpeedTree[J]. Ship Electron Eng, 2015, 35(1):99-101. [5] 王忠芝, 胡逊之.基于Xfrog的树木建模及生长模拟[J].北京林业大学学报, 2009, 31(增刊2):64-68. WANG Zhongzhi, HU Xunzhi. Tree modeling and growth simulation based on Xfrog[J]. J Beijing For Univ, 2009, 31(suppl 2):64-68. [6] 赵赛赛, 汤孟平, 唐思嘉, 等.毛竹林分可视化研究[J].浙江农林大学学报, 2016, 33(5):826-833. ZHAO Saisai, TANG Mengping, TANG Sijia, et al. Visualization for a Phyllostachys edulis stands[J]. J Zhejiang A & F Univ, 2016, 33(5):826-833. [7] 严家璇子.基于Maya的树木三维动画生成方法[D].西安: 西安科技大学, 2012. YAN Jiaxuanzi. A Generation Method of 3D Trees Animation Based on Maya[D]. Xi'an: Xi'an University of Science and Technology, 2012. [8] 白静, 张怀清, 刘闽.合轴分枝树木形态结构三维可视化模拟方法[J].林业科学, 2014, 50(12):73-78. BAI Jing, ZHANG Huaiqing, LIU Min. Three-dimensional visual simulation of sympodial branching trees morphological architecture[J]. Sci Silv Sin, 2014, 50(12):73-78. [9] 鲁萍, 侯筱婷.虚拟植物模型参数优化及仿真[J].计算机工程与科学, 2011, 33(7):132-135. LU Ping, HOU Xiaoting. Virtual plant model parameters optimization and simulation[J]. Comput Engi Sci, 2011, 33(7):132-135. [10] 曾兰玲, 汪国昭.梅花树建模与梅花林景观模拟[J].浙江大学学报(工学版), 2009, 43(12):2191-2195. ZENG Lanling, WANG Guozhao. Plum blossom tree modeling and plum blossom forest landscape simulation[J]. J Zhejiang Univ Eng Sci, 2009, 43(12):2191-2195. [11] 丁欢, 万旺根, 余小清, 等.基于几何参数的植物真实感模拟[J].计算机应用, 2009, 29(1):97-100. DING Huan, WAN Wanggen, YU Xiaoqing, et al. Realistic simulation of plant based on geometry parameter[J]. J Comput Appl, 2009, 29(1):97-100. [12] 叶景晴.树的三维模型自动化生成技术的研究[D].北京: 北京工业大学, 2013. YE Jingqing. Research on the Automatic Generation Technology of 3D Tree Modeling[D]. Beijing: Beijing University of Technology, 2013. [13] 朱山.基于OpenGL的实时阴影算法研究[D].武汉: 华中科技大学, 2011. ZHU Shan. Research on Real Time Shadow Algorithm based on OpenGL[D]. Wuhan: Huazhong University of Science and Technology, 2011. -

-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2019.01.017







 下载:
下载: