-
中国是世界上少数受台风影响最严重的国家之一,平均有台风或热带气旋7个·a-1在东南沿海各省登陆,重创农林种植业。目前,国外对林木抗风机制研究主要集中在樟子松Pinus sylvestris,西家云杉Picea sitchensis,挪威云杉P. abies,西铁杉Tsuga heterophylla等树种,通过动力学理论推导建立了一系列力学方程来描述林木的抗风性,形成了若干关于林木风倒机理的模型[1-5]。国内涉及林木抗风机制的相关研究中,关德新等[6]进行了林带结构与抗风能力关系的理论分析,郑兴峰等[7]从木材纤维的解剖特征来探讨巴西橡胶树Hevea brasiliensis的抗风性能,朱成庆[8]从生长指标、木材密度、造林密度、行间走向等多方面探讨了桉树无性系的抗风性,吴志华等[9]从形态性状、应力波速、基本密度、Pilodyn值等方面探讨木麻黄Casuarina equisetifolia及相思Acacia的抗风性。这些研究均未涉及木材力学性质对树种抗台风效果的影响规律,也未探明影响林木风倒、风折的主要材性因子。木麻黄是华南沿海地区不可替代的海防林主栽树种[10],马占相思Acacia mangium,厚荚相思A. crassicarpa,巨尾桉Eucalyptus grandis × Eu. urophylla是华南沿海地区主要的经济用材树种[11-14],苦楝Melia azedarach和琼崖海棠Calophyllum inophyllum是华南沿海地区乡土树种、滨海盐碱地造林树种及园林绿化景观树种。目前,对于这些树种的培育技术已较为成熟,而对这些树种抗台风性能与材性性状之间关系的研究极少见报道。本研究通过开展风害调查及木材物理、力学性质测定,探讨木材材性对抗台风效果的影响规律,对树种抗台风能力进行评价与预测,为沿海防护林抗风树种的选择和利用提供依据。
HTML
-
试验地位于广东湛江东海岛,为典型的季风气候,年降水量为1 500.0 mm,其中75%以上的降水集中在4-9月;年平均气温为25.0 ℃,最低气温在1月为2.0 ℃,最高气温在7月为38.0 ℃;年均相对湿度为80%,土壤为海滨潮积沙土。木麻黄、苦楝、马占相思、琼崖海棠、巨尾桉、厚荚相思等6个树种在试验地上随机区组排列,40~50株·小区-1,4次重复。2005年造林,林分平均胸径11 cm,平均树高9.5 m。
-
分别树种选择试验林中生长正常,树干较圆满通直而无明显缺陷的平均木3~5株,伐倒,截取原木试材。具体方法参考国家标准GB/T 1927-1991 《木材物理力学试材采集方法》。试样的截取参考国家标准GB/T 1929-1991《木材物理力学试材锯解及试样截取方法》。试样制作、含水率的调整、试验结果的计算等参考国家标准GB/T 1928-1991 《木材物理力学试验方法总则》。
参考国家相应标准[14],测定各树种绝干密度、纤维长度、纤维宽度、纤维长宽比、木材顺纹抗剪、冲击韧性、木材抗弯强度、木材抗弯弹性模量等8个材性指标。
-
2012年13级强台风“启德”在湛江市麻章区登陆,对试验林造成了一定破坏,台风过后7 d内对试验林开展风害调查,并以5级风害等级评估林分风害情况,估算相应的抗风值[15-16]。1级,树干倾斜角度>45°或树干折断,得1分;2级,树干倾斜角度30°~45°或树梢折断,得2分;3级,树干倾斜角度15°~30°,得3分;4级,树干倾斜角度<15°或上端树冠倾斜,得4分;5级,正常而无损害,得5分。
抗风值=(1级风害抗风值×株数+2级风害抗风值×株数+3级风害抗风值×株数+4级风害抗风值×株数+5级风害抗风值×株数)/总株数。
-
应用SAS系统软件[17],进行方差分析、相关分析、逐步回归分析等统计分析。
1.1. 试验地概况
1.2. 木材性质的测定
1.3. 风害调查
1.4. 数据处理
-
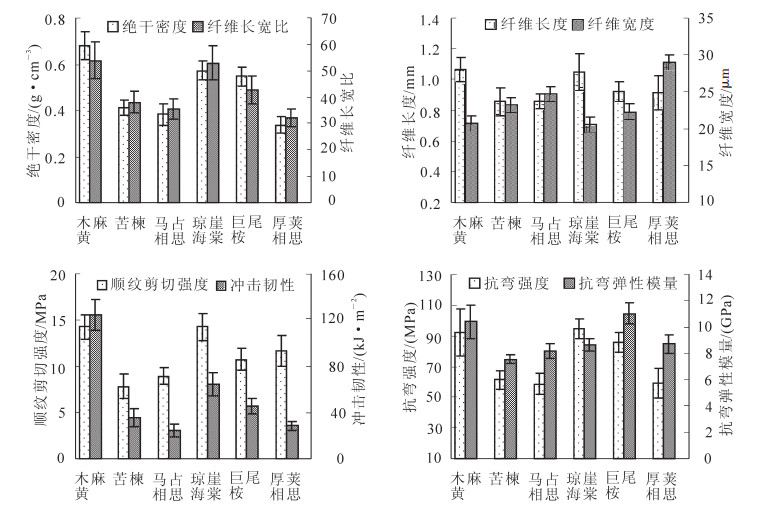
由图 1可以看出:各树种材性性状差异较大,木麻黄绝干密度、纤维长度及其长宽比、冲击韧性的平均值均大于其他树种。厚荚相思的绝干密度最小,纤维宽度最大,纤维长宽比值最小。琼崖海棠纤维宽度平均值最小,顺纹剪切强度、抗弯强度平均值最大。苦楝纤维长度、顺纹剪切强度、抗弯弹性模量平均值均低于其他树种。经方差分析,参试树种各材性性状存在着极显著差异,这些差异性状为探讨林木抗台风性能差异提供了遗传基础。
8个材性性状相关分析(表 1)表明:纤维形态、木材密度、力学性状两两之间相关关系显著,纤维长宽比值越大,木材密度越大,冲击韧性越强,抗弯强度越大。顺纹剪切强度、冲击韧性、抗弯强度、抗弯弹性模量4个力学性状两两之间相关均不显著,抗弯弹性模量与其他材性性状相关关系均不显著。
性状 绝干密度 纤维长度 纤维宽度 纤维长宽比 顺纹剪切强度 冲击韧性 抗弯强度 抗弯弹性模量 绝干密度 1.000 纤维长度 0.844* 1.000 纤维宽度 -0.867* -0.602 1.000 长宽比 0.951** 0.907* -0.884* 1.000 顺纹剪切强度 0.709 0.961** -0.393 0.768 1.000 冲击韧性 0.898* 0.856* -0.662 0.856* 0.736 1.000 抗弯强度 0.942** 0.874* -0.816* 0.938** 0.791 0.756 1.000 抗弯弹性模量 0.673 0.465 -0.360 0.448 0.485 0.539 0.658 1.000 说明:**表示极显著相关(P < 0.01),*表示显著相关(P < 0.05)。 Table 1. Correlation analysis of wood property
-
风害研究结果表明:巨尾桉、马占相思、厚荚相思台风过后风折风倒严重,1级风害率占总风害率的比值最大,分别为72.4%,74.4%,64.7%;台风对琼崖海棠、木麻黄的危害主要是风斜、断梢、枝叶脱落等,2级与3级风害占的比例较大;苦楝以1级和2级风害为主。比较各树种的抗风值,其抗风性能由大到小依次为:琼崖海棠>木麻黄>苦楝>巨尾桉>马占相思>厚荚相思(图 2)。研究结果还表明:台风过后,参试树种树干倾斜角度<30°或只是上端树冠倾斜时,绝大部分植株都能在后期生长中恢复直立,台风对沿海防护林的危害主要是风折、风倒及严重风斜(即1级和2级风害),造成林木的机械破坏、生长势下降及由此可能引发的病虫害。
-
相关分析结果表明(表 2):树种总风害率及1级风害率与纤维宽度呈显著正相关,与纤维长宽比呈显著负相关,与绝干密度、纤维长度、顺纹剪切强度、冲击韧性、抗弯强度、抗弯弹性模量呈不显著负相关;树种抗风值与纤维宽度呈显著负相关,与纤维长宽比呈显著正相关,与其他木材材性性状呈不显著正相关。由以上分析可知,纤维宽度、纤维长宽比与树种总风害率、1级风害率及抗风值大小有着密切的关系;树种抗风效果与木材力学性状间多呈不显著负相关或不显著正相关,2类性状似相互独立,这对育种上开展综合选择非常有利。
性状 绝干密度(x1) 纤维长度(x2) 纤维宽度(x3) 纤维长宽比(x4) 顺纹剪切强度(x5) 冲击韧性x6) 抗弯强度(x7) 抗弯弹性模量(x8) 总风害率 -0.781 -0.607 0.958* -0.868* -0.379 -0.637 -0.734 -0.127 1级风害率 -0.810 -0.716 0.908* -0.909* -0.505 -0.738 -0.757 -0.134 2级风害率 -0.383 -0.014 0.720 -0.379 0.150 -0.026 -0.394 -0.151 抗风值 0.796 0.6555 -0.944* 0.890* 0.433 0.679 0.748 0.129 说明:**表示极显著相关(P < 0.01),*表示显著相关(P < 0.05) Table 2. Correlation analysis between anti-typhoon performance and wood property
-
木材材性性状之间、林木抗风性能与材性性状间存在着复杂的关系。为了确定哪些变量是影响林木抗风性能的主效因子,并寻找这些变量间的规律,分别以绝干密度(x1),纤维长度(x2),纤维宽度(x3),纤维长宽比(x4),顺纹剪切强度(x5),冲击韧性(x6),抗弯强度(x7)及抗弯弹性模量(x8)为自变量,以总风害率(y1),1级风害率(y2),2级风害率(y3),抗风值(y4)为因变量进行逐步回归分析。
结果表明:以总风害率(y1)为因变量进行逐步回归分析时,由于绝干密度、纤维长度、纤维长宽比、顺纹剪切强度、冲击韧性、抗弯强度等6个变量对树种总风害率影响不显著或者变量之间共线性原因,在逐步回归过程中被剔除,只有纤维宽度、抗弯弹性模量这2个性状纳入了方程,回归方程达到显著水平;以1级风害率(y2)为因变量进行逐步回归分析时,只有纤维长宽比、顺纹剪切强度、抗弯弹性模量这3个性状纳入了方程,回归方程达到显著水平;以2级风害率(y3)为因变量进行逐步回归分析时,只有纤维宽度、冲击韧性这2个性状纳入了方程,回归方程达到显著水平;以树种抗风值(y4)为因变量进行逐步回归分析时,只有纤维宽度这个性状纳入了方程,回归方程达到显著水平(表 3)。
因变量 自变量 参数估计 标准误 均方 F值 P值 截距 -167.167 91 25.692 878.655 42.34 0.0074 总风害率 纤维宽度 7.11499 0.697 2 163.895 104.26 0.002 0 抗弯弹性模量 0.003 95 0.002 123.728 5.96 0.0924 截距 70.352 87 14.117 496.214 24.84 0.038 0 纤维长宽比 -2.570 18 0.349 1 082.428 54.18 0.018 0 1级风害率 顺纹剪切强度 2.472 94 1.207 83.926 4.20 0.176 9 抗弯弹性模量 0.003 59 0.002 88.256 4.42 0.1703 截距 -13.709 41 4.496 7.239 9.30 0.055 5 2级风害率 纤维宽度 0.79745 0.168 17.511 22.49 0.017 8 冲击韧性 0.042 72 0.014 7.221 9.28 0.055 6 抗风值 截距 9.229 63 0.958 7.494 92.84 0.000 6 纤维宽度 -0.231 19 0.041 2.625 32.53 0.0047 说明:变量进人模型和留在模型的显著水平分别为0.20和0.18。 Table 3. Regression analysis
以总风害率(y1),1级风害率(y2),2级风害率(y3)和抗风值(y4)作因变量,分别与各自纳入方程的性状建立回归方程如下:${{\hat y}_1} =-167.16791 + 7.11499{x_3} + 0.00395{x_8};$${{\hat y}_2} = 70.35287-2.57018{x_4} + 2.47294{x_5} + 0.00359{x_8};$ ${{\hat y}_3} =-13.70941 + 0.79745{x_3} + 0.04272{x_6};$ ${{\hat y}_4} = 9.22963-0.23119{x_3}。$。
由表 4可以看出进入模型各因子决定系数(R2)均大于0.8,方程拟合程度较高。
因变量 步数 每步选入的变量 模型的变量数 偏R 2 模型R 2 进入变量的F值 P值 1 纤维宽度 1 0.917 8 0.917 8 44.66 0.002 6 总风害率 2 抗弯弹性模量 2 0.057 0.972 5 5.96 0.009 2 1 纤维长宽比 1 0.825 9 0.825 9 18.98 0.012 1 1级风害率 2 抗弯弹性模量 2 0.093 6 0.919 5 3.49 0.158 6 3 顺纹剪切强度 3 0.055 0.974 0 4.20 0.176 9 1 纤维宽度 1 0.818 8 0.818 8 4.31 0.1064 2级风害率 2 冲击韧性 2 0.363 6 0.8824 9.28 0.055 6 抗风值 1 纤维宽度 1 0.890 5 0.890 5 32.53 0.0047 Table 4. Process of regression analysis
2.1. 不同树种间各材性性状比较分析
2.2. 不同树种抗风效果比较分析
2.3. 抗风效果与材性性状的相关分析
2.4. 影响林木抗风性能的主要材性因子分析
-
本研究参试树种均为广东、海南沿海大面积、普遍种植的6个树种,其8个材性性状变异幅度极大,均呈现极显著差异,这为研究木材材性对抗风的影响及抗风树种的选择、评价与利用提供了依据。6个参试树种中,琼崖海棠、木麻黄最抗风,苦楝、马占相思、巨尾桉次之,厚荚相思最不抗风。这些试验结果与王志洁等[18]研究发现木麻黄抗台风的能力强于各种相思树种, 陈胜[19]研究发现厚荚相思抗强风能力较弱等的研究结果基本一致。台风对沿海防护林的破坏以1级风害、2级风害为主,对巨尾桉、马占相思、厚荚相思的危害主要是树干折断、树梢折断,对琼崖海棠、木麻黄的危害主要是风斜、断梢、枝叶脱落等。
相关分析表明:树种抗台风性能与木材纤维形态(纤维宽度、纤维长宽比)存在着直接的线性相关。这可能由于木材纤维形态与木材密度、力学性质指标之间呈显著相关关系,不同树种木材纤维形态直接影响着各树种的木材密度及力学性能,木材密度随着纤维长宽比的增加而增加,力学性能随着纤维长宽比的增加而增强,从而对台风的侵袭表现出不同的抗性。一般来说,纤维长宽比越大、全干密度越大,木材结构就越致密,因此,从本研究来看木材结构越致密的树种相对来说抗风性越强。这与吴志华等[9]研究发现相思树种木材材性较脆,决定其林分抗风折能力弱等研究结果相一致。
逐步回归分析表明:8个材性指标中对总风害率影响最大的是纤维宽度、抗弯弹性模量这2个指标,对树种抗风值影响最大的是纤维宽度,对1级风害率影响最大的是纤维长宽比、顺纹剪切强度、抗弯弹性模量3个指标,对2级风害率影响最大的是纤维宽度、冲击韧性这2个指标。本研究所建立的回归方程可用于其他树种抗风性能的预测及评价。











 DownLoad:
DownLoad:
