-
森林是陆地生态系统的主体,也是生物碳的主要载体,每年固定的碳占整个陆地生态系统碳总量的2/3,对减缓温室效应起着决定性作用[1-2]。精确计量和监测区域森林碳储量及其分布,不仅是区域碳源汇功能评价的基础,也对环境发展和相关决策有重要参考意义。目前,对森林生物量/碳储量,传统估算方法主要有收获法、测树学法、森林资源清查法。传统估计方法以实测数据为基础,需要进行大量的实地调查,工作量大、周期性长,在推测大面积林分生物量时,待测林分的每木检尺数据往往难以获得[3]。遥感技术作为一门综合性探测技术,可以在短时间内对同一地区进行重复探测,获取大面积同步观测数据,并且不受地形阻隔等限制,弥补了传统样地调查方法的不足,具有良好的综合性和现势性[4]。在基于遥感的森林碳储量估测过程中,根据光谱信息与森林植被关系构造的不同遥感信息模型进行分类,可概括为非参数模型和参数模型2种方法。 非参数模型法主要包括:KNN(K-nearest neighbor)法,作为一种较早被国内外学者使用的方法,主要用应用于区域森林蓄积量和生物量的估计[5-7];人工神经网络(ANN)模型估测法,在近几十年中被应用和发展,通过与遥感信息和野外调查数据结合对研究区的森林蓄积量和生物量估计,并在有效性和精确性上得到验证[8-10]。参数模型法有:线性模型估测法,该方法原理简单且应用广泛,以遥感影像信息和实测样地生物量间的线性关系为依据,对森林生物量进行估算[11-13];非线性模型估测法则通过建立两者的非线性模型实现对森林生物量的估计及其动态变化[14-16],也是森林生物量估算的常用方法之一;序列高斯仿真模型估测法,在过去的研究中主要运用在土壤、采矿、油田等方面,近年来在林业应用中有所发展,通过将模型与林业实际生产过程需求结合[17],建立遥感信息及样地清查数据之间的空间关系[18-19],对区域森林碳储量及其分布进行探究。非参数估计中人工神经网络模型外延性较差,并需要依据大量的野外调查数据以及多次测算作为依据[5],KNN法则在原理上过于依赖极限定理,致使在像元尺度上生物量估计的误差较大[20-21]。参数估计方法中主要以回归模拟为主导,采用最小二乘法以降低局部真实性使模拟结果达到整体最优,具有较高的平滑效应[22]。序列高斯协同仿真模拟不仅克服了回归模型的平滑缺陷,真实再现区域森林碳分布的局部特征,还提供了估计结果的不确定性,通过对不确定性传播模型的模拟分析实现对森林碳估计结果的评价[23]。目前,空间仿真方法在区域森林碳储量估计方面的应用研究较少。本研究以浙江省开化县为研究区,基于2014年森林资源清查样地数据与2013年资源3号遥感影像数据(2 m × 2 m分辨率融合影像),采用序列高斯协同仿真算法,对该区域地上部分森林碳储量及其分布进行空间估计,并对模拟误差进行分析。
HTML
-
浙江省衢州市开化县(28°53′25″~29°31′06″N,118°00′07″~118°39′04″E)是浙江主要河流——钱塘江的源头,地处浙江省西北部,浙皖赣三省交界处,拥有多个国家森林公园、风景区,是浙江省主要的林业县之一。
开化县属亚热带季风气候,四季分明,温暖湿润,年均降水量为1 814.0 mm,日照时数1 712.5 h,年平均气温16.4 ℃,昼夜温差平均10.5 ℃,无霜期252 d。全境东西长为63.4 km,南北宽69.5 km,总面积2 234.0 km2,其中85%为山地。
全县属浙西中山丘陵,物种丰富,植被类型多样,其中森林植被主要以马尾松Pinus massoniana,杉木Cunninghamia lanceolata,硬阔,软阔和毛竹Phyllostachys edulis为主。开化全县森林覆盖率达79.6%,林业用地面积19万hm2,林木蓄积840万m3(2007年)。
-
研究采用2013年11月资源3号卫星空间分辨率为2 m × 2 m的融合影像(图 1)为遥感数据源。影像数据在PCI GeoImaging Accelerator(GXL)软件下自动进行正射校正、影像配准、影像融合处理,正射校正误差在1个像元之内。为选出与实测样地碳密度相关性较高的影像因子作为变量参与碳储量估计建模,提取样地位置对应的各波段、波段比值及其植被指数等影像特征值,分析各个像元特征值与其对应样地森林碳之间的相关性,并通过相关性分析选择相关性最好的波段参与序列高斯协同仿真模拟。
-
本研究以开化县全区域2014年森林资源清查固定样地数据为地面实测数据(图 1)。全县有样地95个,样地为正方形,边长28.28 m,面积0.08 hm2,间距为4 km × 6 km。优势树种(组)包含马尾松、杉木、硬阔、软阔和毛竹,共5类,其中无林地22个,有林地73个。借助ArcGIS 9.3软件,随机抽取85%(80个)地面样地数据作为训练样本参与模型模拟,剩余15%(15个)为检验样本对森林碳储量模拟结果的精度进行检验。其中,实测地面样地地上部分森林碳密度与从中随机抽取作为训练样本和检验样本的地上部分碳密度描述性统计如表 1。
数据 样本数量 碳密度/(Mg·hm-2) 标准差 偏值 峰值 变异系数 最小值 最大值 平均值 训练样本(85%) 80 0 142.11 26.700 30.333 1.509 8 5.540 2 1.136 1 检验样本(15%) 15 0 103.31 26.402 30.201 1.163 0 3.799 1 1.143 9 Table 1. Statistical description of the aboveground plot carbon density
-
由于样地数据与资源3号影像采用的地理坐标系统不同,通过对样地坐标参数的转换将两者统一为CGCS_2000国家地理坐标系统。同时,分辨率不同会导致数据匹配误差,影响模型模拟的效果,因此对遥感影像重采样至30 m × 30 m分辨率与样地匹配。
1.1. 研究区概况
1.2. 数据准备
1.2.1. 资源3号遥感影像数据
1.2.2. 森林资源清查样地数据
1.2.3. 数据匹配处理
-
地面实测数据包含样地数据和样木数据(含单株毛竹数据)2个部分,每个样地的森林生物量、碳储量由每株样木(或毛竹)的生物量和碳储量累加而来。以97个地面样地每木检尺记录为基础,按照研究区主要树种的立木胸径—生物量模型(表 2)计算单株样木地上部分生物量,因而选择不含树高的一元模型计算单株生物量。最后根据广泛接受的生物量—碳储量转换系数0.5,将累加样地内所有样木生物量得到的样地森林地上部分生物量转换为样地地上部分碳储量。其中,扣除检尺类型为采伐木、多测木以及枯倒木的部分,由于样木调查不包含树高。
树种类型 生物量回归方程 文献 马尾松 $ w = 0.112243{D^{2.36501}}$ [24] 杉木 $ w = 0.086904{\left\{ {{D^2}\left[ {1.3 + {{\left( {0.232467 + \frac{{2.362912}}{D}} \right)}^{ - 25}}} \right]} \right\}^{0.819180}}$ [25] 硬阔类 $ w = 0.108921{\left\{ {{D^2}\left[ {1.3 + {{\left( {0.2791 + \frac{{1.7661}}{D}} \right)}^{ - 25}}} \right]} \right\}^{0.901726}}$ [26] 软阔类 $ w = 0.097822{\left\{ {{D^2}\left[ {1.3 + {{\left( {0.3063 + \frac{{1.9783}}{D}} \right)}^{ - 25}}} \right]} \right\}^{0.893738}}$ [26] 毛竹 $w = 386.4951{D^{1.6579}} $ [27] 说明:w表示碳储量,单位为Mg·hm-2;D表示胸径,单位为cm。 Table 2. Carbon density and biomass calculated in the aboveground of the study area
-
序列高斯协同仿真模拟(sequential Gaussian co-simulation),以地统计学中变异函数为基础,将已知点x处的观测值Z(x)作为随机变量构造一个概率空间,并依照区域内距离观测点为h(有方向、大小的向量)的所有值Z(x+h),计算此概率空间内随机变量的期望和方差,可得到与该随机变量Z(x)相符的高斯分布概率密度函数以及条件累积分布函数。进而根据Monto-Carlo原理随机抽取累积分布函数中一个值作为服从该分布的一次模拟结果。该模拟方法不但能保持变量的空间相关性不变,还能使观测数据条件化,参与模拟点越多,模拟结果越接近客观实际。
针对森林的分布和自身地理特征,序列高斯模拟可以很好地对区域森林碳储量结构性和随机性进行描述和分析。其中,协方差函数和半变异函数是以区域化变量为理论基础的地统计学基本函数,用这2个模型对森林碳储量进行描述能够兼顾其结构性与随机性。同时,2个相交的半变异函数可以度量其对应的2个随机变量Z(xα)与Z(xα+h)的空间相关性。随机函数的半变异函数γZ(h)和协方差CZ(h)表示为:
在式(1)和式(2)中:h是一个有方向性的向量,决定了2个随机变量之间的距离和位置; N(h)为给定向量h上样本数据对的数量;Z(xα)与 Z(xα+h)分别为在 xα与 xα+h 的2个位置的森林碳储量统计值;m-h与m+h表示结尾和初始数据的均值。
在区域森林碳估计中,仅采用实测样地数据信息相对单一。王广兴等[18]则在此基础上引入信息丰富的遥感影像数据。假设遥感影像的光谱变量为Y,则Y(x)为空间x处的一个随机函数,通过样地与影像相应位置的交叉半变异函数γZY(h)和交叉协方差函数CXY(h)更加精确地描述出森林碳储量的分布和空间变异情况。2个函数分别表示为:
式(3)和(4)中:Y(xα),Y(xα+h)分别表示在 xα和 xα+h这2个位置的光谱值。
序列高斯协同仿真模拟的程序运行步骤可概括为:①采用随机抽样法抽取一个像元作为待估点并设置影像像元的估算顺序;②对已知样点拟合得到半变异函数,以确定模型模拟的变程、基台值、块金值参数;③根据点协同克里格法得到变程内已知样本的均值和方差,以此得到待估像元对应的条件累积分布函数;④在累积分布函数中随机抽取一个值作为该像元的碳密度模拟值;⑤重复步骤③~④遍历整个影像直至得出研究区内每个像元的估计值,即可获得一幅研究区森林碳分布图;⑥重复③~⑤步骤N次,得到N幅森林碳密度分布图,通过计算碳分布图对应像元N次模拟的均值和方差,进而得到用于不确定性分析的森林碳分布方差图和概率图。在本研究中,N的经验值为200。
-
所有测量值估计误差的平均值,用来衡量估值结果的准确性。
-
真实值与估测值之差的平方和,表示随机误差的效应。
-
是一种比较常用的指标,但是需要与其他指标相结合共同完成模型精度的评估。
-
衡量估计值与真实值之间的偏差,能够很好的反映出估测的精度。
-
通过相对均值的离散程度来反映模型的模拟精度。
式(5)~式(9)中:z(xi)为样地真实值,$\hat z\left( {{x_i}} \right) $为样地估计值,$z\left( {\bar x} \right) $为碳密度均值,n为样地个数。
2.1. 实测样地森林植被碳储量估计
2.2. 序列高斯协同仿真模型模拟估计
2.3. 精度验证
2.3.1. 平均误差EME(mean error,ME)
2.3.2. 残差平方和ERSS(residual square sum,RSS)
2.3.3. 平均相对误差EMRE(mean relative error,MRE)
2.3.4. 均方根误差ERMSE(root mean square error,RMSE)
2.3.5. 相对均方根误差ERRMSE(relative root mean square error,RRMSE)
-
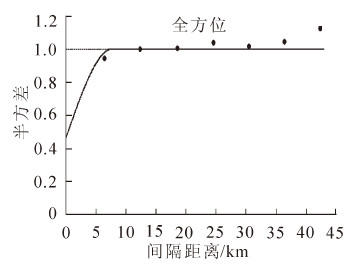
基于开化县全国森林资源清查样地以及资源三号遥感影像融合数据第3波段(用Band3表示),借助统计软件VARIOWIN,采用球状模型进行序列高斯协同仿真模拟样地森林碳密度及其分布,获得Spherical标准化模型:
如图 2所示的变异函数,在变程为7 740 m的范围内,各个测量值相关,而当超出变程时,测量值的相关性消失,可认为其相互独立。
-
在全县区域总量上,序列高斯协同仿真模拟总体总量完全落入按照实测样地数据及其相关模型估算总量的置信区间内,且在分布上与实际的森林碳密度一致。
从图 3A森林碳密度均值分布来看,开化全县整体森林碳密度分布呈中间低周边高趋势,且高密度分布范围集中于全县四周。由于研究区北部和西北部集中了“钱江源森林公园”和“古田山国家自然保护区”等森林公园、自然保护区,森林覆盖面积达到80.4%,因此北部和西北部区域森林碳密度较高。南部及西南部也有部分区域分布较高密度森林,东部森林碳密度相对偏低。在研究区中南部和东部部分区域覆盖了大量的居民区、道路、河流等地物,因而森林覆盖率低,其余区域森林碳密度中等。

Figure 3. Distribution of forest carbon estimation in Kaihua County and contrast with the plots measurements
从图 3B来看,空间仿真模拟的碳分布与样地实测值的高低走势基本一致,样地实测值高处则模拟值高,样地实测值低处则模拟值低。全区域森林碳密度最高达109.178 Mg·hm-2,此结果在森林资源清查样地碳密度范围以内(最大142.11 Mg·hm-2)。
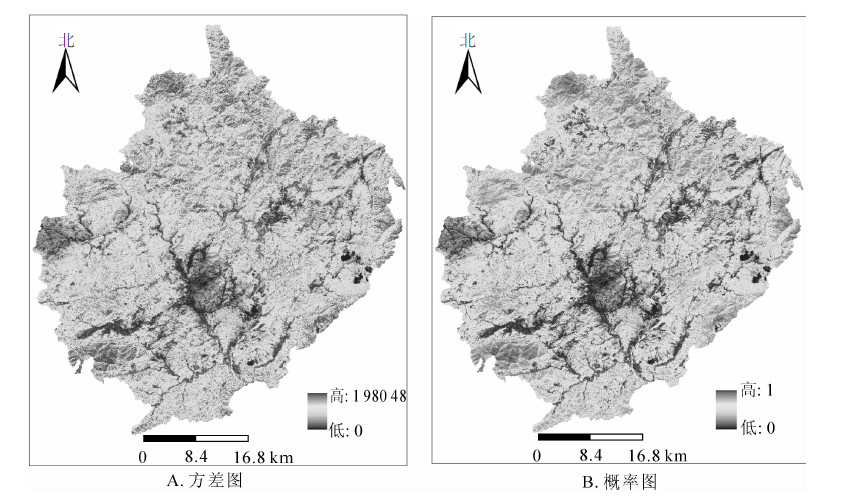
图 4A为空间仿真模拟森林碳密度估计值的方差分布图,表示每一个像元多次(200次)仿真的估计方差,体现了每个位置上估计值的变化程度,同时代表在该位置森林碳密度不确定性大小。从图中分布可以看出,森林碳密度方差与均值的趋势基本一致,北部、西北部和南部、西南部的森林覆盖多,碳密度变化大,空间变异性强,中部、中南部碳密度变化小,空间变异性较弱,表明森林碳密度高的区域均值的变化幅度较大,森林分布不均匀。

Figure 4. Variances distribution of space simulation and probabilities for estimates greater than mean values
图 4B为碳密度大于均值的概率图,表示每个位置上多次(200次)仿真结果大于均值的次数与总的仿真系数之比,反映了森林碳密度大于均值的概率分布情况。从图中分布可以看出,大于均值的概率分布与均值分布基本一致。
-
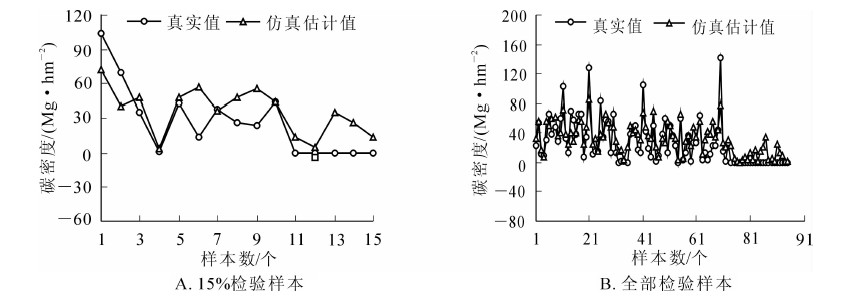
在模型模拟之后,基于15%以及全部样地抽样数据,采用平均误差、残差平方和、平均相对误差以及均方根误差4个指标对空间仿真模拟结果进行综合评估(表 3),并以检验样本与实测样地碳密度值的吻合程度作为模拟精度的参考标准(图 5)。
检验样本/个 平均误差 残差平方和 平均相对误差/% 均方根误差 15(15%) 9.702 2 7 667.262 0 4.565 8 22.608 6 95(100%) 5.272 3 33 505.518 8 0.558 0 18.780 0 Table 3. Analysis in the error of spatial simulation
经统计,15%抽样样地和全部样地作对空间仿真估计结果检验的平均误差分别是9.702 2和5.702 3,平均相对误差分别为4.565%和0.558%,表明序列高斯协同仿真模拟是一种精度较高的估计方法,随着检验样本的增加,模型的模拟精度提高。
均方根误差能够很好地反映真值和估计值之间变化的剧烈程度。数据显示,15%抽样检验以及全部样地检验的均方根误差为22.608 6和18.780 0,根据2种检验样本碳均值26.402 5 Mg·hm-2,26.653 2 Mg·hm-2,得出两者对应的相对均方根误差(RRMSE)分别是0.856和0.705,相对均方根误差越小,相对均值的离散程度越小,模型的精度也就越高。
相比较,2种检验样本除残差平方和外,其余误差均随检验样本的增加而减小,主要因为残差指标是所有参与检验样本的误差之和,样本越大,带来的随机误差就会越大。按照2次检验样本所占比例15%和100%,可发现总体误差的增加程度递减,说明模型的模拟精度提高。
图 5模型模拟检验的结果发现,检验样本仿真估计的结果与实测样地的结果趋势基本一致。通过观察得出,当采用15%检验样本时,由于样本个数较少,造成个别误差明显(图 5A),而全部样本作为检验样本时,误差降低(图 5B)。
3.1. 理论模型结果及分析
3.2. 碳储量模拟结果及分析
3.3. 模型模拟精度分析
-
本研究以森林资源清查数据与资源三号遥感影像数据为基础,对开化县2014年森林碳储量及其分布进行序列高斯协同仿真模拟,得到总碳储量估计结果7.221 573 Tg,碳密度模拟值为0~109.178 0 Mg·hm-2,碳密度平均值为32.376 4 Mg·hm-2。以实测样地数据估计结果作为真实参考,总碳储量为5.953 610 Tg,样地碳密度值为0~142.112 2 Mg·hm-2,碳密度均值26.650 0 Mg·hm-2,总体估计精度达78.7%。
由于开化县拥有森林资源丰富的国家森林公园和自然保护区,因此估计得到较高的碳储量。受人类活动范围的影响,其碳分布主要集中在研究区北部、西北部以及南部、西南部地区,与碳分布的估计结果基本吻合。根据精度分析得出空间仿真模拟对区域碳储量估计具有满意结果,仿真估计的碳总量落在实测样地估算总值的置信区间内。
由于序列高斯协同仿真算法在森林碳储量估计过程中要求样地数据和遥感数据尺度的一致性,因此需要将2 m分辨率的遥感影像重采样至30 m与样地匹配,然而将高分辨率影像降至低分辨率会使信息量减少,并产生一定误差。本研究中,2 m和30 m分辨率遥感影像信息与实测样地碳储量相关性分别为0.352和0.402,表明重采样可以增加影像与样地的匹配度,从而可以提高两者相关性;对重采样前后2种影像进行一元二次回归验证得出,2 m分辨率影像模拟研究区森林碳总量为631.102 8 Mg,平均碳密度28.249 9 Mg·hm-2,30 m分辨率影像模拟得到的森林碳总量为627.296 0 Mg,平均碳密度28.079 5 Mg·hm-2,表明30 m分辨率影像模拟得到的森林碳密度均值和碳总量更接近于样地实测值。重采样后回归模型的拟合优度高于重采样前40.7%,进一步说明对遥感影像重采样的合理性。本研究还发现,将融合影像以5 m为一个间隔重采样至5,10,15,20,25,30 m分辨率影像,地面样地森林碳储量与影像的相关性随空间分辨率的变化而变化,表明样地与影像分辨率不统一对森林碳储量的精确估计有一定阻碍,因此,如何使不同尺度的2种数据有效结合,是下一步需要完善和改进的重点。此外,空间协同仿真模拟依赖于参与模拟的样地数量,样地的多少决定了模型参数量,对模拟结果会造成一定影响,对样地多少的控制也值得进一步探索和研究。













 DownLoad:
DownLoad: