-
近年来，中国温室生产装备发展迅速，智能农机在提高温室生产经济效益方面发挥越来越重要的作用[1]。自动导航技术正成为智能化温室装备的研究热点，其中位置测量和导航路径跟踪控制是自动导航系统的两大核心技术[2]。在位置测量方面，全球定位系统(global position system，GPS)[3]被广泛用于自动导航农机定位研究中，但是大多用于室外大田环境，信号在室内衰减严重，定位效果不佳[4]，在室内应用受到了限制。许多学者选择机器视觉[5]、红外[6]、电磁[7]和无线传感[8-9]等实现室内定位方法。机器视觉可以检测试验环境中丰富的信息，但是受到光照等不可控因素影响较大。红外和电磁需预先铺设引导线，更改或扩充路径麻烦，灵活性较差。超宽带(ultra-wide band，UWB)是一种室内无线定位方法，其数据传输速度快且精度高，适合于温室环境定位使用。林相泽等[10]使用UWB在温室内动态静态定位精度为6.6 cm，动态定位大部分距离误差在15.0 cm以上。孙小文等[11]在仓储环境内为自动导航车(AGV)定位动态试验精度为8.5 cm。在导航控制方面，纯追踪[12]是一种基于几何运算的方法，理论知识不复杂，但是前视距离的确定较困难。模糊控制是建立在以人的知识及经验的基础上的一种智能控制方法，有较强的鲁棒性和容错性。石翔等[13]以横向和航向偏差为输入，根据专家经验制定模糊规则输出前视距离；熊中刚等[14]采用模糊免疫PID控制算法实现前轮转向导航控制，直线跟踪偏差不大于4.0 cm，曲线跟踪偏差平均偏差为12 cm；XUE等[15]结合模糊控制与机器视觉，设计了机器人的路径跟踪控制器；ABIYEV等[16]以误差和误差变化率为输入量，速度为输出量设计模糊控制器，为自行设计的机器人进行导航控制，沿着30.0 m的引导线行驶最大引导误差为15.8 mm。上述研究未充分考虑不同工况时输入量之间的权重，且采用固定模糊控制规则，无法对模糊控制规则进行自调整。本研究采用超宽带技术构建无线定位系统，获取温室生产平台的位置信息，采用一种带有自调整函数的模糊控制器自动调整各输入变量的权重，以实现最佳的前轮转向角输出。最后采用实车进行直线和矩形路径跟踪试验，并与传统纯追踪方法进行对比，以验证本研究方法的有效性。
HTML
-
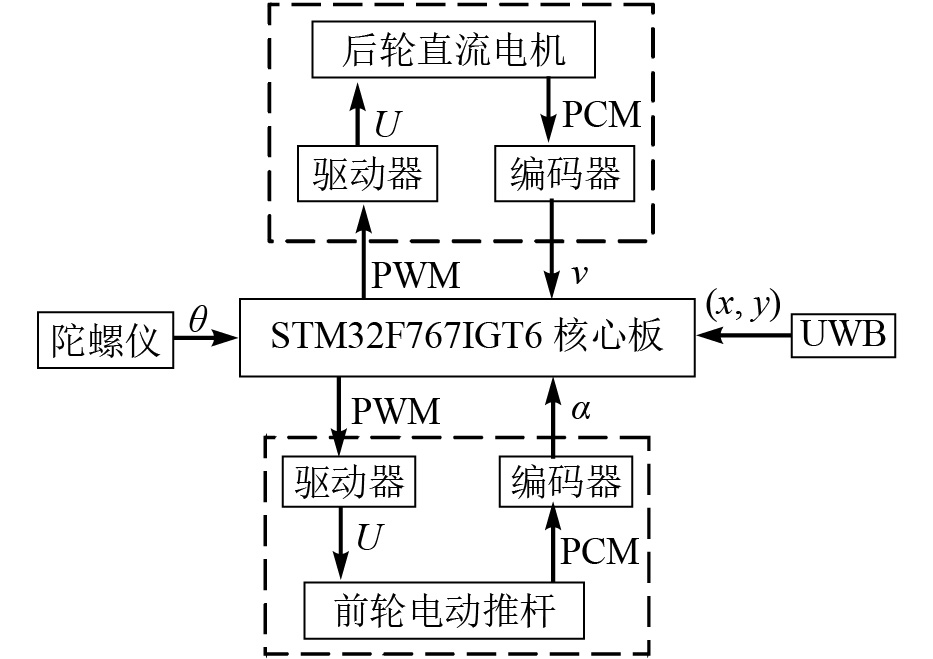
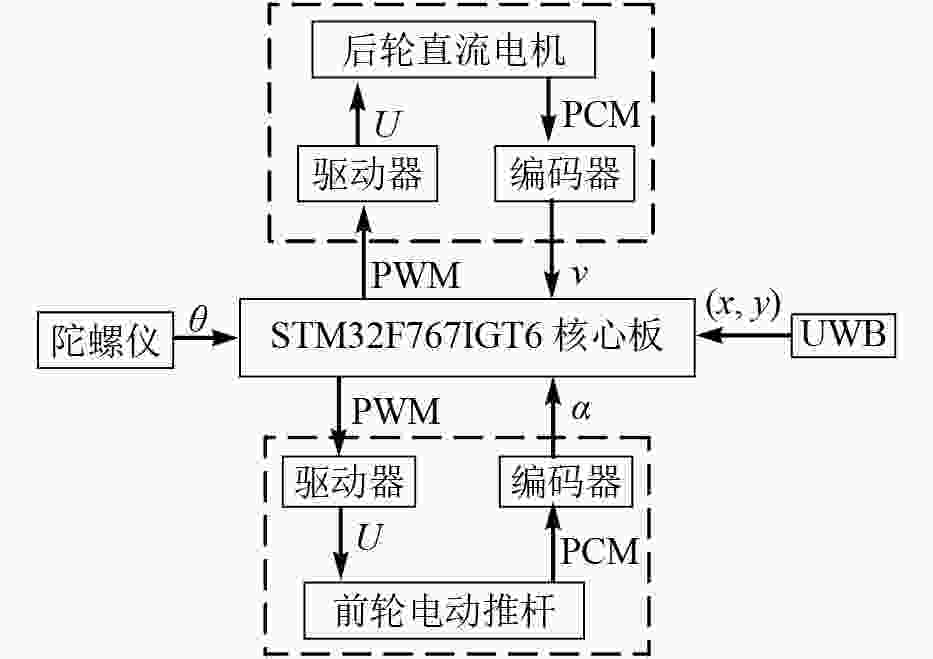
试验平台为纯电动4轮机构，采用前轮转向后轮驱动，由锂电池(48 V，20 Ah)供电，车体长宽高为1 300 mm×700 mm×1 250 mm，轮距和轴距分别为550 mm、840 mm，如图1所示。采用电动推杆推动梯形4杆机构实现转向，推杆行程为200 mm，由L298N驱动器驱动转向角范围为−32°~32°。后轮由直流电机通过减速器与差速器驱动，驱动器型号为AQMD6020BLS。平台的位置信息分别由超宽带无线定位系统和电子陀螺仪提供。超宽带模块数据传输频率为1~50 Hz，陀螺仪(WT901C)为平台提供航向信息，测量范围为−180°~180°，精度为0.1°。采用STM32F767IGT6单片机作为试验平台的主控制器。控制系统原理如图2所示。
Figure 1. Prodsuction platform
Figure 2. Block diagram of control system
-
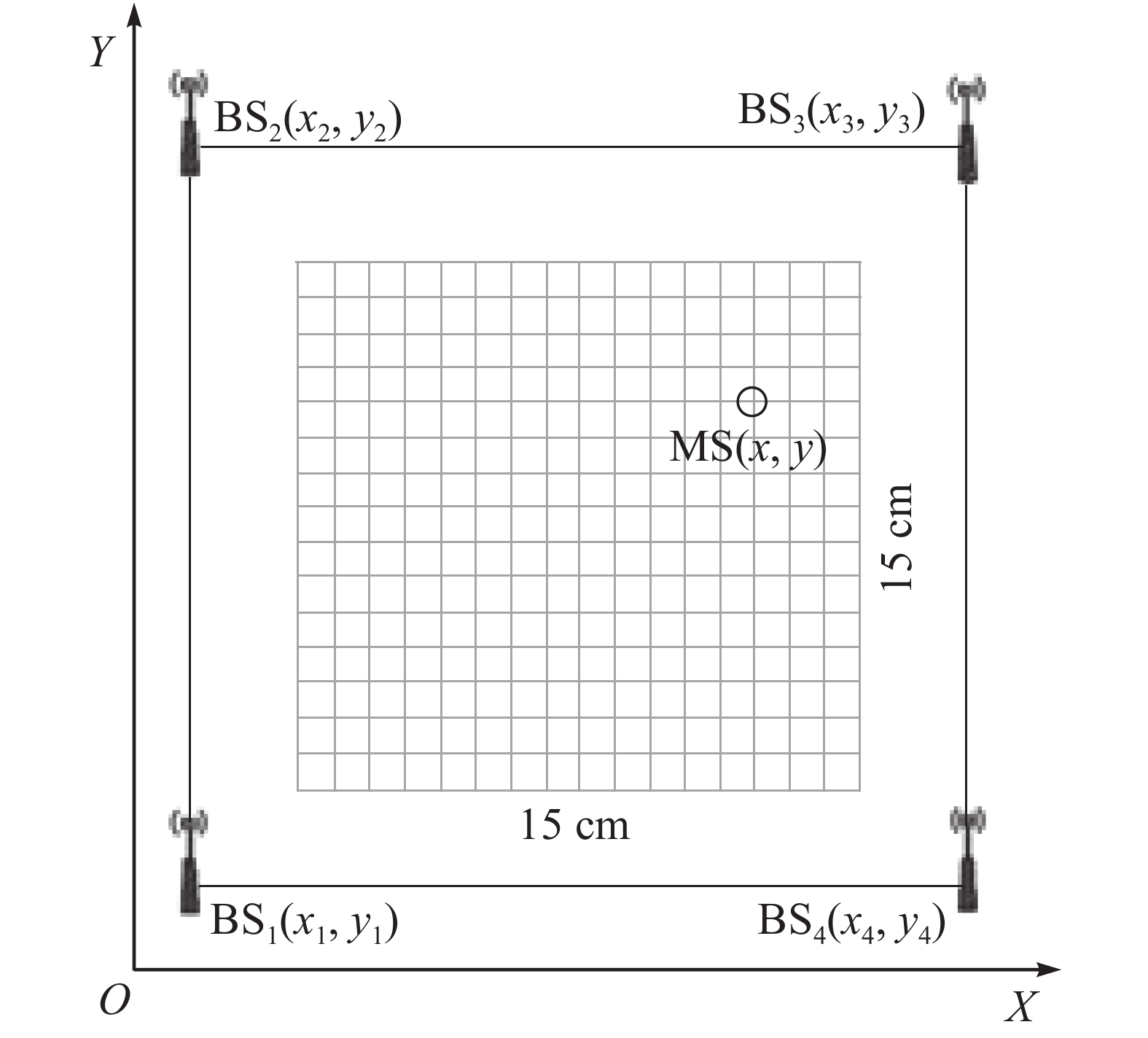
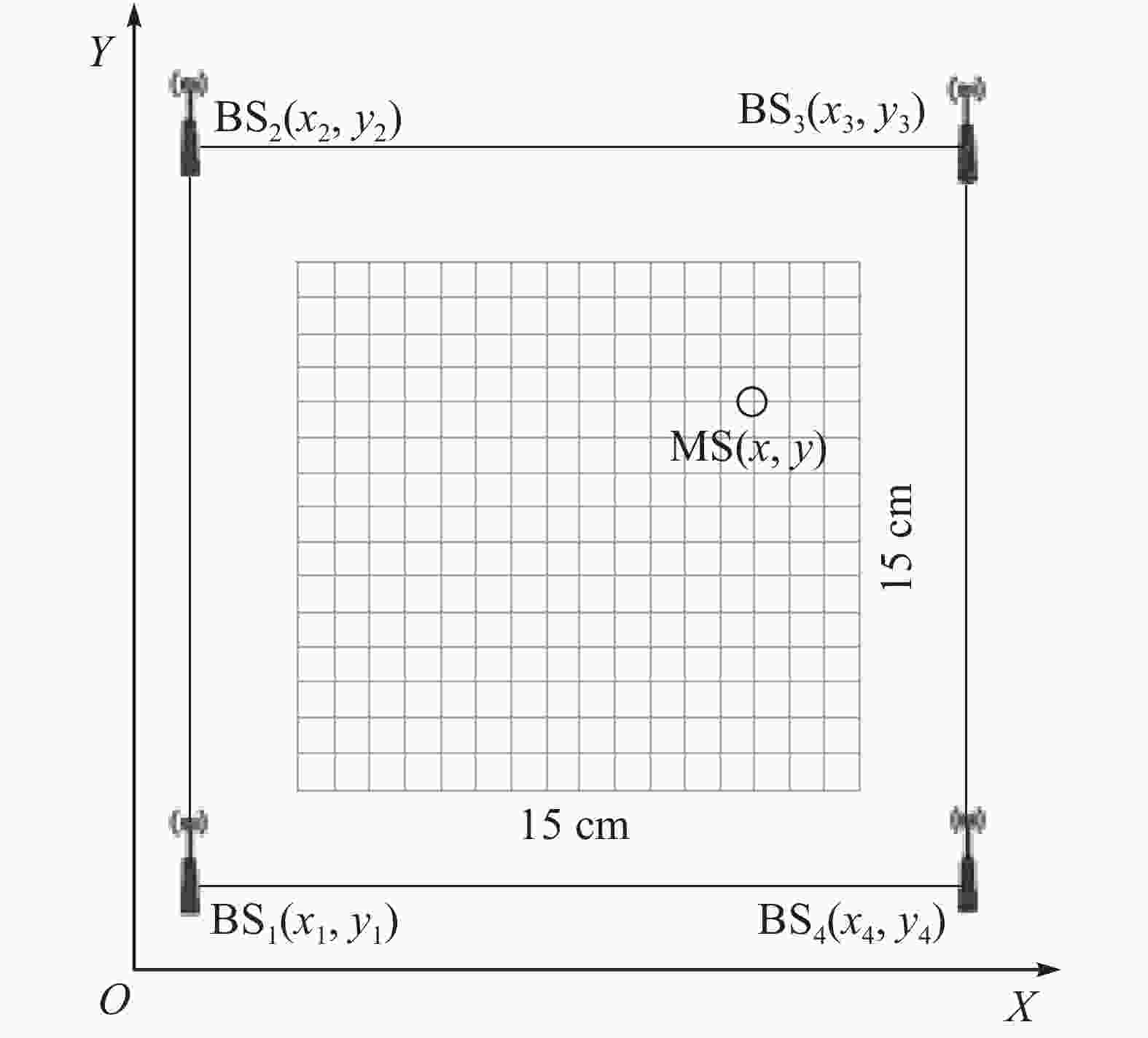
超宽带无线定位系统是由若干固定基站BS和移动标签MS通过一定的通信方式组成。根据超宽带定位原理，获取移动标签3维定位坐标至少需要4个基站。由于本研究默认生产平台行驶在水平地面上，因此定位只需用到水平面横、纵2个坐标参数。增加基站的数量可提高定位的精度。本研究采用4个基站BS1~BS4组成1个平面定位坐标系OXY，如图3所示。
Figure 3. Test area
-
UWB定位方法包含：信号到达时间(TOA)[17]、信号到达时间差(TDOA)[18]、信号到达角度(AOA)[19]、接收信号强度(RSSI)[20]等。AOA定位算法主要参考基站天线阵列获得信号角度，对基站位置依赖较大，且受到非视距传播影响，定位精度不高。RSSI定位算法简易，成本不高，但是用作室内定位时，易受多径传播和信号反射的影响，定位精度误差较大。TOA与TDOA较为常用，时间分辨率高；TDOA较TOA的优势在于，不需要基站与移动标签时钟同步[21]，因此，本研究采用TDOA的定位方法。TDOA定位也称双曲线定位，基本思想为：任选2个坐标已知的基站为某双曲线左右焦点，2基站的距离值即为双曲线焦距值。通过测量这2个基站信号到达移动标签的时间差得到移动标签到2个基站的距离差，根据双曲线的定义可求得实半轴值，并获得该双曲线方程。用1个坐标已知的新基站替换上述2个基站中的任意1个，采用同样的方法可得到另1条双曲线方程，两者的交点即为移动标签的位置。TDOA定位算法具体步骤如下。如图3所示：在坐标系OXY中，移动标签MS的坐标为(x，y)，基站BS1~BS4的坐标分别为(x1，y1)~(x4，y4)。根据TDOA测距原理可得：
式(1)中：ri表示MS到BSi之间的距离，i=1, 2, 3, 4。对式(1)两边平方可得：
式(2)中：Ki=xi2+yi2。令ri,1为MS到BSi和BS1之间的距离差，可得：
式(3)中：c表示光速(3×108 m·s−1)；ti,1表示信号在MS到BSi和BS1的时间差值。联立式(1)、式(2)和式(3)可得：
式(4)中：xi,1=xi−x1，yi,1=yi−y1。令i=2, 3，带入式(4)，可得到：
式(5)中：P1=
$ - {\left[ {\begin{array}{*{20}{c}} {{x_{2,1}}}&{{y_{2,1}}} \\ {{x_{3,1}}}&{{y_{3,1}}} \end{array}} \right]^{ - 1}}$ ，P2=$\left[ \begin{gathered} {r_{2,1}} \\ {r_{3,1}} \\ \end{gathered} \right]$ ，P3=$ - \dfrac{1}{2}\left[ \begin{gathered} {K_2} - {K_1} - r_{2,1}^2 \\ {K_3} - {K_1} - r_{3,1}^2 \\ \end{gathered} \right]$ 。联立式(1)和式(5)，可以得到：式(6)中：a=(P1P2)TP1P2−1，b=(P1P2)T(P1P3−X1)+(P1P3−X1)T(P1P2)，m=(P1P3−X1)T(P1P3−X1)，X1=[x1, y1]T。由于各基站的坐标(x1，y1)~(x4，y4)都为已知，因此将这些数据代入上述所有公式即可解出a、b、m。式(6)是一个关于r1的一元二次方程，可进一步解出r1，最终解出标签的坐标(x，y)。
-
UWB信号在室内直线传播时，会受到多径干扰或障碍物遮挡而产生非视距(NLOS)误差[22]，因此需掌握定位误差产生的规律，并对误差进行必要的修正。
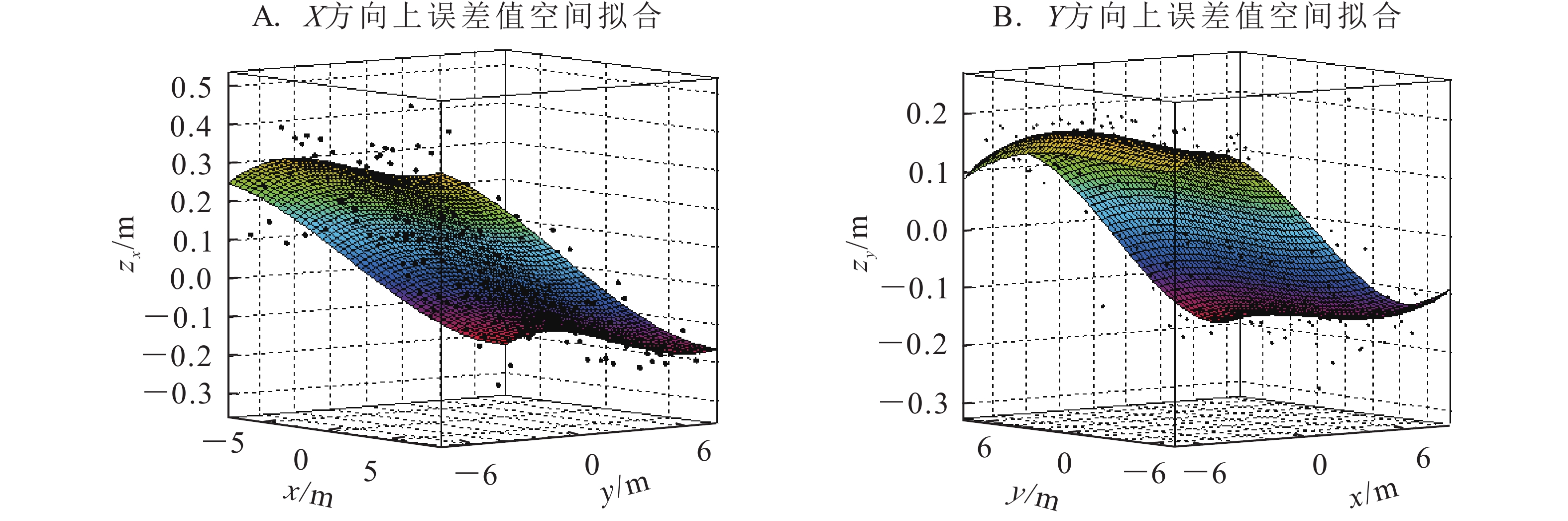
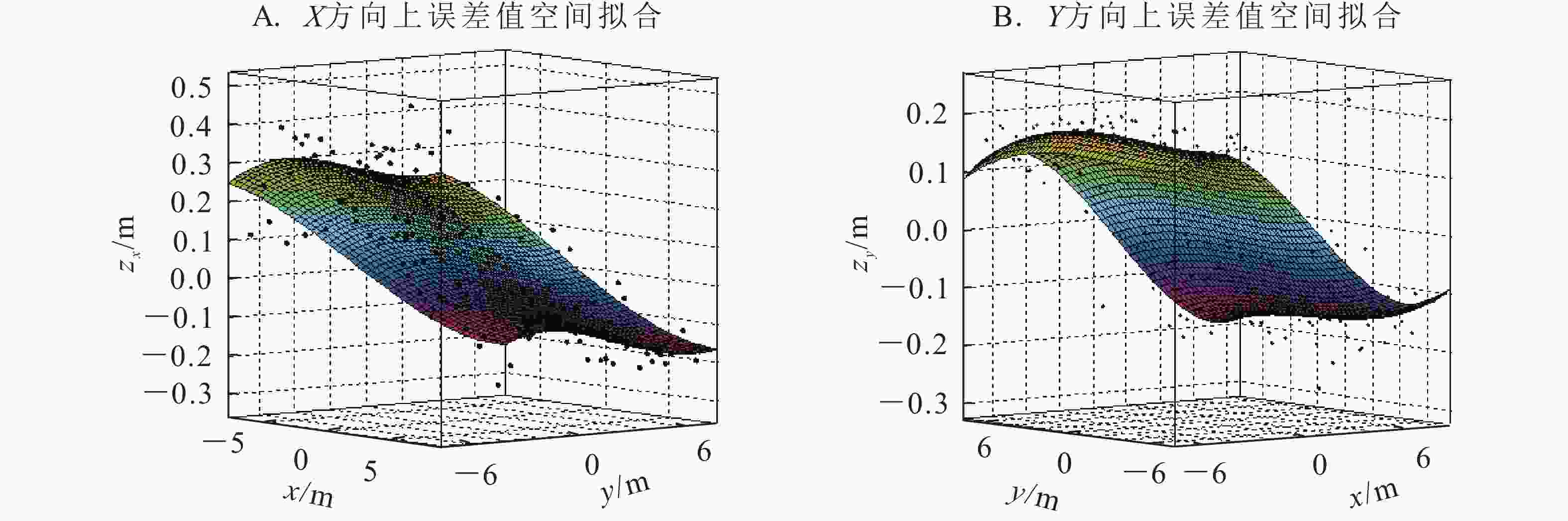
如图3所示：在UWB定位区域中心选定15 m×15 m场地，在场地中画出1 m间隔的单元格，在坐标系OXY中测量每个格点坐标值。这些测量值与格点处的精确值之间存在X和Y方向上的误差。以格点所在的平面为x-y平面，以X和Y方向上的误差值为z轴，分别构建在xyzX和xyzY空间中的误差值三维散点图，为发现误差分布的规律，用MATLAB R2012a对散点图进行二元三次多项式拟合，如图4所示。得出拟合方程如下式，各项系数如表1所示。
方程 m3 m2 m1 n3 n2 n1 p3 p2 p1 p0 zX(x, y) 0.000 31 –0.000 83 –0.038 4 –0.000 07 –0.000 22 0.001 6 –0.000 044 0.000 05 –0.000 101 0.046 7 zY(x, y) 0.000 12 –0.000 59 –0.002 7 0.000 15 0.000 42 –0.042 0 0.000 021 0.000 01 –0.000 167 0.056 4 说明：zX(x, y)为X方向的误差拟合方程，zY(x, y)为Y方向的误差拟合方程 Table 1. Coefficient of error fitting equation
Figure 4. Error fitting
式(7)中：(x, y)为位置坐标的测量值。本研究2个拟合方程的决定系数分别为0.823和0.856，拟合效果较好。则定位修正方程为：
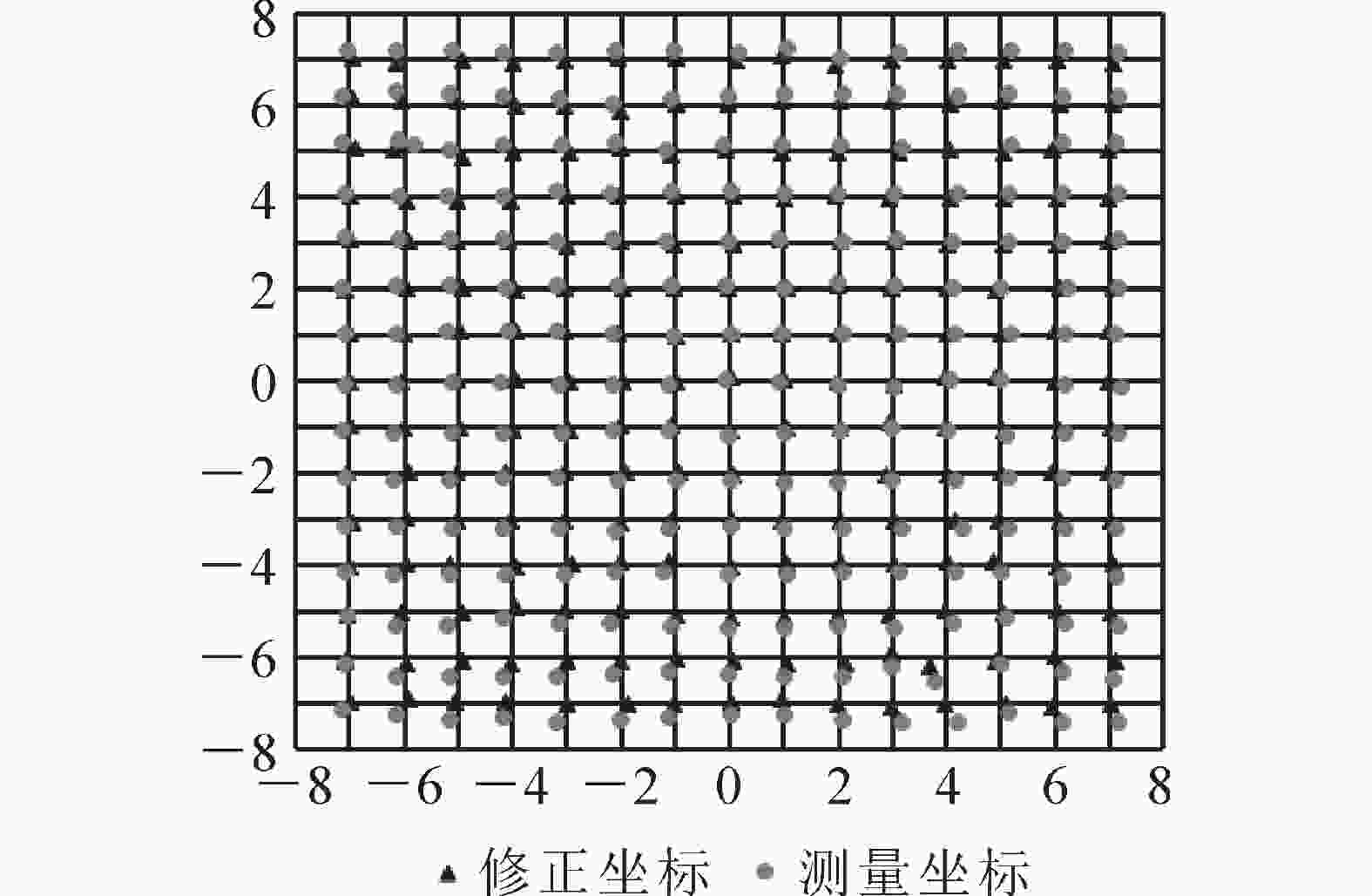
式(8)中：xcorrection和ycorrection分别表示测量点修正后的横、纵坐标。为验证误差修正方法的有效性，将测量值依次带入式(8)计算误差修正后的坐标，修正坐标与测量坐标对比如图5所示，并随机选择了20个不同的静态位置分别采集2 min，100组数据，计算平均值，分别带入定位修正公式，得到修正后坐标和修正前后的平均误差统计值。表2显示：相比修正前坐标，修正后坐标精度得到明显的提升。从表3可见：X方向平均误差减少了0.08 m，定位精度提升了66.7%，Y方向平均误差减少了0.11 m，定位精度提升了68.8%。因此，修正后的点接近实际点，验证了定位误差修正方法的有效性，满足试验需求。
序号 实际坐标/m 修正前坐标/m 修正后坐标/m 序号 实际坐标/m 修正前坐标/m 修正后坐标/m 1 (1.50, 3.50) (1.54, 3.63) (1.53, 3.55) 11 (6.13, 1.58) (6.33, 1.67) (6.17, 1.54) 2 (1.50, –5.50) (1.51, –5.72) (1.5, –5.45) 12 (2.47, 5.39) (2.56, 5.56) (2.50, 5.41) 3 (3.50, 1.50) (3.59, 1.66) (3.51, 1.64) 13 (1.22, –3.66) (1.29, –3.84) (1.19, –3.63) 4 (3.50, –5.50) (3.58, –5.64) (3.50, –5.37) 14 (5.78, –2.32) (6.01, –2.48) (5.86, –2.33) 5 (6.50, 1.50) (6.61, 1.57) (6.46, 1.55) 15 (–4.65, 5.81) (–4.81, 6.03) (–4.66, 5.88) 6 (–3.50, 3.50) (–3.64, 3.63) (–3.49, 3.55) 16 (–0.95, 1.43) (–0.99, 1.50) (–0.91, 1.41) 7 (–3.50, –5.50) (–3.62, –5.73) (–3.47, –5.46) 17 (–2.61, –6.49) (–2.69, –6.73) (–2.56, –6.42) 8 (–4.50, –5.50) (–4.63, –5.67) (–4.47, –5.41) 18 (–5.33, –4.53) (–5.51, –4.72) (–5.34, –4.51) 9 (–5.50, –1.50) (–5.65, –1.68) (–5.47, –1.58) 19 (–5.20, –1.30) (–5.39, –1.38) (–5.24, –1.23) 10 (–5.50, 5.00) (–5.69, 5.13) (–5.53, 4.99) 20 (–1.40, 2.70) (–1.52, 2.81) (–1.42, 2.76) Table 2. Comparison of measured coordinates and corrected coordinates
方向 平均误差 定位精度提升/% 修正前/m 修正后/m X 0.12 0.04 66.7 Y 0.16 0.05 68.8 Table 3. Average error statistics before and after correction
Figure 5. Static positioning measurement and correction
-
本研究设计一种带解析式的模糊控制器，构建车体横向偏差、航向偏差与前轮转向角之间的映射关系，并利用自调整函数动态调整各输入变量的权重，提高生产平台在温室内狭窄空间下路径跟踪的质量。
-
本研究车体横向偏差由UWB无线定位系统采集车辆的当前绝对位置获取，航向偏差由跟踪航向和陀螺仪采集的当前车身航向计算得到。以车体横向偏差d和航向偏差θ作为模糊控制器的输入变量，以前轮转角α作为输出变量，分别对3者模糊化。d的基本论域范围为[−0.6 m，0.6 m]，θ的基本论域范围为[−60°，60°]，α的论域范围为[−32°，32°]。由于Mamdani型模糊推理规则满足人们思维方式的特点[23]，因此，本研究采用Mamdani型模糊推理。将输入输出变量的论域变化范围都归一化为[−6，6]之间的变量，得出d的量化因子
${k_d}$ =10，θ的量化因子${k_\theta }$ =0.1，α的比例因子${k_\alpha }$ =0.17。设定d、θ和α的正负号为：生产平台位于导航线左侧时d为正，右侧为负；θ逆时针为正，顺时针为负；α左转为正，右转为负。 -
设计带有自调整函数的模糊解析表达式[24]。
式(9)中：Α表示前轮转角的模糊变量；D表示横向偏差的模糊变量；Θ表示航向偏差的模糊变量；S表示论域设定值，此处为6；n表示自调整函数。本研究控制器权重设置原则为：生产平台在路径跟踪过程中，若横向偏差较大，则增大横向偏差权重，使其不偏离路径较远；若横向偏差较小，则对航向偏差给予较大权重，使生产平台跟踪路径更稳定。相比于常规模糊控制规则的单一，其提高了控制的灵活性，提升了精度。依据上述思想，建立自调整函数为：
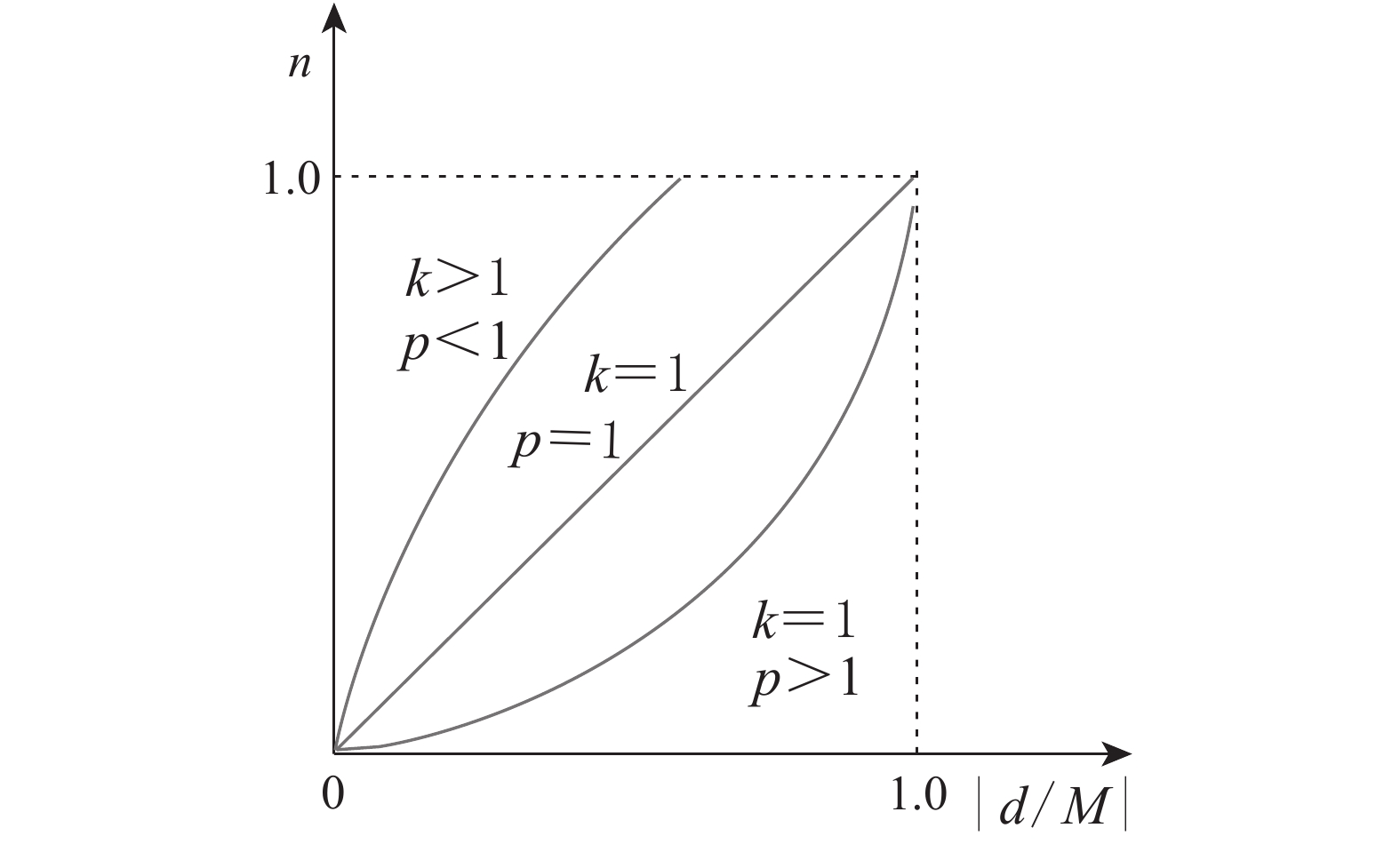
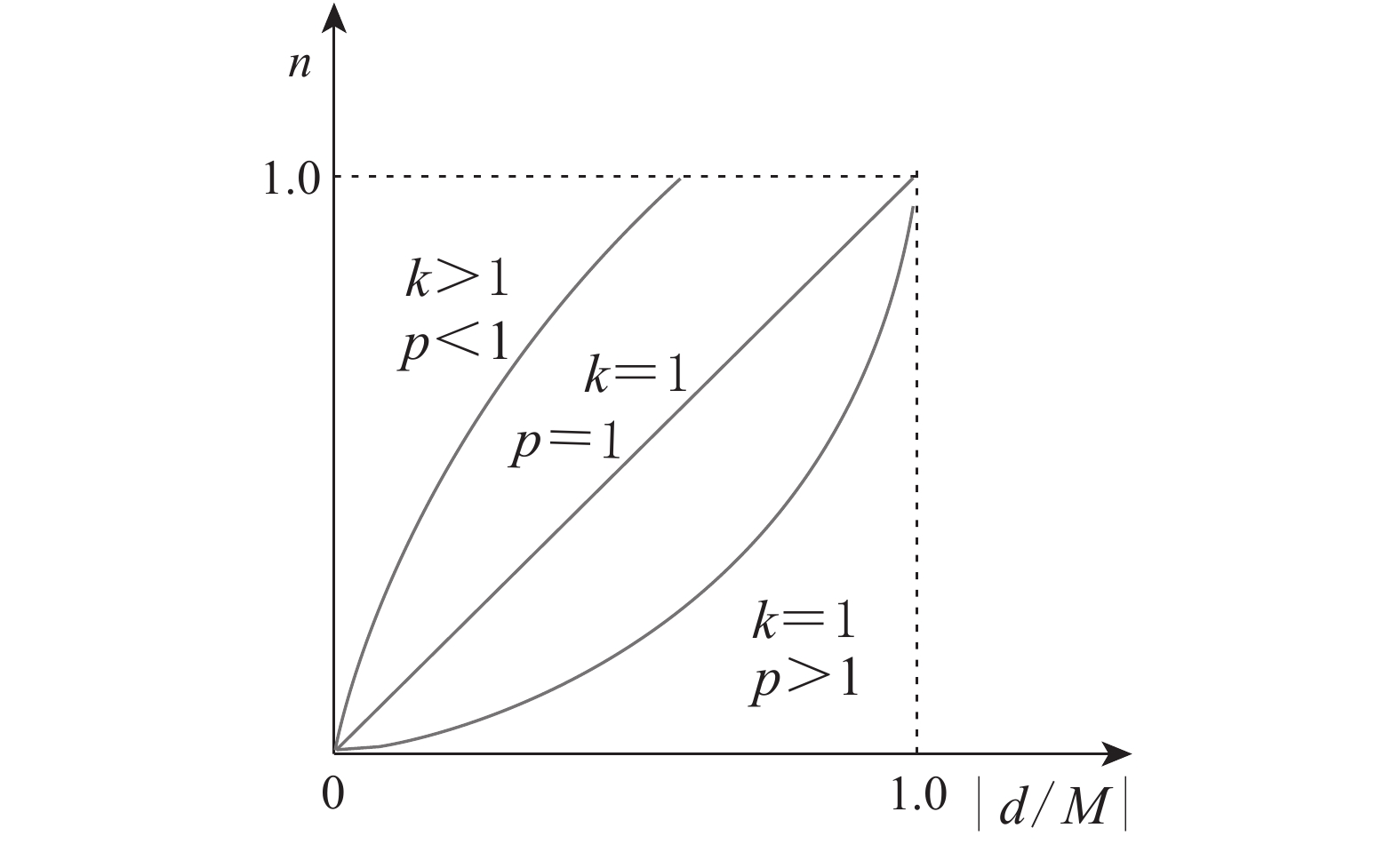
式(10)中：k表示系数；M表示最大误差，此处为0.6 m；p表示自调整函数的幂次；d表示横向偏差。因为式(10)的各参数均为正值，故k≤
${\left( {\dfrac{{{d_{\max }}}}{M}} \right)^{ - p}}$ 时，n≤1。自调整函数的形态根据p取值不同而改变，如图6所示。当p＜1时，n随横向偏差增加较快，横向偏差在系统中占据权重多；当p＞1时，航向偏差的控制作用加强，随着p的增大，其作用越强。由于生产平台在设施温室内行驶时，需频繁更改当前跟踪路径，时常会出现较大横向偏差，且道路宽度有限，因此横向偏差的权重需始终重视。经过MATLAB R2012a仿真，这里自调整函数的参数p=0.8，k=1.1。
Figure 6. Self-adjusting function graph
1.1. 试验材料
1.2. 定位方法
1.2.1. 定位原理
1.2.2. 信号到达时间差定位算法
1.2.3. 定位误差分析及误差修正
1.3. 模糊控制器
1.3.1. 输入输出变量
1.3.2. 带自调整函数模糊解析式
-
为了验证本研究方法的有效性，于2019年3−5月，在浙江农林大学室内体育馆布置场地(图3)进行试验。基站与移动标签距离地面的高度均为1.6 m，移动标签投影点位于生产平台后轮车轴中间。生产平台按照0.5 m·s−1的速度行驶，采样频率为5 Hz。试验类型分为直线跟踪与矩形跟踪2种。同一初始状态的试验重复4次，各数据求平均值。
本研究对偏差的平均值、极值和标准差等进行了统计分析。平均偏差是从试验开始到结束的横向偏差均值；最大偏差是在整个试验过程中横向偏差最大值；稳态偏差是当生产平台从试验开始到第1次横向偏差收敛到0 m的稳定点后横向偏差均值；稳定距离是生产平台到达稳定点行驶的距离。
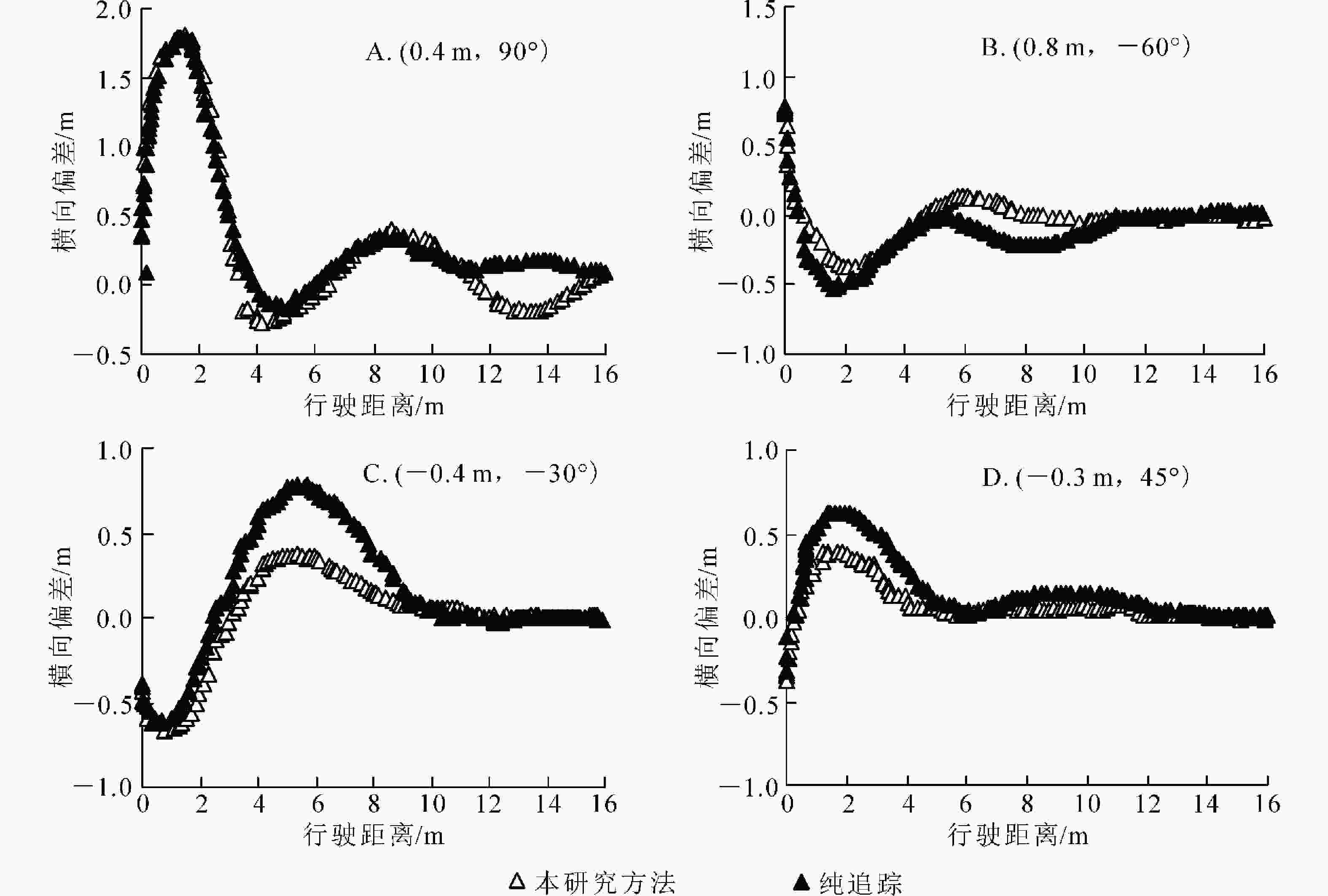
试验1：直线路径跟踪试验。设计4种偏差初始状态来考察本研究方法直线路径的性能，并通过纯追踪法进行对比验证。经多次计算机仿真，纯追踪模型取最佳前视距离为2 m。如图7所示。
Figure 7. Line test
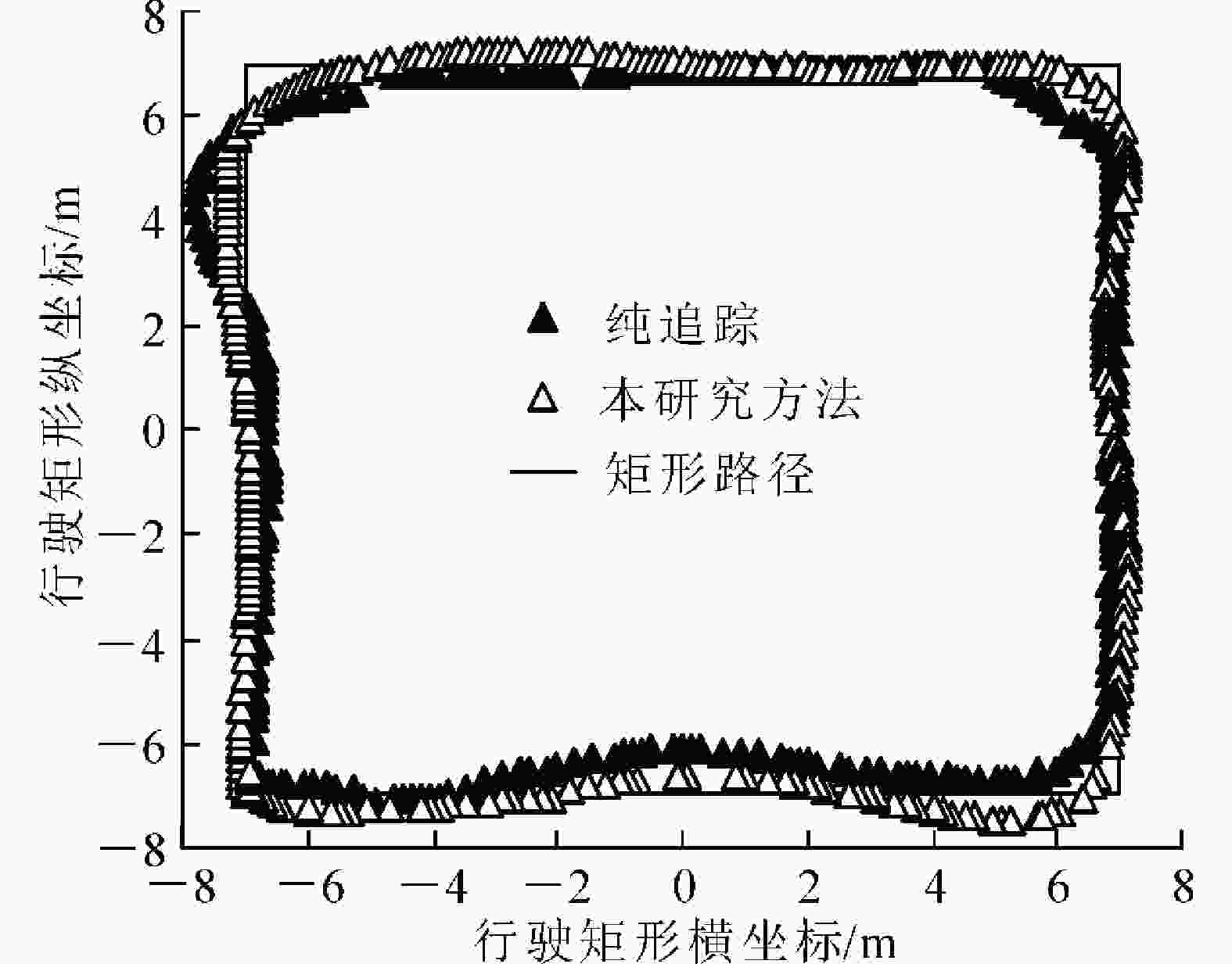
试验2：矩形路径跟踪试验。在温室作业时，农机需频繁沿着设施内道路直角转向，因此需检验生产平台矩形路径跟踪的效果。在试验场地内设计了15 m×15 m的矩形路线。如图8所示：生产平台出发的初始位置为A(−7，−7)，初始横向、航向偏差均为0°，沿顺时针方向行驶。
Figure 8. Rectangle test
-
在进行直线路径跟踪时，本研究提出的方法在4种初始状态下，生产平台平均偏差均值依次为28.7、23.8、16.9、20.1 cm，最大偏差依次为179.5、37.1、66.8、46.4 cm，在纯追踪模型中平均偏差均值依次为37.2、35.3、24.4、28.3 cm，最大偏差依次为180.8、51.3、85.6、62.2 cm。本研究方法的平均偏差比纯追踪模型分别提高了22.8%、32.6%、30.7%和28.9%，最大偏差分别提升了0.7%、27.7%、21.9%和25.4%。直线试验时第1种初始状态下偏差明显大于其他状态，是由于初始位置偏离路径较大，需要进行大幅度转向才能逐渐收敛至跟踪直线。表明相同的环境下，本研究方法具有更好的路径跟踪精度。
采用本研究方法进行直线路径跟踪时，平均偏差值的标准差为5.8 cm；而采用纯追踪模型法的平均偏差值的标准差为9.7 cm。标准差越小，说明数据离散程度越低，前者的标准差比后者小，因此本研究方法具有更好的跟踪稳定性。
在进行直线路径跟踪时，本研究方法4种初始状态下的稳定距离分别为319.9、35.4、310.1和16.8 cm；在纯追踪模型中，稳定距离则为432.1、50.3、250.1和22.4 cm，稳定距离提升率分别为25.9%、29.6%、19.3%和25.0%。这是因为本研究方法在进行转向角计算时，增加航向偏差的权重动态调整转向角，使得车体向期望路径的收敛速度较快。表明相同的试验环境下，本研究方法具有更好的收敛快速性。
在矩形路径跟踪时，生产平台在本研究方法下的平均偏差为14.4 cm，在纯追踪模型中，平均偏差为36.9 cm，平均偏差提升率达60.9%，能基本满足作业需求。在2种方法的矩形试验中，最大偏差都发生在更换路径时，即矩形路径的转角处。这是由于在更换路径时需要做类似于大偏差初始状态的直线跟踪，需要大幅度转向，因此产生大偏差。
2.1. 试验过程
2.2. 数据分析
-
采用UWB模块构建无线定位系统获取生产平台的位置信息，并设计了15 m×15 m的矩形试验区域。在试验区域内随机测量一些点，这些点在原X、Y方向定位平均误差分别为0.12和0.16 m，经误差修正后X、Y方向定位平均误差分别为0.04和0.05 m。使用带自调整函数的解析式模糊控制器，动态调整横向偏差与航向偏差的权重，对前轮转角的输出实现自适应调整,其中自调整函数的参数p=0.8，k=1.1。在生产平台上进行了直线和矩形的路径跟踪，生产平台使用本研究方法的直线跟踪平均稳态偏差在4.7~6.4 cm，矩形路径的平均偏差为14.4 cm，能满足温室内狭窄道路的运输需求。下一步考虑改良生产平台的机械性能，测试在不同的环境下UWB的定位精度，以及在不同的路况下生产平台路径跟踪的平顺性。
DownLoad: