Effect of milling parameters on cutting force and quality of vascular bundle fiber extraction in bamboo

选取浙江湖州5年生毛竹，并截取直径约110 mm，竹壁厚度约10 mm的竹段作为试材。去除竹节后放入烘箱中，在70~80 ℃下烘烤8 h。然后，用破竹器将每段试材分成8根竹条，并去除0.8 mm厚度的竹青表皮，最后对竹条进行切割，得到高度分别为36、40和44 mm的竹板毛坯。加工机床采用宁波其锐达机械有限公司生产的KMD-80120型三轴高速雕铣机，主轴最高转速达到12 000 r·min⁻¹；试验刀具为直径10 mm的双刃直槽硬质合金木工雕刻刀。在试验过程中，刀刃径向跳动调整在6 μm以下。切削力测量系统为宁波灵元测控工程有限公司生产的压电晶体测力仪。

对于纤维增强复合材料，具有大长径比的纤维是理想的^[14−17]，因此本研究以纤维长度、纤维直径和纵横比评判维管束纤维质量。设计正交切削试验并获取各参数下的切削力数据，再基于切削力数据分析切削参数对切削力及维管束纤维质量的影响规律。

参考以往研究^[18−20]，本研究将竹壁沿径向划分为图1所示的内、中、外3层，其中外部维管束纤维呈半开放型，纤维长轴平均长度为0.39 mm，短轴平均长度为0.23 mm。经测量，竹壁外部维管束纤维在水平方向的平均间隙为0.2~0.4 mm。切削过程中，为得到尽可能完整的维管束纤维，切削步进距(A_e)设置为0.4 mm。在以上加工参数的基础上，将切削速度、每齿进给量及切削深度分别定义为因素A、B、C，制定正交试验方案(表1)。试验采用刀刃平行于维管束纤维，沿X轴单向顺铣，干式切削方式进行，对每个试件连续切削3个步距，每组参数重复切削5个试件。通过以上正交试验，可得到135组切削力数据。

Figure 1.  Schematic diagram of bamboo wall layering

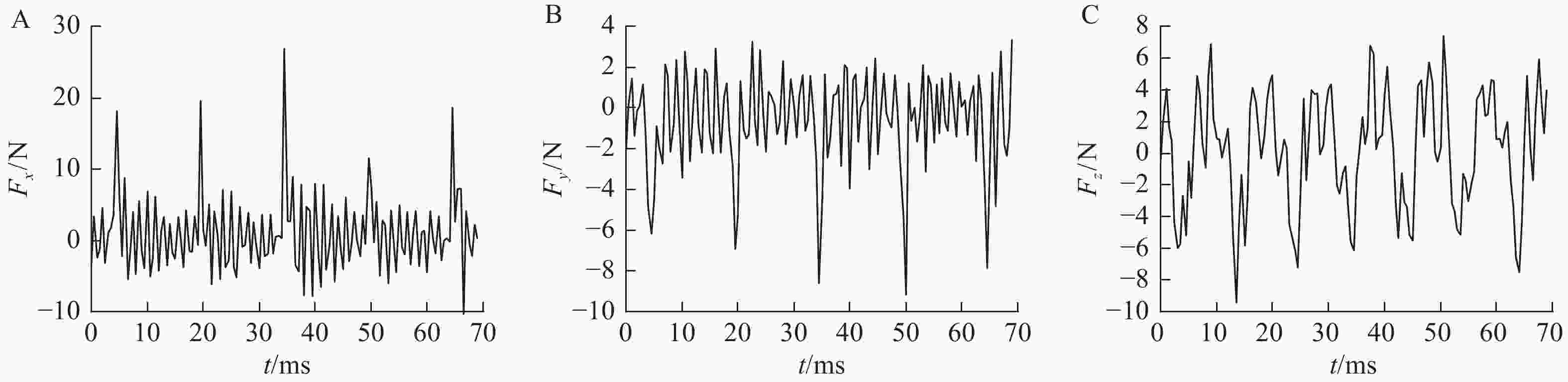
在切削速度为62.8 m·min⁻¹，每齿进给量为0.2 mm，切削深度为4 mm，切削步进距为0.4 mm条件下，对高度为36 mm的竹块毛坯进行切削试验，每个切削刃的部分切削分力(F_x、F_y、F_z)的动态分布曲线如图2所示。切削力呈周期性变化。由于竹壁维管束纤维呈错列排布，铣削过程中维管束纤维的切削厚度不尽相同，因此加工过程中切削力的最大值变化显著。1个切削周期内，F_x先增后减，且为正值，表明在切削过程中，切削刃始终沿进给方向对竹板产生拉力，且随着切削厚度增至最大，切削力也增至最大；F_y向切削刃始终对竹板产生挤压作用，且顺铣时切削刃切出工件侧面过程中，切削厚度逐渐减小为0，故F_y始终为负值。此外，不同于螺旋铣刀，双刃直槽硬质合金木工雕刻刀在切削过程中对材板无Z轴方向作用力，但机床系统振动会导致Z轴方向作用力产生如图2C所示的微小波动^[21]，因此本研究忽略Z轴方向作用力的影响^[22−23]。为保证试验数据的一致性，均在切削力曲线中选取重复频率较高、数值较大的切削力数值进行记录。每组试验参数记录15组切削力数据，并计算其平均值作为该组正交试验参数的切削力，正交试验方案及切削力如表1所示。

Figure 2.  Dynamic distribution of cutting force

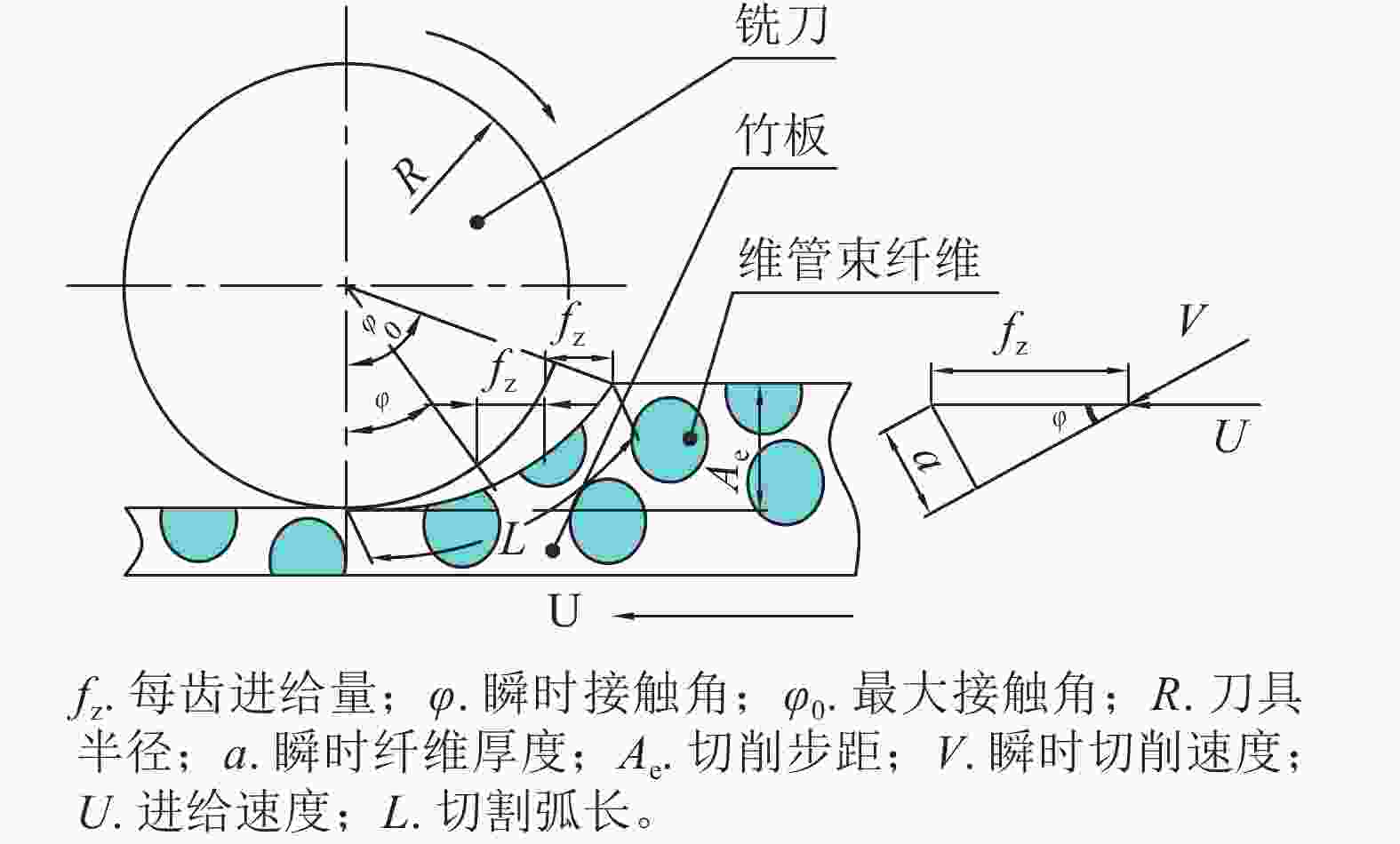
图3为维管束纤维切削瞬态几何模型^[24]。定义纤维纵横比为α=L/a_max，用以标定维管束纤维的长度和窄度，其中L为切割弧长，a_max为最大纤维切削厚度。a_max与L可根据下式得到：

Figure 3.  Transient geometry of vascular bundle fiber cutting

式(1)~(2)中：f_z为每齿进给量，φ₀为最大接触角，R为刀具半径。定义维管束纤维理论直径为D_e=(L+a_max)/2。从每组试验中随机选取的100根维管束纤维，使用游标卡尺分别测量纤维厚度、切割弧长和纤维长度(L₀)，并分别以各自平均值作为对应参数的最终数据。

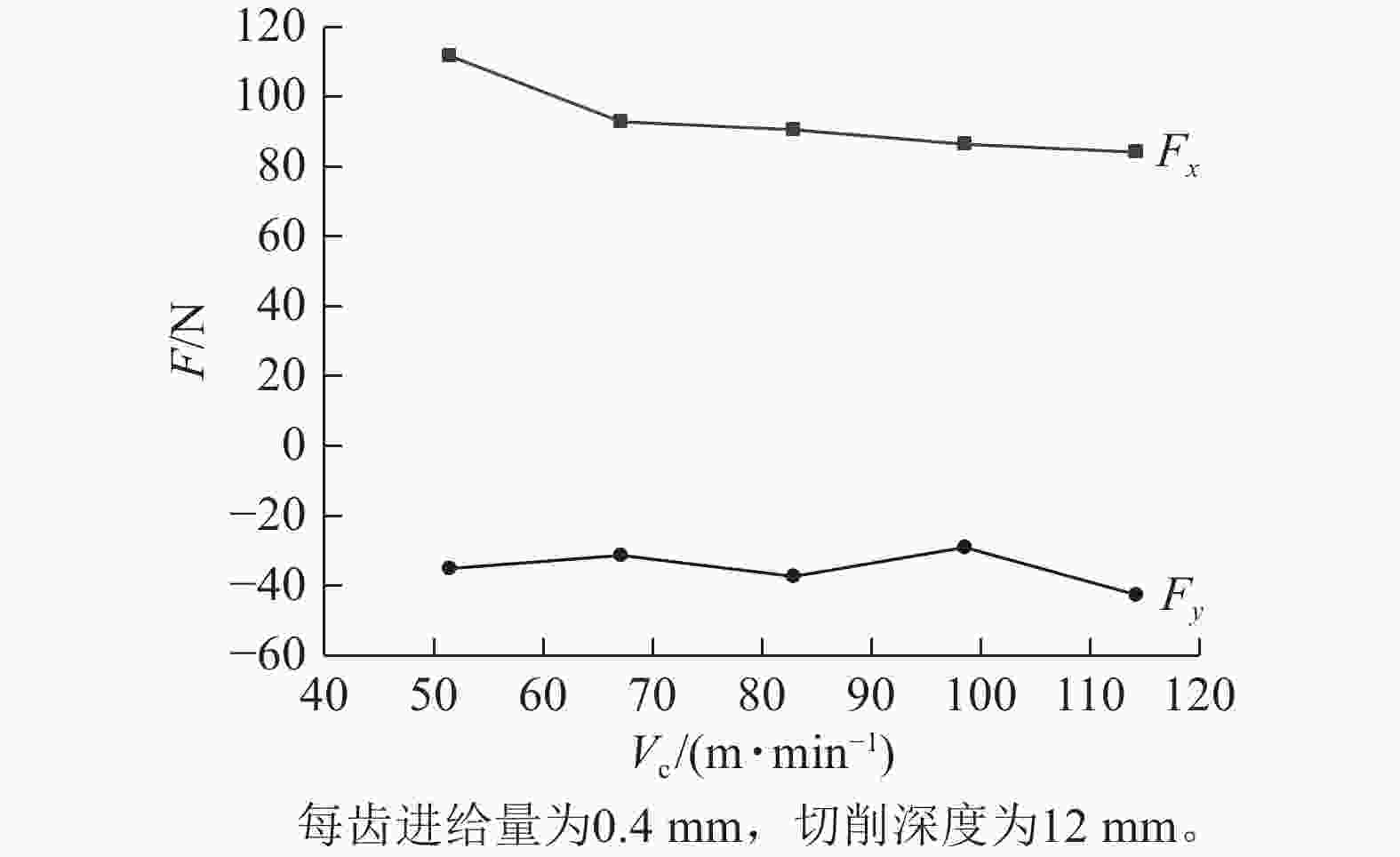
在每齿进给量为0.4 mm，切削深度为12 mm，切削步进距为0.4 mm条件下，切削速度与切削力平均值的关系如图4所示。切削过程中，F_x为正值，为主要切削力。F_y为负值，切削刃对工件产生挤压作用。随着切削速度的增加，刀具单次切削竹维管束的体积减小，单次切削功率也随之减小，因此F_x随切削速度的增加而减小；F_y在−40 N附近轻微波动。由此可见：切削速度的变化对F_y方向的切削力影响不大，其轻微波动主要由切削系统共振造成。

Figure 4.  Influence of cutting speed on cutting force

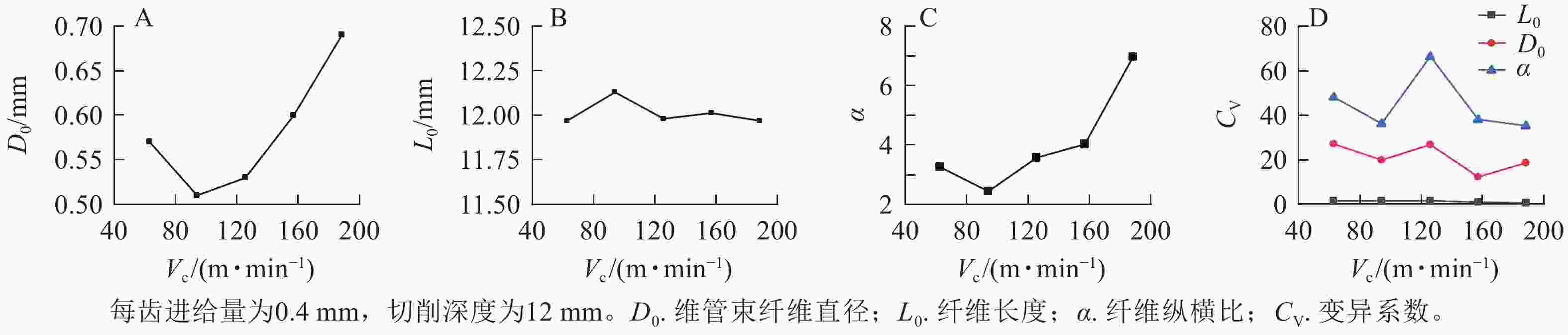
在每齿进给量为0.4 mm，切削深度为12 mm, 切削步进距为0.4 mm条件下，切削速度对维管束纤维形态的影响如图5所示。随着切削速度的增加，维管束纤维直径(D₀)先减小后增大，且数值只有维管束纤维理论直径的0.5~0.7倍(图5A)。这是因为理论切割弧长大于维管束纤维直径，即使维管束纤维被完整切割也无法达到理论值。各参数铣削获得的维管束纤维长度比较稳定，且与理论值的误差极小(图5B)。维管束纤维纵横比随着切削速度的增大而增大，且当切削速度大于125.7 m·min⁻¹时，纤维纵横比有较明显的提高(图5C)。由纤维直径、纤维长度及纤维纵横比的变异系数(C_V)可知(图5D)：随着切削速度的变化，纤维长度并未产生明显的变化，纤维直径和纤维纵横比均在切削速度为160.0~188.5 m·min⁻¹时出现最小值且变化幅度较小。综上，提高切削速度有助于获得尺寸稳定且有较大纵横比和直径的维管束纤维。

Figure 5.  Effect of cutting speed on the shape of bamboo fiber

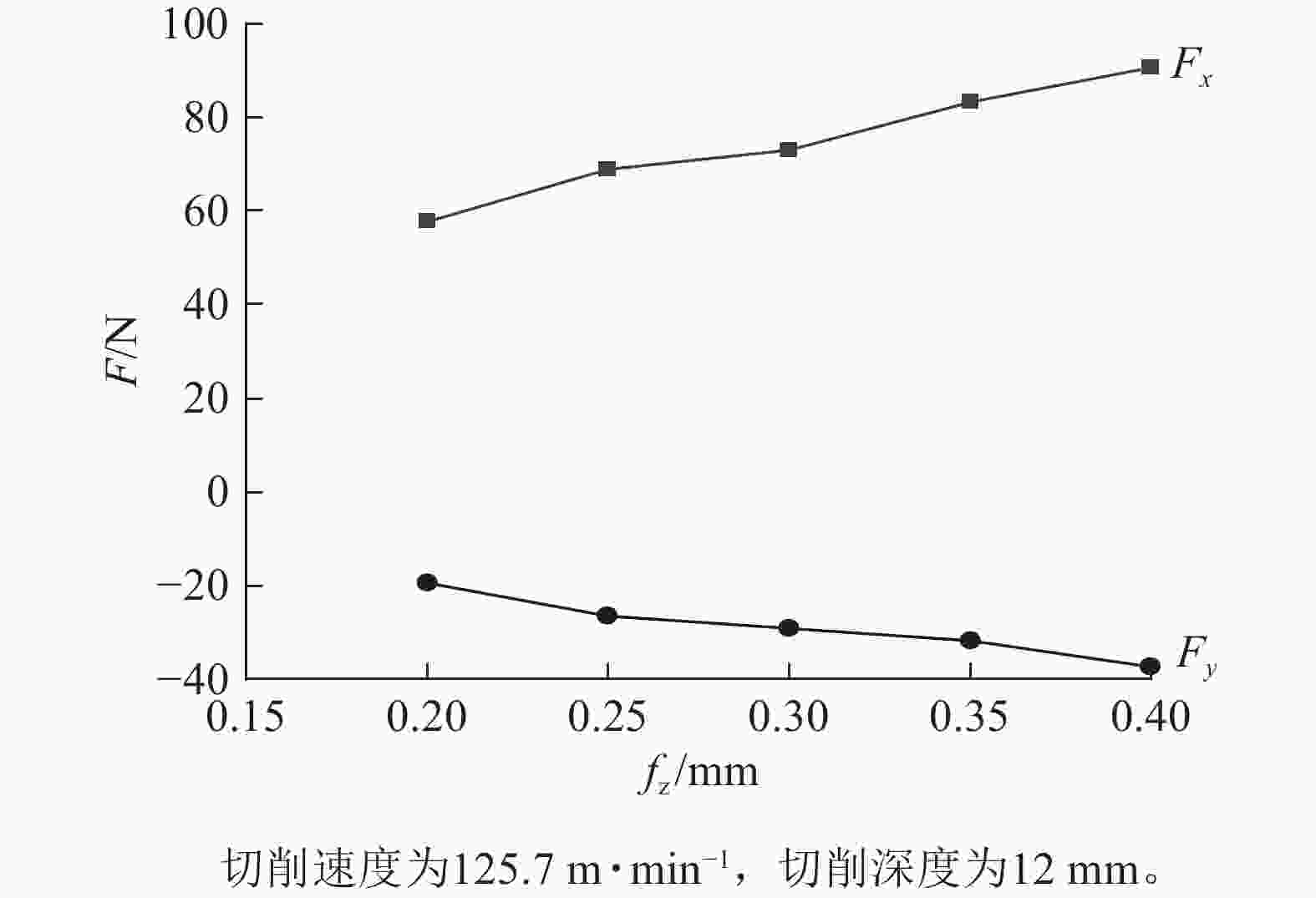
在切削速度为125.7 m·min⁻¹，切削深度为12 mm，切削步进距为0.4 mm条件下，每齿进给量与切削力平均值的关系如图6所示。随着每齿进给量增加，单位时间内切下切屑的体积增大，切削功率也随之增大，因此随着每齿进给量的增加，F_x呈近似线性增大，F_y呈近似线性减小。

Figure 6.  Influence of feed rate per tooth on cutting force

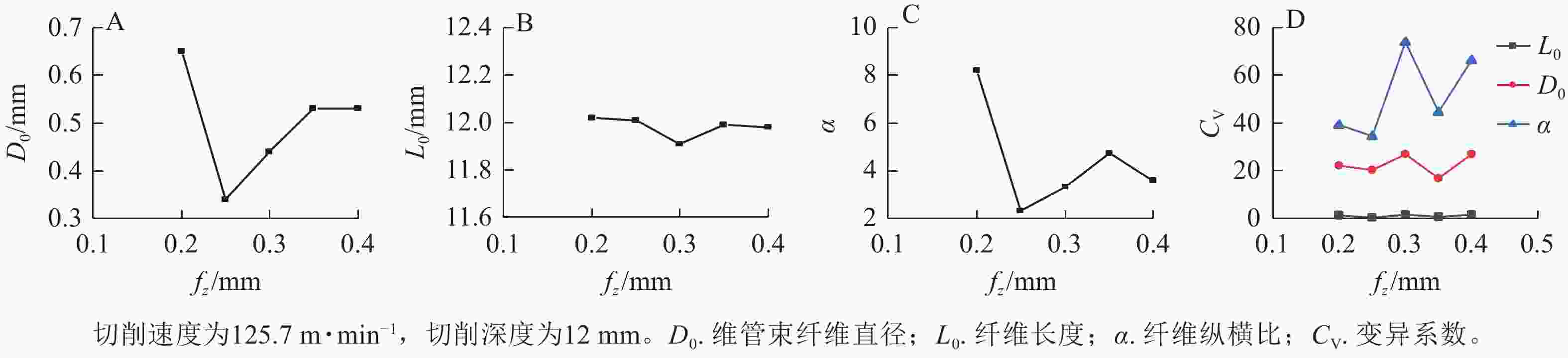
在切削速度为125.7 m·min⁻¹，切削深度为12 mm, 切削步进距为0.4 mm条件下，每齿进给量对维管束纤维形态的影响如图7所示。不同每齿进给量下获得维管束纤维直径先减小后增大，且当每齿进给量为0.2 mm时出现最大值(图7A)；各参数铣削获得的维管束纤维长度比较稳定，且与理论值接近(图7B)；纤维纵横比随着每齿进给量增加，呈先下降后上升再下降的趋势，且当每齿进给量为0.2 mm时出现最大值(图7C)；纤维长度、纤维直径和纤维纵横比随每齿进给量变化而产生明显的变化，但均在每齿进给量为0.2 mm时获得最优维管束纤维(图7D)。综上，减小每齿进给量有利于获得较高质量的维管束纤维。

Figure 7.  Effect of feed rate per tooth on bamboo fiber morphology

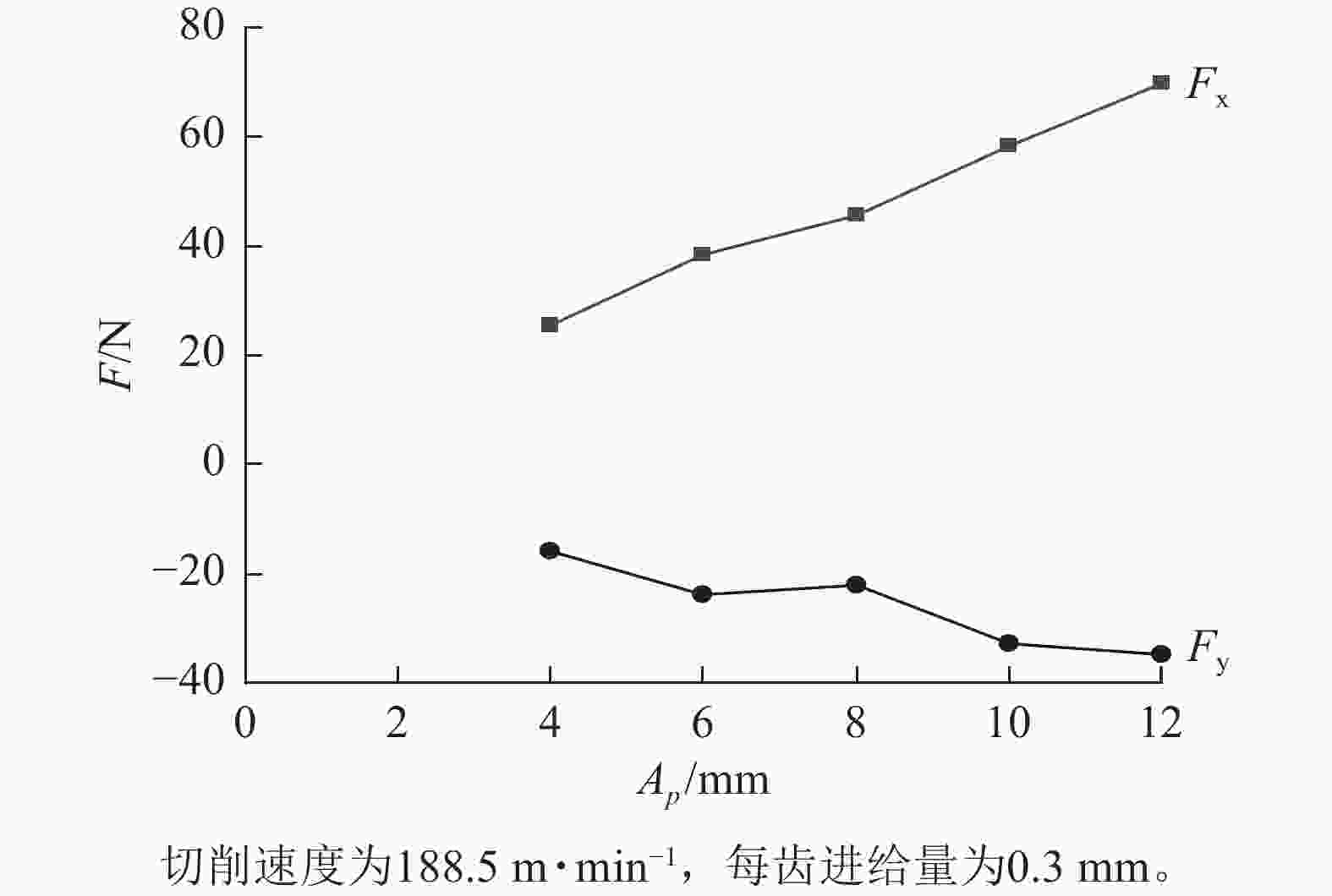
在切削速度为188.5 m·min⁻¹，每齿进给量为0.3 mm，切削步进距为0.4 mm条件下，切削深度与切削力平均值的关系如图8所示。随着切削深度增加，单位时间内切下切屑的体积增大，切削功率也随之增大，因此F_x随切削深度的增加而增大，而F_y随切削深度的增加而减小。

Figure 8.  Influence of cutting depth on cutting force

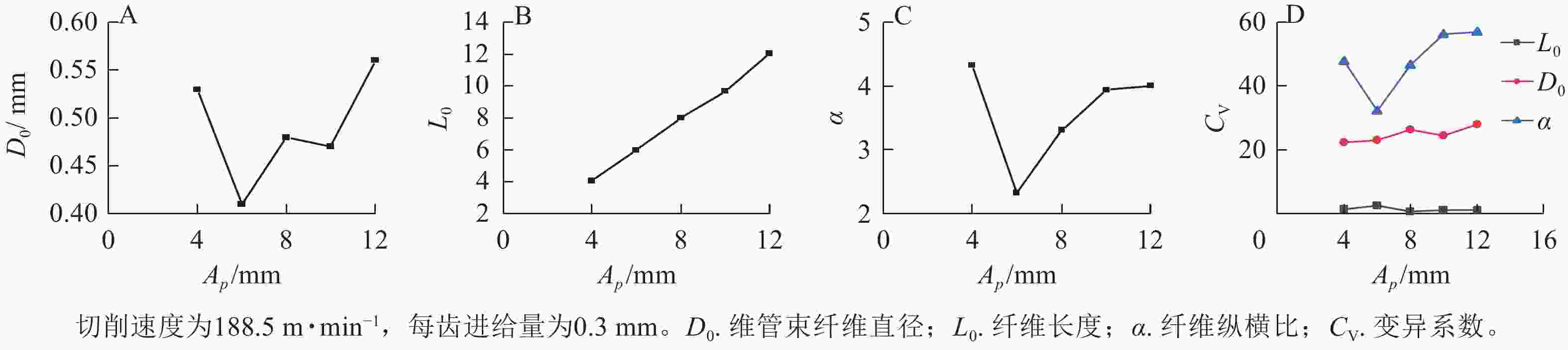
在切削速度为188.5 m·min⁻¹，每齿进给量为0.3 mm, 切削步进距为0.4 mm条件下，切削深度对维管束纤维形态的影响如图9所示。不同切削深度下获得维管束纤维直径变化不大，且为理论值的一半左右(图9A)；维管束纤维长度随切削深度增加而增加，且曲线斜率为1，表明纤维长度与理论值保持一致(图9B)；纤维纵横比随着切削深度增加，呈先下降后上升的趋势(图9C)；图9D为切削深度对纤维形态变异系数的影响，其中纤维长度和纤维直径的变异系数基本保持恒定，纤维纵横比的变异系数先降低后升高且在切削深度大于10 mm后基本保持恒定。综上，增加切削深度有利于获得较高质量的维管束纤维。

Figure 9.  Effect of cutting depth on the shape of bamboo fiber

对切削力正交试验结果进行极差分析，结果如表2所示。由表2可知：切削深度(C)对F_x和F_y的影响最大，切削速度(A)和每齿进给量(B)分别对F_x和F_y的影响最小。因此，可以得到对F_x和F_y影响最小的最优加工参数方案为A₂B₁C₁。

对切削力数据进行方差分析，结果如表3所示。在单向顺铣过程中，切削深度对F_x影响极显著(P＜0.01)，对F_y影响显著(P＜0.05)。每齿进给量对F_x影响显著(P＜0.05)，对F_y影响不显著。切削速度对F_x和F_y切削力影响均不显著。因此，单向顺铣过程中，切削深度是影响切削力的最主要因素，每齿进给量对切削力的影响大于切削速度。方差分析结果与极差分析结果一致，表明正交试验设计的有效性。

对不同切削状态下的切削数据进行多元非线性回归分析^[25−26]。F_x非线性回归方程决定系数(R²)为0.956，说明对应模型能解释95.6%的变异，模型拟合效果很好。F_y非线性回归方程R²为0.697，说明对应模型仅能解释69.7%的变异。

式(3)~(4)中：F_x和F_y为切削分力；A_p为切削深度度；f_z为每齿进给量；V_c为切削速度；R²为决定系数。正交试验与回归方程预测的对比结果如表4所示。F_x的预测值与试验值的误差为±6%左右，说明回归方程具有较高的可靠性。F_y的预测值与试验值的偏差较大，是因为切削刃对竹板反复产生挤压作用，导致切削系统振动。但对比F_y的试验值与预测值可知，预测值与理论值之间的差值在±5 N以内，且F_y的切削力数值相对较小，因此F_y的回归模型能够一定程度上反映其实际切削状态。

为进一步验证回归模型的可靠性，设计各切削要素条件下的非正交试验，试验结果如表5所示。回归方程对各参数的切削力预测与上述非正交试验结果基本一致，说明回归方程具有较高的可靠性。

切削深度对维管束纤维切削力的影响最大，平行于刀具进给方向受力主要为切削力，每齿进给量相对于切削速度对切削力的影响更明显，垂直于刀具进给方向主要受挤压力作用，切削速度比每齿进给量对切削力的影响大。对不同切削状态下的切削数据进行多元非线性回归分析，得到切削力非线性回归模型。试验值与模型预测值的对比结果显示：该模型可以较为准确地计算各方向的切削力。

采用铣削方法可提取长度一致性好的维管束纤维，且可通过控制铣刀的切削深度，得到不同长度的维管束纤维。采用较高切削速度、较大切削深度和较小每齿进给量有助于获得较大长径比和直径的维管束纤维。