-
古树名木是指在人类历史过程中保存下来的具有重要科研、历史、文化价值的树木，是环境的重要组成部分，更是珍贵的不可再生的自然和文化遗产[1]。其文化价值体现在它是区域自然变化及社会发展历史的重要足迹[2]，是研究区域自然地理变迁中植被区系及其演化的活化石[3]，也是研究古代地理和气候的重要依据[4]。自乡村振兴战略提出以来，各地区都把古树名木、古村落、古民居纳入了重点保护对象，这既是对古树名木重要性的体现，同时也说明古树名木集多重价值于一体的综合性作用越来越受到关注。2016年，国家绿化委员会启动全国第二次古树名木普查，建档立户，大多数古树名木重新确立了身份信息。在古树名木普查和乡村振兴战略中最关键的因素是确定古树的树龄，因古树划分标准严格按照自身生长年龄划分，100~299 a为三级古树；300~499 a为二级古树；≥500 a以上的为一级古树。而名木不受年龄限制，且多数树龄有较为清楚的记载。目前，对古树树龄的鉴定主要有文献追踪法、14C交叉定年法、生长锥测定法、CT扫描法等[5-7]，但这些方法存在误差大、成本高、耗时长、破坏性大等缺陷，且树龄较大的古树树干部分存在不同程度的空心、腐烂症状，对树心和年轮取样会造成困难。相关学者对古树树龄的估算研究较少，大多数只分析古树资源特征和分布格局[8]，古树的资源现状和利用[9]，也有学者通过分析梵净山周边地区孑遗植物的古树生长情况与地理分布格局，来解释孑遗植物生境及避难所的具体位置，并提出就地保护策略[10]，而对如何快速、准确估算古树树龄的探索相对缺乏。古树树龄的持续性增长得益于健康的生长环境，无病虫害，还有适合的土壤、水热、光照等是影响古树生理发育的关键因素，而这些因素在地理实体中表现较为密切，不同海拔、不同地理坐标下古树的生长环境差异性较大。古树自身不同生态特征也直观反映古树树龄的大小，如古树的冠幅、胸围和树高不同，其树龄也不尽相同。基于此，本研究对广安市古树名木资源进行了调查，并利用最小二乘法(OLS)模型、地理加权回归模型(GWR)、多元线性回归模型(MRL)等分析了古树树龄与自身生态特征(树高、胸围、平均冠幅)、生长环境(海拔、坡度)之间的回归强度，以期为准确、快捷估算古树树龄提供科学依据。
-
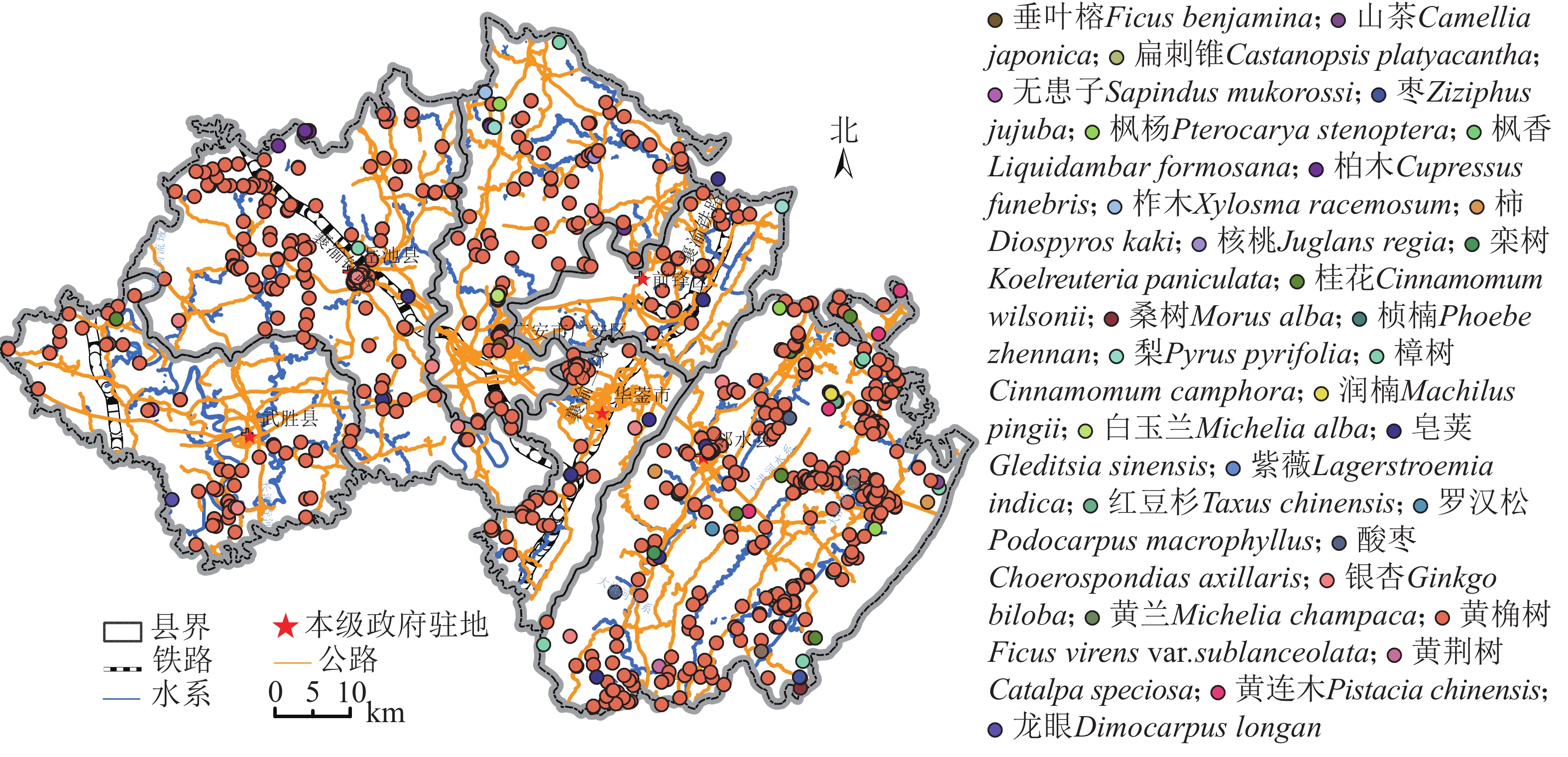
广安市(30°01′~30°84′N，105°56′~107°29′E)位于四川省东部，海拔为195~1 657 m，坡度为0~68°，属典型的川东丘陵地貌区(图1)。该区植被资源丰富，截止目前森林覆盖率达38.5%。古树名木资源有享誉全省的黄桷树Ficus virens var. sublanceolata、银杏Ginkgo biloba、桢楠Phoebe zhennan等。全市古树名木资源主要为黄桷，共计638株，树龄为100~1 500 a，平均树龄为161 a；银杏46株，最小树龄37 a，最大树龄达1 000 a，平均树龄为150 a；柏木Cupressus funebris 32株，树龄为120~350 a，平均树龄为317 a；皂荚Gleditsia sinensis 15株，最小树龄为100 a，最大树龄为250 a，平均树龄为134 a。
图 1 广安市古树名木分布示意图
Figure 1. Distribution of ancient and famous trees in Guang’an City
-
以广安市2017年古树名木普查数据为基准，结合实地调查、复核校正数据为最终研究数据。树高采用深达威手持式激光测距望远镜(SW-1200A)测定，精度±1.00 m；胸围、冠幅采用专业测量皮尺、大型游标卡尺测定，精度分别为±0.50 cm、±0.05 mm。树龄根据LY/2738−2016[11]的文献追踪法、年轮与直径回归估测、针测仪测定法、访谈估测法的顺序测定。
-
数字高程模型(DEM)来源于91卫图助手企业版，空间分辨率为30 m，坐标投影GCS WGS 1984。交通、水系数据来源于地理数据空间云(www.gscloud.cn)。地理经纬度、海拔、坡度信息采用GPS测定。
-
标准差椭圆分布又称利菲弗方向性分布，是定量分析点要素空间分布的常用方法[12]。由方位角、主轴(长轴)、和辅轴(短轴)等要素构成[13]。主轴长半轴代表数据的分布方向，辅轴短半轴代表数据分布的范围。若长短半轴差值越大，则标准差椭圆形状就越扁，数据分布的方向性就越明显，同时，椭圆面积大小可直观反映要素的空间格局集中程度。主要计算公式参见文献[14-15]。
-
地理加权回归是一种用于建模空间变化关系的线性回归的局部形式，作为若干空间回归技术中的一种，越来越多的用于地理学及其他学科。该模型的优点在于能够反映参数在不同空间的非平稳性，使变量间的关系可以随空间位置的变化而变化，其结果更符合客观实际，能真实反映局部变化情况[16-18]。本研究将在最小二乘法(OLS)模型诊断的基础上选择最优模型表达式，借鉴相关文献[19]对模型优化表达。
-
利用筛选后的数据，以树龄为因变量，树高、平均冠幅、胸围、海拔和坡度作为自变量，研究因变量对自变量的影响程度。其模型表达式如：
$y = \sum\limits_{i = 1}^n {{\xi _n}} {x_n} = {\xi _0} + {\xi _1}{x_1} + $ $ {\xi _2}{x_2} +\cdots+ {\xi _n}{x_n}$ 。其中：y表示树龄，${x_1},{x_2},\cdots,{x_n}(n = 5)$ 分别表示树高、胸围、平均冠幅、海拔和坡度，${\xi _0}$ 为常数项或截距，${\xi _1},\cdots,{\xi _n}$ 为回归系数。 -
研究区黄桷树638株，占到全部树种数量的79.85%；银杏46株，占5.75%；柏木32株，占4%；皂荚和桂花分别为15、14株，其他树种均小于10株。根据数据样本容量，选择信息量最大的黄桷树作为建模基础数据，而研究区原始古树名木数据作为空间分布的数据来源。对638株黄桷树的树龄、树高、胸围、平均冠幅、海拔和坡度进行描述性统计分析，并进行异常值剔除，最终得到494株分析样本(表1)。
表 1 广安市古树资源数据处理前后描述性统计表
Table 1. Descriptive statistics of ancient tree resources before and after data processing in Guang’an City
指标 处理前(n=638) 处理后(n=494) 树龄/a 树高/m 胸围/cm 平均冠幅/m 海拔/m 坡度/(°) 树龄/a 树高/m 胸围/cm 平均冠幅/m 海拔/m 坡度/(°) 均值 161.18 55.02 306.64 15.47 350.4 5.11 149.43 53.88 312.15 14.81 347.60 1.18 标准差 78.05 33.89 186.64 6.17 62.94 11.58 45.53 34.40 178.08 5.36 59.42 2.84 偏度 7.03 0.41 0.94 0.51 0.09 3.58 0.99 0.49 0.61 0.18 0.10 2.28 峰度 100.05 −0.65 0.70 0.08 0.04 16.53 0.06 −0.58 −0.61 −0.65 −0.13 3.77 -
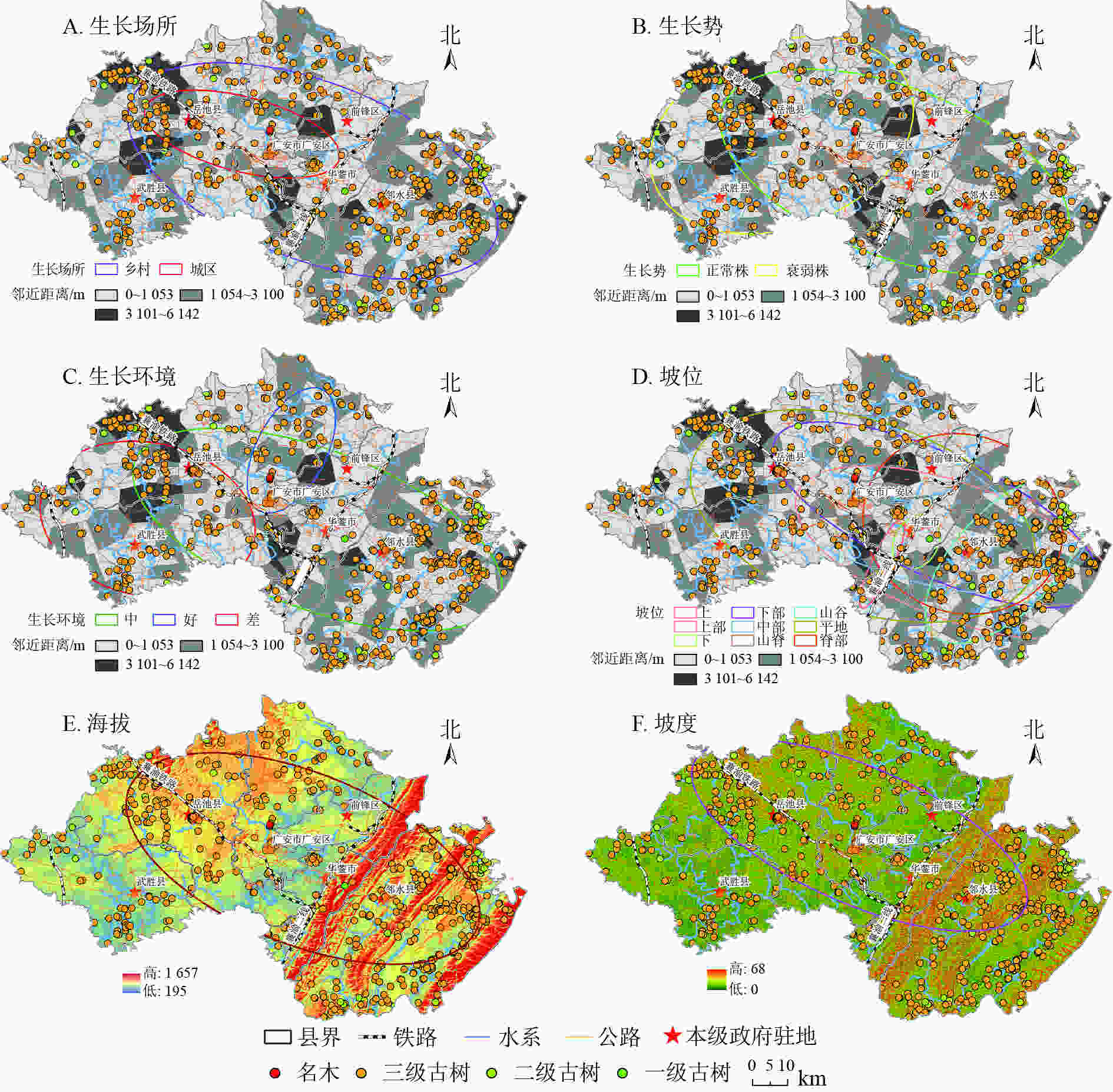
根据古树名木生长位置信息、生长势和周边景观类型，利用ArcGIS 10.6分析古树名木的空间密度和分布方向。由图2A~D可知：古树名木的密集区集中在邻水中部、华蓥南部、前锋中部、广安南部、岳池东部和南部以及武胜南部，且密集区域涵盖了所有政府驻地所在点。稀疏区主要位于华蓥山脉两侧过渡区及岳池县西北部。
图 2 古树名木生态特征方向性空间分布示意图
Figure 2. Directional spatial distribution of ecological characteristics of ancient and famous trees
-
古树名木总体分布以西北的岳池县，横穿广安市、前锋区、华蓥市到东南的邻水县，乡村长轴为0.047，短轴为0.025，扁率为0.469，表明在乡村生长场所主要以东西经向分布；城市生长场所长、短轴分别为0.025、0.010，扁率达0.619，可知古树名木城市生长场所方向性明显。同时，乡村、城市分布面积分别是3 711.687和779.567 km2，说明古树名木80%以上分布在乡村。从生长坡位可知：古树名木主要分布在平地，其次为中部和上部，但坡位分布方向差异较大，上、下、中、山脊、脊部南北纬向分布特别明显，而下部、中部和平地主要以东西经向分布为主。
-
生长势和生长环境是评价古树名木生态状况的2个重要指标。研究区古树名木总体上正常株大于衰弱株，其面积分别为3 407.952和2 746.480 km2。空间分异上正常株主要位于华蓥山山脉东西两侧，涵盖邻水县、华蓥山、前锋和广安南部区；衰弱株则分布在西北方向的岳池、武胜县。其扁率分别为0.490、0.257，表明正常株空间分布方向性更明显。生长环境好的以南北纬向分布，其扁率为−1.142；生长环境中、差的以东西经向分布明显，扁率分别为0.549、0.203。
-
由图2A~2F可知：标准差椭圆覆盖了东南部的大洪河水系、中部的渠江流域、及西部的嘉陵江流域，古树名木沿河分布密集；西部沿邻水县的垫邻高速(垫江—邻水)、304省道分布；中部沿304省道、遂广高速(遂宁—广安)、银昆高速(银川—昆明)分布；西部沿岳广华快速通道、G75兰海高速(兰州—海口)分布。海拔、坡度均是长半轴大于短半轴，方位角分别为117.491°、118.757°，扁率分别为0.498和0.587，表明在海拔和坡度上以高海拔的垂直地带性带状分布明显，同时，东南部高海拔区明显多于西南部低海拔区，经向差异较为突出。
-
标准差椭圆法显示：古树名木涵盖了研究区政府驻地、红色旅游地以及大部分乡镇府所在地，呈以政府驻地为中心向外扩散的圈层结构，尤其是三级古树圈层结构明显(图2A~F)；主要原因是古树名木作为城市生态景观、乡村旅游振兴和红色旅游观光的植被载体具有重大的经济、文化和历史价值，其主体具有多元价值性。同时，也是人类活动变迁、气候变化的重要生态足迹指示器。
-
由表2可知：OLS模型和GWR模型的决定系数(R2)分别为0.249、0.282，GWR模型比OLS模型精度提高了13%，而且阿凯克信息准则(AICc)和Sigma值均比OLS模型小。可见，选择GWR模型，精度更优[20]。因此，本研究对古树树龄估算采用了GWR模型，效果明显优于OLS模型。
表 2 OLS模型和GWR模型结果统计
Table 2. Statistical table of results of OLS model and GWR model
模型 Sigma值 决定系数(R2) 阿凯克信息准则(AICc) OLS 0.636 0.249 5 180.298 GWR 0.485 0.282 5 100.239 -
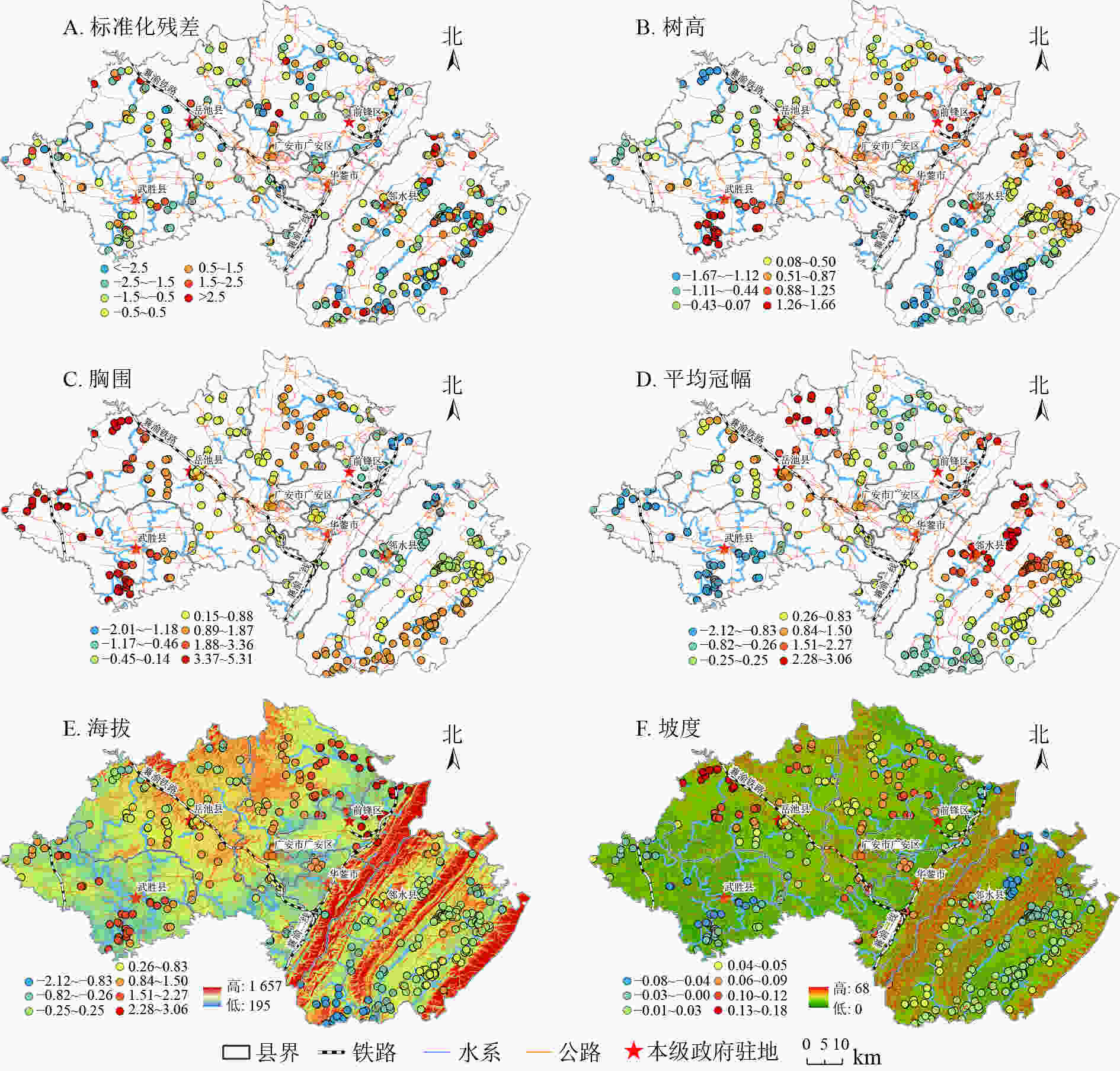
GWR模型回归系数在空间上的变化趋势，可通过样点因变量与各个解释变量之间的空间变异强弱表现出来[21]。结合ArcGIS 10.6中分级色彩，采用自然间断点分级法对GWR模型回归系数进行空间展示(图3A~F)。标准化残差显示：GWR模型残差值在[−2.5，2.5]变动，且大部分区域残差值为[−0.5，0.5]，说明整体模型模拟效果较好。
图 3 GWR模型标准化残差及回归系数空间分布示意图
Figure 3. Spatial distribution of standardized residuals and regression coefficients of GWR Model
-
树高对树龄呈正相关，相关系数为0.111(表3)，空间上呈团簇状分布，差异较为明显(图3B)。前锋区、华蓥市、邻水县北部受树高影响较大，而以华蓥山脉为界的东南部树龄受树高影响较小。中部广安区树高对树龄的回归系数为0.26~1.50，且向西呈递减趋势，到西南部的武胜县树高对树龄的影响又达到最大值。
表 3 古树生态学特征的Pearson相关性分析
Table 3. Pearson correlation analysis of ecological characteristics of ancient trees
指标 树龄 树高 胸围 平均冠幅 海拔 坡度 树龄 1.000 0.111 ** 0.174 ** 0.203 ** −0.012 0.016 树高 0.111 ** 1.000 0.201** 0.457 ** −0.066 0.181** 胸围 0.174** 0.201** 1.000 0.429 ** −0.217** −0.189 ** 平均冠幅 0.203 ** 0.457 ** 0.429 ** 1.000 0.016 0.011 海拔 −0.012 −0.066 −0.217** 0.016 1.000 0.043 坡度 0.016 0.181** −0.189 ** 0.011 0.043 1.000 说明：*表示在0.05水平上相关显著，**表示在0.01水平上相关极显著 -
胸围对树龄呈正相关。胸总体呈低海拔区域向高海拔区域递减，西部总体大于东部，北部大于南部，这与Pearson相关性分析高度一致，海拔与胸围呈显著负相关关系(表3)。
-
平均冠幅对树龄呈高度的正相关关系(表3)。区域间差异较为明显，华蓥山山脉区域的平均冠幅总体影响程度低于西南部的武胜县和岳池县，广安区和岳池县交界处海拔较高地段平均冠幅对树龄影响也较大。表明平均冠幅随着海拔的增加对古树树龄影响的程度在减弱。这与OLS模型中，平均冠幅与树龄、海拔的相关关系极度吻合，同时，与胸围对树龄的空间影响趋同。
-
海拔单一因素对树龄影响较小，总体呈负弱相关关系(表3)。从图3E可知：海拔对树龄的回归系数为−2.12~3.06，广安东部、前锋北部、武胜、岳池区域海拔与树龄呈正相关关系，该区域属研究区内海拔低点，而东部华蓥山脉海拔较高地段普遍回归系数较低。表明海拔对古树树龄的影响较弱、甚至是负相关关系。
-
坡度与树龄呈正相关关系，相关系数为0.016(表3)，华蓥山中部、广安区北部坡度较大区域尤其明显。而武胜地势平坦、坡度较小区域回归系数较弱。表明一定坡度区域对古树生长存续、树龄增加起到积极作用。主要原因是坡度大的区域土壤透水性较好，人类活动影响较小，完全保留了古树自然生长发育、自然新陈代谢和自然生态更新的过程。
-
采用Origin进行多元回归分析显示：树龄(y)与树高(x1)、胸围(x2)、平均冠幅(x3)、海拔(x4)和坡度(x5)的回归方程为
$y = 118.742 + 0.343{x_1} + 0.573{x_2} + 1.267{x_3} - 0.016{x_4} + 0.026{x_5}$ 。多元回归方程自变量标准误均小于0.5，且全部通过5%水平下的t检验，说明模型符合多元回归分析的精度要求。平均冠幅与树龄呈正相关关系。而海拔与回归方程呈负相关关系，树高、胸围、坡度均与树龄回归呈正相关关系。表明古树这一特定时期的综合性景观产物，在积极的人为干扰下，对古树的延续、发育和保护起到了明显促进作用。同时，在实地调查中发现：海拔较低、人口密集区域，古树受到当地政府和相关管理机构重视，对古树做了不同程度的保护措施，如砌树池、土壤改良、松土、挂牌等；而高海拔人口稀少地区古树保护工作较少，部分古树存在树洞空心、树兜腐烂、枝残叶落的衰弱现象，无法及时保护和治理，导致较大年龄的古树自然死亡。 -
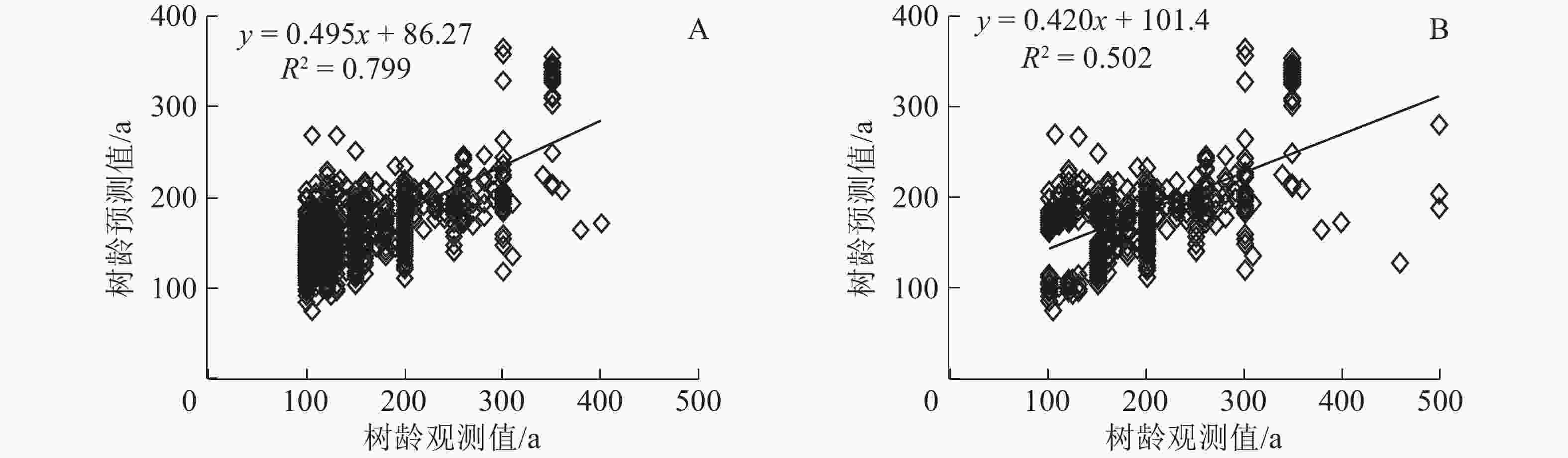
多元线性回归模型(MLR)进行拟合发现：MLR模型的拟合度R2为0.799，拟合精度较高，高于GWR模型的0.502(图4A~B)。MLR模型和GWR模型对300 a以下的树龄拟合效果较好。表明在树龄总体年龄不大(小于300 a)的情况下，模型对树龄的估算精确度较高。
图 4 多元线性回归模型(A)和地理加权回归模型(B)拟合图
Figure 4. Fitting chart of multiple linear regression model (A) and geographical weighted regression model (B)
-
广安市古树名木以政府驻地、交通走廊、水系河流分布为主；乡村古树总量大于城市，地形分布上以平地居多，名木集中分布于红色旅游地。GWR模型综合模拟效果优于OLS模型。且各解释变量回归系数强度空间差异明显，尤其是平均冠幅、胸围、树高对树龄回归响应较强，其中平均冠幅是最大影响因素；海拔与树龄为负相关关系，而坡度与树龄呈正相关趋势。树龄与树高、胸围、平均冠幅、海拔、坡度的多元线性回归方程符合精度要求，且MLR模型各系数回归强度与GWR模型高度一致，模拟精度较高，2种模型都能较好地模拟树龄300 a以下的古树。
Age estimation and spatial distribution characteristics of ancient and famous trees in Guang’an City, Sichuan Province
-
摘要:
目的 广安市古树名木众多。研究古树名木地理分布特征、树龄与生长环境及生态因子间的关系，对古树名木保护具有重要意义。 方法 利用标准差椭圆了解古树名木分布特征，通过地理加权回归模型(GWR)和多元线性回归模型(MLR)模拟树高、胸围、平均冠幅、海拔和坡度对树龄的回归强度。 结果 ①广安市古树名木沿水系、山脉、交通线呈线状分布；政府驻地、红色旅游区向外扩散呈圈层结构；乡村多于城市，平地占主导；正常株多于衰弱株，生长环境适中；高海拔区多于低海拔区，垂直差异明显。②地理加权回归模型优于普通最小二乘法模型(OLS)，平均冠幅、胸围、树高是影响树龄的关键因素，坡度对树龄影响较小，海拔与树龄呈负相关关系。③多元线性回归模型相关系数比地理加权回归模型高0.297，各解释变量与回归变量的系数强度同地理加权回归模型高度一致，且对300 a以下的古树树龄估算精度较高。 结论 标准差椭圆可定量分析古树名木的空间分布特征，地理加权回归模型和多元线性回归模型可准确估算古树树龄。图4表3参21 Abstract:Objective To better protect and preserve the ancient and famous trees in Guang’an City, this study is focused on the geographical distribution characteristics of them and the relationship between tree age, growth environment and ecological factors, which is of vital importance. Method First, the standard deviation ellipse was used to summarize the distribution characteristics of ancient and famous trees. Then, the geographically weighted regression model(GWR) and multivariable linear regression model (MLR)were employed to simulate the regression intensity of tree height, chest circumference, average crown width, altitude and slope to tree age. Result (1) The ancient and famous trees in Guang’an are distributed in a linear pattern along the water system, mountains and traffic lines while in a circular structure along the government residence and the red tourist destinations; more are distributed in the countryside than in the city with flat land as the dominant habitat; there are more normal plants than weak ones with a moderately favorable growing environment; more are distributed in the high-altitude areas than in the low-altitude areas with a significant vertical difference. (2) GWR works better than the ordinary least squares model (OLS); the average crown width, chest circumference and tree height are the key factors that affect tree age; the slope has little effect on tree age and altitude has a negative correlation with tree age. (3) The correlation coefficient of MLR is 0.297 higher than that of GWR. The coefficient intensity of each explanatory variable and regression variable is highly consistent with that of GWR, and the accuracy of estimating the age of ancient trees under 300 a is higher. Conclusion With the employment of standard deviation ellipse, geographically weighted regression model and multivariable linear regression model, the distribution characteristics of ancient and famous trees are better summarized, providing decision-making basis for the estimation of the age of ancient trees and the protection of ancient and famous trees. [Ch, 4 fig. 3 tab. 21 ref.] -
图 2 古树名木生态特征方向性空间分布示意图
拟合椭圆大小代表空间分布范围，椭圆长半轴为生长空间指示方向，短半轴越短代表方向性越明显
Figure 2 Directional spatial distribution of ecological characteristics of ancient and famous trees
图 3 GWR模型标准化残差及回归系数空间分布示意图
Figure 3 Spatial distribution of standardized residuals and regression coefficients of GWR Model
图 4 多元线性回归模型(A)和地理加权回归模型(B)拟合图
Figure 4 Fitting chart of multiple linear regression model (A) and geographical weighted regression model (B)
表 1 广安市古树资源数据处理前后描述性统计表
Table 1. Descriptive statistics of ancient tree resources before and after data processing in Guang’an City
指标 处理前(n=638) 处理后(n=494) 树龄/a 树高/m 胸围/cm 平均冠幅/m 海拔/m 坡度/(°) 树龄/a 树高/m 胸围/cm 平均冠幅/m 海拔/m 坡度/(°) 均值 161.18 55.02 306.64 15.47 350.4 5.11 149.43 53.88 312.15 14.81 347.60 1.18 标准差 78.05 33.89 186.64 6.17 62.94 11.58 45.53 34.40 178.08 5.36 59.42 2.84 偏度 7.03 0.41 0.94 0.51 0.09 3.58 0.99 0.49 0.61 0.18 0.10 2.28 峰度 100.05 −0.65 0.70 0.08 0.04 16.53 0.06 −0.58 −0.61 −0.65 −0.13 3.77 
下载: 导出CSV
表 2 OLS模型和GWR模型结果统计
Table 2. Statistical table of results of OLS model and GWR model
模型 Sigma值 决定系数(R2) 阿凯克信息准则(AICc) OLS 0.636 0.249 5 180.298 GWR 0.485 0.282 5 100.239
下载: 导出CSV
表 3 古树生态学特征的Pearson相关性分析
Table 3. Pearson correlation analysis of ecological characteristics of ancient trees
指标 树龄 树高 胸围 平均冠幅 海拔 坡度 树龄 1.000 0.111 ** 0.174 ** 0.203 ** −0.012 0.016 树高 0.111 ** 1.000 0.201** 0.457 ** −0.066 0.181** 胸围 0.174** 0.201** 1.000 0.429 ** −0.217** −0.189 ** 平均冠幅 0.203 ** 0.457 ** 0.429 ** 1.000 0.016 0.011 海拔 −0.012 −0.066 −0.217** 0.016 1.000 0.043 坡度 0.016 0.181** −0.189 ** 0.011 0.043 1.000 说明：*表示在0.05水平上相关显著，**表示在0.01水平上相关极显著
下载: 导出CSV
-
[1] 贾恒锋, 牟玉梅, 旦增罗布, 等. 西藏尼木县古树年龄鉴定及生长历史分析[J]. 应用生态学报, 2018, 29(7): 2401 − 2410. JIA Hengfeng, MOU Yumei, DANZENG Luobu, et al. Age investigation and growth history analysis of old trees in Nyemo County of Tibet, China [J]. Chin J Appl Ecol, 2018, 29(7): 2401 − 2410. [2] 米锋, 李吉跃, 张大红, 等. 北京地区林木损失额的价值计量研究: 有关古树名木科学文化价值损失额计量方法的探讨[J]. 北京林业大学学报, 2006, 28(增刊 2): 141 − 148. MI Feng, LI Jiyue, ZHANG Dahong, et al. The quantitative estimation of forest tree loss in Beijing: discuss on the computation method of measuring the loss of antique and rare tress, scientific culture value [J]. J Beijing For Univ, 2006, 28(suppl 2): 141 − 148. [3] 邢福武. 中国的珍稀植物 [M]. 长沙: 湖南教育出版社, 2005: 54 − 55. [4] FRITTS H C. Tree Rings and Climate[M]. Caldwell: The Blackburn Press, 2001: 132 − 139. [5] 孟宪宇. 测树学 [M]. 2版. 北京: 中国林业出版社, 1996. [6] 吴祥定. 树木年轮与气候变化 [M]. 北京: 气象出版社, 1990. [7] 王懿祥, 戴文圣, 白尚斌, 等. 古树名木调查方法的改进[J]. 浙江林学院学报, 2006, 23(5): 549 − 553. WANG Yixiang, DAI Wensheng, BAI Shangbin, et al. Improved survey method of ancient and famous trees [J]. J Zhejiang For Coll, 2006, 23(5): 549 − 553. [8] 谢丽宏, 黄钰辉, 温小莹, 等. 广东省新丰江水库古树资源特征与分布格局[J]. 林业与环境科学, 2017, 33(4): 34 − 38. XIE Lihong, HUANG Yuhui, WEN Xiaoying, et al. Resource characteristics and distribution patten of ancient trees in Xinfengjiang reservoir, Guangdong Province [J]. For Environ Sci, 2017, 33(4): 34 − 38. [9] 卢紫君, 刘锡辉, 涂慧萍. 广州市中心城区古树名木的资源现状与开发利用[J]. 林业与环境科学, 2017, 33(1): 77 − 80. LU Zijun, LIU Xihui, TU Huiping. The resources and utilization of ancient and famous trees in central districts of Guangzhou City [J]. For Environ Sci, 2017, 33(1): 77 − 80. [10] LIAO Hongying, REN Mingxun. Distribution patterns of long-lived individuals of relict plants around Fanjingshan Mountain in China: implications for in situ conservation[J]. Collectanea Botanica, 2015, 34: e002. doi: 10.3989/collectbot.2015.v34.002. [11] 国家林业局. 古树名木普查技术规范: Y/2738−2016 [S]. 北京: 中国标准出版社, 2016. [12] 周婷, 牛安逸, 马姣娇, 等. 国家湿地公园时空格局特征[J]. 自然资源学报, 2019, 34(1): 26 − 39. ZHOU Ting, NIU Anyi, MA Jiaojiao, et al. Spatio-temporal pattern of national wetland parks [J]. J Nut Resour, 2019, 34(1): 26 − 39. [13] 蒋金亮, 徐建刚, 吴文佳, 等. 中国人-地碳源汇系统空间格局演变及其特征分析[J]. 自然资源学报, 2014, 29(5): 757 − 768. JIANG Jinliang, XU Jiangang, WU Wenjia, et al. Patterns and dynamics of China’s Human-nature carbon source-sink system [J]. J Nut Resour, 2014, 29(5): 757 − 768. [14] 赵璐, 赵作权. 基于特征椭圆的中国经济空间分异研究[J]. 地理科学, 2014, 34(8): 979 − 986. ZHAO Lu, ZHAO Zuoquan. Projecting the spatial variation of economic based on the specific ellipses in China [J]. Sci Geogr Sin, 2014, 34(8): 979 − 986. [15] FISCHER M M, GETIS A. Handbook of Applied Spatial Analysis[M]. Berlin: Springer-Verlag Berlin Heidelberg, 2010: 27－149. [16] FORTHCOMING A S, CARLTON M, BRONSON C. The geography of parameter space: an investigation of spatial non-stationarity [J]. Geogr Inf Syst, 1996, 10(5): 605 − 627. [17] ANSELIN L. The local indicators of spatial association: LISA [J]. Geogr Anal, 1995, 27(2): 93 − 115. [18] 李记, 徐爱俊. 古树名木旅游最优路线设计与实现[J]. 浙江农林大学学报, 2018, 35(1): 153 − 160. LI Ji, XU Aijun. Design and implementation of the optimal tourist route of ancient trees [J]. J Zhejiang A&F Univ, 2018, 35(1): 153 − 160. [19] 江振蓝, 杨玉盛, 沙晋明. GWR模型在土壤重金属高光谱预测中的应用[J]. 地理学报, 2017, 72(3): 533 − 544. JIANG Zhenlan, YANG Yusheng, SHA Jinming. Application of GWR model in hyperspectral prediction of soil heavy metals [J]. Acta Geogr Sin, 2017, 72(3): 533 − 544. [20] BRUNSDON C, FOTHERINGHAM S, CHARLTON M. Geographically weighted regression-modelling spatial non-stationarity [J]. J Royal Stat Soc, 1998, 47(3): 431 − 443. [21] 杨晴青, 刘倩, 尹莎, 等. 秦巴山区乡村交通环境脆弱性及影响因素: 以陕西省洛南县为例[J]. 地理学报, 2019, 74(6): 1236 − 1251. YANG Qingqing, LIU Qian, YIN Sha, et al. Vulnerability and influencing factors of rural transportation environment in Qinling-Daba mountainous areas: a case study of Luonan county in Shaanxi Province [J]. Acta Geogr Sin, 2019, 74(6): 1236 − 1251. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20190585
点击查看大图
图(4) / 表(3)
计量
- 文章访问数: 1634
- HTML全文浏览量: 270
- PDF下载量: 105
- 被引次数: 0
