-
树种混交是群落发育过程中种群与环境、种群与种群之间长期相互作用的结果。Gadow等[1]提出群落混交程度越大反映出其结构越稳定，生物多样性保护成为森林可持续经营的一个重要指标[2]。定量度量树种混交程度的指标是评价群落结构稳定性的重要依据，如多样性、分离指数、混交度等指标。Fisher等[3]提出的多样性对物种丰富程度进行有效地度量，但缺乏对物种间的空间分布作出明确判定；Pielou[4]提出的分离指数仅说明了2个种的个体分离情况；Gadow等[5]首次提出反映整个混交林中不同树种之间隔离程度的空间结构特征的混交度概念，是评价混交林中林木空间分布格局的重要指标，受到不少研究者的关注。惠刚盈等[5]通过分析对象木与最近相邻林木之间的树种差别提出了传统混交度的概念，并对一些典型混交林进行分析，由于该模型只考虑了单一的影响因子，计算结果不能完全准确的区分不同混交程度的混交林。学者通过增加参考因子来不断修正混交度模型，如，汤孟平等[6]通过分析考虑对象木周围邻近林木的树种差异对混交度的影响，在传统混交度的基础上提出树种多样性混交度的概念；惠刚盈等[7]通过考虑对象木与最近相邻木之间的树种差别以及不同树种的种类数之间的相关关系用来描述相邻木之间的树种分隔程度；汤孟平等[8]通过引入生物多样性指数并提出全混交度的概念，它充分考虑了不同树种、株数对混交度的影响等。这些研究成果为计算混交度提供新思路，但是由于缺乏对一些局部因子的考虑，使得对一些本身混交程度不同的林分所得到混交度却也有可能相等，如对于任意一个结构单元来说，多数混交度却不能够正确描述出完全混交时的状态。常新华等[9]发现不同树种的林木绝大多数在空间距离上都呈现随机分布，使得混交林的空间结构十分复杂。在混交林中，计算任意一个结构单元中对象木的混交度时，不同的林木的组成与空间分布都对其有很大的影响。目前这些对混交林混交度计算的方法都还存在一些不足。本研究在比较分析各种混交度计算方法的基础上，综合考虑相关影响因子，提出一种满足区分任意一个结构单元混交度的改进型混交度模型。
-
混交度调查一般是从局部到整体进行计算，把林中所有单株林木逐一作为对象木，并选取周围邻近木作为一个结构单元，通过一定的计算方法计算出所有单株林木的混交度，再通过计算所有单株林木混交度的均值得出整个混交林的平均混交度。对于纯林，由于其树种单一，不存在不同树种之间的混交，其混交度为0；对于完全混交林，在任一结构单元内，所有林木树种都不相同，其混交度为1。所以，任意一片混交林的混交度都应该在[0, 1]之间，对于混交程度愈强烈的混交林其混交度的值也愈大。整个混交林混交度计算方法如下[5]：
$$\bar{M}=\frac{1}{N}\sum\limits_{i=1}^{N}{{{M}_{i}}}$$ (1) 式(1)中：M为整个混交林的平均混交度，N为林分中所有林木株数，Mi为单株林木混交度。不同混交度计算方法的主要区别就在于单株林木混交度的计算。
-
惠刚盈等[5]通过研究分析发现，当在对象木周围选取4株最近邻木一起作为一个结构单元即可满足对象木的混交度计算，并提出传统混交度的概念用来计算单株林木混交度Mi，其主要通过对象木与周围邻近林木的树种差别比较来计算对象木的混交度。计算方法如下：
$${{M}_{i}}=\frac{1}{n}\sum\limits_{i=1}^{n}{{{V}_{ij}}}$。$ (2) 式(2)中：n为目标树最近林木株数；Vij是以目标树为中心，周围林木树种与目标树树种比较结果，不同记为1，相同记为0。传统混交度概念的提出为林分中不同树种之间的混交程度调查提供了依据。
-
汤孟平等[6]研究发现，在一个结构单元中对象木周围邻近木的树种差别对混交度也有一定影响，而传统混交度缺乏考虑，这使得原本不同树种类型组成的混交林的混交度计算结果可能相等。通过考虑这一因素，汤孟平等在传统混交度的基础上提出树种多样性混交度(Mi0)。其计算方法如下：
$${{M}_{i0}}\text{=}\frac{{{n}_{i}}}{n}\times \frac{1}{n}\sum\limits_{i=1}^{n}{{{V}_{ij}}}$$ (3) 式(3)中：ni是对象木i的n株最近林木种类，Vij与传统混交度中相同。
将式(2)和式(3)对比可以发现，树种多样性混交度在计算方法相当于在传统混交度计算方法的基础上添加一个限制参数ni/n，描述邻近木树种所占比例，这样就能体现出邻近林木不同树种数对混交度的影响。当n取4时发现单木混交度的计算结果从传统混交度中只有5种混交类型增加到11种，使其能够描述出更多不同的混交类型，可以区分出更多的混交林类型。
-
惠刚盈等[7]在一个有4株邻木的结构单元中计算对象木的混交度时发现，树种多样性混交度混淆了对4株邻木中有3株相同种和4株邻木中有2株相同种的对象木混交度，使原本混交程度不同的结构单元所得到的对象木混交度却相同。在此基础上，通过将整个结构单元中的树种数作为研究对象提出了物种空间状态(Msi)的概念，用来反映结构单元中对象木与邻近木的分隔程度。其计算方法如下：
$${{M}_{si}}=\frac{{{S}_{i}}}{5}\times \frac{1}{n}\sum\limits_{j=1}^{n}{{{V}_{ij}}}$。$ (4) 式(4)中：Si表示结构单元中的树种数，n为邻近木株数，Vij与传统混交度中相同。
将式(3)和式(4)对比可以发现，在结构单元中计算树种类型所占比例时，只考虑邻近木树种差别，而将对象木的树种类型也考虑在内。同样使单株林木的混交度类型也达到了11种，区分度较传统混交度有明显地提高。
-
通过分析发现虽然将对象木树种类型添加到混交度的计算当中，但其并没有真正解决在树种多样性中混交度中所出现的混交度混淆问题。汤孟平等[8]引入生物多样性Simpson指数，提出了全混交度(Mci)的概念。其计算方法如下：
$${{M}_{ci}}=\frac{1}{2}\left( {{D}_{i}}+\frac{{{c}_{i}}}{{{n}_{i}}} \right)\times {{M}_{i}}$$ (5) 式(5)中：${{M}_{i}}=\frac{1}{n}\sum\limits_{j=1}^{{{n}_{i}}}{{{V}_{ij}}}$，其中ni是对象木的最近邻木株数；ci是最近邻木中相邻木成对的非同种的对数；Di是空间结构单元的Simpon指数，${{D}_{i}}=1-\sum\limits_{j=1}^{{{s}_{i}}}{p\underset{j}{\mathop{2}}\,}$，表示树种分布均匀度；pj是空间结构单元中第j树种所占比例；si是空间结构单元的树种数。
通过式(3)和式(4)对比发现，全混交度在计算对象木的混交度时不仅考虑了结构单元内的树种差别和树种种类，同时也考虑了任意2株相邻邻近木的种类差别对混交度的影响。不仅很好地解决了树种多样性混交度中存在的混交度混淆问题，也使混交度的计算更加精确。
-
在混交林中计算任意一株对象木的混交度时，在结构单元中，当对象木与周围邻近木所有的林木树种类型都不相同时，对象木与周围邻近木的混交程度达到最大，其混交度等于1。全混交度的计算公式中虽然通过添加生物多样性指数体现不同树种株数对混交度影响，但却忽略了当对象木处于完全混交状态时的混交度值的大小，使其计算所得到的对象木混交度结果实际并不等于1，而是随着邻近木株数n的变化而发生变化，当n分别取3，4，5时，混交度最大时所对应的混交度分别为0.875，0.900和0.920。
在一个结构单元当中，通过树种之间的相互比较，可以得到树种数及不同树种所对应株数。从统计学角度出发，对任意一种树种，当它对应不同株数时，相同树种的对数都会不一样，这样就能够通过不同树种之间的对数与整个单元总的比较次数的比值反映出不同树种株数对混交度的影响。本研究在此基础上，提出一种新的能够明确描述混交林空间隔离状态的结构指数，即改进型混交度(Mwi)。其计算方法如下：
$${{M}_{wi}}=\frac{1}{2}\left( {{p}_{i}}+{{w}_{i}} \right)\times {{M}_{i}}$$ (6) 式(6)中：${{p}_{i}}=\sum\limits_{i=1}^{n\left( n+1 \right)/2}{{{m}_{i}}}/C_{n+1}^{2}$，是单个结构单元中的任意2株林木树种比较相异的累积值与总比较次数的比值。当树种相异时mi取1，反之取0；Pi体现了结构单元中不同树种类型及不同株数对混交度的不同影响，当树种完全混交时P
i值取1，只有1个树种时Pi取0；${{w}_{i}}=\sum\limits_{i=1}^{n}{{{n}_{i}}}/n$是对象木周围n株邻近木中成对相邻木树种不同所占比例，当树种相同ni取0，反之取1，能够很好地体现出邻近木相同树种的不同空间分布对混交度的影响，空间分布不同wi的值也不一样；${{M}_{i}}=\frac{1}{n}\sum\limits_{j=1}^{n}{{{V}_{ij}}}$。 改进型混交度解决了传统混交度和树种多样性混交度所忽略的树种株数对混交度的影响：当树种完全混交时其混交度也达到最大值1。依据惠刚盈提出的“结构4组法”，即选取4株最近邻木与对象木作为一个结构单元，这样不仅方便其单株林木混交类型达到了17种，多于一般混交度的单株林木混交度类型。
-
本研究主要通过构建由3种树种、4种树种和多种树种分别组成的不同的典型混交林类型，用4种不同的混交度的计算方法对这些不同混交程度的混交林进行比较，并用改进型混交度计算模型对天目山样地调查数据进行分析。
-
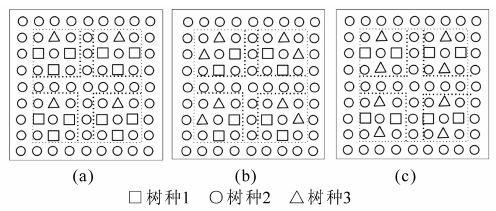
图 1中(a)(b)(c)都是由3种树种组成的典型混交林。它们之间的主要区别是中对象木周围邻近林木之间的各树种的株数及树木分布不同(虚线内)。其中，(a)中对象木的邻近林木2种树种分别是1株和3株；(b)(c)中对象木的邻近林木2种各为2株，(b)中同种树种连续分布，(c)中2种树种间隔分布。3种情况下的物种多样性相同，而邻近木的株数和顺序有所差异，从树种多样性和混交均匀程度可以发现3种混交林的混交程度是(c)最强，(a)最弱。
图 1 3种树种的典型混交林1
Figure 1. A typical mixed forest with different tree species
图 2是由3种树种以不同的混交模式组成的2种不同混交程度的典型混交林。其中，(a)中是3种树种按顺序整列交替混交；(b)中先是树种1和树种3单株交替混交，然后再同树种2进行整列交替混交。2种情况下其物种多样性相同，而不同树种之间的空间排列差异明显，明显可以看出(b)的混交程度比(a)强。
图 2 3种树种的典型混交林2
Figure 2. Another typical mixed forest with three kinds of tree species
图 3是由4种树种组成的不同混交类型的2种典型混交林。(a)中是4种树种一起呈“S”型交替混交；(b)中先是树种1与树种3单株交替混交、树种2与树种4单株交替混交，然后2列交替混交。2种情况下其物种多样性相同，而不同树种的空间排列格局不同，(b)中林木分布得更加均匀，其混交程度也强于(a)。
图 3 4种树种典型混交林
Figure 3. A typical mixed forest with four tree species
图 4是由多种树种组成的典型混交林。该混交林中对于任一个结构单元，对象木与周围邻近林木的树种都互不相同，每一个结构单元的林木都是完全混交状态，对于整个混交林来说混交程度已经达到最大，其混交度应该为1。
图 4 多种树种典型混交林
Figure 4. A typical mixed forest with 8 tree species
-
在天目山选取3块样地，其中2块为天然针阔混交林，第3块内绝大部分为杉木Cunninghamia lanceolata，极少其他阔叶树种，记录样地内每株林木的树种类型及林木相对坐标，调查数据见表 1。
表 1 实际样地调查数据
Table 1. Field data
样地号 样地大小/(m×m) 树木/株 树种类型 主要树种 1 30×30 97 12 枫香 Liquidambar formosana，杉木 Cunninghamia lanceolata，马尾松
Pinus massoniana，白栎 Quercus fabri，山合欢 Albizia kalkora 等2 30×30 114 14 枫香，杉木，马尾松，白栎，山合欢，木荷：chimasuperba等 3 30×30 131 6 杉木，苦储 Castanopsis sclerophylla，楓香等 -
为了消除边缘效应给计算带来的不便，所有混交林的混交度计算都只包括除最边缘林木的其他林木。分别用4种不同计算混交度的方法计算上述不同混交林的混交度，所得结果见表 2和表 3。
表 2 实验样区的5种混交度计算结果对比
Table 2. Compared five kinds of mixed degree calculation results in experimental sample region
表 3 实测数据4种混交度计算结果对比
Table 3. Compared four kinds of mixed degree calculation results in field data
样地号 传统混交度 树种多样性混交度 空间测度指数 改进型混交度 1 0.912 0.824 0.836 0.746 2 0.927 0.829 0.841 0.749 3 0.562 0.463 0.472 0.162 -
传统混交度计算结果分析。能够很好地区分按照顺序排列的3种树种构成的混交林(图 2)，但是由3种树种(图 1)，4种树种以不同方式混交(图 3)所计算得出的混交度分别都为0.612和1.000，表明它们没有正确区分出不同混交程度的混交林。由于只考虑了对象木与邻近木树种差异，难以区分邻近木之间树种差异对混交度的影响，缺乏对比性，影响了混交度计算的准确性。
树种多样性混交度的计算结果分析。由3种树种以不同的方式进行混交所得混交度均为0.250(图 1)和0.375(图 2)；4种树种以不同方式混交(图 3)所得到的混交度均为0.500，也没能够区分出不同混交程度的混交林。结果表明：当邻近木树种多样性一致，但不同树种株数与空间分布存在差异时，树种多样性混交度难以进行区分。
空间测度指数结果分析。从表 2中可以发现空间测度指数所得到的结果与树种多样性混交度的结果类型基本一致，由于Si中考虑了对象木树种类型，使得数值大小发生了变化，但对于混交程度不同的混交林依然没有正确区分。
全混交度的计算结果分析。对于3种或4种树种组成的混交林，它都能够将它们正确区分。当一片混交林处于完全混交的状态时(图 4)，它不能够得到真实的混交度结果，即计算结果不为1。对于一片天然林来说，在一个结构单元里存在完全混交的可能性非常大，这也就使得混交度值会偏低。
改进型混交度的计算结果分析。从图 1至图 4中，对于每一种以不同方式混交的混交林计算所得出的混交度都不相同，并且混交度值的大小与文中所分析的混交强烈程度一致，能够正确区分出由物种多样性、树种不同空间排列组合差异产生的不同混交程度的混交林。
从各种不同混交林所得到的混交度结果来看，改进型混交度的结果与实际相符，随着混交程度的增加而增加，避免了传统混交度和树种多样性混交度那样具有很高的重复性，也并没有像全混交度那样缺少完全混交类型。本实验样区通过由不同树种类型及空间分布构建出不同混交程度的混交林得出改进型混交度要优于其他几种混交度的计算方法。
-
由表 3可见：样地1和样地2的天然针阔混交林由于树种丰富使其不同树种之间的隔离程度明显强于树种数较少的样地3。由于样地3内树种比较少，绝大多数为杉木，可以近似看成杉木纯林，其树种之间隔离程度应该接近0，但传统混交度、树种多样性混交度、空间测度指数所得出的混交度结果明显偏高，显然不符合实际，而改进混交度的计算结果与实际比较接近，显示弱度分隔程度。可见，改进型混交度更能恰当地表达树种分隔程度。
-
混交林中树种之间的隔离程度由树种类型及其不同树种数量和空间分布共同决定，不同的混交类型有不同的混交度。一般来说，树种类型越多，其混交程度也越大。本研究提出的改进型混交度算法考虑了对象木周围邻近木之间树种差别、邻近林木之间树种种类及邻近林木树种的空间分布差异对混交度的影响，通过理论样地与实测样地数据的验证分析，其值域在[0, 1]之间，0代表着纯林的隔离程度，1代表完全混交林的隔离程度。该方法克服了其他混交度算法的缺陷，能够正确区分出不同混交程度林分的混交度，使得计算结果更准确、精度更高，能更客观地反映混交林中不同树种之间的隔离程度，是一个比较理想的混交林混交程度调查的指数。
本研究主要是基于结构单元中不同树种类型及其林木空间分布特征所展开的混交度记算，邻近木的选取过程中并没有考虑林木之间距离是否对混交度有所影响，希望在以后的研究中对此进行分析使得混交度算法进一步完善。
Spatial structure and species diversity with an improved mingling index
-
摘要: 混交度是描述混交林中不同树种之间隔离程度的重要空间结构指数。由于忽略对象木周围邻近木的空间分布,传统混交度、树种多样性混交度和树种分隔程度空间测度指数在计算混交度时,使得一些不同混交程度混交林具有相同混交度;全混交度对只有几株对象木的结构单元,不能够体现出完全混交的状态。这些给混交林的混交度调查和不同混交林之间的混交度比较带来困难。鉴于此,依据物种空间结构特征和树种多样性,考虑结构单元中树种类型及分布差异,提出一种更具普遍意义的改进型混交度。通过不同的理论典型混交林和天目山不同混交程度的样地数据对不同混交度指数进行对比分析。结果得到:①对于混交程度不同的混交林,改进型混交度计算结果不同;②对于混交程度不是很强烈的混交林,改进型混交度描述更加准确。所以,该混交度是一个很好区分混交林的空间结构指数。Abstract: Mingling is an important spatial structure to describe the degree of segregation in mixed forests. Due to ignore the spatial distribution of trees around the object tree,traditional mingling, species diversity mingling and the tree species segregation index may have an equal mingling in mixed forests with different mixed degree. Complete mingling has not accurately described a fully mixed forest when there are few adjacent trees in a unit. Thus,mingling research for an entire mixed forest as well as a mingling index for comparison of different mixed forests was problematic. To surmount these obstacles,an improved mingling index was proposed based on two factors:1)species spatial structure characteristics together with species diversity,and 2)the influence of tree species types and distribution differences within a unit. Comparative analyses of different mingling indices were carried out based on typical mixed forests in theory and different mixed degree's field data in Mount Tianmu. The results show:1)the improving mingling has different mingling for the mixed degree of different forest;and 2)it can describe forest mingling of mixed forests which have low mixed degree more accurately. So it is an available mixed forests spatial structure index.
-
Key words:
- forest mensuration /
- species diversity /
- species space structure /
- mingling /
- improved mingling
-
图 2 3种树种的典型混交林2
Figure 2 Another typical mixed forest with three kinds of tree species
表 1 实际样地调查数据
Table 1. Field data
样地号 样地大小/(m×m) 树木/株 树种类型 主要树种 1 30×30 97 12 枫香 Liquidambar formosana，杉木 Cunninghamia lanceolata，马尾松
Pinus massoniana，白栎 Quercus fabri，山合欢 Albizia kalkora 等2 30×30 114 14 枫香，杉木，马尾松，白栎，山合欢，木荷：chimasuperba等 3 30×30 131 6 杉木，苦储 Castanopsis sclerophylla，楓香等 
下载: 导出CSV
表 2 实验样区的5种混交度计算结果对比
Table 2. Compared five kinds of mixed degree calculation results in experimental sample region
下载: 导出CSV
表 3 实测数据4种混交度计算结果对比
Table 3. Compared four kinds of mixed degree calculation results in field data
样地号 传统混交度 树种多样性混交度 空间测度指数 改进型混交度 1 0.912 0.824 0.836 0.746 2 0.927 0.829 0.841 0.749 3 0.562 0.463 0.472 0.162
下载: 导出CSV
-
[1] von GADOW K,FUELDNER K. Strukturentwicklung eines Buchen-Fichten-Misch[J]. Allg For J Ztg,1997,168(6/7):103-106. [2] 雷向东,唐守正. 林分结构多样性指标研究综述[J]. 林业科学,2002,38(3):20-22. LEI Xiangdong,TANG Shouzheng. Indicators on structural diversity within-stand:a review[J]. Sci Silv Sin,2002,38(3):20-22. [3] FISHER R A,CORBET A S,WILLIAMS C B. The relation between the number of species and the number of individuals in a random of an animal population[J]. Ecology,1943,12:42-58. [4] PIELOU E C. Segregation and symmetry in two-species populations as studied by nearest neighbor relations[J]. Ecology,1961,49:255-269. [5] 惠刚盈,胡艳波. 混交林树种空间隔离程度表达式方式的研究[J]. 林业科学研究,2001,14(1):23-27. HUI Gangying,HU Yanbo. Measuring species spatial isolation in mixed forests[J]. For Res,2001,14(1):23-27. [6] 汤孟平,唐守正,雷相东,等. 2种混交度的比较分析[J]. 林业资源管理,2004,8(4):25-27. TANG Menping,TANG Shouzheng,LEI Xiangdong,et al. Comparison analysis on two minglings[J]. For Resour Manage,2004,8(4):25-27. [7] 惠刚盈,胡艳波,赵中华. 基于相邻木关系的树种分隔程度空间测度方法[J]. 北京林业大学学报,2008,30(4):131-134. HUI Gangying,HU Yanbo,ZHAO Zhonghua,et al. Evaluating tree species segregation based on neighborhood spatial relationships[J]. J Beijing For Univ,2008,30(4):131-134. [8] 汤孟平,娄明华,陈永刚,等. 不同混交度指数的比较分析[J]. 林业科学,2012,48(8):46-53. TANG Mengping,LOU Minghua,CHEN Yonggang,et al. Comparative analyses on different mingling indices[J]. Sci Silv Sin,2012,48(8):46-53. [9] 常新华,赵秀海,曾凡勇,等. 长白山针阔混交林主要树种空间分布及其环境解释[J]. 北京林业大学学报,2009,31(1):7-12. CHANG Xinhua,ZHAO Xiuhai,ZENG Fanyong,et al. Spatial distribution of main tree species and their environment interpretations in conifer and broadleaved mixed forests of Changbai Mountains,northeastern China[J]. J Beijing For Univ,2009,31(1):7-12. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2014.03.002
点击查看大图
图(4) / 表(3)
计量
- 文章访问数: 2725
- HTML全文浏览量: 383
- PDF下载量: 633
- 被引次数: 0
