-
树高和胸径是反映林木生长状况的2个基本且重要的数量指标，然而在外业调查中，树高测量困难，耗时费力且测量结果误差较大。目前，获取树高数据的方法主要有利用测高器直接测量和通过树高曲线模型间接推算2种，但利用测高器进行测量时对该点的地势、立地等有一定的限制要求，且测量结果受人为操作影响较大[1]，因此，目前使用较多的还是树高曲线模型推算法。与树高获取相比，胸径数据具有获取简单、准确等优点，且胸径和树高间存在一定的生物学关系，利用这种密不可分的联系建立合理的树高曲线模型则能有效地推算林分的树高。国内外学者对树高生长模型已经进行了广泛研究，如关于落叶松Larix gmelinii[2-4]，马尾松Pinus massoniana[5]和红松Pinus koraiensis[6]等的树高曲线的报道已有很多，但这些研究多集中在单木水平[7-10]和径阶水平层面，而像2015年高东启等[11]考虑树高、胸径与年龄三者之间的相关关系从而建立蒙古栎Quercus mongolica林分树高曲线这样从林分水平对树高曲线进行的研究较少。杉木Cunninghamia lanceolata是中国特有的针叶商品材树种，在中国南方地区栽培广泛，具有生长快、材质好、经济价值高等优点。众多学者对杉木的胸径、树高、材积生长规律等方面进行了大量深入研究[12-13]。2012年魏晓慧等[14]针对福建杉木人工林建立了Richards树高生长模型，模型的预估能力大幅度提升。2016年姜鹏等[15]先按生长势对杉木成熟林进行分级再对其树高曲线进行研究，对指导杉木的营林生产起到了积极作用。然而，对不同林分起源的杉木树高曲线研究较少。笔者在前人研究的基础上，以湖南省杉木为例，引入以林分起源为特征的哑变量，运用度量误差模型方法，将天然林和人工林合并起来建立林分树高曲线方程组，使得树高、胸径、年龄3个因子互相预测时保持相容性和一致性，并将天然林和人工林不同林龄段的生长状况进行对比分析，以期为湖南省杉木林分的生长和收获预估提供可靠理论依据。
-
湖南省地处长江中游，25°46′~29°38′N，108°47′~114°15′E，全省地貌以山地、丘陵为主。气候类型为大陆性亚热带季风气候，全年日照充足，热量丰富，雨水充沛。湖南省植物资源丰富，种类繁多，主要树种有马尾松，水杉Metasequoia glyptostroboides，樟树Cinnamomum camphora等，此外有银杏Ginkgo biloba，红豆杉Taxus chinensis，珙桐Davidia involucrata等60多种珍贵树种。杉木在湖南全省均有分布，其西南地区是全国著名产地之一。
-
本次研究所用数据为湖南省第6，7，8次3期一类连续清查数据。从数据库中挑选杉木样地，所选样地均为固定复测样地，面积为0.066 7 hm2[16]。剔去记载不详、数据离散异常的样地，最后选出157块样地，其中天然林62块，人工林95块。样地的基本情况如表 1所示。从157块样地中随机抽取119块建模，其中天然林47块，人工林72块；剩余38块样地用于检验，其中天然林15块，人工林23块。
表 1 样地基本情况
Table 1. Basic situation of plots
样地类别 样地数/块 平均年龄/a 平均胸径/cm 平均树高/m 最小 最大 平均 最小 最大 平均 最小 最大 平均 天然林 62 8 47 21 7.1 17.9 11.5 5.3 12.4 8.6 人工林 95 6 50 22 6.5 18.9 12.1 4.5 14.3 9.1 建模样地 119 6 50 23 6.5 18.9 12.0 4.5 13.9 9.0 检验样地 38 6 40 18 7.2 17.5 11.3 4.8 14.3 8.6 -
用来拟合林分生长过程曲线的方程很多，有Schumacher模型、对数型模型、幂函数模型等经验方程和Logistic模型、Mitscherlich模型、Korf模型等理论方程。本研究选取6种常用经验模型对杉木树高生长曲线和胸径生长曲线进行初步拟合，具体模型如表 2所示，同时考虑到林分生长到胸高位置需要一定的年限，故将经验模型进行一定变换作为最终拟合模型。现以Richards方程为例，林分树高曲线方程和胸径生长过程曲线方程的表达式如下：
表 2 常见林分生长过程经验模型
Table 2. Common experience models of stand growth process
模型序号及名称 模型形式 (1) Logistic模型 y=a/[1+bexp(-ct)] (2) Richards模型 y=a [1-exp(-ct)]b (3) Weibull模型 y=a[1-exp(-bt)] (4) Korf模型 y=a exp(-btc) (5) Mitscherlich模型 y=a [1-bexp(-ct)] (6) Schumacher模型 y=aexp(-b/t)] $$ H = 1.3 + a{\left[{1-\exp \left( {-cD} \right)} \right]^b}; $$ (1) $$ D = a{\left[{1-\exp \left( {-c{\rm{ }}\left( {T-{T_{1.3}}} \right)} \right)} \right]^b}。 $$ (2) 式（1）和式（2）中：D为林分平均胸径（cm）；H为林分平均树高（m）；T为林分平均年龄（a）；T1.3为林木生长到胸高时的年龄（由林分平均树高生长曲线推算而得）；a，b，c为待估参数。
-
一般情况下，回归模型都是在自变量的观测值不含误差而因变量的观测值有误差的条件下成立的。导致误差的因素有多种，如抽样方法和测量仪器等，这类误差统称为度量误差。如果自变量和因变量的观测值中均含有误差，则不能再用普通的回归模型估算方法，而必须采用度量误差模型方法[17]。通常在研究林分树高曲线时，假设不含误差的自变量林分胸径的观测值是可能存在抽样或观测等度量误差的，因为林分胸径一般由单木胸径推算而来，此时应使用度量误差方法对其进行研究。以往对于树高曲线和胸径生长过程曲线都是单独建模的，很少考虑它们之间的相关性，事实上林分的平均胸径、平均树高和年龄三者不是相互孤立而是相互关联的，以林分平均胸径D作为桥梁，就可以把树高曲线、胸径生长过程曲线和树高生长过程曲线三者紧密地联系到一起，从而达到保证三者相容性的目的，为此可采用误差变量联立方程组[18-20]。
多元非线性误差变量联立方程组，也称非线性度量误差模型的向量形式为[21]:
$$ \left\{ \begin{array}{l} f\left( {{y_i}, {x_i},c} \right) = 0\\ {Y_i} = {y_i} + {e_i}, i = 1, 2, \cdots, n。\\ E\left( {{e_i}} \right) = 0, {\mathop{\rm cov}} \left( {{e_i}} \right) = {\sigma ^2}\varphi \end{array} \right. $$ (3) 式（3）中：xi是q维无误差变量的观测数据，yi是p维误差变量的观测数据，f是m维向量函数，Yi是yi的未知真值，c是参数，ei是度量误差，E（ei）是ei的期望，cov（ei）=σ2φ渍为误差的协方差矩阵，其中φ渍是ei的误差结构矩阵，σ2为估计误差。
本研究中将式（1）和式（2）联立构成式（4）树高曲线联立方程组。式（4）中的林分胸径（D）是由单木胸径推算而来的，林分树高（H）是估测的，因此将D和H作为误差变量，T作为无误差变量。
$$ \left\{ \begin{array}{l} H = 1.3 + {a_1}{\left( {1- \exp \left( {{a_2}D} \right)} \right)^{{a_3}}}\\ D = {a_4}{\left[{1-\exp \left( {-{a_5}\left( {T-{T_{1, 3}}} \right)} \right)} \right]^{{a_6}}} \end{array} \right.。 $$ (4) -
哑变量又称虚拟变量，是自变量经量化后所得的，一般取值0或者1[21-22]。在本研究中引入哑变量，可以将人工林和天然林2种类型的林分用定性代码0或1来表示。将其中一种起源的林分样地定义为Si，将定性数据Si转化为（0，1）形式。
$$ {S_i} = \left\{ \begin{array}{l} 1, 当S_i为第i个类型林分时 ;\\ 0, 否则。 \end{array} \right. $$ (5) 式（5）中：i=1, 2；S1，S2分别表示人工林分和天然林分的定性代码。
以Richards方程为例，通过试验知在第1个参数上加入哑变量时模型收敛且效果最好，因此，最终加入哑变量的联立方程组形式如下：
$$ \left\{ \begin{array}{l} H = 1.3 + \left( {{b_1}{S_1} + {b_2}{S_2}} \right){\left( {1- \exp \left( {- {b_3}D} \right)} \right)^{{b_4}}}\\ D = \left( {{b_5}{S_1} + {b_6}{S_2}} \right){\left[{1-\exp \left( {-{b_7}\left( {T-{T_{1, 3}}} \right)} \right)} \right]^{{b_8}}} \end{array} \right.。 $$ (6) 式（6）中：D为胸径；H为树高；T为林龄；T1.3为林木生长到胸高时的年龄；S1和S2分别为天然林和人工林的定性代码；b1~b8为待估参数。
-
先运用Excel和SPSS对数据进行初步处理，再利用Forstat中的非线性度量误差联立方程组方法进行参数估计。本研究采用并计算平均绝对偏差（DMAD）, 均方根误差（ERMSE）, 决定系数（R2）和预估精度（P）等几个指标对不同方法的模型进行检验评价分析。
$$ {D_{{\rm{MAD}}}} = \sum\limits_{i = 1}^n {\left( {{y_i}-{{\hat y}_i}} \right)} /n; $$ (7) $$ {E_{{\rm{RMSE}}}} = \sqrt {\frac{{\sum\limits_{i = 1}^n {{{\left( {{y_i}-{{\hat y}_i}} \right)}^2}} }}{n}} ; $$ (8) $$ {R^2} = 1-\frac{{\sum\limits_{i = 1}^n {{{\left( {{y_i}-{{\hat y}_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^n {{{\left( {{y_i}-\bar y} \right)}^2}} }}; $$ (9) $$ P=(1-\frac{{{t}_{0.05}}\sqrt{\frac{\sum\limits_{i=1}^{n}{{{\left( {{y}_{i}}-{{{\hat{y}}}_{i}} \right)}^{2}}}}{n\left( n-p \right)}}}{{\hat{\bar{y}}}})\%。 $$ (10) 式（7）~（10）中：yi为林分胸径（D）或林分树高（H）的实测值，ŷi为林分胸径（D）或林分树高（H）的模型预估值，$ \hat{\bar{y}}$为林分胸径（D）或林分树高（H）的模型预估值的平均值，n为样本数，p为模型参数个数，t0.05为置信水平α=0.05时t分布值。
-
在Forstat软件中拟合林分平均树高生长过程曲线，令树高H=1.3 m时，计算得到杉木生长到胸高时的年龄T1.3=3 a，基本符合杉木的生长习性，将它代入后面模型的拟合计算中。然后用所选6种模型对树高—胸径和胸径—年龄分别进行拟合，各方程的4个拟合评价指标统计如表 3和表 4所示。由表 3和表 4可知，各模型的拟合情况较为相近，树高曲线和胸径生长过程曲线中模型（2）的拟合决定系数分别为0.789 9和0.824 2，都略高于其他模型，因此，最终确定模型（2）即Richards模型为最佳基础模型。
表 3 树高曲线的拟合统计量
Table 3. Fitting statistic of height curve
模型序号及名称 R2 DMAD ERMSE P/% (1) Logistic模型 0.778 6 0.795 9 0.912 3 96.79 (2) Richards模型 0.789 9 0.700 3 0.856 7 97.25 (3) Weibull模型 0.788 5 0.705 7 0.859 6 97.23 (4) Korf模型 0.785 1 0.725 6 0.889 3 97.15 (5) Mitscherlich模型 0.787 6 0.708 9 0.862 9 97.21 (6) Schumacher模型 0.782 7 0.706 9 0.871 3 97.20 表 4 胸径生长曲线的拟合统计量
Table 4. Fitting statistic of DBH growth curve
模型序号及名称 R2 DMAD ERMSE P/% (1) Logistic模型 0.812 3 0.925 4 1.154 6 98.25 (2) Richards模型 0.824 2 0.898 0 1.076 6 98.35 (3) Weibull模型 0.753 4 1.217 1 1.511 7 97.67 (4) Korf模型 0.814 7 0.908 7 1.111 9 98.30 (5) Mitscherlich模型 0.811 5 0.933 2 1.165 4 98.21 (6) Schumacher模型 0.778 2 1.155 6 1.456 7 97.87 利用非线性度量误差联立方程组方法分别求解不含哑变量和引入哑变量的杉木的树高曲线、胸径生长过程曲线联立方程组的参数，统计相关结果如表 5和表 6所示。由表 6可知：哑变量和传统2种方法建立的杉木树高曲线的拟合决定系数都大于0.740 0，胸径生长过程曲线的拟合决定系数达到了0.820 0左右，且建模和检验数据的预估精度均达到了95.00%以上，平均绝对偏差（DMAD）和均方根误差（ERMSE）均较小，说明建立的树高曲线方程组合理，对树高、胸径的预测效果较好。不含哑变量的杉木树高曲线拟合的决定系数0.740 3小于含哑变量的树高曲线决定系数0.758 0，不含哑变量的杉木胸径生长曲线的决定系数0.814 6也小于含哑变量的胸径生长曲线的决定系数0.820 5，而且含哑变量的方程的预估精度高达98.00%以上大于不含哑变量方程的预估精度。引入哑变量之后树高曲线方程的拟合决定系数明显提高，胸径生长曲线的决定系数仅有微弱提高，但预估精度有一定提高，且其他几个评价指标均优于不含哑变量的模型，由此可见引入哑变量之后的模型效果更好，精度更高。
表 5 杉木树高曲线联立方程组参数表
Table 5. Parameters of simultaneous equations of height-DBH curve for Cunninghamia lanceolata
模型公式 参数 H=1.3+a1(1-exp (-a2D))a3 a1=37.212 866 a2=0.029 574 a3=1.303 845 D=a4[1-exp(-a5(T-T1.3))]a6 a4=98.224 975 a5=0.000 099 a6=0.331 043 H=1.3+(b1S1+b2S2)(1-exp(-b3D))b4 b1=34.500 583 b2=35.032 262 b3=0.032 024 b4=1.320 568 D=(b5S1+b6S2) [1-exp(-b7(T-T1.3))]b8 b5=85.512 397 b6=87.866 852 b7=0.000 138 b8=0.329 027 表 6 杉木树高曲线联立方程组的检验指标统计
Table 6. Inspection indexes of simultaneous equations of height-DBH curve for Cunninghamia lanceolata
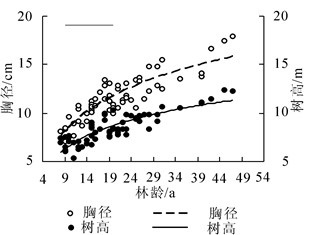
方法 模型 建模数据 检验数据 R2 DMAD ERMSE P/% R2 DMAD ERMSE P/% 传统方法 树高曲线 0.740 3 0.765 2 0.952 5 96.54 0.700 2 0.8107 1.121 7 95.07 胸径生长曲线 0.814 6 0.909 5 1.100 9 97.20 0.826 3 0.848 6 0.821 6 97.32 哑变量方法 树高曲线 0.758 0 0.702 4 0.898 2 98.01 0.724 6 0.775 2 0.967 4 95.74 胸径生长曲线 0.820 5 0.810 3 0.982 1 98.30 0.834 9 0.747 5 0.9143 97.97 杉木天然林和人工林的胸径—林龄、树高—林龄和树高—胸径的散点分布图如图 1~4所示。由图 1可知：在杉木天然林中，林分胸径在林龄为8~21 a间快速生长，11 a左右时其增长速率达到最大，此后增长速率逐渐减小，胸径生长趋于稳定。树高生长在19 a前相对变动较大，林龄到达25 a后，树高生长过程曲线趋于平缓。由图 2可知：杉木人工林平均胸径的生长速度在林龄为5~18 a时均较快，林龄为9 a左右时达到最快，此后生长速度逐年减缓生长趋于稳定。杉木人工林树高生长在17 a前生长较快且相对变动系数较大，林龄到达20 a后树高生长过程曲线趋于平缓。由图 3和图 4可知：树高与胸径之间存在着正相关关系，树高的增长速度随着胸径的生长先增加后减少，杉木天然林的树高在平均胸径为9~11 cm时增长速度最快，杉木人工林的树高在平均胸径为8~10 cm时增长速度最快。通过树高生长过程曲线和胸径生长过程曲线的对比得出，杉木天然林和人工林的树高随林龄增长的生长速率最大值分别出现在14 a和12 a左右，均晚于胸径生长速率达到最大值时的林龄。
图 1 杉木天然林胸径、树高生长过程曲线对比
Figure 1. Comparison of diameter-age and height-age curve for natural forest of Cunninghamia lanceolata
图 2 杉木人工林胸径、树高生长过程曲线对比
Figure 2. Comparison of diameter-age and height-age curve for artifical forest of Cunninghamia lanceolata
图 3 杉木天然林树高曲线
Figure 3. Height-diameter curve for natural forest of Cunninghamia lanceolata
图 4 杉木人工林树高曲线
Figure 4. Height-diameter curve for artifical forest of Cunninghamia lanceolata
据拟合趋势知，杉木人工林与天然林的树高、胸径的总体生长无明显差异，但在各林龄段中的生长变化规律有细小差别，杉木幼中龄生长期，人工林的树高和胸径生长率高于天然林，且人工林的树高与胸径均比天然林先达到最大值。
-
本研究在分析比较初步拟合结果后确定：Richards方程为最优基础模型，引入代表林分起源的哑变量，采用度量误差模型方法，建立了湖南省杉木林分的树高曲线方程组。通过对比分析得出了哑变量方法优于传统方法的结论，所建立的含哑变量的方程组中树高曲线和胸径生长过程曲线的拟合决定系数为0.758 0和0.820 5，且对杉木林分的平均树高和平均胸径的预估精度均达到了98.00%以上。利用特征为林分起源的哑变量将天然林人工林合并建模，不仅减少了建模的工作量还解决了模型间不相容的问题，而且所建立的树高曲线联立方程组保证了树高、胸径和林龄三者在生长模型预测中的相容性。综上所述，采用含哑变量的度量误差模型方法建立的树高曲线联立方程组在考虑树高、胸径的度量误差的基础上解决了多个相容性的问题，使模型具有更高的拟合精度和更好的预估能力，从而为从林分水平预测林木生长情况和统筹管理杉木林分提供了参考依据。
本研究拟合得到的胸径生长过程曲线和树高生长过程曲线的总体走势与前人研究结果一致[14, 23-25]，都呈现出生长速率先增加然后逐渐趋于平稳的倒“J”型，但由于建模数据有限，天然林和成、过熟龄阶段林分的数据样本较少，引入哑变量后方程的拟合系数没有出现大幅度的提升。在下一步研究中，应增加建模的数据量以提高拟合系数和保证树高曲线的完整性，同时还应考虑时间效应和样地效应对模型的影响以期建立更加合理可信的模型，为杉木天然林和人工林的经营提供理论基础。
Compatibility of height-diameter curve equations for Cunninghamia lanceolata stands in Hunan Province
-
摘要: 为了掌握杉木Cunninghamia lanceolata天然林与人工林的树高、胸径生长规律，改进杉木的营林生产模式，利用湖南省杉木一类清查数据，选择了6种常用经验方程拟合杉木树高曲线和胸径生长曲线，从中选出最优模型。在此基础上，考虑林分起源的差异，采用引入哑变量的度量误差模型方法建立不同起源林分相容性树高曲线方程组，并分析比较林分各阶段的生长状况。结果表明：引入哑变量后所建立的树高曲线方程组效果更好，在含哑变量的树高曲线方程组中杉木林分平均胸径生长过程曲线、平均树高曲线的拟合决定系数分别为0.820 5，0.758 0，预估精度分别达到了98.30%和98.01%，且其他各项评价指标均优于不含哑变量的树高曲线方程组；通过对比分析各林分不同林龄段的生长状况知：杉木人工林和天然林的总体趋势一致，但在中幼龄阶段，人工林的树高和胸径生长率高于天然林，且人工林的树高与胸径均比天然林先达到最大值。利用引入哑变量的度量误差模型方法建立树高生长模型，不仅考虑度量误差提高了模型精度，还解决了模型间不相容的问题。Abstract: To improve the forest production mode of Cunninghamia lanceolata artificial and natural forests in Hunan Province, their height-diameter curves were studied. Based on periodic inventory data of C. lanceolata in Hunan, six common empirical models were used to fit height-growth and diameter-growth curves, and selected the best one from them. On the basis of the optimal model, differences in stand origin were considered and compatible height-diameter curve equations for a group of stands with different stand origins were built by introducing dummy variables and using the measurement error model method. These growth status for stand in different origins were compared and analyzed by drawing scatter plots. Results showed that the fitted coefficient of determination for the C. lanceolata height-growth model with the dummy variables was better than this without dummy variables. The fitted coefficients for the tree diameter-growth curve was 0.820 5 with prediction accuracy of 98.30%, and for tree height was 0.758 0 with prediction accuracy of 98.01%. Also, DMAD and ERMSE indicators were superior to the traditional methods. The growth progress of C. lanceolata artificial and natural forests were the same; however, in the young stage, tree height and diameter growth rate of the artificial forest were higher than the natural forest. Moreover, tree height and diameter in the artificial forest reached a maximum value earlier than in natural forests. In conclusion, the model of tree height growth was established using the model with dummy variables, which not only improved the accuracy of the model but also solved the problem of incompatibility between models.
-
图 1 杉木天然林胸径、树高生长过程曲线对比
Figure 1 Comparison of diameter-age and height-age curve for natural forest of Cunninghamia lanceolata
图 2 杉木人工林胸径、树高生长过程曲线对比
Figure 2 Comparison of diameter-age and height-age curve for artifical forest of Cunninghamia lanceolata
图 3 杉木天然林树高曲线
Figure 3 Height-diameter curve for natural forest of Cunninghamia lanceolata
图 4 杉木人工林树高曲线
Figure 4 Height-diameter curve for artifical forest of Cunninghamia lanceolata
表 1 样地基本情况
Table 1. Basic situation of plots
样地类别 样地数/块 平均年龄/a 平均胸径/cm 平均树高/m 最小 最大 平均 最小 最大 平均 最小 最大 平均 天然林 62 8 47 21 7.1 17.9 11.5 5.3 12.4 8.6 人工林 95 6 50 22 6.5 18.9 12.1 4.5 14.3 9.1 建模样地 119 6 50 23 6.5 18.9 12.0 4.5 13.9 9.0 检验样地 38 6 40 18 7.2 17.5 11.3 4.8 14.3 8.6 
下载: 导出CSV
表 2 常见林分生长过程经验模型
Table 2. Common experience models of stand growth process
模型序号及名称 模型形式 (1) Logistic模型 y=a/[1+bexp(-ct)] (2) Richards模型 y=a [1-exp(-ct)]b (3) Weibull模型 y=a[1-exp(-bt)] (4) Korf模型 y=a exp(-btc) (5) Mitscherlich模型 y=a [1-bexp(-ct)] (6) Schumacher模型 y=aexp(-b/t)]
下载: 导出CSV
表 3 树高曲线的拟合统计量
Table 3. Fitting statistic of height curve
模型序号及名称 R2 DMAD ERMSE P/% (1) Logistic模型 0.778 6 0.795 9 0.912 3 96.79 (2) Richards模型 0.789 9 0.700 3 0.856 7 97.25 (3) Weibull模型 0.788 5 0.705 7 0.859 6 97.23 (4) Korf模型 0.785 1 0.725 6 0.889 3 97.15 (5) Mitscherlich模型 0.787 6 0.708 9 0.862 9 97.21 (6) Schumacher模型 0.782 7 0.706 9 0.871 3 97.20
下载: 导出CSV
表 4 胸径生长曲线的拟合统计量
Table 4. Fitting statistic of DBH growth curve
模型序号及名称 R2 DMAD ERMSE P/% (1) Logistic模型 0.812 3 0.925 4 1.154 6 98.25 (2) Richards模型 0.824 2 0.898 0 1.076 6 98.35 (3) Weibull模型 0.753 4 1.217 1 1.511 7 97.67 (4) Korf模型 0.814 7 0.908 7 1.111 9 98.30 (5) Mitscherlich模型 0.811 5 0.933 2 1.165 4 98.21 (6) Schumacher模型 0.778 2 1.155 6 1.456 7 97.87
下载: 导出CSV
表 5 杉木树高曲线联立方程组参数表
Table 5. Parameters of simultaneous equations of height-DBH curve for Cunninghamia lanceolata
模型公式 参数 H=1.3+a1(1-exp (-a2D))a3 a1=37.212 866 a2=0.029 574 a3=1.303 845 D=a4[1-exp(-a5(T-T1.3))]a6 a4=98.224 975 a5=0.000 099 a6=0.331 043 H=1.3+(b1S1+b2S2)(1-exp(-b3D))b4 b1=34.500 583 b2=35.032 262 b3=0.032 024 b4=1.320 568 D=(b5S1+b6S2) [1-exp(-b7(T-T1.3))]b8 b5=85.512 397 b6=87.866 852 b7=0.000 138 b8=0.329 027
下载: 导出CSV
表 6 杉木树高曲线联立方程组的检验指标统计
Table 6. Inspection indexes of simultaneous equations of height-DBH curve for Cunninghamia lanceolata
方法 模型 建模数据 检验数据 R2 DMAD ERMSE P/% R2 DMAD ERMSE P/% 传统方法 树高曲线 0.740 3 0.765 2 0.952 5 96.54 0.700 2 0.8107 1.121 7 95.07 胸径生长曲线 0.814 6 0.909 5 1.100 9 97.20 0.826 3 0.848 6 0.821 6 97.32 哑变量方法 树高曲线 0.758 0 0.702 4 0.898 2 98.01 0.724 6 0.775 2 0.967 4 95.74 胸径生长曲线 0.820 5 0.810 3 0.982 1 98.30 0.834 9 0.747 5 0.9143 97.97
下载: 导出CSV
-
[1] 隋宏大. 树高测量综合技术比较研究[D]. 北京: 北京林业大学, 2009. SUI Hongda. Comparative Study on Comprehensive Technologies of Tree Height Measurement[D]. Beijing:Beijing Forestry University, 2009. [2] 陈东升, 孙晓梅, 李凤日.基于混合模型的落叶松树高生长模型[J].东北林业大学学报, 2013, 41(10):60-64. CHEN Dongsheng, SUN Xiaomei, LI Fengri. Predicting models of tree height growth for larch based on mixed model[J]. J Northeast For Univ, 2013, 41(10):60-64. [3] 代忠迪, 姜立春.大兴安岭不同生态区域兴安落叶松树高曲线的研究[J].植物研究, 2015, 35(4):583-589. DAI Zhongdi, JIANG Lichun. Ecoregion based height-diameter models for Larix gmelinii Rupr. in Daxing' an Mountains[J]. Bull Bot Res, 2015, 35(4):583-589. [4] 肖锐, 陈东升, 李凤日, 等.基于两水平混合模型的杂种落叶松胸径和树高生长模拟[J].东北林业大学学报, 2015, 43(5):33-37. XIAO Rui, CHEN Dongsheng, LI Fengri, et al. Simulating DBH and height growth of trees for hybrid larch plantation with two-level mixed effect model[J]. J Northeast For Univ, 2015, 43(5):33-37. [5] 徐志扬.基于BP神经网络的马尾松树高曲线模型[J].林业调查规划, 2015, 40(2):6-8, 73. XU Zhiyang. Height-diameter model for Pinus massoniana based on BP neural network[J]. For Invent Plan, 2015, 40(2):6-8, 73. [6] 赵俊卉, 亢新刚, 刘燕.长白山主要针叶树种最优树高曲线研究[J].北京林业大学学报, 2009, 31(4):13-18. ZHAO Junhui, KANG Xingang, LIU Yan. Optimal height-diameter models for dominant coniferous species in Changbai Mountain, Northeastern China[J]. J Beijing For Univ, 2009, 31(4):13-18. [7] TEMESGEN H, von GADOW K, Genralized height-diameter models:an application foe major tree species in complex satnds of interior Brotish Columbia[J]. Eur J For Res, 2004, 123(1):45-51. [8] 赖巧玲, 胥辉.核密度估计在构造树高曲线中的应用[J].西南林学院学报, 2009, 29(4):19-22. LAI Qiaoling, XU Hui. Application of kernel density estimation theory to establishment of tree height-diameter curve[J]. J Southwest For Univ, 2009, 29(4):19-22. [9] 岑巨延, 李巧玉, 曾伟生, 等.广西速丰桉人工林相对树高曲线模型研究[J].中南林业科技大学学报, 2007, 27(4):23-27. CEN Juyan, LI Qiaoyu, ZENG Weisheng, et al. Curve models of relative tree height for Eucalyptus plantations in Guangxi[J]. J Cent South Univ For Technol, 2007, 27(4):23-27. [10] 孙拥康, 李际平, 吕勇.西洞庭湖区杉木林分相对树高曲线模型的研究[J].中南林业科技大学学报, 2012, 32(9):47-50. SUN Yongkang, LI Jiping, LÜ Yong. Study on relative tree height curve model of Chinese fir stand in west Dongting lake region[J]. J Cent South Univ For Technol, 2012, 32(9):47-50. [11] 高东启, 邓华锋, 程志楚, 等.基于度量误差模型方法建立的林分相容性树高曲线方程组[J].西北农林科技大学学报(自然科学版), 2015, 43(5):65-70. GAO Dongqi, DENG Huafeng, CHENG Zhichu, et al. Measurement error model based compatible system of equations for height-DBH curve[J]. J Northwest A & F Univ Nat Sci Ed, 2015, 43(5):65-70. [12] 张建国, 段爱国.理论生长方程对杉木人工林林分直径结构的模拟研究[J].林业科学, 2003, 39(6):55-61. ZHANG Jianguo, DUAN Aiguo. Approach to theoretical growth equations for modeling stands diameter structure of Chinese fir plantations[J]. Sci Silv Sin, 2003, 39(6):55-61. [13] 李春明, 张会儒.利用非线性混合模型模拟杉木林优势木平均高[J].林业科学, 2010, 46(3):89-95. LIU Chunming, ZHANG Huiru. Modeling dominant height for Chinese fir plantation using a nonlinear mixed-effects modeling approach[J]. Sci Silv Sin, 2010, 46(3):89-95. [14] 魏晓慧, 孙玉军, 马炜.基于Richards方程的杉木树高生长模型[J].浙江农林大学学报, 2012, 29(5):661-666. WEI Xiaohui, SUN Yujun, MA Wei. A height growth model for Cunninghamia lanceolata based on Richards' equation[J]. J Zhejiang A & F Univ, 2012, 29(5):661-666. [15] 姜鹏, 韩璐, 梁文静, 等.不同生长势杉木成熟林胸径-树高生长曲线研究[J].西北林学院学报, 2016, 31(4):195-200. JIANG Peng, HAN Lu, LIANG Wenjing, et al. Height, DBH growth models of Cunninghamia lanceolata with different growth potentials[J]. J Northwest For Univ, 2016, 31(4):195-200. [16] 国家林业局森林资源管理司. 国家森林资源连续清查技术规定[S]. 北京: 国家林业局森林资源管理司, 2004. [17] 唐守正, 张淑梅.度量误差模型及其应用[J].生物数学学报, 1998, 13(2):161-166. TANG Shouzheng, ZHANG Shumei. Measurement error models and their applications[J]. J Biomath, 1998, 13(2):161-166. [18] 李永慈, 唐守正, 李海奎, 等.用度量误差模型方法编制相容的生长过程表和材积表[J].生物数学学报, 2004, 19(2):199-204. LI Yongci, TANG Shouzheng, LI Haikui, et al. Using the method of measurement error model to compile the compatible growth table and volume table[J]. J Biomath, 2004, 19(2):199-204. [19] 曾伟生, 唐守正.利用度量误差模型方法建立相容性立木生物量方程系统[J].林业科学研究, 2010, 23(6):797-802. ZENG Weisheng, TANG Shouzheng. Using measurement error modeling method to establish compatible single-tree biomass equations system[J]. For Res, 2010, 23(6):797-802. [20] 曾伟生, 夏忠胜, 朱松, 等.贵州人工杉木相容性立木材积和地上生物量方程的建立[J].北京林业大学学报, 2011, 33(4):1-6. ZENG Weisheng, XIA Zhongsheng, ZHU Song, et al. Compatible tree volume and above-ground biomass equations for Chinese fir plantations in Guizhou[J]. J Beijing For Univ, 2011, 33(4):1-6. [21] 唐守正, 郎奎建, 李海奎.统计与生物数学模型计算教程[M].北京:科学出版社, 2009. [22] 冉啟香, 邓华锋, 黄国胜, 等.云南松地上生物量模型研究[J].浙江农林大学学报, 2016, 33(4):605-611. RAN Qixiang, DENG Huafeng, HUAN Guosheng, et al. An aboveground biomass model for Pinus yunnanensis[J]. J Zhejiang A & F Univ, 2016, 33(4):605-611. [23] 王明亮, 唐守正.标准树高曲线的研制[J].林业科学研究, 1997, 10(3):259-264. WANG Mingliang, TANG Shouzheng. Research on universal height-diameter curves[J]. For Res, 1997, 10(3):259-264. [24] 王明亮, 李希菲.非线性树高曲线模型的研究[J].林业科学研究, 2000, 13(1):75-79. WANG Mingliang, LI Xifei. Research on nonlinear height-diameter models[J]. For Res, 2000, 13(1):75-79. [25] 陈丽聪, 邓华锋, 黄国胜, 等.不同起源马尾松与杉木林分树高曲线的拟合及对比[J].西北农林科技大学学报(自然科学版), 2014, 42(1):57-64. CHEN Licong, DENG Huifeng, HUANG Guosheng, et al. Fitting and comparison of tree height curves of Pinus massoniana Lamb. and Cunninghamia lanceolata with different origins[J]. J Northwest A & F Univ Nat Sci Ed, 2014, 42(1):57-64. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2017.06.012
点击查看大图
计量
- 文章访问数: 3814
- HTML全文浏览量: 514
- PDF下载量: 428
- 被引次数: 0
