-
树冠外轮廓模型是指以树木树冠任意位置处半径为因变量，以冠幅、冠长、树高或胸径等因子为自变量的函数，用来模拟树冠形状变化规律的数学表达式[1]。树冠外轮廓模型不仅能够估计树冠任意位置处的树冠半径和推导计算整个树冠体积，而且可以驱动林分树木树冠三维可视化模拟。此外，树冠形态与树冠体积对于间接估算树木树冠部分生物量具有重要意义[2]。为了描述树冠外轮廓形态变化规律和推导计算树冠体积，国内外学者常利用以下方法预测树冠相关变量，包括简单几何形状模拟、经验模型方法、树冠轮廓模型积分法、激光扫描方法等。早期学者们利用规则几何体描述树冠外轮廓二维形状，常采用如下公式定义树冠形状：RCR=（1-RDH）k，其中：RCR表示相对树冠半径，RCH为从树冠基部到任意位置处树冠长度与最大树冠长度的比，k的取值决定了其几何形状，当k为0、0.5、1.0、1.5时分别表示圆柱形、抛物线形、圆锥形或凹面形等，该模型被广泛应用于道格拉斯杉Pseudotsuga douglasii[3]、西部铁杉Tsuga heterophylla[4]、火炬松Pinus taeda[5]、华北落叶松Larix principis-rupprechtii[6]等树冠形状模拟和体积计算研究中。PRETZSCH等[7]、SADONO[8]将树冠分为“阳冠”“阴冠”两部分，分别采用抛物线体和圆锥体表示。由于树冠形状并不是简单规则形式，不同树种树冠形状并不相同，树冠体积大小与冠幅、冠长、胸径、树高等林木因子之间存在相关关系，研究者针对不同树种利用经验模型方法构建幂函数、指数函数等多种形式树冠体积模型，如楠木Phoebe zhennan[9]、樟子松Pinus sylvestris var. mongolica[10]、杉木Cunninghamia lanceolata[11]、长白落叶松Larix olgensis[12]、欧洲赤松Pinus sylvestris和云杉Picea asperata[13]、黑荆树Acacia mearnsii[14]，也有研究者通过构建枝条长度、角度、半径等枝条属性经验方程间接预测树冠半径和模拟树冠形态变化规律，如李凤日[15]、LI等[16]、GILMORE等[17]、姜立春等[18]，但是存在树冠枝条测量困难且误差较大问题。三维激光扫描等技术的发展，不仅提供了快速数据获取方式，而且能够更加准确获取树冠数据[19-21]，但由于数据获取成本高、处理困难、数据量大等限制了它的使用。除了以上方法，为了更加准确预测树冠体积，一些学者利用多项式[22]、幂函数[23]、修正Beta曲线[24]、连续分段函数[25]等曲线形式描述树冠外轮廓形态，并将树冠曲线围绕树干轴旋转得到的旋转体，通过对旋转体积分推导计算树冠体积[26-28]。该方法只需要简单林木因子就能够准确模拟树冠形态与树冠体积。目前，树冠外轮廓模型积分法计算体积研究，一般将树冠外轮廓与树冠体积模型单独进行研究，分别拟合不同模型方程得到2套模型参数；由于外轮廓与体积方程之间存在内在相关性，采用传统最小二乘方法分别求解模型参数，不能保证2个模型误差同时最小，无法满足模型参数估计的渐进无偏性、有效性和一致性。通过对树冠轮廓模型积分推导得到树冠体积方程，将2个方程联立构建一致性方程组，能够有效解决以上模型参数估计存在的问题。目前一致性方程组的研究主要集中在树干削度与材积一致性方程组研究方面[29-30]，关于利用树冠外轮廓与树冠体积一致性模型方面研究还未见报道。本研究以福建地区杉木人工林为研究对象，采用似乎不相关回归方法，构建以最大树冠半径与相对冠长为自变量的树冠外轮廓和树冠体积一致性方程组模型，研究构建的模型能够用于驱动树木树冠三维可视化模拟，直观地反映不同生长条件下树冠生长活力及林木个体间树冠重叠程度，指导林分抚育间伐活动，同时为通过树冠体积间接推算树冠生物量提供新思路。
-
福建省位于中国东南沿海地区（23°33′~28°20′N，115°50′~120°40′E），地势东南低西北高，地形多丘陵少平原，不同区域气候相差较大，其中东南沿海属南亚热带气候，东北与西北区域属中亚热带气候，年平均气温为15.0~22.0 ℃，年平均降水量为1 400~2 000 mm，土壤类型主要包括红土壤、黄土壤、山地草甸土壤，主要用材树种有杉木、马尾松Pinus massoniana、巨尾桉Eucalyptus grandis × E. urophylla等。杉木为杉科Taxodiaceae乔木，幼树树冠尖塔形，大树树冠圆锥形，为中国长江流域、秦岭以南地区栽培最广、生长快、经济价值高的用材树种。
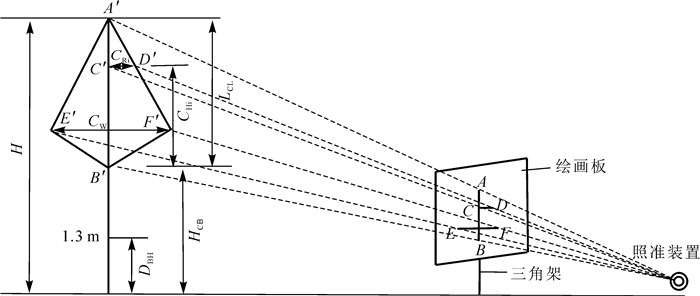
研究数据来自于福建省顺昌县大历和岚下林场布设的杉木人工纯林临时样地，选择不同龄组、林分密度和立地条件类型设置标准样地，共设置98块30 m × 20 m的样地，每个标准地内选择3~5株树木，共413株杉木。测量每株树木胸径（D）、树高（H）、冠幅（CW）、最大冠长（LCL）、枝下高（HCB），树冠长度（CHi）以及相应树冠半径（CRi），其中：i（i=0.10、0.25、0.50、0.75、0.90）表示从树冠基部到树梢顶端的相对位置。树冠因子测量如图 1所示，该装置由透明绘图板、三脚架以及照准装置组成，具体使用方法如下：①根据相似三角形原理，在距离所测树冠一定距离位置处（通常距离1倍树高），将该绘图板固定在三脚架之上保持板面垂直于地面，然后通过透明板观察树冠，往后移动三脚架，保持透明板与地面垂直，直到通过透明板能够观察到整个树冠。②用笔将树冠外轮廓绘制在透明板之上，首先绘制树冠枝下高位置处的点A、树冠顶端的点B以及最大树冠位置处的点C与点D，然后从A点开始到B、C点，将树冠轮廓绘制出来。并将透明板上的树冠轮廓草图复制到有计算网格方格的透明硫酸纸上。③利用测高仪器和皮尺分别测量该树冠的冠长L（LCL=A′B′）和冠幅（CW=E′F′），计算树冠冠长测量值A′B′与绘图纸上AB之间比值以及树冠冠幅测量值E′F′与CD之间比值，根据这2个比值在绘图纸上分别计算树冠冠长0.10、0.25、0.50、0.75、0.90位置处对应的树冠长度和半径值。为了尽可能减少树冠测量误差，应从多个方向观察树冠，取测量均值。通过以上调查方法收集到杉木树冠调查数据情况如表 1所示。
图 1 杉木树冠测量因子示意图
Figure 1. Schematic diagram of crown measurement factors of C. lanceolata
表 1 树冠调查数据的基本概况
Table 1. Summary statistics of measurements of tree variables
项目 t/a N/（株·hm-2） D/cm H/cm CW/m LCR/m LCL/m HCB/m CR/m 平均值 16.00 1 850.00 16.36 12.60 3.50 1.75 6.00 6.40 1.10 最小值 5.00 900.00 5.90 3.00 1.60 0.80 1.10 0.30 0.10 最大值 29.00 4 000.00 33.20 25.50 7.60 3.80 10.30 16.30 3.80 标准差 7.25 60.39 5.52 3.91 1.05 0.53 2.65 3.17 0.56 说明：t为年龄；N为株数密度 -
本研究收集整理了国内外文献研究中常用于描述树冠外轮廓形状的模型方程，具体形式如模型1、模型2、模型3以及模型4所示。其中：模型1被广泛用于模拟多个树种树冠形态[3]，该模型是否可用于杉木树冠模拟需要进一步验证，其他3个模型常用于模拟杉木树冠[23]。本研究将这4个可积分模型方程作为联立方程组中树冠外轮廓模型的备选模型。模型因变量为任意位置处树冠半径（CR），模型自变量为相对树冠冠长（RCH）、最大树冠半径（LCR）。
$$ C_{\mathrm{R}}=L_{\mathrm{CR}}\left(1-R_{\mathrm{CH}}\right)^{a_{0}}； $$ (1) $$ C_{\mathrm{R}}=L_{\mathrm{CR}}\left[a_{0}\left(\frac{R_{\mathrm{CH}}-1}{R_{\mathrm{CH}}+1}\right)+a_{1}\left(R_{\mathrm{CH}}-1\right)\right]； $$ (2) $$ C_{\mathrm{R}}=L_{\mathrm{CR}}\left(a_{0}+a_{1} R_{\mathrm{CH}}+a_{2} R_{\mathrm{CH}}^{2}\right)； $$ (3) $$ C_{\mathrm{R}}=L_{\mathrm{CR}}\left(a_{0}+a_{1} R_{\mathrm{CH}}^{a_{2}}\right)。 $$ (4) 采用积分法计算树冠体积，从树冠基部到树木顶端积分树冠外轮廓模型，得到$V_{\mathrm{c}}=\int_{0}^{L_{a}} {\rm{ \mathsf{ π} }} C_{\mathrm{R}}^{2} \mathrm{d} C_{\mathrm{H}}$体积方程，其中：VC为树冠体积，LCL最大树冠长度，CH为从树冠基部到树冠任意位置处树冠长度，推导得出树冠体积模型方程。
$$ V_{\mathrm{C}}=\frac{{\rm{ \mathsf{ π} }}}{2 a_{0}+1} L_{\mathrm{CR}}^{2} L_{\mathrm{CL}}； $$ (5) $$ V_{\mathrm{C}}={\rm{ \mathsf{ π} }} L_{\mathrm{CR}}^{2} L_{\mathrm{CL}}\left[\left(8 a_{0} a_{1}-4 a_{0}^{2}\right) \ln (2)+3 a_{0}^{2}-5 a_{0} a_{1}+\frac{1}{3} a_{1}^{2}\right]； $$ (6) $$ V_{\mathrm{C}}={\rm{ \mathsf{ π} }} L_{\mathrm{CR}}^{2} L_{\mathrm{CL}}\left(a_{0}^{2}+a_{0} a_{1}+\frac{1}{3} a_{1}^{2}+\frac{2}{3} a_{0} a_{2}+\frac{1}{2} a_{1} a_{2}+\frac{1}{5} a_{2}^{2}\right)； $$ (7) $$ V_{\mathrm{C}}={\rm{ \mathsf{ π} }} L_{\mathrm{CR}}^{2} L_{\mathrm{CL}}\left(a_{0}^{2}+\frac{2 a_{0} a_{1}}{a_{2}+1}+\frac{a_{1}^{2}}{2 a_{2}+1}\right)。 $$ (8) 式（5）~（8）中：RCH为相对冠长（RCH=CH/LCL，树冠基部为0，树冠顶部为1）；a0、a1、a2为模型系数。
-
假设定义如下非线性模型联立方程组，存在一组随机变量Y1，…，Yn与自变量x1，…，xn之间满足非线性关系，如下：
$$ \begin{array} [c]{c} Y_{1}=f_{1}\left(x_{1}, \beta_{1}\right)+\varepsilon_{1}；\\ Y_{2}=f_{2}\left(x_{2}, \beta_{2}\right)+\varepsilon_{2};\\ … \;…\\ Y_{n}=f_{n}\left(x_{n}, \beta_{n}\right)+\varepsilon_n 。 \end{array} $$ 其中：n个模型的同一次观测模型误差εi的各分量间是相关的，即cov（εi）是非对角矩阵[17]。这里多个方程之间存在联系，各方程的扰动项之间存在相关性，同时估计多个方程能够提高模型估计效率。
将树冠外轮廓模型和树冠体积模型两两联立为方程组，即2.1中式（1）与式（5）、式（2）与式（6）、式（3）与式（7）、式（4）与式（8）共4个方程组。每组的2个方程拥有同一套参数，对2个模型共同进行拟合，即解决非线性联立方程组模型的参数估计问题。
为了保证参数估计的一致性和渐进无偏性，利用SAS统计软件proc model程序提供的似乎不相关回归法（SUR），选择SUR法同时拟合树冠外轮廓与体积相容性模型。此外，在林业模型拟合过程中，模型误差项之间可能存在异方差的问题，本研究采用模型回归函数自身作为权函数消除异方差[13]。
-
模型拟合和检验结果通过以下指标评价：决定系数（R2）、均方根误差（RMSE）和平均绝对误差（MAE）、平均偏差（MD）。最优模型选择根据R2最大，RMSE、MAE、MD绝对值最小的原则进行。具体公式如下：
$$ R^{2}=1-\frac{\sum\limits_{i=1}^{m}\left(y_{i}-\hat{y}_{i}\right)^{2}}{\sum\limits_{i=1}^{m}\left(y_{i}-\bar{y}_{i}\right)^{2}}；\\ R_{\mathrm{MSE}}=\sqrt{\frac{\sum\limits_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)^{2}}{n-1}}；\\ M_{\mathrm{AE}}=\frac{1}{n} \sum\limits_{i=1}^{n}\left|y_{i}-\hat{y}_{i}\right|；\\ M_{\mathrm{D}}=\frac{\sum\limits_{i=1}^{n}\left(y_{i}-\hat{y}_{i}\right)}{n}。 $$ 其中：yi为第i因变量实际值，$\hat y_i$为第i因变量预测值，yi为因变量实际值平均，n为样本数。
-
树冠体积数据可采用分层切割法处理得到。本研究在对杉木树冠进行调查时，采用平均断面积求积法，将树冠从树梢到树冠基部按照相对冠长分6部分（0~0.10，0.10~0.25，0.25~0.50，0.50~0.75，0.75~0.90，0.90~1.00）。将树冠最上部分看作圆锥体近似计算体积，其他各部分采用平均断面积法。计算公式如下：
$$ V_{\mathrm{e}}=V_{1}+V_{2}+\cdots+V_{n}=g_{1} l_{1}+g_{2} l_{2}+\cdots+g_{n} l_{n}+\frac{1}{3} g^{\prime} l^{\prime}=\sum\limits_{i=1}^{n} g_{i} l_{i}+\frac{1}{3} g^{\prime} l^{\prime}。 $$ 其中：Vc表示整个树冠体积（m3）；Vi为第i部分树冠体积（m3）；gi为第i区分段中央断面积（m2）；li为第i分段长度（m）；g′为梢头底端断面积（m2）；l′为梢头树冠长度（m）；n为分段个数。
-
利用SAS软件的proc model模块中似乎不相关回归过程SUR方法对树冠外轮廓模型和树冠体积预测模型的一致性方程组同时进行拟合，表 2给出了不同模型拟合的统计量，即决定系数（R2）、均方根误差（RMSE）。
表 2 树冠外轮廓-体积模型拟合结果
Table 2. Fitting results of crown profile and crown volume models
模型 参数 R2 RMSE a0 a1 a2 CR VC CR VC 模型1 0.661 4（0.006 8）* 0.802 5 0.858 1 0.260 3 8.605 4 模型2 1.975 3（0.054 7）* －2.703 0（0.044 4）* 0.808 2 0.860 9 0.256 6 8.518 9 模型3 0.827 9（0.009 1）* 0.138 1（0.138 1）* －0.870 5（0.043 5）* 0.829 2 0.861 0 0.242 1 8.517 6 模型4 0.835 5（0.005 5）* －0.748 7（0.010 0）* 2.277 1（0.078 1）* 0.829 5 0.861 0 0.241 9 8.517 4 说明：a0、a1、a2为模型系数，参数拟合结果数值表示估计值（标准差）；*表示P＜0.000 1 由表 2拟合结果可知：树冠外轮廓模型拟合指标R2的对比结果为模型4＞模型3＞模型2＞模型1，轮廓模型拟合指标RMSE的对比结果为模型4＜模型3＜模型2＜模型1，树冠体积模型拟合指标R2的对比结果为模型4=模型3＞模型2＞模型1，体积模型拟合指标RMSE结果为模型4＜模型3＜模型2＜模型1。根据R2最大且RMSE相对较小的最优模型选择标准，不管从树冠外轮廓还是体积模型结果来看，模型4显示了较好的拟合结果，最终利用模型4来描述福建地区杉木树冠外轮廓和树冠体积。
-
建模数据只能反映模型拟合的好坏，不能反映模型的预测性能。模型系统的独立性检验是采用建模时未使用的独立样本数据，对各模型系统的预测性能进行综合评价。基于表 3的参数估计值和检验数据，利用SAS软件计算各模型系统树冠外轮廓和体积的绝对误差、均方根误差。从表 3可以看出：各树冠外轮廓模型的检验指标R2对比结果为模型4＞模型3＞模型2＞模型1，外轮廓模型RMSE对比结果为模型4＜模型3＜模型2＜模型1，各树冠体积模型检验指标R2对比结果为模型3=模型4＞模型2＞模型1，体积模型RMSE对比结果为模型4＜模型3＜模型2＜模型1，不管是从R2还是RMSE来看，模型4均优于其他模型。此外，模型4的检验指标MAE和MD绝对值最小，真实值与预测值之间误差最小，进一步验证了模型4作为杉木树冠外轮廓-体积模型的合理性。
表 3 不同模型独立性检验
Table 3. Validation results of different crown models
模型 树冠外轮廓模型 体积模型 MAE MD R2 RMSE MAE MD R2 RMSE 模型1 0.170 9 -0.027 3 0.760 1 0.277 6 5.258 3 -0.842 7 0.853 1 8.306 9 模型2 0.197 0 0.026 3 0.781 5 0.264 9 5.156 0 0.337 4 0.855 8 8.232 2 模型3 0.177 8 -0.011 3 0.803 3 0.251 3 5.161 4 0.007 4 0.856 0 8.226 2 模型4 0.177 4 -0.010 2 0.803 9 0.250 9 5.161 2 -0.000 4 0.856 0 8.226 1 -
模型拟合的总体评价反映了总体树冠外轮廓和体积的变化，不能反映各模型是否存在异方差性和无偏性，评价这2个指标最直观的方法就是利用残差分布图。为全面评价模型4效果，分别绘制模型4加权前后的残差分布图。图 2为未增加权函数时相容模型的残差图，左侧为树冠外轮廓模型残差分布，右侧为树冠体积模型残差分布，从图 2可以看出：残差均存在明显喇叭口形状，说明异方差问题显著。图 3为增加权函数后相容模型残差分布图，从图 3可以看出：加权后模型的残差散点图分布变得均匀，说明权函数明显消除了异方差。进一步说明加权后模型4显示了较高的等方差性和无偏性，效果较好。
图 2 未加权的SUR方法拟合的相容模型残差分布图
Figure 2. Residual distribution of models fitted by unweighted SUR method
图 3 加权的SUR方法拟合的相容模型残差分布图
Figure 3. Residual distribution of models fitted by weighted SUR method
-
在树冠模型研究方面，许多学者利用规则几何体模拟树冠形状并计算树冠体积，这类方法具有简单方便特点，但是不灵活且预测精度相对较低。本研究以福建杉木为研究对象，选择4种常用的树冠外轮廓经验模型模拟树冠形状曲线，与简单几何体模拟方法相比，能够更加准确合理地描述树冠形状的变化，而且方程形式更加灵活。
本研究通过树冠外轮廓模型方程推导树冠体积方程，构建一致性的相容的非线性树冠外轮廓-体积联立方程组模型，利用SAS软件模块中的似乎不相关回归过程（SUR）解决复杂分段联立方程组模型系统的参数同时估计，确保了2个方程参数估计的一致性，模型预测效果较好。本研究构建的树冠外轮廓-体积一致性模型方程，可以预测树冠外轮廓形态，驱动林分树木三维可视化并预估树冠体积，实现了树冠外轮廓与体积模型之间互相推导，同时也为进一步估测树木地上部分生物量提供了理论依据。
Crown profile and volume compatibility model of Cunninghamia lanceolata in Fujian Province
-
摘要:
目的 树冠外轮廓模型不仅能够描述任意位置处树冠半径，而且能够推导预测树冠体积与树木地上部分生物量。根据福建地区98块杉木Cunninghamia lanceolata人工林样地的413株杉木调查数据，构建了具有同一套模型参数的树冠外轮廓模型和树冠体积预测联立方程组系统。 方法 选取4种常用的可积分树冠外轮廓备选模型，利用积分法对备选模型进行推导，得到树冠体积预测模型；将模型方程分别两两联立建立树冠外轮廓与体积相容性联立方程组，并利用SAS软件模块中的似乎不相关回归过程估计联立方程组模型系统的参数。为了消除模型异方差，采用加权回归方法拟合模型，并对不同模型系统的拟合精度、预测精度进行对比分析。 结果 基于模型4的联立方程组拟合精度高、预测性能好，其树冠外轮廓和体积拟合精度分别达到0.829 5和0.861 0，预测结果精度分别为0.803 9和0.856 0；通过似乎不相关回归法解决了联立方程组共线性问题，加权回归方法一定程度上消除了模型中存在的异方差性。 结论 所构建的树冠外轮廓-体积一致性模型方程实现了树冠外轮廓与体积模型之间互相推导，为进一步估测树木地上部分生物量提供了理论依据。 Abstract:Objective Crown profile models can not only describe the radius at any position of the crown, but also predict the crown volume and the aboveground biomass. This paper developed a simultaneous equation system of crown profile model and crown volume prediction with the same set of model parameters using the data of 413 trees in 98 sample plots of Cunninghamia lanceolata plantation in Fujian Province. Method Four commonly used and integral crown profile models were selected, and the crown volume prediction models were derived by using integral method. The model equations were set up in pairs to establish the simultaneous equations of tree crown profile and volume compatibility, and the seemingly unrelated regression (SUR) process in SAS software module was used to estimate the parameters of the simultaneous equations model system. In order to eliminate the heteroscedasticity of the model, the weighted regression method was used to fit the model. The fitting accuracy and prediction accuracy of different model systems were compared and analyzed. Result The simultaneous equations based on model 4 had high fitting accuracy and good prediction performance. The fitting accuracy of the crown profile model and crown volume model reached 0.829 5 and 0.861 0 respectively, and the accuracy of prediction was 0.803 9 and 0.856 0 respectively. The collinearity problem of simultaneous equations was solved by the SUR method, and the heteroscedasticity in the model was eliminated to some extent by the weighted regression method. Conclusion The consistency model equation of crown profile-volume constructed in this paper can be used to derive the crown profile and volume model, which provides a theoretical basis for estimating the biomass of the aboveground part of trees. -
图 1 杉木树冠测量因子示意图
Figure 1 Schematic diagram of crown measurement factors of C. lanceolata
图 2 未加权的SUR方法拟合的相容模型残差分布图
Figure 2 Residual distribution of models fitted by unweighted SUR method
图 3 加权的SUR方法拟合的相容模型残差分布图
Figure 3 Residual distribution of models fitted by weighted SUR method
表 1 树冠调查数据的基本概况
Table 1. Summary statistics of measurements of tree variables
项目 t/a N/（株·hm-2） D/cm H/cm CW/m LCR/m LCL/m HCB/m CR/m 平均值 16.00 1 850.00 16.36 12.60 3.50 1.75 6.00 6.40 1.10 最小值 5.00 900.00 5.90 3.00 1.60 0.80 1.10 0.30 0.10 最大值 29.00 4 000.00 33.20 25.50 7.60 3.80 10.30 16.30 3.80 标准差 7.25 60.39 5.52 3.91 1.05 0.53 2.65 3.17 0.56 说明：t为年龄；N为株数密度 
下载: 导出CSV
表 2 树冠外轮廓-体积模型拟合结果
Table 2. Fitting results of crown profile and crown volume models
模型 参数 R2 RMSE a0 a1 a2 CR VC CR VC 模型1 0.661 4（0.006 8）* 0.802 5 0.858 1 0.260 3 8.605 4 模型2 1.975 3（0.054 7）* －2.703 0（0.044 4）* 0.808 2 0.860 9 0.256 6 8.518 9 模型3 0.827 9（0.009 1）* 0.138 1（0.138 1）* －0.870 5（0.043 5）* 0.829 2 0.861 0 0.242 1 8.517 6 模型4 0.835 5（0.005 5）* －0.748 7（0.010 0）* 2.277 1（0.078 1）* 0.829 5 0.861 0 0.241 9 8.517 4 说明：a0、a1、a2为模型系数，参数拟合结果数值表示估计值（标准差）；*表示P＜0.000 1
下载: 导出CSV
表 3 不同模型独立性检验
Table 3. Validation results of different crown models
模型 树冠外轮廓模型 体积模型 MAE MD R2 RMSE MAE MD R2 RMSE 模型1 0.170 9 -0.027 3 0.760 1 0.277 6 5.258 3 -0.842 7 0.853 1 8.306 9 模型2 0.197 0 0.026 3 0.781 5 0.264 9 5.156 0 0.337 4 0.855 8 8.232 2 模型3 0.177 8 -0.011 3 0.803 3 0.251 3 5.161 4 0.007 4 0.856 0 8.226 2 模型4 0.177 4 -0.010 2 0.803 9 0.250 9 5.161 2 -0.000 4 0.856 0 8.226 1
下载: 导出CSV
-
[1] 高慧淋, 董利虎, 李凤日.黑龙江省红松和长白落叶松人工林树冠外部轮廓模拟[J].南京林业大学学报(自然科学版), 2018, 42(3): 10 - 18. GAO Huilin, DONG Lihu, LI Fengri. Modelling outer crown profile for planted Pinus koraiensis and Larix olgensis trees in Heilongjiang Province, China[J]. J Nanjing For Univ Nat Sci Ed, 2018, 42(3): 10 - 18. [2] 罗永开, 方精云, 胡会峰.山西芦芽山14种常见灌木生物量模型及生物量分配[J].植物生态学报, 2017, 41(1): 115 - 125. LUO Yongkai, FANG Jingyun, HU Huifeng. Biomass estimation models and allocation patterns of 14 shrub species in Mountain Luya, Shanxi, China[J]. Chin J Plant Ecol, 2017, 41(1): 115 - 125. [3] MOHREN G M J. Simulation of Forest Growth, Applied to Douglas Fir Stands in the Netherlands [D]. Wageningen: Wageningen University&Research, Mohren, 1987. [4] MARSHALL D D, JOHNSON G P, HANN D W. Crown profile equations for stand-grown western hemlock trees in north[J]. Can J For Res, 2003, 33(11): 2059 - 2066. [5] NEPAL S K. Crown Shape Modeling for Loblolly Pine: A Frontier Approach[D]. Auburn: Auburn University, 1993. [6] HAN Yanyun, WU Baoguo, WANG Kaiyi, et al. Individual-tree form growth models of visualization simulation for managed Larix principis-rupprechtii plantation[J]. Comput Electronics Agric, 2016, 123: 341 - 350. [7] PRETZSCH H, BIBER P, ĎURSKÝ J. The single tree-based stand simulator SILVA: construction, application and evaluation[J]. For Ecol Manage, 2002, 162(1): 3 - 21. [8] SADONO R. Crown shape development of perhutani's teak plus from conal seed orchards in Madiun, Saradan, and Ngawi Forest District, East Java, Indonesia[J]. Adv Environ Biol, 2015, 9(18): 212 - 221. [9] 杜娟, 范志霞, 叶顶英, 等.楠木人工林树冠体积与叶面积指数预估模型的研究[J].浙江林业科技, 2010, 30(4): 37 - 41. DU Juan, FAN Zhixia, YE Dingying, et al. The predicting models of crown volume and LAI for Phoebe zhennan plantation[J]. J Zhejiang For Sci Technol, 2010, 30(4): 37 - 41. [10] 廖彩霞, 李凤日.樟子松人工林树冠表面积及体积预估模型的研究[J].植物研究, 2016, 27(4): 478 - 483. LIAO Caixia, LI Fengri. The predicting model of crown surface area and crown volume for Mongolia pine plantation[J]. Bull Bot Res, 2016, 27(4): 478 - 483. [11] 涂宏涛, 孙玉军, 吴明钦, 等.杉木人工林树冠表面积及体积模型的研究[J].中南林业科技大学学报, 2015, 35(9): 88 - 92, 103. TU Hongtao, SUN Yujun, WU Mingqin, et al. Predicting models of crown surface area and crown volume for Cunninghamia lanceolata plantation[J]. J Cent South Univ For Technol, 2015, 35(9): 88 - 92, 103. [12] 吴明钦, 孙玉军, 郭孝玉, 等.长白落叶松树冠体积和表面积模型[J].东北林业大学学报, 2014, 42(5): 1 - 5. WU Mingqin, SUN Yujun, GUO Xiaoyu, et al. Predictive models of crown volume and crown surface area for Korean larch[J]. J Northeast For Univ, 2014, 42(5): 1 - 5. [13] RAUTIAINEN M, MÕTTUS M, STENBERG P T, et al. Crown envelope shape measurements and models[J]. Silv Fennica, 2008, 42(1): 19 - 33. [14] CADORI C C, SANQUETTA C R, NETTO S P, et al. Analytical approaches for modeling tree crown volume in black wattle (Acacia mearnsii De Wild.) stands[J]. Afr J Agric Res, 2016, 11(49): 4979 - 4989. [15] 李凤日.长白落叶松人工林树冠形状的模拟[J].林业科学, 2004, 40(5): 16 - 24. LI Fengri. Modeling crown profile of Larix olgensis trees[J]. Sci Silv Sin, 2004, 40(5): 16 - 24. [16] LI Fengri, LIU Zhaogang, SUN Jingbo. Models for crown structure of larch plantation[J]. J For Res, 1995, 6(1): 6 - 11. [17] GILMORE D W, SEYMOUR R S. Crown architecture of Abies balsamea from four canopy positions[J]. Tree Physiol, 1997, 17(2): 71 - 80. [18] 姜立春, 潘莹, 李耀翔.兴安落叶松枝条特征联立方程组模型及树冠形状模拟[J].北京林业大学学报, 2016, 38(6): 1 - 7. JIANG Lichun, PAN Ying, LI Yaoxiang. Model systems of branch characteristics and crown profile simulation for Larix gmelinii[J]. J Beijing For Univ, 2016, 38(6): 1 - 7. [19] FERNÁNDEZ-SARRÍA A, MARTÍNEZ L, VELÁZQUEZ-MARTÍ B, et al. Different methodologies for calculating crown volumes of Platanus hispanica trees using terrestrial laser scanner and a comparison with classical dendrometric measurements[J]. Comput Electronics Agric, 2013, 90: 176 - 185. [20] KORHONEN L, VAUHKONEN J, VIROLAINEN A, et al. Estimation of tree crown volume from airborne lidar data using computational geometry[J]. Int J Remote Sensing, 2013, 34(20): 7236 - 7248. [21] STRÎMBU V F, STRÎMBU B M. A graph-based segmentation algorithm for tree crown extraction using airborne LiDAR data[J]. ISPRS J Photogramm Remote Sensing, 2015, 104: 30 - 43. [22] BALDWIN V C, Jr PETERSON K D. Predicting the crown shape of loblolly pine trees[J]. Can J For Res, 1997, 27(1): 102 - 107. [23] 郭艳荣, 吴保国, 郑小贤, 等.杉木不同龄组树冠形态模拟模型研究[J].北京林业大学学报, 2015, 37(2): 40 - 47. GUO Yanrong, WU Baoguo, ZHENG Xiaoxian, et al. Simulation model of crown profile for Chinese fir (Cunninghamia lanceolata) in different age groups[J]. J Beijing For Univ, 2015, 37(2): 40 - 47. [24] FERRARESE J, AFFLECK D, SEIELSTAD C. Conifer crown profile models from terrestrial laser scanning[J]. Silv Fenn, 2015, 49(1): 1106. doi: 10.14214/sf.1106. [25] 高慧淋, 李凤日, 董利虎.基于分段回归的人工红松冠形预估模型[J].北京林业大学学报, 2015, 37(3): 76 - 83. GAO Huilin, LI Fengri, DONG Lihu. Crown-shape model of a Pinus koraiensis plantation in northeastern China[J]. J Beijing For Univ, 2015, 37(3): 76 - 83. [26] 金哲根, 宋德年, 张彦相.浅析树冠结构模型[J].林业勘查设计, 1996(1): 46 - 47. JIN Zhegen, SONG Denian, ZHANG Yanxiang. A brief analysis of crown structure model[J]. For Invest Des, 1996 (1): 46 - 47. [27] 李彦强, 朱祺, 孙小艳, 等.基于SketchUp模拟亚美马褂木树冠及参数估算[J].黑龙江农业科学, 2015(5): 134 - 137. LI Yanqiang, ZHU Qi, SUN Xiaoyan, et al. Simulation and estimation on tree crown of Liriodenron sino-americanum based on SketchUp[J]. Heilongjiang Agric Sci, 2015(5): 134 - 137. [28] 戴超.北京主要树种树冠体积及表面积估测模型研究[D].唐山: 华北理工大学, 2015. DAI Chao. The Predicting Models of Crown Volume and Crown Surface Area about Main Species of Tree of Beijing[D]. Tangshan: North China University of Science and Technology, 2015. [29] 姜立春, 李凤日, 刘瑞龙.兴安落叶松树干削度和材积相容模型[J].北京林业大学学报, 2011, 33(5): 1 - 7. JIANG Lichun, LI Fengri, LIU Ruilong. Compatible stem taper and volume models for dahurian larch[J]. J Beijing For Univ, 2011, 33(5): 1 - 7. [30] BIGING G S. Taper equations for second-growth mixed conifers of Northern California[J]. For Sci, 1984, 30(4): 1103 - 1117. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2020.01.015
点击查看大图
图(3) / 表(3)
计量
- 文章访问数: 2023
- HTML全文浏览量: 520
- PDF下载量: 34
- 被引次数: 0
