-
城市化进程和城乡统筹建设的加速推进，在推动社会经济发展的同时也带来一系列的城市环境问题。如绿地面积不断减少、景观破碎化严重、生物多样性降低、景观功能连通性差等，严重削弱了城市绿地的生态调控能力和城市的可持续发展。面对日益严重的城市环境问题，城市绿地生态规划应考虑如何尽可能利用现有生态空间、综合运用各种空间分析方法/技术构建具有最优生态效能的绿地生态网络结构，并使之成为规划层面上解决生态环境问题的重要手段[1]。目前，城市绿地空间特征及绿地生态网络的构建工作主要根据景观生态学原理，利用地理信息系统（GIS）和景观格局指数等进行[2-3]。一般认为，城市绿地生态网络构建的关键问题是核心绿地斑块以及生态廊道[4]的识别。近年来，由VOGT等[5]提出的基于数学形态学原理的形态学空间格局方法（morphological spatial pattern analysis，MSPA）将土地利用覆盖图的景观分为核心、连接桥、孤岛等相互独立的7种类型，在识别网络结构中的大型绿地斑块并确定相互之间的重要程度上作用明显[6-7]。而最小累积阻力模型（minimal cumulative resistance model，MCR）在综合考虑区域内的自然社会环境、人为干扰等多影响因素后，构建综合阻力面，科学模拟生成区域内的潜在生态廊道；利用重力模型、图谱理论[8-9]、相对生态重要性与相对城镇发展胁迫赋值加权方法[8]等，则能更科学合理地判断生态廊道的相对重要程度。当前大部分研究是将生态环境质量较好或面积相对较大的绿地作为核心斑块，并未考虑斑块间的景观连通性及相对重要程度[10]。本研究利用MSPA方法分析2016年成都市三环区域内的绿地景观空间形态格局，提取对绿地生态网络构建具有重要生态意义的核心区和连接桥区；根据整体连通性（CII），可能连通性（CP）和斑块重要性（DI）等连通性景观指数对核心区和连接桥区景观连接度的评价结果筛选重要生态源地；耦合MCR模型、最小路径方法、重力模型提取重要生态廊道，经中介中心度识别中介作用较好的斑块作为踏脚石，以此构建优化的绿地生态网络。
-
成都市位于四川省中部（30°05′~31°26′N，102°54′~104°53′E），海拔为450~750 m，属亚热带湿润季风气候区，雨水充沛，四季分明；常年最多风向为静风；年平均气温为15.2~16.6 ℃，年平均降水量为873.0~1 265.0 mm；地势差异显著，西北高，东南低，地形地貌复杂，自然生态环境多样，生物资源十分丰富。成都市三环包括武侯区、锦江区、金牛区、成华区、青羊区以及青白江区的部分区域。在以全面建设现代田园城市的发展理念指导下，按照《成都市城市总体规划（2016-2035年）（草案）》和《成都市绿地系统规划（2003-2020）》目标，成都市将建成一个绿量充沛、布局合理、功能完善、生物多样、景观优美、特色鲜明的城市绿地系统。因此，研究绿地生态网络结构对成都市绿化建设具有重要意义。
-
以《成都市绿地系统规划（2003-2020）》和《成都市城市总体规划（2016-2035年）（草案）》为指导，采用2016年成都三环内的QuickBird高分辨率遥感影像，空间分辨率为0.61 m；根据高分辨率遥感影像的特点，采用分类精度较高的目视解译方法获取绿地、水体、道路等城市土地利用数据；通过地形图和实地采点验证，解译精度88.5%，满足研究区景观分析的精度要求。
-
利用地理信息系统（GIS）技术将城市用地类型中的绿地和水体属性值设为2，其他用地类型设为1，空白区域属性值设为0，并将其转化为TIFF格式的二值栅格数据。本研究区面积较小，绿地景观较为破碎，为了准确识别不同面积大小斑块对景观连通性的重要作用并增加核心区域之间的连通性，本研究在MSPA尺度敏感性分析的基础上，选择8领域连通性原则，设定边缘宽度为1，栅格大小为3 m × 3 m的研究尺度分析城市绿地景观空间形态格局。利用Guidos软件对栅格数据进行MSPA分析，得到包括核心、孤岛、连接桥、环、分支、边缘、穿孔7种不同的景观类型[5]。在对结果进行统计分析的基础上提取出具有重要意义的核心区和连接桥区作为景观连通性分析的基础数据。
-
景观连通性水平能够量化表征该景观类型对生态源地斑块内物种迁移的有利程度。本研究利用Conefor软件，选用整体连通性[CII，式（1）]，可能连通性[CP，式（2）]和斑块重要性[DI，式（3）]3个景观指数[6, 11]，对核心区和连接桥区进行景观连接度评价。经过反复计算，将生态源地斑块间的连通距离阈值设置为500 m，连通概率设置为0.5。
$$ {C_{{\rm{II}}}} = \frac{{\sum\limits_{i = 1}^n {} \sum\limits_{j = 1}^n {} \frac{{{a_i}{a_j}}}{{1 + n{l_{ij}}}}}}{{{A_{{L^2}}}}}; $$ (1) $$ {C_{\rm{P}}} = \frac{{\sum\limits_{i = 1}^n {} \sum\limits_{j = 1}^n {} {a_i} \cdot {a_j} \cdot {p_{ij}}^ * }}{{{A_{{L^2}}}}}; $$ (2) $$ {D_{\rm{I}}} = \frac{{I - {I_{{\rm{remove}}}}}}{I} \times 100\% 。 $$ (3) 式（1）~（3）中：n表示研究区内总斑块；ai和aj分别为斑块i和斑块j的面积；nlij为斑块i和斑块j之间的连接；$ {{p_{ij}}^ * }$为斑块i与斑块j之间全部路径概率的最大乘积值；AL为研究区景观总面积；I为某一景观的连接度指数，本研究中为整体连通性指数（CII）和可能连通性指数（CP）；${{I_{{\rm{remove}}}}} $为去除该斑块后的景观连接度指数。
-
利用最小累积阻力（RMC）模型[式（4）]计算生物在不同生境间迁移、扩散的最佳路径[11-12]。
$$ {R_{{\rm{MC}}}} = {f_{{\rm{min}}}}\sum\limits_{j = n}^{i = m} {} \left( {{D_{ij}} \times {R_i}} \right)。 $$ (4) 式（4）中：$ {{D_{ij}}}$表示从源点j到空间单元i的空间距离；Ri表示空间单元i的阻力系数。首先根据景观连通性评价中核心斑块重要性DPC值大小选取生态源地，选取高程、土地利用类型、与城市道路的距离、与河流水系的距离等阻力因子。各景观阻力因子分4个阻力等级分值，分值越高则代表生物扩散阻力越大，各因子的阻力分值及权重主要参考国内外相关研究成果以及专家打分法确定（表 1）。各因子转化为30 m × 30 m栅格单元大小的数据，通过加权叠加计算获得综合阻力面，作为MCR模型的成本数据。然后，利用GIS的Spatial Analyst工具计算生态源地到目标斑块的最小成本路径[6]，并生成由潜在廊道组成的绿地生态网络。利用重力模型[式（5）][6, 12]，计算生态源地间的相互作用矩阵，评价不同生态源地间的相互作用强度，量化分析研究区内潜在生态廊道的相对重要性。
$$ {G_{ij}} = \frac{{{N_i}{N_j}}}{{D_{ij}^2}} = \frac{{\left[ {\frac{1}{{{P_i}}} \times \ln \left( {{S_i}} \right)} \right]\left[ {\frac{1}{{{P_i}}} \times \ln \left( {{S_j}} \right)} \right]}}{{{{\left( {\frac{{{L_{ij}}}}{{{L_{\max }}}}} \right)}^2}}} = \frac{{{L^2}_{\max }\ln \left( {{S_i}{S_j}} \right)}}{{{L^2}_{ij}{P_i}{P_j}}}。 $$ (5) 表 1 不同景观类型的阻力值
Table 1. Impedance values of each landscape type
景观类别 分级指标 景观阻力 权重 高程/m ＜460 1 0.12 460~480 2 480~510 3 ＞510 4 坡度/（°） ＜5 1 0.15 5~15 2 15~25 3 ＞25 4 土地利用类型 绿地 1 0.18 林地、弃置和再建地 2 水体 3 建设用地 4 与铁路的距离/m ＞2 000 1 0.12 1 500~2 000 2 1 000~500 3 ＜500 4 与城市道路距离/m ＞200 1 0.16 150~200 2 100~150 3 ＜50 4 与城市河流距离/m ＞2 000 1 0.15 1 500~2 000 2 1 000~500 3 ＜500 4 式（5）中：${G_{ij}} $是斑块与斑块间的相互作用强度；Ni与Nj为斑块i与斑块j的权重；Dij为斑块i与斑块j之间潜在廊道的标准化阻力值大小；Pi为斑块i的整体阻力值；Si为斑块i的面积；Lij为斑块i与斑块j之间潜在廊道的累积阻力值；Lmax为研究区内所有廊道的最大阻力值。
-
中介中心度（betweeness centrality）是从连通性角度出发识别生态网络中占据中心位置斑块的有效方法，也是判别景观斑块是否为重要踏脚石的量化标准。中介中心度的分值大小为0~1，分值越高，踏脚石斑块的重要程度越大。本研究利用GIS中Matrix Green空间分析模块的中介中心度计算生态网络中绿地斑块的中介作用大小，并根据其分值大小选定生态网络中具有重要枢纽作用的踏脚石斑块。中介中心度公式为：
$$ C_i^B = \frac{1}{{\left( {N - 1} \right)\left( {N - 2} \right)}}\sum\limits_{j = 1;k = 1;j \ne k \ne i}^N {} \frac{{{n_{jk}}\left( i \right)}}{{{n_{jk}}}}。 $$ (6) 式（6）中：N为网络中的节点数；njk为节点j与节点k间最短路径的条数；njk（i）为节点j与节点k之间的最短路径经过节点i的条数。
-
根据景观生态网络连接度理论，采用α指数、β指数、γ指数[13]对优化后的成都市绿地生态网络结构进行评价。$\alpha = \left( {e - v + p} \right)\left( {2v - 5p} \right), \beta = e/v, \gamma = e/3\left( {v - 2p} \right) $。其中：e代表连线数目；v代表节点数目；p代表网络中互不连接的亚图数目，一般取值为1。α指数是衡量网络闭合性的指标，数值范围为0~1，值越接近于1则网络闭合性越好；β指数是衡量网络连通度的指标，数值范围为0~3，数越大则网络结构完善度越高；γ指数用来衡量网络的连通程度，数值范围为0~1，值越接近1则表示网络中每个节点间都存在连线。
-
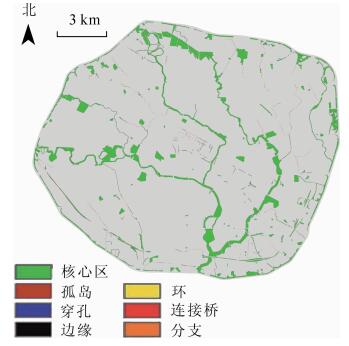
根据MSPA各景观类型统计分析结果（图 1，表 2）可见：研究区核心区面积约为12.972 km2，占总面积的85.85%，主要分布在成都市三环内的清水河、沙河、府南河沿线，空间连通性较好；研究区东北部和西南部核心斑块相对较少，斑块间相互独立，景观连通性较差。连接桥区面积约为0.048 km2，占总面积的0.32%；受绿地斑块较分散、破碎化程度高的影响，作为结构性廊道的连桥接需连接不同的核心斑块，因此分布也较为分散。边缘区是核心区与外部非绿色空间的过渡地带，具有边缘效应和保护核心区不被外界因素干扰的功能，占总面积的11.98%。与边缘区相似的是穿孔区，是核心区与内部非绿色空间的过渡地带，也具有边缘效应，占总面积的0.06%。边缘区与穿孔区作为景观空间格局中的组成要素，可根据其范围大小划定相应的缓冲区域以适应边缘效应。作为“踏脚石”斑块的孤岛，在空间格局中分布相对孤立，面积相对较小，景观连通性低。分支在绿地空间格局中所占比例相对较小，约为总面积的0.86%，它与连接桥、环、穿孔等具有一定的连通性。环是联系同一核心区的内部环状廊道，也是生物迁移的重要通道，约占面积的0.02%。
图 1 基于MSPA的景观类型分析图
Figure 1. Landscape types map based on MSPA
表 2 MSPA分类统计表
Table 2. Classification statistics table of MSPA
景观类型 占MSPA总面积的百分比/% 面积/km2 核心 85.85 12.972 连接桥 0.32 0.048 孤岛 0.92 0.139 边缘 11.98 1.810 穿孔 0.06 0.009 环 0.02 0.003 分支 0.86 0.130 总计 100.00 15.111 -
景观连通性指数计算（图 2，表 3）将DPC值大于4的12个核心斑块作为生态源地，剩余的核心区根据DPC值大小划分为3个等级：极重要核心区（1.0＜DPC≤4.0），重要核心区（0.1＜DPC≤1.0），一般核心区（DPC≤0.1）。连接桥区根据DPC值大小分为极重要连接桥区（DPC＞0.8），重要连接桥区（0.2＜DPC≤0.8），一般连接桥区（DPC≤0.2）。由图 2可看出：连通性较大的核心斑块和连接桥大多分布在研究区的西部，表明该区域内的斑块生境质量高，景观连通性相对较好，利于物种在斑块间的迁移与物质能量的流动。研究区的北部和南部虽然也有一定数量的核心斑块，但数量较少，空间上相对较为分散，不利于生物物种的迁移与扩散。研究区东部核心斑块数量最少，景观连通性相对较差。极重要和重要的连接桥主要分布在研究区的西部、北部、南部，它们对增加核心斑块的景观连通性具有重要作用。然而，研究区的整体连通性相对较差，仅南北区域的连通性相对较好，东西区域的核心斑块间相互独立，尤其是东部的核心绿地斑块面积相对较小且DPC值相对较低，这将不利于绿地生态网络的构建。因此，在绿地生态网络优化中，需要在研究区东部、东北部区域建设踏脚石绿地斑块，以维持景观连通性。
图 2 源地、核心和连接桥分类图
Figure 2. Classification map of source, core, bridge
表 3 基于景观连通性的核心区重要度排序
Table 3. Ranking of the importance of core area based on landscape connectivity
排序 编号 DPC DIIC 1 29 32.88 32.84 2 38 17.82 15.94 3 14 10.03 7.15 4 9 9.54 8.24 5 10 7.78 5.79 6 32 7.54 6.34 7 39 7.30 7.29 8 23 6.92 8.32 9 41 6.67 4.83 10 22 5.28 2.98 11 27 5.01 4.15 12 16 4.76 4.22 说明：DPC和DIIC均为版块重要性值 -
根据重力模型计算结果，提取相互作用强度大于5的廊道作为构建研究区优化绿地生态网络的重要结构性廊道。由表 4和图 3可见：斑块6和斑块9之间相互作用最强，表明斑块间的关联性最强，相互间的景观阻力较小，斑块间的物质和能量流动更紧密，物种迁移与能量流动的可能性较大。因此，斑块6和斑块9之间的连接廊道对维持斑块间的连通性具有重要意义。斑块11和斑块12的相互作用强度最小，其空间距离相对较远，也没有相关的结构廊道将其连通，相互间交流的可能性相对较低，能量流动的景观阻力相对较大，不利于物种在斑块间的迁移与扩散。同时，由于研究区东部和西部区域整体连通性差，重新构建斑块11与斑块12间的连通廊道对东、西部区域间物种迁移与扩散以及绿地生态网络连通性的提高具有重要作用。由图 3可以看出：研究区南部、北部以及西南部有一定的生态廊道连通，利于物种在研究区南北部斑块之间的迁移，但廊道的密集程度相对较低，不能有效地满足物质能量的流动。同时，研究区东部、西部连接的廊道较少，生态网络的完善度有待提高。因此，在整个研究区内构建新的生态源地和生态廊道，提高生态廊道密度对绿地生态网络的优化建设具有重要的指导意义。
表 4 基于重力模型计算的斑块间的相互作用矩阵
Table 4. Node interaction (G) based on the gravity model
斑块编号 1 2 3 4 5 6 7 8 9 10 11 12 1 0 1.04 0.26 0.80 0.40 7.79 2.47 0.99 14.79 43.08 1.48 0.58 2 0 0.25 8.02 0.37 1.73 0.93 1.32 3.33 3.68 0.13 192.70 3 0 0.52 1.19 0.25 0.21 2 200.54 0.42 0.59 0.18 0.17 4 0 0.60 1.00 0.67 2.77 1.78 2.24 0.12 7.86 5 0 0.34 0.33 6.33 0.54 0.81 0.24 0.24 6 0 4.67 0.98 3 099.38 177.44 0.40 0.92 7 0 0.82 8.73 9.67 0.28 0.51 8 0 1.50 2.13 0.63 0.82 9 0 433.15 0.63 1.60 10 0 1.25 1.87 11 0 0.05 12 0 
图 3 研究区潜在生态廊道
Figure 3. Potential ecological corridor map
-
综合考虑MSPA提取的核心斑块以及DPC值，选择重要程度最大的3个斑块进行重点保护与建设，使之成为研究区内重要的生态源地；根据中介中心度计算结果选出分值较高的13个绿地斑块作为踏脚石斑块（图 4），包括沙河公园、望江楼公园、文殊院、东湖公园等，它们对绿地生态功能的提升具有重要意义；根据斑块间的阻力值以及核心区和连接桥区的空间分布规划18条廊道以加强东、西部区域的连接，增大生态网络密度以增强整个网络空间连通的有效性（图 4）。统计对比分析规划前后绿地生态网络连接度表明：规划前α指数、β指数、γ指数分别为0.13，2.20，0.46，规划后为0.51，2.70，0.68，规划后生态网络的空间连通性及有效性较规划前都有较大的提高。
图 4 绿地生态网络规划
Figure 4. Greenspace ecological network planning map
-
本研究基于MSPA分析成都市三环内绿地景观空间形态格局，识别对绿地景观连通性具有重要意义的核心区和连接桥区，利用景观连通性指数确定研究区内绿地生态网络的源地与结构性廊道以及它们的相对重要程度。耦合MCR模型、最小路径方法、重力模型筛选出研究区内相对重要的潜在生态廊道。最后利用中介中心度选择对生态网络连接具有重要意义的踏脚石斑块，以构建优化的绿地生态网络。研究结果表明：MSPA方法、MCR模型、最小路径方法、重力模型以及中介中心度在城市绿地生态网络构建过程的有机结合，打破了传统生态源地选择的单一模式，通过量化分析能够更科学合理地确定核心斑块对绿地景观连通性的重要程度。该方法体系对城市绿地生态网络的构建具有一定的借鉴意义。
本研究中，重点强调踏脚石斑块对物种迁移扩散、增强绿地生态网络连通性的重要作用，在后续研究中，可将踏脚石斑块与城市居民的游憩需求相结合，利用中介中心度，构建城市绿地生态网络中的踏脚石群链接系统，形成“大型绿地斑块+踏脚石斑块+生态绿道+游憩节点”的绿地生态游憩网络结构。城市绿地景观空间形态格局的研究尺度只考虑边缘宽度与栅格像素大小对尺度敏感性的影响，并未考虑研究区的形状、适宜性等因素，在后期研究中将深入探讨和分析不同研究尺度对MSPA绿地网络结构的影响。本研究利用MCR模型构建综合阻力面主要从绿地景观的连通性以及景观格局的稳定性方面入手，并未具体考虑生物物种的迁徙及生活习性对生态网络构建的影响。在利用景观连通指数进行分析时，连通距离阈值设定主要通过反复的对比计算及研究区的范围来设定，未考虑物种的扩散距离，在后续研究中将对连通距离阈值的设定做更为详细的研究。
Developing urban greenspace ecological network in Chengdu City center based on multiple objectives
-
摘要: 基于形态学空间格局分析（MSPA）方法和景观连通性指数，以成都市三环内区域为研究对象，筛选研究区内维持景观连通性最重要的核心斑块作为绿地网络的生态源地；耦合最小累积阻力模型（MCR），最小成本路径方法和重力模型，提取研究区内重要生态廊道，利用中介中心度识别踏脚石斑块，构建研究区优化的绿地生态网络。结果表明：利用MSPA方法可识别研究区内景观结构的核心区及连接桥区；利用景观连通性指数可筛选出具有重要连通性的12个核心绿地斑块作为生态源地。基于MCR模型与最小路径方法识别出的潜在绿地生态网络表明研究区南部、北部以及西南部存在生态廊道，但密集程度较小，东、西部区域生态廊道较少，生态网络结构完善度较差。利用绿地斑块的中介作用选取包括沙河公园在内的13个踏脚石斑块可构建出较为合理的研究区绿地生态网络。相比于其他城市绿地生态网络构建技术，该方法更科学，对城市绿地生态网络优化也更具参考和借鉴意义。
-
关键词:
- 景观生态学 /
- 形态学空间格局分析（MSPA） /
- 景观连通性 /
- 最小累积阻力模型（MCR） /
- 生态网络 /
- 成都市
Abstract: The research took the third ring area of Chengdu as a case study and used the morphological spatial pattern analysis (MSPA) method and landscape connectivity index to identify the most important core patches which maintain landscape connectivity. Then the key corridors were developed using MCR model, the least-cost path method and Gravity model and step stones were identified by using betweeness centrality. Finally, a plan to optimize the ecological network in the study area was put forward. This research indicated that the cores and bridges of ecological networks could be identified through the MSPA method and that landscape connectivity index could effectively extract 12 key core patches as ecological sources in greenspace network. The potential ecological network identified through the MCR model and the least-cost path method indicated that a certain number of ecological corridors were connected in the south, north and southwest part of the study area, but the density of the corridors was relatively small. There were few corridors connecting in the eastern and western parts of the study area; the ecological network was not perfect. On this basis, using the betweeness centrality of green patches, the 13 stepping stones such as Shahe park were selected to construct a reasonable ecological network of green areas in the study area. Compared with other urban green ecological network construction techniques, this method is more scientific and has more significant reference for urban green ecological network optimization. -
表 1 不同景观类型的阻力值
Table 1. Impedance values of each landscape type
景观类别 分级指标 景观阻力 权重 高程/m ＜460 1 0.12 460~480 2 480~510 3 ＞510 4 坡度/（°） ＜5 1 0.15 5~15 2 15~25 3 ＞25 4 土地利用类型 绿地 1 0.18 林地、弃置和再建地 2 水体 3 建设用地 4 与铁路的距离/m ＞2 000 1 0.12 1 500~2 000 2 1 000~500 3 ＜500 4 与城市道路距离/m ＞200 1 0.16 150~200 2 100~150 3 ＜50 4 与城市河流距离/m ＞2 000 1 0.15 1 500~2 000 2 1 000~500 3 ＜500 4 
下载: 导出CSV
表 2 MSPA分类统计表
Table 2. Classification statistics table of MSPA
景观类型 占MSPA总面积的百分比/% 面积/km2 核心 85.85 12.972 连接桥 0.32 0.048 孤岛 0.92 0.139 边缘 11.98 1.810 穿孔 0.06 0.009 环 0.02 0.003 分支 0.86 0.130 总计 100.00 15.111
下载: 导出CSV
表 3 基于景观连通性的核心区重要度排序
Table 3. Ranking of the importance of core area based on landscape connectivity
排序 编号 DPC DIIC 1 29 32.88 32.84 2 38 17.82 15.94 3 14 10.03 7.15 4 9 9.54 8.24 5 10 7.78 5.79 6 32 7.54 6.34 7 39 7.30 7.29 8 23 6.92 8.32 9 41 6.67 4.83 10 22 5.28 2.98 11 27 5.01 4.15 12 16 4.76 4.22 说明：DPC和DIIC均为版块重要性值
下载: 导出CSV
表 4 基于重力模型计算的斑块间的相互作用矩阵
Table 4. Node interaction (G) based on the gravity model
斑块编号 1 2 3 4 5 6 7 8 9 10 11 12 1 0 1.04 0.26 0.80 0.40 7.79 2.47 0.99 14.79 43.08 1.48 0.58 2 0 0.25 8.02 0.37 1.73 0.93 1.32 3.33 3.68 0.13 192.70 3 0 0.52 1.19 0.25 0.21 2 200.54 0.42 0.59 0.18 0.17 4 0 0.60 1.00 0.67 2.77 1.78 2.24 0.12 7.86 5 0 0.34 0.33 6.33 0.54 0.81 0.24 0.24 6 0 4.67 0.98 3 099.38 177.44 0.40 0.92 7 0 0.82 8.73 9.67 0.28 0.51 8 0 1.50 2.13 0.63 0.82 9 0 433.15 0.63 1.60 10 0 1.25 1.87 11 0 0.05 12 0
下载: 导出CSV
-
[1] OPDAM P, STEINGROÖVER E, van ROOIJ S. Ecological networks:a spatial concept for multi-actor planning of sustainable landscapes[J]. Landscape Urban Plann, 2006, 75(3/4):322-332. [2] LI Feng, WANG Rusong, PAULUSSEN J, et al. Comprehensive concept planning of urban greening based on ecological principles:a case study in Beijing, China[J]. Landscape Urban Plann, 2005, 72(4):325-336. [3] MAHMOUD A H A, El-SAYED M A. Development of sustainable urban green areas in Egyptian new cities:the case of El-Sadat City[J]. Landscape Urban Plann, 2011, 101(2):157-170. [4] 李晖, 易娜, 姚文璟, 等.基于景观安全格局的香格里拉县生态用地规划[J].生态学报, 2011, 31(20):5928-5936. LI Hui, YI Na, YAO Wenjing, et al. Shangri-La county ecological land use planning based on landscape security pattern[J]. Acta Ecol Sin, 2011, 31(20):5928-5936. [5] VOGT P, RⅡTTERS K H, ESTREGUIL C, et al. Mapping spatial patterns with morphological image processing[J]. Landscape Ecol, 2007, 22(2):171-177. [6] 许峰, 尹海伟, 孔繁华, 等.基于MSPA与最小路径方法的巴中西部新城生态网络构建[J].生态学报, 2015, 35(19):6425-6434. XU Feng, YIN Haiwei, KONG Fanhua, et al. Developing ecological networks based on mspa and the least-cost path method:a case study in bazhong western new district[J]. Acta Ecol Sin, 2015, 35(19):6425-6434. [7] WICKHAM J D, RⅡTTERS K H, WADE T G, et al. A national assessment of green infrastructure and change for the conterminous United States using morphological image processing[J]. Landscape Urban Plann, 2010, 94(3/4):186-195. [8] WEBER T, SLOAN A, WOLF J. Maryland's green infrastructure assessment:development of a comprehensive approach to land conservation[J]. Landscape Urban Plann, 2006, 77(1/2):94-110. [9] KONG Fanhua, YIN Haiwei, NAKAGOSHI N, et al. Urban green space network development for biodiversity conservation:identification based on graph theory and gravity modeling[J]. Landscape Urban Plann, 2010, 95(1/2):16-27. [10] 吴健生, 张理卿, 彭建, 等.深圳市景观生态安全格局源地综合识别[J].生态学报, 2013, 33(13):4125-4133. WU Jiansheng, ZHANG Liqing, PENG Jian, et al. The integrated recognition of the source area of the urban ecological security pattern in Shenzhen[J]. Acta Ecol Sin, 2013, 33(13):4125-4133. [11] SAURA S. Effects of remote sensor spatial resolution and data aggregation on selected fragmentation indices[J]. Landscape Ecol, 2004, 19(2):197-209. [12] 陈竹安, 况达, 危小建, 等.基于MSPA与MCR模型的余江县生态网络构建[J].长江流域资源与环境, 2017, 26(8):1199-1207. CHEN Zhu'an, KUANG Da, WEI Xiaojian, et al. Development ecological networks based on MSPA and MCR:a case study in Yujiang county[J]. Resour Environ Yangtze Basin, 2017, 26(8):1199-1207. [13] 王海珍, 张利权.基于GIS, 景观格局和网络分析法的厦门本岛生态网络规划[J].植物生态学报, 2005, 29(1):144-152. WANG Haizhen, ZHANG Liquan. A GIS, landscape pattern and network analysis based planning of ecological network for Xiamen island[J]. Acta Phytoecol Sin, 2005, 29(1):144-152. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2019.02.018
点击查看大图
图(4) / 表(4)
计量
- 文章访问数: 2931
- HTML全文浏览量: 684
- PDF下载量: 97
- 被引次数: 0
