-
随着计算机技术和统计学方法的不断发展,机器学习方法被越来越多地运用到各个领域当中。在生态学研究中,物种分布模型(species distribution modelling,SDM)被广泛运用于外来入侵物种潜在分布区预测、珍稀物种潜在分布区预测、保护区规划和全球气候变化背景下的物种分布及迁移等方面[1],为植物保护,造林规划,制定物种多样性保护策略等提供理论依据。物种分布模型的基本原理是利用物种分布数据(包括存在点和不存在点)及不同环境因子,运用不同的模型算法计算物种的生态位,并以概率的形式反映物种对生境的偏好程度,所得结果可以解释为物种出现的概率、生境适宜度或物种丰富度等[2]。目前,学者使用较多的物种分布模型包括随机森林[3]、支持向量机[4]、遗传算法[4]、分类回归树[5]和最大熵模型(MaxEnt)[6]等,种类繁多且各有优势,且在前人研究中都得到了较好的效果。但是随着物种分布模型种类的不断增加,选择合适的模型变得愈加困难。ARAÚJO等[7]报道:每种模型各有优势和局限,且随输入数据的变化模型表现也不稳定,对同一物种的预测的精度差异可能会非常大,因此若通过建立一个模型组,将多个模型的结果整合,产生一个组合模型,将能提高预测结果的准确率。周志华[8]曾提出:单一模型之间较低的相关性可以提高模型的误差校正能力,因此模型结果的差异性越高,最终集成模型的效果也会越好。预测效果不好的模型对于问题的某一特定部分可能会有优势。因此,加入预测效果较差的模型往往不会过拟合,且多个效果较差的模型的集成也可以产生一个较好的模型。目前,常见的集成算法有3种,分别是Bagging,Boosting和Stacking。南方红豆杉Taxus chinensis var. mairei自然分布于中国的华东、中南、西南以及陕西、甘肃、台湾等地,是珍贵的资源植物,材质极佳,因其含紫杉醇而备受关注。本研究以南方红豆杉为例,应用Caret和CaretEnsemble程序包比较和集成多个模型研究其在浙江省丽水市莲都区范围内的潜在分布区,以期为该树种造林及资源保护提供科学依据。
HTML
-
莲都区位于浙江省丽水市,28°06′~28°44′N,119°32′~120°08′E,地处括苍山、洞宫山、仙霞岭3条山脉之间,属于亚热带季风气候,温暖湿润,雨量充沛,四季分明。全境以丘陵山地为主,中间有小块河谷平原。境内地形可分为河谷平原、丘陵、山地3种,平均海拔381 m,低山丘陵和高山丘陵占全区总面积的57.0%,低山、中山面积占全区总面积的30.2%。南方红豆杉是莲都区的乡土树种。由于自然地理条件适合,莲都区是最早发展南方红豆杉的地区之一,开展了人工育苗、造林试验和古树保护等。目前莲都区范围内共有南方红豆杉古树154株,多以村口风水林的形式存在。
-
Stacking模型集成算法是WOLPERT[9]于1992年提出,指训练一个模型用于组合(combine)其他各个模型的方法。Stacking模型分为2层,第0层首先训练多个不同的模型(基学习器),然后再以之前训练的各个模型的输出输入第1层来训练一个模型(元学习器)。在0层首先对训练集S,使用类似k折交叉验证法的方式将数据分成J个部分S1,…,SJ。对于第j次训练,保留Sj的数据,然后将S(-1)=S-Sj用来训练每一个基础分类器Kj,训练完成后,使用每个基础分类器对数据Sj进行预测分类,产生该数据的所属各类别的后验概率,若训练数据存在N个类别,那么每个基础分类器将会产生N个由后验概率组成的新的特征维度pkj,K个分类器将组成K×N个新维度,这些新增的特征维度将作为第1层中的训练数据。根据k折交叉验证的原理,算法结束时将会计算J次,直至训练集中的所有数据都被转换成由后验概率构成的新数据,第0层阶段结束。由于使用了交叉验证技术,故训练集并不会存在数据泄露问题。
-
这是一种基于梯度提升算法(gradient boosting)以及决策树(decision tree)的改进型学习算法。其原理是使用迭代运算的思想,将大量的弱分类器转化成强分类器,以实现准确的分类效果。本研究首次将其用于物种潜在分布区的研究当中。
-
这由BREIMAN[10]在2001年提出的一种基于分类树的算法,利用Bootstrap重抽样方法从原样本中抽取多个样本,对每个样本进行决策树建模,然后将多棵决策树模型组合的预测方法。最终通过投票的方法得出预测结果。
-
分类回归树是一种非参数化的回归及分类技术,无需预先假设响应变量和预测变量之间的关系,而是根据响应变量,利用递归划分法,将由预测变量定义的空间划分为尽可能相同的类别。每一次划分都由预测变量的一个最优划分值来完成,将数据分成2个部分,重复此过程,直到数据不可再分。分类回归树算法由树生长和树剪枝2个步骤组成[11]。
-
它源于古典数学理论,是一种较稳定的有监督分类算法,其分类算法基于贝叶斯定理,在处理大规模数据库时有较高的分类准确率。
-
这是一种基于统计学习理论的机器学习方法[12],具有良好的泛化性能。可以有效解决小样本、非线性及高维模式识别问题,在模式识别和机器学习领域已取得广泛的应用。本研究以上述5个模型作为基学习器,以广义线性模型(GLM)作为元学习器来建模。
-
2017年在莲都区开展野外调查工作,获得154株南方红豆杉的分布点位,将群状古树群视为1个分布点,共得到40个南方红豆杉分布点。
-
数字高程数据(digital elevation model, DEM)来自“地理空间数据云”(),空间分辨率为90 m,使用Arc GIS 10.1软件根据DEM数据提取获得坡度、坡向和海拔高度因子。
-
气象数据由Anusplin软件插值而来,空间分辨率为90 m。Anusplin以DEM为协变量,其局部薄盘样条插值结果与反向距离权重法和普通克吕格法的插值结果相比误差最小[13]。从中国气象数据网()下载地面年值数据集(1981-2010年)数据,范围选取浙江省及其周边省市共132个气象站点进行插值。7个气象因子分别为年最多降水量、年最少降水量、年平均气温、年平均气温日较差、年平均最高气温、年平均最低气温和年平均相对湿度。
-
除地形和气象数据,本研究还增加了土层厚度、距离河流距离、归一化植被指数(normalized difference vegetation index,NDVI)和太阳辐射等因子。数据空间分辨率均为90 m。
-
因模型需要存在和不存在数据,在不能获取真实不存在点的情况下,为了增加模型的可靠性,使用张雷[14]提出的伪不存在点的生成方法,利用MaxEnt模型生成不存在数据。因为MaxEnt模型的运行不需要不存在数据,所以我们先利用MaxEnt模型预测南方红豆杉的潜在分布区。在得出结论以后,从中剔除南方红豆杉的适生区。为了尽量减少误差,将适生区的面积扩大10%剔除,再从剩余的不适生区中随机生成与存在点数量相同的伪不存在点。
-
为验证模型精度,本研究使用k折交叉验证法(k-fold cross-validation)划分训练集(train data)和测试集(test data)。k折交叉验证法是一种用于计算样本识别率的常用算法。k折交叉验证法在小数据集的情况下能够更好地利用数据,取得较好的识别率,更能有效避免过学习和欠学习的发生[15]。本研究使用10折交叉验证。采用Kappa值和准确率来评估模型的预测精度,Kappa值常用于测试空间分布格局的相似性[16],排除了由随机因素导致一致性的可能性,因此是更为稳健、更为保守的指标[17]。Kappa值的计算需要指定一个阈值把物种发生概率转化为二元值(物种发生和不发生)[18]。Kappa值的评估标准为[19]:极好,1.0~0.85;很好,0.7~0.85;好,0.55~0.7;一般,0.4~0.55;失败,<0.4。准确率的计算方法为分类正确的样本数除以所有样本数,准确率越高模型越好。
2.1. 模型集成
2.2. 模型选择
2.2.1. 极端梯度上升(extreme gradient boosting,XGBoost)模型
2.2.2. 随机森林(random forest,RF)模型
2.2.3. 分类回归树(classification and regression tree,CART)模型
2.2.4. 朴素贝叶斯(native bayes,NB)模型
2.2.5. 支持向量机(support vector machine,SVM)模型
2.3. 物种分布记录
2.4. 环境因子
2.4.1. 地形因子
2.4.2. 气象因子
2.4.3. 其他因子
2.5. 伪不存在点的生成
2.6. 模型评估
-
根据Kappa值和准确率对比5个模型和集成模型结果(表 1),单一模型中随机森林模型、极端梯度上升模型、支持向量机模型达到了“很好”的类别,分类回归树模型和朴素贝叶斯模型的预测结果处于“好”的类别。其中极端梯度上升模型预测效果最好,Kappa值和准确率分别为0.77和0.88;其次为随机森林模型和支持向量机模型,Kappa平均值大于0.70,准确率大于0.85;分类回归树模型预测效果最差,Kappa值为0.59,准确率为0.79;朴素贝叶斯模型稍好于分类回归树模型,Kappa值和准确率分别为0.60和0.80。对比5个单一模型和集成模型,集成模型模拟效果最好,其结果显示:Kappa值为0.80,准确率为0.90,较模拟效果最好的单一模型有所提升。
模型 Kappa值 准确率 随机森林模型 0.73 0.87 分类回归树模型 0.59 0.79 朴素贝叶斯模型 0.60 0.80 极端梯度上升模型 0.77 0.88 支持向量机模型 0.73 0.86 集成模型 0.80 0.90 Table 1. Kappa values and accuracy of the model
-
Caretensemble程序包中自带varimp函数,可以计算各环境因子重要性(表 2)。随机森林模型模拟结果显示:海拔高度是影响南方红豆杉分布最重要的因子,其次为年平均最少降雨量、归一化差分植被指数和年平均最多降雨量,其重要性分别为22.58,16.21,15.81和10.55。这4个环境因子的累计重要性为65.15。分类回归树模型模拟结果显示:最重要的因子为海拔高度,其次为年平均最少降雨量、归一化差分植被指数和年平均最多降雨量,重要性分别为24.54,20.24,12.14和11.58。这4个环境因子的累计重要性为68.5。朴素贝叶斯模型模拟结果显示:海拔高度最为重要,其次为年平均最少降雨量、年平均气温和归一化差分植被指数,重要性分别为21.35,13.16,13.05和11.55。这4个环境因子的累计重要性为59.11。极端梯度上升模型模拟结果显示:最重要的因子为海拔高度,其次为归一化差分植被指数、年平均最高气温和年平均最少降雨量,重要性分别为25.75,19.34,10.97和10.02。这4个环境因子的累计重要性为66.08。支持向量机模型模拟结果显示:最重要的环境因子为年平均最低气温,重要性为13.15,为5个模型和集成模型中最高,其次为海拔、年平均气温、年平均最少降雨量、归一化差分植被指数和年平均最高气温,重要性分别为13.13,13.05,12.71,11.55和10.82,这5个环境因子的累计重要性为61.26。
环境因子 随机森林模型 分类回归树模型 朴素贝叶斯模型 极端梯度上升模型 支持向量机模型 集成模型 年平均气温日较差 2.92 0.00 1.43 0.00 0.00 0.75 土层厚度 0.00 0.00 0.79 0.86 1.68 1.03 太阳辐射 0.61 0.00 1.55 3.26 2.60 2.09 年平均湿度 5.51 7.01 4.63 2.62 0.19 2.28 距河流距离 2.23 6.94 3.55 6.12 3.55 3.81 坡度 7.86 0.00 2.65 4.75 2.65 4.23 坡向 1.76 0.00 6.64 7.07 6.64 5.17 年平均最低气温 2.72 0.00 1.92 0.00 13.15 7.63 年平均最多降雨量 10.55 11.58 8.29 4.50 8.29 8.36 年平均最高气温 4.11 7.54 9.47 10.97 10.82 8.98 年平均气温 6.83 9.86 13.05 4.74 13.05 9.89 年平均最少降雨量 16.21 20.41 13.16 10.02 12.71 13.49 归一化差分植被指数 15.81 12.14 11.55 19.34 11.55 14.01 海拔高度 22.85 24.54 21.35 25.75 13.13 18.30 Table 2. Importance of environmental factors
通过模型之间的比较可以看出:影响南方红豆杉在莲都区分布的主要环境因子为海拔高度、归一化差分植被指数和年平均最少降雨量,在每个模型中的重要性均大于10。同时5个单一模型由于其本身侧重不同,所选取参与建模的环境因子和各个环境因子的重要性也不相同。集成模型模拟结果显示每个环境因子都对南方红豆杉的潜在分布区有响应,且每个因子重要性都较为平均,没有特别突出某个环境因子。集成模型中最重要的为海拔高度,其次为归一化差分植被指数和年平均最少降雨量,3个因子重要性均大于10,累计重要性为45.8。通过对比各单一模型和集成模型显示的环境因子重要性可知:海拔高度、归一化差分植被指数和年平均最少降雨量是影响南方红豆杉潜在分布区的主要环境因子。
-
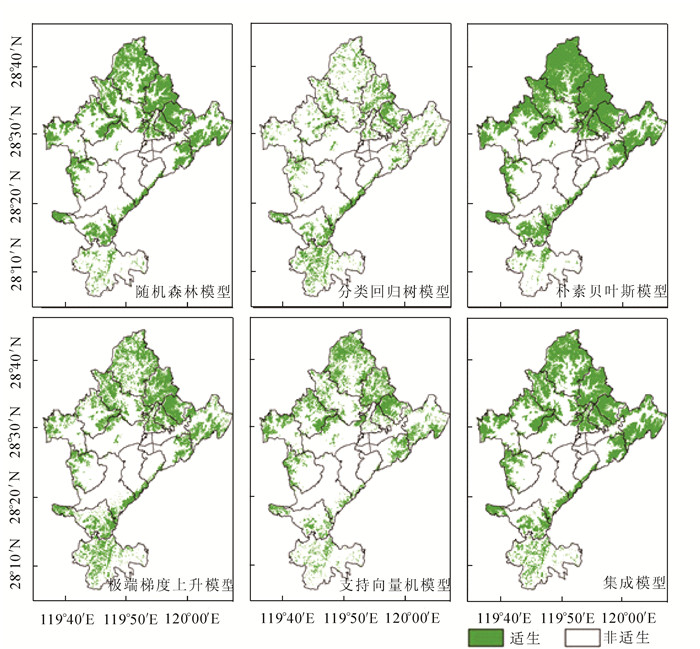
对比5个模型和集成模型,结果由图 1所示。根据集成模型预测结果,南方红豆杉主要分布在莲都区北部及东北部地区的雅溪镇、仙渡乡、双黄乡、黄村乡、太平乡、老竹畲族镇、岩泉街道及白云山林场。莲都区南部的大港头镇和峰源乡也有较多分布。在峰源乡,分布区呈现离散状态。此外,南方红豆杉在丽新畲族乡和高溪乡西侧,富岭街道、紫金街道和碧湖镇东侧亦有分布。
各乡镇潜在分布区面积结果由表 3所示,随机森林模型、极端梯度上升模型、支持向量机模型和集成模型等4个模型均显示雅溪镇的潜在分布区及其所占全区潜在分布区面积比例最大。所有模型预测结果均显示富岭街道的潜在分布区及其面积占比最小。
乡镇 潜在分布区面积/hm2 随机森林模型 分类回归树模型 朴素贝叶斯模型 极端梯度上升模型 支持向量机模型 集成模型 雅溪镇 8 285.30 1 928.64 12 934.92 6 158.25 6 117.03 9 036.40 黄村乡 2 553.49 1 480.30 2 973.48 2 425.94 2 243.00 5 756.30 仙渡乡 4 672.80 2 075.51 6 069.36 4 123.97 3 124.22 4 781.02 太平乡 3 912.68 1 766.31 5 149.49 4 004.16 1 847.48 4 573.60 老竹畲族镇 2 732.57 1 028.09 4 294.03 2 134.78 2 959.31 3 307.16 大港头镇 3 206.67 2 357.66 4 041.52 2 928.39 1 557.60 2 938.70 丽新畲族乡 2 438.82 734.35 2 835.63 1 759.87 2 007.23 2 867.84 峰源乡 1 672.26 3 317.47 1 636.69 3 613.79 1 500.91 2 711.95 双黄乡 2 553.49 1 480.30 2 973.48 3 403.79 2 005.94 2 666.86 高溪乡 2 018.83 981.71 2 070.36 1 495.76 1 345.03 2 192.75 紫金街道 1 938.95 733.06 1 994.35 1 433.92 1 355.33 2 069.07 岩泉街道 1 490.61 582.33 1 853.92 1 366.93 660.92 1 780.48 联城镇 1 360.49 506.32 1 462.26 1 015.21 1 414.60 1 734.10 碧湖镇 1 230.36 1 078.34 1 625.88 1 284.47 615.83 1 396.56 白云山林场 919.87 405.83 1 272.88 971.41 228.04 1 284.47 水阁街道 517.91 529.51 497.30 502.45 230.61 565.58 富岭街道 338.83 247.36 242.21 280.86 86.32 413.56 合计 41 843.93 21 233.09 53 927.76 38 903.95 29 299.40 50 076.40 Table 3. Potential Distribution Area of Taxuschinensis var. mairei in each township
3.1. 不同模型结果比较
3.2. 影响南方红豆杉分布的环境因子
3.3. 南方红豆杉潜在分布区面积
-
对比6个模型结果,集成模型的模拟效果最好,其Kappa值为0.80,准确率为0.90。集成模型结果显示:影响南方红豆杉在莲都区分布的主要环境因子为海拔高度,其次为归一化差分植被指数和年平均最少降雨量,南方红豆杉在莲都区的潜在分布区为5.01万hm2。目前,对于物种潜在分布区研究的空间分辨率主要集中在大尺度的空间上。本研究利用R软件和集成学习方法建立了90 m分辨率的莲都区南方红豆杉潜在分布区的集成模型,能够更好地应用到实际,并直观地反应南方红豆杉在莲都区的潜在分布区,取得较好的结果,对莲都区南方红豆杉的造林工作及资源保护具有指导意义。
-
对于某树种在某地是否适生,判定的标准是该树种能否在当地正常生长发育,繁殖后代,形成稳定的群落并长久生存下去。本研究选取的古树生存时间久,更能反映当地的生态环境,更适合参与建模。
本研究使用14个环境因子建模,但是在现实世界中,影响植物生长的环境因子远不止这些。分辨率为90 m的环境因子,在较小尺度下,影响物种分布的因子主要为地形、土壤及物种之间的交互作用等[20],但是在高分辨率下这类因子却较难获取[21],如能加入其他各类如土壤因子等影响植物生长的环境因子,相信能得到更准确的结果。
以往研究都是按照比例划分数据集,虽然可以重复多次划分,但是在理论上还是有数据泄露的可能。本研究在数据划分与验证上,使用k折交叉验证方法,其优点是可以完整利用整个数据集,虽然增加了运行时间,但提高了数据利用率,尤其适用于较小样本量的数据集。虽然Kappa和准确率能够很好地反应模型精度,但在现实中还有很多在建模过程中并未考虑的因素,HERNANDEZ等[22]和ENGLER等[23]提出,模型只是物种潜在分布的估计。本质还是预测研究,所以在实际的造林活动中,模型模拟的结果并不能当做唯一依据,必须要与当地实际情况相结合,遵循因地制宜,适地适树的原则来确定造林地点或树种。
极端梯度上升模型是近几年提出的一种新的算法,具有速度快,准确率高等优势。极端梯度上升模型和Stacking算法已经被广泛运用于文本分类、图像识别、金融等领域,但是由于在生态学领域人们对各种算法的关注度相对较少,并且使用这类算法较为困难,所以未见其在物种潜在分布模型中应用。本研究将其运用到物种潜在分布区的研究中,希望能够提供一些新的方法,但其中有很多功能,如参数调整、特征选择等,还有待深入研究。










 DownLoad:
DownLoad: