-
根据国家标准GB/T 18107−2017《红木》，红木共5属8类29种。由于不同种类的红木在表层宏观特征不具有唯一性，但在横切面上它们具有十分明显的结构差异，只有少部分红木如乌木的结构特征体现在弦切面上，因此，红木识别目前主要依据红木切片在光学显微镜下的结构特征差异[1]。目前，红木的特征识别主要是通用木材识别技术[2-3]，如红外光谱识技术[4-5]和气相色谱技术[6-7]。此类红木识别方法具有2个主要的缺陷：其一，根据红木切片照片的特征进行人工识别，识别的准确度受限于识别人员的专业素养和经验，特别是对于较为罕见的红木品种，时常发生不同识别人员识别结果不一致的情况；其二，现行的红木识别并没有结合红木的结构特征进行相关优化。由于不同种类红木的结构特征差异使得红木切片上的纹理特征不同[3]，这就可以运用图像识别技术来进行红木分类识别。王学顺等[8]、ESTEBAN等[9]、LAZARESCU等[10]、MOHAN等[3]等已将机器学习和一些图像识别技术应用于木材识别。卷积神经网络[11-12]作为目前图像识别领域中最先进的技术，利用该模型对红木切片纹理特征进行红木识别，可大幅降低红木识别的专业要求，又能提高红木识别率[13]。相比于传统的红木识别技术和一些特殊的技术如应力波[14-15]、热重曲线[16]等，这些方法的识别效果对所提取特征的表示性要求较高，为取得最优的识别效果还需对比众多分类算法[17-19]。卷积神经网络可以自动提取红木切片的纹理特征并分类识别。为了简化红木识别流程，提升识别精度，使用卷积神经网络对红木树种分类识别研究。
HTML
-
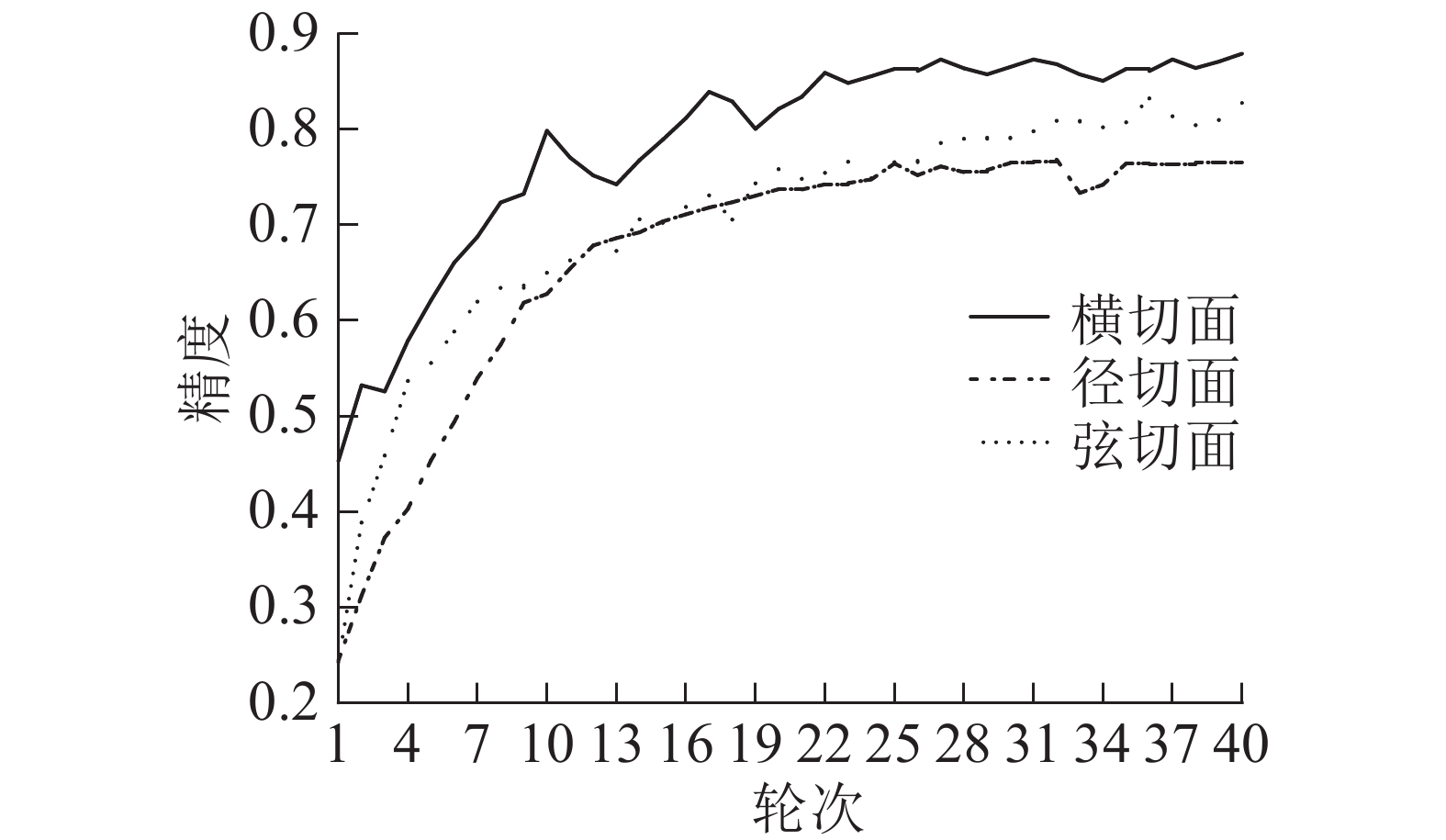
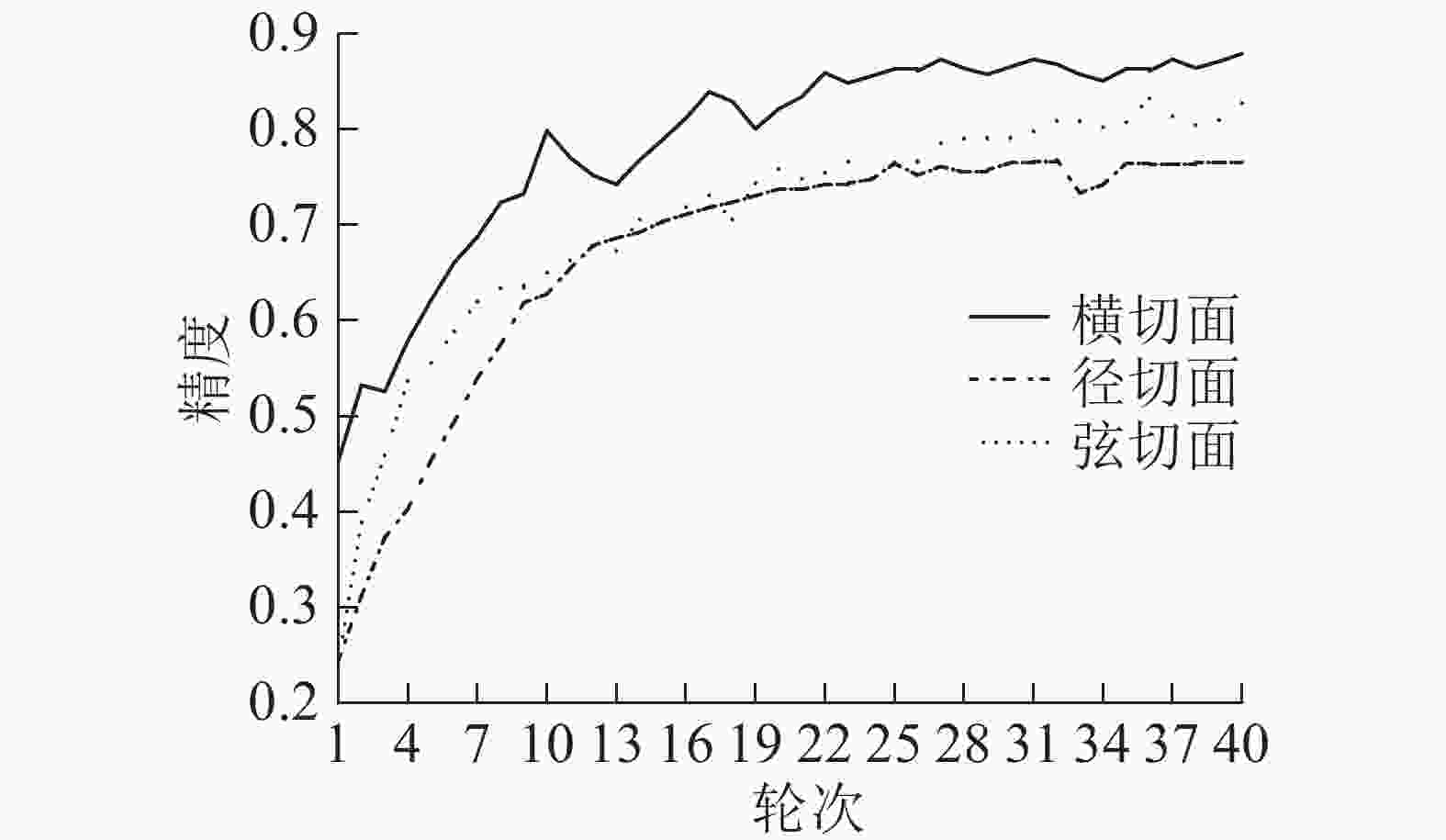
红木切片样本来自国家林业和草原局木材与木竹制品质量检验检测中心(昆明)实际检测业务中累积的数据，包括黄檀属Dalbergia和紫檀属Pterocarpus中交趾黄檀D. cochinchinensis、刀状黑黄檀D. cultrata、卢氏黑黄檀D. louvelii、巴里黄檀D. bariensis、奥氏黄檀D. oliveri、大果紫檀P. macrocarpus、檀香紫檀P. santalinus等7种红木的376个样本。由于在实际木材检验中，结合宏观特征与横切面结构特征就可确定许多红木种类，因此，横切面(显微镜30倍)样本数据较多。在分别针对红木的横切面、径切面、弦切面的部分数据初步建立卷积神经网络时，同样发现针对横切面的数据识别模型精度较高(图1)。因此，选用横切面数据做识别训练。
Figure 1. Comparison of recognition accuracy
-
受试剂的影响，切片图像存在气泡和空白，很容易产生噪声数据影响识别精度，因此设计RGB图像空白处裁剪算法。算法需要先行设置空白率r，1幅图像中1行的白色像素数在整行所占的比列小于r后，则认为从这一行开始包含有效信息，此行后的像素行不再进行裁剪。处理流程为先拷贝图像A的副本A2，对A2进行灰度化处理，使得空白处像素点的值接近于1。从左到右逐列比较空白率，得出x1；再从右到左逐列比较空白率，得出x2；同理从上到下、从下到上比较空白率，得出y1和y2。依据(x1, x2, y1, y2)得矩形的4个点，依据4个点的位置裁剪目标图片(图2)。
Figure 2. Comparison of P. santalinus cross section before and after blank cutting
-
切片在取样时可能存在薄厚不均，在放入载玻片操作时会导致切片折叠产生黑块，且红木切片的颜色很容易受试剂的影响。因此，先将图像从RGB空间转换到HSV空间[20]，再在V通道进行直方图均衡化处理后再转换到RGB空间。均衡化处理后，图像上的黑块变淡、纹理清晰(图3)。
Figure 3. Comparison of D. oliveri cross sections before and after histogram equalization
-
切片大小不一会造成切片图像尺寸和旋转方向不一致，卷积神经网络模型需要输入固定尺寸和方向的图像，会导致图像因缩放纹理结构发生形变，同时样本数量有限，因此提出旋转随机裁剪法来统一和扩充样本。处理流程为每张图片旋转36次，每次旋转10°，每次旋转都依据图片的面积比裁剪出相应数量的子图。为了使子图尽可能小同时又包含更多信息，子图的尺寸被统一为(224, 224)，如输入图像的尺寸为(w, h)，共裁剪出的子图数量n为wh/(224×224)。经过空白处理后的图像在边角部分仍存在连续的空白区块，这使得旋转后的图像存在不少黑色填充区域，导致随机裁剪出的部分图像存在连续的黑色或白色区域。为了减少这种影响，使用白点率、黑点率丢弃法，统计图像中白色或黑色像素点的数量，如果所占比例超过阈值就直接丢弃。黑点丢弃的阈值设置为0.06，考虑到红木切片管孔的空白部分，白点丢弃得阈值为0.17，处理如图4所示。最终，扩展得到可用样本21 495个(表1)。将这些样本按照3∶1∶1的比例划分为训练集、验证集、测试集3部分。
红木种类 原始数据数量/个 扩充后数量/个 交趾黄檀 56 2 673 刀状黑黄檀 53 2 535 卢氏黑黄檀 49 3 102 大果紫檀 51 4 259 奥氏黄檀 52 2 857 巴里黄檀 57 3 216 檀香紫檀 58 2 853 Table 1. Number of samples
Figure 4. Expanded D. bariensis cross section pictures
1.1. 图像采集
1.2. 图像预处理
1.2.1. 去除图像气泡和空白
1.2.2. 图像直方图均衡化处理
1.2.3. 图像尺寸与旋转处理
-
卷积神经网络通过构建人工神经网络[21]，模拟人类的大脑思考过程自动从带有标签的数据中学习特征，进行分类预测。卷积神经网络由3种网络层结构组成，前面部分由卷积层、池化层交替连接，后面部分由全连接层组成。利用卷积神经网络模型进行红木切片识别，先要使用被标注过的切片样本训练模型，然后通过代价函数评估模型的拟合能力，并以反向传播的过程不断调试模型参数，最终使得模型能提取并拟合红木切片的结构特征。
-
红木切片的识别模型有12层，卷积核的数目逐层增多。连续的2个3×3的卷积核，使卷积核的视野与5×5的卷积核一致，而运算量减少28%；同样为了减少卷积的运算量，将裁剪后的图像统一缩放到150×150。模型在卷积层中，设计了多个卷积通道，能以不用角度的视野提取特征。为了能对边缘像素点提取特征，将卷积运算模式设置为填充模式，步长为1。卷积之间加入2×2的最大池化层(maxpool)，选择矩阵中每个2×2区块的最大值为下一层输入，能提取显著特征，减小矩阵尺寸，最后一个卷积层与全局平均池化层(global average pool)相连接将输入矩阵从(37, 37, 128)直接变为(128)，充分减少了模型计算量。模型采用线性整流函数(relu)作为激活函数，克服网络层次变深而梯度消失的情况。最后3层为全连接，最后一层的特征利用归一化指数函数(softmax)做多分类预测。最终模型结构如图5所示，各层参数如表2所示。
类型 核数量 尺寸/步长 输入 输出 类型 核数量 尺寸/步长 输入 输出 卷积层 16 3×3/1 150×150×3 150×150×16 池化层 2×2/2 37×37×64 18×18×64 卷积层 卷积层 128 3×3/1 18×18×64 18×18×128 池化层 2×2/2 150×150×16 75×75×16 全局平均池化层 18×18×128 128 卷积层 32 3×3/1 75×75×16 75×75×32 全连接 128 158 卷积层 全连接 158 58 池化层 2×2/2 75×75×32 37×37×32 全连接 (输出) 58 7 卷积层 64 3×3/1 37×37×32 37×37×64 卷积层 Table 2. Layer parameters of the model
Figure 5. Model structure
-
模型的训练过程实际上是将网络输入以正向传播的过程输入图像逐层提取特征，在卷积层a中，卷积核w以滑动窗口的方式从矩阵最右上角的点运算到最后1个像素点，窗口覆盖的范围与对应的卷积核参数相乘，乘积结果之和加上偏移量b赋值到对应矩阵中卷积核中心的位置，然后在使用激活函数σ将卷积的输出结果z进行激活操作。卷积层的前向传播过程为：
式(1)中：L表示卷积层的层数，zL表示第L层卷积操作的输出，aL表示第L个的卷积层的输出结果。上述只是描述了单个卷积核连接的过程，网络层有多个卷积核时，每个卷积核多需要经相应的运行，并将所有卷积核的输出累加作为卷积层的输出。
选用的池化层大小是2×2，其运算是将一个n×n的矩阵划分成多个2×2的子区域，然后选取每个子区域的最大值输出一个
$\displaystyle\frac{n}{2} \times \displaystyle\frac{n}{2}$ 的矩阵，整个过程中并没有参数需要调整。全连接层$f$ 的传播过程为：式(2)中：当
${f^{L - 1}}$ 层的神经元数为n，${f^L}$ 层的神经元数为m时，w的形状为n×m。全连接的最后一层选用归一化指数函数作为激活函数，提取结果映射到[0, 1]概率区间与标签编码形成的独热码编码比较，得出拟合损失。再利用自适应矩估计(adaptive moment estimation, Adam)优化器将比较结果以反向传播的过程逐层调整网络层参数，使得模型的拟合损失逐步变小。自适应矩估计优化器实现简单计算高效，能自动调整学习率，减少损失函数的震荡，使精度不断上升。 -
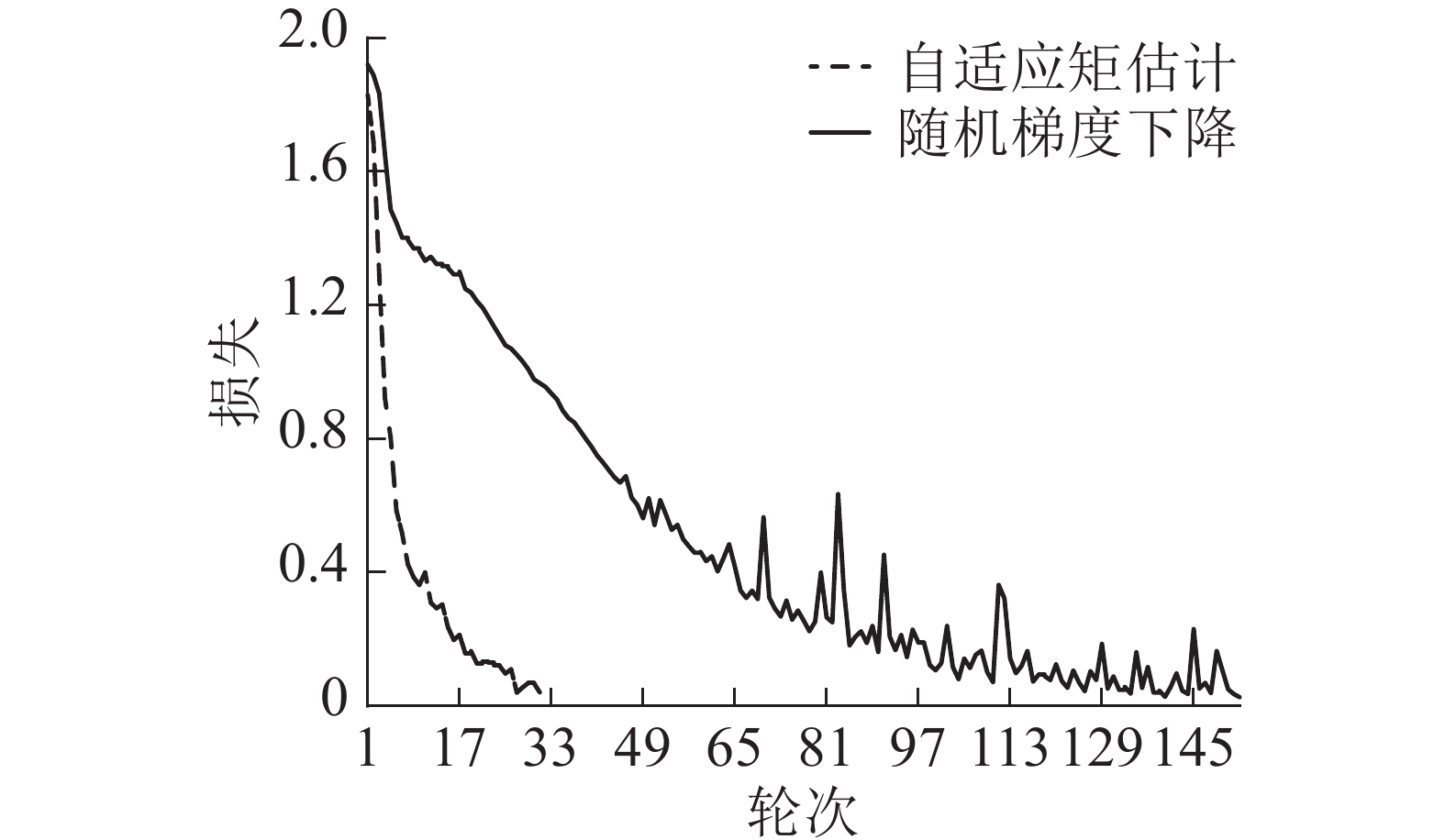
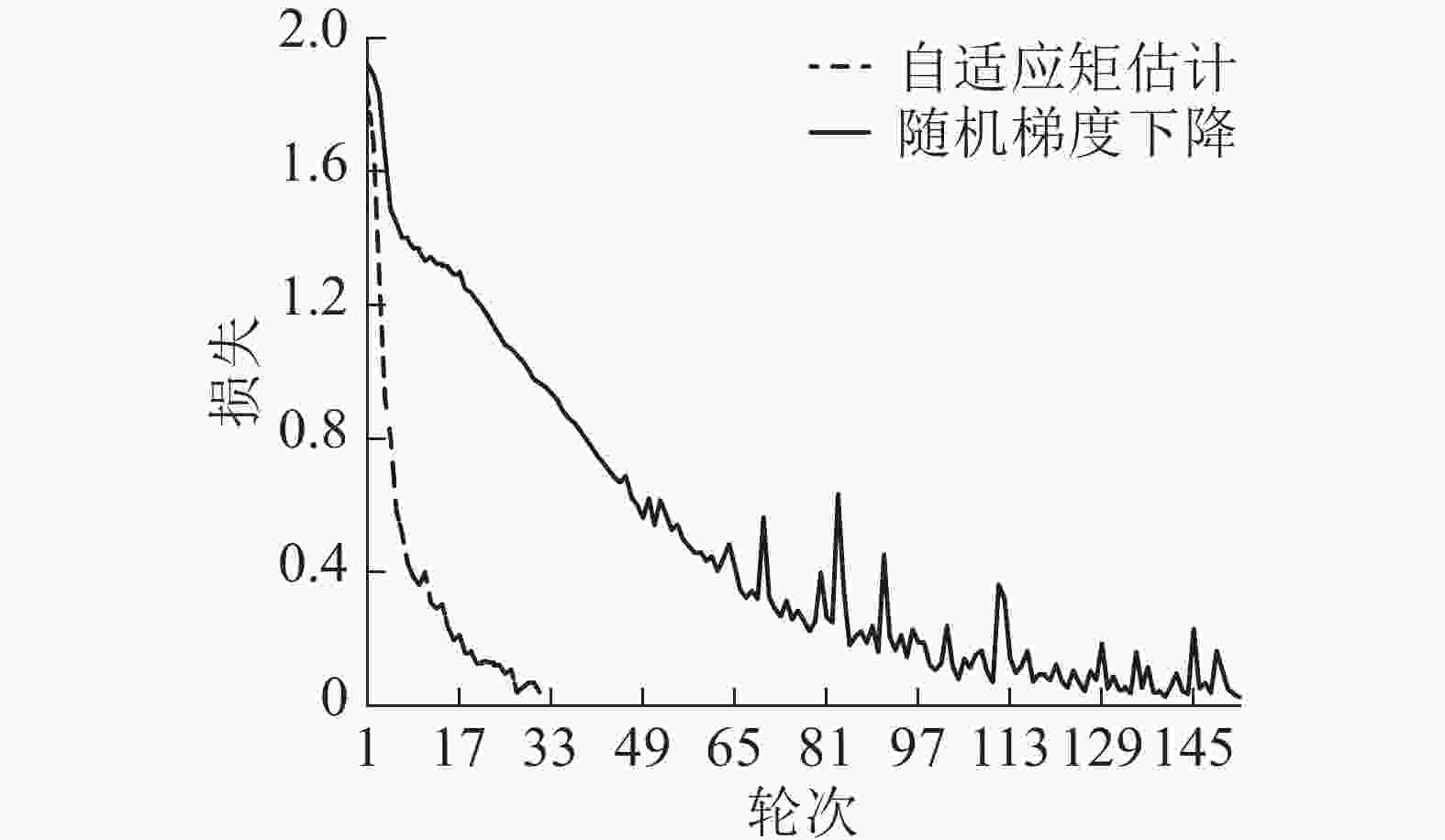
在训练时为了尽量精简模型的体量，起初每层的卷积核通道都比较少，训练出来模型的精度不高。每次训练结束后都依据损失函数的值，适度调整优化器的学习率和衰减率、变更卷积通道数、修改全连接层结构，使模型的测试精度不断上升，直到精度符合实验预期目标时终止调参过程。模型最初选用的优化器是随机梯度下降法(stochastic gradient descent, SGD)，收敛速度较慢，在换成自适应矩估计优化器后模型收敛速度变快，且精度有所提升，如图6所示。在起初模型存在过拟合，引入随机失活(dropout)机制降低过拟合，但调整后又出现数据泄露假象，训练集的重要特征丢失导致验证集精度高于训练集，最终通过降低随机失活的神经元数量的权重加以解决，并经过试验最终采用随机失活的权重为0.2。
Figure 6. Comparison of loss between two optimizers
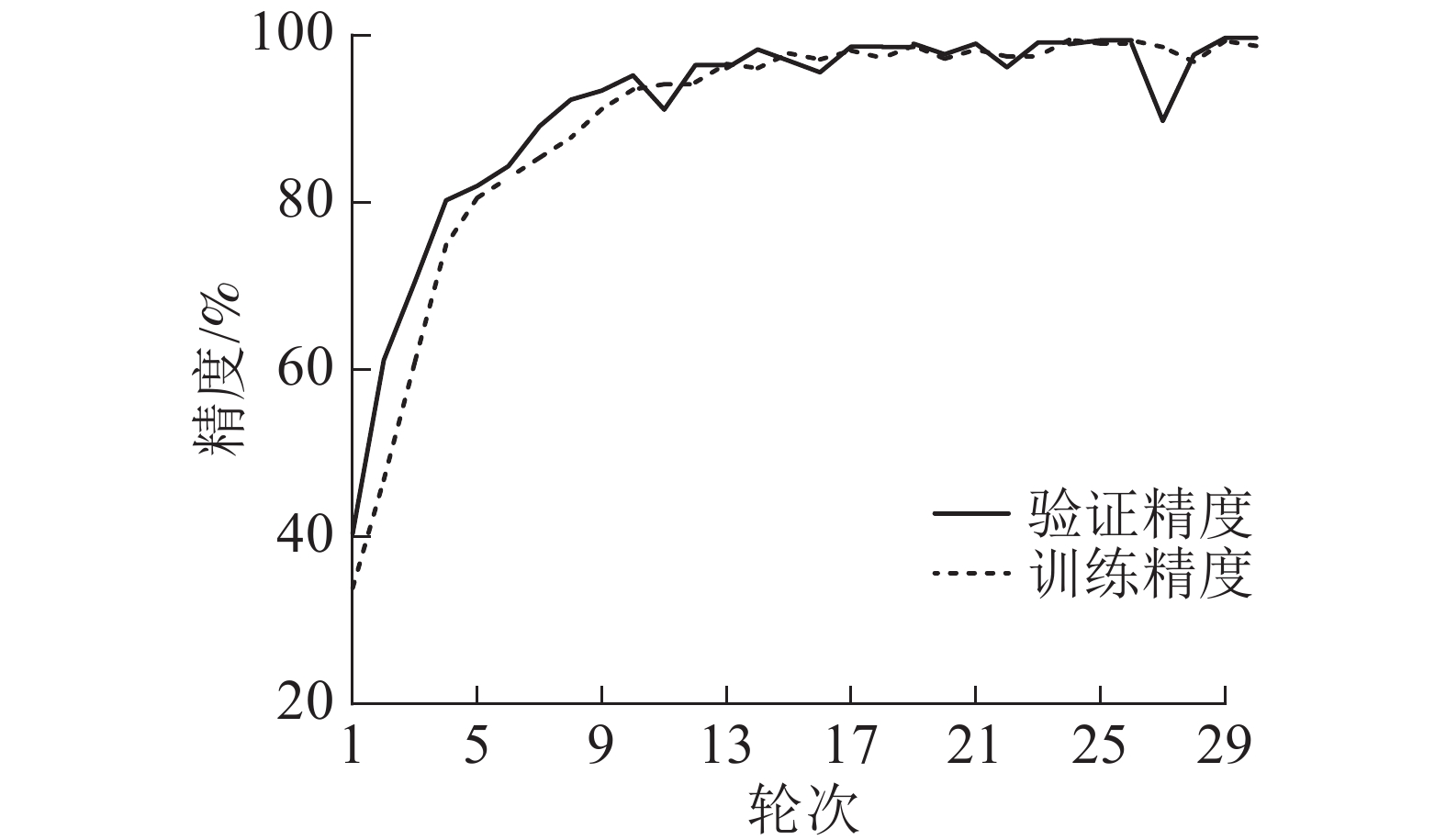
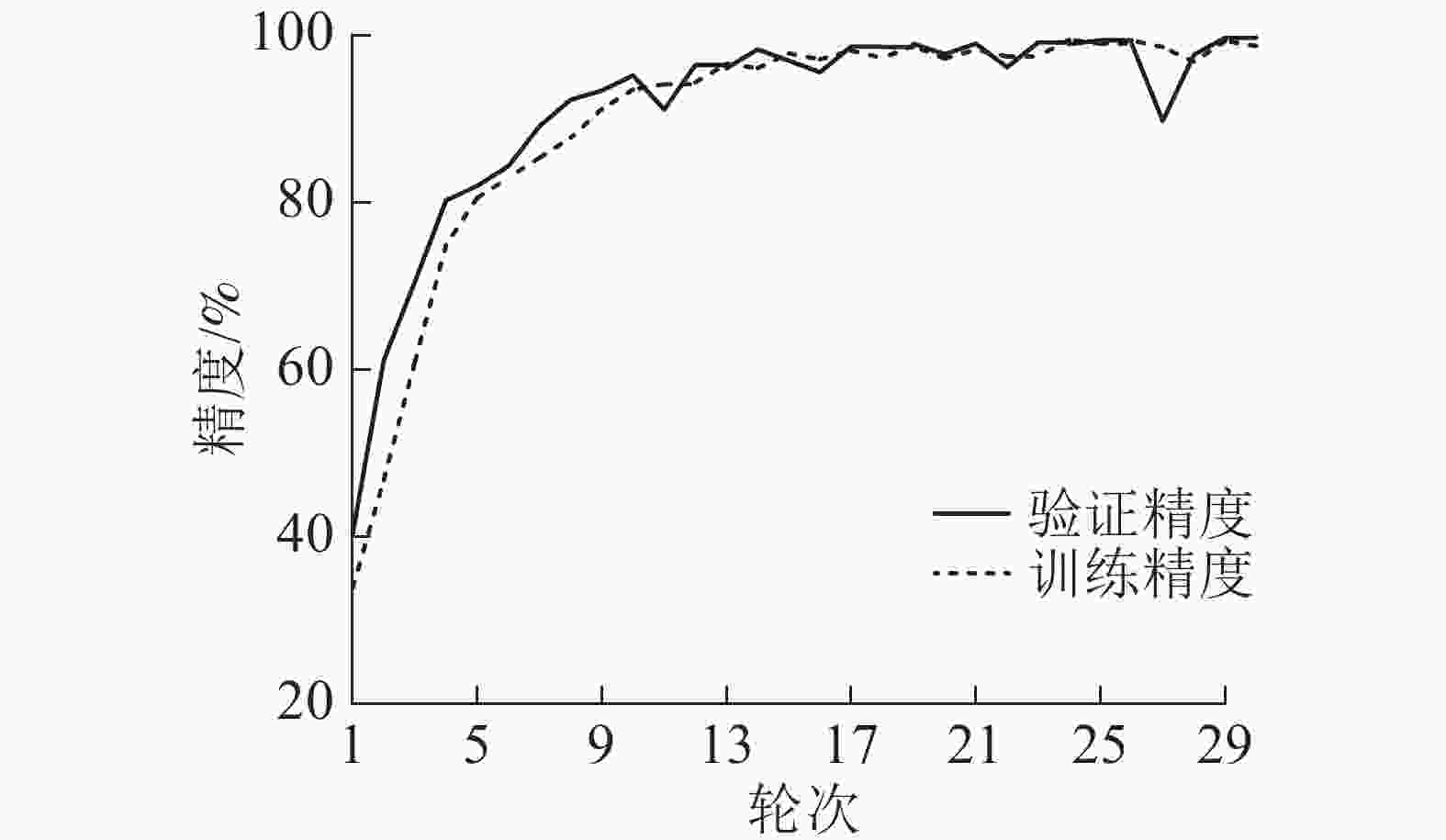
输入图像的尺寸是150×150的RGB三通道图像，在经过卷积层时图像矩阵通道数变成和卷积核数目一致，经过第1个池化层后数据矩阵尺寸变为75×75×16，再通过卷积层、池化层后数据矩阵尺寸变为18×18×128的三维数组。而其后的全连接层输入必须是一维向量，因此使用全局平均池化层在每个18×18的矩阵中求得平均值，将三维数组重塑为128维的向量，第1个全连接层的输出是158。数据再经过卷积层和全连接层时，都利用线性整流函数进行激活操作，而通过最后一个全连接层输出时使用归一化指数函数将数值映射到概率[0, 1]空间。如图7所示：模型的训练轮次为30、批大小为32，模型在第29个轮次后，精度稳定在99%，达到收敛状态。
Figure 7. Accuracy changes during training
2.1. 模型结构设计
2.2. 模型训练原理
2.3. 实验过程
-
如表3所示：利用4 299个测试样本测试后，有4 273个样本预测正确，仅有26个红木样本预测错误，准确率高达99.4%。本方法不需要对特征建立多个识别模型，能够自动提取适合模型分类识别的特征，使用更为便捷。
红木类别 样本数量/个 准确率/% 交趾黄檀 535 99.5 刀状黑黄檀 507 98.7 卢氏黑黄檀 620 99.3 大果紫檀 852 99.6 奥氏黄檀 571 99.9 巴里黄檀 643 100 檀香紫檀 571 98.9 平均值 99.4 Table 3. The recognition accuracy of each category
此外，为进一步论证本方法模型的可靠性，选用卷积神经网络模型AlexNet[22]和VggNet[23]，分别运用迁移学习技术修改它们的最后一层全连接层的数量，微调其全部全连接层的参数建立模型与本方法模型进行了对比。从表4可以看出：本模型参数更少、精度更高。
网络名称 输入尺寸 卷积核个数 卷积参数 全连接参数 总共参数 验证精度/% AlexNet 227, 227 1 152 2 469 696 7 454 508 9 924 204 92.4 VGG16 150, 150 4 224 14 714 688 6 635 308 21 349 996 93.5 本模型(CNN) 150, 150 352 146 206 29 747 175 953 99.4 Table 4. Comparison of model parameters
-
本方法准确率达99.4%，证明了卷积神经网络技术用于红木分类识别的可能性。此外，本方法模型在同样的数据情况下，虽然在调参优化与训练时间大于迁移学习模型，但泛化能力明显高于迁移学习模型，证明了自建模型在应用上优于迁移学习模型。
但是，本方法还存在以下问题：针对交趾黄檀、巴里黄檀、檀香紫檀等7种红木达到实用级的准确率，但要满足实际应用还需更多更全的样本，以保证对于全红木种类的识别精度；模型给定的输入必须为显微镜30倍拍摄图片，在图像输入到模型前可以针对图像的拍摄倍数进行适当缩放，以达到显微镜30倍拍摄的效果；识别结果中仅包括种类信息，无法给出相应的判别依据，后续可借鉴目标检测网络的思想，构建语义化的红木切片识别模型，达到自动识别红木类型并框选出相应红木结构特征的效果。
DownLoad: