Site quality evaluation of Cunninghamia lanceolata plantation based on generalized algebraic difference approach and factor selection

研究区位于浙江省丽水市庆元县(27°25′~27°51′N，118°50′~119°30′E)。2018年庆元县森林覆盖率高达86.06%，森林蓄积量达1321.6万 m³。该地区大部分为山区，海拔为253~1 758 m，地势由东北向西南倾斜。该地区属亚热带季风气候，年均气温为17.4 ℃，年均降水量为1 760.0 mm，无霜期为245.0 d。土壤类型以红壤、黄壤为主，有少量潮土和粗骨土。庆元县森林植被种类丰富，由巾子峰、白坎、百丈3个独立区块组成了大型森林公园，主要针叶树种为福建柏Fokienia hodginsii、南方红豆杉Taxus mairei、杉木等。

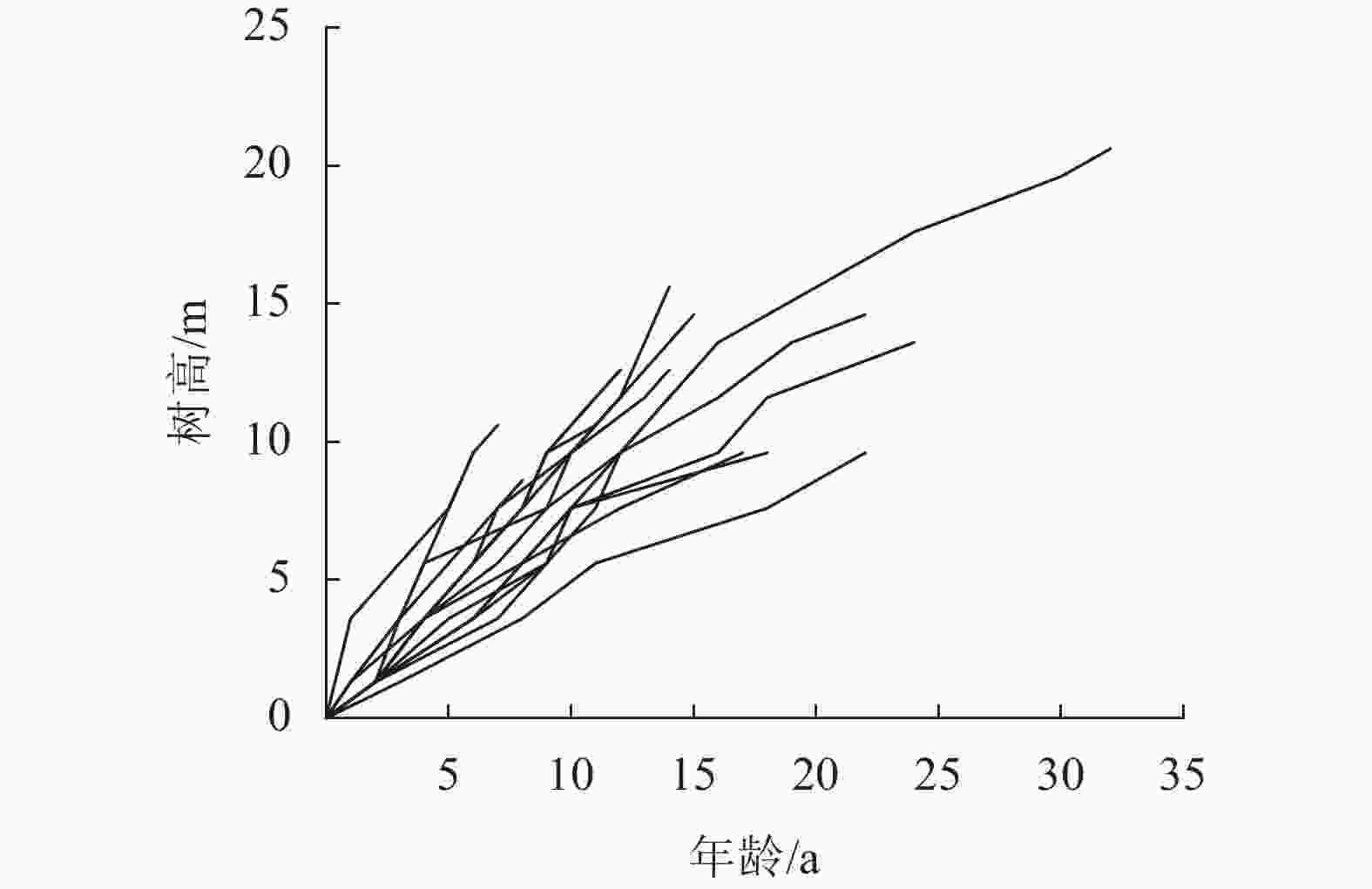
研究数据包括庆元县周边的杉木标准地解析木数据和庆元县杉木二类调查小班数据。解析木数据主要用于地位指数模型的构建。2015年充分考虑了现有林分的立地质量、年龄、密度等因素，设置了18块20 m×20 m具有代表性的林分标准地。每个标准地挑选1株未受损伤的、未受压的、健康的优势木作为研究对象，对其伐倒并截取圆盘进行树干解析。将单株解析木中数据进行排列，共得117个树高和年龄数据，图1是通过解析木得到的树高和年龄分布图。

Figure 1.  Parse tree data statistics

解析木具有代表性，通过解析木构建的地位指数能在一定程度上反映整体小班立地水平。为进一步探索地位指数与立地因子之间的关系，从庆元县2019年度二类调查数据中获取杉木小班资料。对原始数据进行数据完整性检查，以3倍标准差为标准剔除各项异常数据，并删除数据集的缺失值，剔除变量为0的小班数据，得到杉木小班数据4 920条。杉木小班的立地因子包括海拔(263~1 652 m)，地貌(低山、中山)，坡度(缓坡、斜坡、陡坡、急坡)，坡向(阴坡、半阴坡、半阳坡、阳坡)，坡位(上坡、中坡、下坡)，土壤类型(红壤、黄壤)，土层厚度(1~115 cm)，腐殖质厚度(厚、中、薄)。

将地位指数模型应用于二类调查小班的地位指数预测时，需要林分优势木高数据，而二类调查数据中不具备林分优势木高调查数据，因此使用标准地调查数据构建平均木和优势木高模型，计算公式为D=1.054H+2.174，决定系数$ ( $R²)为0.94，其中D为林分优势木高，H为林分平均高，从而得出优势木数据用于小班地位指数的预测。

在地位指数模型构建中，需要选择用于建立广义差分方程的基础理论方程。在基础理论方程的选择中，SCOLFORO等^[16]选择了Korf、修正Weibull等多个理论方程用于巴西桉树Eucalyptus robusta的地位指数研究。SEKI等^[17]运用Richards和Korf方程实现了土耳其克里米亚松Pinus nigra地位指数的模型研究。综合已有研究成果，本研究采用修正Weibull、Korf、Richards方程作为地位指数构建基础模型。

式(1)~(3)中：h为优势木高；t为林分年龄；a、b、c为模型参数。

对于地位指数而言，需要具备以下性质：①多形性；②基准年龄无关性；③具有多条水平渐近线。但使用代数差分法推导的差分地位指数模型时，无法同时满足水平渐近线与多形性的要求。而广义代数差分法允许在推导时设置多个自由参数，能够满足多条水平渐近线和多形性2个性质。

采用广义代数差分法推导步骤为：①选择生长方程为基准方程，并根据理论或经验指定其中的参数为自由参数。②提出一个与立地质量相关的量$ {X}_{0} $，并假设自由参数与$ {X}_{0} $之间具有函数关系。③将上述函数关系带入基准方程，从中解出$ {X}_{0} $的表达式。对于无法求得显式解的$ {X}_{0} $，利用迭代法进行求解。④将地位指数和基准年龄分别带入表达式中的树高和年龄，并将表达式带入基础方程的$ {X}_{0} $，推导出差分地位指数方程。

以修正Weibull为例，参数a影响曲线在时间轴上的位置，c表示曲线的形状参数，影响曲线的弯曲程度，因此选择参数a、c为自由参数。并假设a与$ {X}_{0} $存在指数关系，c与$ {X}_{0} $之间存在线性关系，$ {c}_{1} $、$ {c}_{2} $为线性关系的参数，将基础方程转换为：

从中解出$ {X}_{0} $的表达式为:

式(5)中：$ {t}_{1} $为指定年龄，$ {h}_{1} $为指定年龄下的优势木高，当t₁为基准年龄时，h₁为地位指数。令式(4)中，$ t={t}_{2} $, $ h={h}_{2} $, 其中$ {t}_{2} $为预测年龄，$ {h}_{2} $为预测年龄下的优势木高，将式(5)代入式(4)，得到差分方程模型，表达式为：

在3个基础方程中，b代表生长率参数，是林木固有属性，与立地关系不紧密，因此将a、c指定为自由参数。在理论方程基础上，使用广义代数差分法推导出6个差分方程，如表1所示。

立地质量与立地因子存在密切的关系^[18−20]，从立地因子中提取出主导因子，能够高效地评价林地立地质量。林分的立地质量与立地因子间通常是复杂的非线性关系，传统方法简化了假设条件，难以达到理想的效果。因此，在立地因子的选择上，要选择影响地位指数，又易于测量和获取的数据，同时能保证一定精度的因子。已有研究表明：采用随机森林提取的特征因子能够在不需要先验知识的情况下准确表达因子与林木生长的非线性关联关系^[15]。因此，本研究使用构建好的地位指数模型来计算每个杉木小班的地位指数，使用随机森林算法从立地因子中筛选出影响地位指数的主导因子，并与传统的偏相关分析结果进行比较。

随机森林是基于决策树的机器学习算法^[21]。随机森林能够有效地处理非线性、交互作用、共线性等问题，可以用于回归预测，还可以进行因子特征选择。它主要提供了2种因子特征重要性度量方法，分别是基于内置和置换的因子特征选择方法。

①基于内置的因子特征选择。该方法通过计算随机森林中所有回归树的节点平均值减少程度来确定特征的重要性，其使用基尼指数(B)来测量。在本研究中，用V表示基于内置的特征重要性方法。立地因子j在构成随机森林的回归树子节点m上的重要性，即节点m分枝前后的基尼指数变化量(V_jm)为：

式(7)中：$ {B}_{l} $和$ {B}_{r} $表示分枝后2个新节点l、r的基尼指数，如果立地因子j在第$ i $棵回归树中出现的节点在集合$ M $中，立地因子$ j $在第$ i $棵回归树上的重要性(V_ij)为：

因此对拥有n棵回归树的随机森林而言，立地因子j的重要性评分(V_j)为：

②基于置换的因子特征选择。该方法随机对每个特征进行排序，并计算模型性能的变化，对于特征重要性的评判取决于该特征被随机重排后，模型表现评分的下降程度。过程为：输入训练后的模型E和样本集D，对于样本集D的每个立地因子$ j $，在T次重复实验中的每次迭代次数$ r $，随机重排列立地因子$ j $，构造一个随机重排后的数据集$ {D}_{{c}_{t,j}} $，然后计算模型E在数据集$ {D}_{{c}_{t,j}} $上的参考分数$ {S}_{tj} $，特征$ j $的重要性(P_j)计算如下：

式(10)中：s表示模型的参考分数；T表示实验次数；$ r $表示迭代次数；$ {S}_{tj} $表示选取第t个样本第 j列计算后的参考分数。基于随机森林的因子特征选择分别采用Python中的feature importance和permutation importance进行计算。

当2个变量都与第3个变量相关时，将第3个变量的影响剔除，采用偏相关系数分析另外2个变量之间的相关程度。偏相关系数绝对值越大(越接近1)，表明变量之间的线性相关程度越高，反之越低。本研究运用SPSS 22计算各个立地因子与优势木高的偏相关系数。

使用R语言完成地位指数模型参数的估计和统计检验。在地位指数建模中，使用scorecard包，将数据集分为建模样本与检验样本，其中建模样本占总数据的70%。通过决定系数(R²)评估地位指数模型拟合优度。

采用均方根误差、平均绝对误差、残差对模型进行检验，均方根误差用于反映地位指数模型拟合的误差，平均绝对误差用于反映模型对独立样本的预测能力，残差反映实际优势木高值与估计值之间的差，具体计算公式参考文献[22]。

如表2所示：通过广义代数差分法构建的差分方程中，除M6外，其余拟合结果均较好。以修正Weibull作为基础方程的广义代数差分法的差分方程中，M1、M2的决定系数均达0.99，且拟合系数均通过显著性检验，其中M2比M1拟合效果更好。因此M2可选作为下一步使用的地位指数模型；以Korf方程为生长方程的广义代数差分法拟合中，M3、M4方程的拟合效果较好，但拟合系数并未通过显著性检验，因此不考虑将M3、M4作为下一步进行比较的方程。以Richards方程为基础的广义代数差分法拟合中，M5拟合结果优于M6，且M5的平均绝对误差明显小于M6，说明M5的预测能力更强。因此，综合各项指标，将M2、M5作为较优模型，进行进一步检验。

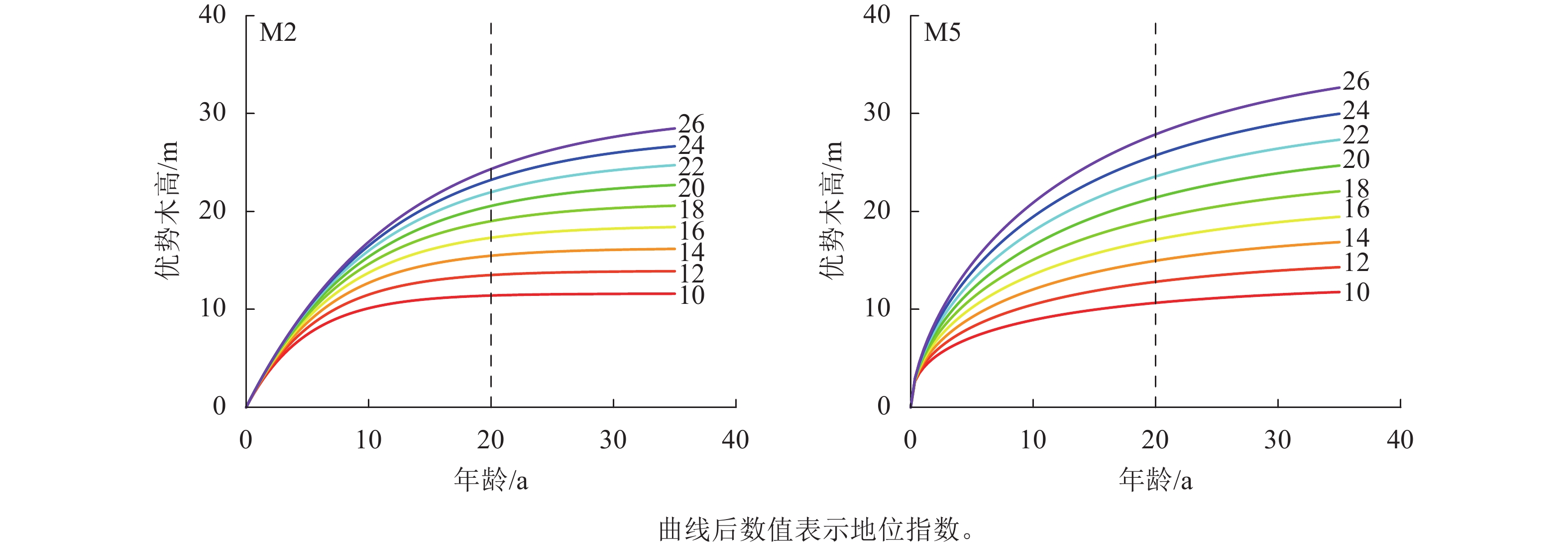
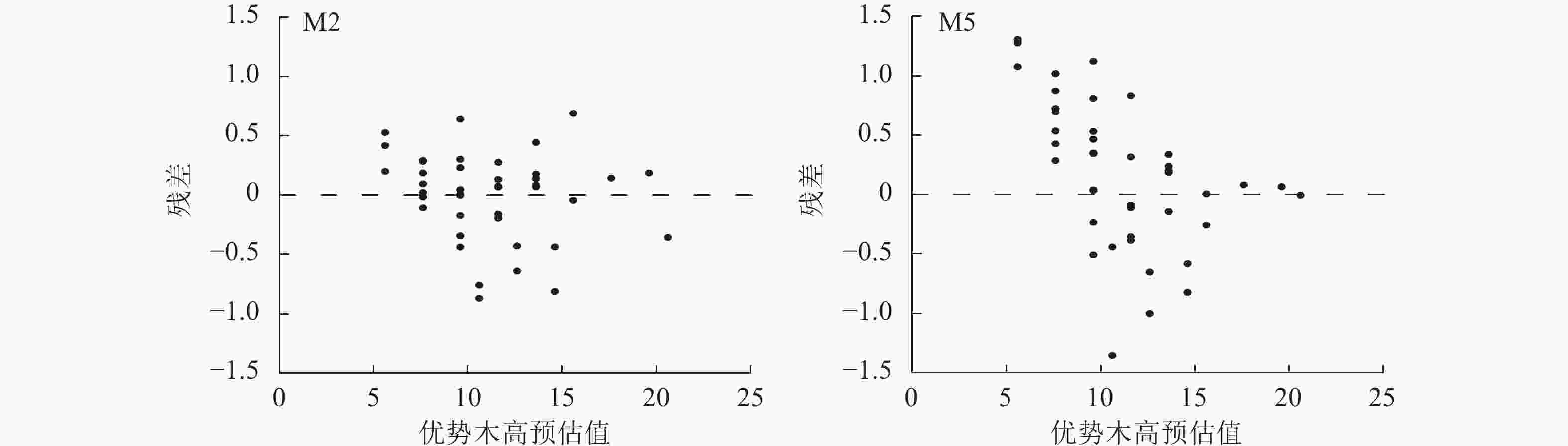
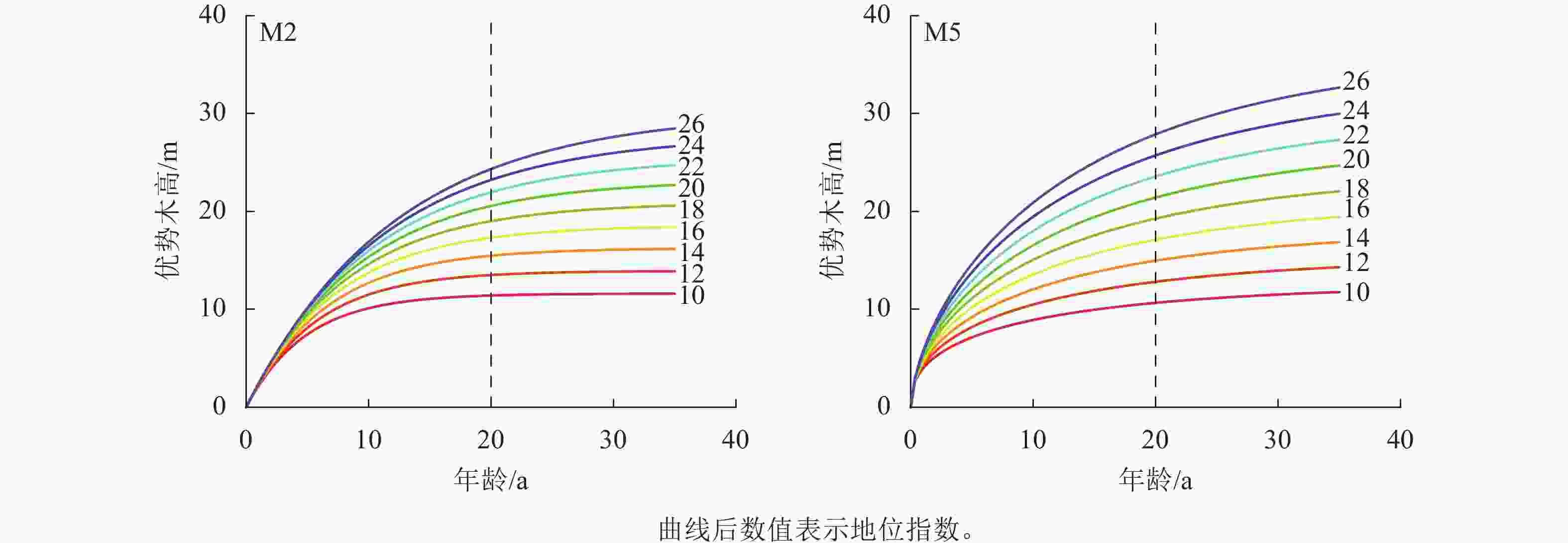
从图2可知：模型M2、M5的残差分布均较为均匀，大部分集中分布在X轴附近。在杉木优势木高较低时，模型M2、M5的拟合残差绝对值较大，为0.5~1.5，而随着优势木高的增大，残差分布的范围呈趋势性减少，因此，M2、M5可用于进行地位指数模型构建。在残差分析上，M2、M5之间精度差距很小，通过绘制以20 a为基准年龄的地位指数曲线簇对方程进一步分析，设定级距为2 m，地位指数为10~26 m (图3)。模型M2具有多条水平渐近线，但图像为非S型的单型生长曲线，在低龄高速生长后，林木生长趋于平缓，近成熟时，生长速率趋近0，这与杉木达到成熟的实际不一致。模型M5的地位指数曲线簇具备多形性，满足地位指数越高，低龄优势木生长越快的实际情况，并呈现林木年龄越趋近20 a，曲线越趋近于平缓的情况，是理想的地位指数模型。在模型检验上，M2、M5之间的差异性不大，而在预测能力上，M5更符合实际的状况。因此选用M5作为最优的地位指数模型，进行下一步研究。将预估参数代入模型M5的$ {X}_{0} $中，并将所得代入差分方程，其表达式为：

Figure 2.  Residuals against predicted dominant tree height for model M2 and M5

其中$ ，{t}_{1} $为指定年龄，$ {h}_{1} $为指定年龄下的优势木高，当$ {t}_{1} $为基准年龄时，$ {h}_{1} $为地位指数；$ {t}_{2} $为预测年龄，$ {h}_{2} $为预测年龄下的树高。

Figure 3.  Site index curves generated with difference site index model M2 and M5

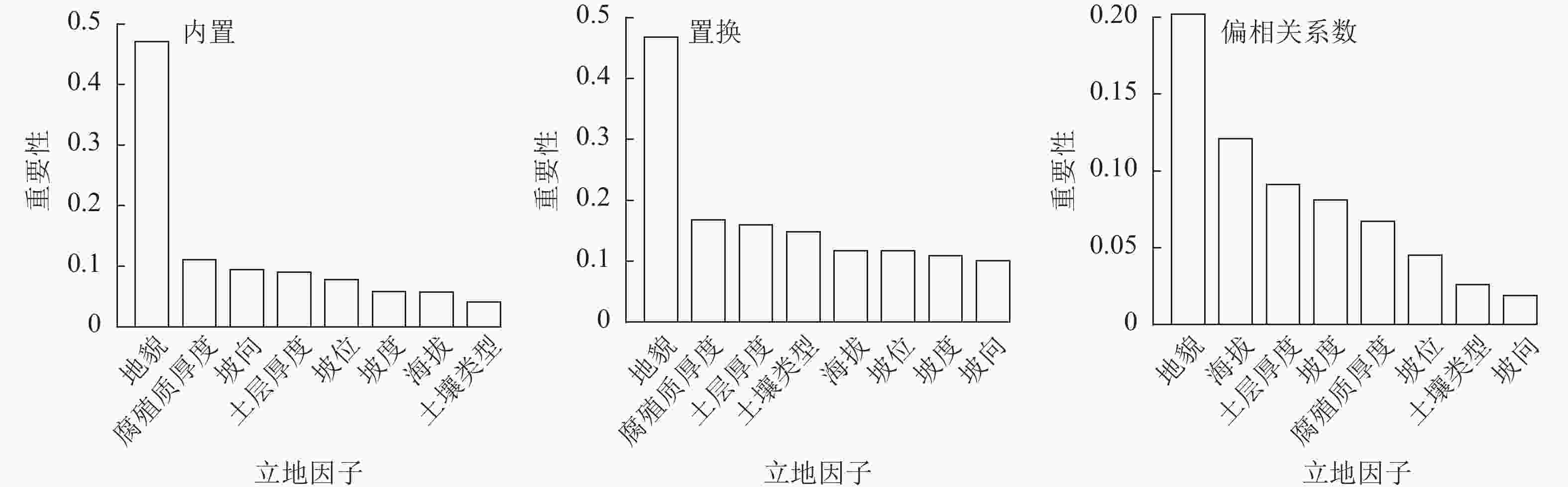
依据基于内置的因子特征得出：各因子对立地质量的影响程度从大到小依次为地貌、腐殖质厚度、坡向、土层厚度、坡位、坡度、海拔、土壤类型。其中重要性占比地貌为0.471，腐殖质厚度为0.111，坡向为0.094，土层厚度为0.090，坡位为0.078，坡度为0.058，海拔为0.057，土壤类型为0.041。依据基于置换的因子特征得出：各因子对立地质量的影响程度从大到小依次为地貌、腐殖质厚度、土层厚度、土壤类型、海拔、坡位、坡度、坡向。其中重要性占比地貌为0.468，腐殖质厚度为0.168，土层厚度为0.160，土壤类型为0.148，海拔为0.117，坡位为0.117，坡度为0.109，坡向为0.101 (图4)。

Figure 4.  Site factores importance ranking based on feature importance, permutation importance and partial correlation

依据偏相关系数对立地因子进行特征性选择得出：各因子对立地质量的影响程度从大到小依次为地貌、海拔、土层厚度、坡度、腐殖质厚度、坡位、土壤类型、坡向。其中重要性占比地貌为0.202，海拔为0.121，土层厚度为0.091，坡度为0.081，腐殖质厚度为0.067，坡位为0.045，土壤类型为0.026，坡向为0.019 (图4)。

通过基于偏相关系数的因子特征选择方法得到前3个因子的贡献度为41.4%；通过基于内置的因子特征选择方法得到前3个因子的贡献度为67.6%；通过基于置换的因子特征选择方法得到前3个因子的贡献度为79.6%(表3)。根据因子选择贡献最高的立地类型进行划分，选取地貌、腐殖质厚度、土层厚度作为主导因子，进行立地类型划分与立地质量评价。

采用地位指数模型预测每个小班的地位指数，根据地位指数值，采用四等分，根据需要将地位指数数值划分为优(＞14.31)、良(＞9.54~14.31)、中(＞4.76~9.54)、差(≤4.76 ) 4个等级。

按照因子特征对庆元县杉木立地进行分类，分别采用地貌、腐殖质厚度、土层厚度来进行立地类型划分，共划分出17个立地类型(表4)。由表4可以看出：庆元县杉木立地质量等级整体属于良好，共有2 564块小班立地质量处于良及以上，占比约52%。说明研究样地的立地水平良好，总体适宜杉木生长，可以进行一定的人工抚育提高林分生产力。

在地位指数模型构建中，广义代数差分法是当前较为理想的方法。庆元县地处浙江省西南地区，杉木生长速度良好，具有一定的代表性。通常认为，分布在长江以南的杉木在20 a左右已经达到生长高峰，这与本研究构建的地位指数模型相一致，而在趋近20 a基准年龄下，曲线逐渐趋于平缓，曹元帅等^[7]、牛亦龙等^[22]也得到了相似的研究结果。本研究选取以Richards为基础方法的广义代数差分方程，构建可用于预测庆元县杉木林达到预测年龄下的优势木高的地位指数模型，模型精度较高，形成的多形地位指数曲线符合杉木的生长特性，可以较好地预估当地的杉木林地位指数。

确定主导立地因子是立地质量评价与立地分类中的一项重要工作。张沛健等^[23]研究得出：影响雷州半岛-海南岛沿海台地地区尾细桉Eucalyptus urophylla×E. tereticornis生长的主要立地因子是土壤质地、成土母岩和土壤密度；郭艳荣等^[13]研究表明：影响杉木人工林生长的主导因子为土层厚度、坡向、腐殖质厚度；杨海宾等^[20]认为：影响杉木的主导因子是坡向、坡位和土壤类型。本研究得出地貌、腐殖质厚度、土层厚度为杉木生长的主导因子。地貌条件直接影响气候和土壤，局部地形对杉木生长有很大影响，随着地势升高，杉木分布高度也随之上升，冻害和断梢现象更为频繁，地貌高低与杉木树高生长呈明显的负相关^[24−25]。因此，地貌为影响杉木生长的主导因子之一。腐殖质是土壤有机质的一种，含有多种养分，能提高土壤的保肥、保水性，并能缓解土壤的酸碱度，有利于微生物活动，促进林木生长，适宜的腐殖质厚度为杉木根系发展提供了良好的环境与空间^[26]，因此腐殖质厚度同样是影响杉木生长的主导因子之一；土层厚度影响土壤养分、水分总储量和根系分布的空间范围，尤其是杉木喜肥沃、深厚、疏松、湿润且排水良好的土壤，对土层厚度的要求较高，因此土层厚度也是影响杉木生长的主导因子之一。林区整体气候温润，导致部分因子差异性不大，这也是坡向、坡位等在因子选择中不明显的原因。本研究采用主导因子对庆元县地区进行立地划分，通过得分值的计算，将立地类型划分为优、良、中、差共4个等级，其中2 564块研究区小班的立地质量为良及以上，表明庆元县立地质量条件良好。

因子特征选择中，偏相关系数是在消除其他变量影响的条件下，计算某2个变量之间的相关系数；基于内置的因子特征选择方法为在树结构的内部节点中，因子按方差减少进行选择，但存在当一个特征被选择后，与其相关的其他特征的重要度则会变得很低等问题。正如研究中当第1个立地因子地貌被确认后，其余因子的重要性都呈现较低的水平；基于置换的因子特征选择方法用于克服使用方差减少计算出的默认特征重要性的缺点，对模型的特征没有偏见，也不局限于特定的模型类别，适用性较广。在以上3种方法中，地貌均被选择，说明地貌的变化导致预测结果波动性最大。而腐殖质厚度、土层厚度在3种方法中均各有体现，在基于内置的因子特征选择中，腐殖质厚度被选择，是其基于树子节点划分时，方差的变化程度较小且导致预测结果变化较大。而在偏相关系数的因子特征选择方法中，消除了其他变量的影响后，其表现性不如土层厚度。立地质量评价中通常使用偏相关系数选择主导因子，而包括随机森林在内的众多机器学习算法均提供了因子选择的方法或参数，因此在主导因子划分这一问题上，可以不局限于偏相关系数去探索更适用于立地质量评价的主导因子选择方法。此外，由于气候、水文等条件难以量化^[27]，因此使用间接因子进行拟合，难免在确信度上有所缺失。在今后运用立地因子对立地质量进行评价时，可以使用降维手段筛选出参与建模的立地因子，进一步提高评价结果的预测精度。