-
森林是陆地生态系统的主体，在全球碳循环中起着十分重要的作用。森林蓄积量作为衡量森林数量的重要的指标之一，能够直观反映森林资源数量和质量，获取森林蓄积量是推算森林生物量和碳储量的必要环节[1-3]。《“十四五”林业草原保护发展规划纲要》明确指出：将增加中国森林蓄积量作为主要目标之一，并将森林蓄积量与森林覆盖率作为两大约束性指标。因此，实现森林资源动态检测、准确获取森林蓄积量等参数信息，已成为当前森林资源调查的迫切需求。激光雷达(light detection and ranging, LiDAR)作为一种新兴的主动式遥感技术，能够从不同空间尺度对生态系统进行高效精准的监测[4]。机载LiDAR发射的激光脉冲能穿透森林冠层并获取树冠上部枝叶的空间信息，通过林分内的空隙，测量冠层结构信息和林下地形信息[5]。而传统方法通过样木、样地等抽样调查进行林分森林参数的推算，调查周期长、成本高且调查范围有限[6-7]。激光雷达在获取森林空间结构因子和地形因子等信息方面具有精度高、范围广等优势。
近年来，基于机载激光雷达的林分蓄积量反演已有许多研究成果，集中在构建参数方法和非参数方法的蓄积量反演模型。PAWE等[8]基于机载LiDAR数据对波兰东南部林区建立多元线性回归蓄积量反演模型，其中均方根误差(root mean square error, RMSE)为15.2%；CHIRICI等[9]以Landsat 5TM、卫星LiDAR数据等预测变量联合气温、降水和地形等辅助变量进行意大利中部地区蓄积量的大尺度反演，其中随机森林回归模型最优，决定系数(R2)为0.69、RMSE为37.2%；陈松等[10]基于Sentinel-2与机载LiDAR数据采用不同回归方法对广西高峰林场界牌、东升分场进行蓄积量反演，构建MLR-Logistic联立模型精度优于随机森林等机器学习方法，R2为0.60、相对均方根误差(relative root mean-squared error, RRMSE)为29.29%；曾伟生等[11]基于机载LiDAR数据，采用线性和非线性参数回归方法对东北林区进行蓄积量反演，其中非线性回归模型R2为0.71~0.82，略优于线性回归。已有多位研究者基于机载LiDAR数据进行林分蓄积量反演模型研究，但对于建模方法中参数回归和非参数回归模型的比较国内研究较少。本研究以广西国有高峰林场桉Eucalyptus树人工林为研究对象，基于机载激光雷达数据及地面调查数据，采用逐步回归、偏最小二乘回归等参数回归和随机森林、支持向量回归等非参数回归进行蓄积量反演模型研建，并通过模型评价指标对以上4种方法进行模型评估，进而选择出拟合优度、泛化能力最优模型。
-
研究区位于广西壮族自治区南宁市兴宁区的国有高峰林场，22°51′~23°02′N，108°06′~108°31′E，该区地处亚热带地区，年平均气温约21 ℃，年平均降水量为1 200~1 500 mm，相对湿度为79%，属丘陵地貌，海拔为100~460 m，坡度为6°~35°，具有较厚的赤红壤，适宜亚热带和热带树种生长，森林覆盖率达87%，主要树种为杉木Cunninghamia lanceolata、巨尾桉Eucalyptus grandis × E. urophylla、马尾松Pinus massoniana等。
-
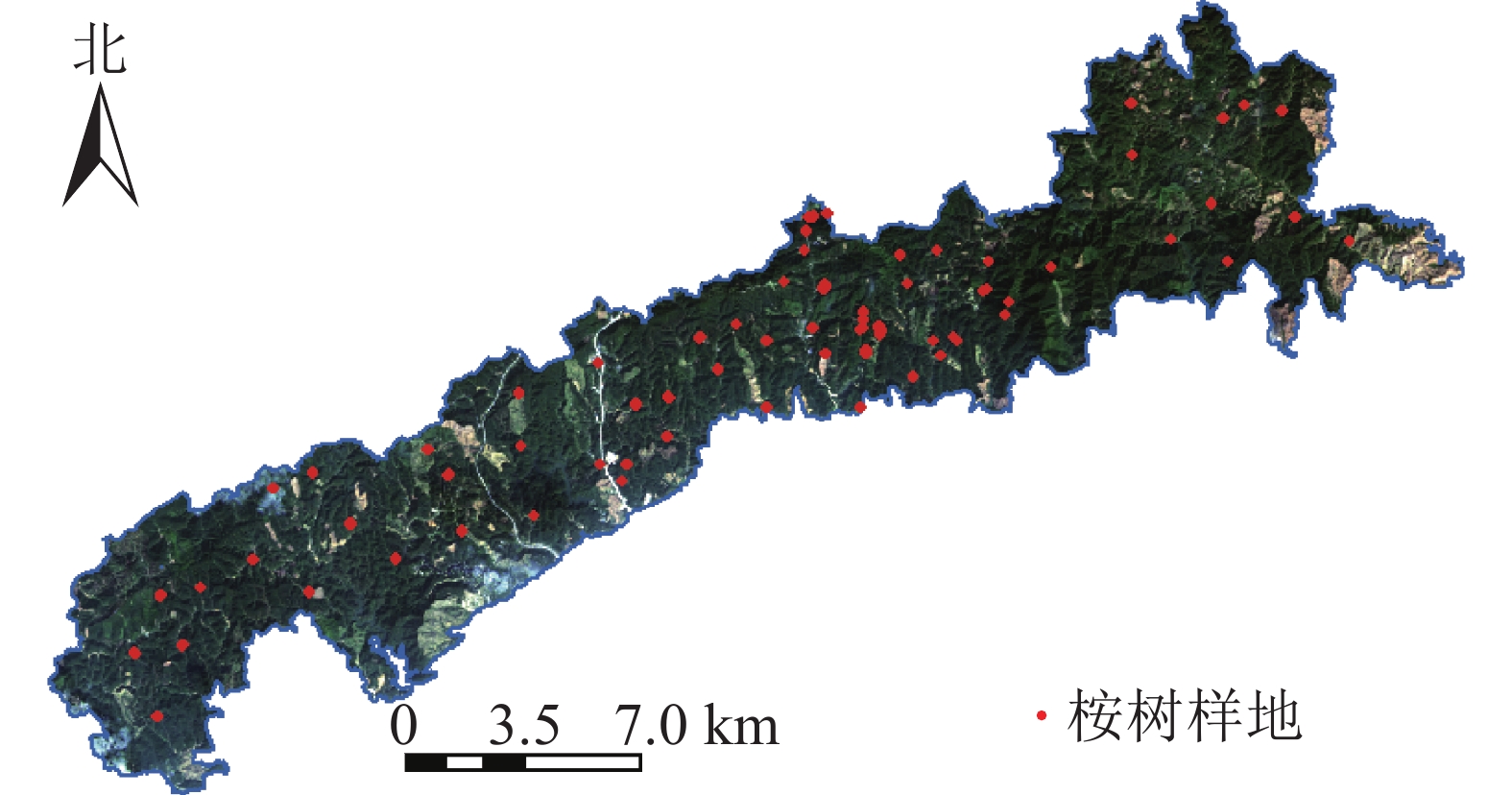
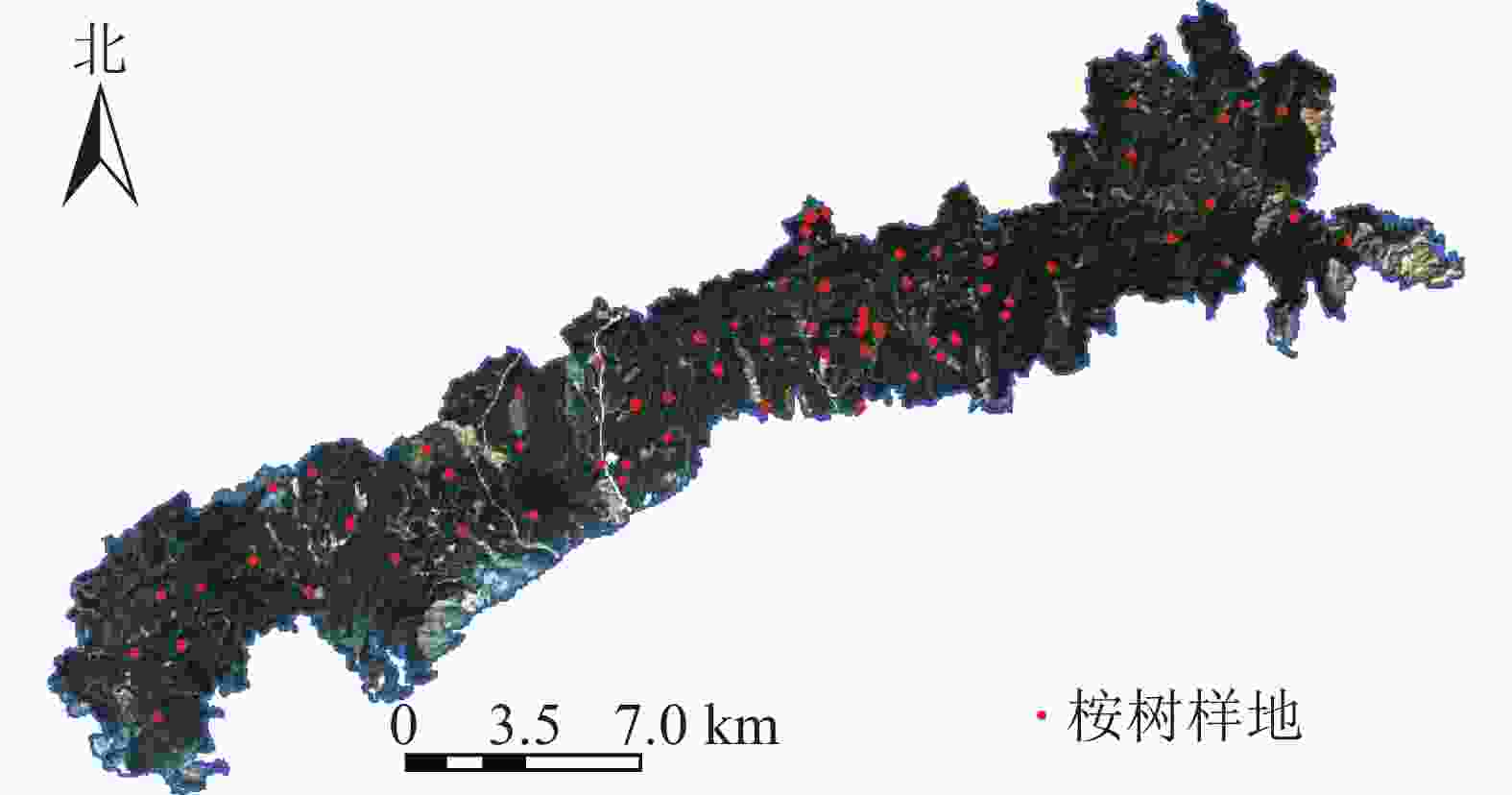
调查时间为2018年1—2月，研究区内共设置71块桉树样地(图1)，其中激光雷达覆盖范围内共57块样地。样地大小为20 m×20 m、25 m×25 m和25 m×50 m。采用实时动态差分技术(real-time Kinematic，RTK)进行样地定位，记录样地中心点及样地角点。采用每木检尺的方法，使用胸径尺、激光测高仪和皮尺逐一测量样地内树木的胸径、树高等数据。统计样地调查数据得到样地算数平均树高、算数平均胸径、样地面积(表1)。通过广西地区桉树二元材积表对单木材积量进行计算[12]，进而计算得到样地尺度的公顷蓄积量值(V样地)：V样地=V公顷S样地/10 000。其中：V公顷为通过二元材积公式计算得的每公顷蓄积量，S样地为桉树样地面积。
表 1 样地参数统计
Table 1. Parameter statistics of sample plots
项目 平均树高/m 平均胸径/cm 单位蓄积量/(m3·hm−2) 最大值 30.40 21.10 320.66 最小值 7.48 5.24 17.79 平均值 15.19 12.06 90.47 标准差 4.22 3.55 65.58 
图 1 研究区样地分布示意图
Figure 1. Location of the sample plots distribution
-
于2018年1月采集机载LiDAR数据，使用有人机并搭载LMS-Q680i激光雷达扫描仪，实际飞行高度为1 000 m，最大扫描角度为30°，波长为1 550 nm，激光脉冲长度为3 ns，采样间隔为1 ns，最大扫描频率为400 KHz，垂直分辨率为0.15 m，点云密度为10 pt·m−2。
使用LiDAR 360软件对机载激光雷达点云进行点云拼接、去噪、地面点分类、基于地面点归一化等预处理，结果如图2所示。根据样地角点以中心点坐标对点云进行裁剪，提取出基于样地尺度特征变量共48个，包括37个点云高度参数、10个密度参数、郁闭度等点云特征变量，具体参数见表2。
图 2 样地点云预处理结果示例
Figure 2. Example of point cloud preprocessing results of sample plots
表 2 提取点云特征变量
Table 2. Extracting point cloud feature variables
变量类型 变量名 特征描述 高度变量 Hmax 归一化后所有点的Z值的
最大值Hmin 归一化后所有点的Z值的
最小值Hmedian_z 高度平均偏差 Hstddev 高度标准差 Hkurtosis 高度峰度 Hsqrt_m 高度二次幂均值 Hcurt_m 高度三次幂均值 HP1, HP5$, \cdots, $ HP99 归一化点云高度分布的百
分位数，共15个HA1, HA2$, \cdots, $ HA99 归一化点云累计高度的百
分位数，共15个密度变量 D1, D2$, \cdots, $ D9 将点云从低到高分成10个
相同高度的切片，该层
回波数点在所有返回点
的所占比例，共9个郁闭度 CC 首次回波中，植被点数与
所有点的比值 -
使用MATLAB激光雷达覆盖范围内57个样本进行随机抽样，按照3∶1的比例选取42个作为训练样本，15个作为验证样本。以样地实测公顷蓄积量为因变量，筛选后点云特征为自变量，采用逐步回归、偏最小二乘回归、随机森林回归、支持向量回归模型进行拟合 。
-
对于逐步回归，采用逐步筛选法对所有特征变量进行变量筛选；再对筛选出特征变量进行多重共线性检验，计算各变量间容忍度或特征变量间方差膨胀因子(FVI) 2个统计量[13]，对于容忍度≤0.2或FVI≥5的变量进行进一步讨论，确定最优特征变量子集。FVI=1/(1−R2)。其中：R为特征变量间相关系数。
-
对于偏最小二乘回归、支持向量机回归、随机森林回归等方法，使用随机森林中重要性排序对特征变量进行优选。其主要原理为随机森林算法在构建各决策树时，对某一特征变量进行取舍，若此时均方误差(mean square error, MSE)有较大变化，则该特征变量重要性高，最终得到所有特征变量重要性排序。
-
逐步回归(stepwise regression, SR)可用于筛选并剔除引起多重共线性的变量，逐步回归建立模型一般形式为：Y=β0+β1X1+β2X2
$+\cdots + $ βiXi+ε。逐步筛选法结合了向前选择变量法和向后选择变量法的优点，对i个自变量X分别与因变量Y建立一元回归模型，计算各变量所对应F值，其中，β0为常数，βi为回归系数，ε为误差项。在建立逐步回归模型时，选择当前未加入模型的预测变量中F的最大值所对应的$ {X}_{i} $ 加入模型，再对已选入预测变量逐个进行t检验，若存在已选入预测变量不再显著，则将其剔除。重复以上步骤，直到既没有显著的解释变量选入回归方程，也没有不显著的解释变量从回归方程中剔除为止，将保留下来的最优子集作为建立模型的特征变量，并将候选变量对应系数保留。 -
偏最小二乘回归(partial least squares regression, PLSR)结合了主成分分析、典型相关分析的优点，实现了数据降维、信息综合[14]。首先对训练样本进行数据标准化处理，调用plsregress函数提取主成分与自变量和因变量组合。分别计算自变量和因变量提取出成分的贡献率进而计算得到累计贡献率，当度量因子Q2h≥0.097 5停止主成分的提取[15]。统计主成分对个数并建立各自变量与因变量的线性表达式，最后根据所建立的各主成分对模型，整理得到PLSR模型。
-
支持向量机算法(support vector machine, SVM)利用内积核函数代替高维空间的非线性映射, 不涉及大数定律和概率测度等有关问题, 且SVM的决策函数仅有少数支持向量决定，该算法在解决小样本多维度回归和分类问题时泛化能力强，具备较好的“鲁棒性”。VAPNIK[16]在SVM分类的基础上引入了不敏感损失函数，得到了支持向量机回归算法(support vector regression, SVR)。
使用Libsvm工具箱实现SVR算法，采用网格搜索法(grid search)对常用的4种核函数进行参数寻优[17]，即线性、多项式、RBF (径向基核函数)、sigmoid (多层感知机核函数)。同时进行十折交叉验证，保证回归模型中惩罚系数(C)与gamma值(g)达到最优。
-
随机森林回归(RFR)算法采用自助采样法(bootstrap sampling)，在以决策树构建Bagging集成的基础上，对样本和特征变量进行随机选择[18]。调用TreeBagger函数进行RFR算法建模，通过对决策树数量(ntree)和最小叶子点数进行参数寻优，直到袋外(out-of-bag，OOB)误差的MSE达到最小，保证模型预测性能达到最优，将寻优结果作为RFR模型的建模参数，用于模型构建。
-
本研究使用决定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)对林分蓄积量估测模型进行定量的精度验证和评价。其计算公式为：
$$\quad\;\;\, {R}^{2}=1-\frac{\displaystyle\sum\limits_{i = 1}^{{n}} {({y}_{i}-{\hat{y}}_{i})}^{2}}{\displaystyle\sum\limits _{i=1}^{n}{({y}_{i}-{\bar{y}}_{i})}^{2}} \text{；} $$ $$ {E}_{\mathrm{R}\mathrm{M}\mathrm{S}}=\sqrt{\frac{\displaystyle\sum \limits_{i=1}^{n}{({y}_{i}-{\hat{y}}_{i})}^{2}}{n}} \text{；} $$ $$ {E}_{\mathrm{M}\mathrm{A}}=\frac{1}{n}\displaystyle\sum\limits _{i=1}^{n}\left|({y}_{i}-{\hat{y}}_{i})\right| 。 $$ 其中：
$ {y}_{i} $ 、$ {\bar{y}}_{i} $ 、$ {\hat{y}}_{i} $ 分别为实测蓄积量值、实测蓄积量均值、模型预测蓄积量值；ERMS为均方根误差；EMA为平均绝对误差；n为验证样本数量。进行评估模型时，R2越趋近于1，代表拟合程度越高；ERMS越小，代表真实值与模型预测值之间离散程度越小；EMA越小，代表真实值与模型预测值之间的误差越小。 -
在采用逐步筛选法进行偏F检验时，取偏F检验拒绝域的临界值为F进＞F出，F进为选入变量时的临界值、F出为删除变量时的临界值。本研究设定F进为0.10，F出为0.11，筛选特征变量结果为D9、HP95、Hmax、Hkurtosis。
对筛选出的变量进行双变量相关性分析，根据相关系数(R)计算各变量间方差膨胀因子(FVI)。计算结果如表3，Hmax与HP95之间FVI为250.25，FVI大于5，认为两者之间存在共线性。因此分别以D9、Hmax、Hkurtosis和D9、HP95、Hkurtos为建模因子。
表 3 各特征变量间的方差膨胀因子
Table 3. FVI calculation of each variable
变量 D9 Hmax HP95 Hkurtosis D9 2.46 2.69 1.00 Hmax 2.46 250.25 1.01 HP95 2.69 250.25 1.01 Hkurtosis 1.00 1.01 1.01 -
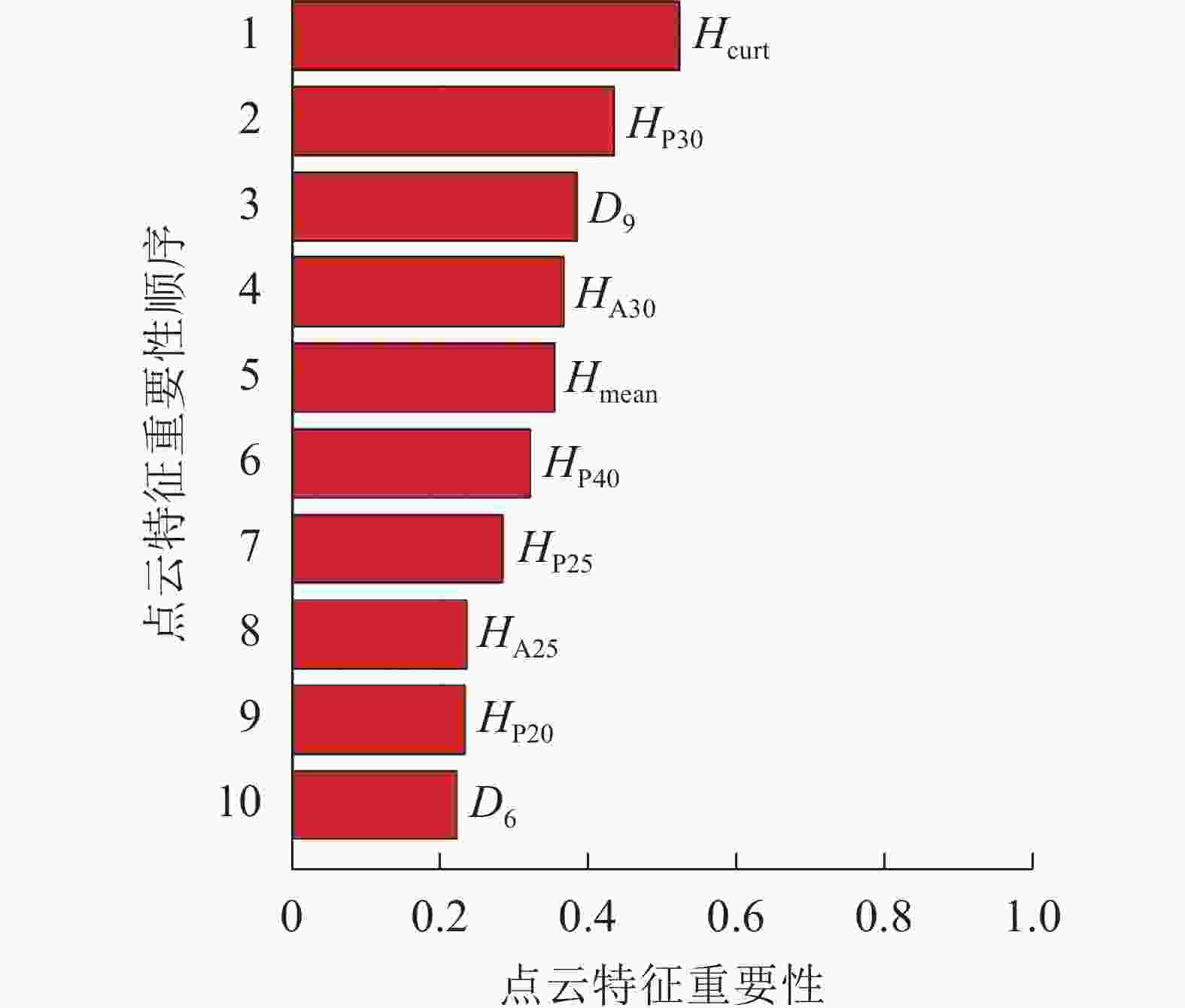
对所有的48个特征变量进行重要性排序，调用随机森林中OOBPermutedVarDeltaError参数，得到所有特征变量的重要性。选择重要性大于0.2的变量作为建模因子，筛选结果如图3，包括8个高度变量、2个密度变量，其中Hcurt重要性最高，达0.52；D6重要性相对最低，为0.22。
图 3 点云特征变量重要性排序
Figure 3. Importance ranking of point cloud characteristic variables
-
根据特征变量优选结果，分别建立以D9、Hmax、Hkurtosis和D9、HP95、Hkurtos为建模因子的多元线性模型:
$$ Y_{\rm{1}} = 470.232D_{\rm{9}} + 4.897H_{\rm{P95}} + 1.453H_{\rm{kurtosis}} - 56.903 \text{；} $$ $$ Y_{\rm{2}} = 482.214D_{\rm{9}} + 4.855H_{\text{max}} + 1.461H_{\rm{kurtosis}} - 65.01 。 $$ 使用SPSS 26对Y1、Y2模型进行初步评估，计算2种模型的相关系数(R)、R2以及标准估算误差(SE)，结果如表4。结果表明Y2中R2、SE均优于Y1，因此选定Y2作为逐步回归模型。
表 4 逐步回归模型初步评估
Table 4. Preliminary evaluation of stepwise regression model
模型 R R2 调整后R2 SE Y1 0.950 0.902 0.894 18.460 Y2 0.953 0.908 0.900 17.904 -
利用PLSR提取的主成分F1、F2与因变量Y关系分别为F1=5.840Y+b和F2=0.271Y+b，b为常数，得到最小二乘回归模型为：
$$ \begin{split} Y=\;&-42.571{-1.344H}_{{\rm{A}}25}-0.513{H}_{{\rm{A}}30}+1.450{H}_{{\rm{curt}}}+\\ \;&1.134{H}_{{\rm{mean}}}+0.705{H}_{{\rm{P}}20}+1.088{H}_{{\rm{P}}25}+{1.337H}_{{\rm{P}}30}+\\ \;&{1.523H}_{{\rm{P}}40}+24.647{D}_{6}+{445.634D}_{9} 。 \end{split} $$ -
调用meshgrid函数对C、gamma进行参数寻优并采用十折交叉验证，调用svmtrain函数，分别构建4种不同核函数的SVR模型并进行模型训练，训练结果如表5。得到拟合结果最优模型为RBF-SVR，其C为8，gamma为0.125。RBF-SVR模型R2为0.85，RMSE为29.24 m3·hm−2，MAE为94.98 m3·hm−2，选定该模型作为本研究的SVR模型。
表 5 SVR不同核函数拟合结果
Table 5. Fitting results of different kernel functions of SVR
核函数 R2 RMSE/(m3·hm−2) MAE/(m3·hm−2) 线性 训练样本 0.89 18.62 14.49 验证样本 0.83 30.43 24.73 多项式 训练样本 0.74 34.34 23.06 验证样本 0.78 52.33 33.54 RBF 训练样本 0.95 13.09 11.65 验证样本 0.85 29.24 23.96 sigmoid 训练样本 0.80 24.91 17.79 验证样本 0.77 35.91 25.71 -
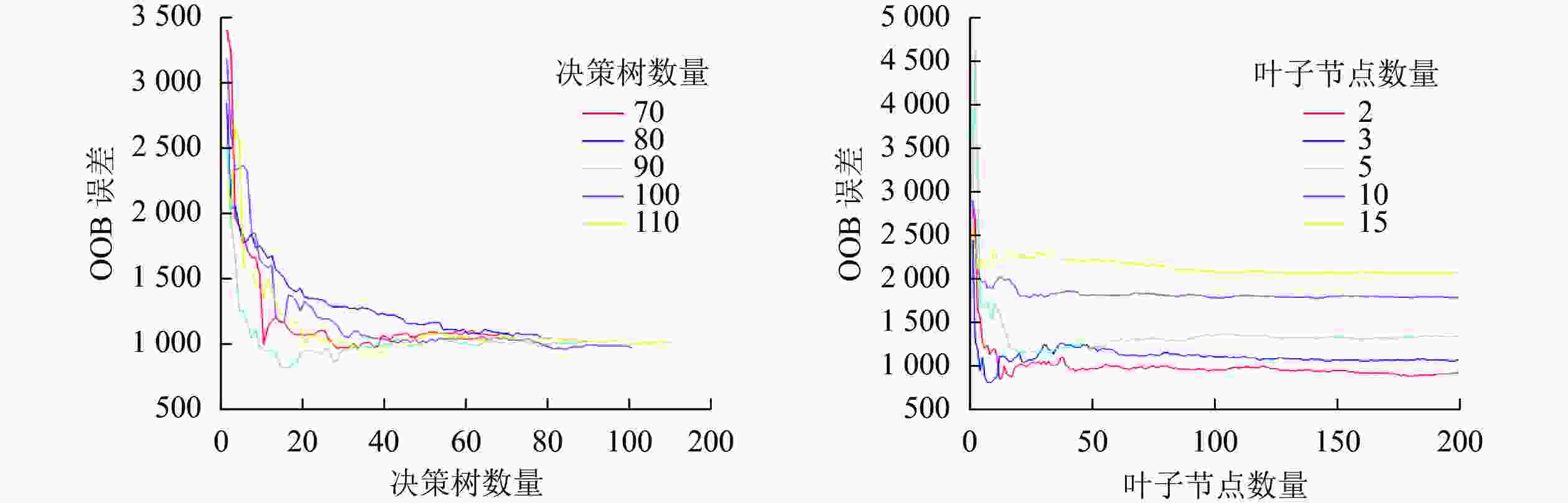
本研究采用穷举法对决策树数量和最小叶子点数进行参数寻优。分别设置决策树数量和最小叶子点数最小值为50和2，每次递增10和1，对寻优过程循环，通过观察OOB误差的MSE变化，直到寻找到本模型最优参数，寻优结果如图4。最终确定决策树数量为90，叶子节点数量为2，将寻优结果作为建模参数，输入训练样本，完成RFR模型构建。
图 4 随机森林参数寻优结果
Figure 4. Evaluation of growing stock volume inversion model
-
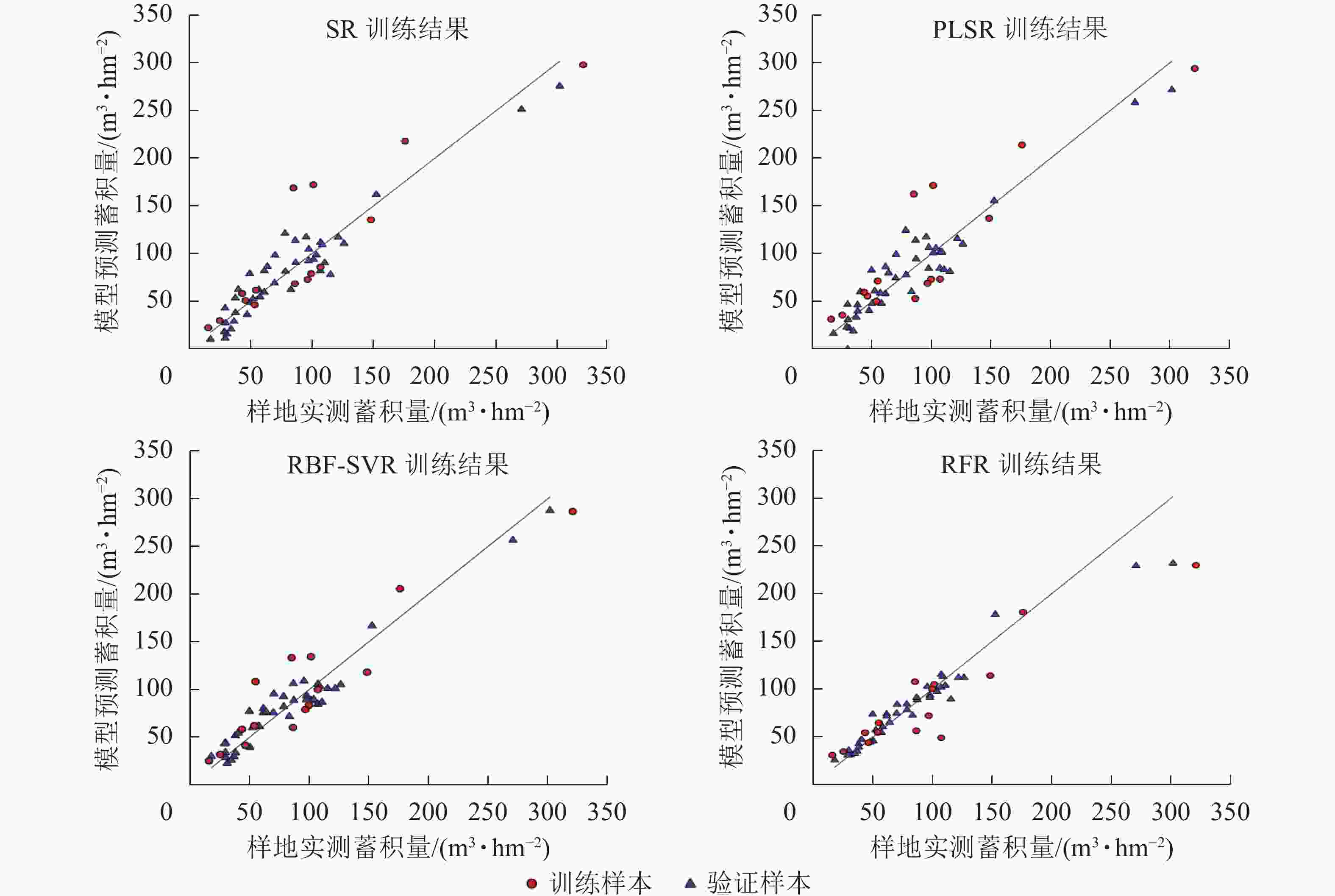
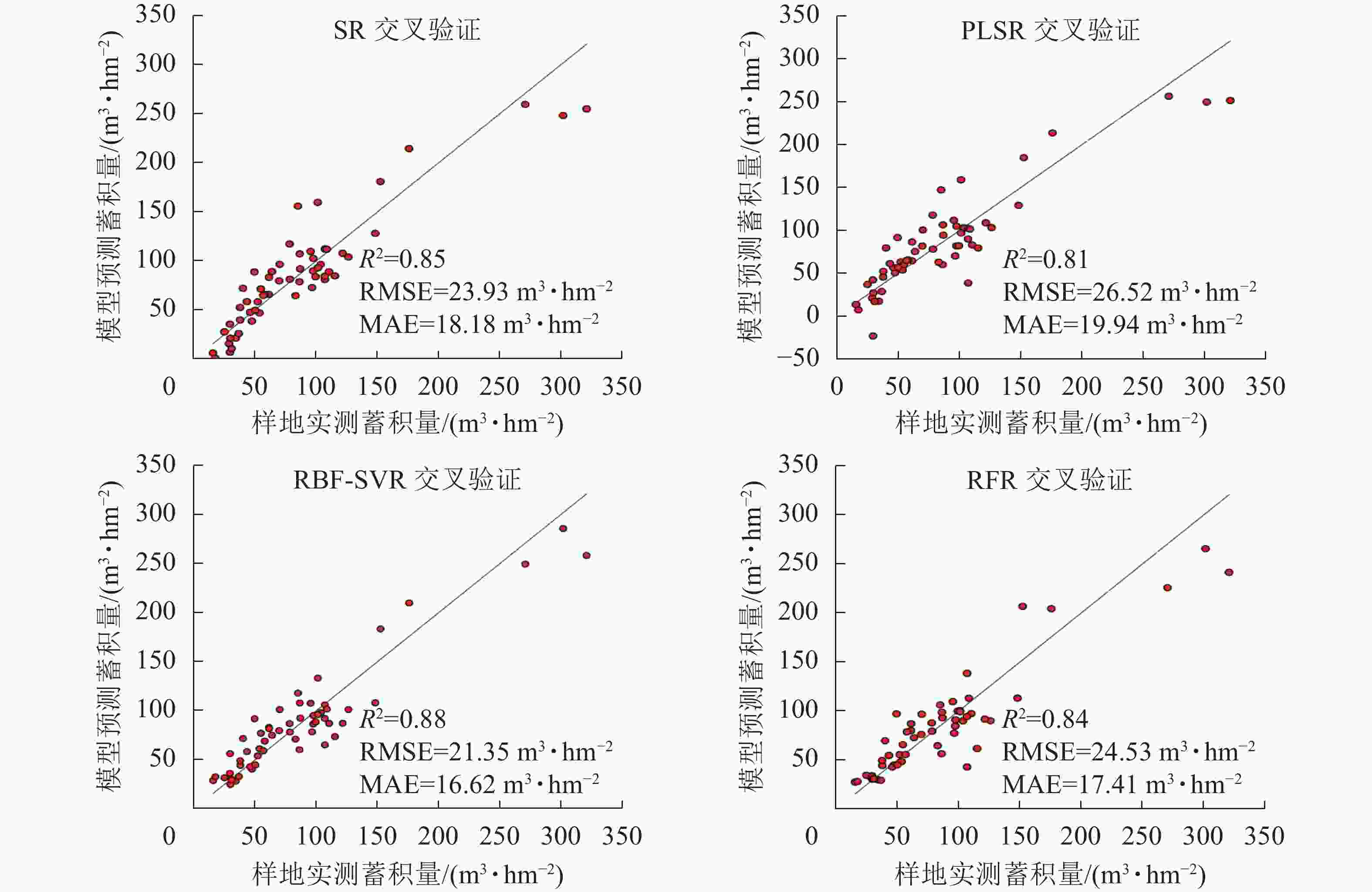
使用验证样本对各模型的预测性能进行评估，结果如表6、图5。可以看出不同的回归模型均表现出较好的拟合结果，其中拟合结果最优模型为RFR模型，模型评价结果R2为0.95，RMSE为12.64 m3·hm−2，MAE为8.00 m3·hm−2，RBF-SVR模型其次，R2为0.94，RMSE为13.09 m3·hm−2，MAE为11.65 m3·hm−2。将验证样本带入模型，检验模型的预测能力，结果显示各模型预测能力与模型的拟合效果一致。通过传统方法的划分训练样本与验证样本，存在一定的偶然性与不确定性，为了进一步确保各模型的稳定性与泛化能力，采用留一法交叉验证(leave-one-out cross validation，LOOCV)对本研究中各模型进行再次评估[19]，如图6所示：RBF-SVR模型表现最优，R2为0.88，RMSE为21.35 m3·hm−2，MAE为16.62 m3·hm−2，与其他模型相比，R2高出0.03~0.07，RMSE减少2.58~5.17 m3·hm−2，MAE减少0.79~3.32 m3·hm−2。
表 6 蓄积量反演模型评估
Table 6. Evaluation of growing stock volume inversion model
模型 样本 R2 RMSE/(m3·hm−2) MAE/(m3·hm−2) SR 训练样本 0.91 17.03 13.27 验证样本 0.82 33.33 24.03 PLSR 训练样本 0.90 17.63 13.49 验证样本 0.80 34.53 27.76 RBF-SVR 训练样本 0.94 13.09 11.65 验证样本 0.85 29.24 23.96 RFR 训练样本 0.95 12.64 8.00 验证样本 0.88 28.11 19.48 
图 5 各模型训练结果与验证结果散点图
Figure 5. Scatter diagram of training results and verification results of each model
图 6 各模型十折交叉验证结果
Figure 6. Ten-fold cross validation results of each model
-
本研究采用SR、PLSR等参数回归方法与RFR、SVR等非参数回归方法进行广西高峰林场桉树人工林的蓄积量反演模型研建，通过对点云特征变量筛选、建模因子优选、参数寻优等方法保证各模型达到最优性能，在此基础上采用留一法对各模型进行交叉验证，保证了模型的稳定性与泛化能力，并将该结果作为本研究各模型性能评估的最终结果。研究结果如下：①核函数为RBF的SVR在4种模型中预测精度最高(ΔR2为0.03~0.07、ΔRMSE为2.58~5.17 m3·hm−2、ΔMAE为0.79~3.32 m3·hm−2)，采用SVR模型在解决林业激光雷达领域的回归预测问题已有广泛应用，肖越[20]结合Landsat 8、高分2号(GF-2)共2种光学遥感数据与极化SAR数据进行旺业甸林场尺度的蓄积量反演，采用SVR模型拟合精度最高(R2为0.48，RMSE为57.27 m3·hm−2)，与MLR、RFR等方法相比，ΔR2为0.10~0.11、ΔRMSE为5.30~6.00 m3·hm−2。赵勋等[21]基于机载激光雷达进行广西高峰林场林分平均树高估测中，通过随机森林特征变量筛选，采用SVR相比较RFR方法，R2增加0.01、RMSE减少0.06 m。以上研究结果与本研究一致，进一步表明解决基于LiDAR点云特征变量的林分蓄积量反演问题时，结合随机森林筛选特征变量与支持向量机回归可作为有效建模方法。
②本研究采用2种方法对特征变量进行筛选，逐步回归法保证入选的特征变量显著且各变量之间不存在共线关系，随机森林则通过计算各特征变量对建模时的贡献度排序进而筛选变量。肖越[20]利用逐步回归法从遥感特征变量中筛选出建模因子用于蓄积量回归模型构建；周蓉等[22]在基于Landsat 8 遥感影像反演地上生物量的研究中，采用随机森林重要性排序方法从遥感因子中筛选出特征变量用于构建模型。这2种方法均广泛应用于构建模型前的变量筛选，合理地选择模型筛选方法，更有利于回归模型构建。
③本研究旨在选取最优桉树蓄积量反演模型，参数方法SR中逐步筛选法已对变量进行筛选，故SR模型不再采用随机森林进行特征变量筛选。在本研究模型评估中，SR模型评估结果均优于PLSR模型，袁钰娜等[23]对东北林区4种不同针叶林蓄积量反演所建立的回归模型中，PLSR模型的拟合结果和预测精度均优于SR (ΔR2为0.05~0.15，ΔRMSE为2.6%~4.2%)，与本研究结果不一致，但由于2种回归方法并未使用同一变量筛选方法，因此，不能直接认为在解决预测回归问题时前者更加可靠，对于以上2种回归方法的模型性能与预测能力需进一步讨论。
④本研究在林场尺度通过较少样本进行桉树林分蓄积量反演，非参数方法总体预测精度较高且RBF-SVR模型略优于RFR模型。SVR核心思想为将低维空间中的向量用非线性函数映射到一个高维特征空间，进而寻求线性回归超平面并解决低维空间中的非线性问题[24]，支持向量机回归解决多维度小样本回归预测问题相较随机森林回归更有优势。在反演尺度较大且训练样本较多的林分蓄积量反演问题时，采用支持向量机回归方法训练效率将明显下降，此时选择随机森林回归将更适用。
⑤本研究采用逐步筛选法筛选出的4个特征变量中，点云密度变量被选择1次；在采用随机森林筛选的10个变量中，点云密度变量被选择2次，且密度变量D9在重要性排序中位于第3位。点云密度变量作为本研究中重要解释变量之一，该类型变量能够描述林分中树木的水平结构信息，与树高(垂直结构变量)等参数结合可解释林分空间结构信息。孙忠秋等[25]加入林分郁闭度作为水平结构的解释变量，与仅用点云高度参数相比较，RMSE下降0.27 m3·hm−2、MAE下降0.08 m3·hm−2，该变量对模型预测性能有一定提升。本研究将郁闭度作为候选变量，但在逐步筛选法中又将其剔除，因为在基于随机森林法的重要性排序中，林分郁闭度参数在48个候选变量中排名第44位。由此可见，在林业激光雷达应用中，将林分密度用于衡量林分水平结构信息更加可靠。
-
本研究通过2种参数回归方法(逐步回归、偏最小二乘回归)与2种非参数方法(随机森林回归、支持向量机回归)对林分蓄积量进行估测。在采用传统方法划分训练样本与验证样本的结果中，非参数方法模型精度均优于参数回归方法；采用留一法对各模型预测精度进行交叉验证时，表现最优模型RBF-SVR属于非参数回归方法，表明解决林业激光雷达领域中的回归预测问题时，非参数方法相较参数方法更有优势。本研究中蓄积量反演模型已在广西高峰林场内取得较好模型精度，但对于大尺度反演森林蓄积量的适用性有待进一步论证。
Estimation model of Eucalyptus stand volume based on airborne LiDAR Point Cloud
-
摘要:
目的 通过2018年1—2月广西国有高峰林场机载激光雷达数据及地面调查数据，采用参数方法和非参数方法建立回归模型，反演桉Eucalyptus树人工林森林蓄积量。 方法 通过点云提取点云高度参数、点云密度参数、林分郁闭度等点云特征变量，采用参数方法(逐步回归、偏最小二乘回归)和非参数方法(随机森林回归、支持向量机回归)进行林分蓄积量构建，通过与样地实测数据对比，进行模型回归预测性能评估，进而选择出表现最优蓄积量反演模型。 结果 采用留一法对以上4种模型进行验证，结果显示：逐步回归模型R2为0.85、均方根误差(RMSE)为23.93 m3·hm−2、平均绝对误差(MAE)为18.18 m3·hm−2；偏最小二乘回归模型R2为0.81、RMSE为26.52 m3·hm−2、MAE为19.94 m3·hm−2；核函数为RBF的支持向量回归模型R2为0.88、RMSE为21.35 m3·hm−2、MAE为16.62 m3·hm−2；随机森林回归模型R2为0.84、RMSE为24.53 m3·hm−2、MAE为17.41 m3·hm−2。 结论 采用随机森林进行变量筛选后，RBF-SVR模型拟合优度及泛化能力最优；通过逐步筛选法结合方差膨胀因子(VIF)方法优选变量的逐步回归模型次之；最后为随机森林回归模型与偏最小二乘回归模型。可见，在解决林业激光雷达领域中的回归预测问题时，采用非参数方法构建RBF-SVR模型更有优势。本研究建立的4种森林类型蓄积量模型，各模型均有较高精度且符合森林资源调查相关技术规定要求。图6表6参25 Abstract:Objective LiDAR, as an active remote sensing technology, has proven to be an effective and efficient means for large-scale dynamic monitoring and investigation for forest resources. With an analysis of the airborne LiDAR data and ground survey data collected of Guangxi state-owned Gaofeng forest farm from January to February 2018, this paper is aimed to establish a regression model by using parametric and nonparametric methods to inverse the forest volume of Eucalyptus plantation. Method First, point cloud characteristic variables such as point cloud height parameters, point cloud density parameters and stand canopy density were extracted from point cloud after which parametric methods (stepwise regression, partial least squares regression) and nonparametric methods (random forest regression and support vector machine regression) were used to construct stand volume. Then the prediction performance of model regression is evaluated by comparing the estimated data of sample plot with the measured ones so that the optimal volume inversion model could be selected. Result After being verified by leaving one method, results are as follows: for the stepwise regression model, R2=0.85, RMSE=23.93 m3·hm−2 and MAE=18.18 m3·hm−2; for the partial least squares regression model, R2=0.81, RMSE=26.52 m3·hm−2 and MAE=19.94 m3·hm−2; for the support vector regression model with RBF kernel function, R2=0.88, RMSE=21.35 m3·hm−2, MAE=16.62 m3·hm−2 whereas for the random forest regression model, R2=0.84, RMSE=24.53 m3·hm−2 and MAE=17.41 m3·hm−2. Conclusion After variable screening with random forest; the RBF-SVR model has demonstrated the best fitness and generalization ability, followed by the stepwise regression model of optimizing variables by stepwise screening method combined with variance inflation factor (VIF) method whereas the random forest regression model and partial least squares regression model came last. It was also shown that nonparametric method is a better choice in the construction of RBF-SVR model in solving the problem of regression prediction in the field of forestry LiDAR and that the volume models of four forest types established in this study have high accuracy and met the requirements of relevant technical regulations of forest resources investigation. [Ch, 6 fig. 6 tab. 25 ref.] -
图 5 各模型训练结果与验证结果散点图
Figure 5 Scatter diagram of training results and verification results of each model
表 1 样地参数统计
Table 1. Parameter statistics of sample plots
项目 平均树高/m 平均胸径/cm 单位蓄积量/(m3·hm−2) 最大值 30.40 21.10 320.66 最小值 7.48 5.24 17.79 平均值 15.19 12.06 90.47 标准差 4.22 3.55 65.58 
下载: 导出CSV
表 2 提取点云特征变量
Table 2. Extracting point cloud feature variables
变量类型 变量名 特征描述 高度变量 Hmax 归一化后所有点的Z值的
最大值Hmin 归一化后所有点的Z值的
最小值Hmedian_z 高度平均偏差 Hstddev 高度标准差 Hkurtosis 高度峰度 Hsqrt_m 高度二次幂均值 Hcurt_m 高度三次幂均值 HP1, HP5$, \cdots, $ HP99 归一化点云高度分布的百
分位数，共15个HA1, HA2$, \cdots, $ HA99 归一化点云累计高度的百
分位数，共15个密度变量 D1, D2$, \cdots, $ D9 将点云从低到高分成10个
相同高度的切片，该层
回波数点在所有返回点
的所占比例，共9个郁闭度 CC 首次回波中，植被点数与
所有点的比值
下载: 导出CSV
表 3 各特征变量间的方差膨胀因子
Table 3. FVI calculation of each variable
变量 D9 Hmax HP95 Hkurtosis D9 2.46 2.69 1.00 Hmax 2.46 250.25 1.01 HP95 2.69 250.25 1.01 Hkurtosis 1.00 1.01 1.01
下载: 导出CSV
表 4 逐步回归模型初步评估
Table 4. Preliminary evaluation of stepwise regression model
模型 R R2 调整后R2 SE Y1 0.950 0.902 0.894 18.460 Y2 0.953 0.908 0.900 17.904
下载: 导出CSV
表 5 SVR不同核函数拟合结果
Table 5. Fitting results of different kernel functions of SVR
核函数 R2 RMSE/(m3·hm−2) MAE/(m3·hm−2) 线性 训练样本 0.89 18.62 14.49 验证样本 0.83 30.43 24.73 多项式 训练样本 0.74 34.34 23.06 验证样本 0.78 52.33 33.54 RBF 训练样本 0.95 13.09 11.65 验证样本 0.85 29.24 23.96 sigmoid 训练样本 0.80 24.91 17.79 验证样本 0.77 35.91 25.71
下载: 导出CSV
表 6 蓄积量反演模型评估
Table 6. Evaluation of growing stock volume inversion model
模型 样本 R2 RMSE/(m3·hm−2) MAE/(m3·hm−2) SR 训练样本 0.91 17.03 13.27 验证样本 0.82 33.33 24.03 PLSR 训练样本 0.90 17.63 13.49 验证样本 0.80 34.53 27.76 RBF-SVR 训练样本 0.94 13.09 11.65 验证样本 0.85 29.24 23.96 RFR 训练样本 0.95 12.64 8.00 验证样本 0.88 28.11 19.48
下载: 导出CSV
-
[1] 张瑜, 陈存友, 胡希军. 应用投影寻踪分类技术的森林生态功能评价[J]. 浙江农林大学学报, 2020, 37(2): 243 − 250. ZHANG Yu, CHEN Cunyou, HU Xijun. Evaluation of forest ecological function based on projection pursuit classification [J]. J Zhejiang A&F Univ, 2020, 37(2): 243 − 250. [2] 程武学, 杨存建, 周介铭, 等. 森林蓄积量遥感定量估测研究综述[J]. 安徽农业科学, 2009, 37(16): 7746 − 7750. CHEN Wuxue, YANG Cunjian, ZHOU Jieming, et al. Research summary of forest volume quantitative estimation based on remote sensing technology [J]. J Anhui Agric Sci, 2009, 37(16): 7746 − 7750. [3] 方精云, 刘国华, 徐嵩龄. 我国森林植被的生物量和净生产量[J]. 生态学报, 1996, 16(5): 497 − 508. FANG Jingyun, LIU Guohua, XU Songling. Biomass and net production of forest vegetation in China [J]. Acta Ecol Sin, 1996, 16(5): 497 − 508. [4] 郭庆华, 刘瑾, 陶胜利, 等. 激光雷达在森林生态系统监测模拟中的应用现状与展望[J]. 科学通报, 2014, 59(4): 459 − 478. GUO Qinghua, LIU Jin, TAO Shengli, et al. Perspectives and prospects of LiDAR in forest ecosystem monitoring and modeling [J]. Chin Sci Bull, 2014, 59(4): 459 − 478. [5] 李增元, 刘清旺, 庞勇. 激光雷达森林参数反演研究进展[J]. 遥感学报, 2016, 20(5): 1138 − 1150. LI Zengyuan, LIU Qingwang, PANG Yong. Review on forest parameters inversion using LiDAR [J]. J Remote Sensing, 2016, 20(5): 1138 − 1150. [6] 徐文兵, 高飞, 杜华强. 几种测量方法在森林资源调查中的应用与精度分析[J]. 浙江林学院学报, 2009, 26(1): 132 − 136. XU Wenbing, GAO Fei, DU Huaqiang. Application and precision analysis of several surveying methods in forest resources survey [J]. J Zhejiang For Coll, 2009, 26(1): 132 − 136. [7] 李春干, 代华兵. 中国森林资源调查: 历史, 现状与趋势[J]. 世界林业研究, 2021, 34(6): 72 − 80. LI Chungan, DAI Huabing. Forest management inventory in china: history, current status and trend [J]. World For Res, 2021, 34(6): 72 − 80. [8] PAWE H, PIOTR T, PIOTR W. Area-based estimation of growing stock volume in Scots pine stands using ALS and airborne image-based point clouds [J]. Forestry, 2017(5): 686 − 696. [9] CHIRICI G, GIANNETTI F, MCROBERTS R E, et al. Wall-to-wall spatial prediction of growing stock volume based on Italian National Forest Inventory plots and remotely sensed data[J/OL]. Int J Appl Earth Observation Geoinf, 2019, 84: 101959[2021-12-30]. doi: 10.1016/j.jag.2019.101959. [10] 陈松, 孙华, 吴童, 等. 基于Sentinel-2与机载激光雷达数据的误差变量联立方程组森林蓄积量反演研究[J]. 中南林业科技大学学报, 2020, 40(12): 44 − 53. CHEN Song, SUN Hua, WU Tong, et al. Study on the forest volume inversion based on the simultaneous equations of error variables of Sentinel-2 and airborne Lidar data [J]. J Cent South Univ For Technol, 2020, 40(12): 44 − 53. [11] 曾伟生, 孙乡楠, 王六如, 等. 基于机载激光雷达数据的森林蓄积量模型研建[J]. 林业科学, 2021, 57(2): 31 − 38. ZENG Weisheng, SUN Xiangnan, WANG Liuru, et al. Development of forest stand volume models based on airborne laser scanning data [J]. Sci Silv Sin, 2021, 57(2): 31 − 38. [12] 黄道年, 廖泽钊. 广西桉树二元材积表编制的研究[J]. 广西农学院学报, 1986(1): 53 − 60. HUANG Daonian, LIAO Zezhao. Study on compiling binary volume table of Eucalyptus in Guangxi [J]. J Guangxi Agric Coll, 1986(1): 53 − 60. [13] 肖武, 陈佳乐, 笪宏志, 等. 基于无人机影像的采煤沉陷区玉米生物量反演与分析[J]. 农业机械学报, 2018, 49(8): 169 − 180. XIAO Wu, CHEN Jiale, DA Hongzhi, et al. Inversion and analysis of maize biomass in coal mining subsidence area based on UAV images [J]. Trans Chin Soc Agric Mach, 2018, 49(8): 169 − 180. [14] 于雷, 洪永胜, 耿雷, 等. 基于偏最小二乘回归的土壤有机质含量高光谱估算[J]. 农业工程学报, 2015, 31(14): 103 − 109. YU Lei, HONG Yongsheng, GENG Lei, et al. Hyperspectral estimation of soil organic matter content based on partial least square regression [J]. Trans Chin Soc Agric Eng, 2015, 31(14): 103 − 109. [15] 刘琼阁, 彭道黎, 涂云燕. 基于偏最小二乘回归的森林蓄积量遥感估测[J]. 中南林业科技大学学报, 2014, 34(2): 81 − 84,132. LIU Qiongge, PENG Daoli, TU Yunya. Estimation of forest stock volume based on partial least squares regression [J]. J Cent South Univ For Technol, 2014, 34(2): 81 − 84,132. [16] VAPNIK V, IZMAILOV R. Intelligent learning: similarity control and knowledge transfer [J/OL]. Ann Math Artif Intell, 2017(1/2)[2022-01-01]. doi: 10.1007/978-3-319-17091-6_1. [17] BAO Yukun, LUI Zhitao. A fast grid search method in support vector regression forecasting time series[R]// [s.l] Intelligent Data Engineering and Automated Learning Vol 4244. Berlin Heidelberg: Springer, 2006: 504 − 511. [18] 方匡南, 吴见彬, 朱建平, 等. 随机森林方法研究综述[J]. 统计与信息论坛, 2011, 26(3): 32 − 38. FANG Kuangnan, WU Jianbin, ZHU Jianping, et al. A review of random forest method research [J]. Stat Inf Forum, 2011, 26(3): 32 − 38. [19] MOLINARO A M, SIMON R, PFEIFFER R M. Prediction error estimation: a comparison of resampling methods[J/OL]. Bioinformatics, 2005, 21(15): 3301-7[2021-012-31]. doi: 10.1093/bioinformatics/bti499. [20] 肖越. 基于多源遥感数据的旺业甸林场森林蓄积量估测方法研究[D]. 长沙: 中南林业科技大学, 2021. XIAO Yue. Research on Estimation Method of Forest Volume of Wangyedian Forest Farm based on Multi-Source Remote Sensing Data[D]. Changsha: Central South University of Forestry & Technology, 2021. [21] 赵勋, 岳彩荣, 李春干, 等. 基于机载LiDAR数据估测林分平均高[J]. 林业科学研究, 2020, 33(4): 59 − 66. ZHAO Xun, YUE Cairong, LI Chungan, et al. Estimation of forest stand mean height based on airborne lidar point cloud data [J]. For Res, 2020, 33(4): 59 − 66. [22] 周蓉, 赵天忠, 吴发云. 基于Landsat 8遥感影像的地上生物量模型反演研究[J]. 西北林学院学报, 2022, 37(2): 186 − 192. ZHOU Rong, ZHAO Tianzhong, WU Fayun. Aboveground biomass model based on landsat 8 remote sensing images [J]. J Northwest For Univ, 2022, 37(2): 186 − 192. [23] 袁钰娜, 彭道黎, 王威, 等. 利用机载激光雷达技术估测东北林区典型针叶林的蓄积量[J]. 应用生态学报, 2021, 32(3): 836 − 844. YUAN Yuna, PENG Daoli, WANG Wei, et al. Estimating standing stocks of the typical conifer stands in Northeast China based on airborne LiDAR data [J]. Chin J Appl Ecol, 2021, 32(3): 836 − 844. [24] 丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 2011, 40(1): 2 − 10. DING Shifei, QI Bingjuan, TAN Hongyan. An overview on theory and algorithm of support vector machines [J]. J Univ Electron Sci Technol China, 2011, 40(1): 2 − 10. [25] 孙忠秋, 高金萍, 吴发云, 等. 基于机载激光雷达点云和随机森林算法的森林蓄积量估测[J]. 林业科学, 2021, 57(8): 68 − 81. SUN Zhongqiu, GAO Jinping, WU Fayun, et al. Estimating forest stock volume via small-footprint LiDAR point cloud data and random forest algorithm [J]. Sci Silv Sin, 2021, 57(8): 68 − 81. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20220108
点击查看大图
图(6) / 表(6)
计量
- 文章访问数: 665
- HTML全文浏览量: 80
- PDF下载量: 41
- 被引次数: 0
