-
树高和胸径不仅是用来预测林分蓄积量[1]、生物量[2]、立地生产力[2-3]及林分结构[4]的重要变量,而且是森林资源调查及经营效果评价的重要因子。在标准地调查过程中,树高测量难度较大且观测成本高,其观测误差也相对较大,给精准林业质量提升带来了一定困难[2,4],而胸径观测方便且精度较高。因此,根据标准地调查数据,建立树高与胸径关系预测模型,可降低调查成本,提高预测精度[5],这对于森林质量精准提升具有重要意义。当前林业研究多采用线性或非线性树高与胸径关系模型来模拟预测两者之间的关系,其参数估计方法多采用最小二乘法来模拟,然而最小二乘法是基于均值回归,利用变量均值来拟合模型参数[6],该方法要求调查数据需满足独立正态同分布等条件。在林业调查中,树高与胸径观测数据不能满足该要求,而分位数回归对调查数据没有严格要求[7],利用变量条件分位数来建模[6],对具有尖峰、厚尾、异方差显著的数据拟合效果更加稳健[8-10]。分位数回归理论框架是由KOENKER[11]提出,已在医学[12]、经济学[13]、教育与政策[14-15]及自然资源管理等领域进行了研究与应用。在林业相关研究中,分位数回归被应用于模拟林分自疏边界线[16]、直径分布规律[17]、林分密度指数[18]及森林病虫害[19]等方面研究。ÖZÇELIK等[20]基于分位数回归建立了树高与胸径关系模型,高慧淋等[21]采用此方法建立了长白落叶松Larix olgensis人工林最大林分密度线模型,提高了模型预测精度及适用性。然而在华北暖温带针阔混交林中,如何基于一个分位数回归模型,预测不同树种树高与胸径关系是亟待解决的科学问题。在混交林中为了描述树种结构对树木生长影响,部分学者[22-25]采用哑变量方法构建了不同间伐方式、不同地域树高曲线及生长量预测模型。然而基于包含哑变量的非线性分位数回归方法来构建不同树种树高与胸径关系模型的研究较少。因此,本研究以河北省塞罕坝华北落叶松Larix principis-rupprechtii与白桦Betula platyphylla针阔混交林为研究对象,基于哑变量方法和分位数回归相结合方法,构建混交林不同树种分位数回归模型,为精确描述树高与胸径的关系提供依据。
-
河北省塞罕坝机械林场(41°22′~42°58′N,116°53′~118°31′E)位于河北省最北部,地势北高南低,属华北暖温带立地类型区,林场总面积约9.2×104 hm2,总蓄积约8.1×106 m3。土壤类型以褐色森林土、棕色森林土及风沙土等为主;成土母质主要为坡积物、残积物及洪积物等;极端最高气温为33.4 ℃,最低气温−43.3 ℃,年均气温−1.3 ℃,年均无霜期64 d,年均降水量460.3 mm,是典型的半干旱半湿润寒温性大陆季风气候。研究区植被类型丰富,主要乔木树种有华北落叶松、白桦、樟子松Pinus sylvestris、云杉Picea asperata等,主要灌木树种有山刺玫Rosa daverica、胡枝子Lespedeza bicolor、沙棘Hippophae rhamnoides等,主要草本植物有地榆Sanguisorba offcinalis、唐松草Thalictrum aquilegifolium、曼陀罗Datura stramonium等。
-
在北曼店、大唤起、阴河、千层板和第三乡等5个林场设立了83块标准地(30 m×30 m),对标准地内各林分因子(林分密度、平均高、平均胸径、树种断面积、林分总断面积、优势高等)和立地因子(海拔、坡度、坡向、坡位、土层厚度等)进行调查,共调查立木10 104株(华北落叶松5 258株,白桦4 846株),林分年龄分布为24~45 a,不同标准地混交度分布为0.39~0.62。研究过程中,分树种将观测数据分别按3∶1分为建模数据(62块标准地)和检验数据(21块标准地),基本信息如表1和表2所示。
表 1 模型建立数据
Table 1. Data of establishment model
统计量 海拔/m 林分断面积/hm2 密度/(株·hm–2) 华北落叶松 白桦 胸径/cm 树高/m 胸径/cm 树高/m 平均值 1 424.00 208.87 1 070.00 15.50 10.60 14.30 10.10 最大值 1 672.00 452.19 1 725.00 34.60 17.90 29.20 16.20 最小值 1 177.00 19.96 675.00 5.00 4.20 5.10 4.60 标准差 149.63 78.69 241.00 4.25 2.34 3.92 1.77 表 2 模型检验数据
Table 2. Data of test model
统计量 海拔/m 林分断面积/hm2 密度/(株·hm–2) 华北落叶松 白桦 胸径/cm 树高/m 胸径/cm 树高/m 平均值 1 464.00 254.00 1 162.00 17.50 11.00 12.50 8.90 最大值 1 540.00 387.40 2 000.00 34.70 17.80 27.20 15.60 最小值 1 396.00 157.83 850.00 5.00 3.20 5.10 4.80 标准差 39.28 73.41 269.76 6.26 2.70 4.47 2.16 -
在描述树木生长及树高与胸径关系的近百种不同模型中,Richard方程不但具有可解释的生物学意义,而且具有易收敛且灵活性高等特性。部分研究基于Richard方程构建了不同林分类型树高与胸径关系的预测模型,均取得了较好的预测结果[18, 20, 26-29]。因此,本研究以Richard方程作为构建华北落叶松与白桦针阔混交林树高与胸径关系基础模型,模型表达如式(1)所示。
$${H_{i\!j}} = 1.3 + a{\left[ {1 - \exp \left( { - b{d_{i\!j}}} \right)} \right]^c} + {\varepsilon _{i\!j}}\text{。}$$ (1) 式(1)中:Hij为第i个样地第j株树的树高(m);dij为第i个样地第j株树的胸径(cm);a、b、c为基础模型的参数;εij为误差项。
-
为了解决模型预测精度的影响,可以在模型中加入哑变量[23, 30-32]。包含哑变量的树高与胸径关系预测模型,不仅可以实现模型对不同树种相容性,而且在一定程度上可以提供模型预测精度及适用性,包含哑变量的树高与胸径关系预测模型表达如式(2)所示。
$${H_{i\!j}} = 1.3 + \left( {{a_1}{M_1} + {a_2}{M_2}} \right){\left\{ {1 - \exp \left[ { - \left( {{b_1}{M_1} + {b_2}{M_2}} \right){d_{i\!j}}} \right]} \right\}^{\left( {{c_1}{M_1} + {c_2}{M_2}} \right)}} + {\varepsilon _{i\!j}}\text{。}$$ (2) 式(2)中:Mi为哑变量,当M1=1、M2=0时为华北落叶松,当M1=0、M2=1时为白桦;ai、bi、ci为模型参数;εij为误差项。
-
由于分位数回归对模型误差不需要严格假设条件,因此本研究基于Richard方程,选取5个分位点(τ=0.1、0.3、0.5、0.7、0.9)构建不同树种的树高与胸径关系预测模型,利用加权最小一乘法可以得到不同分位点参数估计值,具体见式(3)。
$$ S=\sum\limits_{{H_{i\!j}} \geqslant {{\hat H}_\tau }({d_{i\!j}})} {\tau \left[ {{H_{i\!j}} - {{\hat H}_\tau }({d_{i\!j}})} \right]} + \sum\limits_{{H_{i\!j}} < {{\hat H}_\tau }({d_{i\!j}})} {(1 - \tau )\left[ {{{\hat H}_\tau }({d_{i\!j}}) - {H_{i\!j}}} \right]}\text{。} $$ (3) 式(3)中:S为不同分位点估计值;
${\hat H_\tau }$ 、Hij分别为第i个样地第j株树在不同分位点τ树高预测值与树高值(m);dij第i个样地第j株树胸径(cm);τ为分位点。 -
统计分析均基于SPSS 24.0和SAS 9.4中的PROC NLIN和PROC NLP完成,基于模型确定系数(R2)、平均差(MD)、平均绝对误差(MAD)对模型拟合精度及适用性进行评价与比较。
$${R^2} = 1 - \sum\limits_{i = 1}^m {\sum\limits_{i = 1}^{{n_i}} {{{({H_{i\!j}} - {{\hat H}_{i\!j}})}^2}} \Big/\sum\limits_{i = 1}^m {\sum\limits_{i = 1}^{{n_i}} {{{({H_{i\!j}} - {{\overline H}_{i\!j}})}^2}} } }\text{;} $$ (4) $${M_{\rm{D}}} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^{{n_i}} {({H_{i\!j}} - {{\hat H}_{i\!j}})} } \Big/\sum\limits_{i = 1}^m {{n_i}}\text{;}$$ (5) $${M_{{\rm{AD}}}} = \sum\limits_{i = 1}^m {\sum\limits_{j = 1}^{{n_i}} {\left| {{H_{i\!j}} - {{\hat H}_{i\!j}}} \right|} } \Big/\sum\limits_{i = 1}^m {{n_i}} \text{。}$$ (6) 式(4)~(6)中:Hij、
${\hat H_{i\!j}}$ 和${\overline H_{i\!j}}$ 分别为树高观测值、预测值和平均值;m为标准地数量;n为标准地株数。 -
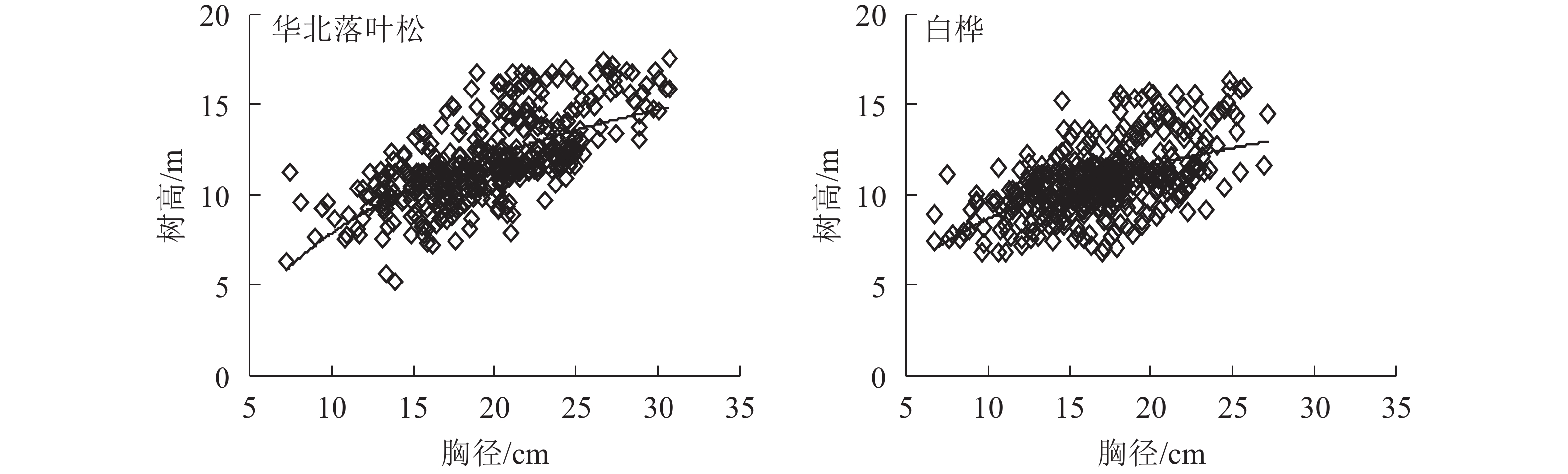
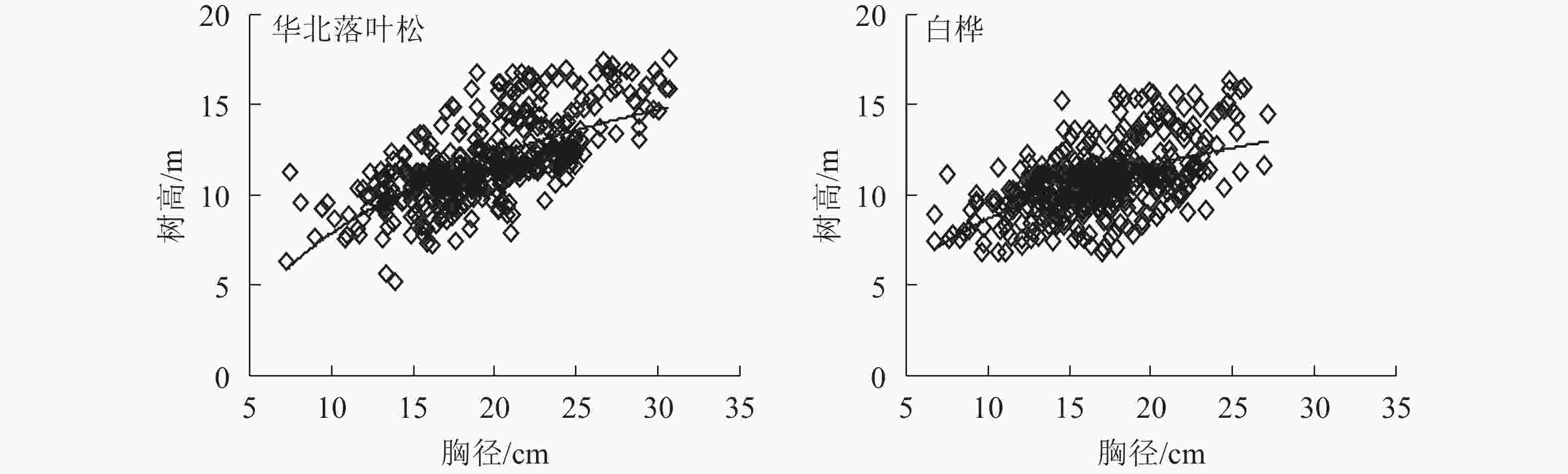
图1为不同树种胸径与树高的关系。华北落叶松和白桦的树高分别为4~18和6~16 m,胸径分别为6~32和6~28 cm。
-
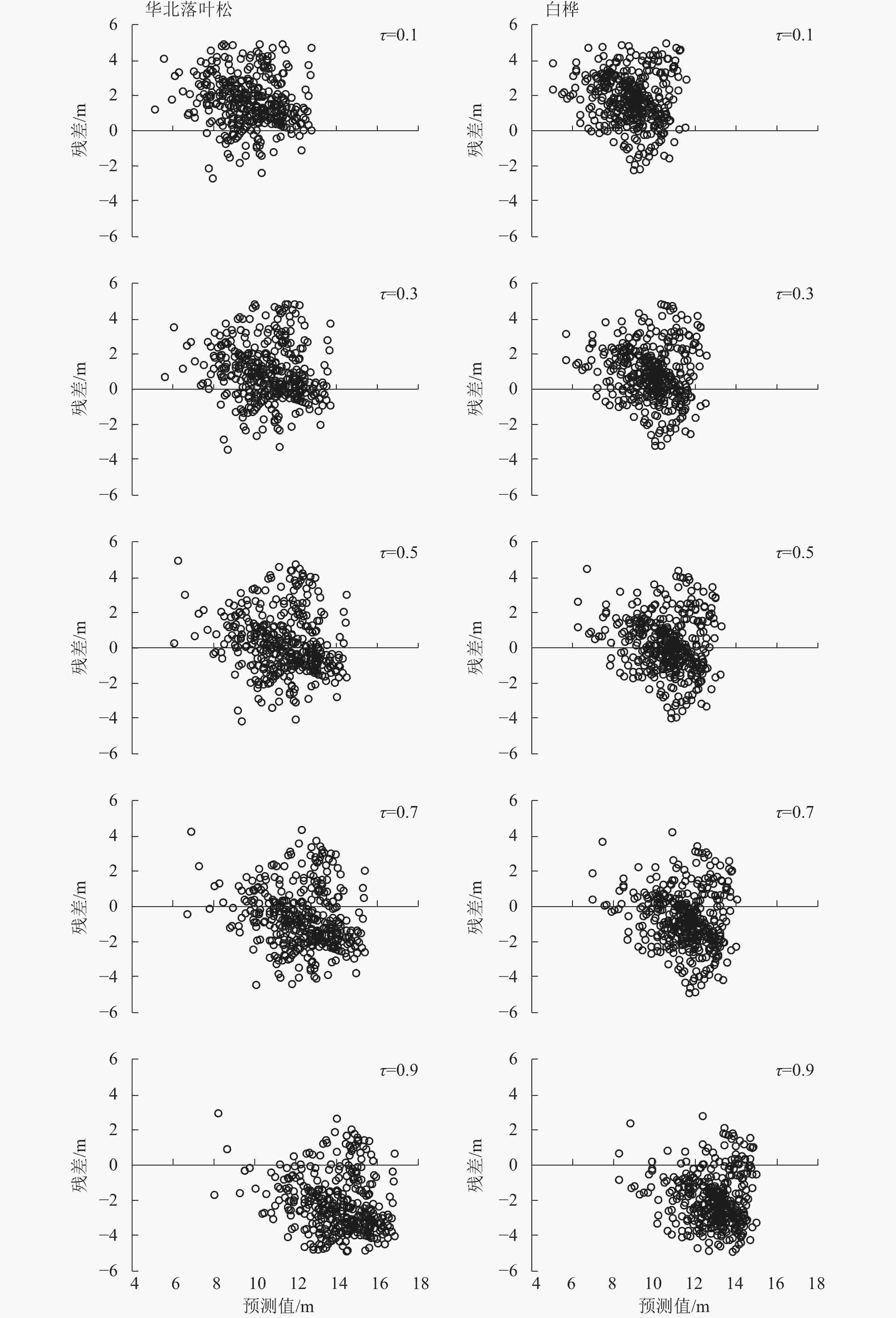
从表3可见:在华北落叶松与白桦针阔混交林中,基于分位数回归的不同树种不同分位点确定系数均大于传统回归方法,平均差及平均绝对误差均小于传统回归方法。在确定的5个分位点中,当分位点τ=0.7时,华北落叶松与白桦的树高与胸径关系预测模型精度最高。基于不同分位点预测模型建立了不同树种在各分位点残差分布图(图2),确定当分位点位为τ=0.7时,华北落叶松与白桦树高与胸径关系模型能够更好描述两者之间的关系。
表 3 基础模型和分位数回归模型拟合与评价
Table 3. Fitting and evaluation of basic model and quantile regression model
模型 参数 评价指标 a b c MD MAD R2 OLSL 20.299 0.001 0.155 1.518 2.447 0.814 OLSB 16.301 0.032 0.906 1.877 2.654 0.787 τL=0.1 17.445 0.033 0.978 0.962 2.032 0.848 τL=0.3 17.576 0.038 0.982 0.725 1.709 0.855 τL=0.5 17.657 0.043 0.992 0.465 1.342 0.872 τL=0.7 17.998 0.051 1.002 0.213 0.561 0.912 τL=0.9 18.005 0.065 1.005 1.432 2.206 0.839 τB=0.1 13.956 0.043 0.892 0.992 2.043 0.848 τB=0.3 14.559 0.052 0.981 0.681 1.882 0.861 τB=0.5 14.703 0.059 0.997 0.428 1.269 0.882 τB=0.7 14.996 0.071 1.001 0.235 0.852 0.921 τB=0.9 15.011 0.092 1.009 1.469 2.322 0.838 说明:L表示华北落叶松,B表示白桦;OLS表示最小二乘法 -
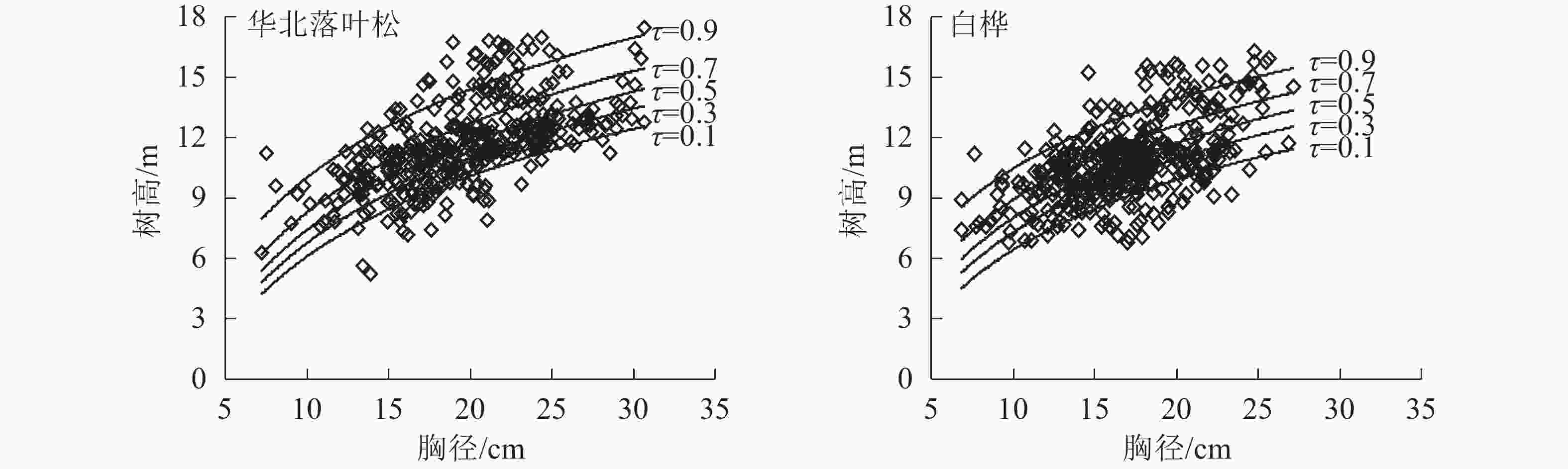
基于不同分位点预测模型,分别对华北落叶松和白桦的树高与胸径关系进行了模拟(图3)。不同树种在不同分位点树高与胸径关系预测趋势及范围基本一致,表明包含哑变量的分位数回归模型预测效果较好。
-
在描述树高与胸径关系的多种线性和非线性预测模型中,通常采用具有生物学意义且灵活性较高的Richard方程来研究不同林分类型树高与胸径的关系[26, 33],因此,本研究将Richard方程作为构建华北落叶松与白桦混交林树高与胸径关系基础模型。对红松Pinus koraiensis人工林、土耳其松Pinus brutia和黎巴嫩雪松Cedrus libani混交林的研究[20, 26-28]表明:Richard方程是描述其树高与胸径关系的最优模型。
在构建树木生长及生物量预测模型中,包含哑变量模型具有更高的预测精度[22, 25, 31-32]。本研究在华北落叶松与白桦针阔混交林中,基于非线性分位数回归构建的包含哑变量树高与胸径的关系模型,其精度高于传统回归预测模型,这与人工林最大密度线确定[21]及树高与胸径关系模型[20]的研究结论相一致,表明非线性分位数回归较传统回归方法更加稳定,可用于人工林和混交林立地潜在生产力的评价。
-
本研究以塞罕坝华北落叶松与白桦针阔混交林调查数据为基础,确定Richard模型为描述不同树种树高与胸径关系的基础模型,在基础模型中构造一个表示树种的哑变量,并利用分位数回归在一个模型中同时估计不同树种及不同分位点的树高与胸径关系模型参数,经过检验不同树种分位数回归模型均能较好反映树高与胸径的关系,当分位点τ=0.7时,分位数回归模型预测精度最高,拟合效果最好。
Relationship between height and diameter at breast height(DBH) in mixed coniferous and broadleaved forest based on quantile regression
-
摘要:
目的 基于包含哑变量的非线性分位数回归方法,构建华北落叶松Larix principis-rupprechtii与白桦Betula platyphylla针阔混交林树高与胸径关系的预测模型,对研究混交林中树种结构及立地生产力预测具有重要意义。 方法 以河北省塞罕坝机械林场华北落叶松与白桦针阔混交林为研究对象,利用83块标准地调查数据,基于哑变量分别采用最小二乘法和非线性分位数回归方法,构建不同树种树高与胸径关系模型。 结果 基于包含哑变量的非线性分位数回归预测模型精度高于最小二乘法,其中利用最小二乘法拟合不同树种模型,其确定系数、平均差及平均绝对误差分别为0.787~0.814、1.581~1.877、2.447~2.654;而利用非线性分位数回归不同树种不同分位点模型,其确定系数、平均差及平均绝对误差分别为0.839~0.921、0.213~1.469、0.561~2.322,经过残差分析确定,当分位点τ=0.7时,不同树种树高与胸径关系预测模型精度较高。 结论 与最小二乘法相比,基于非线性分位数构建的包含哑变量不同树种树高与胸径关系的预测模型精度更高。图3表3参33 Abstract:Objective With the employment of nonlinear quantile regression method using dummy variables, the current study is aimed to establish a prediction model for the relationship between height and diameter at breast height (DBH) in Larix principis-rupprechtii and Betula platyphylla mixed forest so as to better predict the tree structure and site productivity of mixed forests. Method Taking L. principis-rupprechtii and B. platyphylla mixed forest of Saihanba Mechanised Tree farm in Hebei Province as the research object, with 83 pieces of standard land survey data used and dummy variables created, this paper adopted the least square method and nonlinear quantile regression method respectively in the construction of the relationship model of tree height and DBH of different species. Result The accuracy of the nonlinear quantile regression prediction model based on dummy variables was higher than that of the one constructed using the least square method. Specifically, when the least square method was used to fit the tree height and DBH relationship model of different tree species, the determination coefficient, average difference and average absolute error of different tree species models were within the range of 0.787−0.814, 1.581−1.877 and 2.447−2.654 respectively. When the nonlinear quantile regression method was used, the coefficient, average deviation, and average absolute error were within the range of 0.839−0.921, 0.213−1.469, 0.561−2.322. In accordance with the residual analysis, when the quantiles of τ is 0.7, the relationship model of tree height and DBH of different species demonstrated a higher accuracy. Conclusion To sum up, compared with the one constructed employing the least square method, the prediction model of tree height and DBH relationship of different tree species adopting the nonlinear quantile regression method has higher prediction accuracy. [Ch, 3 fig. 3 tab. 33 ref.] -
Key words:
- forest ecology /
- nonlinear quantile regression /
- height-DBH /
- dummy variables /
- mixed forest
-
表 1 模型建立数据
Table 1. Data of establishment model
统计量 海拔/m 林分断面积/hm2 密度/(株·hm–2) 华北落叶松 白桦 胸径/cm 树高/m 胸径/cm 树高/m 平均值 1 424.00 208.87 1 070.00 15.50 10.60 14.30 10.10 最大值 1 672.00 452.19 1 725.00 34.60 17.90 29.20 16.20 最小值 1 177.00 19.96 675.00 5.00 4.20 5.10 4.60 标准差 149.63 78.69 241.00 4.25 2.34 3.92 1.77 表 2 模型检验数据
Table 2. Data of test model
统计量 海拔/m 林分断面积/hm2 密度/(株·hm–2) 华北落叶松 白桦 胸径/cm 树高/m 胸径/cm 树高/m 平均值 1 464.00 254.00 1 162.00 17.50 11.00 12.50 8.90 最大值 1 540.00 387.40 2 000.00 34.70 17.80 27.20 15.60 最小值 1 396.00 157.83 850.00 5.00 3.20 5.10 4.80 标准差 39.28 73.41 269.76 6.26 2.70 4.47 2.16 表 3 基础模型和分位数回归模型拟合与评价
Table 3. Fitting and evaluation of basic model and quantile regression model
模型 参数 评价指标 a b c MD MAD R2 OLSL 20.299 0.001 0.155 1.518 2.447 0.814 OLSB 16.301 0.032 0.906 1.877 2.654 0.787 τL=0.1 17.445 0.033 0.978 0.962 2.032 0.848 τL=0.3 17.576 0.038 0.982 0.725 1.709 0.855 τL=0.5 17.657 0.043 0.992 0.465 1.342 0.872 τL=0.7 17.998 0.051 1.002 0.213 0.561 0.912 τL=0.9 18.005 0.065 1.005 1.432 2.206 0.839 τB=0.1 13.956 0.043 0.892 0.992 2.043 0.848 τB=0.3 14.559 0.052 0.981 0.681 1.882 0.861 τB=0.5 14.703 0.059 0.997 0.428 1.269 0.882 τB=0.7 14.996 0.071 1.001 0.235 0.852 0.921 τB=0.9 15.011 0.092 1.009 1.469 2.322 0.838 说明:L表示华北落叶松,B表示白桦;OLS表示最小二乘法 -
[1] DUCEY M J, KNAPP R A. A stand density index for complex mixed species forests in the northeastern United States [J]. For Ecol Manage, 2010, 260(9): 1613 − 1622. [2] 周晏平,雷泽勇,赵国军,等. 沙地樟子松不同树高-胸径模型比较分析[J]. 华南农业大学学报, 2019, 40(3): 75 − 81. ZHOU Yanping, LEI Zeyong, ZHAO Guojun, et al. Comparing different height-diameter models of Pinus sylvestris var. mongolica in sandy land [J]. J South China Agric Univ, 2019, 40(3): 75 − 81. [3] 樊伟,许崇华,崔珺,等. 基于混合效应的大别山地区杉木树高-胸径模型比较[J]. 应用生态学报, 2017, 28(9): 2831 − 2839. FAN Wei, XU Chonghua, CUI Jun, et al. Comparisons of height-diameter models of Chinese fir based on mixed effect in Dabie Mountain area, China [J]. Chin J Appl Ecol, 2017, 28(9): 2831 − 2839. [4] 徐庆华,杨进良,黄练忠,等. 次生常绿阔叶林群落林冠结构对林下植被的影响[J]. 浙江农林大学学报, 2019, 36(6): 1151 − 1157. XU Qinghua, YANG Jinliang, HUANG Lianzhong, et al. Influence of canopy structure on understory vegetation of secondary evergreen broadleaf forest communities [J]. J Zhejiang A&F Univ, 2019, 36(6): 1151 − 1157. [5] PYA N, SCHMIDT M. Incorporating shape constraints in generalized additive modelling of the height-diameter relationship for Norway spruce [J]. For Ecosyst, 2016, 3(2): 112 − 125. [6] WANG Jing. Bayesian quantile regression for parametric nonlinear mixed effects models [J]. Stat Methods Appl, 2012, 21(3): 279 − 295. [7] GERACI M, BOTTAI M. Linear mixed quantile regression models: extensions and developments [J]. Lifetime Data Anal, 2007, 13(4): 497 − 512. [8] 张兴皖,周石鹏. 人口老龄化与区域产业结构——基于分位数回归的实证研究[J]. 经济数学, 2019, 36(1): 24 − 31. ZHANG Xingwan, ZHOU Shipeng. Population aging and regional industrial structure: empirical research based on quantile regression [J]. J Quant Econ, 2019, 36(1): 24 − 31. [9] 田德超,李凤日,董利虎. 依据分位数回归建立的长白落叶松潜在最大冠幅预测模型[J]. 东北林业大学学报, 2019, 47(8): 41 − 46. TIAN Dechao, LI Fengri, DONG Lihu. Potentila maximum crown width prediction model of Larix olgensis by quantile regression [J]. J Northeast For Univ, 2019, 47(8): 41 − 46. [10] BOHORA S B, CAO Q V. Prediction of tree diameter growth using quantile regression and mixed-effects models [J]. For Ecol Manage, 2014, 319: 62 − 66. [11] KOENKER R. Quantile Regression[M]. London: Cambridge University Press, 2005: 32 − 38. [12] AUSTIN P C, SCHULL M J. Quantile regression: a statistical tool for out-of-hospital research [J]. Acad Emergency Med, 2003, 10(7): 789 − 797. [13] MACHADO P J A F, MATA J. Counterfactual decomposition of changes in wage distributions using quantile regression [J]. J Appl Econ, 2010, 20(4): 445 − 465. [14] HAILE G A, NGUYEN A N. Determinants of academic attainment in the United States: a quantile regression analysis of test scores [J]. Educ Econ, 2008, 16(1): 29 − 57. [15] CADE B S, NOON B R, FLATHER C H. Quantile regression reveals hidden bias and uncertainty in habitat models [J]. Ecology, 2005, 86(3): 786 − 800. [16] ZANG Hao, LEI Xiangdong, ZENG Weisheng. Height-diameter equations for larch plantation in northern and northeastern China: a comparison of the mixed-effects, quantile regression and generalized additive models [J]. Forestry, 2016, 89(4): 434 − 445. [17] MEHTÄTALO L, GREGOIRE T G, BURKHART H E. Comparing strategies for modeling tree diameter percentiles from remeasured plots [J]. Environmetrics, 2010, 19(5): 529 − 548. [18] DUCEY M J. The ratio of additive and traditional stand density indices [J]. Western J Appl For, 2009, 24(1): 5 − 10. [19] EVANS A M, GREGOIRE T G. A geographically variable model of hemlock woolly adelgid spread [J]. Biol Invasions, 2007, 9(4): 369 − 382. [20] ÖZÇELIK R, CAO Q V, TRINCADO G, et al. Predicting tree height from tree diameter and dominant height using mixed-effects and quantile regression models for two species in Turkey [J]. For Ecol Manage, 2018, 419/420: 240 − 248. [21] 高慧淋,董利虎,李凤日. 基于分位数回归的长白落叶松人工林最大密度线[J]. 应用生态学报, 2016, 27(11): 3420 − 3426. GAO Huilin, DONG Lihu, LI Fengri. Maximum density-size line for Larix olgensis, plantations based on quantile regression [J]. Chin J Appl Ecol, 2016, 27(11): 3420 − 3426. [22] 高东启,邓华锋,王海宾,等. 基于哑变量的蒙古栎林分生长模型[J]. 东北林业大学学报, 2014, 21(1): 61 − 64. GAO Dongqi, DENG Huafeng, WANG Haibin, et al. Dummy variables models in Quercus mongolica growth [J]. J Northeast For Univ, 2014, 21(1): 61 − 64. [23] 杨英,冉啟香,陈新云,等. 哑变量在云杉地上生物量模型中的应用研究[J]. 林业资源管理, 2015, 12(6): 71 − 76. YANG Ying, RAN Qixiang, CHEN Xinyun, et al. Research on dummy variable in aboveground biomass models for spruce [J]. For Resou Manage, 2015, 12(6): 71 − 76. [24] 唐守正, 朗奎建, 李海奎. 统计和生物数学模型计算[M]. 北京: 科学出版社, 2009: 12 − 15. [25] 郑冬梅,曾伟生. 用哑变量方法构建东北落叶松和栎类分段地上生物量模型[J]. 北京林业大学学报, 2013, 35(6): 32 − 35. ZHENG Dongmei, ZENG Weisheng. Using dummy variable approach to construct segmented above ground biomass models for larch and oak in northeastern China [J]. J Beijing For Univ, 2013, 35(6): 32 − 35. [26] HUANG S, PRICE D, TITUS S J. Development of ecoregion-based height-diameter models for white spruce in boreal forests [J]. For Ecol Manage, 2000, 129(3): 139 − 141. [27] PENG Changhui, ZHANG Lianjun, LIU Jinxun. Developing and validating nonlinear height-diameter models for major tree species of Ontario’s boreal forests [J]. Northern J Appl For, 2001, 18(3): 87 − 94. [28] 臧颢,雷相东,张会儒. 红松树高-胸径的非线性混合效应模型研究[J]. 北京林业大学学报, 2016, 38(6): 8 − 16. ZANG Hao, LEI Xiangdong, ZHANG Huiru. Nonlinear mixed-effects height-diameter model of Pinus koraiensis [J]. J Beijing For Univ, 2016, 38(6): 8 − 16. [29] 陈义刚,谢正生,张祥生,等. 粤北低山丘陵地区小红栲生长过程分析[J]. 华南农业大学学报, 1994, 14(2): 124 − 128. CHEN Yigang, XIE Zhengsheng, ZHANG Xiangsheng, et al. Analysis of the growth process of Castanopsisc arlesii in north Guangdong mountain and hill areas [J]. J South China Agric Univ, 1994, 14(2): 124 − 128. [30] SANTOS F M, TERRA G, CHAER G M, et al. Modeling the height-diameter relationship and volume of young African mahoganies established in successional agro forestry systems in northeastern Brazil [J]. New For, 2019, 50(3): 389 − 407. [31] 李忠国,孙晓梅,陈东升. 基于哑变量的日本落叶松生长模型研究[J]. 西北农林科技大学学报(自然科学版), 2011, 39(8): 69 − 74. LI Zhongguo, SUN Xiaomei, CHEN Dongsheng, et al. Dummy variables model of increment of Larix kaempferi [J]. J Northwest A&F Univ Nat Sci Ed, 2011, 39(8): 69 − 74. [32] 吕常笑,邓华锋,王秋鸟. 基于哑变量的马尾松生物量模型研究[J]. 河南农业大学学报, 2016, 12(3): 304 − 310. LÜ Changxiao, DENG Huafeng, WANG Qiuniao, et al. Dummy variable models in Masson pine biomass [J]. J Henan Agric Univ, 2016, 12(3): 304 − 310. [33] SHARMA R P, VACEK Z, VACEK S, et al. Modelling individual tree height-diameter relationships for multi-layered and multi-species forests in central Europe [J]. Trees, 2019, 33(1): 103 − 119. -

-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20190461






 下载:
下载: