下载:
-
木材的内部缺陷会严重影响木材的质量。由于应力波的木材无损检测成本低、携带方便及对木材无损的特性，使得其越来越受到人们的青睐。国内外已开展了应力波速度与木材内部缺陷之间的相关研究。如WANG[1]通过应力波在缺陷木材中的传播规律，表明应力波在腐烂或劣化的木材中比在完好的木材中传播速度慢。徐华东等[2]以校园内的活立木作为样本，使用应力波检测仪器对校园树木进行二维成像，表明在活立木的断层横截面上，应力波横向的波速要小于径向的波速，且应力波在木材内部的波速受制于木材内部的缺陷情况。国内学者也对应力波无损检测仪器的可行性进行了研究。杨学春等[3]利用应力波检测仪器对原木内部腐朽进行了研究，结果表明：应力波测试仪能准确判断不同树种原木内部的腐朽程度，并且能够得到原木内部腐朽基本形状的二维图像。LIN等[4]运用应力波断层成像技术，对不同大小的樟树Cinnamomum camphora人造空洞进行了研究，表明应力波断层成像技术可以反映木材的空洞大小及位置，验证了应力波无损成像技术的可行性。以上研究主要针对应力波传播规律与成像技术的应用领域，但对应力波成像算法的研究不多。FENG等[5]提出了一种基于插值的图像重建算法，利用周围点的值估计未知点的速度情况，进而重建树木内部缺陷图像。DU等[6]提出了基于椭圆的空间插值以及速度补偿的方法对木材的横截面进行成像，能够准确地判定缺陷位置，并得到了良好的成像效果。国内外对于应力波在树木内部的传播规律做了大量的研究[8-10]，但是对于木材径切面传播规律和成像方法研究还比较少。翁翔等[7]利用无损检测仪器对木材的径切面进行测量，对应力波横向速度和径向速度的比值进行了回归，得到了应力波在木材径向上的传播速度模型，其结果的拟合度较高。但在木材径切面的缺陷成像方法研究较少。鉴于此，本研究基于应力波在木材径切面中沿直线上传播的假设，提出一种木材径切面内部缺陷的速度修正成像方法。
-
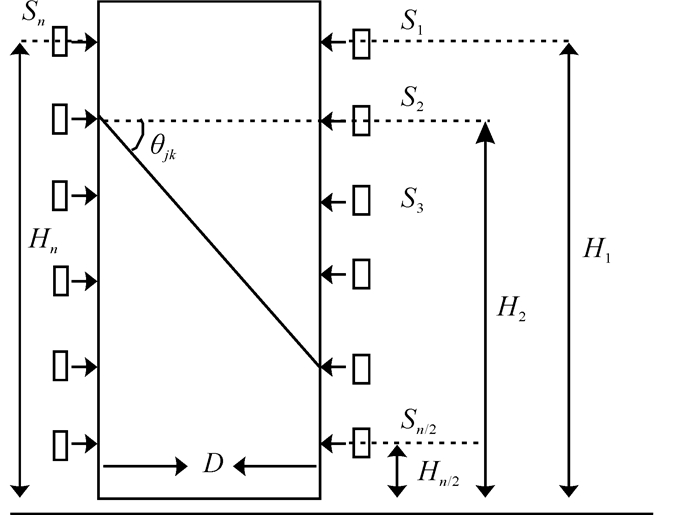
木材可以用圆柱体来近似的表示，那么木材的径切面可以被抽象成一个近似的矩形模型，将n个（n一般为12）传感器放置于被测树木两侧（传感器1至n/2位于同一侧）。每个传感器距离地面的高度（或者某一水平高度的距离）分别为（H1，H2，H3，…，Hn）；S1~Sn表示应力波传感器，传感器按照从右向左，呈U字形进行放置；D表示树木直径；θjk为每个传感器两两之间的相对角度。如图 1所示：定义一个坐标系表示树木径切面。
图 1 木材径切面模型
Figure 1. Radial and longitudinal plane model of wood
令Sn/2+1所在的位置为原点坐标，建立传感器的坐标系。
$$ S\left( {{X_i}, {Y_i}} \right) = \left\{ \begin{array}{l} {X_i} = D/2, {Y_i} = {H_i} - {H_{n/2 + 1}}, \;\;1 \le i \le n/2\\ {Y_i} = 0, {Y_i} = {H_i} - {H_{n/2 + 1}}, \;\;n/2 + 1 \le i \le n \end{array} \right.。 $$ (1) 式（1）中：有1≤i≤n，Xi表示传感器位置横坐标，Yi表示传感器位置纵坐标。根据每个传感器的位置数据，可得到每个传感器两两之间的相对角度θjk为：
$$ {\theta _{jk}} = \left\{ {\begin{array}{*{20}{l}} {\arctan (\frac{{{H_j} - {H_k}}}{D})}&{{H_j} > {H_k}, {H_k} < {H_{n/2 + 1}}}\\ {\arctan (\frac{{{H_j} - {H_{\left( {n/2 + 1} \right)}} - \left( {{H_k} - {H_{\left( {n/2 + 1} \right)}}} \right)}}{D}), }&{{H_j} > {H_k}, {H_k} < {H_{n/2 + 1}}}\\ {\arctan (\frac{{{H_k} - {H_j}}}{D})}&{{H_j} < {H_k}} \end{array}} \right.。 $$ (2) 式（2）中：1≤j≤n/2，n/2+1≤k≤n。
假定应力波在木材中是沿着直线传播的，通过传感器间的距离和应力波传播的时间计算出传感器间应力波的传播速度[11]。
-
为了预测木材离轴的单轴压缩强度，Hankinson公式[12]给出一种数学模型。当应力波在木材径切面上传播时，如果传播方向与垂直于木材纹理角方向所成的角度为θ，那么根据Hankinson公式可以推出如下公式：
$$ {V_\theta } = \frac{{{V_1}{V_{\rm{r}}}}}{{{V_1}{{\sin }^2}\theta + {V_{\rm{r}}}{{\cos }^2}\theta }}。 $$ (3) 式（3）中：V1表示平行于纹理方向上的应力波传播速度；Vr表示垂直于纹理方向上的应力波传播速度；θ表示传播方向与木材纹理方向所形成的角度；Vθ表示在角度为θ时应力波在木材径切面上的传播速度。
翁翔等[7]通过计算得出：
$$ \frac{{{V_\theta }}}{{{V_{\rm{r}}}}} \approx 1 + \frac{{{V_1} - {V_{\rm{r}}}}}{{{V_1}}} \times {\theta ^2}。 $$ (4) 式（4）中：$ \frac{{{V_1} - {V_{\rm{r}}}}}{{{V_1}}}$是常数。那么如图 2所示：假设在空洞木材中有2个对应角度α和β的传播路径Lα和Lβ，其中有α>β。Lα经过缺陷区域，其速度表示为Vα。Lβ是经过正常区域的，其速度表示为Vβ。同时假设在未产生空洞的同一木材中，有L'α经过的是正常的区域，其速度为V'α。那么有：
图 2 应力波在不同缺陷程度的木材中传播
Figure 2. Stress waves propagate in wood of different defect degree
$$ V{'_\alpha } > {V_\beta }, V{'_\alpha } > {V_\alpha } $$ (5) 根据式（5），可以得出:
$$ \frac{{V{'_\alpha }}}{{1 + z \times {\alpha ^2}}} \approx \frac{{V{'_\beta }}}{{1 + z \times {\beta ^2}}} \approx {V_{\rm{r}}}。 $$ (6) 式（6）中：$ z = \frac{{{V_1} - {V_{\rm{r}}}}}{{{V_1}}}$。由式（5）和式（6）可以得出：
$$ \frac{{{V_\alpha }}}{{1 + z \times {\alpha ^2}}} < \frac{{{V_\beta }}}{{1 + z \times {\beta ^2}}}。 $$ 就可以得出速度修正的公式：
$$ {V_{{\rm{c}}\left( {{\theta _{jk}}} \right)}} = \frac{{{V_{{\rm{d}}\left( {{\theta _{jk}}} \right)}}}}{{1 + z \times {\theta _{jk}}^2}}。 $$ (7) 式（7）中：Vc(θjk)表示修正后的速度；Vd(θjk)表示为测量得到的应力波传播速度；k是常数；θjk表示2个传感器间与垂直于木材方向纹理所成的角度。
因此经过缺陷区域的Vα经过速度修正后，就可以反映出应力波经过缺陷区域速度呈现出降低的现象，有效地减少了由木材的各向异性[13]导致的应力波在木材不同方向上传播速度不一致现象的影响，为木材内部缺陷成像提供更精确的数据。
将通过传感器之间的线速度VL转换成木材径切面上交点的速度VP：
$$ {V_{\rm{P}}} = \max \left( {{V_{{\rm{L1}}}}, {V_{{\rm{L2}}}}, \cdots , {V_{{\rm{L}}n}}} \right)。 $$ (8) 式（8）中：VL1至VLn分别表示每条经过该交点的应力波传播路径上修正后的线速度；（VL1, VL2, …, VLn）∈Vc(θjk)。
利用速度修正插值法对木材的径切面进行成像。每个已知点都对插值点具有一定的影响，即权重[14]。权重随着已知点和插值点之间距离的增加而减弱，距离插值点越近的已知点的权重越大。而且当已知点在距离插值点一定范围以外时，权重可以忽略不计。在任一待插值点的值是邻域内已知点权重之和。可以表示为：
$$ {V_{{\rm{q}}i}} = \left( {\sum\limits_{i = 1}^n {\frac{{\max \left( {\frac{{\left( {V{'_{{\rm{L1}}}}} \right)}}{{1 + z \times {\theta _{{\rm{L1}}}}}}} \right), \left( {\frac{{\left( {V{'_{{\rm{L2}}}}} \right)}}{{1 + z \times {\theta _{{\rm{L2}}}}}}} \right), \cdots , \left( {\frac{{\left( {V{'_{{\rm{L}}n}}} \right)}}{{1 + z \times {\theta _{{\rm{L}}n}}}}} \right)}}{{{d^m}_i}}} } \right)/\sum\limits_{i = 1}^n {\frac{1}{{{d^m}_i}}} 。 $$ (9) 式（9）中：Vqi为待插值点的预估值；V'Ln为每条经过该交点的应力波传播路径上未修正的线速度，（V'L1, V'L2, …, V'Ln）∈Vd(θjk)；θLn表示每条经过该交点的应力波传播路径与水平面的所成的夹角，（θL1, θL2, …, θLn）∈θjk；di为第i个已知点与待插值点的距离；n表示邻域内参与插值计算的已知点的个数；m为常数。
成像算法步骤：
步骤1：初始化（建立木材径切面的模型，输入传感器的坐标（x, y），计算传感器间的线速度Vd(θjk)；
步骤2：利用式（7）求出修正后的线速度矩阵Vc(θjk)；
步骤3：传感器两两连线的交点坐标（xc, yc），将邻域内已知属性值的交点的坐标以及每个交点对应的线速度V'Ln代入式（8）计算Vp的属性值；
步骤4：通过将已知点的属性值代入式（9），计算未知点的属性值；
步骤5：重复步骤4，直到计算出所有径切面上的每个点的属性值。
步骤6：将预估点根据属性值的不同进行不同颜色的赋值，并生成二维图像。
-
实验用于采集木材应力波数据的仪器是Fakopp。如图 3所示：将传感器分别放置在原木径切面两边，每边6个传感器，总共12个。实验过程中使用检测仪器自带的重锤以相同的力度，垂直于传感器方向，对各个传感器分别敲击3~5次，采集总共36~60组数据。将数据用于下文的成像中。
图 3 应力波测量装置与传感器的布置
Figure 3. Stress wave measuring device and sensor arrangement
本实验样本编号、样本种类、样本周长、样本测量高度等信息如表 1所示。
表 1 实验样本基本信息
Table 1. Experimental sample information
样本编号 样本种类 样本周长/cm 检测区域面积/cm2 缺陷面积/cm2 1 雪松Cedrus deodara 62.83 1 000 111.20 2 泡桐Paulownia fortunei 73.83 1 175 427.50 3 樟树Cinnamomum camphora 60.95 940 314.15 对样本的空洞面积测量方法如下：利用卷尺测量树木空洞的长和宽，假设样本的长为L，宽为W，则对于长方形的空洞缺陷面积SR计算公式为：
$$ S_{\rm R}=LW。 $$ (10) 假设梯形的空洞，上底长度为A，下底长度为B，缺陷的高度为H，梯形的空洞的面积ST则用公式可以表示为：
$$ {S_{\rm{T}}} = \frac{{\left( {A + B} \right)H}}{2}。 $$ (11) 假设圆形的缺陷孔洞的直径为R，那么缺陷的面积SY可以表示为：
$$ S_{\rm Y}=\mathit{π} R^2。 $$ (12) -
从图 4A可以看出：缺陷为人工挖掘并且形状为长方形。如图 4B所示：未修正的线图将经过缺陷区域的线段表示为黄色，未正确区分缺陷区域。图 4C表示的是修正后的线图，将经过缺陷区域的线段（如1号和7号、2号和8号等传感器之间的连线）错误地表示为缺陷颜色红色。从图 4D可以看出：使用IDW的成像结果，只能粗略反映缺陷位置，对于缺陷大小与形状都不能进行准确成像。对比VCI的成像结果图 4E，VCI可以较好还原缺陷位置，可以看出缺陷的位置是处于第3号、5号与8号、10号传感器之间，与图 4A所示的真实缺陷位置基本吻合。但是对于缺陷形状的成像不够准确。
图 4 雪松样本实验结果
Figure 4. Sample experiment results of Cedrus deodara sample
从图 5A可以看出：样本缺陷位置处于右边2号至5号传感器的下面3 cm，以及左边11号传感器至7号传感器的下面3 cm的位置，形状为矩形。从未修正线图（图 5B）可以看到：仅有少部分经过缺陷区域的线段被表示为缺陷的红色，大部分经过缺陷区域的线段被表示为非缺陷的绿色。修正后的线图（图 5C）较好地区分缺陷区域，并以不同的颜色进行区分。可以看到IDW的成像结果虽然能够还原缺陷的位置（图 5D），但对缺陷还原的准确度较低，对缺陷位置和大小的还原参考价值较低。如图 5E所示：VCI的成像结果可以较好地反映缺陷位置，但存在对缺陷区域成像结果比真实结果偏小的情况，以及对缺陷边缘的重建不够平整，对于样本的缺陷轮廓可以较好还原，可以反映样本的缺陷特征。
图 5 泡桐样本实验结果
Figure 5. Sample experiment results of Paulownia fortunei sample
从图 6A可以看出：树木的缺陷位置位于右边的3号和4号传感器之间，以及左边的9号和10号传感器之间。对比图 6B与图 6C可以看到：未修正的线图将经过缺陷区域的线段（如7号、1号传感器线段以及6号、12号传感器线段）错误地表示为经过正常区域的线段，呈现绿色，与真实情况不符。而修正后的线图，能够较好区分缺陷部位。从IDW成像结果（图 6D）反映缺陷所处的低速度区域，但对于缺陷的形状无法正确成像。缺陷成像结果呈现不规则的块状分布，无法反映样本的缺陷特征。VCI的成像结果（图 6E）显示：缺陷形状呈现一个类似圆形的不规则形状，与真实的缺陷形状较为接近。成像结果表明缺陷位于3号、4号传感器与9号、10号传感器之间，与图 6A的真实缺陷位置也基本相同。
图 6 樟树样本实验结果
Figure 6. Sample experiment results of Cinnamomum camphora sample
-
使用混淆矩阵法对成像效果进行定量的误差分析，混淆矩阵包含由分类系统完成的实际和预测的分类信息[15]。FAWCETT[16]描述了真、假分类系统中4种可能组合（表 2）。
表 2 缺陷与预测的4种组合
Table 2. Four combination of real defects and predict defects
类别 预测缺陷 预测完好 真实缺陷 被正确地预测为缺陷的面积C 被错误地预测为完好的面积E 真实完好 被错误地预测为缺陷的面积F 被正确地预测为完好的面积W 从表 2的矩阵可以推出的常用度量值[17]，如准确率或者正确率（A），精确度（P）和查全率（R）。
$$ A = \frac{{C + W}}{{C + E + F + W}}; $$ (13) $$ P = \frac{C}{{C + F}}; $$ (14) $$ R = \frac{C}{{C + E}}。 $$ (15) 式（13）~（15）中：准确率A表示对木材状态预测正确的百分比；精确度P表示对木材缺陷预测的可靠性水平高低；查全率R表示对木材缺陷的预测能力高低；C，W，E和F所代表含义见表 2。
从表 3可见：3个样本的准确率A为72.32%~95.85%。使用VCI方法的3个样本的平均准确率为93.34%，使用IDW方法的3个样本平均准确率为82.63%。IDW方法在1号、2号样本中的准确率均大于85.00%，其原因应该是IDW方法在成像结果中虽然不能很好地反映木材缺陷的特征，但是对木材完好的部位成像结果较好，所以得到较高的准确率。而3号样本只有72.32%的准确率，对比真实缺陷可以看出：IDW方法将部分正常木材错误地成像为缺陷木材，所以导致准确率下降。IDW和VCI的准确度标准差分别为7.38%和2.04%。可见，VCI在准确率上的标准差较小，说明VCI方法在不同样本中的准确率结果更稳定，准确率相较于IDW方法均有所提高。
表 3 不同样本的准确率
Table 3. Accuracy of different samples
样本编号 准确率A/% IDW方法 VCI方法 1 89.20 95.85 2 86.36 93.30 3 72.32 90.86 从表 4可见：3个样本的精确度P为65.79%~88.35%。使用VCI方法的3个样本的平均精确度为82.26%，使用IDW方法的3个样本平均精确度为70.19%。VCI方法中3号样本的结果要好于其他样本，其原因是3号样本中的预测缺陷大部分与真实缺陷重合，且预测缺陷大部分落在真实缺陷上，所以得到较高的精确度。IDW和VCI方法的精确度标准差分别为5.00%和4.70%。VCI方法在准确度上的标准差较小，VCI方法在精确度的稳定性略高于IDW方法。同时VCI方法在不同样本上的精确度均好于IDW方法。
表 4 不同样本的精确度
Table 4. Precision of different samples
样本编号 精确度P/% IDW方法 VCI方法 1 67.60 76.92 2 77.18 88.35 3 65.79 81.51 从表 5可见：3个样本的查全率R为17.98%~94.03%。使用VCI方法的3个样本的平均查全率为92.65%，使用IDW方法的3个样本平均查全率为36.64%。VCI方法中的查全率高于IDW方法。可见，VCI方法可以较好地反映木材的真实缺陷结果，且对木材的缺陷位置成像结果更好。在真实缺陷大小不变的情况下，由于VCI方法可以更好地反映木材的缺陷情况，因此得到了更高的查全率，与真实的成像结果相吻合。IDW和VCI方法的查全率标准差分别为：15.59%和1.93%。说明VCI方法的查全率标准差要远小于IDW方法，在查全率的稳定性上要好于IDW方法。
表 5 不同样本的查全率
Table 5. Recall rate of different samples
样本编号 查全率R/% IDW方法 VCI方法 1 17.98 89.92 2 56.14 94.03 3 35.80 94.00 -
本研究提出了一种应用于木材无损检测领域的，基于应力波的木材径切面成像方法。通过与IDW的成像效果比较发现：不论是在定量还是定性方面，VCI方法对木材径切面的缺陷成像结果都好于IDW方法。与真实的缺陷进行对比得到较小的误差，可以准确反映木材内部的真实缺陷情况，具有较高的成像精度。利用传感器测量得到的不同应力波数据，通过对不同缺陷的样本进行实验，验证了该算法对于木材的径切面成像效果的可行性。利用混淆矩阵对成像结果进行了定量分析发现：VCI方法的平均准确度为93.34%，平均精确度为82.26%，平均查全率为92.65%，均高于IDW方法，但对于缺陷具体形状的成像结果，其准确度有待进一步提高。
A stress wave tomography algorithm for internal defects in radial and longitudinal (RL) planes of wood
-
摘要: 为了获得木材径切面上的缺陷形状、大小和位置，提出一种木材径切面内部缺陷成像的方法。首先，基于应力波在木材径切面上的传播规律，提出一种木材径切面上的应力波速度修正方法。将应力波速度转换为径切面上的若干个预估点的值，结合反距离加权插值（IDW）法提出一种速度修正插值（VCI）方法。最后，使用VCI方法在不同树木样本上进行了木材径切面缺陷的二维成像实验。结果表明：①VCI方法可以重建木材内部缺陷大小以及缺陷位置，缺陷成像结果与真实的缺陷情况相吻合。②对比IDW方法的成像结果，VCI方法对缺陷的大小以及缺陷形状、位置的成像结果有较大提高。③利用混淆矩阵方法对VCI与IDW方法进行定量分析表明，VCI方法的平均准确率、平均精确度和平均查全率均高于IDW方法，说明VCI方法成像效果的可行性和有效性。Abstract: To generate and obtain the shape, size, and position of defects in the radial and longitudinal (RL) planes of wood, this study presented a new method for imaging defects on the RL planes in wood. First, based on the propagation law of stress waves for the RL planes of wood, a modified method of propagating the velocity of stress waves was proposed. Then the propagation velocity of the stress wave was converted into a value at estimated points. Finally, a velocity correction interpolation method (VCI) was proposed to reconstruct any defects in different tree samples. Imaged results were then compared to the inverse distance weighted (IDW) interpolation method and quantitatively analyzed using the method of confusion matrix. Experimental results showed that (1) the proposed method could reconstruct the size of the internal wood defects and their location with imaging results of the defects being basically consistent with real defects. (2) Compared to imaged results from IDW, the proposed method has higher accuacy rate when reconstructing the size, shape, and location of the defect. (3) The quantitative analyses showed that the proposed method improved in average accuracy, average precision, and the average recall. Thus, imaged results of defects with different shapes showed the effectiveness of the proposed method in reconstruction defects in RL plans of wood.
-
杜鹃群落是以杜鹃属Rhododendron植物为优势种的植被类型,主要分布于中国西南地区海拔较高的山地[1]。全世界杜鹃属植物约960种,中国约650种,是杜鹃属分布中心,也是杜鹃花生物多样性最高的国家,除新疆地区之外,全国其他省(市、自治区)均有分布,其中以西南地区分布最为广泛。贵州省是杜鹃原生种分布区数量最多的省份之一,是杜鹃花中国中心分布区向外扩张的过渡地带,有着丰富的原生种和大量可能的新种和变种[2]。有关学者先后对杜鹃植物开展了种子萌发特性、形态解剖、抗旱评价、引种驯化、繁殖利用、群落特征以及多样性保护及保育研究[3-5]。但对于杜鹃群落生物多样性的研究较少,尤其采用群落数量分类学方法对杜鹃群落生物多样性研究鲜有报道。采用群落数量分类方法结合群丛特性进行分析,能够定量解析群丛特性、组成特点,更加准确地反映杜鹃与其他植物种类间的关系。在对退化杜鹃群落进行恢复中,以群丛为单位进行恢复,提高了其可操作性。本研究选择贵阳市乌当区万亩杜鹃群落作为研究对象,采用典型样地调查、群落数量分类及多样性分析等方法展开研究,旨在筛选出万亩杜鹃群落生物多样性最高的群丛,为杜鹃群落生物多样性保护提供技术指导,奠定理论基础。
1. 材料与方法
1.1 研究区域概况
本研究选择贵阳市乌当区典型杜鹃群落为研究对象。乌当区位于贵阳市东北部,属贵阳城市规划的9个组团之一,地处26°55′～26°33′N,106°30′～107°03′E。乌当区属亚热带季风湿润气候,具有明显的高原性气候的特点,冬无严寒,夏无酷暑,光、热、水同季,垂直气候差异明显,年平均降水量1 179.8~1 271.0 mm。年平均气温14.6 ℃。森林覆盖率达49.36%。由于地形、地貌类型多样,形成多种小气候,宜于农业生产,大部分地区可满足农作物1 a 2熟,蔬菜1 a 3~4熟的需要。主要灾害性天气有干旱、倒春寒、冰雹、秋季连阴雨、秋风、凝冻[6]。区境内河流均属于长江流域乌江水系,河床狭窄,比降大,流速较快。全区土壤为黄壤区,黄棕壤、石灰土、紫色土和冲积土[7]。植被属于黔中山原湿润性灰岩常绿栎林、常绿落叶混交林及马尾松Pinus massoniana林区,主要树种有青栲Cyclobalanopsis glauca,丝栗栲Castanopsis fargesii,细叶青冈栎Cyclobalanopsis gracilis,柞木 Quercus mongolica等,落叶树种有枫香Liquidambar formosana,光皮桦 Betula luminifera等。次生植被有大面积天然牧草和灌丛草坡[8-9]。
1.2 研究方法与材料
采用典型样地调查法,对贵阳市乌当区杜鹃群落进行调查。在贵阳市乌当区杜鹃群落分布区域随机布设调查样点15处,分别在每个调查样点区域内随机设置10 m × 10 m典型群落调查样方3个,共计调查样方45个,统计每个调查样方内的植物种类、生活型、密度、高度、盖度、频度等群落特征指标,用于群落数量分类与多样性等指标的计算。
1.3 统计分析
贵阳乌当杜鹃群落调查数据统计分析与整理,均采用SPSS 18.0软件和Microsoft Office Excel 2007软件完成。
1.3.1 群落数量分类
结合《中国植被》和实际生态学意义,采用TWINSPAN分类法,对贵阳乌当杜鹃群落进行群落数量分类。
1.3.2 重要值
采用重要值(Ⅵ,对贵阳乌当杜鹃群落进行分析,计算公式[10-11]：
$I{V_{Ii}} = \left( {\frac{{{D_i}}}{{\sum {{D_i}} }} + \frac{{{F_i}}}{{{{\sum F }_i}}} + \frac{{{C_i}}}{{\sum {{C_i}} }}} \right) \div 3 \times 100\% $
其中： VIi表示第i种物种的重要值；Di表示第i种物种的密度；Fi表示第i种物种的频度；Ci表示第i种物种的盖度(乔木层中Ci表示第i中物种的显著度)。
1.3.3 α多样性测度
采用Margalef指数、Simpson指数和Shannon-Wiener指数对贵阳乌当杜鹃群落物种多样性进行分析,计算公式为[10-13]：
$\begin{array}{l} {\rm{M}}\arg {\rm{alef}}指数R = \frac{{S - 1}}{{\ln N}};\\ {\rm{Simpson}}指数D = \sum\limits_{i = 1}^s {{{({p_i})}^2}} ;\\ {\rm{Simpson}} - {\rm{Wiener}}指数H = - \sum\limits_{i = 1}^s {({p_i}ln{p_i})} \end{array}。$
其中：S表示植被群落中物种数目,N表示群丛中全部物种个体总数,Pi为第i种的相对重要值。
1.3.4 均匀性测度
采用Pielou均匀性指数对贵阳乌当杜鹃群落进行分析,计算公式为[11]：
${\rm{Pielou}}均匀性指数E = \frac{H}{{\ln S}}。$
其中：H 表示Shannon-Wiener多样性指数,S表示植被群落中物种数目。
2. 结果与分析
2.1 万亩杜鹃群落分类
采用TWINSPAN分类法,对贵阳乌当杜鹃群落15个调查样点进行等级分类,经过4次划分,得到为4组。结合《中国植被》和实际生态意义,采用第4级的分类结果,将贵阳乌当杜鹃群落划分为4组(图 1),结合分类将4个组命名为4个植物群丛。群丛Ⅰ：锈叶杜鹃Rhododendron siderophyllum+白栎Quercus fabrei群丛,包括样点2和样点6。群丛Ⅱ：锈叶杜鹃+白栎+麻栎Quercus acutissima群丛,包括样点1,样点4,样点9,样点3,样点5和样点7。群丛Ⅲ：锈叶杜鹃+麻栎群丛,包括样点10,样点12,样点13和样点15号。群丛Ⅳ：锈叶杜鹃+麻栎+藤黄Garcinia hanburyi群丛,包括样点8,样点11和样点14。
图 1 乌当杜鹃群落15个样点TWINSPAN树状分类图Figure 1. TWINSPAN classification of 15 sampling pointies in the Wudang of the Rhododendron community表 1 贵阳乌当杜鹃群丛重要值特征Table 1. Important values trait of the Rhododendron communities in Wudang，Guiyang科名 种名 生活型 重要值 群丛I 群丛Ⅱ 群丛Ⅲ 群丛Ⅳ 杜鹃花科Ericaceae 镑叶杜鹃Rhododendron siderophyllum S 48.72 29.80 36.23 48.74 杜鹃花科Ericaceae 小果南烛Lyonia ovalifolia S 6.02 5.51 5.26 — 杜鹃花科Ericaceae 映山红Rhododendron S 7.32 8.12 8.27 4.66 壳斗科Dagaceae 麻栋Quercus acutissima T 8.91 28.55 11.34 10.28 壳斗科Dagaceae 栲 Castanopsis fargesii T — 3.55 5.80 0.80 壳斗科Dagaceae 白栋Quercus fabrei S 13.66 11.45 1.90 7.90 禾本科Gramineae 五节芒 Miscanthus floridulus P — 0.17 — — 禾本科Gramineae 茅叶荩草 Arthraxon lanceolatus P — — 0.64 — 禾 本 科 Gramineae 芒 Miscanthus sinensis P — — 0.88 1.04 蕨科 Pteridiaceae 蕨 Pteridium aquilinum P — 1.32 2.13 — 蕨科 Pteridiaceae 密毛蕨 Pteridium reyolutum P — — 0.76 5.07 桑科 Moraceae 小构树 Broussonetia CasinoCi S — — 0.40 — 桑科 Moraceae 專草 Humulus scandens P — — 0.67 — 藤黄科 Guttiferae 藤黄 Farcinia hanburyi T — — — 8.82 藤黄科 Guttiferae 金丝桃 Hypericum monogynum S — 1.11 — — 百合科Liliaceae 拔葜 Smilax china CS 0.67 8.34 — — 车前科 Plantaginaceae 车 前 草 Plantago asiatica P — — 0.37 — 豆科 Leguminosae 三叶崖豆藤 Millettia unijuga CS — 1.39 — — 金缕梅科 Hamamelidaceae 枫香 Liquidambar formosana T — — — 2.23 菊科 Compositae 艾蒿 Artemisia vulgaris P — — 0.46 — 茜草科Rubiaceae 鸡矢藤 Paederia scandens CS — — 1.19 — 蔷薇科Rosaceae 插田泡Rubus coreanus S — — 1.52 2.88 忍冬科 Caprifoliaceae 珍珠荚莲 liburnum/oetidum S 3.88 — 7.40 — 莎草科 Cyperaceae 莎 草 Cyperus rotundus P — 0.34 — — 山茶科Theaceae 怜木 Juryajaponica S 3.33 — 5.96 4.36 杉科 Taxodiaceae 杉木 Cunninghamia lanceolata T 7.50 — — — 石松科 Lycopodiaceae 石松 Lycopodium clavatum P — — 2.71 — 石竹科 Caryophyllaceae 银柴胡 Fypsophilaoldhamiana P — — 0.37 — 五加科 Araliaceae 檧木 Aralia chinensis S — — 5.75 2.53 虎耳草科 Saxifragaceae 滇鼠刺 Ktea ilicifolia S — 0.36 — — 苋科 Amaranthaceae 牛漆 Achyranthes bidentata P — — — 0.69 说明：共计植物31种，其中群丛Ⅰ9种，群丛Ⅱ13种，群丛Ⅲ21种，群丛Ⅳ13种。“—”表示该样地中未发现该种植物；“T”表示乔木植物（tree）；“P”表示多年生植物（perennial plant）；“S”表示灌木（shrubbery）；“CS”表示攀援灌木（climbing shrub）。 2.2 乌当杜鹃群落数量特征
群丛Ⅲ中,杜鹃花科Ericaceae,壳斗科Fagaceae分别共出现3种植物,分别占群丛出现种的14.29%；禾本科Gramineae,蕨科Pteridiaceae,桑科Moraceae分别出现2种植物,分别占群丛出现种的9.52%,其他科共出现9种植物,占群丛出现种的42.86%。群丛Ⅳ中,壳斗科出现3种植物,占群丛出现种的23.08%,杜鹃花科出现2种植物,占群丛出现种的15.38%；其他科共出现7种植物,占群丛出现种的53.85%。
对贵阳乌当杜鹃群落植物生活型分析发现,乔木植物5种,占群落出现种的16.13%；灌木植物14种(其中攀援灌木植物3种,占群落出现种的9.68%),占群落出现种的45.16%；草本植物12种(均为多年生草本植物)占群落出现种的38.71%。对贵阳乌当杜鹃群落4种群丛植物组成生活型分析发现,群丛Ⅰ中共出现9种植物,其中乔木2种,占群丛出现植物种的22.22%；灌木植物7种(其中攀援植物1种,占群丛出现种的11.11%),占群丛出现种的77.78%；群丛中未出现草本植物种类。群丛Ⅱ中共出现13类植物,其中乔木2种,占群丛出现植物种的15.38%；灌木植物8种(其中攀援植物2种,占群丛出现种的15.38%),占群丛出现种的61.54%；草本植物3种,占群丛出现种的23.08%。群丛Ⅲ中共出现21种植物,其中乔木2种,占群丛出现植物种的9.52%；灌木植物10种(其中攀援植物1种,占群丛出现种的4.76%),占群丛出现种的47.62%；草本植物9种,占群丛出现种的42.86%。群丛Ⅳ中共出现13种植物,其中乔木4种,占群丛出现植物种的30.77%；灌木植物6种,占群丛出现种的46.15%；草本植物3种,占群丛出现种的23.08%。
对贵阳乌当杜鹃群丛植物重要值分析发现,群丛Ⅰ中,锈叶杜鹃重要值最高,为48.72%,白栎次之,为13.66%；群丛Ⅱ中,锈叶杜鹃重要值最高,为29.80%,麻栎次之,为28.55%,白栎重要值为11.45%；群丛Ⅲ中,锈叶杜鹃重要值最高,为36.23%,麻栎次之,为11.34%；群丛Ⅳ中,锈叶杜鹃重要值最高,为48.74%,麻栎次之,为10.28%。
综上所述,乌当杜鹃群落是以锈叶杜鹃为主,白栎、麻栎为辅的群落类型。
2.3 杜鹃群落α多样性分析
贵阳乌当杜鹃群落Margalef丰富度指数分析如表 2所示。Margalef丰富度指数从高到低的变化趋势为群丛Ⅲ(4.714),群丛Ⅱ(3.306),群丛Ⅳ(3.081),群丛Ⅰ(2.111)。
表 2 贵阳乌当杜鹃群落α多样性与均匀性指数特征Table 2. Index trait of α diversity and evenness of Rhododendron communities in Wudang，Guiyang群丛 R D H E Ⅰ 2.111 0.719 1.665 0.758 Ⅱ 3.306 0.798 1.873 0.730 Ⅲ 4.714 0.828 2.270 0.745 Ⅳ 3.081 0.729 1.830 0.714 贵阳乌当杜鹃群落Simpson多样性指数、Shannon-Wiener多样性指数分析如表 2所示。Simpson多样性指数从高到低的变化趋势为群丛Ⅲ(0.828),群丛Ⅱ(0.798),群丛Ⅳ(0.729),群丛Ⅰ(0.719)；Shannon-Wiener多样性指数从高到低的变化趋势为群丛Ⅲ(2.270),群丛Ⅱ(1.873),群丛Ⅳ(1.830),群丛Ⅰ(1.665)。
贵阳乌当杜鹃群落Pielou均匀性指数分析如表 2所示。Pielou均匀性指数从高到低的变化趋势为群丛Ⅰ(0.758),群丛Ⅲ(0.745),群丛Ⅱ(0.730),群丛Ⅳ(0.714)。
综上所述,贵阳乌当杜鹃群落Margalef丰富度指数、Simpson多样性指数、Shannon-Wiener多样性指数均呈现出群丛Ⅲ＞群丛Ⅱ＞群丛Ⅳ＞群丛Ⅰ的趋势,而Pielou均匀性指数则呈现出群丛Ⅰ＞群丛Ⅲ＞群丛Ⅱ＞群丛Ⅳ。
3. 结论与讨论
3.1 结论
贵阳乌当杜鹃群落可分为4种植物群丛,依次为群丛Ⅰ：锈叶杜鹃+白栎群丛；群丛Ⅱ：锈叶杜鹃+白栎+麻栎群丛；群丛Ⅲ：锈叶杜鹃+麻栎群丛；群丛Ⅳ：锈叶杜鹃+麻栎+藤黄群丛。杜鹃群落主要以杜鹃科、壳斗科、禾本科植物为主；在贵阳乌当杜鹃群落中锈叶杜鹃种群占绝对优势,麻栎、白栎种群次之,因此,杜鹃群落主要是以锈叶杜鹃为主,麻栎、白栎为辅的植物群落结构类型。贵阳乌当杜鹃群丛Margalef丰富度指数、Simpson多样性指数、Shannon-Wiener多样性指数均呈现出群丛Ⅲ＞群丛Ⅱ＞群丛Ⅳ＞群丛Ⅰ的趋势,而Pielou均匀性指数则呈现出群丛Ⅰ＞群丛Ⅲ＞群丛Ⅱ＞群丛Ⅳ。贵阳乌当杜鹃群落多样性保护应当遵从群丛Ⅲ的植物结构类型进行保护,对群丛Ⅰ,群丛Ⅱ和群丛Ⅳ进行适当修复,使其结构接近群丛Ⅲ的结构类型。
3.2 讨论
本研究针对贵阳乌当万亩杜鹃林群落进行多样性研究,按植物群落的自然演替规律,该群落处于灌木或灌丛群落阶段,正向乔灌群落阶段演替,并非顶级群落及地带性植被类型,因此,处于不稳定阶段。目前,贵阳市乌当区想要打造万亩杜鹃林,作为贵阳城郊以观赏杜鹃花的休闲旅游区,但随着群落演替的进行,杜鹃群落的变化会直接影响旅游观光效果,因此,进一步研究贵阳乌当万亩杜鹃林最佳群落结构、物种组成、物种多样性、人工正向干扰或结构调整,对旅游观光效果及群落的相对稳定性有重要意义。正如黔西的百里杜鹃,目前观光效果很好,在长期人为正向干扰下,其群落结构具相对稳定性,但从物种多样性及演替规律来看,目前的结构是否为最佳,有待于进一步研究。
-
图 2 应力波在不同缺陷程度的木材中传播
Figure 2 Stress waves propagate in wood of different defect degree
表 1 实验样本基本信息
Table 1. Experimental sample information
样本编号 样本种类 样本周长/cm 检测区域面积/cm2 缺陷面积/cm2 1 雪松Cedrus deodara 62.83 1 000 111.20 2 泡桐Paulownia fortunei 73.83 1 175 427.50 3 樟树Cinnamomum camphora 60.95 940 314.15 
下载: 导出CSV
表 2 缺陷与预测的4种组合
Table 2. Four combination of real defects and predict defects
类别 预测缺陷 预测完好 真实缺陷 被正确地预测为缺陷的面积C 被错误地预测为完好的面积E 真实完好 被错误地预测为缺陷的面积F 被正确地预测为完好的面积W
下载: 导出CSV
表 3 不同样本的准确率
Table 3. Accuracy of different samples
样本编号 准确率A/% IDW方法 VCI方法 1 89.20 95.85 2 86.36 93.30 3 72.32 90.86
下载: 导出CSV
表 4 不同样本的精确度
Table 4. Precision of different samples
样本编号 精确度P/% IDW方法 VCI方法 1 67.60 76.92 2 77.18 88.35 3 65.79 81.51
下载: 导出CSV
表 5 不同样本的查全率
Table 5. Recall rate of different samples
样本编号 查全率R/% IDW方法 VCI方法 1 17.98 89.92 2 56.14 94.03 3 35.80 94.00
下载: 导出CSV
-
[1] WANG Xiping. Acoustic measurements on trees and logs:a review and analysis[J]. Wood Sci Technol, 2013, 47(5):965-975. [2] 徐华东, 王立海, 游祥飞, 等.应力波在旱柳立木内的传播规律分析及其安全评价[J].林业科学, 2010, 46(8):145-150. XU Huadong, WANG Lihai, YOU Xiangfei, et al. Analysis of stress wave propagation in Hankow Willow standing trees and stability assessment[J]. Sci Silv Sin, 2010, 46(8):145-150. [3] 杨学春, 王立海.红松木材结构缺陷对应力波传播参数的影响[J].东北林业大学学报, 2005, 33(1):30-31. YANG Xuechun, WANG Lihai. Impacts of structure defaults on propagation parameters of stress wave in wood of Korean pine[J]. J Northeast For Univ, 2005, 33(1):30-31. [4] LIN C J, CHANG T T, JUAN M Y, et al. Stress wave tomography for the quantification of artificial hole detection in camphor trees (Cinnamomum camphora)[J]. Taiwan J For Sci, 2011, 26(1):17-32. [5] FENG Hailin, LI Guanghui, FU Sheng, et al. Tomographic image reconstruction using an interpolation method for tree decay detection[J]. Bioresources, 2014, 9(2):3248-3263. [6] DU Xiaochen, LI Saozhi, LI Guanghui, et al. Stress wave tomography of wood internal defects using ellipse-based spatial interpolation and velocity compensation[J]. Bioresources, 2015, 10(3):3948-3962. [7] 翁翔, 李光辉, 冯海林, 等.应力波在树木径切面内的传播速度模型[J].林业科学, 2016, 52(7):104-112. WENG Xiang, LI Guanghui, FENG Hailin, et al. Stress wave propagation velocity model in rl plane of standing trees[J]. Sci Silv Sin, 2016, 52(7):104-112. [8] 徐华东, 王立海.杨木径切面准纵波传播路径追踪及速度变化试验研究[J].声学学报, 2012(1):62-67. XU Huadong, WANG Lihai. Experiment study on the propagation path tracing and velocity change of quasi-P wave in the radial section of poplar wood[J]. Acta Acust, 2012(1):62-67. [9] LI Guanghui, WANG Xiping, FENG Hailin, et al. Analysis of wave velocity patterns in black cherry trees and its effect on internal decay detection[J]. Comput Electron Agric, 2014, 104(2):32-39. [10] 冯海林, 李光辉, 方益明, 等.应力波传播模型及其在木材检测中的应用[J].系统仿真学报, 2010, 22(6):1490-1493. FENG Hailin, LI Guanghui, FANG Yiming, et al. Stress wave propagation modeling and application in wood testing[J]. J Syst Simulation, 2010, 22(6):1490-1493. [11] LI Li, WANG Xiping, WANG Lihai, et al. Acoustic tomography in relation to 2D ultrasonic velocity and hardness mappings[J]. Wood Sci Technol, 2012, 46(1/3):551-561. [12] HU Yingcheng, NAKAO T, NAKAI T, et al. Dynamic properties of three types of wood-based composites[J]. J Wood Sci, 2005, 51(1):7-12. [13] BRANCHERIAU L, ASHKAN G, GALLET P, et al. Application of ultrasonic tomography to characterize the mechanical state of standing trees (Picea abies)[J]. J Phys Conf Ser, 2012, 253(1):1-13. [14] 贾悦, 崔宁博, 魏新平, 等.基于反距离权重法的长江流域参考作物蒸散量算法适用性评价[J].农业工程学报, 2016, 32(6):130-138. JIA Yue, CUI Ningbo, WEI Xinping, et al. Applicability evaluation of different algorithms for reference crop evapotranspiration in Yangtze River Basin based on inverse distance weighted method[J]. Trans Chin Soc Agric Eng, 2016, 32(6):130-138. [15] SAMMUT C, WEBB G I. Encyclopedia of Machine Learning[M]. New York:Springer, 2010. [16] FAWCETT T. An introduction to ROC analysis[J]. Pattern Recogn Lett, 2006, 27(8):861-874. [17] POWERS D M W. Evaluation:from precision, recall and F-Factor to ROC, informedness, markedness & correlation[J]. J Mach Learn Technol, 2011, 2(1):37-63. 期刊类型引用(4)
1. 付婷，欧静，龙海燕，黄家涌，郝磊. 淡紫杜鹃典型植物群落结构及其多样性特征分析. 北方园艺. 2022(04): 62-68 . 
百度学术2. 黄梅，戴晓勇，杨成华，邓伦秀，袁丛军，李鹤，龙海燕，冯育才. 阔柄杜鹃典型植物群落的结构及其多样性特征分析. 西部林业科学. 2020(02): 113-120+136 . 百度学术3. 韦海霞，袁丛军，李鹤，龙海燕，杨冰，冯邦贤，戴晓勇. 梵净山稀果杜鹃群落结构及物种多样性初步研究. 四川林业科技. 2020(04): 38-43 . 百度学术4. 葛英亮，于水利，时文歆，杨帆，漆晴. 应用Illumina MiSeq高通量测序技术解析O_3-BAC饮用水处理过程细菌多样性变化. 食品科学. 2016(16): 223-228 . 百度学术其他类型引用(4)
-
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2019.02.001
点击查看大图
计量
- 文章访问数: 3538
- HTML全文浏览量: 795
- PDF下载量: 181
- 被引次数: 8
