-
木材无损检测技术可以对木材的力学性能、内部腐朽进行准确检测，对充分利用木材资源有着重要的意义。应力波技术是一种非常有效的木材无损检测方法[1-2]，其原理是利用脉冲锤敲击木材，使其内部产生应力波的传播，通过测量应力波的传播时间和传播速度的变化确定木质材料的性能（如弹性模量、腐朽等）。国外诸多科研院所以及企业均投入大量精力，新产品层出不穷。孟瑞华等[3]、冯国红等[4]、肖江等[5]、Hayes等[6]采用不同方法，实现了应力波传播时间、传播速度的测量。在这些研究中，大多通过应力波信号的阈值比较或过零比较等操作，计算应力波在木材中的传播时间。由于应力波在木材中传播过程复杂，这种通过简单的比较运算获取的传播时间分散性较大，抗干扰能力弱。本研究提出一种高阶统计量[7]和小波变换[8]相结合的广义相关算法，通过抑制应力波信号中的噪声，提高应力波传播时间的测量精度。
-
互相关法利用空间上2个独立传感器接收到的信号获取时间差。根据应力波木材无损检测的原理，建立信号模型如下：
$$\begin{align} & {{y}_{1}}\left( n \right)=x\left( n \right)+{{s}_{1}}\left( n \right) \\ & {{y}_{2}}\left( n \right)=Ax\left( n-D \right)+{{s}_{2}}\left( n \right) \\ \end{align}$$ (1) 式（1）中：y1（n），y2（n），为2个传感器采集到的信号，x（n）表示纯净应力波信号，A为应力波信号在木材中传播过程中出现的衰减系数，D表示应力波从1号传感器传播至2号传感器所需时间，s1（n）和s1（n）表示y1（n）和y2（n）中混杂的噪声信号。
y1（n）和y2（n
）的互相关函数为： $${{R}_{12}}\left( \tau \right)=E\left[ {{y}_{1}}\left( n \right){{y}_{2}}\left( n-\tau \right) \right]={{R}_{xx}}\left( \tau -D \right)+{{R}_{xs1}}\left( \tau -D \right)+{{R}_{xs2}}\left( \tau \right)+{{R}_{s1s2}}\left( \tau \right)$$ (2) 式（2）中：Rxx为x（n）的自相关函数，Rxs1为x（n）和s1（n
）的互相关函数，Rxs2为x（n）和s2（n）的互相关函数，Rs1s2为s1（n）和s2（n）的互相关函数。 由于x（n）与s1（n），s2（n）之间互不相关，所以存在：
$$\begin{align} & {{R}_{xs1}}\left( \tau -D \right)=0; \\ & {{R}_{xs2}}\left( \tau \right)=0; \\ & {{R}_{s1s2}}\left( \tau \right)=0 \\ \end{align}$$ (3) 式（3）定义的互相关函数等于纯净应力波信号的自相关函数，即：
$${{R}_{12}}\left( \tau \right)={{R}_{xx}}\left( \tau -D \right)$$ (4) 由自相关函数性质可以得出$\left| {{R}_{xx}}\left( \tau -D \right) \right|\le {{R}_{xx}}\left( 0 \right)$，那么当τ-D＝0时R
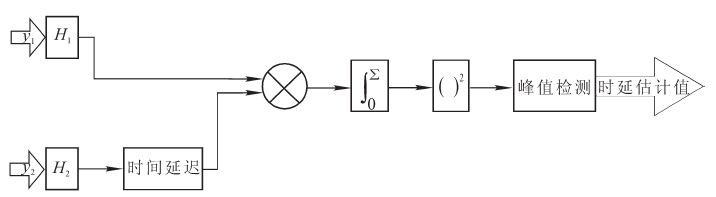
12（τ）取得最大值，通过寻找互相关R12（τ）函数峰值对应的时间可估计出应力波信号y1（n）传播至第2个传感器所需的时间D。 广义相关法是Knappy等[9]和Hero等[10]提出的，它是在基本相关法基础上对信号提前进行处理，提高信噪比，从而有效提高时延估计精度。图 1描述了广义相关法的原理，它的步骤包括对信号去噪、求两路信号的互相关函数、计算互相关函数的峰值时刻等，最后得到应力波信号的传播时间。
图 1 广义互相关算法原理图
Figure 1. Schematic diagram of generalized cross correlation algorithm
-
在广义相关算法中，需利用滤波算法对信号去噪以便提高时延估计的精度。由于在高阶统计量中，高斯噪声的双谱为0，能够彻底消除信号中的高斯噪声。小波变换又能够很好地保留信号的峰值特征和信号信息。因此将高阶统计量和小波变换结合的滤波方法具有更好的降噪滤波功能。
算法具体步骤如下：①对含噪信号进行小波变换，将原始波形分解为高频部分和低频部分；②使用小波分层阀值降噪对低频小波系数进行处理；③处理高斯噪声后的小波系数仍是高斯分布的，对高频部分进行高阶统计量的双谱估计法进行滤波；④利用小波反变换对去噪后的波形进行重构。
-
本节提出基于小波变换与高阶统计量的广义互相关应力波传播时延估计方法。时延估计的输入信号为初始应力波信号在经过高阶统计量和小波变换相结的滤波算法滤波去噪后的信号，然后对输入信号求互相关函数，找到互相关函数峰值对应的时刻。算法原理如图 2所示。
图 2 基于广义互相关的应力波时延估计算法原理
Figure 2. Scheme of wood nondestructive detection of stress wave time delay estimation
算法实现步骤如下：第1步，数据采集。利用搭建好的实验平台采集所需的2列应力波信号，通过Openchoice软件以Excel数据保存。第2步，数据处理。剔除有用信号之前的大量的0数据，保留长度为2 048的信号，分别记为y1（n），y2（n）。第3步，滤波。利用Matlab软件编写程序对波形进行3层尺度分解，分解后得到高频部分cD1，cD2，cD3和低频部分cA1，cA2，cA3的小波系数。对cA1，cA2，cA3进行阀值处理，阀值选取采用小波默认阀值。对cD1，cD2，cD3则采用高阶统计量中的双谱滤波法进行滤波，因为高阶统计量中的高斯噪声双谱为0。将处理完后的小波系数进行重构，反变换得到去噪波形$y_{1}^{'}\left( n \right),y_{2}^{'}\left( n \right)$。第4步，时延估计。求互相关函数R12（τ）。利用Matlab软件的工具箱函数max（ ）求出R12（τ）的最大值及最大值所在位置D。应力波信号的传播时间t传播就可以根据下式求出：
$${{t}_{传播}}=D/{{f}_{s}}$$ (5) 式（5）中fs为信号采集时所用的采样频率。
-
把原始信号y1（n）（抽样频率100 kHz，数据长度为2 048）向右平移10个点，得到延迟信号y2（n），用于测试提出的算法对应力波传播时延估计的效果。
首先进行滤波处理，去除噪声信号。本研究利用Matlab工具箱设计了实验。先用小波工具箱中的wavedec（ ）函数对小波信号进行3层分解，提取小波系数。输出部分包括分解结构中小波分解矢量C和相应的记录向量L。随后用小波变换和高阶累计量相结合的滤波方法对含噪信号进行滤波处理，得到小波系数。最后在Matlab软件平台上用互相关法求出应力波传播时延的估计值为100 μs。
为了比较本研究提出的广义相关法与传统相关法的效果，还利用相关法直接估计y1（n）和y2（n）的时延，估计结果为80 μs。因为y2（n）是y2（n）右移10个采样点得到的，滤波后的互相关算法比不滤波直接求互相关函数的算法更加准确，时延估计精度提高了81.5%。
-
时延估计算法引入应力波木材无损检测中，提高时间测量的准确性。利用项目组自行研发的Wopeck木材无损检测仪完成了本组实验，实验场景如图 3和图 4所示，Wopeck木材无损检测仪采用传统计时器计时方法。根据Wopeck仪器使用方法，将12个传感器均匀地安装在腐朽木材周围并根据编号记录下来，分别敲击传感器，利用Wopeck仪器测量出各对传感器之间的传播时间，并产生木材内部缺陷的断层图像，如图 5所示。
图 3 Wopeck木材无损检测系统
Figure 3. Wopeck wood nondestructive testing system
图 4 木材缺陷以及传感器分布图
Figure 4. Wood defect and sensor distribution map
图 5 Wopeck检测仪（传统计时法）的检测结果
Figure 5. Experimental results of Wopeck tester (traditional timing method)
为了验证本研究提出的时延估计方法，拆除木材上的传感器，根据事先记录下来的编号，利用数据采集平台的2个传感器分别采集2个测量点的信号波形。然后在Matlab软件上用基于小波变换和高阶统计量滤波的互相关时延估计算法分别求取时延值，导入Wopeck仪器的软件上，生成木材内部缺陷断层图像。如图 6所示。
图 6 时延估计法的检测结果
Figure 6. Experimental results of time delay estimation algorithm
从图 5和图 6可以看出：本研究提出的时延估计法和传统的计时器计时法都能判断出木材的腐朽位置和程度，但采用本研究提出的时延估计方法后，生成的图像中腐朽位置更加突出，颜色对比更加明显，测量结果的准确性更高。
-
在实际的木材无损检测过程中，通常会遇到震动和声音对测量信号等干扰，为了验证本算法的抗干扰能力，采用高分贝喇叭在传感器附近模拟外界声音，并用震动机模拟来自地面的震动。按照高、中、低三级信噪比完成了3组不同实验。3种情况下采集到的信号波形如图 7所示。
图 7 不同干扰强度下采集到的应力波信号
Figure 7. Signal waveform under there levels interference
采用本研究提出的方法估计不同情况下的采样点延迟以及传播时间如表 1所示：从表 1可以看出：3种不同信噪比下的延时估计方差仅为2/3×10-8，说明本研究提出的时延估计算法性能稳定，能够适应木材无损检测环境下不同等级的信噪比。该算法法提高了应力波传播时间的测量精度，使木材无损检测的准确性得到进一步的提高。
表 1 不同干扰情况下传播时间估计结果
Table 1. Results under there levels interference
干扰强度 采样点延迟(D） 传播时间（t传播)/s 低 1 059 0.021 2 中 1 052 0.021 0 高 1 053 0.021 0 -
为了克服木材无损检测技术中传统计时方法的不足，本研究提出了一种小波变换和高阶统计量相结合的滤波算法以及广义互相关时延估计算法，用于木材无损检测中的应力波传播时间估计。大量的实验结果表明：该算法能够准确测量木材内部应力波传播时间，断层成像效果好，并具有较强的抗干扰能力。
Stress wave propagation time estimation algorithm for nondestructive testing of wood
-
摘要: 为了准确测量应力波在木材内部的传播时间,提高木材内部缺陷识别的精度,提出了一种基于小波变换和高阶统计量的广义相关时延估计算法。该方法利用滤波算法,将采集到的应力波信号进行滤波去噪,然后输入到广义互相关时延模型,求出传播时延估计值。仿真和实际的木材检测实验结果表明:提出的算法比传统的定时器计时法时延估计精度提高81.5%,并具有较强的抗干扰能力。Abstract: The purpose of this study is to measure the stress wave propagation time and improve the accuracy of identifying the internal decay of wood. An algorithm of stress wave propagation time estimation combining high order cumulants with wavelet transformation was presented. The proposed algorithm removed the noise of stress wave signal with filtering algorithm, then input the filtered signal to the generalized cross-correlation time delay model, and calculated the estimation of the stress wave propagation time. The results of simulation and experiments showed that the accuracy of the measured stress wave propagation time was improved by 81.5 per cent. Further more, under low, medium and high signal to noise ratios (SNR), the experimental results demonstrated the anti-interference ability of the new algorithm.
-
图 2 基于广义互相关的应力波时延估计算法原理
Figure 2 Scheme of wood nondestructive detection of stress wave time delay estimation
图 5 Wopeck检测仪（传统计时法）的检测结果
Figure 5 Experimental results of Wopeck tester (traditional timing method)
表 1 不同干扰情况下传播时间估计结果
Table 1. Results under there levels interference
干扰强度 采样点延迟(D） 传播时间（t传播)/s 低 1 059 0.021 2 中 1 052 0.021 0 高 1 053 0.021 0 
下载: 导出CSV
-
[1] WANG Xiping,ROSS R J,MCCLELLAN M,et al. Nondestructive evaluation of standing trees with a stress wave method[J]. Wood Fiber Sci,2001,33(4):522-533. [2] 李光辉,尹建新. 基于应力波的木材无损检测技术研究进展[C]//中国自动化学会制造技术专门委员会. 第6届制造业自动化与信息化技术研讨会论文集. 桂林:[出版者不祥],2007:189-193. [3] 孟瑞华,胡勤龙,刘毅. 应力波时间仪的研制和应用[J]. 南京化工大学学报:自然科学版,2000,22(6):55-57. MENG Ruihua,HU Qinlong,LIU Yi. Research and design of stress wave time instrument and its applications[J]. J Nanjing Univ Chem Technol Nat Sci Ed,2000,22(6):55-57. [4] 冯国红,王立海,杨慧敏,等. 应力波木材无损检测信号采集系统[J]. 森林工程,2008,24(2):22-24. FENG Guohong,WANG Lihai,YANG Huimin,et al. Signal collection system of stress wave nondestructive testing of wood[J]. For Eng,2008,24(2):22-24. [5] 肖江,杨建华,李黎. 基于单片机的单板层积材抗弯强度应力波波速检测系统[J]. 木材加工机械,2008,19(1):1-5. XIAO Jiang,YANG Jianhua,LI Li. The detecting system of stress velocity for laminated veneer lumber bending strength based on single chip[J]. Wood Proc Mach,2008,19(1):1-5. [6] HAYES M P,CHEN J. A portable stress wave measurement system for timber inspection[C]//ENZC. Proceedings of the Electronics New Zealand Conference. Wellington:[s. n.],2003:1-6. [7] 何涛. 基于DSP的小波降噪技术研究及应用[D]. 郑州:河南工业大学,2011. HE Tao. Research and Application on Technology of Wavelet Denoising Based on DSP[D]. Zhengzhou:Henan University of Technology,2011. [8] 栾风虎,李玉峰,于学明,等. 基于高阶累计量的时延估计研究[J]. 黑龙江大学自然科学学报,2010,27(2):260-263. LUAN Fenghu,LI Yufeng,YU Xueming,et al. Research of time delay estimation based on higher-order cumulant[J]. J Nat Sci Heilongjiang Univ,2010,27(2):260-263. [9] KNAPPY C H,CARTER G C. Generalized correlation method or estimation of time delay[J]. IEEE Trans Acoust Speech Sign Proc,1976,24(4):320-327. [10] HERO A O,SCHWARTZ S C. New generalized cross correlator[J]. IEEE Trans Acoust Speech Sign Proc,1985,33(1):38-45. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2014.03.010
点击查看大图
图(7) / 表(1)
计量
- 文章访问数: 3205
- HTML全文浏览量: 450
- PDF下载量: 536
- 被引次数: 0
