Bioremediation of 4-bromine biphenyl ether polluted water using biosorption and microbial degradation

4-溴联苯醚(BDE-3)高效降解菌株Sphingomonas sp. DZ3 (GenBank accession No. KJ658629)为浙江农林大学林业与生物技术学院森林保护学实验室分离保藏。

海藻酸钠为国产分析纯，购自国药集团化学试剂有限公司；4-溴联苯醚(BDE-3)，纯度为99%，购自Sigma-Aldrich(上海)有限公司；生物碳由玉米Zea mays秸秆在350 ℃限氧条件下热解制备所得，粉碎后过筛，烘干至恒量，冷却后保存在密封袋中备用。Luria-Bertani培养基(LB，pH 7.1)：10 g·L^-1蛋白胨，5 g·L^-1酵母膏，10 g·L^-1氯化钠，固体培养基含质量分数为2%的琼脂，在115 ℃灭菌30 min用于微生物培养。4-溴联苯醚溶液配制设置：配制成质量浓度为500 mg·L^-1的母液(以甲醛为溶剂)保存，用时稀释到试验所需质量浓度。微球菌剂降解研究所用的无机盐培养基配方为：5.1 g·L^-1磷酸二氢钾，30.0 g·L-1磷酸氢二钾，5.0 g·L^-1氯化钠，pH 7.0。

称取一定质量的海藻酸钠粉末加入到100 mL水溶液中，磁力搅拌过夜，使海藻酸钠充分溶解，配制成质量分数分别为1.5%，2.0%，2.5%，3.0%的海藻酸钠溶液。在海藻酸钠溶液中加入生物碳，质量分数为2.0%，搅拌均匀。将上述各海藻酸钠-生物碳溶液用装有5号针头的注射器逐滴滴到凝结液中(40 g·L^-1氯化钙溶液)，制得直径为3~5 mm、海藻酸钠质量分数分别为1.5%，2.0%，2.5%，3.0%的多孔凝胶微球。海藻酸钠-生物碳微球制成后，在室温下放置过夜，然后用蒸馏水洗至中性，于4 ℃冰箱中保存待用。微球制剂的海藻酸钠浓度对BDE-3吸附量的影响实验设计：分别称取1 g上述所制海藻酸钠-生物碳微球加入到100 mL质量浓度为200 mg·L^-1，pH 7.0的4-溴联苯醚溶液中，在恒温30 ℃，120 r·min^-1条件下振荡25 h后分别取不同处理的上清液，用高效液相色谱测定溶液中4-溴联苯醚的质量浓度，实验设3组重复。吸附量的计算方法：q_e=(C₀－C_e)V/m。其中：q_e为吸附量(mg·g^-1)，C₀和C_e分别为初始和平衡液质量浓度(mg·L^-1)，V为溶液体积(L)，m为吸附剂质量(g)。

根据1.2.1实验结果，选取合适质量分数海藻酸钠溶液，同上方法加入质量分数为2%生物碳，再加入干质量为0.05 g的菌株Sphingomonas sp. DZ3制成微球菌剂。

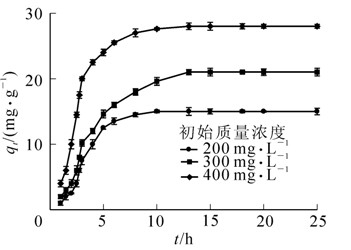
称取1 g海藻酸钠-生物碳微球加入到100 mL初始质量浓度分别为200，300和400 mg·L^-1的BDE-3溶液中，在温度30 ℃、转速120 r·min^-1条件下25 h时间范围内多次取样测定BDE-3质量浓度，计算吸附量。试验至少重复3次·组^-1。

反应在100 mL 锥形瓶中进行，将1 g微球菌剂加入20 mL BDE-3质量浓度为300 mg·L^-1的无机盐培养基中，在温度30 ℃、转速120 r·min^-1的条件下，隔10 h取样测定溶液中BDE-3的质量浓度，实验分别设置添加纯材料微球颗粒以及仅添加降解菌的对照，重复3次·处理^-1。

使用Weber-Morris吸附动力学模型研究海藻酸钠质量分数对微球内部扩散的影响，从而确定海藻酸钠的最佳质量分数，以及微球内部的传质过程^[8]。模型表达如下：q_t=K_wt^0.5+I，式中：K_w是粒子内部传质速率常数(mg·g^-1·min_-0.5)，t^0.5 是时间的平方根(min^-0.5)，q_t是单位质量微球在时间t吸附BDE-3的吸附量(mg·g^-1)，I是截距的值(mg·g^-1)，用于描述边界层的厚度。图 1a显示的是随着时间推移海藻酸钠-生物碳微球对BDE-3的吸附量的变化曲线。结果表明：在海藻酸钠添加量不同的情况下，制得的微球的吸附速率不同，但最大吸附量相同。当海藻酸钠质量分数为1.5%时，吸附速率最快，7 h即可达到吸附高峰，随着微球内海藻酸钠添加量的提高，吸附速率逐渐降低，在海藻酸钠质量浓度为3.0%时，吸附速率最低。

Figure 1.  Adsorption of microspheres for BDE-3 (a) and the fitting adsorption process using Webber-Morris model (b)

以吸附量q_t和t^0.5的线性关系可制得图 1b，通过模型数据拟合，拟合参数结果见表 1。 表 1显示，Weber-Morris吸附模型能完美描述整个吸附过程(R²均大于0.99)，随着微球中海藻酸钠质量分数的增加，边界层的厚度(I)也逐渐增加，粒子内部传质速率常数(K_w)逐渐降低，说明海藻酸钠质量分数的提高使得微球内的孔隙数量和大小逐渐减少，所以BDE-3在微球内的传质速率逐渐降低，从而造成高质量分数海藻酸钠微球不利于吸附BDE-3^[9]。微球中海藻酸钠的添加量也决定了微球的机械强度，当微球内海藻酸钠质量分数低于1.0% 时就无法成形，添加量在1.0%~2.0%时制得的微球较软，在震荡过程中容易破碎。本研究中制备微球的目的是将它用于水体修复，需要一定的机械强度。综合考虑吸附效果和机械强度，确定海藻酸钠的最佳质量分数为2.0%。

预实验发现，在一定范围内，微球对BDE-3的吸附量随着溶液中BDE-3质量浓度的增加而增加，但当溶液中BDE-3质量浓度超过400 mg·L^-1时，微球的吸附量不再增加。选择200，300，400 mg·L^-1 3个梯度对制得的海藻酸钠-生物碳微球的吸附动力学进行了研究。图 2显示的是BDE-3不同初始质量浓度条件下，海藻酸钠-生物碳微球对BDE-3的吸附情况。结果表明：各处理组微球对BDE-3的吸附量均呈现出先快速增加，到达高峰后逐渐趋于平衡的态势。当BDE-3初始质量浓度越高时，海藻酸钠微球对BDE-3吸附速率也越大。本试验中，在初始质量浓度为400 mg·L^-1 时10 h后吸附量达到最大28.6 mg·g^-1，之后吸附量保持不变。初始质量浓度为BDE-3吸附到微球上提供动力，这也许是在一定范围内初始质量浓度越高吸附量越大的主要原因，但当吸附剂表面的吸附位点已经达到饱和时，吸附停止。应用Lagergren准一级动力学方程与准二级动力学方程模型对图 2的吸附动力学数据进行分析^{[11, 12]}。2个动力学模型的线性方程分别表达如下：q_t=q_e(1-e^-k₁·t)，t/q_t=1/k₂q_e2+t/q_e。其中：q_t为t时刻的吸附量(mg·g^-1)；q_e为达到平衡时的吸附量(mg·g^-1)；k1为准一级动力学速率常数(min^-1)，k₂为准二级动力学速率常数(g·mg^-1·min－1)。数据拟合后的模型参数如表 3所示。由表 3证实，本试验结果与Lagergren准一级动力学方程拟合效果较好，R²均大于0.99。随着BDE-3初始质量浓度的增大，吸附量逐渐增大，吸附速率增加。

Figure 2.  Effect of initial concentration of BDE-3 on adsorption of BDE-3

对吸附动力学试验数据进一步分析，利用Elovich方程对吸附过程中的吸附作用与解吸附作用进行研究，方程表达如下^[13]：q_t=ln(α·β)/β+ln t/β。式中：q_t为t时刻的吸附量(mg·g^-1)；α为吸附速率常数(g·mg^-1·min^-1)；β为解吸附常数(g·mg^-1)。经分析发现，本试验所得数据与Elovich方程有良好的拟合，R²均在0.99以上(表 3)，随着初始质量浓度的增加，吸附常数α逐渐增大，解吸附常数β逐渐降低，吸附常数远远大于解吸附常数，表明在该过程中吸附作用远大于解吸附作用，即吸附占据主导地位，试验结果进一步证明了海藻酸钠-生物碳微球具有优良的吸附性能。

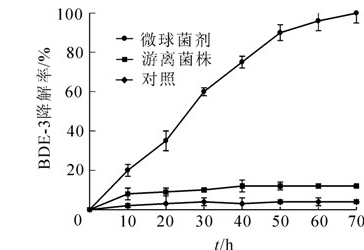
修复试验在人工模拟较高初始质量浓度300 mg·L^-1的BDE-3污染水体中进行。图 3表明：与仅添加降解菌和仅添加纯材料微球的处理相比，微球菌剂能快速高效地吸附、降解水体中的BDE-3(经SPSS单因素方差分析，差异达极显著水平，P<0.01)，至70 h时已检测不到BDE-3的存在。游离菌株的降解效果优于纯材料微球，但可能是由于高质量浓度污染物对微生物自身也有毒性和抑制作用，菌株DZ3仅在最初的10 h内保持较强降解活性，而后活性逐渐丧失，至40 h时BDE-3的降解率达到峰值12%，而后不再增加。微球菌剂对BDE-3的降解是微球的吸附作用和微生物的降解作用的协同效应。Monod降解动力学方程广泛用于有机污染物的降解过程研究。本研究用Monod方程对微球菌剂降解BDE-3的数据进行分析，其方程表达式如下^[14]：$\frac{1}{\upsilon }=\frac{1}{{{\upsilon }_{\max }}}+\frac{{{K}_{s}}}{{{\upsilon }_{\max }}}\centerdot \frac{1}{S}$。其中：υ表示有机底物的比降解速率(min^-1)，υ_max表示有机底物的最大比降解速率(min^-1)，K_s表示饱和常数(mg·L^-1)，S表示有机底物的质量浓度(mg·L^-1)。

Figure 3.  Remediation of BED-3 contaminated water by microsphere-microbe complex

图 4是微球菌剂处理的溶液中随着时间的推移BDE-3的质量浓度变化情况。通过对图 4降解曲线求导，可计算出反应区间10~60 h的瞬时降解速率等S—v数据，详情见表 4。

Figure 4.  Concentration variation of BDE-3 in solution

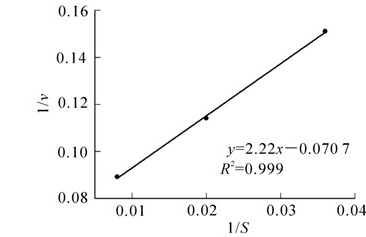
在线性区间内采用线性简化的方法，以1/υ对1/S作图，即以BDE-3降解速率的倒数对BDE-3质量浓度作图(图 5)，通过与Monod方程拟合，对方程参数求解。 最终，拟得关联式$\frac{1}{\upsilon }=A+\frac{B}{S}$，其中A=0.070 7，B=2.22。由纵轴截距$A=\frac{1}{{{\upsilon }_{\max }}}$，可得υ_max=14.29。由斜率$B=\frac{{{K}_{s}}}{{{\upsilon }_{\max }}}=2.22$，计算得到K_s=31.71 mg·L^-1。所以在液相中微球菌剂对BDE-3的降解动力学方程为：$\upsilon =\frac{{{\upsilon }_{\max }}\centerdot S}{{{K}_{s}}+S}=\frac{14.29\centerdot S}{31.71+S}$。

Figure 5.  Linear relationship of 1/S and 1/υ

生物碳空隙丰富、表面积大，并且可以通过π—π键固定芳香烃类的有机化合物^{[15, 16, 17]}，因而成为有效的有机污染吸附剂。本研究首次用海藻酸钠和生物碳制成微球颗粒，以4-溴联苯醚(BDE-3)为模式物研究了制得的微球对多溴联苯醚的吸附潜能。结果表明：海藻酸钠的质量分数对微球制剂的质量影响较大，添加质量分数过高，制得的微球孔隙数量少，不利于吸附作用的发生。但若添加质量分数低于2.0%时，制得的微球较软，在震荡过程中容易破碎。兼顾考虑成本、吸附效果和机械强度，本研究最终确定海藻酸钠的添加质量分数为2.0%，制得的微球凝胶颗粒用于后续的吸附实验。

海藻酸钠-生物碳微球在液相环境中对BDE-3的吸附动态过程符合Lagergren准一级动力学方程，所得数据与Elovich方程有良好的拟合，吸附常数远远大于解吸附常数，表明在该过程中吸附作用远大于解吸附作用，即吸附占据主导地位，试验结果证实制得的海藻酸钠-生物碳微球BDE-3具有优良的吸附特性。目前，修复水体中有机污染物的方式主要有物理吸附和添加外源微生物2种方法。只利用吸附剂的纯物理方法无法彻底从环境中去除污染物，而向污染水中添加外源微生物却常因为微生物自身对环境的耐受性差，无法在较高浓度污染物条件下存活。利用河底淤泥中筛选得到的菌株对PBDEs的耐受最高质量浓度为50 mg·L^-1，利用白腐真菌降解对PBDEs的耐受最高质量浓度为35 mg·L^{-1[18, 19, 20]}。在上述背景下，本研究首次尝试将吸附剂和高效降解菌株相结合，利用海藻酸钠进行包埋制成微球菌剂对4-溴联苯醚(BDE-3)进行降解。结果证实，微球本身较强的吸附特性加快了BDE-3在水体的传质速率，而微生物经过包埋后极大地提高了菌株DZ3对周边环境的耐受性，可在BDE-3质量浓度为300 mg·L^-1的溶液中进行降解。数据显示，添加微球菌剂的溶液中BDE-3的降解率与仅使用游离微生物相比降解效率提高了88%。本研究结果可为微球菌剂在多修联苯醚污染水体的实际修复提供初步理论指导。