-
应用于木材检测领域的无损检测方法多达十几种，在立木材质和内部缺陷辨识过程中应用较为广泛的方法是应力波检测[1-3]。随着森林资源的日益减少和需求量的日益增加，木材无损检测技术的发展对木材的保护显得尤为重要。国内外的相关研究主要集中在应力波横向二维传播规律领域[4-6]，ROSS等[7]认为木材的弹性模量E与应力波速度v和木质材料密度ρ有关，并可通过测量应力波传播速度来确定木质材料的弹性模量。在对应力波的木材缺陷二维成像技术[8]研究中，学者们发现应力波可以有效检测样本内部缺陷状况[9-10]。应力波在木材内部的传播速度易受外界因素影响，徐华东等[11-12]提出红松Pinus koraiensis木材中应力波传播速度随含水率增加或温度升高呈逐渐下降趋势。为提高应力波技术在木材无损检测应用领域的可行性，刘光林等[13]分析了应力波在健康树木中的传播规律，并建立了应力波传播速度数学模型，发现在健康树木中，方向角θ与传播方向速度vT和径向速度vR比值之间的关系为vT/vR=-0.2θ2+1，与冯海林等[14]提出的理论模型吻合；方向角θ与应力波传播速度v之间的线性回归模型拟合度较高，决定系数高于0.95，从而认为应力波传播速度模型不受树种变化影响。随着应力波无损检测技术的不断发展和成像系统的不断完善，该模型还被应用到云杉Picea aspoerata等缺陷材的监测上[15]。目前，应力波在木材无损检测领域内的应用大多集中在树木横截面上的传播规律的研究上[16]，在树木纵向上的传播规律还有待研究。本研究以应力波在树木不同角度纵截面上的传播规律为切入点，建立理论模型，通过对不同角度纵截面上应力波传播规律、不同树种纵截面上传播速度模型验证、应力波传播模型影响因素的研究、有缺陷活立木纵截面上的应力波传播速度模型等4个方面对应力波在纵截面上的传播做出相关分析，以期为高精度的三维成像技术提供新的理论依据。
HTML
-
木材具有中空的细胞组成的蜂窝状结构，而细胞壁的主体是厚度最大的次生壁中层，其中微细纤维紧密靠拢，与纵轴呈10°~30°的交角，这是木材各向异性的原因。大量试验和研究表明，木材的这种各向异性可以简化为正交各向异性，即在3个相互垂直的材料主轴，横纹径向、横纹切向和顺纹纵向，分别具有不同的物理力学性质。木材的这种材料性质对其破坏特征具有显著的影响。
在实际应用中，木材的受力方向可能与木材天然形成的木纹方向不同，此时需要考虑木材斜纹的承受能力。1921年，HANKINSON在大量试验结果的基础上总结出了木材斜纹抗压强度公式，即HANKINSON公式：
式（1）中：θ为作用力方向与木纹方向的夹角；fc, θ为木材斜纹抗压强度；fc, 0为木材顺纹抗压强度；fc, 90为木材横纹抗压强度。从HANKINSON公式可以推导出应力波传播速度，若传播方向与木材纹理方向所成角度为θ，则有：
式（2）中：vl表示顺木材纹理方向的应力波速度，vr表示木材横纹方向的应力波速度。公式（2）可转变为：
令y＝v（θ）/vr，若θ＝90°，则有y＝vl/vr；若θ＝0°，则有y＝1。在θ＝0°处用二阶泰勒展开公式（3）得到：
DIKRALLAH等通过导波实验分析了湿材的声学各向异性，研究了应力波与纵截面夹角之间的数学关系，得到应力波速度v与纵截面夹角α之间的数学关系。方程如下：
式（5）中：v（α），vR，ER，ET，GRT分别代表纵截面夹角为α的传播速度、径向速度、径向弹性模量、切向弹性模量、剪切模量。令f（α）=v（α）/vR，可得：
式（6）中：g（α）＝ $\sqrt {\left[ {1 + {E_{\rm{T}}}/{E_{\rm{R}}} \cdot {{\tan }^4}\alpha + 2 \cdot {G_{{\rm{RT}}}}/{E_{\rm{R}}} \cdot {{\tan }^2}\alpha } \right]} $ ；由式（6）可知：f（0）＝1，f ′（0）＝0，f ″（0）＝-2（1-GRT /ER）。当θ＝0时，通过麦克劳林公式将方程展开为一个关于多项式和一个余项的和，化简得到如下方程：
由式（7）可知：在横截面近似为理想圆的情况下，v（α）/vR与α间的曲线近似为二次抛物线，且关于α＝0对称。而在计算应力波在纵截面上传播的速度时应考虑方向角和纵截面夹角大小，将木材任意2点间的应力波传播速度定义为方向角θ和纵截面夹角α，所测树木的纵向传播速度vl，径向应力波传播速度vr。由式（2）和式（6）可得出：v（θ, α）＝vl·vr /（vl·sin2θ+vr·cos2θ）＝vl·vR（-0.2α2+1）/[vl·sin2θ+vR（-0.2α2+1）·cos2θ]，令f（θ, α）＝v（θ, α）/vr，即：
理论分析表明，在纵截面夹角α固定的情况下，沿方向角θ的应力波速度和径向速度比值近似为一条二次曲线，我们把式（8）作为健康树木中应力波在纵截面上的传播理论模型，将方向角θ定义为x，k＝[vl-vR（-0.2α2-1）] /vl，则可将式（8）转化为y＝1+kx2。从中可知：应力波在纵截面上的传播速度曲线图呈二次曲线型，α的大小决定着k的大小，即决定着二次曲线开口大小，增长速率的快慢。
-
选取浙江农林大学植物园樟树Cinnamomum camphora，白杨Populus alba，鹅掌楸Liriodendron chinensis，雪松Cedrus deodara等4个树种为测试样本。实验分为2个部分：一是针对正常活立木检测应力波在其内部的传播规律；二是通过比较雪松健康部位与缺陷部位之间的应力波传播速度差异，得出缺陷木材中应力波传播方式的变化。实验选用ArborSonic 3D木材无损检测仪（匈牙利Fakopp公司），该仪器包含12个传感器及主机和成像软件，能够测量各个传感器间的应力波传播时间及速度，并生成2D断层图像和检测报告。
-
选取健康活立木样本和带有缺陷的样本共40株，皮卷尺、卡尺测得立木样本的胸径、直径，将传感器布置在立木纵截面两侧（图 1A），6个·侧-1，同侧传感器间距10 cm·个-1。测试时按1~12号传感器顺序敲击，4次·个-1。同个截面测量3次取平均值。换至不同角度的纵截面重复上述进行测量。立木所测纵截面间的夹角为15°·个-1，共测得纵截面数量6个·样本-1（图 1B，图 1C）。ArborSonic 3D木材无损检测仪获取传播速度、时间等数据并传送至电脑端。
Figure 1. Cross-section and the number of test samples
为进一步了解纵截面应力波传播规律，分析不同的方向角和纵截面夹角对应力波传播速度的影响，将敲击传感器产生应力波的敲击方向与传播速度方向之间的夹角称为方向角θ（图 1A），所测纵截面与径切面的夹角称为截面夹角α；取所选树种不同尺寸的样本各3株，分析传播速度模型在不同树种上的变化；分析敲击力度，测量时的起始高度，木材本身缺陷等客观影响因素对实验的影响。选取人工凿的缺陷雪松，缺陷大小为长度10 cm的正方形缺口，检测应力波经过缺陷和不经过缺陷时的传播速度。如图 2所示，测量4个不同纵截面，其中2个经过缺陷（图 2A，图 2B），2个不经过缺陷（图 2C，图 2D）。
Figure 2. Cedrus deodara containing defects detected stress wave propagation velocity at different longitudinal cross sections
2.1. 材料与设备
2.2. 实验方法及内容
-
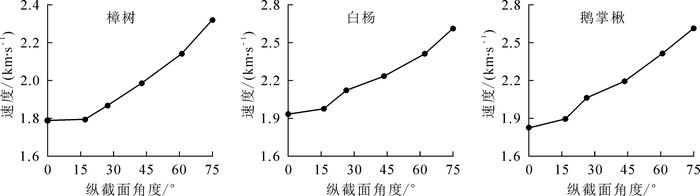
分析所测健康活立木样本的应力波传播速度数据，得到应力波传播速度散点图并进行曲线拟合，由图 3可知：在不同纵截面上（以α为15°为例）应力波传播速度随着方向角θ的增大而增大，水平方向上传播速度最小。
Figure 3. Stress wave propagation velocity trend longitudinal section of different trees
为了更加直观地观测到纵截面上应力波传播模型，使速度模型更具有代表性，表 1给出了相对应的拟合方程。其中令y＝v（θ, α） /v0，vθ表示方向角速度，v0表示水平方向应力波速度，x表示方向角θ，得出一条一次项系数为0的二次曲线，回归分析中决定系数R2均在0.93以上，拟合度较高。从拟合结果来看，在纵截面上应力波传播速度与方向角θ和截面夹角α具有较强的相关性，随着θ的增大，速度随之变大。通过图 3和表 1可以看出，在不同纵截面上随着θ的增大，速度随之增大。而随着α的增大，木材内部应力波传播速度增长加快。随着方向角θ的增大，应力波速度会呈二次曲线式增长，α的增大会使增长的二次曲线增长率增加。θ和α的变化与前文提出的理论传播模型具有较强一致性。
树种 拟合方程 R2 樟树 y=0.253x2+0.987 0.935 白杨 y=0.256x2+1.013 0.941 鹅掌楸 y=0.381x2+0.986 0.932 Table 1. The regression model between v(θ, α)/v0 and θ in healthy tree radial longitudinal section
通过分析可以知道应力波在木材纵截面上的传播速度大于在横向上的传播速度，这是由木材内部各向异性所导致，纵截面上的传播是顺着木材纹理方向，传播速度较快。不同角度纵截面上的应力波传播速度随着α的增大会使传播速进一步增大。这是由于随着α的增大，所测量的纵截面越来越靠近木材表层，所受木材内部各向异性的影响逐渐减小造成。
-
同一纵截面上任意2点间的传播速度随着方向角度的变化而变化，同一纵截面上速度随着方向角的增大而增大；在不同纵截面上，随着截面夹角α的增大应力波传播速度的增长率加大，即在方向角θ不变的情况下，α的增大速度随之增大；相同树种胸径较大则应力波在纵截面上传播的速度将更快。而在不同角度的纵截面上，由于内部的各向异性，应力波速度也各不相同。随着截面夹角α的变化k值的大小也随之改变，由k＝[vl-vR（-0.2α2+1）]/vl得出理论k值。表 2为樟树不同角度纵截面上应力波传播速度回归方程。
不同纵截面角度/(°) 拟合方程 理论k值 R2 0 y=0.253x2+0.987 0.29 0.935 15 y=0.431x2+0.988 0.41 0.934 30 y=0.493x2+0.983 0.47 0.958 45 y=0.592x2+0.969 0.53 0.946 60 y=0.597x2+0.958 0.56 0.938 75 y=0.582x2+1.012 0.57 0.949 Table 2. Each longitudinal cross-section regreeion mode of cinnamomum camphora
由表 2可知：拟合曲线满足一元二次方程。为使结论更具普遍性，增加鹅掌楸、白杨实验样本数据，采用与樟树样本相同的数据处理方式，得到不同树种在不同角度纵截面上的拟合方程，如表 3所示。结果表明：该模型具有很好的拟合优度，且对不同树种都适用，能够很好地反映应力波在不同角度纵截面上的传播规律；对于所检测健康树种，应力波在不同角度纵截面上的传播回归模型与本研究建立的理论模型（8）非常吻合。上述实验和数据分析同时说明，应力波在不同树种上传播时，木材密度越大，则传播速度越大；相同树种的不同纵截面，随着纵截面角度α的不断增大，其速度的增长率也逐渐增大。推测原因是应力波作为一种声波，在质地坚硬密度大的树种内传播速度较快；相同树种中随着α的增大，应力波在木材内部的传播逐渐从髓心转向木质部，而其速度发生明显变化，即木质部内的应力波传播速度大于髓心的传播速度。
树种 截面角度/(°) 拟合方程 理论k值 R2 0 y=0.253x2+0.987 0.24 0.935 樟树 15 y=0.431x2+0.988 0.43 0.934 30 y=0.493x2+0.983 0.48 0.958 0 y=0.381x2+0.986 0.37 0.932 鹅掌楸 15 y=0.446x2+0.989 0.44 0.932 30 y=0.521x2+1.014 0.52 0.936 0 y=0.256x2+1.013 0.25 0.941 白杨 15 y=0.389x2+0.946 0.38 0.933 30 y=0.513x2+0.976 0.50 0.945 Table 3. Regression models of different species on each longitudinal section
-
选取与径切面夹角为15°的一个纵截面，在传感器布置位置不变的情况下，邀请6位实验人员，分别编号为1~6号，每人采用其常用的敲击力度完成测试。由于实测时每个人的力度均不同，所以以此来探究敲击力度对本研究建立的传播速度模型的影响。6组数据采集完成后，拟合方程如表 4所示。
实验次数 拟合方程 理论k值 R2 1 y=0.438x2+0.993 0.44 0.932 2 y=0.463x2+0.992 0.45 0.927 3 y=0.427x2+0.989 0.43 0.928 4 y=0.412x2+0.976 0.41 0.932 5 y=0.445x2+0.996 0.44 0.939 6 y=0.436x2+0.988 0.43 0.938 Table 4. Relationship between v(θ, α)/vr and θ, α under different forces
由6次测试结果可以看出：拟合曲线整体趋势为一条开口向上的抛物线，符合本研究提出的传播速度模型；k值相差不大，也可以说明在一般情况下敲击力度大小对所提出模型的影响不大。
为测量在不同起始高度下应力波在木材内部传播速度的变化。实验选取离地80 cm，100 cm，120 cm处为起始位置，按照之前的测试方法进行实验，记录数据。完成采集后对应不同离地高度的数据进行拟合，得到拟合方程如表 5所示。
树种 离地高度/cm 拟合方程 理论k值 R2 80 y=0.354x2+1.027 0.36 0.934 樟树 100 y=0.356x2+1.022 0.36 0.951 120 y=0.366x2+1.033 0.36 0.946 80 y=0.442x2+1.011 0.44 0.977 鹅掌楸 100 y=0.436x2+0.993 0.44 0.974 120 y=0.454x2+0.989 0.45 0.943 80 y=0.381x2+1.016 0.38 0.931 白杨 100 y=0.376x2+0.994 0.38 0.962 120 y=0.386x2+0.975 0.39 0.938 Table 5. Relationship between v(θ, α)/vr and θ, α at different heights
由表 5可知：3个不同样本在不同起始高度下的曲线均符合所提出的模型，并且k值大致相同。相同树种内部，不同的起始高度对理论模型的影响不大；这是由于在木材内部不同高度上的结构大致相同，应力波在其内部传播速度也大致相同。同时应力波作为振动波，不同力度所产生的振动效果是一致的，因此在合理的力度范围内其传播速度变化较小。
-
对缺陷木材中应力波的传播分析可知，在不同夹角的纵截面上，经过缺陷位置的应力波传播速度明显低于正常数值；推测原因是应力波经过缺陷位置时会绕过缺陷传播，传播时间变长，相应的传播速度会变小。图 4为应力波经过缺陷时，3D木材无损检测仪精确定位到的缺陷位置及大小。
Figure 4. Cedrus deodara dimensional stress wave with defects in different longitudinal section showing diagram
通过判断是否符合前文所建传播模型可以确定树木内部是否含有缺陷。对15°纵截面和30°纵截面上的应力波传播数据进行拟合，得到拟合曲线（图 5）。从图 5可知：当应力波经过3~9，3~10传感器时，其速度拟合曲线明显下降，波速比先前所测树种的拟合曲线降低15%以上，可判断该路径经过缺陷区域。这与王立海等[17]认为的在树木横截面上测得某条传播路径上应力波传播时间大于其参考值10%时，可视为缺陷的观点一致。
Figure 5. Stress wave velocity different longitudinal section of the fitting curve
DownLoad: