Measuring method of tree attributes based on consumer-grade binocular camera

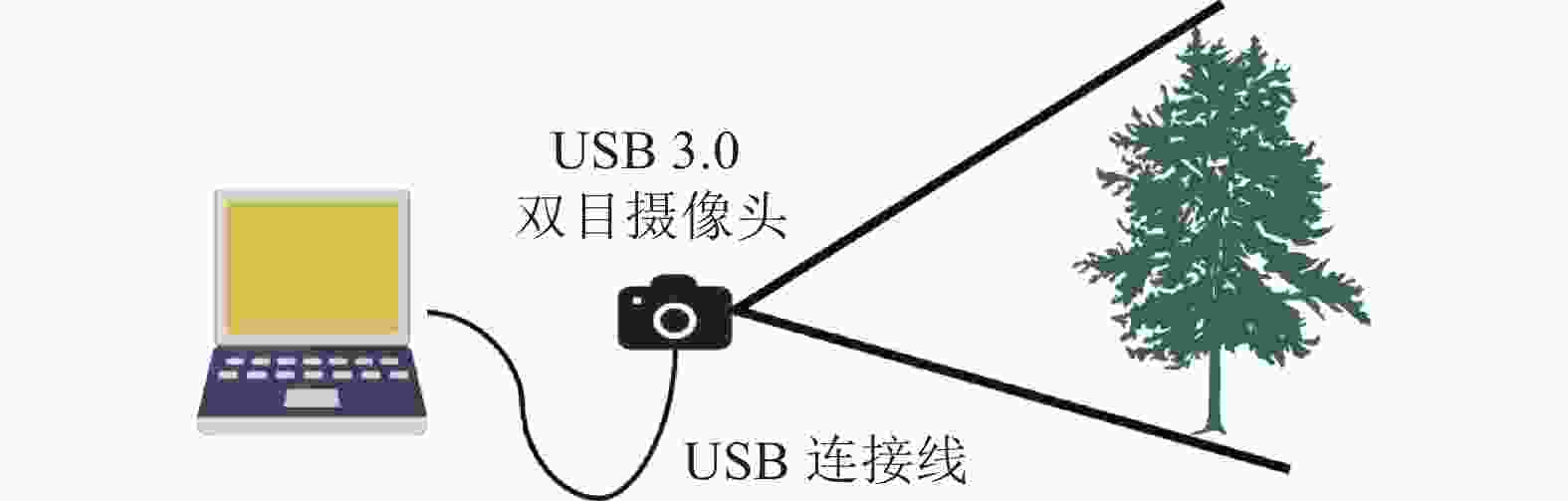
利用高帧率固定基线(6 cm)的USB 3.0双目相机，借助Opencv开源库在浙江农林大学东湖校区以及周边街道共采集20组不同场景的立木图像，图像分辨率统一设置像素为1280×720。另因立木品种不同，高矮存在差异，拍摄距离为1.8~4.0 m，相机距离地面垂直高度约95 cm，为保证目标立木在相机拍摄范围内且位于中心位置，拍摄过程中相机存在仰视角度，确保左右图像最低点均为树木根部或地面，最高点均为立木生长方向的最高处。图1为立木图像采集示意图。

Figure 1.  Schematic diagram of tree image collection

相机标定是立体匹配、三维重建的基础，直接影响立木三维点云重建效果。采用张氏经典棋盘格标定法^[24]，选取GP400专业标定板(黑白格子数为12×9，每个棋盘格边长为30 mm)，把相机固定在标定板正前方80 cm处，拍摄22张不同角度的棋盘格照片，且拍摄全程使标定板全部位于图像的中心，无遮挡、无反光。

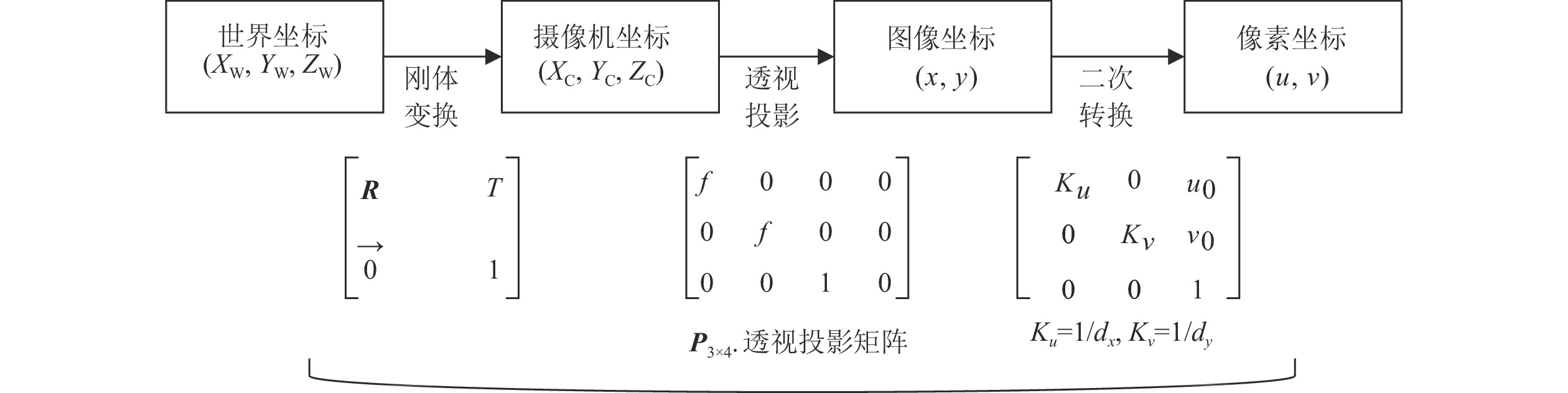
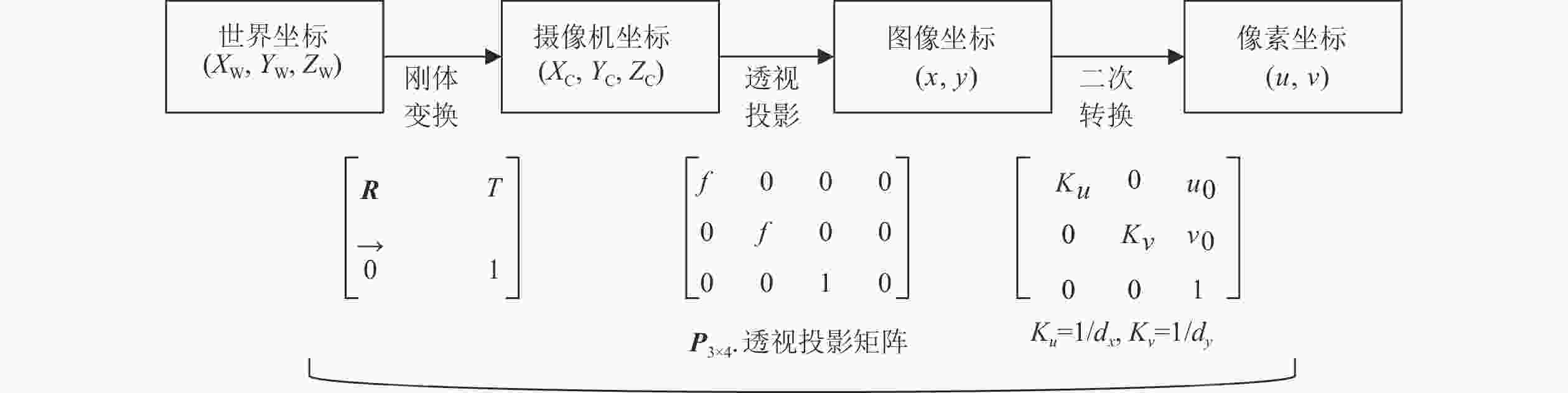
相机成像过程中，摄像机坐标系、世界坐标系、图像坐标系以及像素坐标系的转换如图2所示，像素坐标系、图像坐标系、摄像机坐标系以及世界坐标系中的坐标分别用(u, v)，(x，y)，(X_c, Y_c, Z_c)，(X_w, Y_w, Z_w)表示。

Figure 2.  Transformation of four coordinate systems

图2中，R为3×3的旋转矩阵，T为平移向量，$\vec {\boldsymbol{O}}$为1×3的矩阵。根据图2坐标系的转换关系，本研究中的立木因子测量点是从像素坐标系转化到世界坐标系，计算公式为：

式(1)中，Z_c表示点与光轴的距离，d_x、d_y表示单位长度内像素的实际大小，f为双目相机焦距。

通过拍摄左右2幅不同视角的立木图片将二维图像信息转化为三维信息，可实现三维重建。根据相似三角原理可得到立木深度与视差的关系，见式(2)。

式(2)中，D为深度，B为双目相机之间的固定基线距离，d为视差。

本方法由立木三维点云生成、立木点云数据处理和立木因子测量3个部分组成，其流程如图3所示。先利用改进的SGM算法生成视差图，通过三角原理转换为深度图，深度图通过坐标转换生成初始三维点云；为了准确去除立木三维点云的噪声点，提出基于空间密度聚类和混合滤波的方法进行点云去噪，速度快且普适性强，再分别利用主成分分析法和随机采样一致性算法进行方向矫正和点云分割，提取只包含目标立木的点云；最后，利用最值遍历法和椭圆拟合法实现树高、胸径的无接触测量。

Figure 3.  Technical flow chart

先使用标定后的USB 3.0双目视觉相机采集立木图像，并根据标定结果对图像进行立体矫正；针对传统SGM算法生成立木视差图效果不佳，Census变换过于依赖中心像素，以及仅通过比较邻接像素值与中心像素值大小进行取值受光照、噪声影响较大等问题，对SGM算法中的Census变换进行了改进，并利用其生成初始视差图；然后针对初始视差图中无效点的问题提出自适应窗口优化方法；根据相似三角原理将视差图转换成高质量的深度图，既包含了立木图像的二维信息，又保留了相机与立木之间的深度信息；最后，通过坐标系转换生成原始立木三维点云。其中，改进的Census变换和自适应窗口优化方法分2个步骤。步骤1：将中心像素值用其周围8个窗口像素点的中值代替，抗干扰能力强，计算结果较为准确。

步骤2：通过改进的Census生成的初始视差图有无效点(空洞点、失真点)，根据无效点的类型，利用自适应窗口对视差图进行填充，完成优化，生成高质量视差图。若式(3)成立且视差值为0，则判定为空洞；否则，判定为失真点。其中D_L(x, y)表示左视差图某点视差值，D_R(x, y)表示右视图某点视差值。

若点Y为失真点，以Y点为像素中心与周围窗口8个像素点视差值进行比较，寻找最大与最小视差值，并对二者求平均。Z表示失真点相邻视差值的集合，失真点填充表达式如式(4)所示。

式(4)中，M_min为最小视差值，M_max为最大视差值，M_avg为最大与最小视差的平均视差值。

若D_L(Y )＜M_min，则失真点视差以最小值视差值填充；若M_min≤D_L (Y )≤M_max，以平均视差值进行填充；若D_L(Y)＞M_max，以最大视差值填充，如式(5)所示：

若点Y为空洞点，则分别从x，y方向进行遍历，寻找视差值不为0的点Y_x和Y_y，构造一个以孔洞点Y(x, y)的坐标为起点，d_y为高，d_x为宽的矩阵N_dx×dy，形成一个自适应窗口矩阵N，见式(6)。

空洞点填充的表达式如式(7)所示。

式(7)中，S表示矩阵N对应元素总和，矩阵非0元素为n个，S_avg为平均值。根据上述公式及填充方法，直到检测完所有像素点，并进行视差优化，采用中值滤波平滑图像去除噪声。

由于三维点云生成后的立木场景复杂、数据量大，包含了若干噪声点，且三维点云模型与真实世界三维空间尺度、方向也不一致，因此需要对点云进行去噪、坐标和方向矫正等预处理操作。预处理后的点云包含了其他背景立木以及地面点云，还需进行点云分割，提取只包含目标立木的三维点云。通过USB 3.0双目相机生成的立木点云噪声点较多，主要分布于立木的树干周围或叶片之间，为此提出一种基于空间密度聚类和混合滤波的三维点云去噪方法。

①去噪。首先，对X、Y、Z轴进行阈值范围的设定，通过直通滤波将点云中不在该范围内的点滤除，提取只包含目标立木的感兴趣区域，减少其他背景立木噪声。再采用统计滤波删除立木点云数据中聚集的噪声点：步骤1，读取三维点云数据集P，建立kd-tree数据结构。步骤2，对点云数据中每个点P_i的邻域进行统计分析，计算其到k (k取50)个临近点的平均距离，如式(8)和式(9)所示。其中d_ij是p_i与p_j两点之间的空间距离，d_i是平均距离。

步骤3，计算点云数据的标准差(d_std)，如式(10)所示：

步骤4，假设得到的结果是一个高斯分布，其形状是由平均值和标准差(d_std)决定，平均距离在标准范围L (由全局距离平均值和方差定义)之内的点进行保留，否则被定义为离群点并从数据中剔除。如式(11)所示：

步骤5，遍历点云中的所有点，直到处理完所有点云数据。步骤6，然后利用空间密度聚类算法移除离散噪声点，在三维点云中任意选择一个点(既没有指定到一个类也没有特定为外围点)，通过计算其邻域内的数据点数是否大于设定的阈值，判断是否为该点。若是，则在该点周围建立一个类，否则，将其设定为外围点。步骤7，遍历其他点，直到建立一个类。把密度直达(directly-reachable)的点和密度可达(density-reachable)的点依次加入到类中。如果标记为外围的点被加进来，则修改其状态为边缘点。步骤8，重复步骤6和步骤7，直到所有的点满足在类中(核心点或边缘点)或者为外围点。

综上，基于空间密度聚类和混合滤波的去噪步骤为：步骤1，首先进行参数初始化，输入点云的数据；步骤2，计算点云数据的k (k取50)个近邻点；步骤3，采取统计滤波去除点云聚集的噪声点；步骤4，选定任意一点为核心点，利用密度聚类算法去除离散的噪声点；步骤5，计算完成，输出点云数据。

该去噪方法充分利用直通滤波和统计滤波对聚集噪声点的优势、空间密度聚类对离散噪声点的敏感性，大大提高了点云去噪的效率。

②点云坐标矫正。将点云模型比例(h_m)与实际比例(h_r)矫正，缩放成R=h_r/h_m的比例，在进行树高、胸径测量时可按照比例换算到实际尺度。

③方向矫正。计算三维点云模型初始质心点(p₀)的三维坐标，利用主成分析法将三维点云模型进行质心化，并求解三维点云中方差矩阵和特征向量(立木三维点云的主方向)的值，根据立木三维点云模型的主方向创建旋转矩阵(N)，将初始质心点(p₀)为中心转换到主方向的位置，得到一个新的三维点云模型P_new=Np₀。

④点云分割。矫正后的点云数据包含地面以及其他背景立木，利用随机采样一致性(RANSAC)算法将地面拟合成一个平面，再提取该平面的点云，从而将地面点云与目标立木点云进行分割。首先手动设置一个阈值，计算三维点与拟合平面(地面)之间的距离，若超过该阈值，被判定为无效数据，否则进行保留，在多次迭代的过程中随机拟合多个平面，选取包含最多有效数据的平面为最终的拟合结果。RANSAC算法只对主体数据进行拟合，在偏移量大且无效数据较多的情况下，拟合效果较佳。

将立木在生长方向的最高点与最低点的高度差定义为树高。将三维点云进行坐标矫正，使立木生长方向与Z轴方向一致，且立木底部区域位于oxy平面，遍历三维点云所有的点，Z轴坐标的最大值(Z_max)与最小值(Z_min)的差值为立木的高度H。

将立木位于地面1.3 m胸高处断面直径视为胸径(干径)。在生成的立木三维点云中，立木的主干可近似看作为椭圆，可利用矫正后的坐标比例(R)求得1.3 m处的点云坐标：Z=1.3/R，对该位置做3 cm厚度的切片，再将点云切片投影至oxy平面，对立木胸径测量处的点云数据利用最小二乘法进行椭圆拟合，椭圆的一般方程式为：

式(12)中，A、B、C、D、E、F分别表示拟合求得的系数，x、z表示立木主干待测区域点云数据投影后的坐标。利用式(13)可求得椭圆的中心${X}_{{\rm{c}}}$、$ {Z}_{\mathrm{c}} $，利用式(14)可求得椭圆的长半轴L (立木的胸径为2L)。

本研究中立木因子测量方法验证的软硬件平台均使用PC电脑[Intel(R) Core(TM) i5-7200U CPU @2.50 GHz 2.70 GHz]、Windows 10操作系统和Visual Studio2017+opencv库以及开源点云库(point cloud library，PCL)，C++语言实现。

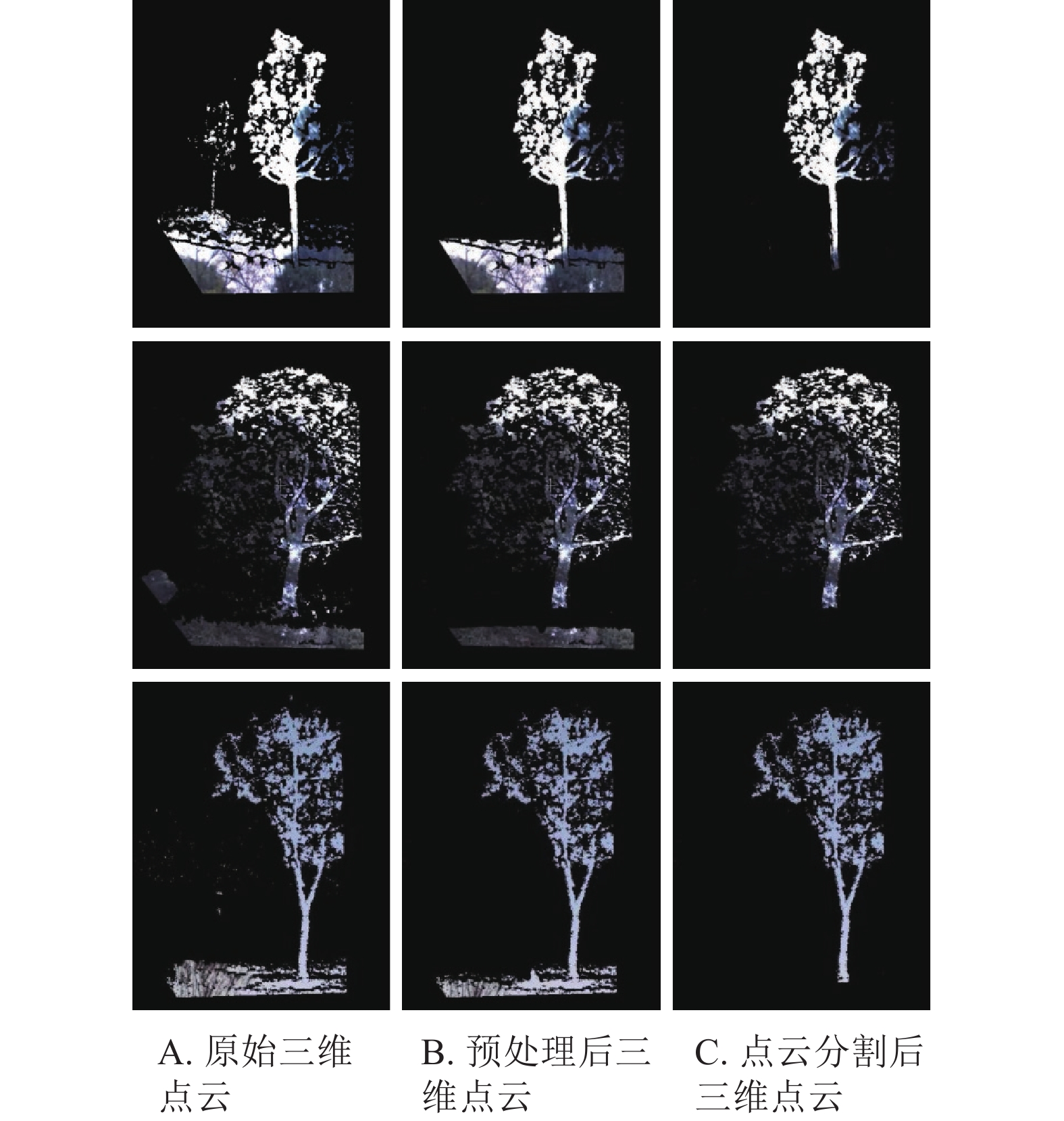
图4为随机选取的3株不同种类立木的三维点云处理结果。其中：图4A为原始立木点云，可以看出包含大量离散噪声点以及地面、背景立木等；图4B为预处理后的三维点云，保持目标立木三维点云的整体形状不变化的同时去除了背景立木以及树干、地面周围的噪声点，且三维点云坐标方向得到矫正；图4C为立木点云分割后的结果，将目标立木点云与嘈杂的地面点云准确分割。

Figure 4.  Processing results of tree point cloud

表1是原始三维点云(图4A)与点云分割后三维点云(图4C)的数量变化对比结果。由表1可知：在保证目标立木三维点云完整的前提下，处理后的有效点云数量比初始点云数量总体减少约2/3。

将本研究方法得到的树高和胸径值与实际测量值(利用胸径尺、博世激光测距仪分别测量胸径、树高10次，取平均值作为实际测量值)进行对比，来评价本研究方法的准确性与稳定性。

由表2可知：立木高度的误差范围为0.012~0.079 m，测量值与真实值的最大相对误差为2.219%，最小相对误差为0.339%，平均相对误差为1.525%。立木胸径的误差范围为0.065~0.429 m，测量值与真实值的最大相对误差为5.620%，最小相对误差为0.457%，平均相对误差为2.084%。

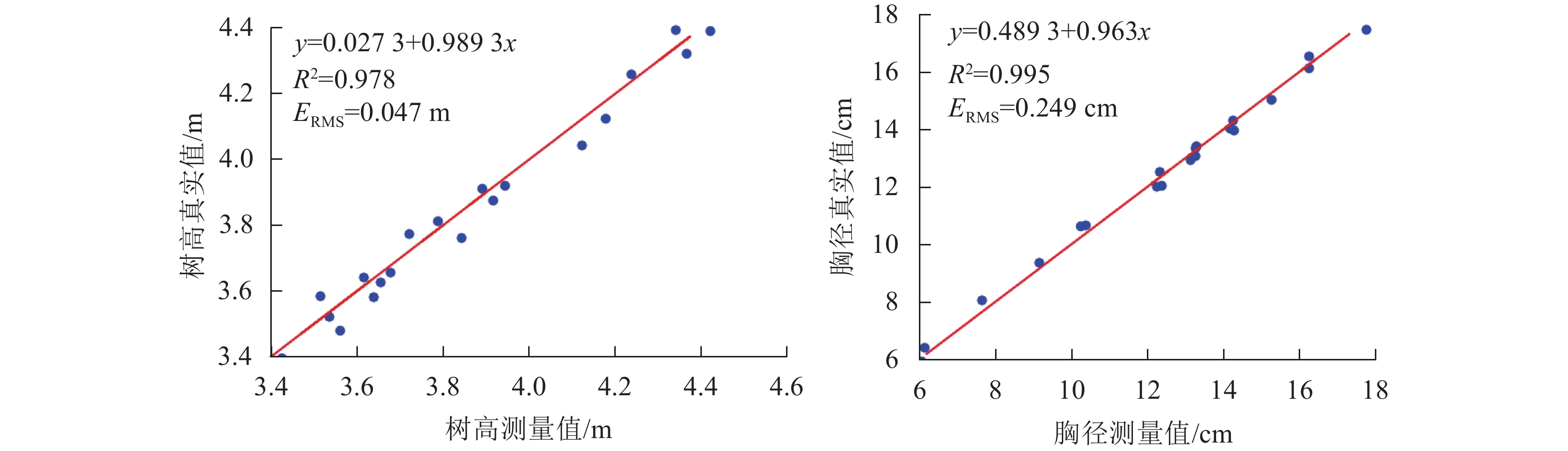
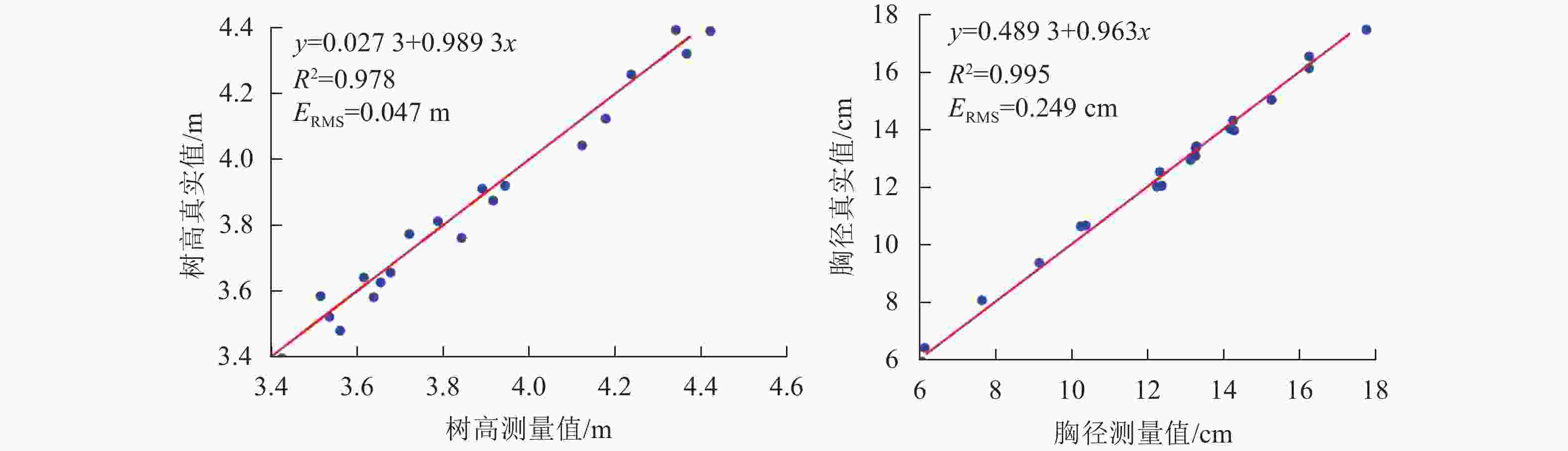
图5为立木高度、胸径真实值与测量值的线性回归分析图，结果表明：使用本研究方法测量的立木高度、胸径与真实值均存在着显著的线性相关关系，树高的相关系数R²为0.978，均方根误差为0.047 m；胸径的相关系数R²为0.995，均方根误差为0.249 cm。

Figure 5.  Linear regression diagram of measured and true values of tree height and DBH

针对现有立木因子测量方法成本高、效率低、仪器携带不便等问题，本研究提出一种新的方法，即基于消费级双目相机的立木因子测量方法。利用双目相机拍摄左右两幅不同视角的立木图片获得二维图像信息，通过改进的Census变换形成高可靠初始视差值，再采用自适应窗口填充黑洞点和剔除无效点，使立体匹配结果更加精确，从而生成层次分明、边缘清晰的视差图，并转化为三维信息，进而生成高质量的立木三维点云；提出一种基于空间密度聚类和混合滤波的三维点云去噪方法，可快速去除聚集、离散的噪声点，获得较高精度的立木测量值。结果表明：树高平均相对误差为1.092%，测量值与真实值的相关系数(R²)为0.978，均方根误差(E_RMS)为0.047 m；胸径的平均相对误差为2.084%，R²为0.995，均方根误差(E_RMS)为0.249 cm。

本方法树高的平均相对误差均低于顾雯钧等^[25]和杨全月等^[26]的研究结果，胸径的平均相对误差低于顾雯钧等^[25]和吴铮等^[27]研究结果，略高于杨全月等^[26]的研究结果，但杨全月等^[27]的方法需要较为昂贵的三维激光扫描仪，而本研究仅需要便携式双目相机，方法简单、容易实现。本方法测量值与真实值比较结果表明：胸径、树高测量精度较高，但树高测量值总体低于实际值，主要是因为立木生长环境复杂，包含大量背景噪声，树冠顶部枝叶稀疏，生成树冠顶部的三维点云也较为离散，在点云去噪阶段可能当作噪声剔除；部分立木高度较高、树干较细，拍摄的不够清晰完整，导致视差图效果不是很好，影响立木三维点云生成效果，可能会存在点云缺失、数量少的现象。利用最小二乘法椭圆拟合时，由于树干点云分布不均匀或者有效点云数量较少，这是胸径误差的主要来源，导致胸径计算结果不理想。因此，未来可进一步对树冠和胸径部分的三维点云进行稠密化处理，减少因树冠和胸径点云分布不均匀或数量较少所带来的影响。