下载:
-
雷达探测木材内部异常结构主要通过分析发射的电磁波的反射信息来实现。当木材内部存在孔洞时，因孔洞与木材本身具有不同的介电性能，进入木材的电磁波在穿过内部孔洞时会在两者的界面上发生反射。分析反射回波波形资料，可以推断木材内部孔洞情况。利用雷达对木材进行扫描可以快速获知木材内部是否存在孔洞。雷达波在不同含水率不同树种等条件下具有不同的传播速度，其检测图像若采取统一的方法进行分析会存在一定误差。大量研究表明：木材孔洞的探测精度与被测对象的介电常数密切相关，而木材的含水率、纤维密度和纤维方向等均会对介电常数产生一定影响[1]，其中木材含水率与介电常数密切相关[2]，因此分析木材含水率与介电常数的关系对开展雷达检测木材内部缺陷研究非常重要[3]。由此也可逆向通过雷达回波信号进行木材含水率的预估[4]。在实际应用过程中，针对雷达探测木材内部缺陷存在解析困难、探测精度不高、可视化程度低等不足，国内外学者展开了广泛研究。可行性及可靠性方面，LORENZO等[5]研究了雷达波对树干以及树根检测的可行性；邸向辉等[6]指出：电磁波信号解释分析的困难性是树木无损探测的主要制约因素；JEZOVA等[7]开展了树木内部残损的雷达图像特征研究；WU等[8]评估了探地雷达技术在探测不同树种内部损伤方面的可靠性。成像精度及算法方面，DEVARU等[9]阐述了探地雷达在树木无损检测方面的优点，并设计试验研究了探地雷达对树干内部缺陷的自动检测算法；BUTNOR等[10]采用阈值法对针叶树木内部缺陷进行了探测，并获得了较好的效果；李伟林等[11]对颐和园界河桥旁6株古柳Salix spp.进行雷达探测，并采用匹配滤波器算法计算回波时延以提高检测精度；肖夏阳等[12]通过比较阈值法、匹配滤波器法和希尔伯特积算法在树木内部层位探测的准确性，得出希尔伯特积算法对树木内缺陷区域的检测更加准确。陈勇平等[13]研究也发现：木材含水率等对雷达检测孔洞面积的影响较大，并开展树种、含水率等对雷达预估孔洞面积的初步分析。本研究旨在探究基于雷达检测的木材内部孔洞面积预估修正方法，提高雷达检测精度，从而为木材内部残损检测提供理论和数据支撑。
-
马尾松Pinus massoniana木材采集于湖南省攸县，造林年度为1966年，树龄50 a，胸径约51 cm，树高约22 m。杉木Cunninghamia lanceolata木材采集于湖南省攸县，造林年度为1982年，树龄34 a，胸径约46 cm，树高约25 m。
-
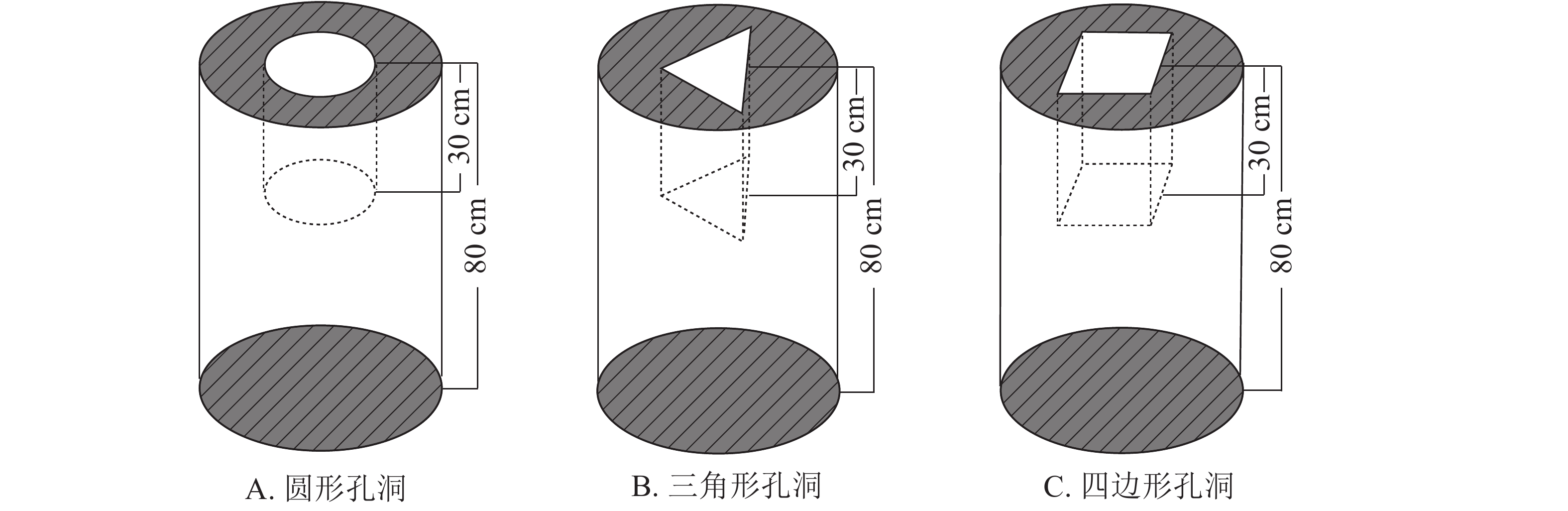
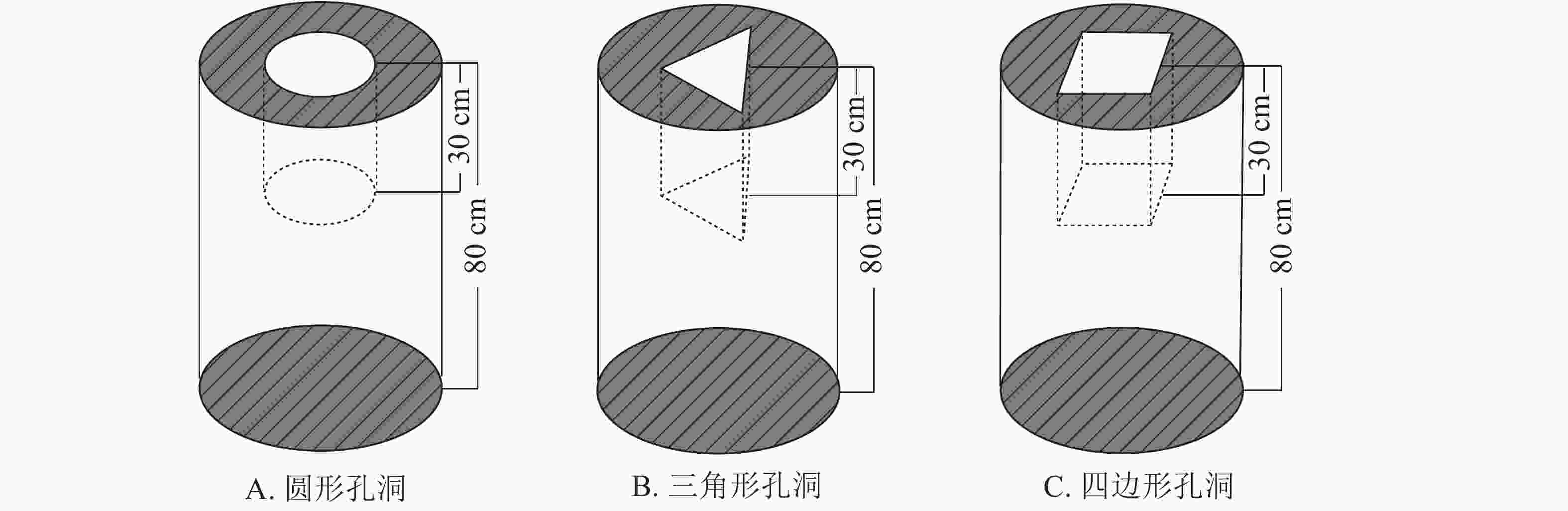
马尾松和杉木原木伐倒后，自树根位置80 cm起按每段长约80 cm逐个截取木段，以模拟短柱；截断后的部分木段通风干燥3 a，使其达到北京地区的平衡含水率。对干燥后的木段进行挑选并分别编号为S1、S2、S3、S4、S5、S6和C1用于实验研究，每个木段标记其起始检测点，其中S1~S6为马尾松试件，C1为杉木试件。取S2、S3、S4木段在其内部加工大小不一致的圆形孔洞；取S5木段在其内部加工三角形孔洞；取S6木段在其内部加工四边形孔洞；取C1木段在其内部加工圆形孔洞；S1为备用木段。以上木段的孔洞加工均位于中心位置，孔洞深度约30 cm(图1)。
图 1 孔洞加工示意图
Figure 1. Schematic of internal cavity in wood columns
-
采用树木雷达对上述试材进行雷达扫描[13]，其中S3、S4、S5、S6为试验用材，S2和C1为数据分析验证试材。本次测试研究采用美国树木雷达检测系统[Tree Radar Unit(TRU)]，主要参数设置为：频率900 MHz，最大扫描直径4.2 m，深度分辨率1.9 mm，数据采集间隔5 mm。
-
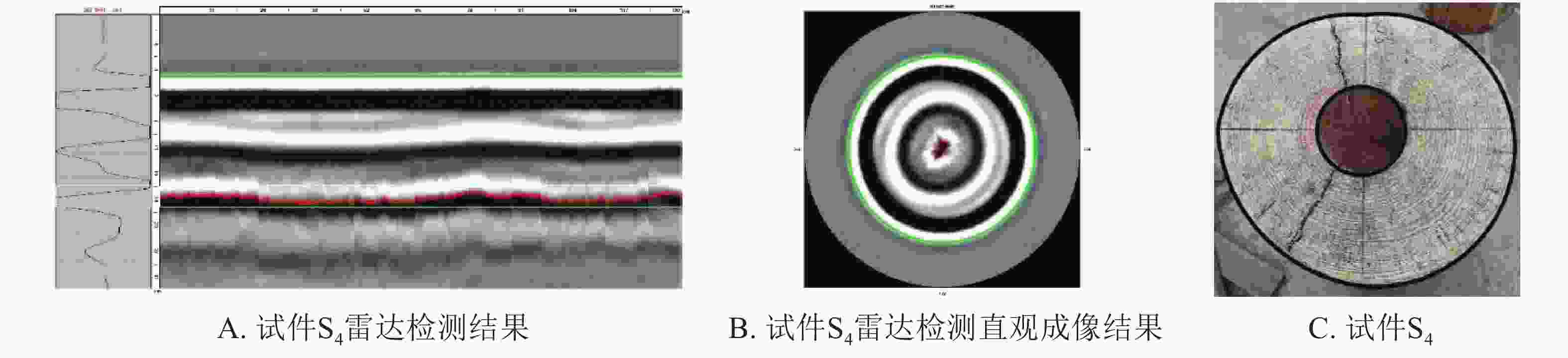
采用雷达扫描技术对带孔试材进行检测。以S4试件为例，通过分析雷达波反射波形和检测图像可以直观判定木材内部孔洞存在(图2A)，但雷达预测孔洞面积(图2B)与实际孔洞面积(图2C)存在较大的偏差。
图 2 雷达成像直观结果
Figure 2. Intuitionistic results of the cavity areas in wood columns by TRU
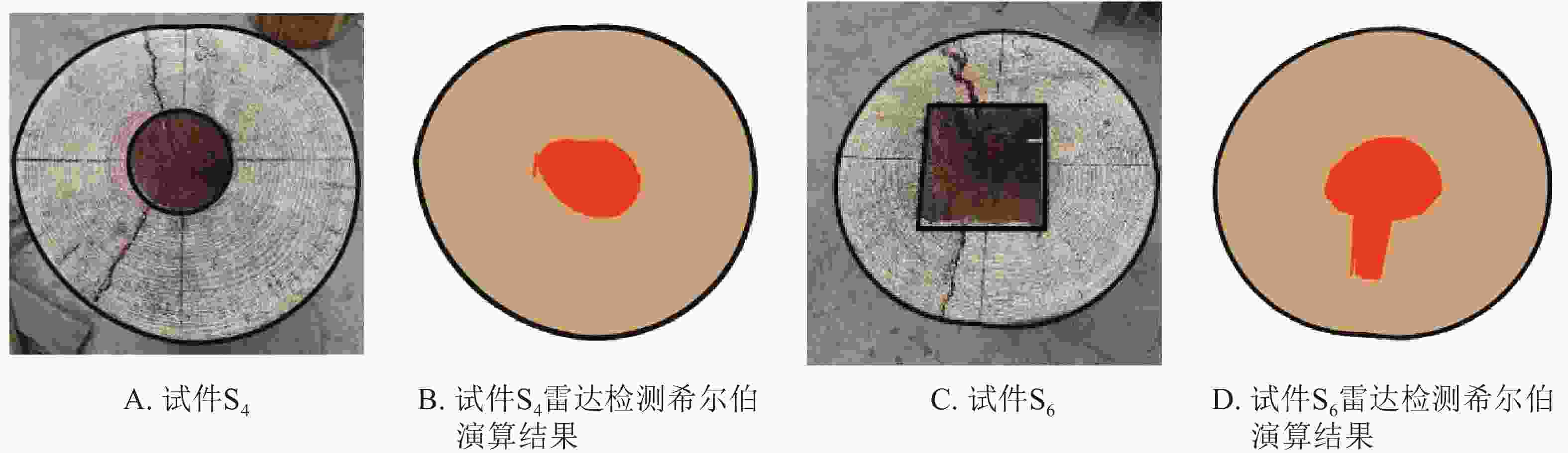
基于直观成像的误差，且希尔伯特积算法相较于阈值法和匹配滤波器法对木质体内部缺陷识别效果更好[12,14]，本研究首先对上述检测结果进行希尔伯特积算法修正，其部分检测结果如图3所示。本研究采用层剥反演法获得木材介电常数并对其内部孔洞进行定位，结合检测对象外轮廓数据，可实现内部孔洞较准确定位。
图 3 希尔伯特积算法演算结果
Figure 3. Analysis results of the cavity areas in wood columns by Hilbert
结合图2和图3可以看出：利用希尔伯特积算法对雷达检测图像进行修正，提高了检测精度，但还是存在一定误差，修正面积仍低于实际孔洞面积，其中试件S4修正图像的相对误差为20.57%，试件S6修正图像的相对误差为41.49%。这主要是因为希尔伯特积算法是根据层剥反演获得相对介电常数，从而对木材内部的传输速度进行在线估测，而实际过程该介电常数可能与估算的介电常数存在一定得误差。为此，本研究根据希尔伯特积算法原理，采取提取单路径检测数据，并使用曲线偏移、介电常数修正、辅助系数校正等方法尝试进一步的修正研究。
-
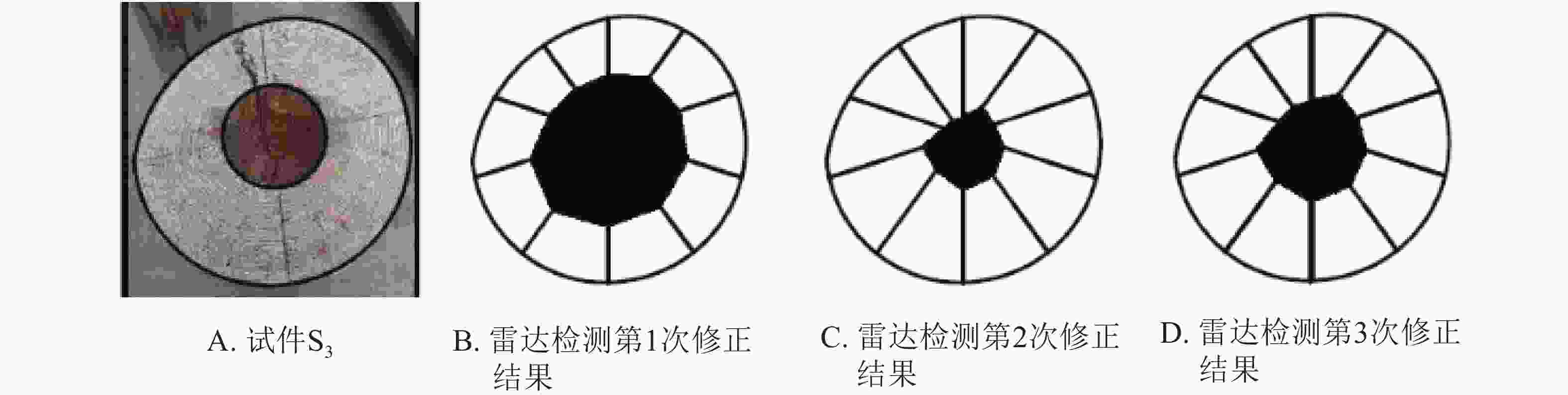
根据雷达检测原理，树木雷达工作时雷达天线绕该木柱一周相当于虚拟钻孔机对该木柱进行了360°的“钻孔”操作。本研究对检测对象进行圆周10等分，并提取等分点上每一次的“钻孔”结果。每一次“钻孔”结果即对应雷达检测中每一个位置的回波图形。通过回波图形分析可获得对应位置木材边缘与孔洞边缘距离，其中孔洞边缘即高介电常数物质(木材)与低介电常数物质(孔洞)交界面，交界面位置在回波图形中的特征为谷—峰—谷，叠加后在雷达检测图像中表现的形态为黑—白—黑。根据“钻孔”检测结果，将得到10个孔洞边界点，将边界点进行连线，即形成了内部孔洞轮廓。以试件S3为例，结果如图4。
图 4 雷达检测初步分析结果
Figure 4. Preliminary results of the cavity areas in wood columns by TRU
图4A为试件S3；图4B为图4A的断面轮廓提取，其目的是便于检测对象横断面及孔洞面积的计算；图4C为雷达检测初步分析图像。为了便于数据比对，本研究对试件S3、S4、S5、S6的雷达初步检测结果进行了测算和统计。结果见表1。
表 1 雷达检测初步测算与统计
Table 1. Preliminary calculation and statistics of the cavity areas in wood columns by TRU
序号 孔洞类型 实际孔洞百分比/% 雷达测算孔洞百分比/% S3 圆形孔洞 14.67 2.15 S4 圆形孔洞 9.66 0.84 S5 三角形孔洞 12.82 1.59 S6 四边形孔洞 20.26 2.53 从表1和图4可以看出：通过雷达检测可以快速判定木材内部孔洞的存在，但其预估的孔洞面积与实际面积相差较大。这主要是因为雷达检测内部孔洞的轮廓线产生了一定的偏移，且实际检测对象的介电常数与预设常数相差较大，导致预估孔洞面积与实际孔洞面积相差甚远。从表1和图4结果也可以看出：雷达检测预估内部孔洞面积若不加以修正，其数值远小于实际孔洞面积，无法直接应用于古建筑木构件内部残损的定量评估。
-
雷达波在介质中的传播速度可以简化为
$ v=\dfrac{c}{\sqrt{{\rm{\varepsilon }}}} $ ，其中：c为雷达波在真空中的传播速度；ε为介质的介电常数[15]。由此，木材边缘与孔洞边缘的距离可以简化为$ s=\dfrac{{\rm{c}}t}{2\sqrt{{\rm{\varepsilon }}}} $ ，其中：t为雷达波传播时间。假设“钻孔”操作中木材边缘与孔洞边缘的距离为sr，实测偏移量为a，则雷达检测中木材边缘与孔洞边缘距离第1次修正为s1c=sr−a。同时，根据雷达检测系统预设介电常数ε1和马尾松木材介电常数ε2[16-17]，设定介电常数修正系数为$ {k}_{1}=\dfrac{\sqrt{{{\rm{\varepsilon }}}_{1}}}{\sqrt{{{\rm{\varepsilon }}}_{2}}} $ ，则雷达检测中木材边缘与孔洞边缘距离第2次修正为s2c=(sr−a)k1。以试件S3为例，修正结果见图5。
图 5 雷达检测数据修正结果
Figure 5. Corrected results of the cavity areas in wood columns by TRU
图5A为试件S3；图5B为根据偏移量进行第1次修正后的孔洞图像；图5C为根据介电常数进行第2次修正后的孔洞图像；图5D为3次修正后的孔洞图像。为了便于分析，同样对试件S3、S4、S5、S6的雷达检测数据修正结果进行了计算和统计。从表2和图5可以看出：根据偏移量进行第1次修正后，识别精度得到一定得提升，但其与实际孔洞相比均表现为偏大，这主要是因为修正距离s1c是根据雷达检测系统预设介电常数ε1计算得来，但实际检测对象的介电常数为ε2，在气干木材的检测中预设介电常数ε1大于检测对象介电常数ε2，故而s1c距离偏小，导致孔洞识别偏大。从表2和图5也可以看出：根据介电常数进行第2次修正后，其检测修正面积与实际孔洞面积仍存在一定偏差。从图5也可以看出：无论是否修正，雷达识别孔洞形状的能力均较差，这可能是因为外部形状等因素引起了内部图像的扭曲。
表 2 雷达检测数据修正与统计
Table 2. Corrected calculation and statistics of the cavity areas in wood columns by TRU
序号 残损类型 第1次修正后孔洞百分比/% 第2次修正后孔洞百分比/% 第3次修正后孔洞百分比/% S3 圆形孔洞 30.21 6.85 13.26 S4 圆形孔洞 26.51 6.39 12.49 S5 三角形孔洞 38.03 8.70 15.30 S6 四边形孔洞 37.71 8.75 15.29 上述研究结果表明：单独依靠介电常数比值进行修正，其孔洞识别面积与实际孔洞仍存在一定偏差。为此，本研究设置了另一辅助修正系数k2，即雷达检测中木材边缘与孔洞边缘距离按照s3c=(sr−a)k1k2进行修正，其中辅助修正系数k2为常数。经过前期的研究分析和数据拟合，可初步确定常数k2取值为0.80~0.90，本研究k2取值为0.85。从表1和表2可以看出：雷达检测结果进行3次修正后，其识别精度得到明显提升，总体相对误差小于30%。
-
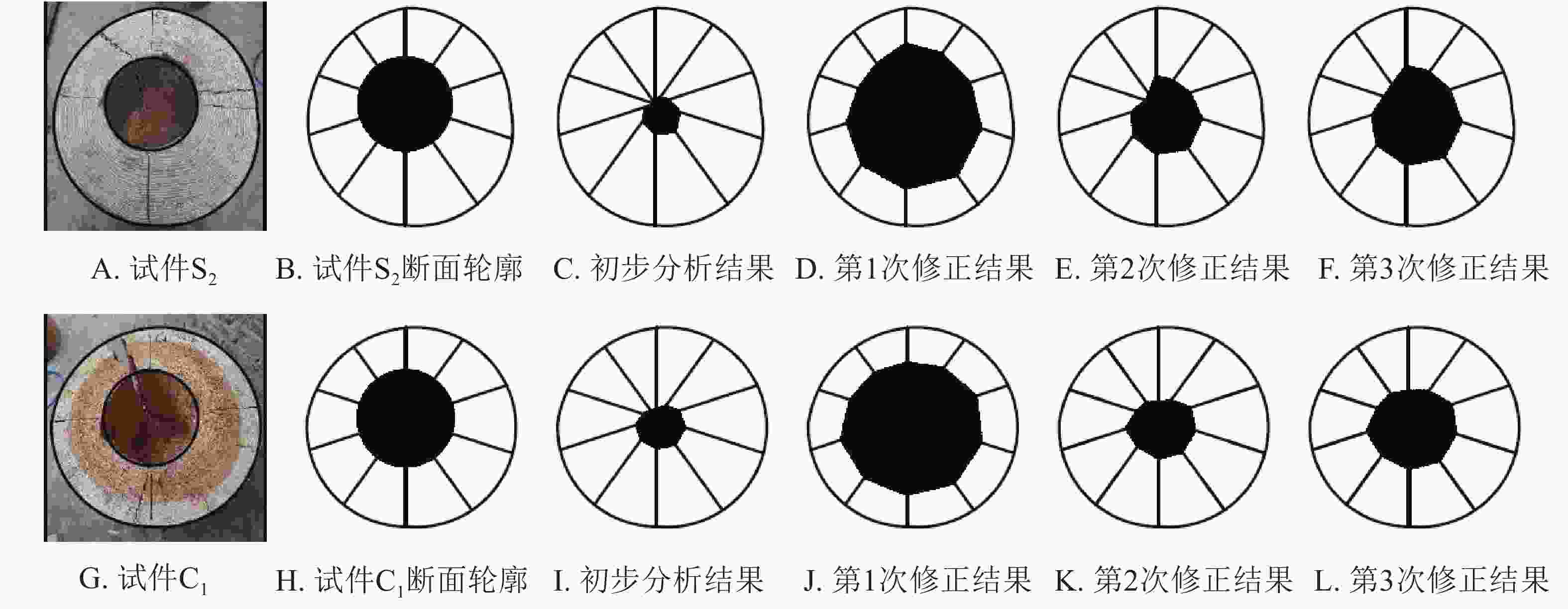
为验证上述结论，本研究选取了具有不同大小孔洞马尾松试材S2和杉木试材C1进行补充试验，并根据上述研究步骤获取其断面轮廓、雷达检测初步结果、第1次修正结果、第2次修正结果和第3次修正结果，经数据整理见图6。
图 6 雷达检测数据修正过程
Figure 6. Corrected process of the cavity areas in wood columns by TRU
从验证试验可以得出同样结论，未修正或按照一定含水率下特定树种的介电常数修正的雷达图像其预估孔洞面积与孔洞实际面积均存在一定误差，按照s3c=(sr−a)k1k2对图像进行3次修正后精度较高。3次修正后，试材S2雷达检测预估孔洞面积相对误差为9.47%，试材C1预估相对误差为28.72%，检测结果可能会因为个体差异产生一定的偏差，但大致趋势相同。
-
通过分析雷达回波图形和检测图像可以快速判定松木和杉木木材内部孔洞的存在，但其直观成像技术在定量评估方面误差较大，需进行一定的数据处理和修正。①对带孔木材进行雷达扫描，未经修正的雷达图像其预估孔洞面积小于实际孔洞面积，按介电常数进行修正的雷达图像其预估孔洞面积与实际孔洞面积仍存在一定的误差。②无论是否进行数据处理和修正，利用雷达扫描进行内部孔洞的形状预估难度较大，难以准确识别三角形、四边形、圆形等各种形状的孔洞，应开展进一步研究。③实际应用中，根据树种和含水率所得到的介电常数应进行再次修正，即实际应用中根据树种和含水率所得到的介电常数仅为多参数校正中的一个因素。④利用该雷达检测与修正方法进行木材内部孔洞探测，综合树种和含水率等参数，可确保孔洞面积的识别误差小于30%。此项技术可应用于古建筑木构件内部残损的检测评估。⑤在开展古建筑木构件内部残损的雷达检测与定量评估前，应首先调查分析木结构建筑常用的树种类型，并建立常用树种、含水率与介电常数之间的关系模型。
Calculation and correction of wood internal cavity area based on radar detection
-
摘要:
目的 开展木材内部孔洞的雷达检测研究，探讨该检测手段下孔洞成像的准度和精度，实现木材内部孔洞的雷达快速识别和定量表征。 方法 以古建筑木结构常用的马尾松Pinus massoniana木材和杉木Cunninghamia lanceolata木材为研究对象，采取人工模拟的方法在木段端部制作异型孔洞，并利用雷达扫描仪对带孔木段进行检测，比较分析直观成像技术与希尔伯特积算法、单路径数据提取合成以及成像轮廓多参数校正等处理方法之间的差异，提出基于雷达检测的木材内部孔洞面积测算与可行的修正方法。 结果 利用雷达无损检测技术可以对马尾松和杉木木材内部孔洞的存在进行快速识别，但其直观成像技术在定量评估方面误差较大，需进行相关的数据处理和修正；未经修正的雷达图像其预估孔洞面积小于实际孔洞面积，通过希尔伯特积算法演算或介电常数修正的雷达图像其预估孔洞面积与实际孔洞面积仍存在一定的误差；木材边缘与孔洞边缘的距离应按s3c=(sr－a)k1k2进行修正，即实际应用中根据树种和含水率所得到的介电常数仅为多参数校正中的一个因素；无论是否进行数据处理和修正，雷达检测难以准确识别孔洞的具体形状，应开展进一步研究。 结论 该雷达检测及修正方法应用于木材内部孔洞探测，综合树种和含水率数值，可确保孔洞面积识别误差小于30%。图6表2参17 Abstract:Objective The objective of this study is to realize the rapid recognition and quantitative characterization of the internal cavities in wood by evaluating the accuracy and precision of the cavity imaging under radar detection method. Method Pinus massoniana and Cunninghamia lanceolata, commonly used in ancient building timber structure, were taken as the research object. Artificial simulation was used to make special-shaped cavities at the end of the logs to simulate the internal damages, and then the radar scanner was used to detect the cavities. The differences between the visual imaging technology and the processing methods such as the Hilbert integral method, single path data extraction and synthesis, and the multi-parameter correction of the image contour were compared and analyzed. The calculation and feasible correction method of wood internal cavity area based on radar detection was proposed. Result The internal cavity of P. massoniana and C. lanceolata wood could be recognized rapidly by the radar nondestructive testing technology, but the visual imaging technology had a large error in quantitative evaluation, which required further relevant data processing and correction. The estimated cavity area of the unmodified radar image was smaller than that of the actual one. There was still a certain error between the actual cavity area and the estimated cavity area of the radar image calculated by Hilbert integral method or modified by dielectric constant. The distance between the wood edge and the cavity edge should be corrected according to the formula s3c=(sr−a)k1k2, that was to say, the dielectric constant obtained by tree species and moisture content in practical application was only one factor in the multi-parameter correction. Therefore, it was difficult for radar scanner to accurately recognize the specific shape of the cavity, regardless of data processing and correction, and further research should be carried out. Conclusion The radar detection and correction technology can be applied to the detection of cavities in wood and the error of cavity area identification can be less than 30% by integrating tree species and moisture content values. [Ch, 6 fig. 2 tab. 17 ref.] -
Key words:
- wood science /
- ancient building timber structure /
- cavity /
- radar /
- quantitative evaluation /
- dielectric constant
-
农业面源污染已成为全球许多国家流域水污染和水体富营养化的首要污染来源[1-2]。近年来，国内诸多流域尺度的污染源调查解析表明：中国许多河湖、水库等地表水体中的氮磷输入主要来自农田种植、畜禽水产养殖等农业生产以及农村生活所产生的非点源污染，其中种植业所引起的农田退水污染正逐步成为污染的主要贡献者[3-5]。农田退水污染具有排放时间瞬时多变，迁移途径复杂多样，污染负荷时空变化幅度大等特点，治理难度相对更大[1-2]。目前基于生态工程原理的生态沟渠、人工湿地等技术受到格外重视[6-8]。此类通常建立在培植大型水生植物基础上的生态拦截工程具有建设成本低且可控、技术难度低、生态友好等优点，近年来在中国许多地区特别是生态敏感区域得到了较大规模的推广应用。2018年以来，浙江省在全省范围内实施了300项农田面源污染氮磷生态拦截沟渠示范推广项目[9]。研究已表明：水生植物对包括氮磷营养物质在内的众多污染物的净化效率及其稳定性具有重要的影响[10-11]。沉水植物占据了根系-基质(根际)、水-基质和植物茎叶-水3个关键微界面，由其介导形成的微环境结构更为复杂，往往能够表现出更加稳定和持续的水质净化潜力[12-14]。近几年以沉水植物为先锋物种的“水下植被”技术拓展应用到农业面源污染的拦截处理[15-17]。目前，国内外对挺水植物型人工湿地去污动力学已开展了比较深入的研究[18-20]，但对“水下植被”型净化系统污染物去除动力学特征还十分欠缺，特别是对拦截净化农田退水、池塘养殖尾水等具有瞬间排放特点的非点源污染的除磷动力学研究至今还未见报道。在动力学模型应用研究方面，一级动力学、Grau二级动力学和Monod动力学因具有模型构式可线性化处理、参数求解过程简单、适用范围广等优点而被广泛采用[19-22]；近年来，修正的Gompertz模型作为一种多参数非线性模型在污染物去除动力学研究领域逐步被重视，并且已被成功应用于新型生物处理系统的工艺设计和污染物去除效率的预测[23-25]。本研究以苦草Vallisneria natans和金鱼藻Ceratophyllum demersum等2种典型沉水植物为供试材料，研究苦草型和金鱼藻型2种“水下植被”型净化系统对农田退水中磷污染的净化效率。在此基础上，采用一级动力学、Grau二级动力学、Monod 动力学和修正的Gompertz模型模拟总磷的去除过程并进行统计验证，获取相关动力学参数，进而探讨2种沉水植物净化系统除磷效率的差异，以期为“水下植被”型生态净化系统的工艺调控及其设计应用提供理论依据和技术参考。
1. 材料与方法
1.1 供试材料
选择不同生长型的沉水植物苦草和金鱼藻作为供试植物，这2种植物均为长江中下游流域常见的优势沉水植物，偏好于富营养化水体，在溪沟、河流、池塘、湖泊等水域中均有分布。2种供试植物均取自浙江农林大学乌镇大学生实践基地。采集时选取生长状态良好且株高相近的植株，运至实验基地培养10 d，统一修剪至株高25 cm，去离子水清洗干净后用作试验材料。
受降雨强度、降雨历时、施肥量、土壤类型、土地利用类型等因素影响，农田退水中总磷质量浓度波动极大，低值时可低于地表水Ⅳ类标准，而峰值时高达5.00 mg·L−1以上[26-27]。本研究人工配置中，农田退水总磷质量浓度处于相对较高水平，试验原水取自浙江农林大学平山实验基地内的池塘，原水中总磷质量浓度为 0.17 mg·L−1，铵态氮(NH3-N)质量浓度为0.39 mg·L−1，重铬酸盐指数(CODcr)为8.56 mg·L−1。经配置后的试验用水总磷质量浓度为4.17 mg·L−1。
1.2 试验方案
考虑到农田退水排放的瞬间性、间歇性等特征以及池塘、相对封闭河道等受纳水体的水动力特点，本研究采用批式试验考察2种供试植物净化系统对农田退水总磷的去除效果及其动力学特征。试验共设置3组，分别为苦草组、金鱼藻组和无植物对照组，每组均重复3次。试验于浙江农林大学平山实验基地温室大棚内进行，试验装置采用白色聚乙烯塑料箱(长×宽×高为40 cm×80 cm×60 cm)，各塑料箱内注入试验用水，试验水深50 cm，计为160 L。每个塑料箱底部铺设1层厚度为10 cm的火山石基质(过10目筛)。为避免植物直接定植在基质上导致基质分布不均，先将经预培养的供试植物(鲜质量300 g)定植于渗排水网垫网上(厚度为5 mm)，然后再铺设于基质层上。
试验周期共计49 d (2018年7—8月)，试验期间平均最高气温为34.0 ℃，平均最低气温为25.0 ℃，隔1周采样1次。采用虹吸管抽取方式采集水样，分别于水面以下15和25 cm处采集等体积水样组成混合样(100 mL)。每次取样后添加去离子水以弥补蒸发、蒸腾以及取样所带来的水损耗。水样及试验用水总磷采用过硫酸钾氧化-钼锑抗分光光度法测定。
1.3 总磷去除负荷及动力学方法
分别利用一级动力学[20]、Grau二级动力学[18]、Monod动力学[20]和修正的Gompertz模型[28]对批式试验数据进行拟合分析。
1.3.1 总磷去除负荷
总磷去除负荷表达式为：
$$ \sum\limits_{t = 0}^t {C'} = \frac{{\left( {{C_0} - {C_t}} \right)V}}{{L W}}{\text{。}} $$ (1) 式(1)中：t为反应时间(d)；C0为总磷初始质量浓度(mg·L−1)；Ct为反应时间t时的总磷质量浓度(mg·L−1)；C′为总磷累计去除负荷(mg·m−2)；V为试验用水体积(L)；L为试验装置长度(m)；W为试验装置宽度(m)。
1.3.2 一级动力学
一级动力学模型通用表达式在边界条件下积分处理为：
$$\ln \left( {\frac{{{C_0}}}{{{C_t}}}} \right) = {F_{\rm{a}}}t{\text{。}}$$ (2) 式(2)中：Fa为总磷一级动力学速率常数(d−1)。
1.3.3 Grau二级动力学
Grau二级动力学通用表达式边界条件下积分并线性化处理为：
$$\frac{{{C_0}t}}{{{C_0} - {C_t}}} = t + \frac{{{C_0}}}{{{S_{\rm{a}}}X}}{\text{。}}$$ (3) 令：m=C0/SaX，则式(3)可整理成：
$$\frac{{{C_0}t}}{{{C_0} - {C_t}}} = m + nt{\text{。}}$$ (4) 式(4)中：m和n为Grau二级动力学常数。其中：n为接近1的无量纲常数；m代表总磷去除效率(d)，其值越大，去除效率越低。
1.3.4 Monod动力学
Monod动力学通用表达式经积分和线性化处理为：
$${C_0} - {C_t} + {C_{\rm{h}}}\ln \frac{{{C_0}}}{{{C_t}}} = {M_{\max }}t{\text{。}}$$ (5) 式(5)中：Mmax为Monod动力学总磷最大体积去除速率常数(mg·m−3·d−1)；Ch为Monod动力学总磷半饱和速率常数(mg·L−1)，取0.2 mg·L−1[22]。
1.3.5 修正的Gompertz模型
Gompertz模型经修正可用于描述污染物质量浓度与处理时间的定量关系。表达式为[28]：
$${C_t} = {C_0} - {C_0}\exp \left\{ { - \exp \left[ {\frac{{{\rm{e}} {G_{{\rm{max}}}}}}{{{C_0}}}\left( {{t_{\rm{a}}} - t} \right) + 1} \right]} \right\}{\text{。}}$$ (6) 式(6)可转化为：
$$R_{\rm{E}} = 100 \times \exp \left\{ { - \exp \left[ {\frac{{{\rm{e}} {G_{{\rm{max}}}}}}{{{C_0}}}\left( {{t_{\rm{a}}} - t} \right) + 1} \right]} \right\}{\text{。}}$$ (7) 式(7)中：RE为总磷去除率(%)；Gmax为Gompertz模型总磷最大体积去除速率常数(mg·m−3·d−1)；ta为迟滞时间(d)；e为数学常数。
1.4 数据统计与分析
采用Excel和SPSS进行数据统计与分析(显著水平设为P＜0.05)，采用Origin 9.1软件进行模型创建、拟合和图形绘制。图表中所列数据均为3个重复的平均值。引入判定系数(R2)和相对均方根误差(RRMSE)评价动力学模型的准确性和适用性。其中：R2反映2组数据线性回归拟合优度，该值接近于1(取值为0~1)表明两者之间高度线性相关；RRMSE反映模型预测值与试验实测值之间的整体偏差，RRMSE越小(取值为0~∞)，表明预测值与实测值间越接近。各统计参数计算公式为：
$${R^2} = \frac{{\displaystyle \sum\limits_{i = 1}^N {{{\left[ {\left( {{X_i} - \overline X} \right)\left( {{Y_i} - \overline Y} \right)} \right]}^2}} }}{{\displaystyle \sum\limits_{i = 1}^N {{{\left( {{X_i} - \overline X} \right)}^2}} \displaystyle \sum\limits_{i = 1}^N {{{\left( {{Y_i} - \overline Y} \right)}^2}} }};$$ (8) $$R_{\rm{RMSE}} = \frac{{\sqrt {\dfrac{1}{N}\displaystyle \sum\limits_{i = 1}^N {{{\left( {{Y_i} - {{\hat Y}_i}} \right)}^2}} } }}{{\overline Y}}{\text{。}}$$ (9) 式(8)~(9)中：Xi和Yi分别为2组数据(反应时间和试验实测值)，
$\overline X$ 和$\overline Y$ 分别为2组数据的平均值；${\hat Y_i}$ 为动力学模型预测值；N为样本数。2. 结果与分析
2.1 总磷去除效率的时间变化
随着处理时间的延长，2组植物净化系统总磷累计去除负荷呈逐渐增加趋势(图1)。至试验结束时(第49 天)，苦草组和金鱼藻组净化系统的累计去除负荷分别为1 151.17和1 167.50 mg·m−2，对应总磷去除率分别为82.8%和84.0%。方差分析表明：试验结束时2组植物系统总磷去除效率无显著差异(P＞0.05)，但均显著好于无植物的对照组(P＜0.05)。进一步对各周总磷去除负荷分析发现(图2)：2组植物系统各周之间的总磷去除负荷均存在较大波动，并且均在第3周出现峰值，单周贡献了整个试验期间(共7周)总磷累计去负荷的28.5%(苦草组)和16.7%(金鱼藻组)。无植物的对照组总磷去除负荷在第1周出现峰值。
图 1 沉水植物净化系统总磷累计去除负荷随处理时间的变化Figure 1 Total phosphorus removal loading over treatment time in the submerged plant treatment systems
图 2 沉水植物净化系统各周总磷去除负荷Figure 2 Total phosphorus weekly removal loading for the submerged plant treatment systems在不同时间尺度上比较2组植物净化系统总磷去除效率发现(图1)：尽管在试验结束时(第49 天)和试验中期(第21 天和第28 天)两者差异不显著，但在试验初期(第7 天和第14 天)和中后期(第35 天和第42 天)2组植物净化系统总磷去除效率存在差异显著(P＜0.05)。其中试验初期，金鱼藻组净化系统总磷去除效率显著高于苦草组净化系统；而当处理时间增至35和42 d时，苦草组又显著高于金鱼藻组。这种不同沉水植物系统除磷效率的差异在不同时间尺度上出现偏离甚至逆转的现象可能具有一定的普通性，如文献[29]、文献[30]和文献[31]的研究中均存在这种现象。值得注意的是，忽视植物效应差异的不确性，可能会导致水生植物净化系统工艺优化，特别是水生植物的筛选结果出现偏离甚至失真，因此，有必要借助污染物去除动力学模拟分析获取用于指示和预测污染物去除效率的相关特征参数。
2.2 一级动力学和Grau二级动力学模拟与验证
分别运用一级动力学[公式(2)]和Grau二级动力学[公式(4)]模型对2组沉水植物净化系统试验数据进行拟合，并进行模型统计验证分析，结果见图3和表1。一级动力学模型具有较高的拟合度(判定系数R2＞0.930)，模型预测值与实测值之间吻合程度较好(相对均方根误差RRMSE＜0.200)，表明一级动力学模型可用来描述沉水植物净化系统批式运行周期内总磷的去除过程。2组净化系统回归求得的总磷去除一级动力学常数(Fa)分别为0.039 d−1(苦草组)和0.035 d−1(金鱼藻组)。不同于一级动力学，Grau二级动力学模型拟合度较差(R2＜0.600)，表明该模型不适用于模拟本试验沉水植物净化系统总磷的去除过程，获取的动力学参数(n和m)也不具有现实意义。
图 3 2种沉水植物净化系统总磷去除一级动力学模型拟合曲线Figure 3 Regression of first-order kinetic model for TP removal over time in the submerged plant treatment systems表 1 2种沉水植物净化系统总磷去除一级动力学和Grau二级动力学拟合结果Table 1 Fitting result of First-order and Grau second-order kinetic models for total phosphorus removal in the submerged plant treatment systems沉水植物型生态净化系统 一级动力学模型 Grau二级动力学模型 Fa/d−1 R2 RRMSE m/d n R2 RRMSE 苦草组 0.039 0.931 0.196 109.90 −1.35 0.588 0.324 金鱼藻组 0.035 0.937 0.169 57.25 0.03 0.081 0.127 一级动力学模型已被广泛应用于挺水植物型人工湿地系统中有机物、营养物、悬浮物等污染物去除效果的预测[19-22]，但该模型是否适用于模拟沉水植物型净化系统的污染物去除动力学至今还未得到证实。本研究发现：一级动力学模型可用于描述沉水植物型净化系统在批式模式下的总磷去除过程。
一级动力学常数(Fa)代表着反应器系统在相对稳定运行状态下的去污能力，该参数不仅可用于反应器放大设计所需有效体积或面积的测算，还可以用于处理系统的工艺调控和比较优化。如在同等污染物质量浓度水平下，Fa越大，达到同一出水质量浓度所需的处理时间越短，即污染物的去除效率越高。方差分析结果表明：2组沉水植物系统的总磷去除一级动力学常数Fa存在显著差异(P＜0.05)，说明植物种类对总磷的净化效率产生显著影响。基于Fa及其物理意义可知：试验条件下苦草组净化系统的总磷去除效率显著好于金鱼藻组净化系统。
2.3 Monod动力学模拟与验证
图4为Monod动力学模型f(C0, Ct, Ch)与净化处理时间(t)之间的回归曲线，表2列出了由回归系数求得的总磷最大体积去除速率常数(Mmax)以及统计验证参数。结果表明：Monod动力学模型可以较好地拟合2组沉水植物系统总磷的去除过程(R2＞0.970，RRMSE＜0.110)。2组植物系统拟合得到的总磷最大体积去除速率分别为87.14 mg·m−3·d−1(苦草组)和78.15 mg·m−3·d−1(金鱼藻组)，并且差异达到显著性水平(P＜0.05)。
图 4 2种沉水植物净化系统总磷去除Monod动力学拟合曲线Figure 4 Regression of Monod kinetic model for total phosphorus removal over time in the submerged plant treatment systems表 2 2种沉水植物净化系统总磷去除Monod动力学和修正的Gompertz模型拟合结果Table 2 Fitting result of Monod kinetic and modified Gompertz model for total phosphorus removal in the submerged plant treatment systems沉水植物型生态净化系统 Monod动力学模型 修正的Gompertz模型 Mmax/(mg·m−3·d−1) R2 RRMSE Gmax/(mg·m−3·d−1) ta/d R2 RRMSE 苦草组 87.14 a 0.974 0.108 107.96 a 8.70 a 0.991 0.062 金鱼藻组 78.15 b 0.999 0.020 84.82 b 3.37 b 0.992 0.041 说明：不同字母表示差异显著(P＜0.05) Monod动力学模型表征了污染物去除速率与其质量浓度之间的关系由一级向零级反应过渡的状态，因而可以避免单纯使用一级动力学模型时可能造成的设施尺寸过大问题。作为一种在经典的米-门方程基础上建立起来的半经验模型，Monod动力学模型起初主要用于辅助活性污泥法、生物接触氧化法等污水生物处理工程设计。近年来Monod动力学模型越来越多地被应用于挺水植物型人工湿地系统有机物和氮素污染物去除能力的预测[19-22]。本研究证实：Monod动力学模型可用于沉水植物型净化系统批式运行模式下总磷去除过程的模拟及其去除效果的预测 (表2)。
2.4 修正的Gompertz模型模拟与验证
自FAN等[28]于2004年首次对Gompertz模型进行修正，并将其用于描述好氧生化处理过程中邻苯二甲酸降解动力学特征以来，这种可以同时输出用于指示污染物去除效率和初始延迟时间的多参数模型越来越多地应用于厌氧反应器、好氧反应器等工艺系统污染物去除过程的模拟[23-25]。本研究采用修正的Gompertz模型[公式(7)]对2组沉水植物型净化系统总磷去除过程进行非线性拟合，结果见图5和表2。
图 5 2种沉水植物净化系统总磷去除Gompertz模型动力学拟合曲线Figure 5 Regression of modified Gompertz model for total phosphorus removal over time in the submerged plant treatment systems结合图5和表2可以看出：修正的Gompertz模型可以很好地拟合本试验条件下沉水植物净化系统总磷去除效率与处理时间之间的关系(R2＞0.990，RRMSE＜0.110)。2组植物净化系统拟合获得的总磷最大体积去除速率和除磷延迟时间均有所不同(P＜0.05)，其中苦草组净化系统总磷最大体积去除速率为107.96 mg·m−3·d−1，显著高于金鱼藻组净化系统(84.82 mg·m−3·d−1) (P＜0.05)，表明苦草组净化系统总磷去除效率显著高于金鱼藻组净化系统。但苦草组净化系统拟合获得的除磷延迟时间(8.70 d)显著长于金鱼藻组净化系统(3.37 d)，表明苦草型沉水植物净化系统相较于金鱼藻型需要更长的生境适应周期。
3. 讨论
3.1 动力学模型的比较
污染物去除动力学是指导工程设计的重要基础。许多动力学模型已用于模拟污水生物处理和人工湿地系统污染物的去除过程，其中一级动力学、Grau二级动力学和Monod 动力学模型简化了污染物去除过程中所涉及的生物、化学、物理及其相互影响等复杂过程，模型构式可线性化处理而使得参数求解十分简单，拟合求得的动力学参数又可以较好地代表处理系统污染物的去除能力。这些有利因素促使此类模型越来越多地应用到包括水平潜流[32]、垂直流[33]、潮汐流[34]、静止状态[35]及其组合工艺[19]等多种人工湿地系统中污染物的去除动力学特征的研究。但近年来研究发现：此类建立在众多假定条件基础上的表观动力学模型的适用性，不仅与湿地工艺类型(水平潜流和垂直流)及其水动力模式(推流或完全混合态)有关，还与所描述的污染物类型有关[19-20]。本研究结果表明：一级动力学和Monod 动力学模型均可以用来描述沉水植物型净化系统批式试验周期内的总磷去除过程，而Grau二级动力学却不适用；相较于一级动力学，Monod 动力学模型具有更高的拟合优度。
近年来，修正的Gompertz模型作为一种多参数非线性模型，在污染物去除动力学研究领域逐步被重视。众多研究已发现：这种非线性预测模型描述异养硝化菌、厌氧氨氧化等新型好氧或厌氧生物处理系统的脱氮除磷效果具有较好的拟合精确度[23-25]。但该模型能否用于模拟人工湿地、植物塘等生态处理系统中污染物的去除过程至今还未见报道。本研究发现：修正的Gompertz模型可以很好地模拟沉水植物净化系统总磷的去除动力学过程。相较于一级动力学和Monod动力学模型，修正的Gompertz模型的拟合除了可以输出代表着污染物去除能力的关键性能参数(如最大体积去除速率)，还可以输出可用于指示前期阶段污染物去除的迟缓时间。这些参数的获取有助于对污染物去除机制的理解，也可用于协助工艺系统的优化设计和过程调控。
3.2 沉水植物种类对总磷去除效率的影响
本研究发现：2组植物系统总磷去除效率的差异在时间尺度上存在明显的不确定性；这种不同种类植物净化效率的差异，在时间尺度上出现偏离甚至逆转的现象极有可能普遍存在。如李琳等[31]针对不同种类沉水植物氮磷净化效率的对比研究发现：当处理时间为7和21 d时金鱼藻组总磷净化效率显著好于苦草组(P＜0.05)，但持续处理至第35 天时，两者总磷的净化效率无显著差异。究其原因，一方面可能是由于不同种类的沉水植物对磷的吸收量存在时间变异，但更为重要的原因可能是不同植物所介导的间接增效作用也存在时间尺度上的差异。
众多研究已表明：在由沉水植物、基质(自然沉积物或人工填料)、微生物和水体四大基本要素构成的水生态系统或由其衍生而来的“水下植被”型生态拦截净化系统中，沉水植物、基质和微生物以及三者相互之间通过一系列物理(沉积、挥发等)、化学(基质吸附、沉淀等)和生物(动植物吸收、微生物降解转化等)作用，实现对污染物的有效去除，其中沉水植物的作用被证实是磷去除的主要机制[6, 30]。一直以来，植物的直接吸收作用被认为是“水下植被”净化系统除磷的主要途径，但近年来越来越多的证据显示：因沉水植物所介导的间接增效作用(如根际效应、茎叶生物膜效应等)对总磷去除的贡献强度远超过植物的直接吸收作用，并且该作用途径对总磷去除的贡献强度也与植物的种类密切相关[30-31]。这种尚未引起重视的现象给水生植物的筛选带来了不确定性，有必要借助诸如动力学模型分析等手段加以分析。本研究通过动力学分析发现：2组沉水植物系统总磷去除一级动力学速率常数Fa、Monod动力学速率常数Mmax以及修正的Gompertz模型拟合常数Gmax均存在显著差异，并且一致地表现为苦草组指标大于金鱼藻组指标。据此可以推断，苦草型净化系统对总磷的去除效率好于金鱼藻型。
4. 结论
苦草型和金鱼藻型2种植物净化系统总磷去除效率无显著差异，总磷去除率分别为82.8%和84.0%，但两者总磷去除效率在不同时间尺度上的差异存在不确定性。4种动力学模型模拟与验证结果表明：除Grau二级动力学外，一级动力学、Monod 动力学模型和修正的Gompertz模型均可以有效描述2种沉水植物型净化系统试验条件下总磷的去除过程，其中Monod动力学和Gompertz模型的模拟具有更高的拟合优度，模型预测值与实测值之间吻合程度更好。3种有效模型拟合获得的动力学常数在植物种类之间均存在显著差异(P＜0.05)，其中指示除磷效率的动力学速率常数一致表现为苦草组大于金鱼藻组，表明苦草型净化系统对总磷的去除效率好于金鱼藻型。但苦草组除磷延迟时间显著长于鱼藻组(P＜0.05)，表明其生境适应周期相对较长。
-
图 2 雷达成像直观结果
Figure 2 Intuitionistic results of the cavity areas in wood columns by TRU
图 3 希尔伯特积算法演算结果
Figure 3 Analysis results of the cavity areas in wood columns by Hilbert
图 4 雷达检测初步分析结果
Figure 4 Preliminary results of the cavity areas in wood columns by TRU
表 1 雷达检测初步测算与统计
Table 1. Preliminary calculation and statistics of the cavity areas in wood columns by TRU
序号 孔洞类型 实际孔洞百分比/% 雷达测算孔洞百分比/% S3 圆形孔洞 14.67 2.15 S4 圆形孔洞 9.66 0.84 S5 三角形孔洞 12.82 1.59 S6 四边形孔洞 20.26 2.53 
下载: 导出CSV
表 2 雷达检测数据修正与统计
Table 2. Corrected calculation and statistics of the cavity areas in wood columns by TRU
序号 残损类型 第1次修正后孔洞百分比/% 第2次修正后孔洞百分比/% 第3次修正后孔洞百分比/% S3 圆形孔洞 30.21 6.85 13.26 S4 圆形孔洞 26.51 6.39 12.49 S5 三角形孔洞 38.03 8.70 15.30 S6 四边形孔洞 37.71 8.75 15.29
下载: 导出CSV
-
[1] RAZAFINDRATSIMA S, SBARTAI Z M, FRANCOIS D. Permittivity measurement of wood material over a wide range of moisture content [J]. Wood Sci Technol, 2017, 51(6): 1421 − 1431. [2] MAI T C, RAZAFINDRATSIMA S, SBARTAI Z M, et al. Non-destructive evaluation of moisture content of wood material at GPR frequency [J]. Constr Build Mater, 2015, 77: 213 − 217. [3] 吕静霞. 基于雷达波的木材内部缺陷检测方法研究[D]. 北京: 北京林业大学, 2015. LÜ Jingxia. Research on Wood Internal Defects Detection Method Based on the Radar Wave[D]. Beijing: Beijing Forestry University, 2015. [4] HANS G, REDMAN D, LEBLON B, et al. Determination of log moisture content using early-time GPR signal [J]. Wood Mater Sci Eng, 2015, 10(1): 112 − 129. [5] LORENZO C H, PÉREZ G M de la V, NOVO A, et al. Forestry applications of ground-penetrating radar [J]. For Syst, 2010, 19(1): 5 − 17. [6] 邸向辉, 王立海. 探地雷达(GPR)在木材无损检测应用中的可行性探讨[J]. 无损检测, 2013, 35(11): 51 − 54. DI Xianghui, WANG Lihai. Study on the feasibility about GPR applied on wood nondestructive testing [J]. Nondestr Test, 2013, 35(11): 51 − 54. [7] JEZOVA J, MERTENS L, LAMBOT S. Ground-penetrating radar for observing tree trunks and other cylindrical objects [J]. Constr Build Mater, 2016, 123: 214 − 225. [8] WU Xi, LI Guanghui, JIAO Zhi, et al. Reliability of acoustic tomography and ground-penetrating radar for tree decay detection[J]. Appl Plant Sci, 2018, 6(10): e1187. doi: 10.1002/aps3.1187. [9] DEVARU D, HALABE U B, GOPALAKRISHNAN B, et al. Algorithm for detecting defects in wooden logs using ground penetrating radar [J]. Proc SPIE- Int Socr Opt Eng, 2005, 5999: 110 − 121. [10] BUTNOR J R, PRUYN M L, SHAW D C, et al. Detecting defects in conifers with ground penetrating radar: applications and challenges [J]. For Pathol, 2009, 39(5): 309 − 322. [11] 李伟林, 文剑, 肖中亮, 等. 颐和园古树内部异常的雷达波检测[J]. 福建农林大学学报(自然科学版), 2017, 46(6): 665 − 670. LI Weilin, WEN Jian, XIAO Zhongliang, et al. Detection of internal anomaly for trees in the Summer Palace based on radar [J]. J Fujian Agric For Univ Nat Sci Ed, 2017, 46(6): 665 − 670. [12] 肖夏阳, 文剑, 肖中亮, 等. 基于雷达波的树木躯干内部缺陷探测识别[J]. 林业科学, 2018, 54(5): 127 − 134. XIAO Xiayang, WEN Jian, XIAO Zhongliang, et al. Detection and recognition of tree trunk internal structure based on radar [J]. Sci Silv Sin, 2018, 54(5): 127 − 134. [13] 陈勇平, 高甜, 李德山, 等. 马尾松木材内部空洞的雷达检测与定量评估[J]. 林业科学, 2017, 53(10): 139 − 145. CHEN Yongping, GAO Tian, LI Deshan, et al. Detection and quantitative evaluation of internal cavity of Pinus massoniana wood by radar testing technology [J]. Sci Silv Sin, 2017, 53(10): 139 − 145. [14] 文剑, 李伟林, 肖中亮, 等. 活立木内部缺陷雷达波检测研究[J]. 农业机械学报, 2017, 48(10): 185 − 193. WEN Jian, LI Weilin, XIAO Zhongliang, et al. Radar wave detection of standing treesinternal defect [J]. Trans Chin Soc Agric Mach, 2017, 48(10): 185 − 193. [15] 郭秀军, 王淼, 张刚, 等. 高频电磁波传播速度在水及淤积砂土中影响因素实验研究[J]. 地球物理学进展, 2010, 25(5): 1820 − 1824. GUO Xiujun, WANG Miao, ZHANG Gang, et al. Research on influence factors of GPR wave velocity in water and sandy soil in laboratory [J]. Prog Geophys, 2010, 25(5): 1820 − 1824. [16] 吴晔. 木材介电常数的研究[J]. 安徽农学院学报, 1989, 16(1): 59 − 74. WU Ye. Study on the dielectric constant of wood [J]. J Anhui Agric Univ, 1989, 16(1): 59 − 74. [17] 季亚春, 季亚坤. 木材介电常数的测量[J]. 黑龙江电子技术, 1997(5): 24 − 28. JI Yachun, JI Yakun. Measurement of wood dielectric constant [J]. Heilongjiang Electron Tech, 1997(5): 24 − 28. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20190709
点击查看大图
计量
- 文章访问数: 1087
- HTML全文浏览量: 294
- PDF下载量: 32
- 被引次数: 0
