下载:
-
森林蓄积量是一定森林面积上所有活立木材积的总和[1]。作为森林生物量和碳储量的重要评价指标，森林蓄积量能直接反映森林资源的数量与质量，是森林资源调查的重要因子之一。随着无人机遥感技术的快速发展，无人机载可见光/多光谱遥感影像在森林资源调查领域得以快速推广，为森林蓄积量调查提供了快速高效的技术手段。传统的森林蓄积量调查主要以地面调查为主，此类调查周期长，对人力、物力的需求量巨大[2]。20世纪90年代以来，国内外学者通过获取单一或多源遥感影像，以地面调查数据作为因变量，以各类植被指数、纹理特征、地形因子等作为自变量，采用主成分分析、偏最小二乘法、逐步回归、随机森林、k邻近模型等方法建立回归模型，估测森林蓄积量，进行了较多有益的探索[3−5]。卫星遥感影像具有长时序、大尺度、易获取等优势，但其影像易受天气影响，且难以兼顾分辨率和成本。无人机具有成本低、机动灵活、影像分辨率高等优点，作为传统遥感估测的补充手段，在森林资源调查中得到了广泛应用。通过搭载可见光、多光谱、高光谱、激光雷达等多种传感器，可获得低空地表有关森林资源的多层面数据[6]。大量研究表明：基于无人机航拍影像估测森林蓄积量具有较高的可行性。利用无人机航拍影像估测森林蓄积量主要包括2个角度：① 基于数字正射影像(DOM)、数字表面模型(DSM)、冠层高度模型(CHM)获取林分株数、胸径、冠幅、树高等因子，从单木、林分2个角度进行蓄积量估测[7−12]；② 基于影像提取各类植被指数、纹理特征、地形因子等，建立森林蓄积量估测模型，或是建立单株材积估测模型，再进一步计算森林蓄积量[13−14]。
无人机多光谱影像较可见光影像具有更丰富的光谱信息，可计算对森林蓄积量敏感的各类植被指数，已被广泛用于植被参数信息的提取研究，在未来森林蓄积量估测研究中具有较大的潜力[14]。现有研究大多以无人机获取的可见光影像为基础，对无人机载多光谱影像的尝试相对较少。本研究基于大疆精灵4多光谱版无人机拍摄的多光谱影像，在不进行影像分割的情景下，提取研究区单波段反射率、各类植被指数、纹理特征等因子，计算标准地范围内的均值，建立云南松Pinus yunnanensis林蓄积量估测模型，分析其在森林蓄积量估测建模中的可行性和适用性，旨在为今后森林蓄积量的遥感估算研究提供有益的方法参考。
-
研究区位于云南省昆明市富民县罗免乡(25°16′21″~25°25′26″N，102°20′46″~102°29′14″E)。该地区属天然云南松林分布的典型区域，地势西南、西北高，东南低。属于低纬度亚热带高原季风气候区，四季温差小，干湿季分明，年平均气温为15.8 ℃，年平均降水量为847.0 mm，研究区内以典型的天然云南松纯林为主。
-
于2022年10月在研究区内选取能充分代表林分总体特征平均水平的地块，设置大小为25 m×25 m的标准地，共63个。对标准地内胸径≥5.0 cm的所有活立木进行每木定位，并测量胸径、树高、最长冠幅、最短冠幅。标准地林分因子见表1。根据实测的胸径、树高，利用二元立木材积公式计算单木材积，在此基础上计算标准地的蓄积量。云南松林二元立木材积公式：
表 1 标准地林分因子汇总
Table 1. Summary of stand factors in sample plots
项目 蓄积量/
(m3·hm−2)株数 平均胸
径/cm平均树
高/m郁闭度 最小值 7.90 2 12.8 5.0 0.21 最大值 79.49 42 32.6 14.7 0.79 平均值 41.97 14 21.9 8.4 0.45 $$ V=0.000\;058\;290\;117\;5{\times D}^{1.979\;634\;4}\times {H}^{0.907\;151\;55}\mathrm{。} $$ 其中：V为材积(m3)；D为胸径(cm)；H为树高(m)。
-
大疆精灵4多光谱无人机作为多光谱影像采集平台，集成了1个可见光相机和5个多光谱相机[包括红光(B1)、绿光(B2)、蓝光(B3)、红边(B4)和近红外(B5)波段]。于2022年11月14日利用大疆精灵4多光谱无人机，采用DJI GS PRO地面站软件从各标准地获取多光谱影像数据。飞行高度设置为100 m，航向和旁向重叠率均设置为85%。利用DJI Terra软件对原始图像进行预处理，生成数字正射影像(DOM)和数字表面模型(DSM)。将5个单波段的合成图像在ArcGIS中合成为多光谱影像(影像分辨率为5.3 cm)，计算所需的各类特征变量。
-
植被指数是指多光谱遥感数据经过线性或非线性数学运算，产生能反映植被生长状况的数值，已广泛用于森林蓄积量建模反演[15]。提取多光谱影像中红光、绿光、蓝光、红边、近红外等5个波段的反射率(b1、b2、b3、b4、b5)，计算蓄积量估测中常用的植被指数：归一化植被指数(NDVI)，比值植被指数(RVI)，差值植被指数(DVI)，大气抗阻植被指数(ARVI)，以及根据可见光波段计算的植被指数：过绿指数(EXG)[16]，绿蓝比值指数(GBRI)[17]，绿红比值指数(GRRI)[18]，归一化绿蓝差异指数(NGBDI)[19]，归一化绿红差异指数(NGRDI)[20]，可见光波段差异植被指数(VDVI)[21]等10个植被指数。
-
在蓄积量估测中加入纹理特征有助于提高蓄积量的估算精度[22−24]。为避免影像高频空间信息的丢失，选择较小的3×3窗口提取纹理特征[25]。借助ENVI 5.3的纹理提取工具，在3×3窗口下，通过灰度共生矩阵提取纹理特征，主要包括方差(VA)，均值(ME)，协同性(HO)，熵(EN)，对比度(CO)，二阶矩(SM)，相异性(DI)和相关性(CC)[14]。5个波段共40个纹理特征。
-
由于标准地为方形标准地，且部分样地郁闭度较低，所以以标准地中的某一点提取各特征变量值不能充分反映标准地特征。本研究以标准地边界为矢量区域，借助ArcGIS的分区统计工具计算标准地范围内各特征变量的平均值作为自变量，建立蓄积量估测模型[26]。可用于建立蓄积量估测模型的因子会随着研究区、数据源、成像时间等的差异而不同，在建立模型之前对蓄积量与各特征变量进行Pearson相关性分析，筛选与蓄积量相关性较高的特征变量构建模型。
-
根据相关性分析的结果，选择在0.01水平与蓄积量极显著相关的特征变量为自变量，按照7∶3比例随机划分训练集和测试集，采用多元线性回归(MLR)、支持向量机(SVR)、随机森林(RF)等3种回归方法建立蓄积量估测模型。
-
利用决定系数(R2)、均方根误差(ERMS)、平均绝对误差(EMA)、平均相对误差(EMR)进行精度评价[26]。
-
将单波段反射率、植被指数、纹理特征与蓄积量进行相关分析(表2)，5个波段反射率中，蓄积量与b1、b2无显著相关性，与b3呈极显著负相关(P＜0.01)，与b4、b5呈极显著正相关(P＜0.01)。
表 2 蓄积量与单波段反射率、植被指数的相关性
Table 2. Correlation between forest volume and single band reflectance and vegetation indexes
植被指数 相关性 植被指数 相关性 单波段反射率 相关性 RVI 0.533** ARVI 0.548** b1 −0.126 NDVI 0.463** GBRI 0.341** b 2 −0.194 DVI 0.541** GRRI 0.541** b 3 −0.333** VDVI 0.532** NGRDI −0.117 b 4 0.342** EXG 0.508** NGBDI 0.310* b 5 0.381** 说明：b1、b2、b3、b4、b5分别为红光、绿光、蓝光、红边、近红外反射率；**表示在0.01 (双侧)水平上极显著相关，*表示在0.05 (双侧)水平上显著相关。 在植被指数中，NGRDI与蓄积量不相关，NGBDI与蓄积量呈显著正相关(P＜0.05)外，其余植被指数均与蓄积量呈极显著正相关(P＜0.01)。
如表3所示：在8个纹理特征中，HO、EN与蓄积量的相关性较高，VA、CO、DI次之，CC、SM、ME与蓄积量的相关性较低。比较5个波段提取的纹理特征，与蓄积量显著相关的纹理特征数由大到小依次为B5、B4、B1、B2、B3。
表 3 蓄积量与纹理特征的相关性
Table 3. Correlation between forest volume and texture factors
波段 CO CC DI EN HO ME SM VA B1 0.115 −0.139 0.165 0.362** −0.381** −0.380** −0.253* 0.088 B2 0.297* −0.053 0.257* 0.428** −0.499** −0.189 −0.213 0.306* B3 0.092 0.201 0.113 0.337** −0.173 −0.239 −0.115 0.111 B4 0.413** −0.123 0.405** 0.189 −0.507** 0.067 −0.218 0.392** B5 0.408** −0.210 0.395** 0.409** −0.499** 0.129 −0.186 0.390** 说明：B1、B2、B3、B4、B5分别为红光、绿光、蓝光、红边、近红外波段；**表示在0.01 (双侧)水平上极显著相关，*表示在0.05 (双侧)水平上显著相关。0.115表示红光波段(B1)提取的对比度(CO)与蓄积量的相关系数，其余值同理。 根据相关性分析结果，筛选出26个在0.01水平与蓄积量显著相关的因子，分别为单波段反射率b3、b4、b5，植被指数RVI、NDVI、DVI、VDVI、EXG、ARVI、GBRI、GRRI，纹理特征B1-EN、B1-HO、B1-ME、B2-EN、B2-HO、B3-EN、B4-CO、B4-DI、B4-HO、B4-VA、B5-CO、B5-DI、B5-EN、B5-HO、B5-VA。
-
传统的线性回归模型易受自变量间共线性的影响，利用主成分分析可将原始的多个变量转化为少数主成分因子，每个主成分之间相互独立，克服自变量间的多重共线性的同时保留了原始变量的绝大部分信息[3−4]。根据特征根和累计方差解释率确定主成分个数(表4)。当主成分个数为4个时，累计方差解释率达93.66%，因此确定主成分为C1、C2、C3、C4。
表 4 主成分分析结果
Table 4. Principal component analysis
主成分 特征根 方差解释率/% 累积方差解释率/% C1 14.80 56.92 56.92 C2 4.66 17.91 74.83 C3 3.24 12.45 87.29 C4 1.66 6.38 93.66 提取的4个主成分因子与原始变量的线性关系如表5，利用提取出的4个主成分因子建立多元线性回归模型：$M=41.569+11.949C_{1}-2.162C_{2}+ 2.020C_{3}- 2.706C_{4} $。其中：M为蓄积量(m3·hm−2)；C1、C2、C3、C4为主成分分析提取的主成分因子。
表 5 主成分与原始变量的线性关系
Table 5. Linear relationship between principal components and original variables
原始变量 C1 C2 C3 C4 原始变量 C1 C2 C3 C4 RVI 0.050 0.088 0.149 −0.064 B1-ME −0.030 −0.112 −0.134 0.296 NDVI 0.044 −0.029 0.000 0.052 B2-EN 0.048 −0.125 0.037 −0.187 DVI 0.051 0.009 0.189 0.108 B2-HO −0.055 0.111 0.003 0.142 VDVI 0.057 0.092 0.084 −0.034 B3-EN 0.043 −0.157 −0.008 −0.120 EXG 0.058 0.014 0.110 0.092 B4-CO 0.058 0.046 −0.133 0.037 ARVI 0.051 0.086 0.143 −0.124 B4-DI 0.060 0.029 −0.130 0.053 GBRI 0.041 0.087 −0.062 0.292 B4-HO −0.065 0.045 0.035 0.028 GRRI 0.054 0.089 0.112 −0.086 B4-VA 0.057 0.053 −0.138 0.049 B3 −0.025 −0.165 0.008 0.216 B5-CO 0.058 0.053 −0.130 0.035 B4 0.033 −0.081 0.161 0.350 B5-DI 0.060 0.038 −0.116 0.068 B5 0.036 −0.064 0.190 0.284 B5-EN 0.058 −0.082 −0.071 0.020 B1-EN 0.038 −0.161 0.023 −0.167 B5-HO −0.065 0.031 0.064 −0.007 B1-HO −0.043 0.151 0.029 0.121 B5-VA 0.057 0.060 −0.132 0.057 -
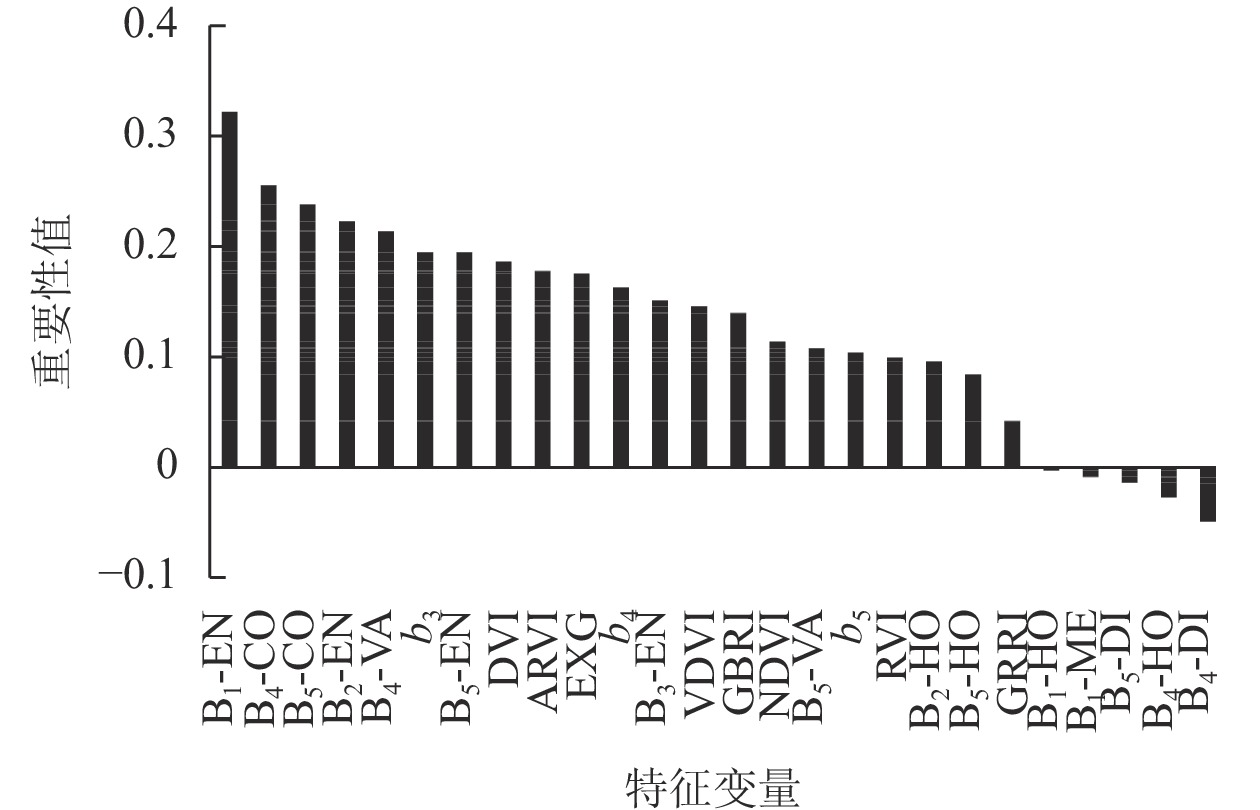
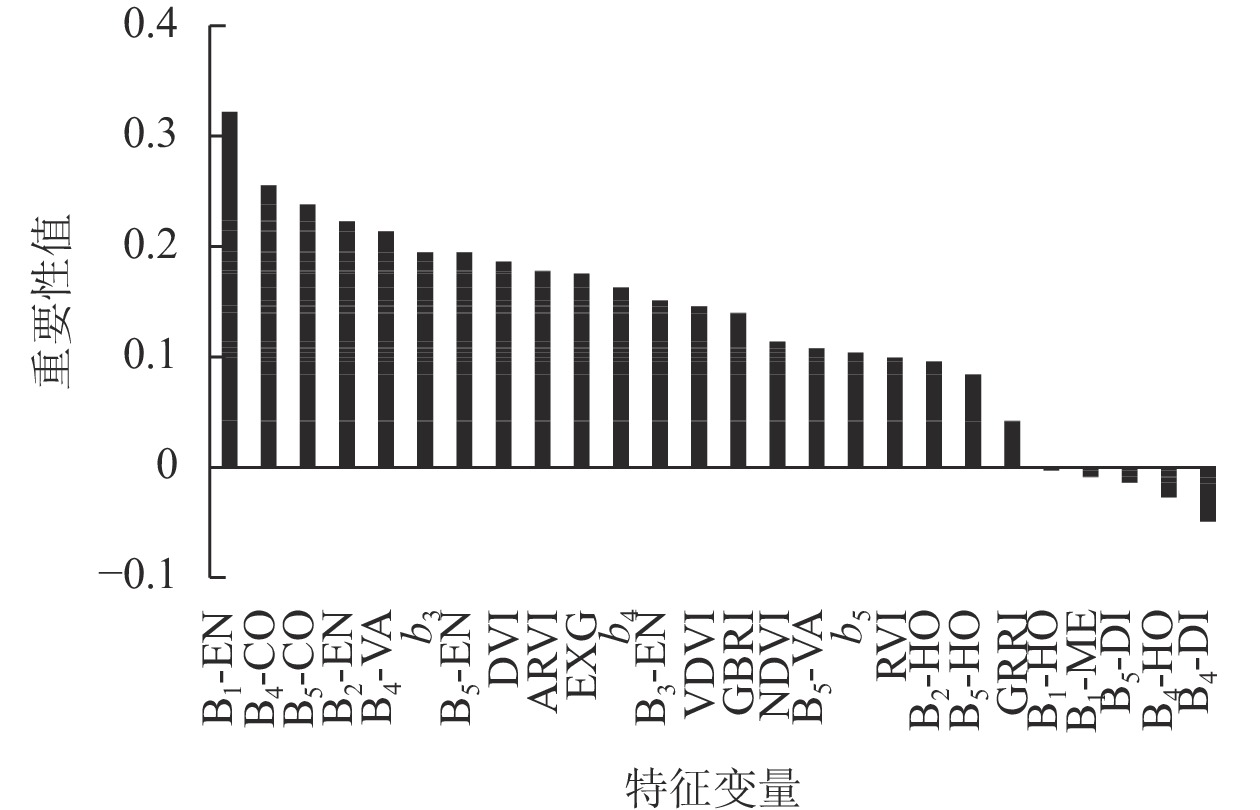
本研究使用Matlab建立随机森林回归模型，决策树数目为100，最小叶子数为1，其余参数均为默认值。如图1所示：随机森林模型中，变量重要性前5位的均为纹理特征，说明纹理特征对于蓄积量估测模型的重要性不可忽视。纹理特征间的重要性程度差异大，不同波段间也存在较大差异；植被指数对模型的影响比较稳定，植被指数间除GRRI外无明显差异。
图 1 随机森林模型变量重要性
Figure 1. Importance of random forest model variables
-
基于Matlab借助LIBSVM工具箱构建支持向量回归(SVR)模型，支持向量机(SVM)类型为e-SVR，函数选择径向基核函数(RBF)，涉及惩罚系数(c)和径向基核函数的参数$(\gamma) $这2个重要参数。利用格网化寻优，得到最佳c、$\gamma $分别为4、0.0625。
-
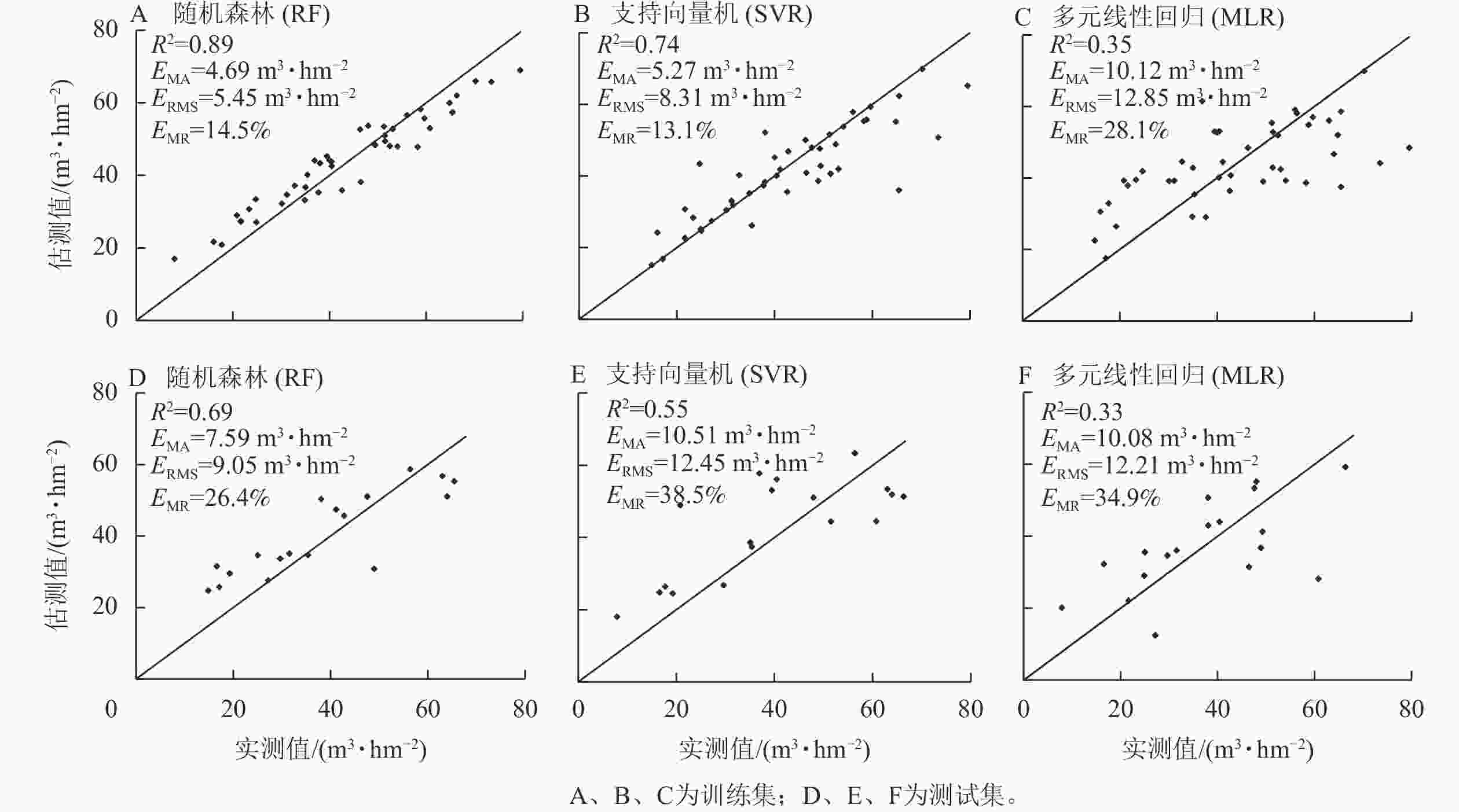
精度评价结果：在训练集上，随机森林模型精度最高(R2=0.89，EMA=4.69 m3·hm−2，ERMS=5.45 m3·hm−2，EMR=14.5%)，支持向量机次之(R2=0.74，EMA=5.27 m3·hm−2，ERMS=8.31 m3·hm−2，EMR=13.1%)，多元线性回归精度最低(R2=0.35，EMA=10.12 m3·hm−2，ERMS=12.85 m3·hm−2，EMR=28.1%)。在测试集上，随机森林精度仍最高(R2=0.69，EMA=7.59 m3·hm−2，ERMS=9.05 m3·hm−2，EMR=26.4%)，其次是支持向量机(R2=0.55，EMA=10.51 m3·hm−2，ERMS=12.45 m3·hm−2，EMR=38.5%)，多元线性回归最低(R2=0.33，EMA=10.08 m3·hm−2，ERMS=12.21 m3·hm−2，EMR=34.9%)。3种模型的测试集精度均有降低。
根据估测蓄积量与实测蓄积量绘制散点图。在训练集上(图2A~C)，随机森林和支持向量机模型离散程度较小，散点在两侧分布较均匀，模型拟合效果较好；多元线性回归模型散点在两侧分布较均匀，但离散程度较高，模型拟合较差。在测试集上(图2D~F)，3种模型散点在两侧分布不均匀，随机森林离散程度小，其余2种模型离散程度大。3种模型在训练集、测试集上均存在一定的低值高估和高值低估现象。
图 2 实测蓄积量与估算蓄积量之间的相关关系
Figure 2. Correlation between measured forest volume and estimated forest volume
-
本研究基于无人机多光谱影像提取单波段反射率、各类植被指数、纹理特征，并计算其标准地均值，利用结合主成分分析的多元线性回归、随机森林、支持向量机等建立蓄积量估测模型，结果表明：随机森林模型的精度最高，支持向量机次之，多元线性回归最低。
苏迪等[10]根据平均胸径、平均树高、坡度、坡向等因子建立蓄积量估测模型(模型R2=0.738，ERMS=5.1358 m3·hm−2)，曾霞辉[11]提取平均冠幅、郁闭度、平均树高、株数密度建立蓄积量估测模型(模型对应的R2、EMR分别为0.64~0.78、18.93%~39.68%)。本研究所建立随机森林模型和支持向量机模型的误差水平与其基本一致，多元线性回归模型精度较低。
于东海[13]在对辽宁老秃顶子国家级自然保护区的蓄积量估测研究中，提取植被指数、纹理特征、地形因子，并通过主成分分析提取主成分因子建立多元线性回归模型，模型R2为0.88，拟合效果良好，测试集平均相对误差为9.96%。与该研究相比，本研究结合主成分分析法建立的多元线性回归模型R2为0.35，测试集的平均相对误差为34.9%，精度较低。对研究区进行对比发现，于东海[13]所选研究区森林覆盖率97%，郁闭度、样地单位面积蓄积量高；本研究区郁闭度差异大，标准地单位面积蓄积量低，最大值为79.49 m3·hm−2，最小值低至7.90 m3·hm−2，平均值为41.97 m3·hm−2。2个研究区森林郁闭度存在较大差异，估测精度可能受到郁闭度的影响。
不同窗口下提取的纹理特征对蓄积量估测精度存在一定影响，提取窗口过大或过小都会造成纹理特征的错误分割进而影响估测精度[27]。基于无人机多光谱影像，在不同窗口大小下提取的纹理特征对蓄积量估测精度的影响有待进一步研究。
研究区林分较稀疏，在部分标准地中，有少量的树木位于标准地边界附近，其部分树冠在标准地边界之外。计算各变量均值时，此部分树冠所对应的特征变量没有参与均值计算，可能对估测精度产生一定的影响。
-
以大疆精灵4无人机获取滇中地区典型天然云南松林多光谱影像，提取并计算标准地单波段反射率、植被指数、纹理特征均值，共55个特征变量，经相关性分析筛选出26个变量参与模型构建。通过对随机森林、支持向量机、多元线性回归3种模型进行精度评价，最佳估测模型为随机森林。3种模型在估测蓄积量时均存在一定的低值高估和高值低估现象。与同类型研究的蓄积量估测误差水平基本一致，表明在不进行单木分割的情况下，利用无人机多光谱影像提取各因子，以各因子的标准地均值建立模型估测蓄积量具有一定的可行性。
Pinus yunnanensis volume estimation model based on UAV multispectral image
-
摘要:
目的 无人机多光谱遥感影像较可见光影像具有更丰富的光谱信息，在森林蓄积量估测中具有较大潜力。以无人机载多光谱遥感影像为主要数据源，探索森林蓄积量的遥感估测模型，以克服传统地面调查工作量大、耗时长、成本高等弊端。 方法 以滇中地区典型天然云南松Pinus yunnanensis纯林为研究对象，利用无人机多光谱影像提取单波段反射率、各类植被指数、纹理特征等，计算各特征变量的标准地均值；筛选与云南松林蓄积量相关性显著的特征变量，采用多元线性、随机森林、支持向量机建立云南松林蓄积量估测模型，以决定系数(R2)、平均绝对误差(EMA)、均方根误差(ERMS)、平均相对误差(EMR)评价模型精度。 结果 ① 3种模型中，随机森林的精度最高(R2=0.89，EMA=4.69 m3·hm−2，ERMS=5.45 m3·hm−2，EMR=14.5%)，其次为支持向量机(R2=0.74，EMA=5.27 m3·hm−2，ERMS=8.31 m3·hm−2，EMR=13.1%)，最低为多元线性回归模型(R2=0.35，EMA=10.12 m3·hm−2，ERMS=12.85 m3·hm−2，EMR=28.1%)；3种模型在测试集上的估测精度均有所降低，随机森林的模型表现最好，支持向量机次之，多元线性最差。② 3种模型在云南松林蓄积量估测中均存在一定的低值高估和高值低估现象。③ 基于无人机多光谱影像估测云南松林蓄积量，纹理特征仍是不可忽视的重要因子。 结论 基于无人机多光谱影像，在不进行单木分割的情景下，提取标准地的单波段反射率、植被指数、纹理特征均值，筛选适用于蓄积量估算的变量构建估测模型。通过对3种模型进行精度评价，随机森林为云南松林蓄积量估测的最佳模型。图2表5参27 Abstract:Objective Unmanned aerial vehicle (UAV) multispectral remote sensing images, with richer spectral information than visible light images, have great potential in forest volume estimation. Taking UAV-borne multispectral remote sensing images as the main data source, this study aims to explore the remote sensing estimation model of forest volume, so as to overcome the drawbacks of traditional ground survey, such as heavy workload, long time consumption and high cost. Method Taking the typical natural pure Pinus yunnanensis forest in Luomian Township, Fumin County, Kunming City as the research object, the single-band reflectance, vegetation index and texture feature were extracted according to the UAV multispectral image, and the standard ground mean of each characteristic variable was calculated. The characteristic variables significantly correlated with the forest volume were screened, and the forest volume estimation model was established using multiple linear regression, random forest and support vector machine. The model accuracy was evaluated by coefficient of determination (R2), root mean square error (ERMS), mean absolute error (EMA) and mean relative error (EMR). Result (1) Among the three models, the random forest had the highest accuracy (R2=0.89, EMA=4.69 m3·hm−2, ERMS=5.45 m3·hm−2, EMR=14.5%), followed by the support vector machine (R2=0.74, EMA=5.27 m3·hm−2, ERMS=8.31 m3·hm−2, EMR=13.1%). The multiple linear regression model had the minimum accuracy (R2=0.35, EMA=10.12 m3·hm−2, ERMS=12.85 m3·hm−2, EMR=28.1%). The estimation accuracy of the three models in the test set decreased. The random forest had the best performance, followed by the support vector machine, and the multivariate linearity was the worst. (2) The three models had certain underestimation and overestimation in the estimation of P. yunnanensis forest volume. (3) Texture feature was still an important factor that could not be ignored in estimating the forest volume of P. yunnanensis based on UAV multispectral images. Conclusion Based on the multi-spectral images of UAV, the single-band reflectance, vegetation index, and texture factor mean values of the standard ground were extracted without individual tree segmentation, and the variables suitable for volume estimation were screened to construct an estimation model. Through the precision evaluation of the three models, the random forest is the best model for estimating P. yunnanensis volume. [Ch, 2 fig. 5 tab. 27 ref.] -
木材的内部缺陷会严重影响木材的质量。由于应力波的木材无损检测成本低、携带方便及对木材无损的特性，使得其越来越受到人们的青睐。国内外已开展了应力波速度与木材内部缺陷之间的相关研究。如WANG[1]通过应力波在缺陷木材中的传播规律，表明应力波在腐烂或劣化的木材中比在完好的木材中传播速度慢。徐华东等[2]以校园内的活立木作为样本，使用应力波检测仪器对校园树木进行二维成像，表明在活立木的断层横截面上，应力波横向的波速要小于径向的波速，且应力波在木材内部的波速受制于木材内部的缺陷情况。国内学者也对应力波无损检测仪器的可行性进行了研究。杨学春等[3]利用应力波检测仪器对原木内部腐朽进行了研究，结果表明：应力波测试仪能准确判断不同树种原木内部的腐朽程度，并且能够得到原木内部腐朽基本形状的二维图像。LIN等[4]运用应力波断层成像技术，对不同大小的樟树Cinnamomum camphora人造空洞进行了研究，表明应力波断层成像技术可以反映木材的空洞大小及位置，验证了应力波无损成像技术的可行性。以上研究主要针对应力波传播规律与成像技术的应用领域，但对应力波成像算法的研究不多。FENG等[5]提出了一种基于插值的图像重建算法，利用周围点的值估计未知点的速度情况，进而重建树木内部缺陷图像。DU等[6]提出了基于椭圆的空间插值以及速度补偿的方法对木材的横截面进行成像，能够准确地判定缺陷位置，并得到了良好的成像效果。国内外对于应力波在树木内部的传播规律做了大量的研究[8-10]，但是对于木材径切面传播规律和成像方法研究还比较少。翁翔等[7]利用无损检测仪器对木材的径切面进行测量，对应力波横向速度和径向速度的比值进行了回归，得到了应力波在木材径向上的传播速度模型，其结果的拟合度较高。但在木材径切面的缺陷成像方法研究较少。鉴于此，本研究基于应力波在木材径切面中沿直线上传播的假设，提出一种木材径切面内部缺陷的速度修正成像方法。
1. 应力波木材径切面成像原理
1.1 树木径切面模型的建立
木材可以用圆柱体来近似的表示，那么木材的径切面可以被抽象成一个近似的矩形模型，将n个（n一般为12）传感器放置于被测树木两侧（传感器1至n/2位于同一侧）。每个传感器距离地面的高度（或者某一水平高度的距离）分别为（H1，H2，H3，…，Hn）；S1~Sn表示应力波传感器，传感器按照从右向左，呈U字形进行放置；D表示树木直径；θjk为每个传感器两两之间的相对角度。如图 1所示：定义一个坐标系表示树木径切面。
令Sn/2+1所在的位置为原点坐标，建立传感器的坐标系。
$ S\left( {{X_i}, {Y_i}} \right) = \left\{ \begin{array}{l} {X_i} = D/2, {Y_i} = {H_i} - {H_{n/2 + 1}}, \;\;1 \le i \le n/2\\ {Y_i} = 0, {Y_i} = {H_i} - {H_{n/2 + 1}}, \;\;n/2 + 1 \le i \le n \end{array} \right.。 $
(1) 式（1）中：有1≤i≤n，Xi表示传感器位置横坐标，Yi表示传感器位置纵坐标。根据每个传感器的位置数据，可得到每个传感器两两之间的相对角度θjk为：
$ {\theta _{jk}} = \left\{ {\begin{array}{*{20}{l}} {\arctan (\frac{{{H_j} - {H_k}}}{D})}&{{H_j} > {H_k}, {H_k} < {H_{n/2 + 1}}}\\ {\arctan (\frac{{{H_j} - {H_{\left( {n/2 + 1} \right)}} - \left( {{H_k} - {H_{\left( {n/2 + 1} \right)}}} \right)}}{D}), }&{{H_j} > {H_k}, {H_k} < {H_{n/2 + 1}}}\\ {\arctan (\frac{{{H_k} - {H_j}}}{D})}&{{H_j} < {H_k}} \end{array}} \right.。 $
(2) 式（2）中：1≤j≤n/2，n/2+1≤k≤n。
假定应力波在木材中是沿着直线传播的，通过传感器间的距离和应力波传播的时间计算出传感器间应力波的传播速度[11]。
1.2 速度修正插值方法
为了预测木材离轴的单轴压缩强度，Hankinson公式[12]给出一种数学模型。当应力波在木材径切面上传播时，如果传播方向与垂直于木材纹理角方向所成的角度为θ，那么根据Hankinson公式可以推出如下公式：
$ {V_\theta } = \frac{{{V_1}{V_{\rm{r}}}}}{{{V_1}{{\sin }^2}\theta + {V_{\rm{r}}}{{\cos }^2}\theta }}。 $
(3) 式（3）中：V1表示平行于纹理方向上的应力波传播速度；Vr表示垂直于纹理方向上的应力波传播速度；θ表示传播方向与木材纹理方向所形成的角度；Vθ表示在角度为θ时应力波在木材径切面上的传播速度。
翁翔等[7]通过计算得出：
$ \frac{{{V_\theta }}}{{{V_{\rm{r}}}}} \approx 1 + \frac{{{V_1} - {V_{\rm{r}}}}}{{{V_1}}} \times {\theta ^2}。 $
(4) 式（4）中：$ \frac{{{V_1} - {V_{\rm{r}}}}}{{{V_1}}}$是常数。那么如图 2所示：假设在空洞木材中有2个对应角度α和β的传播路径Lα和Lβ，其中有α>β。Lα经过缺陷区域，其速度表示为Vα。Lβ是经过正常区域的，其速度表示为Vβ。同时假设在未产生空洞的同一木材中，有L'α经过的是正常的区域，其速度为V'α。那么有：
图 2 应力波在不同缺陷程度的木材中传播Figure 2. Stress waves propagate in wood of different defect degree$ V{'_\alpha } > {V_\beta }, V{'_\alpha } > {V_\alpha } $
(5) 根据式（5），可以得出:
$ \frac{{V{'_\alpha }}}{{1 + z \times {\alpha ^2}}} \approx \frac{{V{'_\beta }}}{{1 + z \times {\beta ^2}}} \approx {V_{\rm{r}}}。 $
(6) 式（6）中：$ z = \frac{{{V_1} - {V_{\rm{r}}}}}{{{V_1}}}$。由式（5）和式（6）可以得出：
$ \frac{{{V_\alpha }}}{{1 + z \times {\alpha ^2}}} < \frac{{{V_\beta }}}{{1 + z \times {\beta ^2}}}。 $
就可以得出速度修正的公式：
$ {V_{{\rm{c}}\left( {{\theta _{jk}}} \right)}} = \frac{{{V_{{\rm{d}}\left( {{\theta _{jk}}} \right)}}}}{{1 + z \times {\theta _{jk}}^2}}。 $
(7) 式（7）中：Vc(θjk)表示修正后的速度；Vd(θjk)表示为测量得到的应力波传播速度；k是常数；θjk表示2个传感器间与垂直于木材方向纹理所成的角度。
因此经过缺陷区域的Vα经过速度修正后，就可以反映出应力波经过缺陷区域速度呈现出降低的现象，有效地减少了由木材的各向异性[13]导致的应力波在木材不同方向上传播速度不一致现象的影响，为木材内部缺陷成像提供更精确的数据。
将通过传感器之间的线速度VL转换成木材径切面上交点的速度VP：
$ {V_{\rm{P}}} = \max \left( {{V_{{\rm{L1}}}}, {V_{{\rm{L2}}}}, \cdots , {V_{{\rm{L}}n}}} \right)。 $
(8) 式（8）中：VL1至VLn分别表示每条经过该交点的应力波传播路径上修正后的线速度；（VL1, VL2, …, VLn）∈Vc(θjk)。
利用速度修正插值法对木材的径切面进行成像。每个已知点都对插值点具有一定的影响，即权重[14]。权重随着已知点和插值点之间距离的增加而减弱，距离插值点越近的已知点的权重越大。而且当已知点在距离插值点一定范围以外时，权重可以忽略不计。在任一待插值点的值是邻域内已知点权重之和。可以表示为：
$ {V_{{\rm{q}}i}} = \left( {\sum\limits_{i = 1}^n {\frac{{\max \left( {\frac{{\left( {V{'_{{\rm{L1}}}}} \right)}}{{1 + z \times {\theta _{{\rm{L1}}}}}}} \right), \left( {\frac{{\left( {V{'_{{\rm{L2}}}}} \right)}}{{1 + z \times {\theta _{{\rm{L2}}}}}}} \right), \cdots , \left( {\frac{{\left( {V{'_{{\rm{L}}n}}} \right)}}{{1 + z \times {\theta _{{\rm{L}}n}}}}} \right)}}{{{d^m}_i}}} } \right)/\sum\limits_{i = 1}^n {\frac{1}{{{d^m}_i}}} 。 $
(9) 式（9）中：Vqi为待插值点的预估值；V'Ln为每条经过该交点的应力波传播路径上未修正的线速度，（V'L1, V'L2, …, V'Ln）∈Vd(θjk)；θLn表示每条经过该交点的应力波传播路径与水平面的所成的夹角，（θL1, θL2, …, θLn）∈θjk；di为第i个已知点与待插值点的距离；n表示邻域内参与插值计算的已知点的个数；m为常数。
成像算法步骤：
步骤1：初始化（建立木材径切面的模型，输入传感器的坐标（x, y），计算传感器间的线速度Vd(θjk)；
步骤2：利用式（7）求出修正后的线速度矩阵Vc(θjk)；
步骤3：传感器两两连线的交点坐标（xc, yc），将邻域内已知属性值的交点的坐标以及每个交点对应的线速度V'Ln代入式（8）计算Vp的属性值；
步骤4：通过将已知点的属性值代入式（9），计算未知点的属性值；
步骤5：重复步骤4，直到计算出所有径切面上的每个点的属性值。
步骤6：将预估点根据属性值的不同进行不同颜色的赋值，并生成二维图像。
2. 实验材料与方法
实验用于采集木材应力波数据的仪器是Fakopp。如图 3所示：将传感器分别放置在原木径切面两边，每边6个传感器，总共12个。实验过程中使用检测仪器自带的重锤以相同的力度，垂直于传感器方向，对各个传感器分别敲击3~5次，采集总共36~60组数据。将数据用于下文的成像中。
本实验样本编号、样本种类、样本周长、样本测量高度等信息如表 1所示。
表 1 实验样本基本信息Table 1. Experimental sample information样本编号 样本种类 样本周长/cm 检测区域面积/cm2 缺陷面积/cm2 1 雪松Cedrus deodara 62.83 1 000 111.20 2 泡桐Paulownia fortunei 73.83 1 175 427.50 3 樟树Cinnamomum camphora 60.95 940 314.15 对样本的空洞面积测量方法如下：利用卷尺测量树木空洞的长和宽，假设样本的长为L，宽为W，则对于长方形的空洞缺陷面积SR计算公式为：
$ S_{\rm R}=LW。 $
(10) 假设梯形的空洞，上底长度为A，下底长度为B，缺陷的高度为H，梯形的空洞的面积ST则用公式可以表示为：
$ {S_{\rm{T}}} = \frac{{\left( {A + B} \right)H}}{2}。 $
(11) 假设圆形的缺陷孔洞的直径为R，那么缺陷的面积SY可以表示为：
$ S_{\rm Y}=\mathit{π} R^2。 $
(12) 3. 结果与分析
3.1 速度修正插值法（VCI）与反距离加权插值法（IDW）成像结果对比
从图 4A可以看出：缺陷为人工挖掘并且形状为长方形。如图 4B所示：未修正的线图将经过缺陷区域的线段表示为黄色，未正确区分缺陷区域。图 4C表示的是修正后的线图，将经过缺陷区域的线段（如1号和7号、2号和8号等传感器之间的连线）错误地表示为缺陷颜色红色。从图 4D可以看出：使用IDW的成像结果，只能粗略反映缺陷位置，对于缺陷大小与形状都不能进行准确成像。对比VCI的成像结果图 4E，VCI可以较好还原缺陷位置，可以看出缺陷的位置是处于第3号、5号与8号、10号传感器之间，与图 4A所示的真实缺陷位置基本吻合。但是对于缺陷形状的成像不够准确。
从图 5A可以看出：样本缺陷位置处于右边2号至5号传感器的下面3 cm，以及左边11号传感器至7号传感器的下面3 cm的位置，形状为矩形。从未修正线图（图 5B）可以看到：仅有少部分经过缺陷区域的线段被表示为缺陷的红色，大部分经过缺陷区域的线段被表示为非缺陷的绿色。修正后的线图（图 5C）较好地区分缺陷区域，并以不同的颜色进行区分。可以看到IDW的成像结果虽然能够还原缺陷的位置（图 5D），但对缺陷还原的准确度较低，对缺陷位置和大小的还原参考价值较低。如图 5E所示：VCI的成像结果可以较好地反映缺陷位置，但存在对缺陷区域成像结果比真实结果偏小的情况，以及对缺陷边缘的重建不够平整，对于样本的缺陷轮廓可以较好还原，可以反映样本的缺陷特征。
从图 6A可以看出：树木的缺陷位置位于右边的3号和4号传感器之间，以及左边的9号和10号传感器之间。对比图 6B与图 6C可以看到：未修正的线图将经过缺陷区域的线段（如7号、1号传感器线段以及6号、12号传感器线段）错误地表示为经过正常区域的线段，呈现绿色，与真实情况不符。而修正后的线图，能够较好区分缺陷部位。从IDW成像结果（图 6D）反映缺陷所处的低速度区域，但对于缺陷的形状无法正确成像。缺陷成像结果呈现不规则的块状分布，无法反映样本的缺陷特征。VCI的成像结果（图 6E）显示：缺陷形状呈现一个类似圆形的不规则形状，与真实的缺陷形状较为接近。成像结果表明缺陷位于3号、4号传感器与9号、10号传感器之间，与图 6A的真实缺陷位置也基本相同。
3.2 成像结果误差分析
使用混淆矩阵法对成像效果进行定量的误差分析，混淆矩阵包含由分类系统完成的实际和预测的分类信息[15]。FAWCETT[16]描述了真、假分类系统中4种可能组合（表 2）。
表 2 缺陷与预测的4种组合Table 2. Four combination of real defects and predict defects类别 预测缺陷 预测完好 真实缺陷 被正确地预测为缺陷的面积C 被错误地预测为完好的面积E 真实完好 被错误地预测为缺陷的面积F 被正确地预测为完好的面积W 从表 2的矩阵可以推出的常用度量值[17]，如准确率或者正确率（A），精确度（P）和查全率（R）。
$ A = \frac{{C + W}}{{C + E + F + W}}; $
(13) $ P = \frac{C}{{C + F}}; $
(14) $ R = \frac{C}{{C + E}}。 $
(15) 式（13）~（15）中：准确率A表示对木材状态预测正确的百分比；精确度P表示对木材缺陷预测的可靠性水平高低；查全率R表示对木材缺陷的预测能力高低；C，W，E和F所代表含义见表 2。
从表 3可见：3个样本的准确率A为72.32%~95.85%。使用VCI方法的3个样本的平均准确率为93.34%，使用IDW方法的3个样本平均准确率为82.63%。IDW方法在1号、2号样本中的准确率均大于85.00%，其原因应该是IDW方法在成像结果中虽然不能很好地反映木材缺陷的特征，但是对木材完好的部位成像结果较好，所以得到较高的准确率。而3号样本只有72.32%的准确率，对比真实缺陷可以看出：IDW方法将部分正常木材错误地成像为缺陷木材，所以导致准确率下降。IDW和VCI的准确度标准差分别为7.38%和2.04%。可见，VCI在准确率上的标准差较小，说明VCI方法在不同样本中的准确率结果更稳定，准确率相较于IDW方法均有所提高。
表 3 不同样本的准确率Table 3. Accuracy of different samples样本编号 准确率A/% IDW方法 VCI方法 1 89.20 95.85 2 86.36 93.30 3 72.32 90.86 从表 4可见：3个样本的精确度P为65.79%~88.35%。使用VCI方法的3个样本的平均精确度为82.26%，使用IDW方法的3个样本平均精确度为70.19%。VCI方法中3号样本的结果要好于其他样本，其原因是3号样本中的预测缺陷大部分与真实缺陷重合，且预测缺陷大部分落在真实缺陷上，所以得到较高的精确度。IDW和VCI方法的精确度标准差分别为5.00%和4.70%。VCI方法在准确度上的标准差较小，VCI方法在精确度的稳定性略高于IDW方法。同时VCI方法在不同样本上的精确度均好于IDW方法。
表 4 不同样本的精确度Table 4. Precision of different samples样本编号 精确度P/% IDW方法 VCI方法 1 67.60 76.92 2 77.18 88.35 3 65.79 81.51 从表 5可见：3个样本的查全率R为17.98%~94.03%。使用VCI方法的3个样本的平均查全率为92.65%，使用IDW方法的3个样本平均查全率为36.64%。VCI方法中的查全率高于IDW方法。可见，VCI方法可以较好地反映木材的真实缺陷结果，且对木材的缺陷位置成像结果更好。在真实缺陷大小不变的情况下，由于VCI方法可以更好地反映木材的缺陷情况，因此得到了更高的查全率，与真实的成像结果相吻合。IDW和VCI方法的查全率标准差分别为：15.59%和1.93%。说明VCI方法的查全率标准差要远小于IDW方法，在查全率的稳定性上要好于IDW方法。
表 5 不同样本的查全率Table 5. Recall rate of different samples样本编号 查全率R/% IDW方法 VCI方法 1 17.98 89.92 2 56.14 94.03 3 35.80 94.00 4. 结论
本研究提出了一种应用于木材无损检测领域的，基于应力波的木材径切面成像方法。通过与IDW的成像效果比较发现：不论是在定量还是定性方面，VCI方法对木材径切面的缺陷成像结果都好于IDW方法。与真实的缺陷进行对比得到较小的误差，可以准确反映木材内部的真实缺陷情况，具有较高的成像精度。利用传感器测量得到的不同应力波数据，通过对不同缺陷的样本进行实验，验证了该算法对于木材的径切面成像效果的可行性。利用混淆矩阵对成像结果进行了定量分析发现：VCI方法的平均准确度为93.34%，平均精确度为82.26%，平均查全率为92.65%，均高于IDW方法，但对于缺陷具体形状的成像结果，其准确度有待进一步提高。
-
图 2 实测蓄积量与估算蓄积量之间的相关关系
Figure 2 Correlation between measured forest volume and estimated forest volume
表 1 标准地林分因子汇总
Table 1. Summary of stand factors in sample plots
项目 蓄积量/
(m3·hm−2)株数 平均胸
径/cm平均树
高/m郁闭度 最小值 7.90 2 12.8 5.0 0.21 最大值 79.49 42 32.6 14.7 0.79 平均值 41.97 14 21.9 8.4 0.45 
下载: 导出CSV
表 2 蓄积量与单波段反射率、植被指数的相关性
Table 2. Correlation between forest volume and single band reflectance and vegetation indexes
植被指数 相关性 植被指数 相关性 单波段反射率 相关性 RVI 0.533** ARVI 0.548** b1 −0.126 NDVI 0.463** GBRI 0.341** b 2 −0.194 DVI 0.541** GRRI 0.541** b 3 −0.333** VDVI 0.532** NGRDI −0.117 b 4 0.342** EXG 0.508** NGBDI 0.310* b 5 0.381** 说明：b1、b2、b3、b4、b5分别为红光、绿光、蓝光、红边、近红外反射率；**表示在0.01 (双侧)水平上极显著相关，*表示在0.05 (双侧)水平上显著相关。
下载: 导出CSV
表 3 蓄积量与纹理特征的相关性
Table 3. Correlation between forest volume and texture factors
波段 CO CC DI EN HO ME SM VA B1 0.115 −0.139 0.165 0.362** −0.381** −0.380** −0.253* 0.088 B2 0.297* −0.053 0.257* 0.428** −0.499** −0.189 −0.213 0.306* B3 0.092 0.201 0.113 0.337** −0.173 −0.239 −0.115 0.111 B4 0.413** −0.123 0.405** 0.189 −0.507** 0.067 −0.218 0.392** B5 0.408** −0.210 0.395** 0.409** −0.499** 0.129 −0.186 0.390** 说明：B1、B2、B3、B4、B5分别为红光、绿光、蓝光、红边、近红外波段；**表示在0.01 (双侧)水平上极显著相关，*表示在0.05 (双侧)水平上显著相关。0.115表示红光波段(B1)提取的对比度(CO)与蓄积量的相关系数，其余值同理。
下载: 导出CSV
表 4 主成分分析结果
Table 4. Principal component analysis
主成分 特征根 方差解释率/% 累积方差解释率/% C1 14.80 56.92 56.92 C2 4.66 17.91 74.83 C3 3.24 12.45 87.29 C4 1.66 6.38 93.66
下载: 导出CSV
表 5 主成分与原始变量的线性关系
Table 5. Linear relationship between principal components and original variables
原始变量 C1 C2 C3 C4 原始变量 C1 C2 C3 C4 RVI 0.050 0.088 0.149 −0.064 B1-ME −0.030 −0.112 −0.134 0.296 NDVI 0.044 −0.029 0.000 0.052 B2-EN 0.048 −0.125 0.037 −0.187 DVI 0.051 0.009 0.189 0.108 B2-HO −0.055 0.111 0.003 0.142 VDVI 0.057 0.092 0.084 −0.034 B3-EN 0.043 −0.157 −0.008 −0.120 EXG 0.058 0.014 0.110 0.092 B4-CO 0.058 0.046 −0.133 0.037 ARVI 0.051 0.086 0.143 −0.124 B4-DI 0.060 0.029 −0.130 0.053 GBRI 0.041 0.087 −0.062 0.292 B4-HO −0.065 0.045 0.035 0.028 GRRI 0.054 0.089 0.112 −0.086 B4-VA 0.057 0.053 −0.138 0.049 B3 −0.025 −0.165 0.008 0.216 B5-CO 0.058 0.053 −0.130 0.035 B4 0.033 −0.081 0.161 0.350 B5-DI 0.060 0.038 −0.116 0.068 B5 0.036 −0.064 0.190 0.284 B5-EN 0.058 −0.082 −0.071 0.020 B1-EN 0.038 −0.161 0.023 −0.167 B5-HO −0.065 0.031 0.064 −0.007 B1-HO −0.043 0.151 0.029 0.121 B5-VA 0.057 0.060 −0.132 0.057
下载: 导出CSV
-
[1] 孟宪宇. 测树学[M]. 北京: 中国林业出版社, 2002. MENG Xianyu. Forest Mensuration[M]. Beijing: China Forestry Publishing House, 2002. [2] 陈忠明. 基于无人机影像的杉木蓄积量反演研究[D]. 长沙: 中南林业科技大学, 2019. CHEN Zhongming. Study on Cunninghamia lanceolata Volume Estimation Based on UAV Image[D]. Changsha: Central South University of Forestry and Technology, 2019. [3] 刘明艳, 王秀兰, 冯仲科, 等. 基于主成分分析法的老秃顶子自然保护区森林蓄积量遥感估测[J]. 中南林业科技大学学报, 2017, 37(10): 80 − 83, 117. LIU Mingyan, WANG Xiulan, FENG Zhongke, et al. Estimation of Laotudingzi Nature Reserve forest volume based on principal component analysis [J]. Journal of Central South University of Forestry &Technology, 2017, 37(10): 80 − 83, 117. [4] 王海宾, 彭道黎, 高秀会, 等. 基于GF-1 PMS影像和k-NN方法的延庆区森林蓄积量估测[J]. 浙江农林大学学报, 2018, 35(6): 1070 − 1078. WANG Haibin, PENG Daoli, GAO Xiuhui, et al. Forest stock volume estimates in Yanqing District based on GF-1 PMS images and k-NN method [J]. Journal of Zhejiang A&F University, 2018, 35(6): 1070 − 1078. [5] 刘兆华. 基于多源遥感数据的森林蓄积量估测研究[D]. 长沙: 中南林业科技大学, 2020. LIU Zhaohua. Research on Forest Volume Estimation Based on Multi-source Remote Sensing Data[D]. Changsha: Central South University of Forestry and Technology, 2020. [6] 谢巧雅, 余坤勇, 邓洋波, 等. 杉木人工林冠层高度无人机遥感估测[J]. 浙江农林大学学报, 2019, 36(2): 335 − 342. XIE Qiaoya, YU Kunyong, DENG Yangbo, et al. Height measurement of Cunninghamia lanceolata plantations based on UAV remote sensing [J]. Journal of Zhejiang A&F University, 2019, 36(2): 335 − 342. [7] 樊江川. 无人机航空摄影测树技术研究[D]. 北京: 北京林业大学, 2014. FAN Jiangchuan. Study of the Tree Measurement Technology by UAV Aerial Photography[D]. Beijing: Beijing Forestry University, 2014. [8] 李赟. 基于UAV高分影像的林木冠幅提取与蓄积量估测研究[D]. 南京: 南京林业大学, 2017. LI Yun. Study on Crown Extraction and Forest Volume Estimation Based on UAV High Resolution Image[D]. Nanjing: Nanjing Forestry University, 2017. [9] 应兴亮. 基于无人机遥感的森林蓄积量估测研究[D]. 福州: 福建农林大学, 2017. YING Xingliang. Estimation of Forest Volume Based on Unmanned Aerial Vehicle Remote Sensing[D]. Fuzhou: Fujian Agriculture and Forestry University, 2017. [10] 苏迪, 高心丹. 基于无人机航测数据的森林郁闭度和蓄积量估测[J]. 林业工程学报, 2020, 5(1): 156 − 163. SU Di, GAO Xindan. Estimation of forest canopy density and stock volume based on UAV aerial survey data [J]. Journal of Forestry Engineering, 2020, 5(1): 156 − 163. [11] 曾霞辉. 基于无人机影像的林分蓄积量估测研究[D]. 长沙: 中南林业科技大学, 2020. ZENG Xiahui. Study on Forest Stand Volume Estimation Based on UAV Image[D]. Changsha: Central South University of Forestry and Technology, 2020. [12] 孙钊. 基于无人机航拍图像的杉木树冠参数提取与模型研建[D]. 北京: 北京林业大学, 2020. SUN Zhao. Extraction of Tree Crown Parameters and Model Development Based on UAV Image[D]. Beijing: Beijing Forestry University, 2020. [13] 于东海. 无人机航测林分及单木信息提取方法研究[D]. 北京: 北京林业大学, 2017. YU Donghai. Research on Methods of Forest Stand & Individual Tree Information Extraction Using UAV-based Aerial Photography[D]. Beijing: Beijing Forestry University, 2017. [14] 卯光宪. 基于无人机多光谱影像的马尾松林蓄积估测研究[D]. 贵阳: 贵州大学, 2021. MAO Guangxian. Estimation of Pinus massoniana Forest Stock Volume Based on Multi-spectral UAV Image[D]. Guiyang: Guizhou University, 2021. [15] 吴胜义, 王义贵, 王飞, 等. 基于多距离度量kNN模型的森林蓄积量反演[J]. 中南林业科技大学学报, 2023, 43(2): 10 − 18. WU Shengyi, WANG Yigui, WANG Fei, et al. Forest stock volume inversion based on multi-distance metric kNN models [J]. Journal of Central South University of Forestry &Technology, 2023, 43(2): 10 − 18. [16] TORRES-SÁNCHEZ J M, PEÑA J M, de CASTRO F, et al. Multi-temporal mapping of the vegetation fraction in early-season wheat fields using images from UAV [J]. Computers and Electronics in Agriculture, 2014, 103: 104 − 113. [17] SELLARO R, CREPY M, TRUPKIN S A, et al. Cryptochrome as a sensor of the blue/green ratio of natural radiation in Arabidopsis [J]. Plant Physiology, 2010, 154(1): 401 − 409. [18] GAMON J A, SURFUS J S. Assessing leaf pigment content and activity with a reflectometer [J]. New Phytologist, 1999, 143(2): 105 − 117. [19] HUNT E R J, CAVIGELL M, DAUGHTRYC S T, et al. Evaluation of digital photography from model aircraft for remote sensing of crop biomass and nitrogen status [J]. Preccision Agriculture, 2005, 6(4): 359 − 378. [20] MEYER G E, NETO J C. Verification of color vegetation indices for automated crop image application [J]. Computers and Electronics in Agriculture, 2008, 63(2): 282 − 293. [21] 汪小钦, 王苗苗, 王绍强, 等. 基于可见光波段无人机遥感的植被信息提取[J]. 农业工程学报, 2015, 31(5): 152 − 159. WANG Xiaoqin, WANG Miaomiao, WANG Shaoqiang, et al. Extraction of vegetation information from visible unmanned aerial vehicle images [J]. Transactions of the Chinese Society of Agricultural Engineering, 2015, 31(5): 152 − 159. [22] 房秀凤, 谭炳香, 刘清旺, 等. 基于纹理信息的森林蓄积量估计[J]. 东北林业大学学报, 2017, 45(11): 21 − 25. FANG Xiufeng, TAN Bingxiang, LIU Qingwang, et al. Estimation of forest stock volume by texture information [J]. Journal of Northeast Forestry University, 2017, 45(11): 21 − 25. [23] 尤静妮. 基于高分遥感纹理信息的森林蓄积量估测研究[D]. 西安: 西安科技大学, 2017. YOU Jingni. The Research on High Resolution Texture Information of Remote Sensing in Forest Volume Estimate[D]. Xi’an: Xi’an University of Science and Technology, 2017. [24] 王月婷, 张晓丽, 杨慧乔, 等. 基于Landsat8卫星光谱与纹理信息的森林蓄积量估算[J]. 浙江农林大学学报, 2015, 32(3): 384 − 391. WANG Yueting, ZHANG Xiaoli, YANG Huiqiao, et al. Forest volume estimation based on spectral and textural informationfrom the Landsat 8 satellite [J]. Journal of Zhejiang A&F University, 2015, 32(3): 384 − 391. [25] 崔博文. 基于机器学习的森林蓄积量估测研究[D]. 长沙: 中南林业科技大学, 2022. CUI Bowen. Estimation of Forest Stock Volume Based on Machine Learning [D]. Changsha: Central South University of Forestry and Technology, 2022. [26] 刘永新. 基于遥感技术的北京市森林蓄积量估测研究[D]. 长春: 吉林大学, 2021. LIU Yongxin. Estimation of Forest Stock Volume in Beijing Based on Remote Sensing[D]. Changchun: Jilin University, 2021. [27] 叶子林, 周普良, 林辉, 等. 纹理特征对森林蓄积量反演模型的影响[J]. 中南林业科技大学学报, 2020, 40(9): 49 − 56. YE Zilin, ZHOU Puliang, LIN Hui, et al. Texture features influences on inversion model of forest stock volume [J]. Journal of Central South University of Forestry &Technology, 2020, 40(9): 49 − 56. 期刊类型引用(8)
1. 夏甜甜，杜秋硕，刘鹏. 基于数字赋能的泰山古柏生态修复技术应用探究. 山东林业科技. 2024(02): 77-83 . 
百度学术2. 熊海贝，龙有为，陈琳，丁叶蔚. 木结构无损检测技术研究与应用综述. 结构工程师. 2023(01): 191-201 . 百度学术3. 郑强，赵玮，徐锋，刘云飞. 基于非对称椭圆的应力波木材缺陷断层成像算法. 林业工程学报. 2023(04): 137-143 . 百度学术4. 付志伟，王奇光. 数控机床在我国木材加工行业的应用现状. 林产工业. 2021(03): 77-79 . 百度学术5. 袁霄，陈勇平，郭文静，唐启恒. 古建筑木构件隐蔽式残损适宜性检测技术. 木材科学与技术. 2021(06): 9-15 . 百度学术6. 张慧娟. 木材应力波检测精度的影响因素研究. 中国林副特产. 2020(01): 27-30 . 百度学术7. 黄鹏桂，赵璠，李晓平，吴章康，汤正捷，张严风. 卷积神经网络在红木树种识别中的应用. 浙江农林大学学报. 2020(06): 1200-1206 . 本站查看8. 孙丽萍，许述正，魏喜雯，岳琪，王一凡. 应力波木材无损检测技术应用及研究进展. 世界林业研究. 2020(06): 39-43 . 百度学术其他类型引用(10)
-
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20230263
点击查看大图
计量
- 文章访问数: 574
- HTML全文浏览量: 177
- PDF下载量: 40
- 被引次数: 18
