-
森林是陆地生态系统的主体，给人类的生存与发展提供了生态系统服务和丰富的物质基础[1−2]。森林为人类提供储存碳、承载生物多样性和调节气候等服务并提供能源、建筑材料和食物[3]，在维护全球生态平衡中起着重要的作用。但是全球气候和土地利用变化、移民开垦、乱砍滥伐、过度放牧等严重损害了森林的健康和复原力，对生态环境造成了不可逆的破坏[4−5]。中国西北干旱区生态环境脆弱，植被覆盖率较低，土地沙漠化严重，水资源匮乏，生态系统稳定性差[6]。胡杨Populus euphratica是干旱荒漠区的特有种，具有较强的耐旱耐盐碱能力，其密集的林冠能够降低地表风速，减少风蚀作用，从而有效保护土壤不被风化和侵蚀[7]。作为许多珍稀野生动植物的重要栖息地，胡杨林为生物多样性的保护和维持提供了重要的生态环境。它为多种动物提供了食物和栖息地，有助于维持生态系统的平衡[8]，保障生态安全。
克里雅河是中国新疆南部的第四大水系，其尾闾达里雅布依深入塔里木盆地腹地300 km，是极具科学研究价值的“原始绿洲”。胡杨为该区主要树种，由于干旱条件制约，胡杨林的生存状况正面临严重的威胁[9]。虽然有很多学者开展了胡杨特征的研究，但是对胡杨的健康评价研究很少，大部分集中在无人机[10]、生物多样性地下水和植被关系[11]等方面。为了确保这一珍贵资源的可持续利用和保护，需要采取有效措施，如加强生态恢复、合理规划土地利用和加强管理等[12]。因此，本研究对达里雅布依绿洲胡杨进行林健康评价，以摸清胡杨林健康状况，这对发挥绿洲的生态作用具有重要意义。
-
达里雅布依绿洲地处新疆维吾尔自治区于田县境内(38°16′~38°37′N，81°05′~81°46′E)，海拔1 100~1 300 m，是塔里木盆地南缘第二大河流克里雅河的尾闾绿洲[13]。克里雅河从南到北汇入绿洲，是该地区主要水分来源。该区域处于塔克拉玛干沙漠腹地，降水量极低，蒸发过程强烈，风沙活动频繁，气候极度干燥，生态环境脆弱[14]。属于大陆性沙漠气候。该地区的光热资源却相当充足，全年≥10 ℃的积温为4 208 ℃，无霜期长达192~235 d。研究区气温年际间变化稳定，年平均气温为11.6 ℃。然而，该地区的降水量非常有限，不足20 mm，与此同时，年平均蒸发量高达2 480 mm，是降水量的124倍，这使得大气极度干燥。绿洲群落主要由胡杨、柽柳Tamarix ramosissima、芦苇Phragmites australis、骆驼刺Alhagi sparsifolia等组成[15]，由上述优势物种构成的群落有效地抑制了荒漠的扩张。
-
于2018年设立了地下水监测井监测地下水位，已经建好17口地下水监测井。设置50 m×50 m的样地，并划分为4个25 m×25 m的样方，共计68个。记录每个样方内乔灌木的数量、胸径、树高、冠幅等指标。并在样方内随机布设了5个1 m×1 m的草本小样方，调查草本植物的多度、高度、盖度等指标，并运用手持全球定位系统(GPS)记录各调查样地的经纬度信息。植被调查时间在2023年夏季。
-
每个样地中随机挖取3处深度为100 cm的土壤剖面，分为6层(0~5、5~20、20~40、40~60、60~80、80~100 cm)，将不同剖面的同一深度土壤进行充分混合后，将获取的土壤样品放置在铝盒与塑封袋内保存，用于测量土壤含水率、有机质、全氮、全磷与全钾等土壤理化性质。
-
根据国内外相关研究，结合达里雅布依绿洲胡杨林的实际情况[16−19]，构建了胡杨林健康评价体系，指标体系由森林生产力指标、森林群落结构指标、生境因子指标等3个一级指标和17个二级指标构成，二级指标包括平均树高、平均胸径、郁闭度、灌木盖度、草本盖度、乔木密度、Shannon-Wiener指数、Simpson指数、Pielou指数、Margalef指数、地下水埋深、土壤含水率、土壤有机质、全氮、全磷、全钾和人为干扰。使用Margalef指数、Simpson指数、Pielou指数和Shannon-Wiener指数的公式，计算生物群落的丰富度和生物多样性；人为干扰按照受干扰程度分为轻度干扰、中度干扰、重度干扰3类[20]；地下水埋深根据地下水井的均值计算。通过计算不同土层深度的土壤指标平均值，获得土壤含水率、土壤有机质、全氮、全磷和全钾质量分数。
-
对达里雅布依绿洲地下水埋深进行K-means聚类分析，将其分为浅地下水埋深(2.00~2.59 m)、中地下水埋深(2.59~5.00 m)、深地下水埋深(5.00~7.25 m)。
-
采用主成分分析法进行降维，从17个指标中选取主成分指标，计算综合得分，利用聚类分析法对沙漠腹地达里雅布依绿洲的胡杨林进行分类，得出胡杨林健康状况。
先对指标数据进行标准化处理，得到标准化矩阵；对17项指标数据进行KMO和Bartlett检验，KMO检验值为0.607 (＞0.5)，Bartlett检验的P＜0.05，说明各检验量的相关性足够小。综上，可以采用主成分分析进行胡杨林健康评价，处理各样地指标数据。由表1可见：提取的5个主成分特征值均＞1，累计方差解释率达78.093%，表明这些指标能充分反映原变量信息，主成分分析结果可靠。
表 1 主成分因子的特征值和方差贡献率
Table 1. Eigenvalues and variance contribution rates of principal component factors
名称 特征值 方差解释率/% 累计方差解释率/% 权重/% 主成分1 5.088 29.932 29.932 38.329 主成分2 2.763 16.252 46.185 20.811 主成分3 2.472 14.540 60.724 18.618 主成分4 1.840 10.824 71.548 13.860 主成分5 1.113 6.546 78.093 8.382 根据公式(1)的计算结果，各主成分因子的权重分别为：第1个主成分因子占38.329%、第2个主成分因子占20.811%、第3个主成分因子占18.618%、第4个主成分因子占13.860%以及第5个主成分因子占8.382%。结合公式(2)~(3)，利用之前计算得到的各主成分因子的权重，计算各样地的森林健康指数，全面评估达里雅布依绿洲胡杨林的森林健康状况。计算公式如下：
$$ {W_i} = \frac{{{\lambda _i}}}{{\displaystyle \sum_{i=1}^n {\lambda_i } }} \text{；} $$ (1) $$ {F_i} = \sum\limits_{i = 1}^n {{C_{ij}}} \times Z_{{\mathrm{X}}j} \text{；} $$ (2) $$ {H_i} = \sum\limits_{i = 1}^n {{W_i}} \times {F_i} 。 $$ (3) 式(1)~(3)中：Wi为第i个主成分的权重；λi为第i个主成分的方差贡献率；Fi为第i个主成分得分；Cij为第i个主成分的第j个指标的得分系数；ZXj为第j个指标的标准化值；Hi为第i个样地的健康指数；n为主成分因子个数。
结合干旱区实际情况，运用系统聚类方法，基于胡杨林健康指数，将胡杨林健康划分为4个等级：健康，健康指数为[0.91, 0.97]；亚健康，健康指数为[0.59, 0.91)；中健康，健康指数为[0.23, 0.59)；不健康，健康指数为[−0.15, 0.23)。
-
采用Excel 2019进行数据整理与计算，利用SPSS 23.0进行主成分分析、聚类分析和非参数检验，使用Origin 2022作图。
-
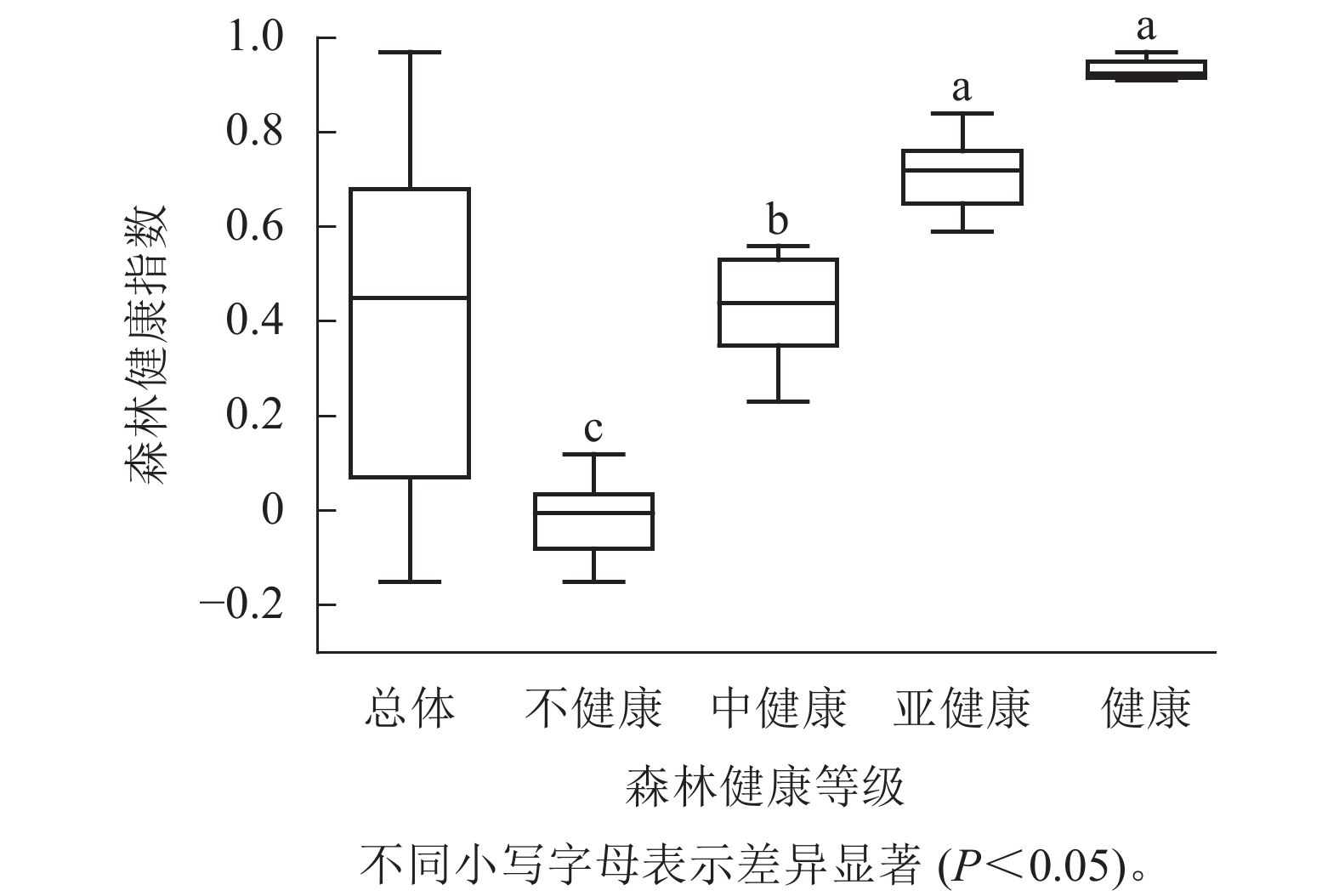
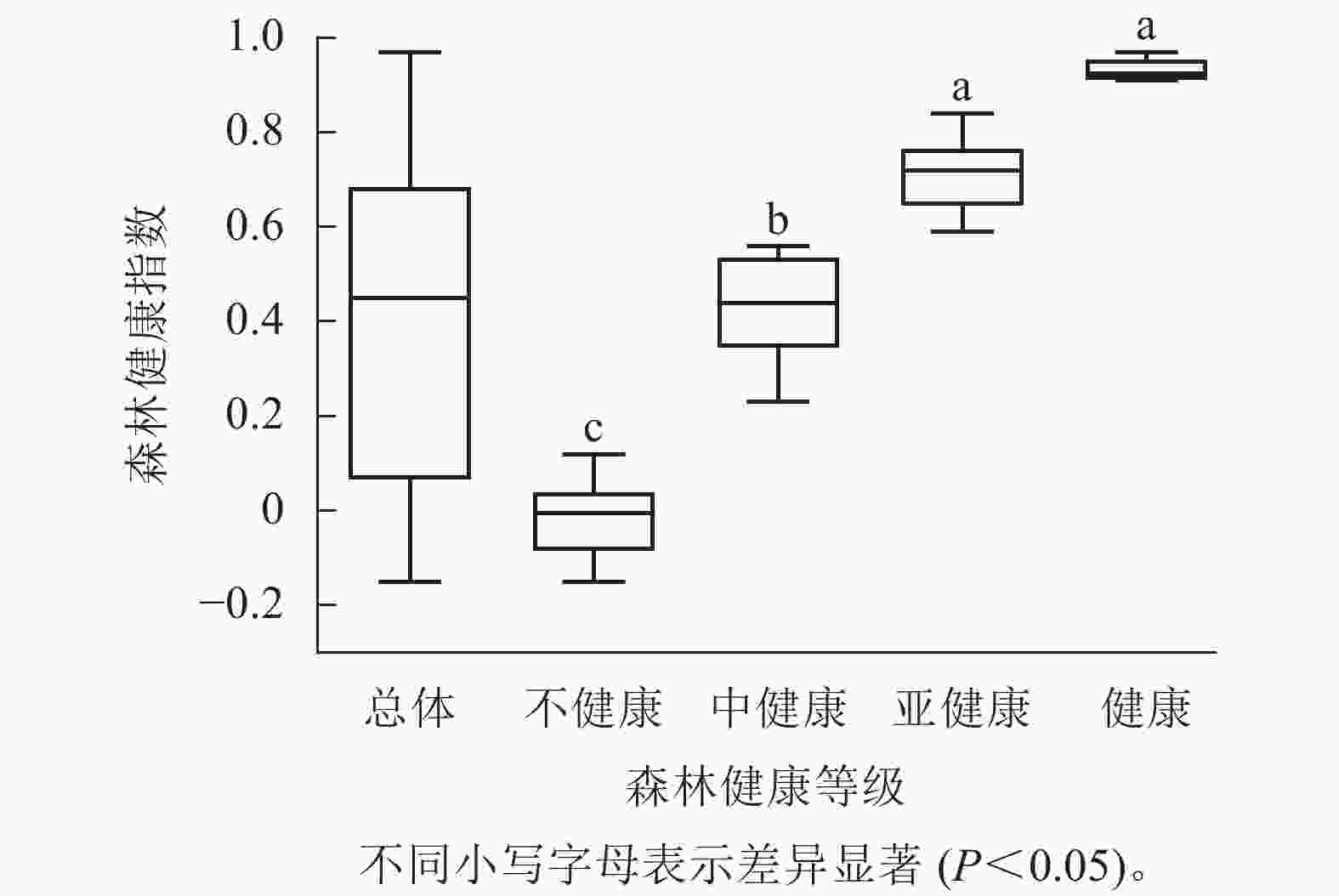
聚类分析(图1)表明：68个达里雅布依绿洲胡杨林样地中，23个样地处于中健康状态，这占据了总样地数量的33.8%，森林健康指数范围为[0.23, 0.59)，中位数0.44；21个样地处于亚健康状态，约占30.9%，森林健康指数范围为[0.59, 0.91)，中位数0.72；20个样地处于不健康状态，占29.4%，森林健康指数范围为[−0.15, 0.23)，中位数−0.01；4个样地处于健康状态，占5.9%，森林健康指数范围为[0.91, 0.97]，中位数0.93。其中，达里雅布依绿洲胡杨林的整体森林健康指数的中位数为0.45，处于中健康指数范围[0.23, 0.59)。
图 1 达里雅布依绿洲的胡杨林整体健康状况
Figure 1. Overall health status of P. euphratica forests in Dali Yabuyi Oasis
-
Spearman相关性分析(表2)表明：影响达里雅布依绿洲胡杨林健康状况的多个因子与各样地的森林健康指数显著相关。其中，森林生产力指标与森林健康指数的相关系数：郁闭度(0.681)＞平均树高(0.375) ＞灌木盖度(0.306)＞乔木密度(0.323)＞草本盖度(0.254)＞平均胸径(0.101)；森林群落结构指标与森林健康指数的相关系数：Simpson指数(0.558)＞Shannon-Wiener指数(0.509)＞Pielou指数(0.364)＞Margalef指数(0.226)；生境因子指标与森林健康指数的相关系数： 地下水平埋深(0.797)＞全氮(0.749)＞土壤含水率＞(0.444)＞土壤有机质(0.285)＞全钾(0.167)＞全磷(−0.283)＞人为干扰(−0.741)。
表 2 达里雅布依绿洲胡杨林健康指数与各因子的相关性系数
Table 2. Correlation coefficients of health indices of poplar forests in Dali Yabuyi Oasis with factors
指标 影响因子 相关系数 指标 影响因子 相关系数 森林生产力 平均树高 0.375(0.002***) Margalef指数 0.226(0.063*) 平均胸径 0.101(0.415) 郁闭度 0.681(0.000***) 生境因子 地下水埋深 0.797(0.000***) 灌木盖度 0.306(0.011**) 土壤含水率 0.444(0.000***) 草本盖度 0.254(0.036**) 土壤有机质 0.285(0.018**) 乔木密度 0.323(0.007***) 全氮 0.749(0.000***) 全磷 −0.283(0.020**) 森林群落结构 Shannon-Wiener指数 0.509(0.000***) 全钾 0.167(0.174) Simpson指数 0.558(0.000***) 人为干扰 −0.741(0.000***) Pielou指数 0.364(0.002***) 说明：***、**、*分别表示1%、5%、10%的显著性水平。括号内数值为P值。 综合来看，达里雅布依绿洲胡杨林的健康指数主要受森林生产力指标、生境因子指标和群落结构指标的影响。其中，地下水埋深、全氮、郁闭度、Simpson指数以及Shannon-Wiener指数是影响森林健康程度的主要因子。森林群落指标因子中Simpson指数和Shannon-Wiener指数对胡杨健康影响较大，这些因子在本质上充当了森林生态系统物种多样性的指示器。森林内物种的丰富程度和林分结构的复杂性，直接关联着生态系统的稳定性。简而言之，物种越多、结构越复杂的森林，其生态系统越稳固，进而反映出森林的健康状况更为优越。在生境因子指标中，地下水埋深和全氮是影响森林健康的主要因子，与森林健康指数呈现显著相关性，全磷、全钾以及土壤有机质与达里雅布依绿洲胡杨林健康指数的相关性较弱，对森林健康水平的影响程度较低。人工干扰与森林健康呈负相关，可能是由于人工干扰严重的地方水源充足，胡杨能够得到更好的水源供给和生长。
结合图1和表2，可以得出森林的健康状态主要体现为较高的胸径、树高及生物量指标，还体现在植被类型丰富、群落结构完整，具有出色的生产力和稳定性，以及强大的恢复力和抗干扰能力，并且地下水埋深较浅，能够得到充分的水分供给。相反，当森林呈现不健康状态时，其胸径、树高及生物量指标相对较低，物种多样性减少，群落结构单一，生产力和稳定性下降，恢复力和抗干扰能力减弱，从而更容易受到外界干扰和病虫害的威胁，并且所处位置的地下水埋深较深，胡杨无法得到太多的水源补充。达里雅布依地区的森林普遍处于不健康和亚健康状态，因此，亟需采取科学合理的抚育管理措施，以优化森林结构，提升其生产力和稳定性，进而全面提高达里雅布依地区森林的健康水平。
-
对达里雅布依绿洲地下水埋深进行K-means聚类分析，分为深地下水埋深、中地下水埋深、浅地下水埋深，并针对绿洲内不同地下水埋深条件下胡杨林的森林健康指数进行了差异性分析(图2A)。研究显示：绿洲3种不同地下水埋深胡杨林的森林健康指数整体上差异显著(P＜0.05)，其中，深地下水埋深森林健康指数显著低于浅地下水埋深和中地下水埋深(P＜0.05)，深地下水埋深的森林健康指数中位数(0)处于不健康的指数范围[−0.15, 0.23) ；浅地下水埋深森林健康指数中位数(0.65)处于亚健康的指数范围[0.59, 0.91)；中地下水埋深中位数(0.45)处于中健康的指数范围[0.23, 0.59)；浅地下水埋深(0.65)和中地下水埋深(0.45)的森林健康指数差异不显著，2种地下水埋深的森林健康状况相近。整体来看，不同地下水埋深森林健康指数：浅地下水埋深(0.65)＞中地下水埋深(0.45)＞深地下水埋深(0)。
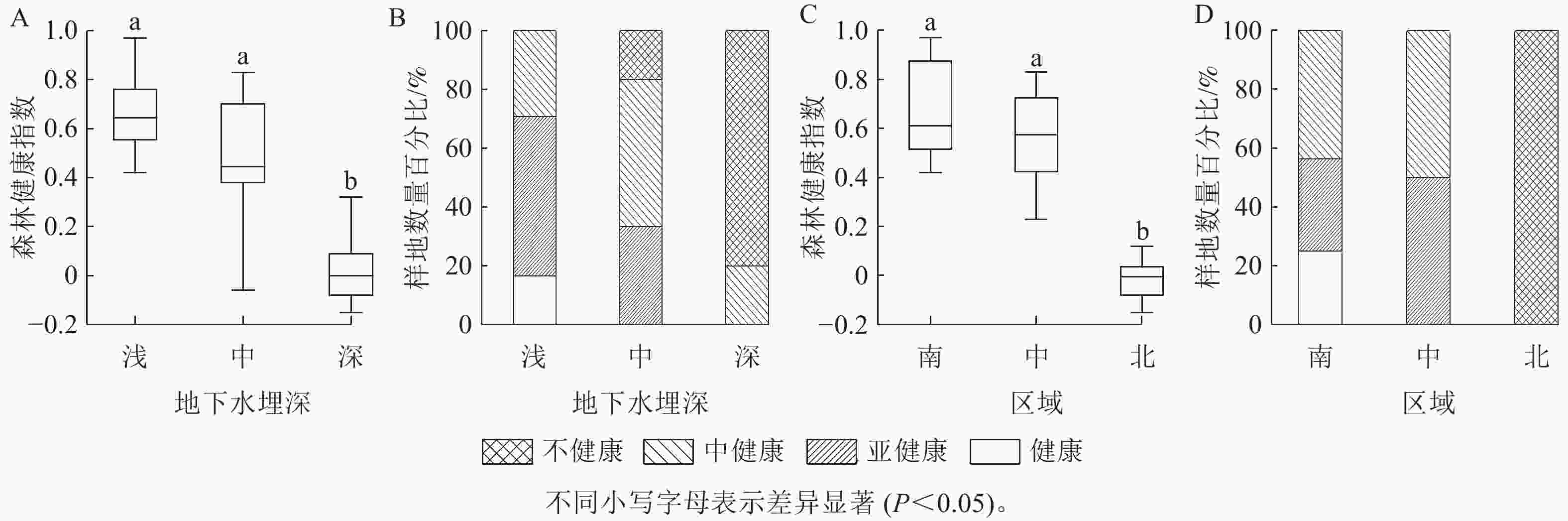
图 2 达里雅布依绿洲不同地下水埋深和不同区域胡杨林健康状况和构成
Figure 2. Forest health status and composition of P. euphratica forests in different grourdwater depths and regions of Dali Yabuyi Oasis
图2B结果显示：在达里雅布依绿洲胡杨林的不同地下水埋深中，浅地下水埋深条件下的森林健康状态集中在亚健康(54.2%)、中健康(29.2%)和健康(16.7%)水平，显示出相对较高的森林健康水平。相比之下，中地下水埋深条件下的森林健康状态则主要处于中健康(50.0%)、亚健康(33.3%)和不健康(16.7%)水平，森林健康水平相对中等。而深地下水埋深条件下的森林健康状态集中在不健康(80.0%)和中健康(20.0%)水平，显示出相对较低的森林健康水平。这一结果表明：随着地下水位的变浅，森林健康指数相应提高。
-
本研究按照绿洲内的植被状况和环境变化梯度将绿洲划分为北部、中部和南部3个部分，并分别对这3个部分胡杨林的森林健康指数进行差异性分析，结果如图2C所示。达里雅布依绿洲北部胡杨林的森林健康指数显著低于中部和南部地区(P＜0.05)，森林健康指数中位数(−0.01)处于不健康指数范围[−0.15, 0.23)；南部和中部的森林健康指数差异不显著，南部森林健康指数中位数(0.61)处于亚健康指数范围[0.59, 0.91)；中部森林健康指数中位数(0.58)处于中健康指数范围[0.23, 0.59)。整体来看，从北部、中部到南部，森林健康指数呈增加趋势，各区域森林健康指数：南部(0.61)＞中部(0.58)＞北部(−0.01)。
根据图2D的分析结果，达里雅布依绿洲不同区域的森林健康构成情况存在差异。在绿洲南部，胡杨林主要呈现中健康(43.8%)、亚健康(31.3%)和健康(25.0%)状态，这表明该区域的森林健康水平相对较高。在中部区域，胡杨林主要处于亚健康(50.0%)和中健康(50.0%)状态，森林健康水平相对中等。然而，北部区域的胡杨林全部处于不健康状态，显示出较低的森林健康水平。这些结果表明：从北部、中部到南部，森林健康指数相应提高。
-
本研究采用主成分分析法构建达里雅布依绿洲胡杨林森林健康评价模型，对该地胡杨林的森林健康状况进行评价。目前，森林健康评价方法有很多种，层次分析是最常用的方法，但其在确定权重时，人为影响太大，会导致结果有很大主观性[21]。本研究采用主成分分析法，将原先的17个复杂指标简化为5个独立主成分因子，优化了指标体系，在决定权重的过程中，基于各主要成分因子的真实贡献度来进行，而不是手动赋权，这样确保了评估结果的客观性和合理性。该方法不仅简化了数据的构造，还增强了评估的精确度和信赖度[22]。
达里雅布依绿洲深地下水埋深森林健康指数显著低于浅地下水埋深和中地下水埋深。这与在塔里木河北部[23]和克里雅河北部[24]的植被生长与地下水关系相吻合。深地下水埋深的胡杨林，由于地下水埋深较深，胡杨得不到充分的水分供给，森林结构较为简单，随着地下水埋深变高，胡杨能够得到充分的水分供给，森林结构变得复杂，生产力水平提高，森林健康指数也随之提高。达里雅布依绿洲南部和中部的胡杨林健康指数显著高于北部胡杨林健康指数。根据前人研究可知：绿洲南部森林结构较为完整[25]，克里雅河从此处开始汇入绿洲，丰富的地表水和较高的地下水位使得较多植物种类在这里出现[26]。水作为干旱区重要的环境因素之一，是荒漠植物生长发育的主要限制因子，对胡杨的健康生长具有至关重要的作用[27]。达里雅布依绿洲胡杨林水源补给主要来自克里雅河，河水从南部汇入绿洲，南部和中部地区获得的水分要比北部获得的水分多。
对达里雅布依绿洲胡杨林整体森林健康状况的评价结果表明：胡杨林处于中健康、亚健康和不健康状态的比例分别为33.8%、30.9%和29.4%，整体森林健康水平有待提高。结合前人对绿洲胡杨的研究结果[28−29]，达里雅布依绿洲胡杨林受水资源影响较大。不健康胡杨林大多处于深地下水埋深或较难获得水分补给的北部区域，应适当增加输水频率，通过部分河道改道，使缺水地区得到水分供给，提升胡杨林健康指数。旅游资源开发和牧民过度放牧等人为干扰也会影响胡杨林健康，应对人为干扰较大的胡杨林进行保护，提高当地居民生态环保意识，适度放牧，划定胡杨保护区，增强森林生态系统的抗干扰能力，改善森林健康状态，从而抑制沙漠化扩大的速度。
-
达里雅布依绿洲胡杨林总体健康状况不佳，有29.4%处于不健康状态，33.8%处于中健康状态，30.9%处于亚健康状态，仅有5.9%处于健康状态。地下水埋深、全氮、郁闭度、Simpson指数以及Shannon-Wiener指数是影响森林健康程度的主要因子。达里雅布依绿洲胡杨林中，深地下水埋深森林健康水平相对较低。浅地下水埋深森林健康水平相对较高。整体来看，不同地下水埋深森林健康指数：浅地下水埋深(0.65)＞中地下水埋深(0.45)＞深地下水埋深(0)。从达里雅布依绿洲的不同区域，总体趋势来看，从北部、中部到南部，森林健康指数逐渐上升。各区域森林健康指数：南部(0.61)＞中部(0.58)＞北部(−0.01)。
Health evaluation of Populus euphratica forest in Dali Yabuyi Oasis in the hinterland of the desert
-
摘要:
目的 胡杨Populus euphratica林的普遍退化严重威胁着干旱区绿洲的生态安全，因此，摸清胡杨林的健康状况，对胡杨林的可持续经营具有重要意义。 方法 以沙漠腹地达里雅布依绿洲胡杨林为研究对象，在对区域内68个典型样地进行野外调查的基础上，从森林生产力、森林群落结构和生境因子指标等方面选取了17项指标，运用主成分分析和聚类分析法，构建适用于该区域胡杨林的健康评价指标体系和模型，计算森林健康指数，综合评价该地区胡杨林的健康状况。 结果 ①达里雅布依绿洲胡杨林整体森林健康状况较差，有29.4%处于不健康状态，33.8%处于中健康状态，30.9%处于亚健康状态，5.9%处于健康状态。地下水埋深、全氮、郁闭度、Simpson指数以及Shannon-Wiener指数是影响森林健康程度的主要因子。②达里雅布依绿洲胡杨林中，深地下水埋深森林健康指数显著低于浅地下水埋深和中地下水埋深(P＜0.05)，森林健康水平相对较低。浅地下水埋深森林健康水平相对较高。整体来看，不同地下水埋深森林健康指数：浅地下水埋深(0.65)＞中地下水埋深(0.45)＞深地下水埋深(0)。③在达里雅布依绿洲不同区域胡杨林中，北部胡杨林的森林健康指数显著低于中部和南部，显示出较低的健康水平，南部森林健康水平相对较高。从北部、中部到南部，森林健康指数总体呈现逐渐上升的趋势，各区域森林健康指数：南部(0.61)＞中部(0.58)＞北部(−0.01)。 结论 达里雅布依绿洲整体胡杨林健康水平较差，地下水位越浅，胡杨健康指数就越高，不同区域中，从南部、中部到北部胡杨林健康指数呈现降低趋势。图2表2参29 Abstract:Objective The widespread degradation of Populous euphratica forests seriously threatens the ecological security of oases in arid zones. Therefore, mapping the health of P. euphratica forests is important for their sustainable management. Method The P. euphratica forests in Dali Yabuyi Oasis in the desert hinterland were taken as the object, and based on the field survey of 68 typical sample plots in the region, 17 indexes were selected from the aspects of forest productivity, forest community structure and habitat factors, and the health evaluation index system and health evaluation model applicable to the P. euphratica forests in the region were constructed by using the principal component analysis and the cluster analysis method, the forest health indexes were calculated, and the health of the P. euphratica forests in the region was comprehensively evaluated. Result (1) The overall forest health of oasis P. euphratica forests was poor, with 29.4% in an unhealthy state, 33.8% in a medium-healthy state, 30.9% in a sub-healthy state, and 5.9% in a healthy state. Groundwater burial depth, total nitrogen, depression, Simpson index, and Shannon-Wiener index were the main factors affecting forest health. (2) In the P. euphratica forests of Dali Yabuyi Oasis, the forest health index of deep groundwater burial depth is significantly lower than that of shallow and medium groundwater burial depth (P＜0.05), and the forest health level is relatively low. Shallow groundwater burial depths have relatively high levels of forest health. Overall, the forest health indices of different groundwater depths: shallow groundwater depth (0.65)＞medium groundwater depth (0.45)＞deep groundwater depth (0). (3) Among the P. euphratica forests in different regions of the oasis, the forest health index of the P. euphratica forests in the north is significantly lower than that in the center and south, and the forest health level is relatively low. Forest health is relatively high in the south. Overall, the forest health index showed an increasing trend from the north, center to the south, and the forest health index in different regions: south (0.61)＞center (0.58)＞north (−0.01). Conclusion The overall health level of P. euphratica forests in the oasis is poor, the shallower the water table is, the higher the health index of P. euphratica forests is, and the health index shows a decreasing trend from the south, the center to the north in different regions. [Ch, 2 fig. 2 tab. 29 ref.] -
图 1 达里雅布依绿洲的胡杨林整体健康状况
Figure 1 Overall health status of P. euphratica forests in Dali Yabuyi Oasis
图 2 达里雅布依绿洲不同地下水埋深和不同区域胡杨林健康状况和构成
Figure 2 Forest health status and composition of P. euphratica forests in different grourdwater depths and regions of Dali Yabuyi Oasis
表 1 主成分因子的特征值和方差贡献率
Table 1. Eigenvalues and variance contribution rates of principal component factors
名称 特征值 方差解释率/% 累计方差解释率/% 权重/% 主成分1 5.088 29.932 29.932 38.329 主成分2 2.763 16.252 46.185 20.811 主成分3 2.472 14.540 60.724 18.618 主成分4 1.840 10.824 71.548 13.860 主成分5 1.113 6.546 78.093 8.382 
下载: 导出CSV
表 2 达里雅布依绿洲胡杨林健康指数与各因子的相关性系数
Table 2. Correlation coefficients of health indices of poplar forests in Dali Yabuyi Oasis with factors
指标 影响因子 相关系数 指标 影响因子 相关系数 森林生产力 平均树高 0.375(0.002***) Margalef指数 0.226(0.063*) 平均胸径 0.101(0.415) 郁闭度 0.681(0.000***) 生境因子 地下水埋深 0.797(0.000***) 灌木盖度 0.306(0.011**) 土壤含水率 0.444(0.000***) 草本盖度 0.254(0.036**) 土壤有机质 0.285(0.018**) 乔木密度 0.323(0.007***) 全氮 0.749(0.000***) 全磷 −0.283(0.020**) 森林群落结构 Shannon-Wiener指数 0.509(0.000***) 全钾 0.167(0.174) Simpson指数 0.558(0.000***) 人为干扰 −0.741(0.000***) Pielou指数 0.364(0.002***) 说明：***、**、*分别表示1%、5%、10%的显著性水平。括号内数值为P值。
下载: 导出CSV
-
[1] 邹为民, 丁俊, 黄子豪, 等. 浙江省松阳县亚热带森林干扰与恢复遥感监测[J]. 浙江农林大学学报, 2024, 41(2): 353 − 361. ZOU Weimin, DING Jun, HUANG Zihao, et al. Remote sensing monitoring of subtropical forest disturbance and restoration in Songyang County, Zhejiang Province[J]. Journal of Zhejiang A&F University, 2024, 41(2): 353 − 361. [2] 申小娟, 杜盛. 甘肃省5种典型人工林健康状况[J]. 水土保持研究, 2023, 30(3): 295 − 300. SHEN Xiaojuan, DU Sheng. Health assessment of five typical plantation forests in Gansu Province[J]. Research of Soil and Water Conservation, 2023, 30(3): 295 − 300. [3] TRUMBORE S, BRANDO P, HARTMANN H. Forest health and global change[J]. Science, 2015, 349(6250): 814 − 818. [4] PAUTASSO M, SCHLEGEL M, HOLDENRIEDER O. Forest health in a changing world[J]. Microbial Ecology, 2015, 69(4): 826 − 842. [5] HARTMANN H, BASTOS A, DAS A J, et al. Climate change risks to global forest health: emergence of unexpected events of elevated tree mortality worldwide[J]. Annual Review of Plant Biology, 2022, 73: 673 − 702. [6] LI Suyuan, MIAO Lijuan, JIANG Zhihong, et al. Projected drought conditions in Northwest China with CMIP6 models under combined SSPs and RCPs for 2015−2099[J]. Advances in Climate Change Research, 2020, 11(3): 210 − 217. [7] YUSUP A, HALIK Ü, ABLIZ A, et al. Population structure and spatial distribution pattern of Populus euphratica riparian forest under environmental heterogeneity along the Tarim River, northwest China [J/OL]. Frontiers in Plant Science, 2022, 13 : 844819[2024-01-10]. doi: 10.3389/fpls.2022.844819. [8] LI Mengyi, DENG Mingjiang, LING Hongbo, et al. Constructing a new irrigation model for desert riparian forests based on response of canopy EVI loss and tree rings growth to groundwater fluctuation [J/OL]. Ecological Indicators, 2023, 148 : 110060[2024-01-10]. doi: 10.1016/j.ecolind.2023.110060. [9] WAN Yanbo, PENG Lei, ANWAIER A, et al. Effects of meteorological factors and groundwater depths on sap flow density of Populus euphratica in a desert oasis, Taklamakan Desert, China [J/OL]. Frontiers in Plant Science, 2024, 15 : 1330426[2024-01-10]. doi: 10.3389/fpls.2024.1330426. [10] PENG Lei, WAN Yanbo, SHI Haobo, et al. Influence of climate, topography, and hydrology on vegetation distribution patterns: oasis in the Taklamakan Desert Hinterland [J/OL]. Remote Sensing, 2023, 15 (22): 5299[2024-01-10]. doi: 10.3390/rs15225299. [11] SHI Haobo, SHI Qingdong, ZHOU Xiaolong, et al. Influence of surface water and groundwater on functional traits and trade-off strategies of oasis communities at the end of the Keriya River, China [J/OL]. Frontiers in Plant Science, 2024, 15 : 1340137[2024-01-10]. doi: 10.3389/fpls.2024.1340137. [12] ZHU Yonghua, CHEN Yaning, REN Lilang, et al. Ecosystem restoration and conservation in the arid inland river basins of northwest China: problems and strategies[J]. Ecological Engineering, 2016, 94: 629 − 637. [13] 师庆东, 郭玉川, 周小龙, 等. 塔克拉玛干沙漠克里雅河尾闾达理雅博依绿洲地表水、地下水对植被格局的影响机制[J]. 新疆大学学报(自然科学版中英文), 2019, 36(3): 253 − 259, 286. SHI Qingdong, GUO Yuchuan, ZHOU Xiaolong, et al. Mechanism of the influence of surface water and groundwater on vegetation pattern in Daliyaboyi Oasis at the tail of Keriya River in Taklamakan Desert[J]. Journal of Xinjiang University (Natural Science Edition in Chinese and English), 2019, 36(3): 253 − 259, 286. [14] 万彦博, 师庆东, 戴岳, 等. 沙漠腹地天然绿洲不同林龄胡杨水分利用来源[J]. 应用生态学报, 2022, 33(2): 353 − 359. WAN Yanbo, SHI Qingdong, DAI Yue, et al. Water sources of Populus euphratica with different tree ages in the oasis of desert hinterland[J]. Chinese Journal of Applied Ecology, 2022, 33(2): 353 − 359. [15] SHI Haobo, ZHANG Feng, SHI Qingdong, et al. Responses of arid plant species diversity and composition to environmental factors[J]. Journal of Forestry Research, 2023, 34(6): 1723 − 1734. [16] 李雪宁, 徐先英, 郑桂恒, 等. 石羊河下游人工梭梭林健康评价体系构建及应用研究[J]. 干旱区研究, 2022, 39(3): 872 − 882. LI Xuening, XU Xianying ZHEN Guiheng, et al. A health evaluation of a Haloxylon ammodendron plantation in the Shiyang River lower reaches[J]. Arid Zone Research, 2022, 39(3): 872 − 882. [17] 闫晋升, 王永东, 娄泊远, 等. 哈萨克斯坦首都努尔苏丹人工林健康评价[J]. 干旱区研究, 2021, 38(5): 1474 − 1483. YAN Jinsheng, WANG Yongdong, LOU Boyuan, et al. Health assessment of plantations in Nursultan, capital of Kazakhstan[J]. Arid Zone Research, 2021, 38(5): 1474 − 1483. [18] 曹小玉, 委霞, 赵文菲, 等. 基于结构方程模型的森林健康评价[J]. 生态学杂志, 2021, 40(8): 2635 − 2647. CAO Xiaoyu, WEI Xia, ZHAO Wenfei, et al. Evaluation of forest health based on structural equation model[J]. Chinese Journal of Ecology, 2021, 40(8): 2635 − 2647. [19] 何苗, 宁虎森, 罗青红. 甘家湖典型防风固沙林健康评价[J]. 生态科学, 2022, 41(4): 78 − 83. HE Miao, NING Husen, LUO Qinghong, et al. Health evaluation of typical windbreak and sand-fixation forest in Ganjiahu[J]. Ecological Science, 2022, 41(4): 78 − 83. [20] 谭继旭. 青海省高寒黄土区典型小流域人工生态公益林健康评价[D]. 北京: 北京林业大学, 2020. TAN Jixu. Health Evaluation of Artificial Ecological Public Welfare Forest in Typical Small Watershed of Alpine Loess Area in Qinghai Province [D]. Beijing: Beijing Forestry University, 2020. [21] 王秋燕, 陈鹏飞, 李学东, 等. 森林健康评价方法综述[J]. 南京林业大学学报(自然科学版), 2018, 42(2): 177 − 183. WANG Qiuyan, CHEN Pengfei, LI Xuedong, et al. Review of forest health assessment methods[J]. Journal of Nanjing Forestry University (Natural Sciences Edition), 2018, 42(2): 177 − 183. [22] 滕芝妍, 崔雨同, 应学兵, 等. 不同南瓜品种的综合评价[J]. 浙江农林大学学报, 2020, 37(1): 143 − 150. TENG Zhiyan, CUI Yutong, YING Xuebing, et al. Comprehensive evaluation of pumpkin cultivars based on a principal component analysis[J]. Journal of Zhejiang A&F University, 2020, 37(1): 143 − 150. [23] 玉米提·哈力克, 柴政, 艾尔肯·艾白不拉, 等. 塔里木河下游输水恢复过程中胡杨生长对地下水位的响应[J]. 水土保持通报, 2011, 31(5): 18 − 22. Umut Halik, CHAI Zheng, Arkin Habibulla, et al. Response of Populus euphratica to groundwater level after water diversion to lower reaches of Tarim River[J]. Bulletin of Soil and Water Conservation, 2011, 31(5): 18 − 22. [24] 王雅梅, 张青青, 李骊, 等. 新疆克里雅河下游植被与地下水埋深关系初探[J]. 干旱区研究, 2020, 37(3): 562 − 569. WANG Yamei, ZHANG Qingqing, LI Li, et al. Preliminary study on the relationship between vegetation and groundwater depth in the lower reaches of the Keriya River[J]. Arid Zone Research, 2020, 37(3): 562 − 569. [25] 张文奇, 周小龙, 尼加提·卡斯木, 等. 沙漠腹地达理雅博依天然绿洲植物群落特征分析[J]. 新疆大学学报(自然科学版中英文), 2019, 36(3): 276 − 286. ZHANG Wenqi, ZHOU Xiaolong, Nijiati Kasimu, et al. Study of plant community characteristics in Daliyaboyi natural oasis in desert Hinterland[J]. Journal of Xinjiang University (Natural Science Edition in Chinese and English), 2019, 36(3): 276 − 286. [26] 吴宏伟. 大气-植被-土体相互作用: 理论与机理[J]. 岩土工程学报, 2017, 39(1): 1 − 47. WU Hongwei. Atmosphere-plant-soil interactions: theories and mechanisms[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(1): 1 − 47. [27] 陈亚宁, 李忠勤, 徐建华, 等. 中国西北干旱区水资源与生态环境变化及保护建议[J]. 中国科学院院刊, 2023, 38(3): 385 − 393. CHEN Yaning, LI Zhongqin, XU Jianhua, et al. Changes and protection suggestions in water resources and ecological environment in arid region of northwest China[J]. Bulletin of Chinese Academy of Sciences, 2023, 38(3): 385 − 393. [28] WAN Yanbo, SHI Qingdong, DAI Yue, et al. Water use characteristics of Populus euphratica Oliv. and Tamarix chinensis Lour. at different growth stages in a desert oasis [J/OL]. Forests, 2022, 13 (2): 236[2024-01-10]. doi: 10.3390/f13020236. [29] 麦尔哈巴·尼加提, 戴岳, 师庆东, 等. 沙漠腹地天然绿洲胡杨和柽柳叶片δ13C值对不同地下水埋深的响应[J]. 应用生态学报, 2020, 31(4): 1083 − 1087. Marhaba Nijiat, DAI Yue, SHI Qingdong, et al. Response of foliar δ13C in Populus euphratica and Tamarix sp. to different groundwater depths in the oasis of desert hinterland[J]. Chinese Journal of Applied Ecology, 2020, 31(4): 1083 − 1087. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20240148
点击查看大图
图(2) / 表(2)
计量
- 文章访问数: 113
- HTML全文浏览量: 33
- PDF下载量: 5
- 被引次数: 0
