-
立木材积表作为林业行业标准，编制于20世纪70年代末中国森林资源连续清查体系初建时期，至今已经使用约30 a。为保证材积表的精度不受气候条件、立地条件的影响，国家规程中明确规定，应该每20 a对材积表进行重新检核修订[1]。由于中国森林资源结构在这些年发生了较大变化，部分原有材积表在应用中可能存在难以接受的偏差。曹忠[2]对部分华北山杨Populus spp.材积模型进行了检验，速生杨Populus × euramericana与毛白杨Populus tomentosa的总体相对误差（TRE）分别为-3.59%和7.31%，超过国家规定的±3%。因此，原有材积表部分树种已经不能满足林业调查和生产工作需求，亟待重新编制[3]。材积表是根据树干材积与胸径、树高和干形间的回归关系，建立材积模型编制的[4-5]，因此，材积模型直接影响材积表的精度和适用性。自1846年二元立木材积表问世至今，很多学者提出了不同的材积模型，如纳斯伦德、山本和藏、卡松、斯泊尔等经验模型[6-7]。随着现代机器学习理论和技术的发展，新的智能算法为建立高精度的材积模型和编制精准的材积表提供了新的机会。材积模型实质是一种根据立木胸径、树高等因子估算材积的方法。一般来说，样本量越大测量越精准，材积模型的代表性越大，其工作量也越大；又由于受地形、天气等因素影响，样本量越大，同一树种的干形可能表现出较大的差异性，这对模型抗噪能力要求越高。传统的经验模型要想获得较好的估算效果需要大量精准测量的样本。支持向量机（Support Vector Machine，SVM）在解决小样本、非线性、高维数、局部极小点等实际问题表现较好，具有很强的泛化能力[8-9]。最小二乘支持向量机（Least Squares Support Vector Machines，LSSVM）针对标准SVM算法抗噪能力较差的问题做了改进[10]。但实现LSSVM的优点依赖于参数的优化选择，目前参数的选择主要以经验为主，过分依赖于使用者的水平，这在很大程度上限制了它的应用。近年来，已经出现应用快速交叉验证、遗传算法、蚁群算法、粒子群算法等改进方法优化支持向量机参数，但优化的效果与优化算法的选择有很大关系。量子粒子群优化算法（quantum-behaved particle swarm optimization，QPSO）是SUN等[11]从量子力学的角度提出的一种改进的粒子群优化算法（particle swarm optimization，PSO）。QPSO算法相比PSO算法具有全局搜索性能强、参数个数少、稳健性好、收敛速度快等优点。试验采集北京地区侧柏Platycladus orientalis与落叶松Larix principis-rupprechtii数据，通过查询北京市落叶松一元立木材积表和河北承德地区侧柏一元立木材积表，计算得到部颁材积表总体相对误差依次为11.33%和-11.02%，超过国家规定的±3%，需要重新编制材积表。为解决精准估算立木材积的难题，本研究以北京地区侧柏与落叶松为研究对象，提出了一种基于QPSO优化LSSVM算法建立高精度材积估算模型的方法，以期为立木材积表的编制提供科学依据。
-
以北京地区侧柏和落叶松2种树种为建模对象，选择范围包括北京市的昌平、房山、门头沟、海淀、怀柔、密云、平谷、延庆等各个区县。标准木的选取根据各树种蓄积量的占比，按机械抽样原理将拟选标准木数量分配到各个区县，采用典型选样方法分立地条件选取不同径阶和树高级的标准木。选取的标准木为干形通圆竖直、主稍明显，以避免因树干弯曲或倾斜所导致的观测误差。每种树种的建模样本按照胸径值划分为6，8，10，12，16，20，24，28，32和36 cm等10个径阶。
采集建模样本于2014年12月8日至2015年12月31日进行。共采集样木810株，其中落叶松456株，侧柏354株。样木统计指标见表 1。
表 1 建模样本统计指标
Table 1. Statistical indicators for modeling samples
树种 统计指标 胸径/cm 地径/cm 树高/m 材积/m3 侧柏 最小值 5.10 6.50 3.86 0.005 9 最大值 41.20 50.10 17.51 0.728 6 平均值 16.20 19.80 9.47 0.147 2 标准差 8.30 9.60 3.03 0.166 2 变动系数/% 51.27 48.23 32.00 112.97 落叶松 最小值 5.00 7.10 4.25 0.005 7 最大值 43.50 56.20 24.10 1.293 9 平均值 19.30 24.40 13.21 0.308 4 标准差 10.20 12.30 5.23 0.335 3 变动系数/% 52.69 50.48 39.55 108.7 -
获取编制材积表的建模样本一般采用伐倒解析法。该方法精度较高，但破坏性大、成本较高。长期以来，国内外学者致力于无损、快速、精准测量立木材积方法的研究。传统的无损材积测量方法有望高法、正形数法、实验形数法、形点法等，但普遍精度不高，不易操作[12]。近年来，随着三维激光扫描仪、全站仪、CCD数码相机、电子经纬仪、便携式数字化智能测树仪等高精度测量仪器的出现，一些学者针对这些高精度测量仪器进行了测量树木方法的相应研究[13-21]。其中，电子经纬仪无损立木材积精测法是一种高精度，低成本，易操作的立木材积无损观测方法，但该方法对小规格树木测量精度影响较大[22-23]。为了获取高精度的建模样本，克服电子经纬仪无损立木材积精测技术对小规格树木观测精度影响较大的不足，采集建模样本时采用电子经纬仪无损立木材积精测法结合伐倒解析法进行，其中6~10 cm径阶的采用伐倒解析技术获取，12 cm及以上径阶的采用电子经纬仪无损立木材积精测技术获取。
电子经纬仪无损立木材积精测方法，采用南方测绘生产的电子经纬仪（DT-2），利用两站式方法观测标准木的树高，并按树高将标准木分为10段依次测量对应高度处的树干直径，最后使用区分求积法计算立木材积[24-25]。在每段逐步向上测量过程中，选择可以清楚观测树干的位置为观测点，避开树木的节疤及分叉部分，以保证观测精度。
伐倒解析方法，将样木伐倒后使用钢尺量测地径位置至树梢的长度（树高），每株样木测量相对树高0.2/10，0.5/10，1/10，2/10，3/10，4/10，5/10，6/10，7/10，8/10，9/10处的带皮直径，按区分求积法计算材积。
-
SVM是由CORTES等[8]和VAPNIK[9]在20世纪90年代提出的一种基于统计学习理论的机器学习算法。SUYKENS等[10]为了提高标准SVM的训练效率，对其进行了改进，提出了LSSVM算法。LSSVM利用结构风险最小化（structural risk minimization，SRM）原则时，损失函数采用最小二乘线性系统，并用等式约束替换不等式约束来取代传统的二次规划方式解决问题，只需求解一个线性方程组即可得出结果，降低了计算复杂度，提高了求解效率。LSSVM采用式（1）对样本数据进行建模。
$$ y = {\mathit{\boldsymbol{w}}^T}\varphi \left( x \right) + b。 $$ (1) 式（1）中：x∈Rn为给定n维训练样本集的输入向量；y∈R为相应输出向量；R为样本空间；w∈Rnh为权重向量，wT为w的转置向量；b∈R为偏置量；φ（x）为非线性映射函数：Rn→Rnh将输入数据映射到高维特征空间。
LSSVM回归可以表示为约束优化问题，式（1）的优化目标函数为：
$$ \left\{ \begin{array}{l} \mathop {\min }\limits_{w, e, b} J\left( {\mathit{\boldsymbol{w}}, \mathit{\boldsymbol{e}}} \right) = \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + \frac{C}{2}\sum\limits_{i = 1}^N {e_i^2} \\ s.t.\;{y_i} = {\mathit{\boldsymbol{w}}^T}\varphi \left( {{x_i}} \right) + b + {e_i}, \;\;\;i = 1, \;\; \cdots, \;\;\;N \end{array} \right.。 $$ (2) 式（2）中：J（w, e）为自变量w和e的函数；b∈R为偏置量；ei∈R为误差变量；C为可调正则化参数；N为训练样本数量。
根据式（2）定义拉格朗日函数L为：
$$ L\left( {\mathit{\boldsymbol{w}}, b, \mathit{\boldsymbol{e}}, \mathit{\boldsymbol{a}}} \right) = \frac{1}{2}{\left\| \mathit{\boldsymbol{w}} \right\|^2} + \frac{C}{2}\sum\limits_{i = 1}^N {e_i^2}-\sum\limits_{i = 1}^N {{a_i}} \left( {{\mathit{\boldsymbol{w}}^T}\varphi \left( x \right) + b + {e_i}-{y_i}} \right)。 $$ (3) 式（3）中：ai∈R为拉格朗日乘子。
根据KKT（Karush-Kuhn-Tucker）最优化条件，通过分别求取w, b, e, a的偏导数并置为0，消去w, e，求解的优化问题转化为求解线性方程组，通过解该方程组可得a, b的值，得到LSSVM的回归模型为：
$$ f\left( x \right) = \sum\limits_{i = 1}^N {{a_i}K} \left( {x, {x_i}} \right) + b。 $$ (4) 式（4）中：K（x, xi）为核函数；x∈Rn为给定n维训练样本集的输入向量；xi为核函数中心。
立木材积与胸径、树高为非线性关系，因此本研究建模选用核函数为具有强大的非线性处理能力和广阔实用性且核参数最少的径向基核函数（RBF）：
$$ K\left( {x, {x_i}} \right) = \exp \left( {-\frac{{{{\left\| {x-{x_i}} \right\|}^2}}}{{2{\sigma ^2}}}} \right)。 $$ (5) 式（5）中：σ2为核参数。
影响LSSVM回归模型的主要参数为正则化参数C和核参数σ2，2个参数对模型的泛化能力和学习能力有很大的影响[26-27]。在立木材积模型估算中，为了提高LSSVM的估算精度，合理选择正则化参数C和核参数σ2非常重要。
-
量子粒子群优化算法克服了粒子在收敛过程中最大速度的限制，使粒子在整个可行解空间中能够寻求到最优解，在搜索能力与收敛速度上优于标准PSO算法，且参数个数更少，公式简单，易于控制[28-29]。在量子空间中，粒子的速度和位置是不能同时确定的，可通过波函数来描述粒子的状态，并通过求解薛定谔方程得到粒子在空间某一点出现的概率密度函数，随后通过蒙特卡罗方法随机模拟的方式得到粒子的位置。粒子位置更新方程为：
$$ \left\{ \begin{array}{l} {x_{id}}\left( {t + 1} \right) = {p_d} \pm \beta \left| {{m_{{\rm{best}}d}}-{x_{id}}\left( t \right)} \right|\ln \left( {\frac{1}{u}} \right)\\ {m_{{\rm{best}}d}} = \frac{1}{M}\sum\limits_{i = 1}^M {{p_{id}}} \\ {p_d} = \varphi {p_{id}} + \left( {1-\varphi } \right){p_{gd}}\\ \beta = 0.5 + 0.5\left( {{T_{\max }}-t} \right)/{T_{\max }} \end{array} \right.。 $$ (6) 式（6）中：xid（t），xid（t+1）分别为第t，t+1次迭代后i粒子在第d维中的位置；t为迭代次数；Tmax为最大迭代次数；β为收缩扩张系数，可控制算法的收敛速度；M为群体中所含粒子数量；mbestd为第d维中粒子群中值最优位置；pd为第d维中每个粒子收敛于自身的随机点；pid为粒子i在第d维的个体历史最优位置（Pbest）；pgd为整个粒子群在第d维的全局最优位置（Gbest）。φ，u是在（0, 1）之间产生的随机数。
优化LSSVM算法中的正则化参数C和RBF核函数参数σ2为一个优化问题，可描述为：
$$ \left\{ \begin{array}{l} \min f\left( {C, {\sigma ^2}} \right) = \min \left( {{F_{{\rm{itness}}}}} \right)\\ s.t.\;\;{C_{\min }} < C < {C_{\max }}\\ \;\;\;\;\sigma _{\min }^2 < {\sigma ^2} < \sigma _{\max }^2 \end{array} \right.。 $$ (7) 本研究选择适应度函数为：
$$ {F_{{\rm{itness}}}}\sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {{{\left( {{{\hat y}_i}-{y_i}} \right)}^2}} }。 $$ (8) 式（8）中：yi为样本输出值；${\hat y_i}$为样本估测值；N为样本数量。
采用QPSO优化确定LSSVM参数（C，σ2），建立材积与胸径、树高估测模型的具体实现步骤如下：①对样本数据集进行归一化处理，消除量纲影响；②设置粒子群数量M，并初始化所有粒子的2维位置向量（C，σ2），确定QPSO的收缩扩张系数的取值范围、最大迭代次数Tmax等参数；③利用当前粒子的位置向量，用训练样本训练LSSVM，根据式（8）计算每个粒子的适应度值；④根据计算得到的适应度值，更新粒子个体最优值Pbest和全局最优值Gbest；⑤根据式（6）计算势中心点mbest和随机点P，更新每个粒子的新位置；⑥检查粒子位置是否满足结束条件，若适应度值小于给定精度或t达到设定的最大迭代次数，则结束寻优，输出当前最优粒子位置作为LSSVM参数，否则，t = t+1，返回步骤③继续迭代寻优。
-
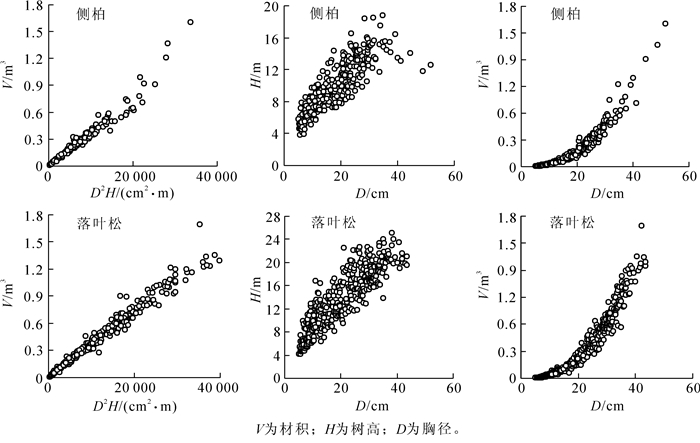
按树种分别绘制胸径平方和树高乘积（横轴，D2/H）与立木材积（纵轴，V）的散点图、胸径（D）与树高（H）的散点图、胸径（D）与立木材积（V）的散点图（图 1）。利用散点图法对数据进行去噪整理，侧柏和落叶松依次过滤异常数据10组和8组，得到合格的样木数据侧柏344组，落叶松448组。将样本数据集根据径阶分为训练集和测试集，数据集结构见图 2。侧柏训练集样本共250组，占侧柏样本总数的72.67%，测试集样本共94组；落叶松训练集样本共300组，占落叶松样本总数的66.96%，测试集样本共148组。
图 1 外业采集样本数据散点图
Figure 1. Scatter plot of sample data collected in the field
图 2 侧柏与落叶松样本数据分布情况
Figure 2. Distribution of sample data of Platycladus orientalis and Larix principis-rupprechtii
-
用QPSO算法进行寻优时，其参数设定为：粒子维度D=2，种群数量M=30，最大迭代次数Tmax=300。通过MATLAB实现算法，得到侧柏与落叶松的一元材积估算模型最优粒子位置依次为（249.43，1.00）和（746.22，3.01），得到侧柏与落叶松的二元材积估算模型最优粒子位置依次为（389.67，1.56）和（812.39，3.99）。
为了说明QPSO-LSSVM的效果，分别采用PSO-LSSVM和BP神经网络（BPNN）算法以及常用的传统一、二元材积方程建立材积估算模型并与之进行比较。其中PSO参数设为：粒子维度D=2，种群数量M=30，最大迭代次数Tmax=300，加速度系数C1=C2=2，初始惯性权值W=0.9。神经网络算法BPNN参数设为：隐藏层数量L=1，隐藏层神经元数量为10。传统一元材积模型采用伯克霍特（Berkhout）方程（9），二元材积模型采用山本式（Yamamoto Kazuhide）方程（10）：
$$ V = a{D^b} + \varepsilon ; $$ (9) $$ V = a{D^b}{H^c} + \varepsilon 。 $$ (10) 式（9）~（10）中：V为立木材积（m3）；D为胸径（cm）；H为树高（m）；a，b，c为参数；ε为误差项。
由于立木材积数据普遍存在着异方差性，在求解模型参数时必须采取措施消除异方差的影响。常用的方法是采用对数回归或加权回归。本次材积模型建立采用非线性加权回归方法，每个方程的权函数W=1/De（e为参数）根据普通最小二乘法独立拟合的二元材积方程的残差平方与胸径的幂函数回归关系确定。利用训练集数据分别建立一元与二元材积回归模型，得材积模型参数（表 2）。
表 2 侧柏和落叶松一、二元材积模型参数
Table 2. Parameters of the one-variable and two-variable tree volume models of Platycladus orientalis and Larix principis-rupprechtii
树种 模型 权函数W 参数 a b c 侧柏 V=aDb 1/D2.3 1.365×10-4 2.374 V=aDbHc 1/D2.3 6.470×10-5 1.815 1.0140 落叶松 V=aDb 1/D1.8 1.274×10-4 2.489 V=aDbHc 1/D2.4 6.348×10-5 1.881 0.955 1 本研究选用以下4项指标作为材积模型性能评价指标：决定系数（R2），总相对误差（TRE），相对误差绝对值的平均值（MARE）和平均相对误差（MRE）。各指标表达式定义为：
$$ {R^2} = 1-\frac{{\sum\limits_{i = 1}^N {{{\left( {{y_i}-{{\hat y}_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^N {{{\left( {{y_i}-{{\bar y}_i}} \right)}^2}} }}; $$ (11) $$ {T_{{\rm{RE}}}} = \frac{{\sum\limits_{i = 1}^N {{{\left( {{y_i}-{{\hat y}_i}} \right)}^2}} }}{{\sum\limits_{i = 1}^N {{{\bar y}_i}} }} \times 100\% ; $$ (12) $$ {M_{{\rm{RE}}}} = \frac{1}{N}\sum\limits_{i = 1}^N {\frac{{{y_i}-{{\hat y}_i}}}{{{{\hat y}_i}}}} \times 100\% ; $$ (13) $$ {M_{{\rm{ARE}}}} = \frac{1}{N}\sum\limits_{i = 1}^N {\left| {\frac{{{y_i}-{{\hat y}_i}}}{{{{\hat y}_i}}}} \right|} \times 100\% 。 $$ (14) 式（11）~（14）中：yi和${\hat y_i}$分别为第i株样木的实测值和预估值，y为全部样木实测值的平均值。
利用测试集数据，对比侧柏与落叶松的一、二元材积方程的性能指标（表 3）可以看出：在决定系数（R2）指标上，QPSO-LSSVM算法的拟合度均优于其他3种模型，PSO-LSSVM与传统一、二元材积方程基本相当，而BPNN算法拟合度则相对较差一些。QPSO-LSSVM材积估算模型的总相对误差（TRE），相对误差绝对值的平均值（MARE）和平均相对误差（MRE）均优于传统一、二元材积方程。
表 3 材积估算模型性能指标对比
Table 3. Comparison of performance indicators for the volume models
模型类型 树种 材积模型 R2 TRE/% MARE/% MRE/% 一元 侧柏 QPSO-LSSVM 0.978 6 0.75 12.49 2.16 PSO-LSSVM 0.971 8 -1.03 13.62 2.88 BPNN 0.970 7 -0.84 19.61 9.43 Berhout 0.976 6 -0.90 13.22 2.70 落叶松 QPSO-LSSVM 0.946 1 -0.16 15.59 1.79 PSO-LSSVM 0.945 1 -0.87 15.23 2.61 BPNN 0.933 7 -1.31 16.94 1.86 Berhout 0.944 6 -0.18 15.76 2.11 二元 侧柏 QPSO-LSSVM 0.987 0 0.64 7.43 0.85 PSO-LSSVM 0.986 5 0.39 7.49 0.33 BPNN 0.980 7 0.72 8.27 1.85 Yamamoto 0.986 8 0.85 7.63 1.12 落叶松 QPSO-LSSVM 0.990 1 -0.50 5.72 -0.06 PSO-LSSVM 0.987 8 -1.44 6.62 -0.59 BPNN 0.986 3 -1.81 8.07 -0.40 Yamamoto 0.987 6 -0.59 5.81 -0.11 在执行材积估算模型代码过程中，QPSO-LSSVM的平均收敛速度要优于PSO-LSSVM。以侧柏二元材积模型为例，连续执行材积估算建模代码15次并计算测试集估算结果的相对误差最大值REmax和相对误差绝对值的平均值MARE（图 3）。经计算得到传统一、二元材积模型，QPSO-LSSVM，PSO-LSSVM和BPNN算法的MARE的标准差依次为0.00，0.03，0.09，0.88，可以看出BP神经网络估算结果的REmax和MARE变化较大，4种材积估算模型的稳健性由强到弱排序为：传统材积估算方法＞QPSO-LSSVM＞PSO-LSSVM＞BPNN。综合材积估算模型的性能指标，平均收敛速度和稳健性，QPSO-LSSVM材积模型要优于其他3种材积模型。
图 3 侧柏二元材积估算模型指标
Figure 3. Indicator of the estimate model of the two-variable volume of Platycladus orientalis
QPSO-LSSVM，PSO-LSSVM，BPNN等3种模型为机器学习算法，模型参数较多，不同于传统模型表达直观，但模型使用MATLAB编程实现，具有可重用性和可移植性，在应用模型时，可将训练好的模型封装为独立的可执行程序发布使用，也可移植到林业相关系统中进行材积的自动化计算，还可利用MATLAB的编译器功能将模型进行重新编译嵌入手机、平板电脑等智能终端。另外，可直接利用训练好的模型编制立木材积表。
-
采用电子经纬仪无损立木材积精测法与伐倒解析法结合的方案获取样本数据，利用传统一、二元材积方程，QPSO-LSSVM，PSO-LSSVM和BPNN算法建立材积模型，通过分析计算结果发现，侧柏与落叶松的一、二元QPSO-LSSVM材积模型测试集的估算值与实测值的决定系数（R2）均优于其他3种算法；侧柏和落叶松的传统的一、二元材积模型的总体相对误差（TRE）依次为-0.90%，-0.18%，0.85%，-0.59%，QPSO-LSSVM材积模型的总体相对误差优于传统一、二元材积模型；4种材积估算模型的稳健性强弱关系为传统材积方程＞QPSO-LSSVM＞PSO-LSSVM＞BPNN。QPSO-LSSVM材积模型虽然在稳健性上比传统材积方程稍弱一些，但相差无几，且在估算精度上要优于传统材积方程。
综上所述，QPSO-LSSVM材积模型综合性能要优于其他3种模型，相比传统材积模型无需在多种经验方程中进行选择，且具有估算精度高，收敛速度快，稳健性强等优点，该方法在高精度材积估算中具有较好的应用前景。
Tree volume estimates based on QPSO-LSSVM
-
摘要: 基于材积方程建立的材积表是森林资源调查工作中重要的工具，估算立木材积的精度是编制材积表的关键。为了解决已有立木材积方程复杂多样、测算准确率低等不足，以北京地区侧柏Platycladus orientalis和落叶松Larix principis-rupprechtii为研究对象，提出利用量子粒子群优化最小二乘支持向量机（QPSO-LSSVM）算法建立材积方程的方法。通过伐倒解析法结合电子经纬仪无损立木材积精测法获取建模样本，对250株侧柏与300株落叶松数据分别建立一元与二元材积方程，计算得到侧柏与落叶松的一元材积方程测试集的决定系数（R2）为0.978 6和0.946 1，二元材积方程测试集决定系数（R2）为0.987 0和0.990 1，均在0.940 0以上，总体相对误差（TRE）依次为0.75%，-0.16%，0.64%，-0.50%，均满足国家规程小于±3%的要求，表明QPSO-LSSVM模型估算效果良好。最后引用传统一、二元材积方程、BP神经网络和粒子群优化最小二乘支持向量机（PSO-LSSVM）算法建立材积方程并与之进行对比分析。结果表明：QPSO-LSSVM材积方程在估测精度、收敛速度和稳健性等综合性能指标上优于其他材积方程。该方法在高精度材积估测中具有较好的应用前景。
-
关键词:
- 森林计测学 /
- 立木材积 /
- 量子粒子群(QPSO) /
- 最小二乘支持向量机(LSSVM) /
- 材积方程
Abstract: A volume table with calculations based on a volume equation, is an important tool for estimating tree volume in forest resources inventory. To overcome the large total relative error (TRE) that sometimes occurs, making the volume tables unable to meet the precision requirements of forest surveys and production, a Quantum-Behaved Particle Swarm Optimization (QPSO)-Least Squares Support Vector Machines (LSSVM) Model was used to estimate the volume of Platycladus orientalis and Larix principis-rupprechtii in Beijing. The traditional method of analyzing cut trees and the method of electronic theodolite standing timber volume were used to measure diameter at breast height (DBH), tree height, and volume of small diameter class (6-10 cm) and large diameter classe (12 cm or more) were used. A total of 792 trees were collected, including 344 P. orientalis and 448 L. principis-rupprechtii. Then, one-variable and two-variable tree volume equations of P. orientalis and L. principis-rupprechtii were established based on the QPSO-LSSVM algorithm. Also the volume model was established using the traditional empirical volume equation, BP neural network, and the PSO-LSSVM algorithm to test comprehensive performance indexes such as estimate accuracy, convergence speed, and robustness. The sample data set was divided into train set and test set according diameter class in the experiment. There were 250 train set samples of Platycladus orientalis, accounting for 72.67% of the total number, and 94 test set samples of it. Also, there were 300 train set samples of Larix principis-rupprechtii, accounting for 66.96% of the total number, and 148 test set samples of it. Results of the regression analysis on the improved one-variable and two-variable tree volume equations of P. orientalis and L. principis-rupprechtii showed R2 (the coefficient of determination of the test sets)=0.978 6, 0.946 1, 0.987 0, and 0.990 1, with the TRE of 0.75%, -0.16%, 0.64%, and -0.50%, all within ±1%. The QPSO-LSSVM has higher comprehensive performance indexes for the volume equation than the other three volume equations, including traditional empirical volume equation, BP neural network and the PSO-LSSVM algorithm. Thus, the proposed QPSO-LSSVM method should have a favorable application prospect with high precision volume estimates. -
图 2 侧柏与落叶松样本数据分布情况
Figure 2 Distribution of sample data of Platycladus orientalis and Larix principis-rupprechtii
图 3 侧柏二元材积估算模型指标
Figure 3 Indicator of the estimate model of the two-variable volume of Platycladus orientalis
表 1 建模样本统计指标
Table 1. Statistical indicators for modeling samples
树种 统计指标 胸径/cm 地径/cm 树高/m 材积/m3 侧柏 最小值 5.10 6.50 3.86 0.005 9 最大值 41.20 50.10 17.51 0.728 6 平均值 16.20 19.80 9.47 0.147 2 标准差 8.30 9.60 3.03 0.166 2 变动系数/% 51.27 48.23 32.00 112.97 落叶松 最小值 5.00 7.10 4.25 0.005 7 最大值 43.50 56.20 24.10 1.293 9 平均值 19.30 24.40 13.21 0.308 4 标准差 10.20 12.30 5.23 0.335 3 变动系数/% 52.69 50.48 39.55 108.7 
下载: 导出CSV
表 2 侧柏和落叶松一、二元材积模型参数
Table 2. Parameters of the one-variable and two-variable tree volume models of Platycladus orientalis and Larix principis-rupprechtii
树种 模型 权函数W 参数 a b c 侧柏 V=aDb 1/D2.3 1.365×10-4 2.374 V=aDbHc 1/D2.3 6.470×10-5 1.815 1.0140 落叶松 V=aDb 1/D1.8 1.274×10-4 2.489 V=aDbHc 1/D2.4 6.348×10-5 1.881 0.955 1
下载: 导出CSV
表 3 材积估算模型性能指标对比
Table 3. Comparison of performance indicators for the volume models
模型类型 树种 材积模型 R2 TRE/% MARE/% MRE/% 一元 侧柏 QPSO-LSSVM 0.978 6 0.75 12.49 2.16 PSO-LSSVM 0.971 8 -1.03 13.62 2.88 BPNN 0.970 7 -0.84 19.61 9.43 Berhout 0.976 6 -0.90 13.22 2.70 落叶松 QPSO-LSSVM 0.946 1 -0.16 15.59 1.79 PSO-LSSVM 0.945 1 -0.87 15.23 2.61 BPNN 0.933 7 -1.31 16.94 1.86 Berhout 0.944 6 -0.18 15.76 2.11 二元 侧柏 QPSO-LSSVM 0.987 0 0.64 7.43 0.85 PSO-LSSVM 0.986 5 0.39 7.49 0.33 BPNN 0.980 7 0.72 8.27 1.85 Yamamoto 0.986 8 0.85 7.63 1.12 落叶松 QPSO-LSSVM 0.990 1 -0.50 5.72 -0.06 PSO-LSSVM 0.987 8 -1.44 6.62 -0.59 BPNN 0.986 3 -1.81 8.07 -0.40 Yamamoto 0.987 6 -0.59 5.81 -0.11
下载: 导出CSV
-
[1] 中华人民共和国国家林业局.二元立木材积表编制技术规程: LY/T 2102-2013[S].北京: 中国标准出版社, 2013. [2] 曹忠.立木材积无损精测与建模方法研究[D].北京: 北京林业大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10022-1015319444.htm CAO Zhong. Study on Nondestructive Measurement and Modeling Methods for Standing Tree Volume[D]. Beijing: Beijing Forestry University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10022-1015319444.htm [3] 刘琪璟.中国立木材积表[M].北京:中国林业出版社, 2017. [4] 陈章水.杨树二元立木材积表的编制[J].林业科学研究, 1989, 2(1):78-83. http://d.old.wanfangdata.com.cn/Periodical/lykjkf200702010 CHEN Zhangshui. The establishment of binomial stock volume tables of poplar[J]. For Res, 1989, 2(1):78-83. http://d.old.wanfangdata.com.cn/Periodical/lykjkf200702010 [5] 李晖, 曾伟生.不同区域落叶松二元立木材积表的检验及差异分析[J].林业科学, 2016, 52(6):157-162. http://d.old.wanfangdata.com.cn/Periodical/lykx201606019 LI Hui, ZENG Weisheng. Validation and comparison of two-variable tree volume tables for Larix spp. in different regions of China[J]. Sci Silv Sin, 2016, 52(6):157-162. http://d.old.wanfangdata.com.cn/Periodical/lykx201606019 [6] STOLARIKOVÁ R, ŠÁLEK L, ZAHRADNíK D, et al. Comparison of tree volume equations for small-leaved lime (Tilia cordata Mill.) in the Czech Republic[J]. Scand J For Res, 2014, 29(8):757-763. doi: 10.1080/02827581.2014.980316 [7] BI H Q, HAMILTON F. Stem volume equations for native tree species in southern New South Wales and Victoria[J]. Aust For, 1998, 61(4):275-286. doi: 10.1080/00049158.1998.10674752 [8] CORTES C, VAPNIK V. Support-Vector networks[J]. Mach Learn, 1995, 20(3):273-297. http://d.old.wanfangdata.com.cn/Periodical/hwyhmb200803006 [9] VAPNIK V N. The nature of statistical learning theory[J]. IEEE Trans Neural Networks, 2002, 8(6):1564. http://d.old.wanfangdata.com.cn/OAPaper/oai_doaj-articles_aa60477f3b98d64446b1353cf89cadee [10] SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers[J]. Neural Process Lett, 1999, 9(3):293-300. doi: 10.1023/A:1018628609742 [11] SUN Jun, FENG Bin, XU Wenbo. Particle Swarm Optimization with Particles Having Quantum Behavior[M]. Portland, USA:IEEE, 2004:325-331. [12] 孟宪宇.测树学[M]. 3版.北京:中国林业出版社, 2008. [13] 何诚, 冯仲科, 袁进军, 等.基于数字高程模型的树木三维体积测量[J].农业工程学报, 2012, 28(8):195-199. doi: 10.3969/j.issn.1002-6819.2012.08.030 HE Cheng, FENG Zhongke, YUAN Jinjun, et al. Three-dimensional volume measurement of trees based on digital elevation model[J]. Trans Chin Soc Agric Eng, 2012, 28(8):195-199. doi: 10.3969/j.issn.1002-6819.2012.08.030 [14] 陈金星, 岳德鹏, 冯仲科, 等.手持式树径自动识别测树仪的研制与应用[J].浙江农林大学学报, 2016, 33(4):589-598. http://zlxb.zafu.edu.cn/CN/abstract/abstract1329.shtml CHEN Jinxing, YUE Depeng, FENG Zhongke, et al. A handheld dendrometer for automatic tree diameter measurement[J]. J Zhejiang A&F Univ, 2016, 33(4):589-598. http://zlxb.zafu.edu.cn/CN/abstract/abstract1329.shtml [15] 王佳, 杨慧乔, 冯仲科.基于三维激光扫描的树木三维绿量测定[J].农业机械学报, 2013, 44(8):229-233. http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201308039 WANG Jia, YANG Huiqiao, FENG Zhongke. Tridimensional green biomass measurement for trees using 3-D laser scanning[J]. Trans Chin Soc Agric Mach, 2013, 44(8):229-233. http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201308039 [16] 赵芳, 冯仲科, 高祥, 等.树冠遮挡条件下全站仪测量树高及材积方法[J].农业工程学报, 2014, 30(2):182-190. http://d.old.wanfangdata.com.cn/Periodical/nygcxb201402025 ZHAO Fang, FENG Zhongke, GAO Xiang, et al. Measure method of tree height and volume using total station under canopy cover condition[J]. Trans Chin Soc Agric Eng, 2014, 30(2):182-190. http://d.old.wanfangdata.com.cn/Periodical/nygcxb201402025 [17] 冯仲科, 刘金成, 杨立岩. CCD组合全站仪摄影基站摄影测量方法: CN201510602572.1[P/OL].[2017-03-08]. http://www.vipzhuanli.com/patent/201510602572.1. [18] 于东海, 冯仲科, 曹忠, 等.全站仪测量立木胸径树高及材积的误差分析[J].农业工程学报, 2016, 32(17):160-167. doi: 10.11975/j.issn.1002-6819.2016.17.022 YU Donghai, FENG Zhongke, CAO Zhong, et al. Error analysis of measuring diameter at breast height and tree height and volume of standing tree by total station[J]. Trans Chin Soc Agric Eng, 2016, 32(17):160-167. doi: 10.11975/j.issn.1002-6819.2016.17.022 [19] 王智超, 冯仲科, 闫飞, 等.全站仪测树的内外业一体化方法研究[J].西北林学院学报, 2013, 28(6):134-138. doi: 10.3969/j.issn.1001-7461.2013.06.27 WANG Zhichao, FENG Zhongke, YAN Fei, et al. Integrated indoor and field forest measurement by using total station[J]. J Northwest For Univ, 2013, 28(6):134-138. doi: 10.3969/j.issn.1001-7461.2013.06.27 [20] 韦雪花, 王永国, 郑君, 等.基于三维激光扫描点云的树冠体积计算方法[J].农业机械学报, 2013, 44(7):235-240. http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201307041 WEI Xuehua, WANG Yongguo, ZHENG Jun, et al. Tree crown volume calculation based on 3-D laser scanning point clouds data[J]. Trans Chin Soc Agric Mach, 2013, 44(7):235-240. http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201307041 [21] 刘金成, 黄晓东, 杨立岩, 等.基于CCD超站仪的森林样地建立与精测方法研究[J].农业机械学报, 2016, 47(11):316-321. doi: 10.6041/j.issn.1000-1298.2016.11.043 LIU Jincheng, HUANG Xiaodong, YANG Liyan, et al. Establishment and precise measurement of forest sample plot based on CCD super station[J]. Trans Chin Soc Agric Mach, 2016, 47(11):316-321. doi: 10.6041/j.issn.1000-1298.2016.11.043 [22] 焦有权, 冯仲科, 高原, 等.用光电经纬仪对无伐倒活立木材积精准计测[J].中南林业科技大学学报, 2013, 33(10):25-29. doi: 10.3969/j.issn.1673-923X.2013.10.006 JIAO Youquan, FENG Zhongke, GAO Yuan, et al. Live standing tree volume through the photoelectric theodolite accurate measurement[J]. J Cent South Univ For Technol, 2013, 33(10):25-29. doi: 10.3969/j.issn.1673-923X.2013.10.006 [23] 曹忠, 巩奕成, 冯仲科, 等.电子经纬仪测量立木材积误差分析[J].农业机械学报, 2015, 46(1):292-298. http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201501041 CAO Zhong, GONG Yicheng, FENG Zhongke, et al. Error analysis on standing tree volume measurement by using electronic theodolites[J]. Trans Chin Soc Agric Mach, 2015, 46(1):292-298. http://d.old.wanfangdata.com.cn/Periodical/nyjxxb201501041 [24] 焦有权, 冯仲科, 赵礼曦, 等. PSO嵌入SVM算法的活立木材积预报研究[J].光谱学与光谱分析, 2014, 34(1):175-179. doi: 10.3964/j.issn.1000-0593(2014)01-0175-05 JIAO Youquan, FENG Zhongke, ZHAO Lixi, et al. Research on living tree volume forecast based on PSO Embedding SVM[J]. Spectrosc Spectr Anal, 2014, 34(1):175-179. doi: 10.3964/j.issn.1000-0593(2014)01-0175-05 [25] HE Cheng, HONG Xiafang, LIU Kezhen, et al. An improved technique for non-destructive measurement of the stem volume of standing wood[J]. South For A J For Sci, 2016, 78(1):53-60. doi: 10.2989/20702620.2015.1108617 [26] SCHÖLKOPF B, SUNG K K, BURGES C J C, et al. Comparing support vector machines with Gaussian kernels to radial basis function classifiers[J]. IEEE Trans Sign Process, 1996, 45(11):2758-2765. http://bioinformatics.oxfordjournals.org/external-ref?access_num=10.1109/78.650102&link_type=DOI [27] FERNANDEZ-MARTINEZ J L, GARCIA-GONZALO E. Stochastic stability analysis of the linear continuous and discrete PSO models[J]. IEEE Trans Evol Comput, 2011, 15(3):405-423. doi: 10.1109/TEVC.2010.2053935 [28] 管芳景, 须文波, 孙俊, 等. QPSO算法求解无约束多目标优化问题[J].计算机工程与设计, 2007, 28(14):3285-3287, 3290. doi: 10.3969/j.issn.1000-7024.2007.14.001 GUAN Fangjing, XU Wenbo, SUN Jun, et al. QPSO algorithm for unconstraint multi-objective optimization problem[J]. Comput Eng Des, 2007, 28(14):3285-3287, 3290. doi: 10.3969/j.issn.1000-7024.2007.14.001 [29] 李玉军, 汤晓君, 刘君华.基于粒子群优化的最小二乘支持向量机在混合气体定量分析中的应用[J].光谱学与光谱分析, 2010, 30(3):774-778. doi: 10.3964/j.issn.1000-0593(2010)03-0774-05 LI Yujun, TANG Xiaojun, LIU Junhua. Application of least square support vector machine based on Particle Swarm Optimization in quantitative analysis of gas mixture[J]. Spectrosc Spectr Anal, 2010, 30(3):774-778. doi: 10.3964/j.issn.1000-0593(2010)03-0774-05 -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2018.05.011
点击查看大图
图(3) / 表(3)
计量
- 文章访问数: 3530
- HTML全文浏览量: 370
- PDF下载量: 929
- 被引次数: 0
