-
理论生长方程是指在生物生长模型研究中，根据生物学原理作出某种假设，建立有关生物体大小的微分方程，解出并代入其初始条件或边界条件而导出的模型。理论生长方程逻辑性强，适用性大，参数可作出生物学解释，并且可从理论上对尚未观察的事实进行预测。观察林木的整个生长周期可发现，它们的生长遵循“S”型曲线，即“慢—快—慢”直至稳定不变的态势，尽管受到环境的影响会出现一些波动，但总的生长趋势是稳定的[1]。用数学模型来描述“S”型曲线，即理论生长方程，目前研究应用较多的主要有：坎派兹式（Gompertz方程）、逻辑斯蒂式（Logistic方程）、米切尔里希式（Mitscherlich方程）、贝塔兰菲式（Bertalanffy方程）、理查德式（Richards方程）、舒马赫式（Schumacher方程）和Korf方程等7种[2]。不同植物或者林木类型适用的生长方程不同。目前，生长模型可分为3类：全林分模型、径阶分布模型以及单木模型。全林分模型或径阶分布模型的预测侧重的是整体，而单木模型侧重的则是单株林木。单木模型能直接预测每株林木的生长情况及潜力，全林分模型则做不到。但目前单木模型的实际应用还是受到很多因素限制，如林木实际生长过程复杂，人类认识比较局限，导致目前单木模型预测精度较低。全林分模型和径阶分布模型虽然预测精度较单木模型高，但其涉及的因子较多，各因子之间关系复杂，不方便林分的生长建模。目前，对于林分生长预测的研究主要集中在理论层面，即通过相关数学模型预测增长量，再将得到的数据用图表的形式展示出来，以此形象地表示林分各个生长因子整体的预测生长量，对林分中单株林木的生长情况却少有研究，这样对林分生长的预测是不够真切的，而且对于计算机模拟林分生长建模也是十分困难的。如果要预测单株林木的生长，就必须研究竞争情况，但竞争因子复杂多样，甚至多达上百种，对林分生长预测建模带来很大困难。因此，本研究提出了基于生长方程与增长量分配模型的林分生长预测建模方法，并有效地将林分整体平均增长量付诸到林分中单木模型的预测生长上。该方法既可避免林木之间复杂的竞争模型研究，又使得林分预测建模变得简便、高效、快速，并实现林分按生长规律生长。
HTML
-
本研究以杉木Cunninghamia lanceolata为例，采用湖南省攸县黄丰桥林场和尚岭杉木不同年份的同龄林分实测数据。该样地坐标为27°19′27″N，113°45′14″E，大小为40 m×80 m，样地共955株10年生杉木。本实验均基于该林分样地2.5~10.0年生杉木的实测数据进行分析建模。
-
式（1）中：当0≤m＜1时取“-”，m＞1时取“+”。其中：参数A为y的最终值即上渐近线；参数B决定x=0时生长因子的大小；参数k与生长速度有关系。为了便于求解，本研究中取m=2/3，则(1)式可化为y=A(1±Be(-kx))3。设点集P={p1(x1, y1), p2(x2, y2), …, pn(xn, yn)}为待拟合的点，采用最小二乘法将它们拟合成Richards方程的曲线。方法如下：点pi到Richards方程曲线的偏移量可定义为di=(y-yi)2，即:
则所有点到Richards方程曲线的偏移量之和为：
对式（2）分别求A，B，k的偏导数并令其等于0，可得：
令1-Be-kxi=ai，则上式可化为:
将数据点代入式（3），可得到A, B, k的值。
-
林分生长模型由1个或1组数学函数来表达，它能准确描述林木生长与林分状态以及立地条件的关系。目前，林分生长模型主要分为3类：全林分模型、径阶分布模型以及单木模型。为了方便建模以及更真实地模拟林分生长，本研究结合了全林分模型和单木模型的优点，简化了林木之间复杂的竞争，提出全林分—单木模型，使得每株林木得到合理的增长，同时保持了一定的预测精度。全林分—单木模型是指根据所得到的生长方程预测某林分的某一因子平均量，如平均胸径、平均树高等，然后根据整个林分的某一因子的平均增长量按一定的原则或规则（即增长量分配模型）分配到每株林木上，使得每株林木在整体上得到合理的增长。通过全林分模型得到整个林分各个生长因子的平均增长量，然后根据增长量分配模型为每株林木分配增长量，由此转化为单木模型，完成全林分模型到单木模型的过渡。
-
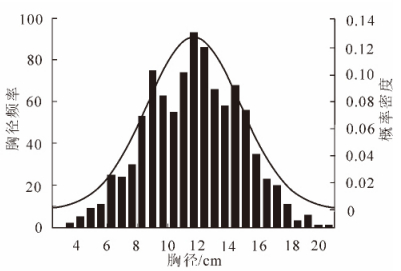
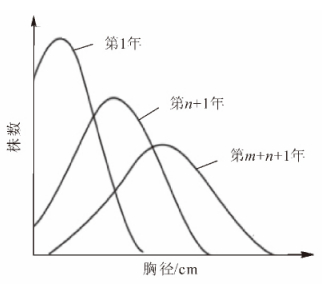
林分调查基本因子中仅有林分的总体特征，如林分面积、株数；预测得到的也是林分的总体特征，如平均胸径、平均树高等，却不能取得每株林木的胸径、树高等因子信息。如果给林分中的每株林木都赋予全林分的平均胸径和树高，则与林木的真实状况有较大差别。同龄纯林的直径结构规律一般为以林分平均直径为峰值的单峰山状近似正态分布曲线。多年来，林学家利用正态分布函数来拟合，描述同龄纯林的直径分布取得了良好的效果。根据林分结构规律，无论是人工林还是天然林，林分内的胸径、树高等因子信息普遍遵循一定的林分结构规律。同龄纯林的胸径—株数成正态分布，不同龄林分的胸径分布函数也有着特定的变化规律。图 1中最高的正态分布曲线为时间最前的，而最低的为时间最后的。从图 1中可看出，同龄纯林胸径分布在开始时各径阶内的林木株数差别较大，峰值较高，说明胸径分布在均值附近的较多。随着时间的推移，胸径分布正态曲线整体向右移，且各径阶内林木株数差别缩小，峰值降低，说明林木间由于竞争使得胸径分布差距渐渐增大。对黄丰桥林场和尚岭10年生同龄纯林样地955株杉木的胸径数据进行分析，可知同龄纯林的胸径成正态分布（图 2）。从图 2中可以看出：同是10年生的杉木，胸径却大小不一，甚至相差较大。这是由于林木生长时，林木与林木之间存在竞争。由于要对外界因子，如阳光、水分、土壤养分等，进行一一研究，费时费力，实施起来也不太现实。结合图 1中的生长规律，本研究提出一种基于“强者越强，弱者越弱”的竞争原则。生长了10 a的杉木，尽管胸径不一，但呈正态分布。“强者越强，弱者越弱”的竞争原则可以从整体上把握林木的竞争状况，得到整体的林木增长量，而不需要研究每个因子的影响再综合得到增长量，避免了复杂的竞争模型的研究。虽然避免了单木之间复杂竞争因子、竞争模型的研究，但实际生活中每株林木的增长量不可能全一样，其增长量有大有小，在建模过程中为了使林分符合自然生长规律，要对增长量分配模型的“强”和“弱”给定标准，即对林分中每株林木赋予竞争力，以此排定每株林木的“强弱”。对于林木竞争力的强弱，本研究用每株林木的竞争指数来表示。竞争指数表达了林木承受的竞争压力。通常分为2种：一种与距离有关，一种与距离无关。本研究选取与距离有关的胸径简单竞争指数[6-7]，表达式如下：
Figure 1. Diameter at breast height of the same age pure stand with the change of time
Figure 2. Frequency histogram and normal distribution curve of diameter at breast height (the 10 years old Cunninghamia lanceolata in Huangfengqiao)
式（4）中，CIi是对象木i的竞争指数，Dj是相邻木j的胸径，Di是对象木i的胸径，Lij是对象木i和相邻木j之间的距离，n是对象木i周围竞争木株数。该竞争指数是相邻木即竞争木对对象木的竞争指数，其值越大，对象木所受的干扰越大，则对象木在竞争中处于劣势；其值越小，所受的干扰程度越小，对象木在竞争中处于优势。因此，该竞争指数不能完全代表林木在林分中的竞争强弱，而该竞争指数与某一生长因子相结合，如上一时刻某林木胸径大小减去其竞争指数，将这个差值作为该株林木在整个林分中的竞争力，差值越大，竞争力越强，反之，越弱。则单株林木的竞争力CP可表示为以下形式：
以胸径为例，主要思想是：所求时刻的胸径平均值Y为上一时刻的胸径平均值y加上增长量Ir，即Y=y+Ir。具体分配过程如下：首先根据Richards生长方程获得下一时刻的林分平均胸径，与前一时刻的林分平均胸径相减得到林分的胸径平均增长量Δavg。随机生成n个增长量，分别作为林分中n株林木的增长量。由于强竞争力林木的增长量会高于平均值，弱竞争力林木的增长量会低于平均值，因而，可以把随机增长量的范围设定为（0，（1+s）Δavg），s为所求林分某时刻的生长曲线斜率，即增长率，增长率越大说明林分长得越快，反之，越慢。Richards生长方程求导即可得到增长率方程，如下所示：
（6）对生成的随机增长量要保证总和要等于总增长量。然后根据式（4）和式（5）计算每株林木的竞争力并排序，对于竞争力最大的林木分配最大的增长量，对竞争力第二大的林木分配第二大的增长量，以此类推。建模过程中若考虑自然稀疏带来的林木枯损，可选定合适的枯损模型，计算得到该年份林分中枯损木株数便可得到预测年份时林分中的活立木株数n。方法如下：选用Logistic模型建立杉木林分的枯损模型，该模型形式为：
式（7）中: Pi为第i径阶林木枯损概率或第i株树枯损概率；y=a0+a1x1+a2x2+…+anxn, x1~xn为选择的自变量；a0~an为待定参数。自变量可选择林木直径大小的径阶中值、相对直径（即径阶中值与林分平方平均直径的比值）、每公顷断面积、平方平均直径、郁闭度、大于所估径阶的林木直径平方和等。自变量的数量一般为2~5个，在拟合模型（7）时采用的是逐步引进法，通过检测的自变量最终才可被引进。具体方法参见文献[12]。若枯损模型的结果为有枯损，则活立木数量相应变更，改变分配模型中所需要生成的随机数数量即可；若为单木枯损模型，在绘制时直接根据位置坐标剔除枯损的林木；若为径阶枯损模型，则根据林木胸径或者树高的大小确定该径阶内枯损的林木，胸径或树高较小的枯损，在绘制时再根据相应的位置坐标剔除枯损的林木；若枯损模型的结果为无枯损，则活立木株数n与上个年份的数量相同。然后采用前文所述增长量分配算法，构建自然稀疏和他疏的林分生长模型。
1.1. 试验地概况
1.2. 研究方法
1.2.1. Richards生长方程及其参数求解Richards方程表达式如下：
1.2.2. 全林分-单木模型
1.2.3. 增长量分配模型
-
以所述试验地同龄纯林杉木林分样地2.5~10.0年生树木的胸径数据为依据。部分数据如表 1。
树龄/a 胸径/cm 2.5 2.0 3.0 2.4 4 3.2 - - 8.0 6.4 10.0 17.4 Table 1. Cunninghamia lanceolata data of diameter at breast height in Huangfengqiao
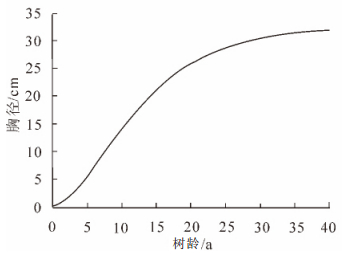
根据1.2.1节方法以及表 1数据可得，该杉木林分的Richards生长方程参数分别为A=32.645 3，B=0.820 0，k=0.120 0，其曲线方程如图 3所示。根据式（4），得到该方程对应的曲线斜率方程，如图 4所示。
Figure 3. Richards equation of Cunninghamia lanceolata in Huangfengqiao
Figure 4. Slope curve of Richards equation in Huangfengqiao
由图 3可知：该杉木林分样地平均胸径长到32.645 3 cm左右趋于稳定。由图 4可知：该杉木林分样地胸径先增长较慢，然后快速增长一段时间后，在10年生左右达到最大增长率，其中5.0~15.0年生左右属于快速增长期，然后增长率开始下降，直至达到稳定，增长率趋于0。
-
根据2.1节求得的Richards生长方程可得：15.0年生时该杉木林分的平均胸径为21.088 6 cm。另外，根据该10.0年生杉木样地实测的955株杉木数据，得到林分平均胸径为11.757 7 cm。根据求得的生长曲线斜率方程可得到15.0年生时的斜率即增长率为1.190 4，按1.2.3节中的生长量分配原则给每株林木分配生长量。再根据以上步骤建立树高、枝长等关系的生长量，得到15.0年生时的数据建立林分。系统林分建模是基于DirdectX3D，以C#为开发语言，开发环境为VS2008，分别对黄丰桥国有林场和尚岭10.0年生杉木林分和预测的15.0年生时的杉木进行3D建模与模拟，结果见图 5与图 6。
Figure 5. 10 years old Cunninghamia lanceolata stand
Figure 6. 15 years old Cunninghamia lanceolata stand
图 5和图 6分别为该林场10.0和15.0年生杉木的林分整体图。由图 5和图 6以及林分生长曲线可知，10.0~15.0年生处于生长曲线“慢—快—慢”的“快”时期。
2.1. Richards方程结果与分析
2.2. 林分建模结果与分析
-
本研究以湖南省攸县黄丰桥林场不同年份杉木的实测数据为基础，对Richards方程采用最小二乘法求解方程参数，得到方程表达式后，再以该林场1块10.0年生同龄纯林杉木样地的实测数据为基础，结合Richards生长方程预测15.0年生时的林分平均胸径、平均树高等林木因子，然后根据“强者越强，弱者越弱”的自然选择法为林分中的每株林木分配增长量，由此可得到每株林木的增量情况。基于这样的增长量分配原则，提出相应算法，实现全林分生长模型向单木生长模型转换，既避免了林木之间复杂的竞争模型研究，又使得林分按生长规律生长。实验表明了该方法的简便性和有效性，预测的生长模型真实度较高，并有利于林分生长建模系统的高效、快速仿真与可视化模拟。
DownLoad: