-
大气中温室气体浓度上升引起的全球气候变化，导致极端气候事件频发，严重威胁着人类生存与社会经济的可持续发展，成为各国政府和科学家关注的重大环境问题。在应对全球气候变化背景下，森林碳汇的相关研究成为科学界关注的热点[1-3]。生物量是森林生态系统碳汇潜力评估的重要基础，如何快速、准确地获取森林生物量信息，在20世纪90年代就成了森林生态系统与全球气候变化研究的关键[4]。准确评估森林碳储量的时空变化，不仅可以为森林资源的经营管理和林业可持续发展提供的科学依据，而且对碳循环及碳汇研究具有重要的意义。随着遥感技术的不断发展，利用数学模型结合实测样地数据进行生物量的大尺度快速估测变得有效可行。k-最近邻法（k-nearest neighbor, k-NN）作为一种非参数方法，已被广泛用于多源林业调查和森林参数估计的反演。1990年，TOMPPO[5]首次将k-NN技术应用于芬兰森林资源监测中并取得了较好的效果。MCROBERTS[6]记录了该技术在国际范围内被广泛用于林业应用领域，包括森林调查空间插值预测、数据库监测、反演制图、小区域估测和统计推理。从数据层面上来讲，k-NN与Landsat影像，机载激光扫面数据和MODIS数据联合使用估测评价森林属性的研究较多，并且将机载激光扫描指标等主动遥感变量与光学遥感、大尺度森林变量等参数结合使用有助于提高k-NN模型的预测精度[7]。国外研究者在遗传算法的优化下，利用k-NN和机载激光扫描数据对森林资源调查、森林参数估测与评价等方面取得了较好的研究成果[8-10]。KATILA等[11]和TOMPPO等[12]运用数字地图进行数据分层和使用遗传算法对特征变量进行加权来作为一种提高预测精度的手段后，该方法得到了加强。利用遗传算法对卫星影像数据特征变量加权优化将会提高估测精度，并且将优化好的模型应用于单一森林属性变量（如某个树种）比同时应用于多变量的精度会提高许多[13]。然而，国内的研究学者缺少对k-NN模型算法进行优化改良的研究，仅局限于将传统的k-NN运用于不同的森林参数估计。如陈尔学等[14]运用Landsat数据和传统的k-NN法对小面积统计单元森林蓄积量估测，其结果表明采用k-NN法对县市级统计单元森林参数的估测效果明显优于只利用固定样地数据的传统参数估测方法。郭颖[15]利用k-NN非参数回归模型对甘肃省西水林场的森林地上生物量进行估测，并用随机森林算法（RF）进行特征选择后估测精度得以提升，优化后的算法在处理错误样本时具有良好的容错能力。本研究使用遗传算法对k-NN模型进行优化，使模型预测结果的偏差、均方根误差等最小化，以期提高模型的估测精度，实现对研究区高山松Pinus densata地上生物量储量估计与空间反演制图。
HTML
-
研究区位于滇西北迪庆藏族自治州香格里拉市境内（26°52′11.44″~28°50′59.57″N，99°23′6.08″~100°18′29.15″E）（图 1）。研究区地势高耸，热量不足，气温偏低，海拔为1 503~5 545 m，多年平均气温为5.5 ℃，历年平均降水量为618.4 mm，平均降雪日为35.7 d，年日照率为40%~50%，属山地寒温带季风气候。境内密集的金沙江水系支流、冰雪融水和高原湖泊等水资源以及以棕壤、红壤为主的森林土壤类型孕育了丰富的植物资源。森林植被面积大，覆盖率高，南北差异分布明显，主要分布有10种植被类型，常见的树种有云杉Picea asperata，冷杉Abies fabri，高山松，云南松Pinus yunnanensis和高山栎Quercus semicarpifolia等。其中，高山松适应性广，更新能力强，是喜光、耐旱、耐瘠薄的优势树种。一般分布于云杉、冷杉林下限，海拔为2 800~3 500 m，林分外貌整齐，成片分布，以同龄单层林常见，占全市乔木林面积的22.7%。
Figure 1. Location of the study area
变量 数量 公式及说明 $\rho_{{{{\rm{B}}i}}}$ 6 Landsat 8/OLI数据第i波段原始发生率拖$\rho_{{\rm{B}} i}(i=2, 3, 4, 5, 6, 7)$ $V_{{\rm{IS}} 234}$ 1 ${V_{{\rm{IS}}234}} = \sum\limits_{i = 2}^4 {{\rho _{{\rm{B}}i}}} $ $A_{\text { lledo }}$ 1 ${A_{{\rm{lhedo}}}} = \sum\limits_{i = 2}^7 {{\rho _i}} $ ${P_{{\rm{CA}}j}}, {I_{{\rm{CA}}j}}, {M_{{\rm{NF}}j}}$ 9 分别为主成分分析、独立主成分分析、MNF变换的第j成分(j=1, 2, 3) $T_{{\rm{CB}}}, T_{{\rm{CG}}}, T_{{\rm{CW}}}$ 3 分别为缨穗变换的亮度、绿度、湿度分量 $D_{{\rm{VI}}}$ 1 差值植被指数${D_{{\rm{VI}}}} = {\rho _{{\rm{NIR}}}} - {\rho _{\rm{R}}}, \;{\rho _{{\rm{NIR}}}}, \;{\rho _{\rm{R}}}$分别为近红外波段、红波段的反射率 ${N_{{\rm{DVI}}}}$ 1 归一化植被指数:${N_{{\rm{DVI}}}} = \left( {{\rho _{{\rm{NIR}}}} - {\rho _{\rm{R}}}} \right)/\left( {{\rho _{{\rm{NIR}}}} + {\rho _{\rm{R}}}} \right)$ ${E_{{\rm{VI}}}}$ 1 增强植被指数:${E_{{\rm{VI}}}} = 2.5\left[ {\frac{{\left( {{\rho _{{\rm{NIR}}}} - {\rho _{\rm{R}}}} \right)}}{{\left( {{\rho _{{\rm{NIR}}}} + 6.0{\rho _{\rm{R}}} - 7.5{\rho _{{\rm{BLUE}}}} + 1} \right)}}} \right]$，$\rho_{{\rm{BLUE}}}$为蓝波段的反射率 $R_{{\rm{VI}}}$ 1 比值植被指数:${R_{{\rm{VI}}}} = \left( {{\rho _{{\rm{NIR}}}}/{\rho _{\rm{R}}}} \right)$ $S_{{\rm{AVI}}}$ 1 土壤调节植被指数：${S_{{\rm{AVI}}}} = \frac{{(1 + L)\left( {{\rho _{{\rm{NIR}}}} - {\rho _{\rm{R}}}} \right)}}{{\left( {{\rho _{{\rm{NIR}}}} + {\rho _{\rm{R}}} + L} \right)}}$，L为土壤调节系数，因研究区植被覆盖率大，本研究取0.25 Bi_N_T 96 纹理特征，即第i波段N×N窗口下的纹理滤波T。i=2, 3, 4, 5; N=3, 5, 9;T为纹理滤波，依次分为：均值ME，方差VA，协同性HO, 对比度CO, 相异性DI，信息熵EN，二阶矩SM，相关性CR $E_{\text { levation }}$ 1 海拔 $S_{\rm{lope}}$ 1 DEM派生的坡度因子 Table 1. A list of factors derived from remote sensing
-
从地理空间数据云（http://www.gscloud.cn/）获取Landsat 8/OLI影像3景覆盖整个研究区：2015年11月9日（2景），轨道号分别为132/040和132/041；2015年12月20日（1景），轨道号为131/041（图 1）。并采用软件ENVI 5.3对卫星影像进行辐射定标、大气校正（FLAASH）和几何精校正等预处理后提取单波段、多波段组合、主成分变换、缨帽变换、植被指数、纹理和地形特征（由DEM提取）等共计123个因子，作为建模因子备选参数（表 1）。
-
地面实测数据49块标准地和116株高山松样木数据（表 2）：实测标准地数据于2014年10－11月，在云南省香格里拉市境内的高山松分布范围内采集，在高山松分布范围布设了49个大小为30 m × 30 m的样地，记录了树高、胸径、样地差分GPS定位坐标和海拔等。其中：林分地上生物量依据式（1）进行计算。
变量 样木数据(N=116) 标准数据(N=49) 树高/m 胸径/cm 单株地上生物量/kg 标准树高/m 标准胸径/cm 均值 15.061 24.094 276.381 9.275 15.295 最大值 33.00 76.00 2 058.50 14.77 23.10 最小值 4.20 5.60 4.03 5.61 8.62 标准差 6.480 14.082 370.847 2.092 3.373 Table 2. Basic information of biomass measured data
高山松样木数据记录了不同龄组下（包括幼龄林、中龄林、近熟林、成熟林、过熟林）116株高山松胸径（DBH）和树高（H），并测定了树干、树皮、树叶、树枝、树冠生物量，用于拟合高山松地上生物量计算模型。本研究中的地上生物量由树干、树枝和树叶3个部分的生物量构成，生物量调查参照胥辉等[16]生物量测定方法。
首先，采用随机抽样法将116株样木数据分成2个部分：2/3样本作为建模样本建立生物量估算模型，1/3作为检验样本对模型进行检验。其次，采用相对生长模型（非线性模型），运用最小二乘法对高山松单木地上生物量（W）模型进行拟合，结果见式（1），拟合决定系数R2为0.980 7，均方根误差RMSE等于46.73 kg，模型的验证结果如图 2所示，检验决定系数R2等于0.995 7。
Figure 2. Validation of Pinus densata aboveground biomass model
-
在k-NN的专业术语中，将待测变量及其特征变量的观测值样本指定为参考集，将待测变量的预测集指定为目标集，特征变量定义的空间成为特征空间。对于诸如生物量或蓄积量等连续性变量M在像元p上的预测值mp的计算方法如下：
式（2）中：mi为变量M参考样地点i上的实测值；k为计算预测值mp时考虑的近邻个数；wip为像元权重值，其计算如下：
式（3）中：i是参考集样本；p是目标集像元；pj是与参考集样本j对应的样本；$d_{{\rm{pvp}}}^{ - t}$为距离分解因子；k, t为常量，一般通过实验反复测试选取最佳值；$\left\{ {{i_1}(p), \cdots , {i_k}(p)} \right\}$是与待测像元p在特征空间上最相似的k个参考集样本。特征变量空间相似度由度量dpi, p，其计算方法如下：
式（4）中：${f_{l, {p_j}}}$和fl, p分别为参考集和目标集样本对应的遥感影像光谱波段及其派生因子等特征变量；nf为特征变量个数；p为目标集像元；pi为参考集样本i对应的像元；ωl, f为赋予特征空间中第l个特征变量的权值。
-
ik-NN与k-NN在方法原理上是一样的，改进之处在于前者使用遗传算法赋予了特征空间里的所有变量一个评价其重要性指标的权重向量，即式（4）中的ωl, f；而后者则赋予所有变量相同的权值。优化的非单位矩阵ωl, f降低了不相关因子对因变量的影响，间接的起到了因子筛选的作用。
遗传算法优化ωl, f过程：（1）初始化。便于描述，将初始化权重向量群体比作染色体群体，权重向量的元素个体比作基因。随机生成大小为[npop，nf]的数组作为初始化群体，运用二进制（0/1）对基因进行编码，并计算每一个染色体的适应度γ，其计算公式见式（5），用于对初始染色体及子代染色体选择的评价指标。（2）选择。采用随机遍历采样，根据自定义选择概率ps将已有的优良染色体复制后添入新染色体群体中，删除劣质染色体；染色体是否被选择的依据是其适应度的大小，适应度大者被复制，小者被淘汰，确保新群体中的基因总数和初始群体相同。（3）交叉。利用交叉算子对染色体的基因编码进行重组，发生的概率为pc，通过交叉操作可以得到新一代染色体，子代的染色体组合了父辈的特性。交叉是遗传算法中最主要的操作，体现了信息交换的思想。（4）变异。变异首先在染色体群体中随机选择1个个体，对于选中的个体以突变概率pm随机地改变其基因的编码。同生物界一样，遗传算法中变异发生的概率很低，通常取值很小。
-
留一法交叉验证，即对于N个样本，每次从N个样本中抽出1个样本作为测试集，利用剩余的N－1个样本作为参考集，重复N次循环，直至结束。本研究将N个样本的模型预测值${\hat y_i} = (i = 1, \cdots , N)$与对应样本的实测值（yi）进行统计分析，利用均方根误差$\hat{\sigma}$[式（6）]和偏差$\hat{\overline{e}}$[式（7）]及相对标准误差百分比RMSE[式（8）]来检验模型的精度。
式（5）~（8）中：γ为遗传算法适应度；ω为赋予特征变量的权值；nf为特征变量个数；yi和$\hat{y}_{i}$分别为第i个样本的实测值与模型预测值；$\overline {\hat y} $为模型预测值的平均值。
2.1. 遥感数据及信息提取
2.2. 地面实测数据及处理
2.3. 基于传统和优化k-NN模型的生物量估测
2.3.1. 传统k-最近邻法（k-NN）
2.3.2. 优化k-最近邻法（ik-NN）
2.4. 模型的精度评价方法
-
筛选特征变量的目的在于：①降低特征空间的维数提高算法的运行速率，保证研究的可行性；②排除不相干变量、选择相关性显著的特征变量来提高模型的精度。在SPSS软件中分析特征变量与生物量之间的相关性显著水平，综合考虑特征空间的维度和模型精度后，从123个特征变量中选取16个与生物量极显著相关的特征变量作为建模变量。表 3是将特征变量分为原始、显著相关和极显著相关3个等级后逐一评价的结果，客观地反映了不同特征变量等级下的模型精度。
特征变量等级 数量 $\widehat \sigma $/(t·hm-2) $\hat{\overline{e}}$/(t·hm-2) RMSE/% 原始 123 33.96 0.03 61.6 显著相关 35 33.34 -2.7 63.6 极显著相关 16 29.95 -0.42 54.8 显著或极显著相关 51 34.52 0.01 62.6 Table 3. Comparison of model accuracy under different level feature variables
-
k-NN模型需要确定3个重要的参数：评估特征变量空间相似度的距离参数$d_{p_{i}, p}$；计算待测像元p的预测值时考虑的在特征空间上最相似的参考集样本个数k及其加权方案wip。依据CHIRICI等[17]和谢福明等[18]的研究，在k-NN模型距离参数指标度量方式中，最常用的是欧氏距离（70%），其次是马氏距离（3.5%），以及典型相关分析度量（1.9%），故本研究选取欧氏距离作为特征变量空间相似度的评价标准。k的选择通常介于1~10，本研究结合相应的实验数据选取的k=5，如图 3A：k≤5时，模型精度随k的增大而提高，并在k=5时达最佳精度；k＞5时，模型的精度逐渐降低。t即距离分解因子，在模型中的应用见式（3），t通常取0~2内的值，其对模型精度的影响较小（图 3B），本研究t取2。
Figure 3. Change curve of model accuracy with the value of k and t
-
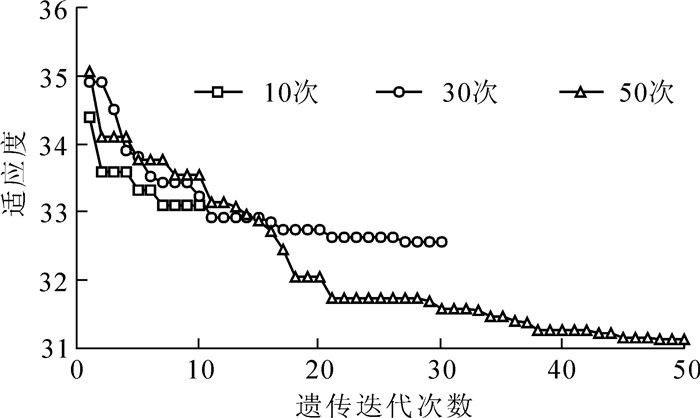
遗传算法最终的目的是为每一个特征变量计算出权重，并将其运用于k-NN模型来提高生物量的预测精度。算法中的主要函数调用于Sheffield遗传算法工具箱，其中的参数值在实验中反复测试、调试后确定。其中，图 4表明了适应度$\gamma (\omega , \hat \sigma , \hat{\overline{e}})$随着遗传迭代次数（10，30或50）的增加呈缓慢下降，当迭代次数大于50时，适应度随迭代次数的变化比较平稳，并趋向于稳定。表 4记录了算法的最佳初始参数值和调用的主要算子。
Figure 4. Reduction of fitness value curve with the number of generations in optimization of genetic algorithm
自定义有效参数值 主要算子(算法调用于Sheffield遗传算法工具箱) 初始化染色体群体个数npop: 50 crtbp.m，创建任意离散随机种群 遗传迭代次数ngen:30~80 bs2rv.m，二进制串到实值的转换 染色体选择操作概率ps: 0.95 ranking.m，基于排序的适应度分配 染色体基因交叉操作概率Pc:0.7 sus.m，随机遍历采样选择方式 染色体变异操作概率Pm: 0.01 xovsp.m，单点交叉；mut.m，离散变异 优化权重上限值: 0.5 reins.m，一致随机和基于适应度的重插入 Table 4. Parameters and main functions of genetic algorithm
-
k-NN模型及其优化算法在MATLAB环境下调试、运行，算法给予每个特征变量初始化的权重值均相等（第0代），表 5为第50代优化的特征变量权重值（算法的参数设置同2.2所述），表 5数据为标准化后的数值，其和为1。
项目 B2 B2_3_ME B2_3_HO B2_3_DI B3_3_HO B3_3_DI B3_3_EN B3_3_SM B4_3_ME B2_5_ME B3_5_ME B3_5_EN B3_5_SM B4_5_ME B2_9_ME B3_9_ME 权重 2.10×l0-3 2.50×10-2 7.53×10-2 1.41×10-1 1.14×10-1 1.24×10-1 1.16×10-1 6.12×10-2 2.42×10-2 2.88×10-2 2.29×10-2 2.75×10-2 9.52×10-2 2.59×10-2 4.04×10-2 7.50×10-2 说明：Bi_N_T为纹理特征，即第i波段N×N窗口下的纹理滤波T。纹理滤波依次分为：均值ME，方差VA，协同性HO，对比度CO，相异性DI，信息熵EN，二阶矩SM，相关性CR。如B2_3_ME，即第2波段3×3窗口下的均值（ME）纹理滤波，依次类推 Table 5. Values of the elements of the weight vector for feature variables for the 50th optimization (with upper bounds 0.5 and 50 generations)
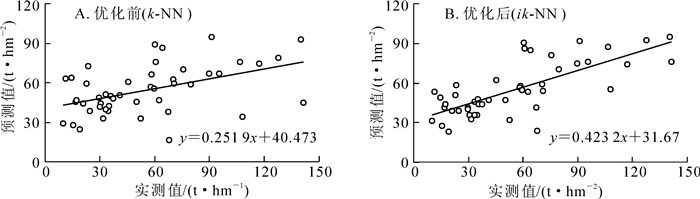
本研究的主要目标是通过优化方法降低像元尺度下模型的估测误差，提高对高山松地上生物量的估测精准度。表 6和图 5表明：（1）基于传统k-NN模型的样本生物量预测结果为16.2~92.6 t·hm－2，平均值为54.7 t·hm－2，模型均方根误差为30.0 t·hm－2, 偏差为－0.418 t·hm－2，RMSE为54.8%（图 5A）；（2）遗传算法优化后的ik-NN模型精度得到了提升，均方根误差为24.0 t·hm－2，偏差为－0.123 t·hm－2，RMSE为43.7%（图 5B）。与传统k-NN模型相比，ik-NN模型的精度均方根误差值降低了约6.0 t·hm－2，偏差下降比例达75.6%，模型精度RMSE提高了11.1%；（3）ik-NN模型的样本估计值为23.3~95.2 t·hm－2，在均值上与实测值比较相近，约55.0 t·hm－2。但对于高生物量或低生物量区域的估测残差仍较大，均出现高值低估，低值高估的现象。
变量 生物量/(t·hm-2) 最小值 最大值 均值 标准差 样地实测 10.2 141.2 55.1 34.9 k-NN预测 16.2 92.6 54.7 18.9 ik-NN预测 23.3 95.2 55.0 20.1 Table 6. Statistics of observations and model predictions of aboveground biomass of Pinus densata
Figure 5. Comparison of estimation accuracy of aboveground biomass of Pinus densata between k-NN and ik-NN model
-
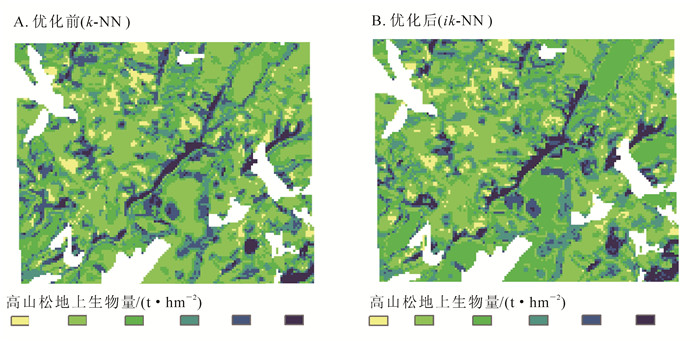
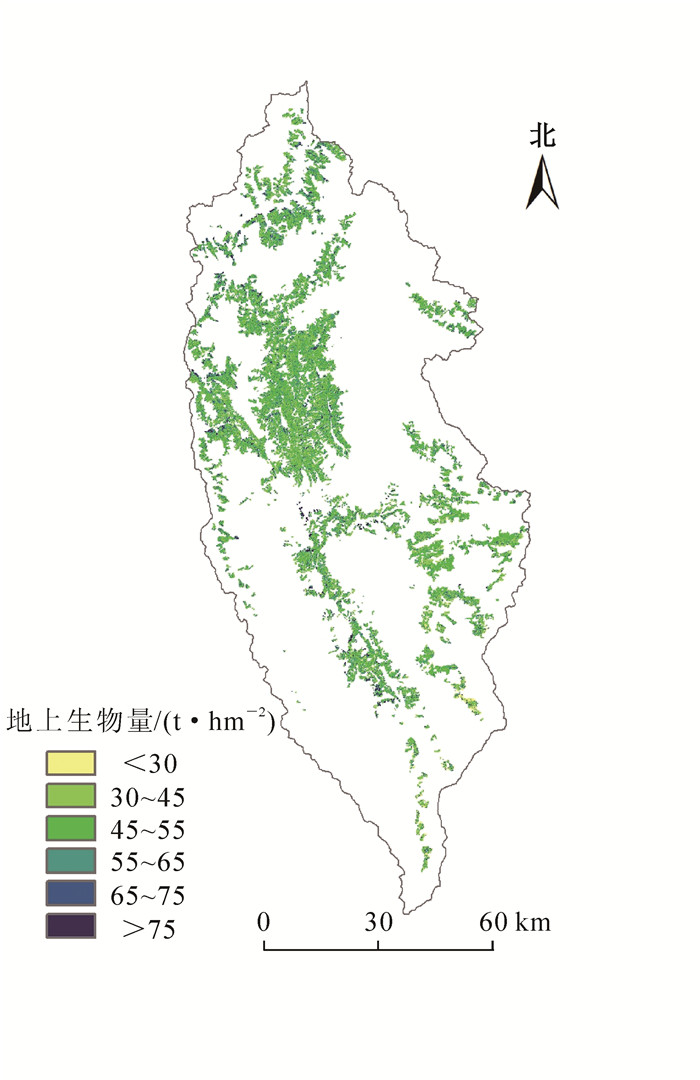
像元尺度下的定量反演是一项极其密集的任务，需要逐一计算研究区内的每一个像元，对计算机内存需求大，故本研究把研究区分成多块区域后再逐一估测反演。图 6为k-NN和ik-NN 2个模型局部反演结果：k-NN模型的预测为20.0~97.5 t·hm－2，平均值为49.5 t·hm－2，标准差为13.1 t·hm－2（图 6A）；ik-NN模型的预测值则为18.4~113.7 t·hm－2，平均值为49.3 t·hm－2，标准差为13.5 t·hm－2（图 6B）。模型的反演结果中离散分布的像元较少，近邻相关性好，更好地体现了变量的区域相关性。依据森林资源二类调查统计数据，研究区高山松分布区面积为1.74×105 hm2，其地上总生物量估测结果为0.89×107 t。图 7为ik-NN模型的高山松地上生物量空间分布等级图，生物量等级在16.8~108.9 t·hm－2之内，主要分布在45~75 t·hm－2。
Figure 6. Comparison of local inversion of k-NN/ik-NN model on pixel scale
Figure 7. Spatial distribution of Pinus densata aboveground biomass in Shangri-la at the pixel scale
3.1. 建模特征变量的筛选
3.2. 模型参数优化配置
3.2.1. k-NN模型参数优化配置
3.2.2. 遗传算法参数说明
3.3. 模型效果分析
3.4. 生物量估计与反演
-
本研究使用遗传算法实现对k-NN模型中的特征变量赋予相应的权重值后，构建加权欧氏距离，结合卫星数据和地面实测样地数据建立了优化的k-NN估测回归模型，估算出香格里拉高山松地上生物量储量，反演出地上生物量分布等级图。结果显示：k-NN算法参数k和t分别取值为5和2时，模型的预测效果最佳；基于遗传算法优化的ik-NN模型预测精度优于传统的k-NN模型，均方根误差为24.0 t·hm－2，偏差为－0.123 t·hm－2，RMSE为43.7%。研究区像素级水平下高山松地上生物量的预测值为16.8~108.9 t·hm－2，总估计值为0.89×107 t。
CHIRICI等[17]研究显示：使用卫星光谱数据作为特征变量时，需要大量的样本来获取较小的相对标准误差百分比，这与本研究结果相符合。本研究k-NN模型的参考样本偏少，且参考样本在空间分布上相对集中（图 1），所以生物量的预测结果残差较大，出现高值低估，低值高估的现象；造成这一现象的另一个原因是k-NN法本身存在的缺陷，即只能局限于实测值范围内对未知单元进行估测，预测值不会超出实测值的范围，模型算法中k个参考样本间的加权求和降低了估计值的方差，从而产生了更大的估测误差。但k-NN在大尺度区域上的森林资源监测中有很大的潜力，不仅适用于森林参数的估测反演，还适用于森林调查空间插值预测、数据库监测、小区域估测和统计推理等研究[19-20]，并且从以下方面做出突破可以有效提升其预测能力，为生活生产实践提供更好的技术借鉴：①k-NN在搜索最近邻个体时应限制搜寻的范围，如限制一个搜寻半径或在指定的图斑区域，而不是全局搜索，充分利用区域化变量的特性来提高模型的估测精度。②利用地物光谱的差异性，结合星载、机载高光谱数据和地面实测高光谱数据或者其他能够区分地物的单波段，利用最近邻法或其他机器学习算法实现对地物的精细识别，提高区域尺度上的地物分类精度，进而提高对其生理生化参数定量估测的准确性。
DownLoad: