本站查看
-
立木胸径和树高是衡量立木生长状况的重要因子[1]，立木因子的获取是森林资源调查中最重要的工作之一[2-3]。传统的立木因子测量主要依靠人工或二维图像完成。人工测量方法中，使用皮尺、测距仪等测树工具[4]，工作量大且主观误差较大；电子经纬仪、全站仪等精密设备[5-6]专业性强，但操作复杂。随着计算机视觉技术的发展，基于二维图像的测量方法[7-9]取得了一定的成果，但由于维度的限制，这类方法对于遮挡严重的场景测量精度不高。近几年，三维重建方法被广泛用于植物表形参数的测量[10-11]。其中地面激光扫描技术(terrestrial laser scanning, TLS)[12-13]测量精度高，但地面激光扫描仪价格昂贵，产生点云数据量大，对计算机的运行速度、传输容量等有较高要求，使其在植株表型参数提取与分析方面的应用受到了制约，难以满足社会化的需求。运动恢复结构(structure from motion，SfM)[14]是一种通过特征点匹配建立不同视角的二维图像的关系，从而恢复相机参数与目标三维信息的算法。该算法为植株表型参数测量提供了一种新思路[15]。梁秀英等[16]使用户外小车自动拍摄田间玉米Zea mays植株，基于SfM 算法首先获取玉米植株稀疏三维点云，然后再进一步得到植株稠密点云，通过点云数据测得玉米株高、茎粗和叶面积等参数。HUI等[17]基于SfM算法，利用Visual SFM软件对茄Solanum melongena、辣椒Capsicum annuum和黄瓜Cucumis sativus等3种蔬菜进行了重建和表型解析，获取了植物叶片数、叶长、叶宽和叶面积数据。该方法除用于小型作物表型参数的测量外，在立木因子测量方面也有应用。MILLER等[18]、徐慧丹等[19]围绕单株立木拍摄重叠度约70%的图片，并基于SfM算法获取其三维点云模型，从而估计树高、胸径等参数。孙英伟等[20]在室外围绕单株立木进行拍摄，并基于SfM算法获取立木三维点云，将点云最高和最低的差值作为树高数据，对1.3 m处点云拟合圆提取胸径值。这些方法虽然能够有效替代传统方法和TLS测量立木因子，但均是围绕立木人为控制拍摄间隔获取图像，步骤繁琐且精度难以保障，仅能测量单株立木，效率较低。
本研究提出基于运动恢复结构的多株立木因子测量方法，围绕立木场景拍摄视频，使用关键帧提取算法自动提取三维重建所需的立木图像，减少拍摄的复杂程度；基于SfM算法获取立木三维点云后，进行多株立木点云分割，实现立木单株点云的提取和树高、胸径的自动测量，为多株立木因子的自动测量提供了新思路。
-
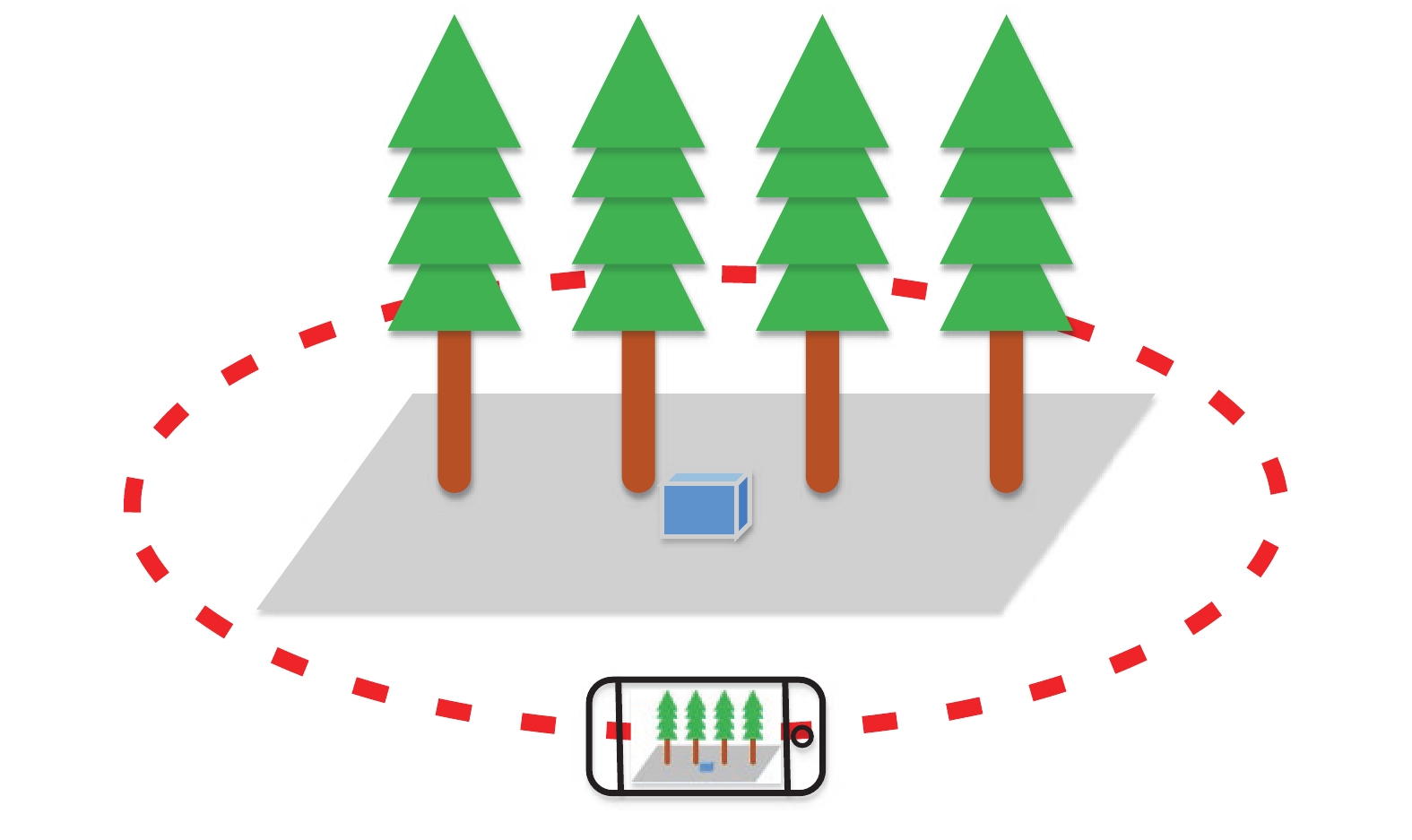
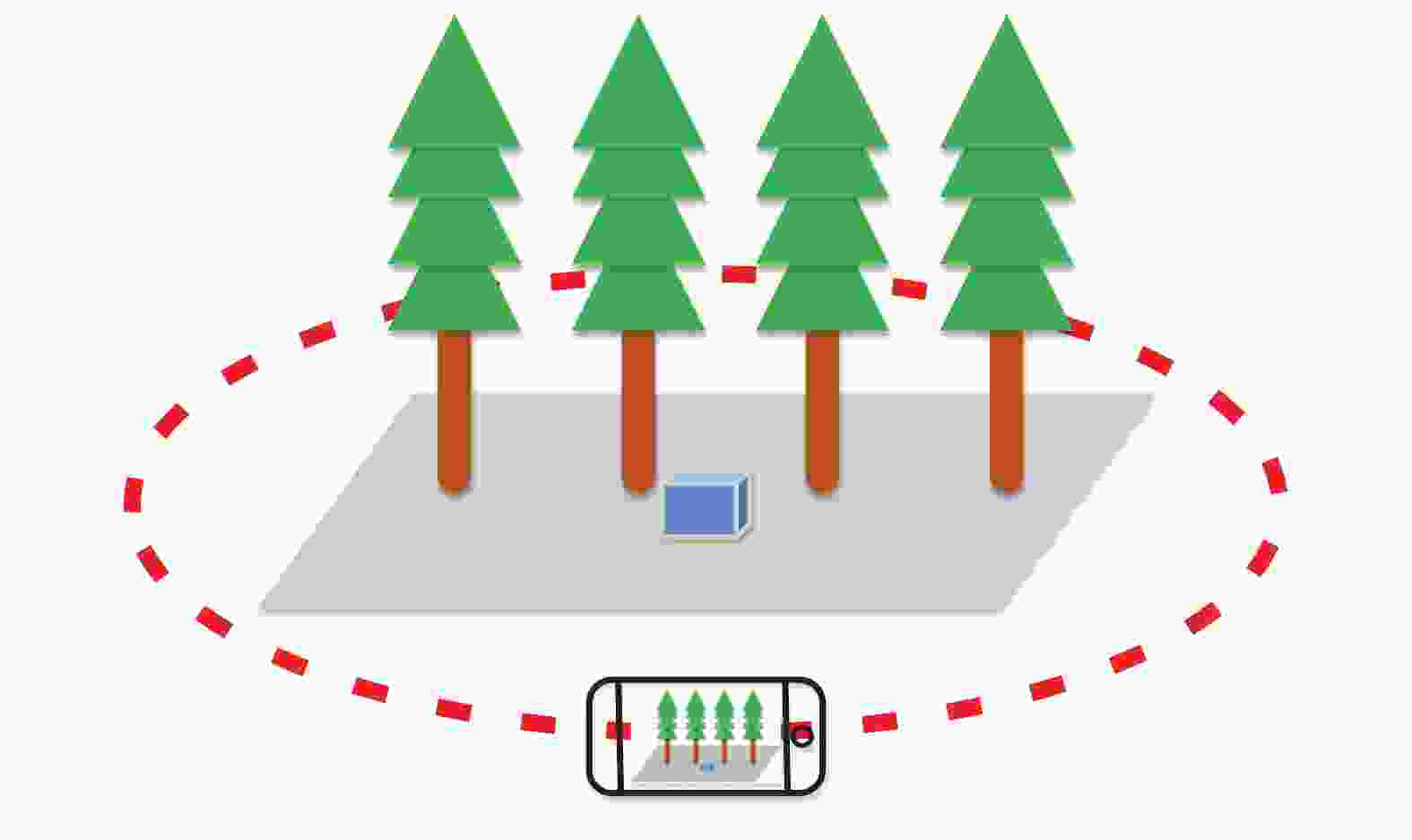
以浙江农林大学校园内的立木为研究对象，在自然条件下使用智能手机环绕包含多株立木的场景拍摄一段视频。拍摄时将手机移动速度尽量保持均匀并减少晃动，尽可能拍到立木的全部，并将相机镜头始终指向场景中心。由于每个场景中的立木数量、高度、间距均不相同，因此拍摄路线也不同。图1为某场景的拍摄路线示意图，场景中放置的蓝色长方体尺寸已知，有助于将立木三维点云的尺度恢复到与实际相同。
Figure 1. Schematic diagram of shooting route
-
视频相比图像能够传达更为丰富的信息，但是一个完整的视频序列包含较多冗余数据，关键帧提取算法能够从视频中选择满足特定要求的帧，使得提取的关键帧序列能够在满足后续立木三维点云获取所需基本信息的基础上尽量减少冗余。将固定采样法和相似度度量法相结合，对立木视频进行关键帧提取。先用固定采样法提取视频帧作为候选帧，即以视频的第1帧作为候选帧的开始，使用固定间隔为t帧的采样算法At对包含L帧的视频VL进行候选帧提取，得到候选帧序列Fc，其中
${f_1},{f_{1 + t}}, \cdots ,{f_{1 + nt}}$ 为候选帧序列中的每帧，(1±nt)≤L。式(1)中，将所有的候选帧提取完成后，以候选帧的第1帧作为关键帧的开始，采用差异值哈希(dHash)算法[21]计算当前关键帧与候选帧之间的相似度。该算法首先将2幅图像分别缩小并灰度化，然后比较每行相邻元素的大小，根据比较结果赋值1或0，得到2幅图像的哈希值，最后利用汉明距离计算2幅图像之间的相似度S。
式(2)中：Ii表示当前关键帧，fj表示候选帧，dH(Ii)和dH(fj)分别表示2幅图像的哈希值，D表示汉明距离。
计算出相似度S之后，设定相似度阈值S1、S2 (分别取值为0.6和0.8)。当S＞0.8时，将筛选出的关键帧序列进行三维重建时立木三维模型的效果并没有明显提升，但是关键帧图像大量增加导致效率降低；当S＞0.6可以较好地排除视频中突然出现的干扰(如车辆)。因此，若0.6≤S≤0.8，则将该候选帧加入到关键帧序列，并将该帧设置为当前关键帧。然后继续计算当前关键帧与下一候选帧的相似度，直至筛选完所有候选帧，得到视频关键帧序列Fe。
-
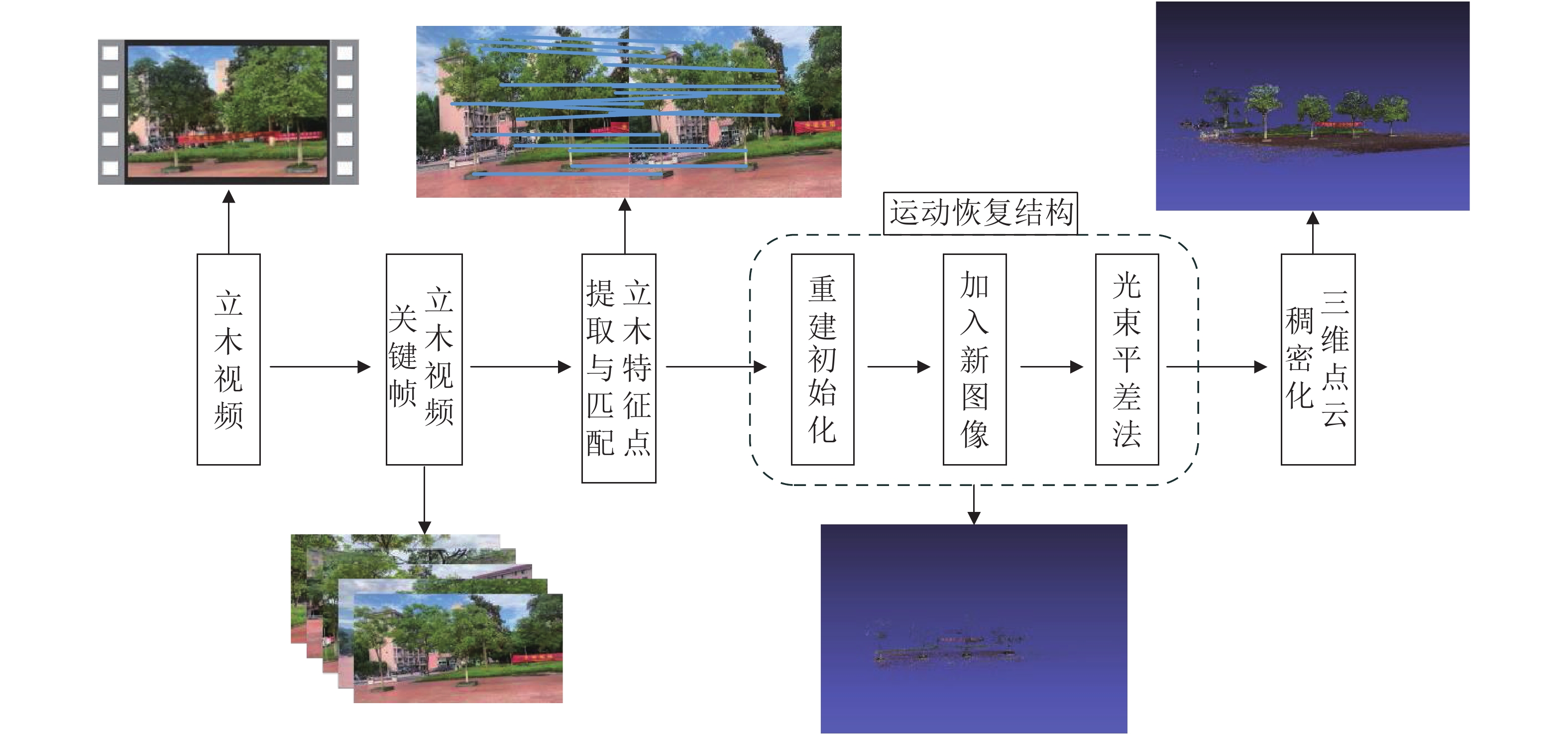
在立木视频关键帧序列(即有序图像集)提取的基础上，基于运动恢复结构算法生成立木三维点云，基本流程如图2所示。①特征点提取与匹配。通过尺度不变特征变换算法(scale-invariant feature transformation，SIFT)[22]对图像进行特征点提取，并计算每2幅图像特征点描述子之间的欧几里得距离来完成特征点匹配，得到所有图像的特征匹配关系
$M \left\{m_{1,2}, m_{2,3}, \cdots, m_{n-1, n}\right\}$ ，其中n为关键帧图像的数量，m中储存了2幅图像间的特征点匹配对$m\left\{\left(x_{1}, x_{1}^{\prime}\right),\left(x_{2}, x_{2}^{\prime}\right), \cdots,\left(x_{i}, x_{i}^{\prime}\right)\right\}$ ，其中i为特征点匹配对的数量。②使用2幅图像进行重建初始化。首先将第1幅图像与第2幅图像中的匹配点对x和x'代入对极几何约束条件[式(3)]求得基础矩阵F，该矩阵代表了2幅图像匹配点之间的空间几何关系。
Figure 2. Flow chart of creating 3D point cloud of trees
再通过已知的相机内参K和式(4)求得本质矩阵E和，对E进行奇异值分解后得到第2幅图像相对第1幅图像的相机旋转矩阵R和平移向量T。
在此基础上，可通过式(5)求得2个相机的投影矩阵P1和P2：
通过P1和P2建立二维匹配点x和x'及其对应的三维空间点X的关系：
并将匹配点x和x'的齐次坐标[u, v, 1]T及[u', v', 1]T代入上式，得：
式(7)中：Pi1、Pi2、Pi3是Pi的行向量，对A进行奇异值分解后得到二维图像特征点的三维坐标。
③加入新的图像。根据新加入的一幅图像与已重建的上一幅图像上特征点的匹配关系，获得已知的三维点X对应新图像上的二维点x，将对应的二维点和三维点代入式(8)可求得投影矩阵Pi，然后重复使用步骤②中的方法获得新图像上其余未重建的匹配点的三维坐标。
④利用光束平差(bundle adjustment，BA)[23]算法进行集束调整，减小相机姿态R、T和重建三维点坐标的误差。将所有三维点通过重新映射的方式到得到其在图像上的二维点坐标，然后计算与其真实二维点之间的距离，并将该距离最小化以完成优化。即：
式(9)中：xij是第i个特征点在第j幅图像上的坐标，Pj为投影矩阵，Xi为第i个特征点的三维坐标。每重建一幅图像进行一次集束调整，当所有图像重建完成后，再次进行集束调整，获得优化后的稀疏三维点云。
⑤三维点云稠密化。采用多视角立体集群算法(cluster multi-view stereo，CMVS)和多视角拼接算法(patch-based multi-view stereo，PMVS)对重建出来的稀疏点云进行稠密化[24]。
-
由于立木场景三维点云数据量大，夹杂了许多噪声点，且点云模型与真实世界三维空间的方向、尺度上也存在不一致，因此需要对点云模型进行下采样、去噪、比例校正、坐标校正、方向校正等预处理，以减少后续算法运行时间。①采用三维体素栅格法对点云进行下采样。首先为输入的点云数据创建由大量指定边长的微小立方体包围的集合，即三维体素栅格；然后在每个体素内计算所有点的重心，利用重心代替该体素内的其余点，这样所有的三维点云最终都由各个体素内的重心表示。②去噪。使用直通滤波器对X、Y、Z阈值范围进行设定，划分出感兴趣的立木范围区域，从而减少背景噪声点。接着采用统计滤波方法去除离群噪声点，计算直通滤波后的每个点pi，计算其与k(取50)个近邻点的平均距离
$\bar{d}\left(p_{i}\right)$ ，假设得到的结果服从高斯分布，得平均距离均值(μ)和标准差(σ)，如果这些点的平均距离$\bar{d}\left(p_{i}\right)$ 大于阈值Cσ(C为常量，取1)，则将被视为离群值去除。③坐标校正。首先进行点云模型与实际的比例校正，由放置物体实际尺寸hr和放置物体的模型尺寸hm得到坐标缩放比例r=hr/hm，在进行立木因子测量时可按比例将其换算到与实际相同的尺度。④方向校正。计算三维点云模型质心点的三维坐标，并基于主成分分析法(principal component analysis，PCA)[25]将点云模型进行质心化，求解点云模型协方差矩阵的特征值和特征向量，特征向量为立木三维点云模型的主方向，根据该主方向创建旋转矩阵M，将原始点云Po以质心点为中心转换到主方向的位置，得到新的三维点云模型Pn=MPo。 -
预处理后的三维点云模型中包含多株目标立木及地面，为此需要进行点云分割，分别提取单株立木三维点云。首先使用RANSAC算法将地面点云拟合成一个平面，然后提取属于该平面内的点云，从而将地面点云与立木点云进行初步分割。
在初步分割后的点云中，同一立木的点云总是紧邻的，而不同立木的点云之间存在间距，因此，根据空间点的欧氏距离采用条件欧几里得聚类算法进行多株立木三维点云的分割。对于三维点云中的某一点P，通过KD树找到三维点云中离点P最近的k个点，这些点与P点的距离若小于阈值d则聚类到集合Q中。然后从集合Q中选取点P以外的点，重复上述过程，直到集合Q中点的数量不再增加，则聚类过程结束。最后将多株立木三维点云分割到不同的点云集合中，从而提取出单株立木三维点云。
-
将立木在z轴方向的最高点与最低点的差值默认为其高度，如图3所示。由于点云坐标校正后单株立木的生长方向均与z轴的正方向一致，且立木底部平面位于oxy平面，所以提取出单株立木点云后，遍历所有点，找到单株立木z轴坐标的最大值与最小值，两者差值的绝对值即为单株立木的高度h (h=|Zmax−Zmin|)。
Figure 3. Schematic diagram of tree height extraction
-
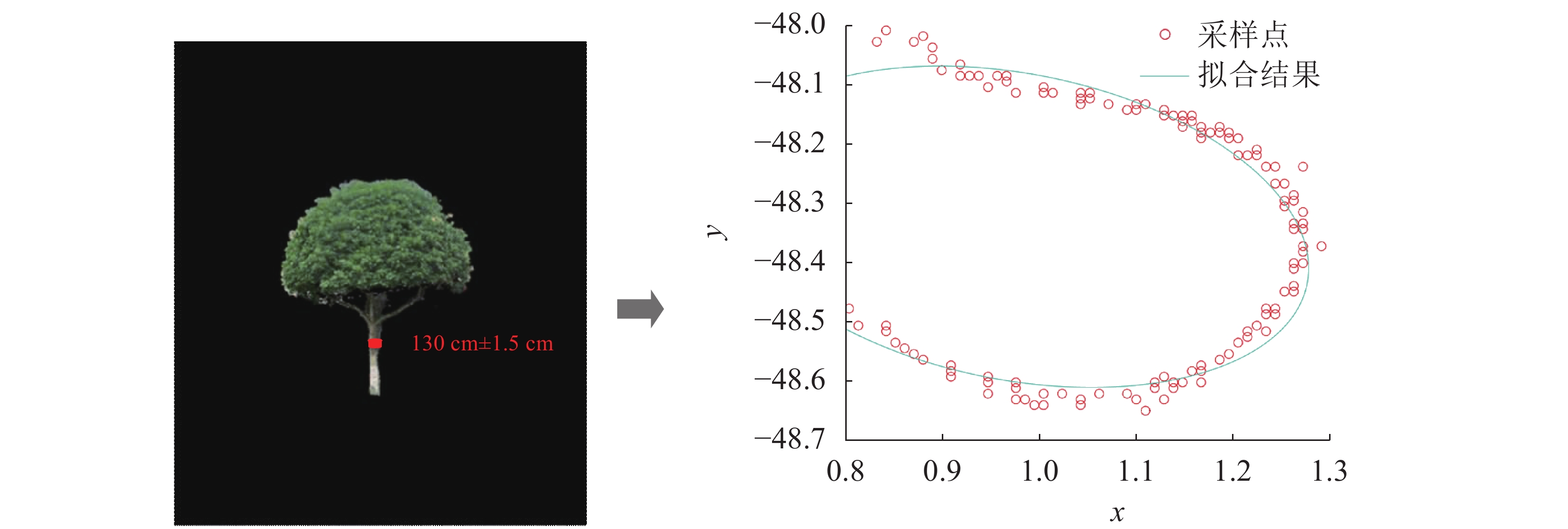
将立木位于距地面1.3 m处断面直径的最大值和最小值的平均视为其胸径，如图4所示。在单株立木的三维点云中，利用校正后的比例r求得1.3 m处点云坐标：z=1.3/r。对该处做3 cm厚度的切片，然后再将点云切片投影至oxy平面，利用非线性最小二乘法进行椭圆拟合求解椭圆一般方程式：Ax2+Bxy+Cy2+Dx+Ey+1=0。其中：A、B、C、D、E是待求解参数。求得椭圆一般方程式后，根据式(10)和式(11)求得椭圆的短轴a和长轴b：
Figure 4. Schematic diagram of tree DBH extraction
然后将椭圆的短轴与长轴的平均值作为立木的胸径(Φ)：Φ=(a+b)/2。
-
基于软件平台Visual Studio 2017和计算机视觉Opencv库提取立木视频关键帧图像并基于运动恢复结构算法获取立木三维点云；基于C++开源点云库(point cloud library，PCL)对点云数据进行预处理及分割操作。
-
立木视频关键帧提取后，基于运动恢复结构算法获取的立木场景三维点云如图5A所示。可以看出该原始三维点云不仅包含了4株立木，还包含了地面、背景及离群噪声点。由图5B所示：进行点云下采样之后点云数据减少了约3倍，这并不影响立木三维点云的整体形状，且经过预处理后的点云成功滤除了背景及大量离群噪声点，点云模型的坐标方向也得到了校正(该场景中种植立木的花坛长度已知，无需在场景中放置用于比例校正的物体)。图5C是将地面点云与立木点云进行初步分割后的结果，图5D是点云通过条件欧几里得聚类算法分割后得到的4株立木。
Figure 5. 3D point cloud processing results of trees
-
由表1可见：经过计算得出树高测量的绝对误差为0.03~0.24 m，测量值与实际值之间的相对误差为0.63%~3.93%，平均相对误差为1.96%。树高测量值总体上比实际值低，主要是因为树冠顶部的枝叶稀少，导致生成的三维点云在树冠顶部较为稀疏，在点云处理阶段被视为噪声点去除，并且在一些枝叶较细或者高度较高的立木上，由于视频拍摄不够清晰导致特征点匹配数量不足，使得立木三维重建时存在点云部分缺失的现象。立木的胸径测量的绝对误差为0.20~0.85 cm，测量值与实际值之间的相对误差为1.45%~6.92%，平均相对误差为3.19%。测量误差主要是由于拍摄时立木之间的遮挡，导致部分立木树干重建效果不佳，并且在使用非线性最小二乘法进行椭圆拟合时，由于利用的点云数量较少且分布不均匀，使得拟合不够准确。
立木
编号树高 胸径 实际
值/m测量
值/m相对误
差/%实际
值/cm测量
值/cm相对误
差/%1 6.14 6.10 0.63 15.60 14.85 4.85 2 4.98 4.87 2.15 13.06 13.33 2.07 3 5.49 5.53 0.84 12.74 13.00 2.09 4 5.64 5.49 2.60 14.97 15.58 4.06 5 3.42 3.39 0.93 10.83 10.62 1.87 6 3.49 3.55 1.69 12.26 13.11 6.91 7 4.53 4.40 2.78 12.90 12.25 4.99 8 4.31 4.21 2.39 14.33 14.09 1.70 9 6.65 6.60 0.71 19.43 19.14 1.44 10 6.19 6.08 1.79 18.63 19.35 3.87 11 7.17 6.93 3.40 18.80 18.42 1.94 12 5.63 5.73 1.67 18.72 19.39 3.58 13 7.52 7.35 2.18 16.97 17.27 1.77 14 7.47 7.20 3.56 19.04 18.59 2.37 15 5.58 5.69 1.93 15.13 14.36 5.08 16 5.01 5.05 0.64 11.94 12.20 2.16 17 5.41 5.27 2.57 12.67 12.46 1.68 18 7.18 6.98 2.78 16.08 16.88 4.93 平均值 1.96 3.19 Table 1. Measured and actual values of tree height and DBH
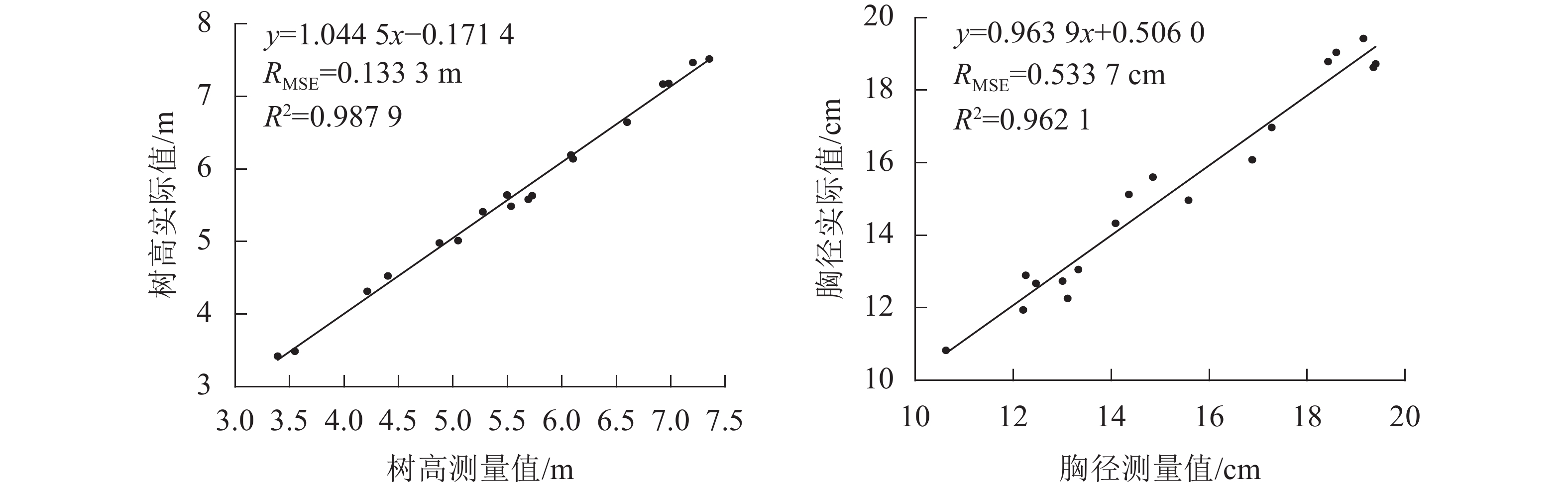
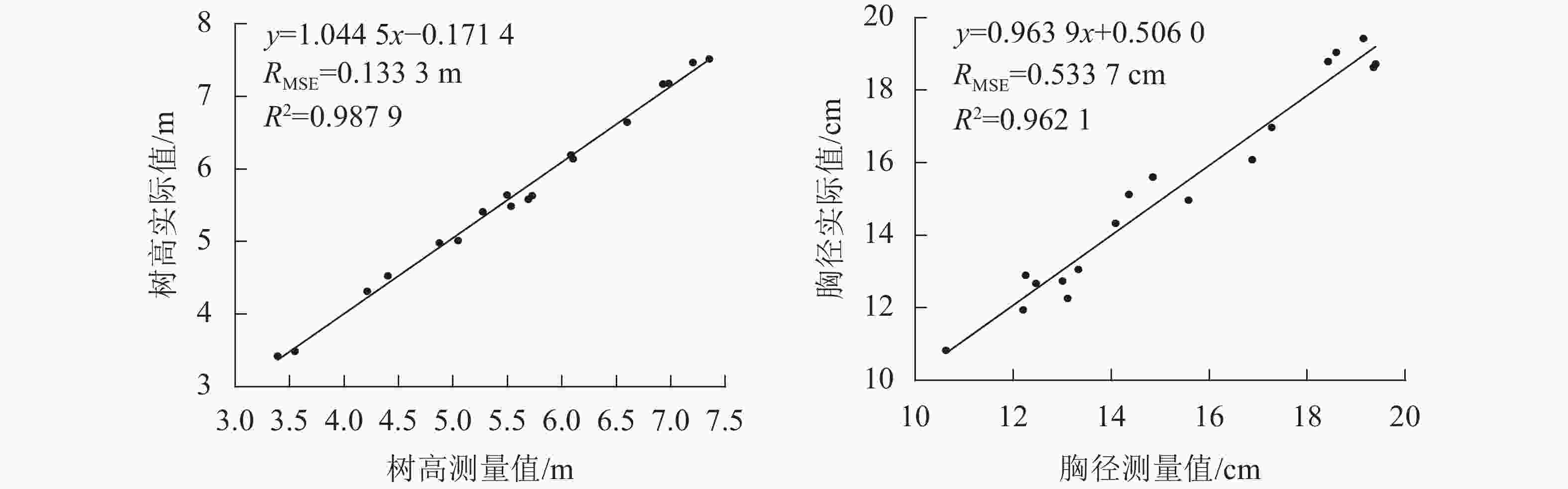
图6为树高和胸径测量值与实际值的线性回归分析图，使用本研究方法测量的立木树高和胸径与实际值之间均存在着显著的线性相关关系，树高相关系数(R2)为0.987 9，均方根误差(RMSE)为0.133 3 m；胸径R2为0.962 1，RMSE为0.533 7 cm。
Figure 6. Regression analysis of measured and actual values of tree height and DBH
-
针对当前基于三维点云的立木因子测量方法效率低或成本高的问题，本研究提出了一种基于运动恢复结构的多株立木因子测量方法，使用普通智能手机实现了自然环境下多株立木树高和胸径的灵活、有效测量。本研究表明：使用本方法测量树高的平均相对误差为1.96%，相关系数为0.987 9，均方根误差为 0.133 3 m；测量胸径的平均相对误差为3.19%，相关系数为0.962 1，均方根误差为0.533 7 cm。本方法测量树高的平均相对误差均低于文献[26-27]，具有更高的树高测量精度；测量胸径的平均相对误差低于文献[26]，略高于文献[27]，但是文献[26-27]分别需要使用三维激光扫描仪和ToF手机，而本方法仅需使用普通智能手机，具有更好的普适性。
本方法具有较高的精度，但是测量胸径和树高仍有一定的误差，可能原因为：①树冠顶部的枝叶稀少，导致生成的三维点云在树冠顶部较为稀疏，在点云处理阶段被视为噪声点去除，导致树高测量值总体上比实际值低。②在一些枝叶较细或者高度较高的立木上，由于视频拍摄不够清晰导致特征点匹配数量不足，使得立木三维重建时点云部分缺失。③采用非线性最小二乘法拟合椭圆时由于树干点云的数量较少或分布不均导致立木胸径计算结果不理想。因此，可尝试采用高分辨率无人机等设备进行树冠顶部视频的拍摄，以获得立木清晰且全面的图像，同时进一步研究立木图像特征点提取与匹配算法，增加树干与树冠顶部枝叶的特征点匹配对数量，以提高重建立木的三维点云质量。
Measuring method of multiple trees attributes based on structure from motion
doi: 10.11833/j.issn.2095-0756.20210547
- Received Date: 2021-08-09
- Accepted Date: 2022-01-18
- Rev Recd Date: 2021-09-10
- Available Online: 2022-07-20
- Publish Date: 2022-08-20
-
Key words:
- tree attribute measurement /
- video key frame /
- structure from motion (SfM) /
- point cloud segmentation
Abstract:
| Citation: | GU Wenjun, XU Aijun, YIN Jianxin. Measuring method of multiple trees attributes based on structure from motion[J]. Journal of Zhejiang A&F University, 2022, 39(4): 792-799. DOI: 10.11833/j.issn.2095-0756.20210547
|
DownLoad: