Pinus yunnanensis volume estimation model based on UAV multispectral image

研究区位于云南省昆明市富民县罗免乡(25°16′21″~25°25′26″N，102°20′46″~102°29′14″E)。该地区属天然云南松林分布的典型区域，地势西南、西北高，东南低。属于低纬度亚热带高原季风气候区，四季温差小，干湿季分明，年平均气温为15.8 ℃，年平均降水量为847.0 mm，研究区内以典型的天然云南松纯林为主。

于2022年10月在研究区内选取能充分代表林分总体特征平均水平的地块，设置大小为25 m×25 m的标准地，共63个。对标准地内胸径≥5.0 cm的所有活立木进行每木定位，并测量胸径、树高、最长冠幅、最短冠幅。标准地林分因子见表1。根据实测的胸径、树高，利用二元立木材积公式计算单木材积，在此基础上计算标准地的蓄积量。云南松林二元立木材积公式：

其中：V为材积(m³)；D为胸径(cm)；H为树高(m)。

大疆精灵4多光谱无人机作为多光谱影像采集平台，集成了1个可见光相机和5个多光谱相机[包括红光(B₁)、绿光(B₂)、蓝光(B₃)、红边(B₄)和近红外(B₅)波段]。于2022年11月14日利用大疆精灵4多光谱无人机，采用DJI GS PRO地面站软件从各标准地获取多光谱影像数据。飞行高度设置为100 m，航向和旁向重叠率均设置为85%。利用DJI Terra软件对原始图像进行预处理，生成数字正射影像(DOM)和数字表面模型(DSM)。将5个单波段的合成图像在ArcGIS中合成为多光谱影像(影像分辨率为5.3 cm)，计算所需的各类特征变量。

植被指数是指多光谱遥感数据经过线性或非线性数学运算，产生能反映植被生长状况的数值，已广泛用于森林蓄积量建模反演^[15]。提取多光谱影像中红光、绿光、蓝光、红边、近红外等5个波段的反射率(b₁、b₂、b₃、b₄、b₅)，计算蓄积量估测中常用的植被指数：归一化植被指数(NDVI)，比值植被指数(RVI)，差值植被指数(DVI)，大气抗阻植被指数(ARVI)，以及根据可见光波段计算的植被指数：过绿指数(EXG)^[16]，绿蓝比值指数(GBRI)^[17]，绿红比值指数(GRRI)^[18]，归一化绿蓝差异指数(NGBDI)^[19]，归一化绿红差异指数(NGRDI)^[20]，可见光波段差异植被指数(VDVI)^[21]等10个植被指数。

在蓄积量估测中加入纹理特征有助于提高蓄积量的估算精度^[22−24]。为避免影像高频空间信息的丢失，选择较小的3×3窗口提取纹理特征^[25]。借助ENVI 5.3的纹理提取工具，在3×3窗口下，通过灰度共生矩阵提取纹理特征，主要包括方差(VA)，均值(ME)，协同性(HO)，熵(EN)，对比度(CO)，二阶矩(SM)，相异性(DI)和相关性(CC)^[14]。5个波段共40个纹理特征。

由于标准地为方形标准地，且部分样地郁闭度较低，所以以标准地中的某一点提取各特征变量值不能充分反映标准地特征。本研究以标准地边界为矢量区域，借助ArcGIS的分区统计工具计算标准地范围内各特征变量的平均值作为自变量，建立蓄积量估测模型^[26]。可用于建立蓄积量估测模型的因子会随着研究区、数据源、成像时间等的差异而不同，在建立模型之前对蓄积量与各特征变量进行Pearson相关性分析，筛选与蓄积量相关性较高的特征变量构建模型。

根据相关性分析的结果，选择在0.01水平与蓄积量极显著相关的特征变量为自变量，按照7∶3比例随机划分训练集和测试集，采用多元线性回归(MLR)、支持向量机(SVR)、随机森林(RF)等3种回归方法建立蓄积量估测模型。

利用决定系数(R²)、均方根误差(E_RMS)、平均绝对误差(E_MA)、平均相对误差(E_MR)进行精度评价^[26]。

将单波段反射率、植被指数、纹理特征与蓄积量进行相关分析(表2)，5个波段反射率中，蓄积量与b₁、b₂无显著相关性，与b₃呈极显著负相关(P＜0.01)，与b₄、b₅呈极显著正相关(P＜0.01)。

在植被指数中，NGRDI与蓄积量不相关，NGBDI与蓄积量呈显著正相关(P＜0.05)外，其余植被指数均与蓄积量呈极显著正相关(P＜0.01)。

如表3所示：在8个纹理特征中，HO、EN与蓄积量的相关性较高，VA、CO、DI次之，CC、SM、ME与蓄积量的相关性较低。比较5个波段提取的纹理特征，与蓄积量显著相关的纹理特征数由大到小依次为B₅、B₄、B₁、B₂、B₃。

根据相关性分析结果，筛选出26个在0.01水平与蓄积量显著相关的因子，分别为单波段反射率b₃、b₄、b₅，植被指数RVI、NDVI、DVI、VDVI、EXG、ARVI、GBRI、GRRI，纹理特征B₁-EN、B₁-HO、B₁-ME、B₂-EN、B₂-HO、B₃-EN、B₄-CO、B₄-DI、B₄-HO、B₄-VA、B₅-CO、B₅-DI、B₅-EN、B₅-HO、B₅-VA。

传统的线性回归模型易受自变量间共线性的影响，利用主成分分析可将原始的多个变量转化为少数主成分因子，每个主成分之间相互独立，克服自变量间的多重共线性的同时保留了原始变量的绝大部分信息^[3−4]。根据特征根和累计方差解释率确定主成分个数(表4)。当主成分个数为4个时，累计方差解释率达93.66%，因此确定主成分为C₁、C₂、C₃、C₄。

提取的4个主成分因子与原始变量的线性关系如表5，利用提取出的4个主成分因子建立多元线性回归模型：$M=41.569+11.949C_{1}-2.162C_{2}+ 2.020C_{3}- 2.706C_{4} $。其中：M为蓄积量(m³·hm⁻²)；C₁、C₂、C₃、C₄为主成分分析提取的主成分因子。

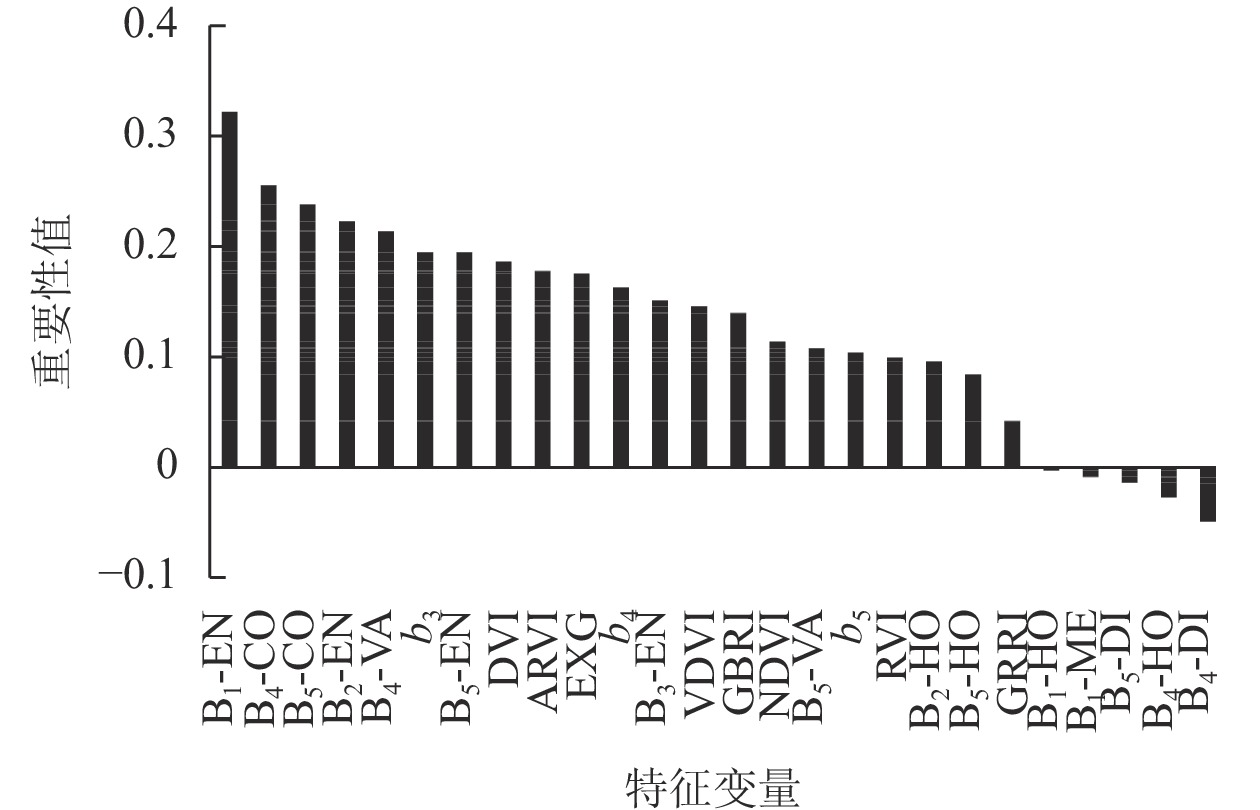
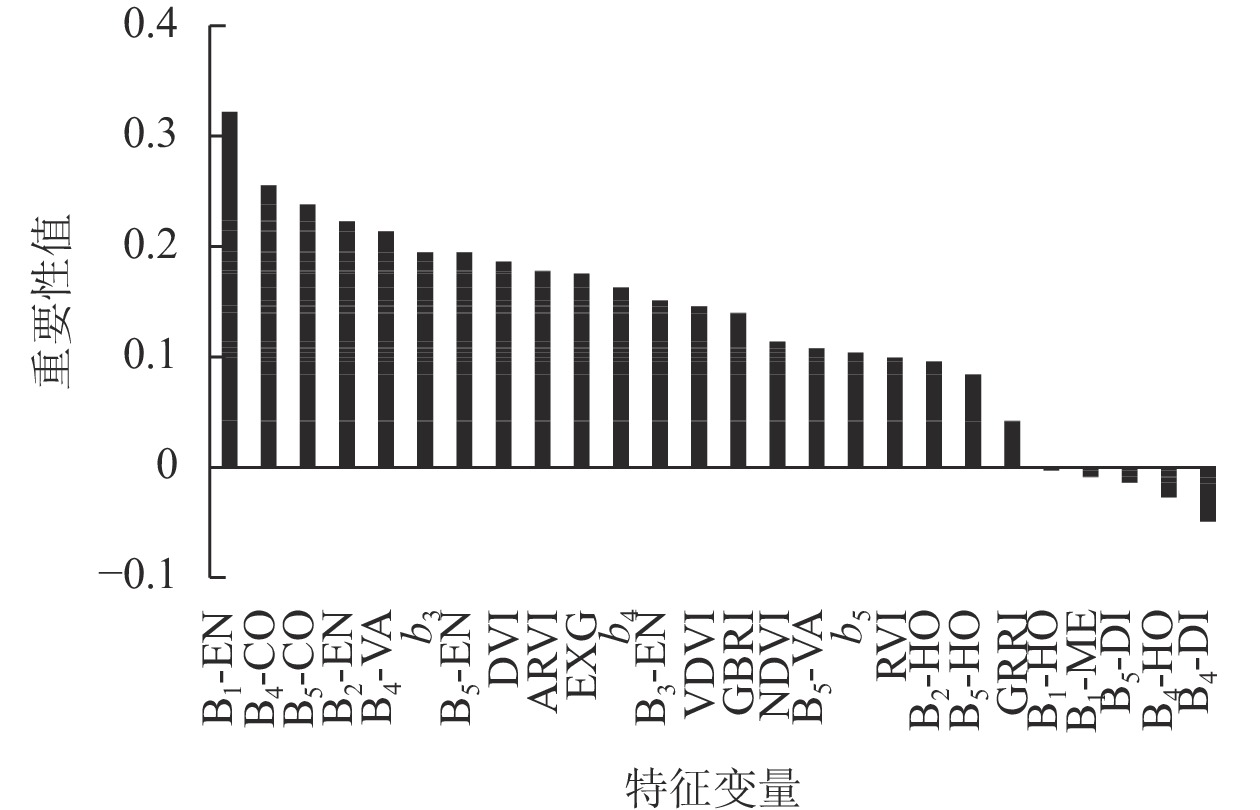
本研究使用Matlab建立随机森林回归模型，决策树数目为100，最小叶子数为1，其余参数均为默认值。如图1所示：随机森林模型中，变量重要性前5位的均为纹理特征，说明纹理特征对于蓄积量估测模型的重要性不可忽视。纹理特征间的重要性程度差异大，不同波段间也存在较大差异；植被指数对模型的影响比较稳定，植被指数间除GRRI外无明显差异。

Figure 1.  Importance of random forest model variables

基于Matlab借助LIBSVM工具箱构建支持向量回归(SVR)模型，支持向量机(SVM)类型为e-SVR，函数选择径向基核函数(RBF)，涉及惩罚系数(c)和径向基核函数的参数$(\gamma) $这2个重要参数。利用格网化寻优，得到最佳c、$\gamma $分别为4、0.0625。

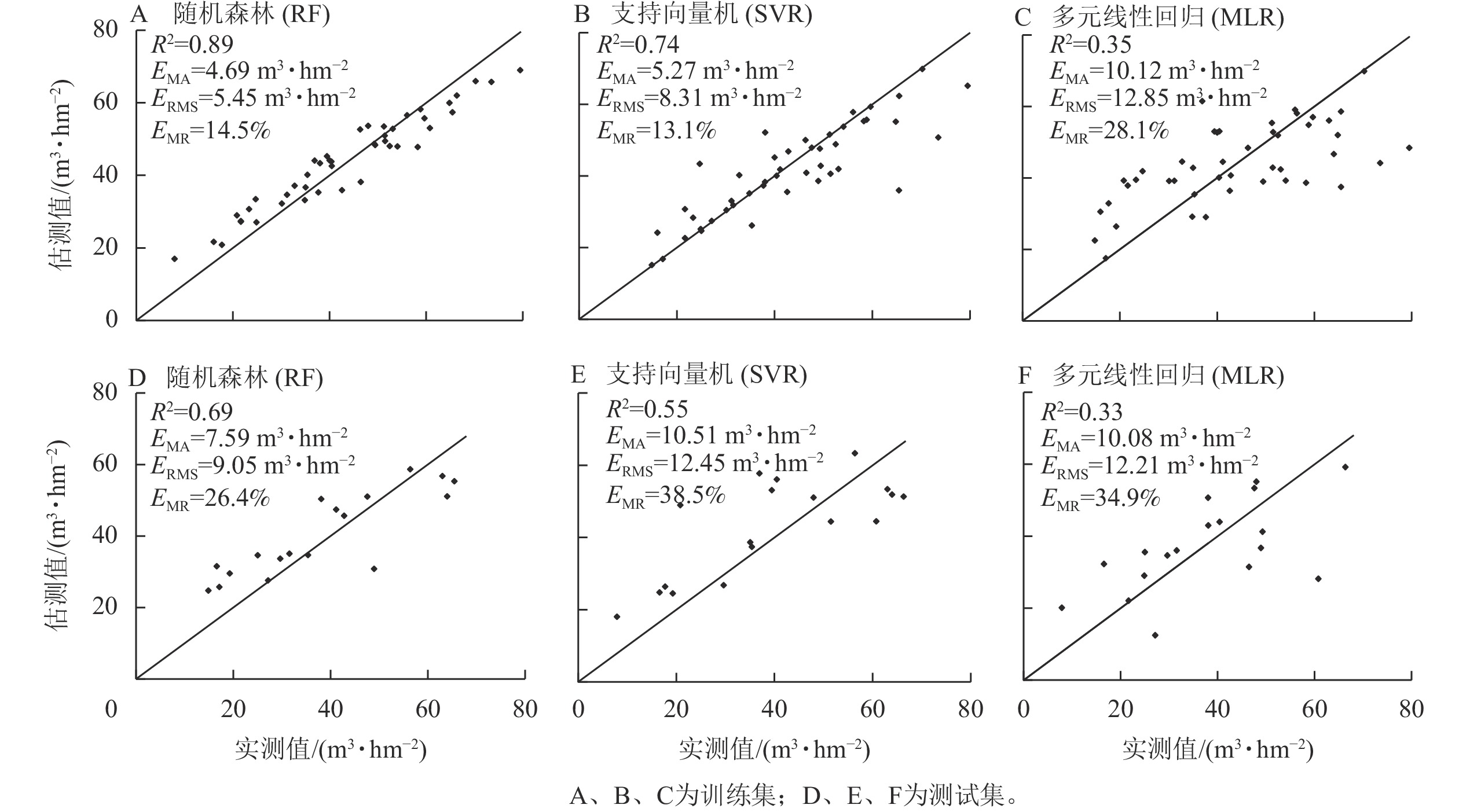
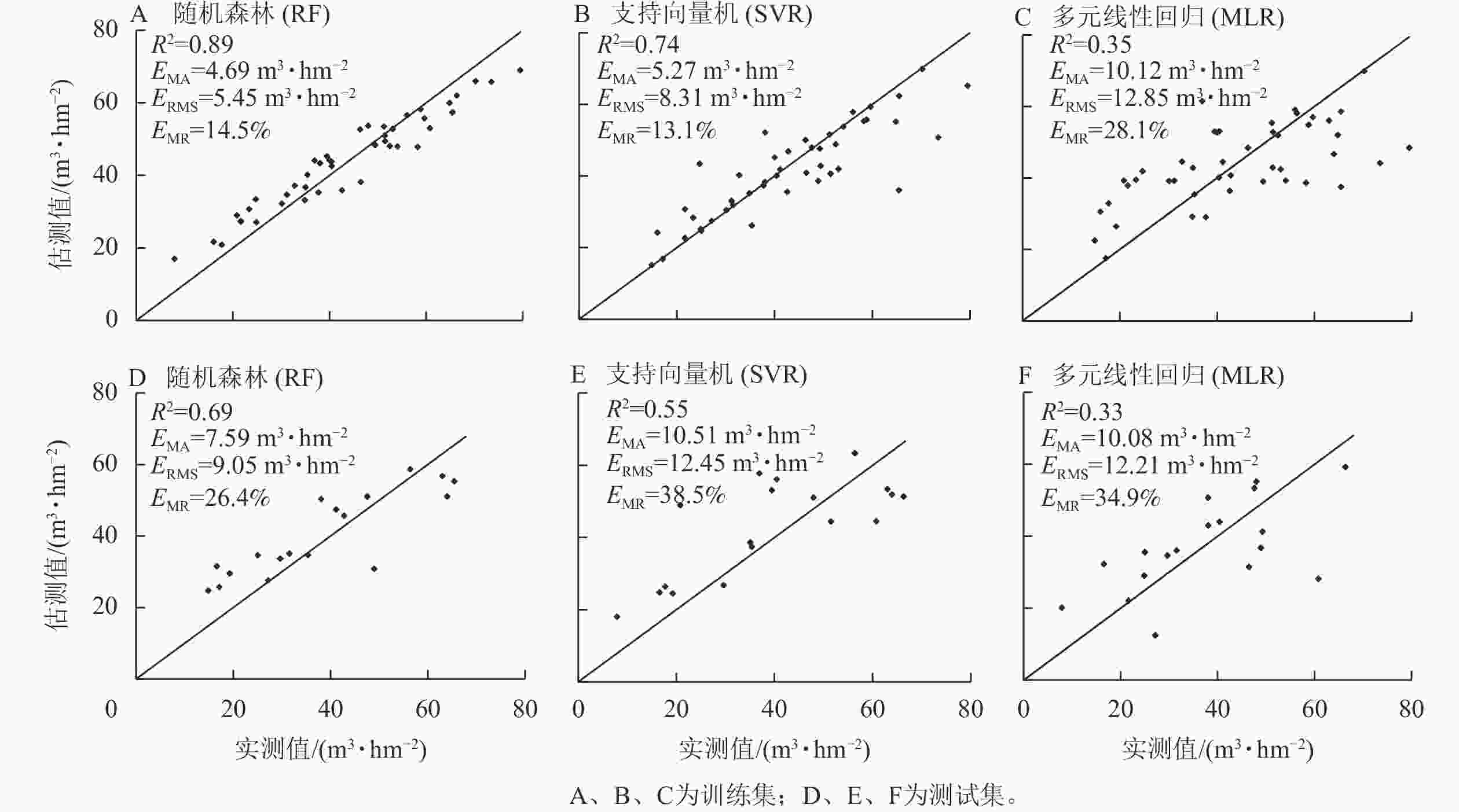
精度评价结果：在训练集上，随机森林模型精度最高(R²=0.89，E_MA=4.69 m³·hm⁻²，E_RMS=5.45 m³·hm⁻²，E_MR=14.5%)，支持向量机次之(R²=0.74，E_MA=5.27 m³·hm⁻²，E_RMS=8.31 m³·hm⁻²，E_MR=13.1%)，多元线性回归精度最低(R²=0.35，E_MA=10.12 m³·hm⁻²，E_RMS=12.85 m³·hm⁻²，E_MR=28.1%)。在测试集上，随机森林精度仍最高(R²=0.69，E_MA=7.59 m³·hm⁻²，E_RMS=9.05 m³·hm⁻²，E_MR=26.4%)，其次是支持向量机(R²=0.55，E_MA=10.51 m³·hm⁻²，E_RMS=12.45 m³·hm⁻²，E_MR=38.5%)，多元线性回归最低(R²=0.33，E_MA=10.08 m³·hm⁻²，E_RMS=12.21 m³·hm⁻²，E_MR=34.9%)。3种模型的测试集精度均有降低。

根据估测蓄积量与实测蓄积量绘制散点图。在训练集上(图2A~C)，随机森林和支持向量机模型离散程度较小，散点在两侧分布较均匀，模型拟合效果较好；多元线性回归模型散点在两侧分布较均匀，但离散程度较高，模型拟合较差。在测试集上(图2D~F)，3种模型散点在两侧分布不均匀，随机森林离散程度小，其余2种模型离散程度大。3种模型在训练集、测试集上均存在一定的低值高估和高值低估现象。

Figure 2.  Correlation between measured forest volume and estimated forest volume

本研究基于无人机多光谱影像提取单波段反射率、各类植被指数、纹理特征，并计算其标准地均值，利用结合主成分分析的多元线性回归、随机森林、支持向量机等建立蓄积量估测模型，结果表明：随机森林模型的精度最高，支持向量机次之，多元线性回归最低。

苏迪等^[10]根据平均胸径、平均树高、坡度、坡向等因子建立蓄积量估测模型(模型R²=0.738，E_RMS=5.1358 m³·hm⁻²)，曾霞辉^[11]提取平均冠幅、郁闭度、平均树高、株数密度建立蓄积量估测模型(模型对应的R²、E_MR分别为0.64~0.78、18.93%~39.68%)。本研究所建立随机森林模型和支持向量机模型的误差水平与其基本一致，多元线性回归模型精度较低。

于东海^[13]在对辽宁老秃顶子国家级自然保护区的蓄积量估测研究中，提取植被指数、纹理特征、地形因子，并通过主成分分析提取主成分因子建立多元线性回归模型，模型R²为0.88，拟合效果良好，测试集平均相对误差为9.96%。与该研究相比，本研究结合主成分分析法建立的多元线性回归模型R²为0.35，测试集的平均相对误差为34.9%，精度较低。对研究区进行对比发现，于东海^[13]所选研究区森林覆盖率97%，郁闭度、样地单位面积蓄积量高；本研究区郁闭度差异大，标准地单位面积蓄积量低，最大值为79.49 m³·hm⁻²，最小值低至7.90 m³·hm⁻²，平均值为41.97 m³·hm⁻²。2个研究区森林郁闭度存在较大差异，估测精度可能受到郁闭度的影响。

不同窗口下提取的纹理特征对蓄积量估测精度存在一定影响，提取窗口过大或过小都会造成纹理特征的错误分割进而影响估测精度^[27]。基于无人机多光谱影像，在不同窗口大小下提取的纹理特征对蓄积量估测精度的影响有待进一步研究。

研究区林分较稀疏，在部分标准地中，有少量的树木位于标准地边界附近，其部分树冠在标准地边界之外。计算各变量均值时，此部分树冠所对应的特征变量没有参与均值计算，可能对估测精度产生一定的影响。

以大疆精灵4无人机获取滇中地区典型天然云南松林多光谱影像，提取并计算标准地单波段反射率、植被指数、纹理特征均值，共55个特征变量，经相关性分析筛选出26个变量参与模型构建。通过对随机森林、支持向量机、多元线性回归3种模型进行精度评价，最佳估测模型为随机森林。3种模型在估测蓄积量时均存在一定的低值高估和高值低估现象。与同类型研究的蓄积量估测误差水平基本一致，表明在不进行单木分割的情况下，利用无人机多光谱影像提取各因子，以各因子的标准地均值建立模型估测蓄积量具有一定的可行性。