-
植物种群的空间分布格局是指种群在水平空间上的配置和分布状况[1]，除了种群自身特性和环境条件因素与其形成密切相关外[2]，种间关系也是促使其形成的主要动力之一[3]，在判断植物种间关系时，生态学家们通常会运用种间联结性分析来探究物种之间的内在联系[4]。此外，生态位的重叠程度在一定程度上能够反映物种联结关系以及空间配置关系[5-6]。对植物种间关系及空间分布格局的研究，有助于认识种群与生境的相互关系、空间资源获取能力与生态适应对策，预测群落消长动态，是深入了解维持树木物种共存机制，并了解产生空间格局的过程的重要手段[7-9]，对于正确认识群落的组成、功能及演替规律具有重要意义。次生林是中国森林资源的主体，它既保持着原始森林的物种组成成分与生境，又与原始森林在结构组成、林木生长、生产力、林分环境和生态功能等诸多方面有着显著的不同，原始林退化导致的次生林面积扩大将引起森林生态系统中生物多样性的下降[10]。如何恢复和保护次生林群落的物种多样性成为生态学家面临的重要问题。而对森林木本植物的空间分布格局及种间关系的研究有助于揭示群落结构的形成机制与潜在的生态学过程，对次生林的经营抚育具有一定指导意义[11]。以松林、松阔混交林和常绿阔叶林中幼龄林为主体的天然次生林是浙江省建德市的森林资源主体，主要由被过度干扰破坏的天然林地逐渐恢复、演替而来[12]。次生林中仍保有原始森林的部分物种，但不同类型次生林在群落结构、林木年龄组成、植物生产力及生境等方面都存在显著差异[13]。本研究对浙江建德的次生林群落进行每木调查，分析主要树种间的相互关系及空间分布格局特征，以增强对该区域次生林群落结构特征和空间分布格局的认识，促进区域生物多样性保护与木本植物资源的可持续利用，预测群落的演替方向并探索其驱动力来源，进而为该区域次生林群落的恢复、改造及抚育经营提供依据，更好发挥其生态社会效益。
-
研究区位于浙江省建德市新安江林场(29°29′N，119°16′E)，属亚热带北缘季风气候，温暖湿润，四季分明，年平均气温为16.9 ℃，最冷月平均气温为4.7 ℃，最热月平均气温为29.2 ℃，年均降水量为1 504.0 mm。据《中国植被》区划，该地区森林植被属亚热带常绿阔叶林北部亚地带，地带性植被为常绿阔叶林。主要森林植被类型有常绿阔叶林、落叶阔叶林、常绿落叶阔叶混交林、针阔混交林等[14]。
-
在实地踏查的基础上，在浙江建德典型常绿阔叶林、松阔混交林和松林群落中分别设置面积为100 m×100 m的样地(表1)，用木桩、塑料带进行围封标记。将每块样地划分为25小块(20 m×20 m)，并以此为基本单位对乔木层进行每木调查。记录样地群落类型、海拔、坡度、坡向、土壤等环境因子；记录样方中胸径≥5 cm的木本植物的基础数据，包括种名、树高、胸径、冠幅及其相对应的坐标[15-16]。
表 1 样地基本信息
Table 1. Basic information of sample plots
样地类型 海拔/m 纬度(N) 经度(E) 坡度/(°) 坡向 土壤类型 地点 常绿阔叶林 172 29°40′ 119°23′ 44 西 红壤 杨村桥镇徐坑村 松阔混交林 165 29°28′ 119°12′ 38 南 红壤 新安江林场朱家埠林区 松林 90 29°21′ 119°09′ 33 东 红壤 新安江林场朱家埠林区 -
重要值(IV)计算[17]：IV=(相对多度+相对显著度+相对频度)/3×100%。
-
采用Pianka重叠指数计算物种间的生态位重叠系数，公式[18]如下：
$${O_{ik}}{\rm{ = }}\mathop \sum \limits_{j = 1}^w \left( {{P_{i\!j}}{P_{k\!j}}} \right) \div \sqrt {{{\left( {\mathop \sum \limits_{j = 1}^w {P_{i\!j}}} \right)}^2}{{\left( {\mathop \sum \limits_{j = 1}^w {P_{k\!j}}} \right)}^2}} \text{。}$$ 其中：Oik为种i和种k的生态位重叠系数[1]；w为划分的资源位总数；Pij和Pkj分别是种i和种k在资源位j中的重要值占该物种在整个资源中总重要值的比例。Oik的值域为[0，1]，当2个种对群落中所有的资源都不存在共享状态时，该种对之间生态位完全不重叠，其值为0；当2个种对群落中所有资源利用完全重叠时，该种对的生态位重叠程度为1，达到最大状态。
-
Ripley’s K(r)函数是进行种内空间分布格局分析的基础函数，公式如下[19]：
$$ K\left( r \right) = \frac{A}{{{n^2}}}\sum\limits_{p = 1}^n {\sum\limits_q^n {e_{pq}^{ - 1}} } {I_r}{\rm{(}}{u_{pq}}{\rm{)}}\text{。} $$ 其中：r为分析的空间尺度(m)，A为样方面积(m2)，n为植物种个体数，upq表示点p和点q之间的距离(m)；Ir(upq)为指示函数，当upq≤r时，Ir(upq)=1，当upq＞r时，Ir(upq)=0；epq为权重值，用于边缘校正。为了更直观地解释实际的空间格局，通常用Ripley’s L(r)函数表示：
$$L\left( r \right) = \sqrt {\frac{{K\left( r \right)}}{\text{π} }} {\rm{ - }}r\text{。}$$ 当L(r)=0，种群分布类型为随机分布，对种群的聚集分布研究基于随机分布的基础，以样地中的任意一点为圆心，r为半径画圆，如果在圆中出现的个体数多于随机状态下的个体数，那么表示该种群呈现聚集分布；当圆中出现的个体数少于随机分布状态下的个体数时，该种群呈现均匀分布[20-22]。采用Monte-Carlo模拟99%置信区间，进行结果偏离随机状态的显著性检验。若L(r)值位于置信区间之上，种群呈聚集分布，L(r)值位于置信区间之下，种群呈均匀分布，L(r)值位于置信区间之内，种群呈随机分布[23]。
-
种间空间分布格局基础函数计算公式[24]如下：
$${K_{12}}\left( r \right) = \frac{A}{{{n_1}{n_2}}}\sum\limits_{g = 1}^n {\sum\limits_f^n {w_{gf}^{ - 1}} } {I_r}({u_{gf}})\text{。}$$ 其中：n1和n2分别为种1和种2的个体数，f和g分别代表种1和种2的个体。同样，用L12(r)取代K12(r)，公式为：
$${L_{12}}\left( r \right) = \sqrt {\frac{{{K_{12}}\left( r \right)}}{\text{π} }} {\rm{ - }}r\text{。}$$ 当L12(r)=0，表明2个种在r尺度下无关联；当L12(r)＞0，表明两者为空间正关联；当L12(r)＜0，表明两者为空间负相关。采用Monte-Carlo模拟99%置信区间，进行结果偏离随机状态的显著性检验。当L12(r)值位于置信区间之上，2个变量显著正相关；L12(r)值位于置信区间之下，2个变量显著负相关；L12(r)值位于置信区间之内，2个变量相互独立[23]。本研究根据实际样地面积，在参考同类研究及毗邻地区森林群落空间格局研究的基础上[25-26]，将格局分析的尺度限定为0~25.0 m。
-
采用方差比率法来测定各类型次生林群落中主要树种间的总体联结性，并利用统计量W来检验总体联结是否显著，计算公式[27]如下：
$${V_{\rm{R}}} = \frac{{\dfrac{1}{N}\displaystyle\sum\limits_{z = 1}^N {{{({T_z} - t)}^2}} }}{{\displaystyle\sum\limits_{i = 1}^S {(1 - {P_i})} }}\text{。}$$ 其中：VR为方差比率，N为样方总数，
$ T_z $ 为样方$ z $ 内出现的目标物种总数；t为样方中物种的平均数，S为总物种数，Pi为物种i的频度。以VR作为不同类型次生林中主要树种总体联结性指数，在独立性零假设条件下，VR期望值为1，即当VR=1时认为种间无联结；若VR＜1则表示物种间存在正联结；若VR＜1则表示物种间存在负联结。对于VR偏离1的显著程度采用统计量W来验证，W=VRN，若$W{\text{＜}}$ ${\textit{χ}}_{0.95}^2\left( N \right)$ 或$W{\text{＞}}{\textit{χ}} _{0.05}^2\left( N \right)$ 则说明种间总体联结性性显著，若${\textit{χ}} _{0.05}^2\left( N \right) {\text{＞}}W {\text{＞}} {\textit{χ}}_{0.95}^2\left( N \right)$ 则说明种间总体联结性不显著[28]。 -
采用经Yates连续校正系数纠正的χ2统计量对种间联结性进行定性研究。公式[18]如下：
$${\textit{χ} ^2} = \frac{{N{{[ad - bc - 0.5N]}^2}}}{{(a + b)(b + d)(a + c)(c + d)}}\text{。}$$ 其中，N为取样总数，
$ a $ 为2物种均出现的样方数，b、c分别为2个种单独出现的样方数，d为2物种均不出现的样方数。当$ ad-bc=0 $ 时，2个种相互独立；$ ad-bc{\text{＞}}0 $ 时，2个种之间呈正联结；$ ad- $ bc＜0时，2个种之间呈负联结。${\textit{χ}}^{2}$ ＜3.841时，表示种间联结性不显著；当3.841＜${\textit{χ}}^{2}$ ＜6.635时，表示种间联结性显著；当${\textit{χ}}^{2}$ ＞6.635时，表示种间联结性极显著[17]。为避免出现分母为0无法计算分析的状况，把a、b、c、d凡是为0的都加权为1[29-30]。 -
本研究以多度作为Spearman秩相关系数的数量指标，对种对间的线性关系做定量分析，计算公式[31]如下：
$$r\left( {i,k} \right) = 1 - \frac{{6\displaystyle\sum\limits_{z = 1}^N {{{\left( {{x_{iz}} - {{\bar x}_i}} \right)}^2}} {{\left( {{x_{kz}} - {{\bar x}_k}} \right)}^2}}}{{{N^3} - N}}\text{。}$$ 其中，
$ r\left(i,k\right) $ 是种$ i $ 和种$ k $ 在样方$ z $ 中的Spearman秩相关系数；$ N $ 为样方总数；$ {x}_{iz} $ 和$ {x}_{kz} $ 分别是种$ i $ 和种$ k $ 在样方$ z $ 中的秩；$ {\bar{x}}_{i} $ 和$ {\bar{x}}_{k} $ 分别是种$ i $ 和种$ k $ 在所有样方中多度的平均值。$ r\left(i,\;k\right) $ 的值域为[−1, 1]，正值表示正相关，负值表示负相关。 -
根据重要值大于5%选出各植被类型主要树种。常绿阔叶林中主要树种是青冈Cyclobalanopsis glauca、石栎Lithocarpus glaber、苦槠Castanopsis sclerophylla及木荷Schima superba等4种；松阔混交林的主要树种分别是马尾松Pinus massoniana、苦槠、杉木Cunninghamia lanceolata、檵木Loropetalum chinense、石栎等5种；松林的主要树种分别是马尾松、杉木、苦槠、化香Platycarya strobilacea、枫香Liquidambar formosana等5种。
-
从表2可以看出：在常绿阔叶林中，主要树种之间生态位重叠程度最高的是木荷-石栎(0.861 4)、其次是苦槠-青冈(0.615 4)，最低的是苦槠-木荷(0.377 2)；在松阔混交林中，重叠程度最高的是檵木-苦槠(0.801 8)，其次是马尾松-石栎(0.753 1)，最低的是石栎-杉木(0.340 9)；在松林中，重叠程度最高的是枫香-化香(0.757 5)，其次是枫香-苦槠(0.720 1)，最低的是苦槠-马尾松(0.442 7)。
表 2 不同森林类型主要树种生态位重叠数值矩阵
Table 2. Niche overlap of dominant tree species of different forest types
常绿阔叶林 松阔混交林 松林 树种 苦槠 木荷 青冈 树种 檵木 苦槠 马尾松 石栎 树种 枫香 化香树 苦槠 马尾松 木荷 0.377 2 苦槠 0.801 8 化香 0.757 5 青冈 0.615 4 0.518 2 马尾松 0.631 2 0.632 4 苦槠 0.720 1 0.625 8 石栎 0.421 9 0.861 4 0.473 3 石栎 0.451 3 0.458 4 0.753 1 马尾松 0.676 9 0.567 6 0.442 7 杉木 0.393 7 0.521 8 0.646 2 0.340 9 杉木 0.466 2 0.470 7 0.600 1 0.567 5 -
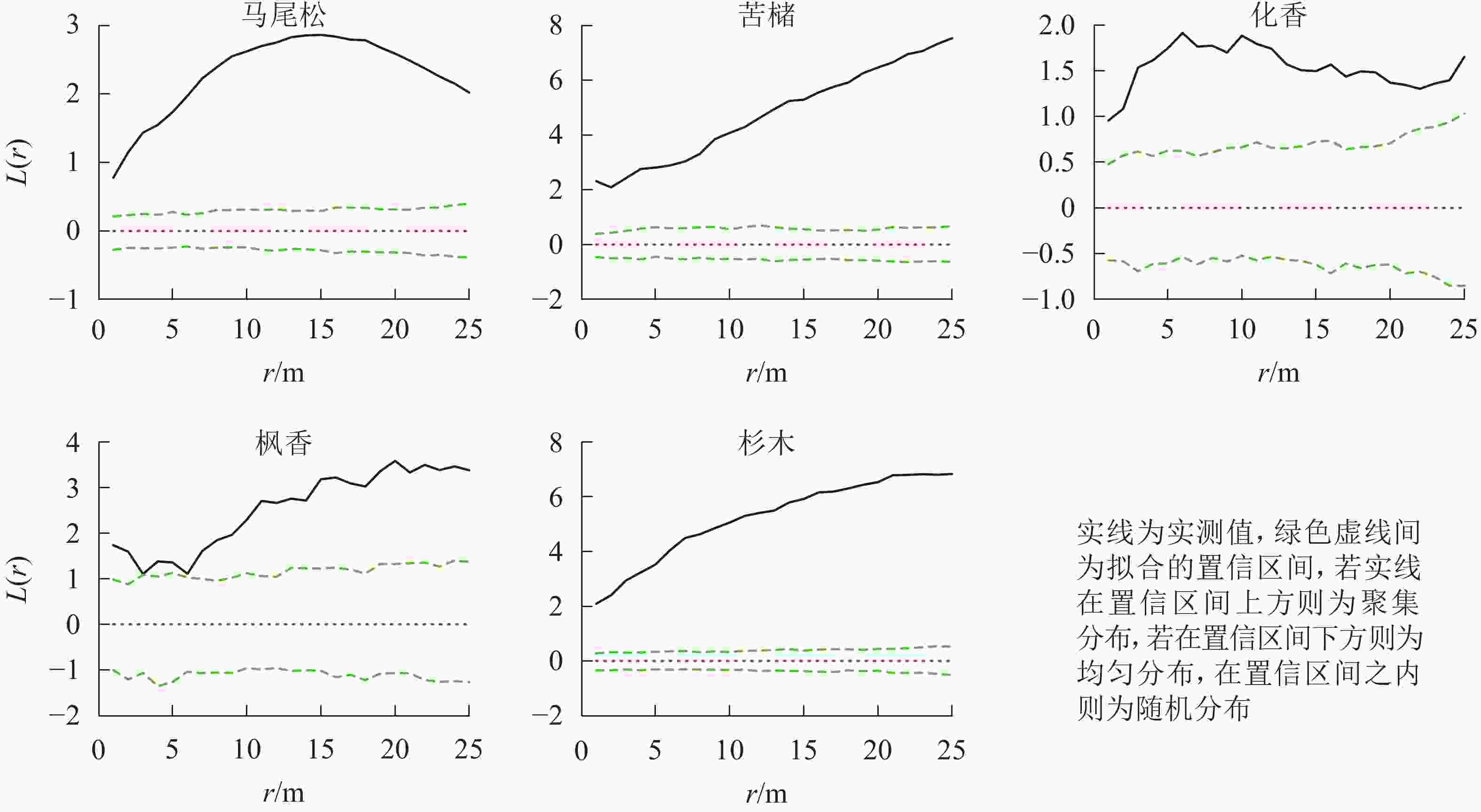
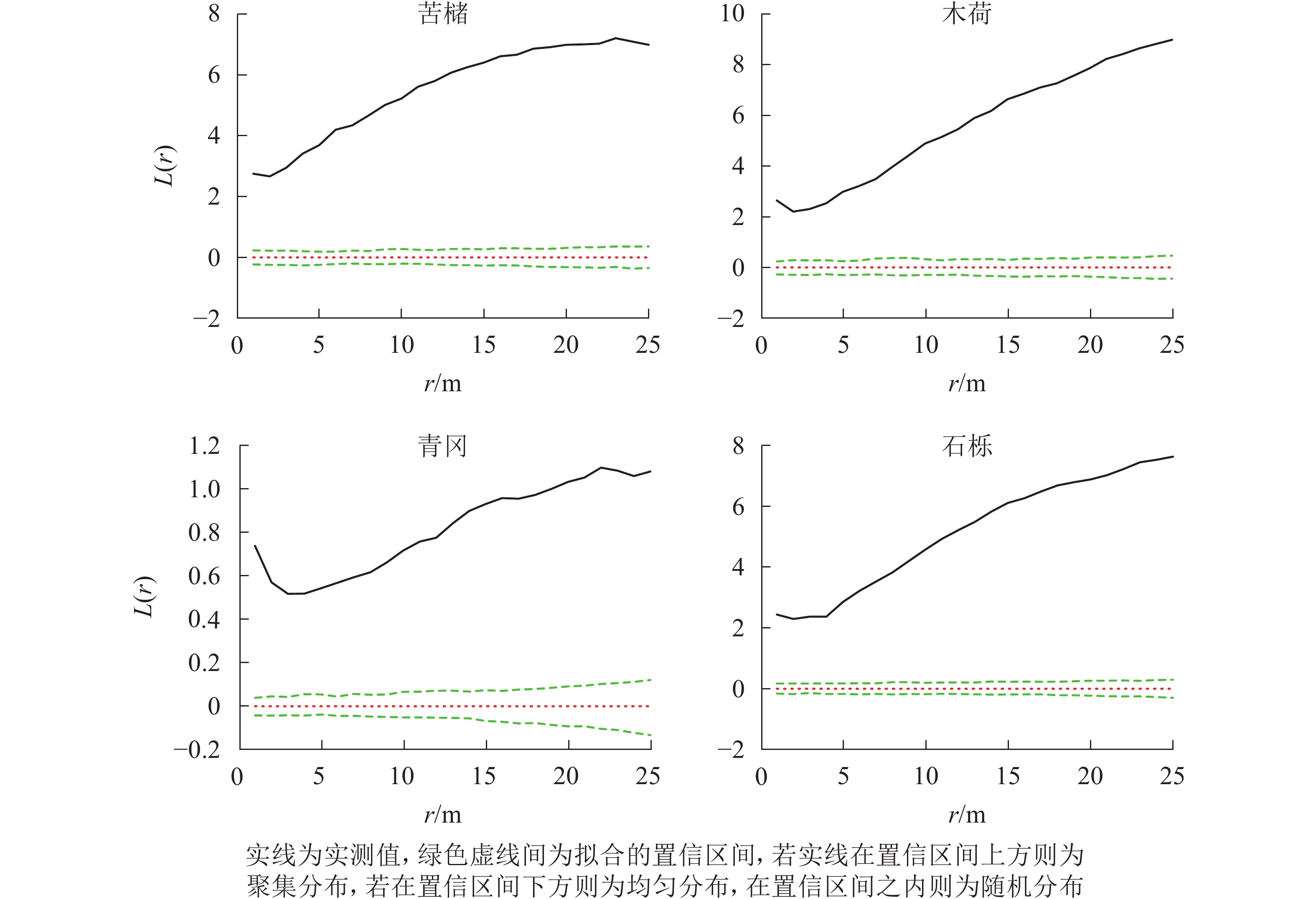
在所有研究样地中，主要树种在0~25.0 m的尺度内均表现为显著的聚集分布(P＜0.05)(图1~3)。
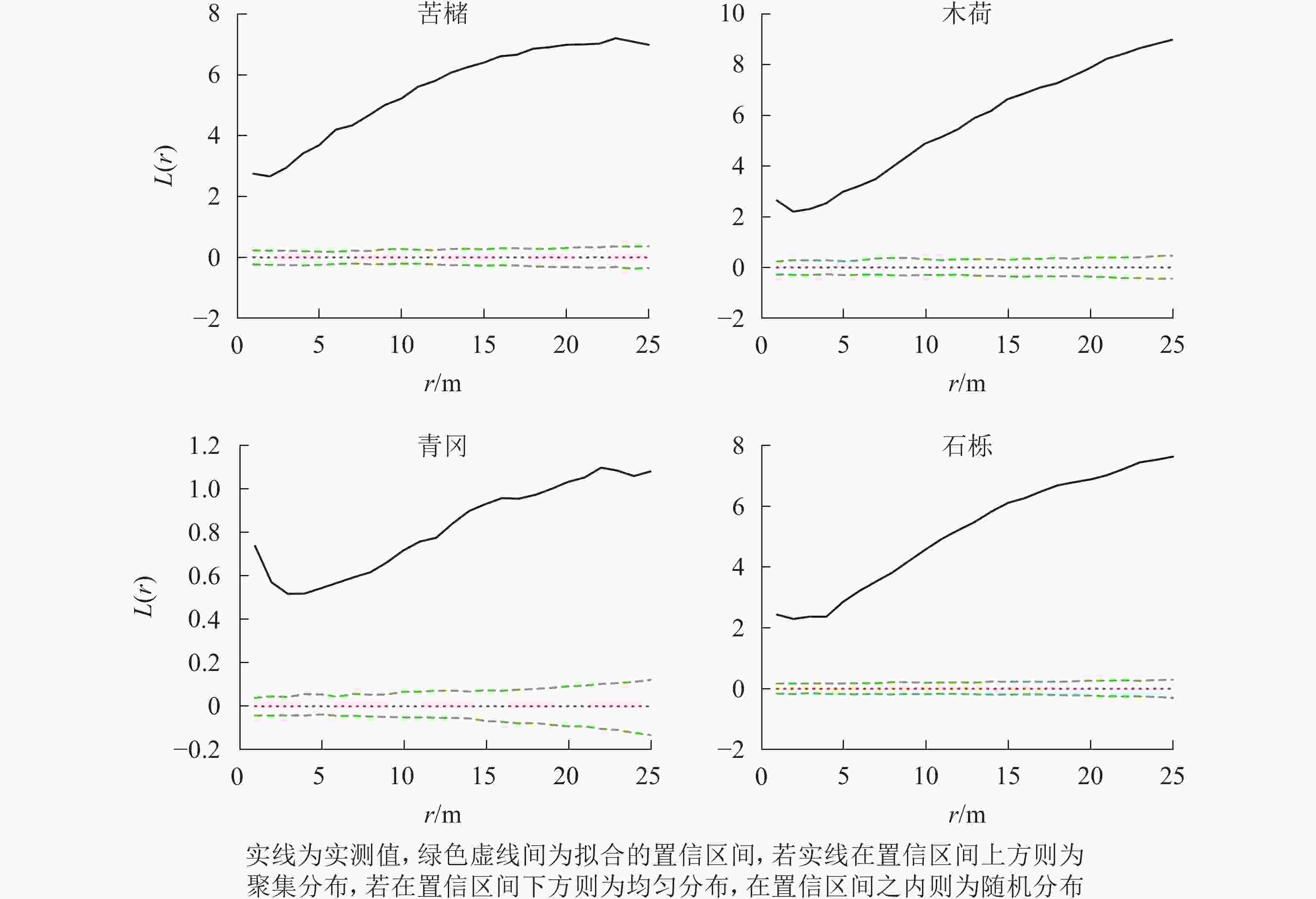
图 1 常绿阔叶林主要树种空间分布格局
Figure 1. Spatial distribution pattern of dominant tree species in evergreen broad-leaved forest
图 2 松阔混交林主要树种空间分布格局
Figure 2. Spatial distribution pattern of dominant tree species in mason pine and broad-leaved mixed forest
图 3 松林主要树种空间分布格局
Figure 3. Spatial distribution pattern of dominant tree species in mason pine forest
-
常绿阔叶林主要树种空间分布格局特征如下(图4)：青冈-石栎在0~25.0 m尺度上均呈现负相关，其中6.0~10.0 m、15.0~17.0 m尺度上负相关达到显著(P＜0.05)；青冈-木荷在0~25.0 m尺度上均为负相关，其中8.0~14.0 m尺度范围内达到显著(P＜0.05)；石栎-木荷在0~25.0 m尺度上均呈现显著的正相关(P＜0.05)。其他种对的空间关联性则以不显著相关为主。
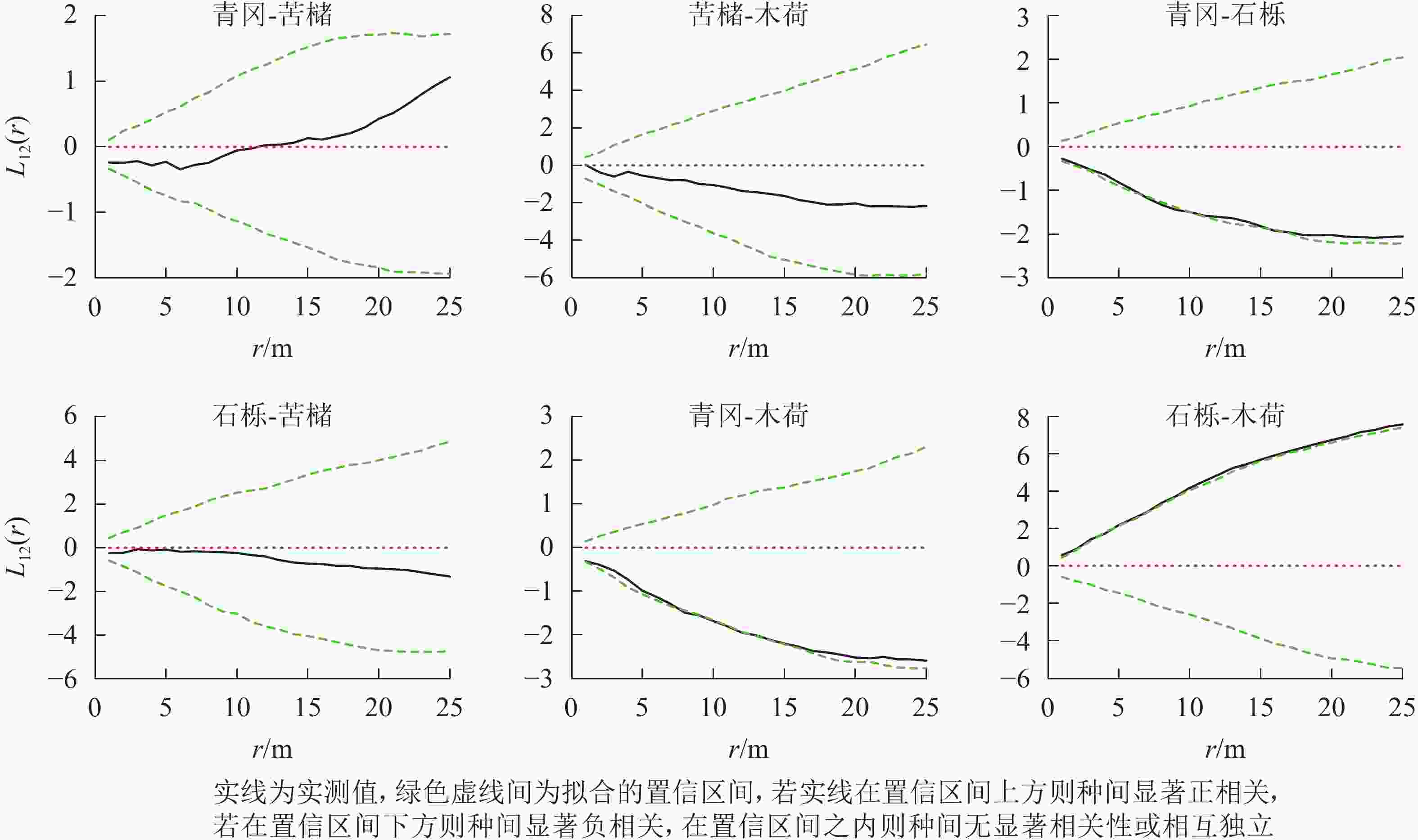
图 4 常绿阔叶林主要树种间空间分布格局图
Figure 4. Spatial distribution pattern of dominant tree species in evergreen broad-leaved forest
松阔混交林主要树种空间分布格局特征如下(图5)：马尾松-石栎在0~25.0 m尺度上呈现正相关，10.0~25.0 m尺度内达到显著(P＜0.05)；苦槠-石栎在0~20.0 m尺度范围内为正相关，其中7.0~8.0 m尺度上达到显著(P＜0.05)，而在20.0~25.0 m尺度范围内呈现不显著负相关。其他种对的空间关联性以不显著相关或无关联为主。
图 5 松阔混交林主要树种间空间分布格局图
Figure 5. Spatial distribution pattern of dominant tree species in mason pine and broad-leaved mixed forest
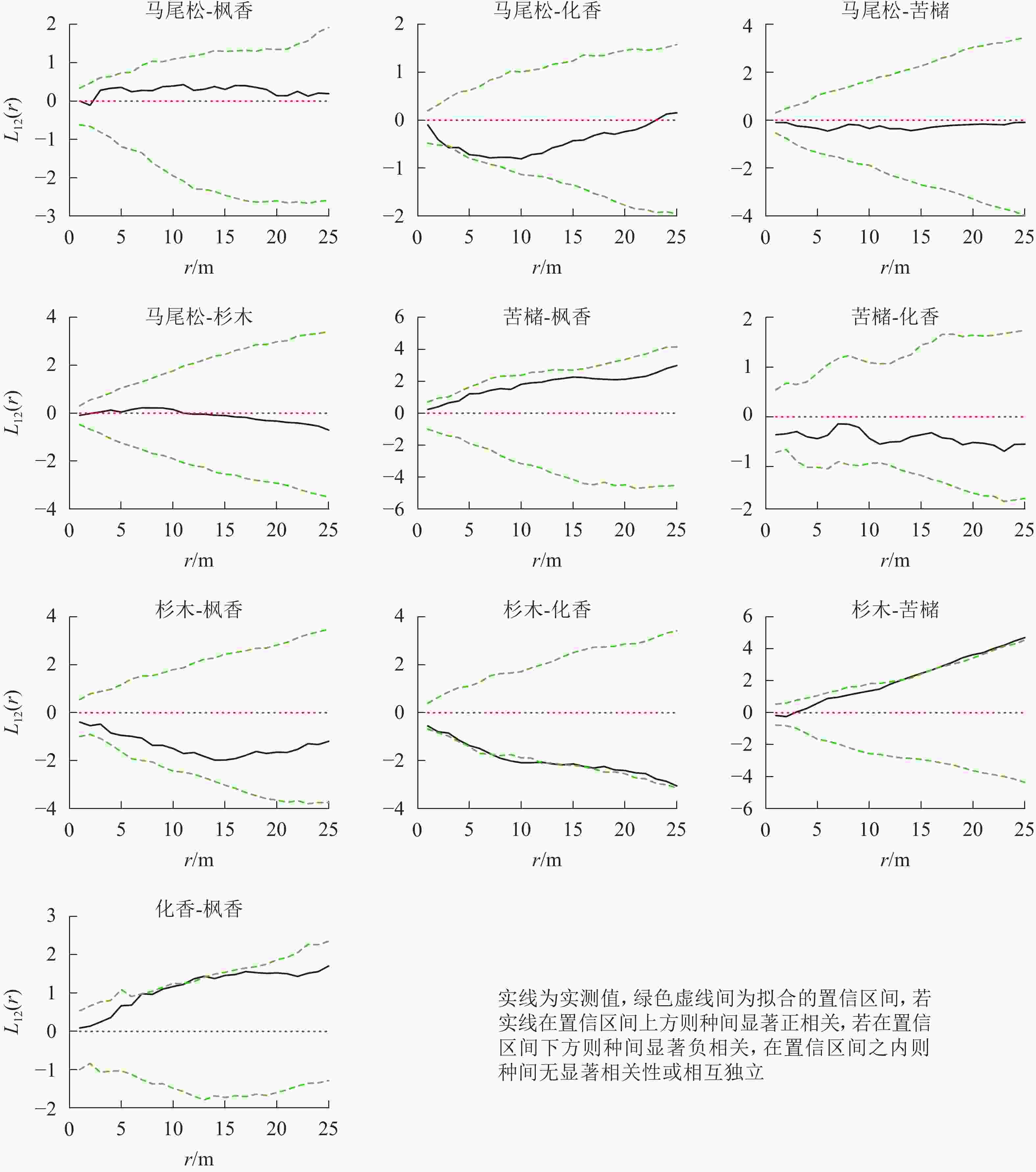
松林主要树种间空间分布格局特征如下(图6)：马尾松-化香在0~25.0 m尺度上为负相关，其中4.0 m时达到显著(P＜0.05)；杉木-苦槠在0~25.0 m尺度范围内为正相关，其中15.0~25.0 m尺度上达到显著(P＜0.05)；杉木-化香在0~25.0 m尺度范围内为负相关，其中7.5~17.0 m尺度上达到显著(P＜0.05)；化香-枫香在0~25.0 m尺度范围内表现为正相关，其中12.0~13.0 m尺度上达到显著(P＜0.05)。除此之外其他种对的空间关联性表现为不显著相关或无关联。
图 6 松林主要树种间空间分布格局图
Figure 6. Spatial distribution pattern of dominant tree species in mason pine forest
-
各类型次生林的方差比率(表3)结果表明：3种类型次生林主要树种的总体关联性均为不显著正关联。
表 3 不同森林类型主要树种的总体关联性
Table 3. Overall interspecific associations among dominant tree species of different forest types
样地类型 方差比率 W ${\; \textit{χ}^{2}_{0.95}(N)} $，${ \; \textit{χ}^{2}_{0.05}(N)} $ 结果 常绿阔叶林 1.389 34.722 14.611, 37.652 不显著正关联 松阔混交林 1.397 34.930 14.611, 37.652 不显著正关联 松林 1.199 29.966 14.611, 37.652 不显著正关联 -
χ2检验结果表明(表4)：样地中所有类型次生林的主要树种种对均呈不显著的正联结(χ2＜3.841，
$ ad-bc $ ＞0)。表 4 不同森林类型的种间联结χ2统计量矩阵
Table 4. Value of χ2 of different forest types
常绿阔叶林 松阔混交林 松林 树种 苦槠 木荷 青冈 树种 檵木 苦槠 马尾松 杉木 树种 枫香 化香 马尾松 杉木 木荷 0.001 苦槠 1.223 化香 0.179 青冈 0.230 0.092 马尾松 1.103 1.103 马尾松 0.230 1.103 石栎 0.039 0.001 0.230 杉木 0.001 0.001 0.010 杉木 0.020 0.179 0.230 石栎 0.089 0.089 0.069 0.110 苦槠 2.214 0.069 0.038 0.368 -
据图7可知：在常绿阔叶林中，呈负相关的种对有苦槠-木荷、木荷-青冈和青冈-石栎等3对，其中木荷-青冈和青冈-石栎种对的负相关达极显著(P＜0.01)；呈正相关的有苦槠-青冈、苦槠-石栎和木荷-石栎等3对，其中木荷-石栎种对的正相关达到极显著(P＜0.01)。在松阔混交林中，呈现负相关的种对有檵木-杉木、檵木-石栎2对；其余8对均呈正相关，其中马尾松-石栎的正相关达极显著(P＜0.01)。在松林中，呈现负相关的种对有枫香-杉木、化香-马尾松、化香-杉木、化香-苦槠和马尾松-苦槠等5对，其中化香-杉木的负相关达显著(P＜0.05)；其余5对呈正相关，其中枫香-苦槠的正相关达显著(P＜0.05)。
图 7 不同森林类型种间Spearman秩相关半矩阵图
Figure 7. Semi-matrix of Spearman’s rank correlation coefficients of dominant tree species of different forest types
-
森林在向顶级群落演替的过程中，植物种内空间分布格局一般会由聚集分布渐渐过渡为随机分布[12]，而在本研究中，0~25.0 m尺度上不同类型次生林的主要树种均呈显著(P＜0.05)聚集分布，这说明样地群落还未进入演替成熟期。物种自身的生物学特性是造成群落演替过程中物种聚集分布的主要原因，即相同物种对环境等条件有着相似的需求[32]。样地群落种间生态位重叠程度也能佐证其所处的演替阶段，顶级群落中树种间的生态位重叠程度一般处在较低的水平，即树种间的竞争并不活跃，这是因为经过长时间演替后，群落趋于稳定，内部树种间达到了一种相对平衡的状态[33-34]，主要树种间的生态位重叠程度仍普遍较高，群落整体呈正关联，正相关种对仍有较高占比。这反映了群落中的主要树种具有相似的环境需求和生态适应性，由此造成了样地中主要树种的聚集分布。此外，种子的扩散限制和生境异质性也被认为是影响物种分布的主要因素[20]，样地中主要树种的种子传播方式以重力传播为主，种子传播距离有限，多聚集在母树周围，离母树越远种子越少，这也导致了树种的聚集分布。在松林中，马尾松和杉木作为建群早期先锋种最先入侵林地，在光竞争中占据优势，对光的有效利用是形成林分空间格局的主要决定因素[35]，因而马尾松和杉木与群落中其他优势树种多呈负空间关联。枫香幼树稍耐荫，所以与群落中其他优势树种多呈正空间关联。在松阔混交林中，主要树种间空间关联显著程度较低，这或许与群落中的针叶树种同群落中其他较晚发育起来的常绿阔叶树种产生了垂直分层现象有关，这种垂直分层现象能够减轻群落内的光竞争，进而影响群落内的树种空间分布格局。马尾松和杉木作为早期先锋树种入侵林地后，逐渐改善了立地条件，为其他树种进入群落创造了条件，使得松林能够向松阔混交林方向演替。随后由于马尾松和杉木生物学特性在垂直结构上与其他树种产生了分层现象，加之密度制约和扩散限制等因素[12]共同作用，群落中的常绿阔叶树种逐渐获得更多的环境资源并对针叶树种和落叶阔叶树种的幼苗更新产生负作用，松阔混交林逐渐向常绿阔叶林演替。这种演替机制与XIANG等[9]的研究结果一致，即在不发生干扰的情况下，次生林群落中的不耐荫落叶树种将逐渐被耐荫的常绿阔叶树种所取代。
通过比较不同森林类型主要树种组成可以发现：3类森林群落的主要树种组成存在差异，落叶阔叶树种枫香和化香仅出现在松林主要树种中，而松阔混交林中已经没有落叶树种，但出现了常绿阔叶树种石栎和檵木。在常绿阔叶林中，主要树种则由木荷及青冈、石栎和苦槠等3种壳斗科Fagaceae树种组成。树种组成的变化是群落演替的结果，森林经营管理可根据此对松林和松阔混交林进行适当抚育，伐除部分针叶树种及清理林内枯立木，改善林分内的光照条件，促进常绿阔叶树种的生长。在常绿阔叶林中，则可通过修枝来改善林内光照条件，也可通过为森林土壤施加养分来改善目标树种的营养状况，通过人为栽种苗木等手段来加快木荷、石栎等目标树种的更新、生长和郁闭，促进森林群落向顶级群落发展并促进生物多样性的恢复。
本研究通过方差比率法、χ2检验和Spearman秩相关系数检验，对不同类型次生林群落种间的联结性和相关性进行了分析。其中，χ2检验结果是由种对的二元数据转换计算而来，反映的是物种能否共存和共存的概率，不能表达低显著度种对的内在相关性情况和强度。Spearman秩相关系数属定量检验方法，能够在一定程度上检验种对数量关系上的变化，对种对间的相关性及其显著性水平更为敏感。Spearman秩相关系数属定量检验与定性的方差比率法、χ2检验结合使用能够更全面地反映物种的种间关系[36]。
-
通过测度常绿阔叶林、松阔混交林和松林群落中主要树种的生态位重叠程度、空间分布格局和种间联结分析可以发现：本研究各群落乔木层主要树种在空间分布格局中独立性相对较强，物种间虽存在比较相似的环境资源需求，但种间联结关系比较松散，群落演替尚未进入成熟期。此外也可以看出：树种间的空间分布格局、联结性与种群的生态位重叠之间存在密切关联。一般情况下，群落内优势树种种间正联结性越强，其生态位重叠程度越高，种间负联结性越强，生态位重叠程度越低[37]。样地群落的总体关联性检验结果显示：各群落种间总体关联性呈不显著的正相关。χ2检验发现：多数种对都呈不显著的正联结，这与各群落物种生态位重叠程度的分析结果基本吻合。各群落主要树种间的Spearman秩相关分析结果与种间空间关联性结果也有比较一致的表现，这也说明植物种间关系对植物种群空间分布格局的形成有重要意义。本研究可为进一步揭示物种自身生物特性、环境条件及种间关系等综合作用下的种群空间分布格局形成机制提供依据，但群落中植物种间关系及空间分布格局是处在动态变化过程中的，本研究结果仅反映某一特定时间节点的群落状态，有待长期的群落动态监测研究。
Spatial distribution patterns and interspecific relationship of dominant tree species in the tree layer of typical natural secondary forest communities in Jiande, Zhejiang Province
-
摘要:
目的 探究天然次生林群落主要乔木树种空间分布格局及种间关系，为区域次生林群落的恢复、改造及抚育经营提供科学依据。 方法 于浙江建德典型的天然常绿阔叶次生林、松阔混交次生林和松林次生林3类群落中分别设置面积为1 hm2 (100 m×100 m)的样地，在每木调查基础上，运用Pianka生态位重叠指数、点格局分析方法、方差比率法(VR)、χ2检验和Spearman秩相关系数对各群落乔木层主要树种进行空间分布格局和种间关系的分析。 结果 ①样地中各次生林群落主要树种在所有尺度上呈现聚集分布；②在0~25.0 m尺度内，各群落空间关联性以不显著相关关系为主，负相关种对数多于正相关种对数；③各群落主要树种种间总体关联性及χ2检验种间联结性均以不显著的正联结为主，Spearman秩相关分析显示种对间以不显著相关关系为主，与主要树种空间关联性分析结果及生态位重叠程度较吻合。 结论 样地中各群落乔木层主要树种在各自分布格局中独立性相对较强，物种间虽存在比较相似的环境资源需求，但种间联结关系比较松散，群落演替尚未进入成熟期。图7表4参37 Abstract:Objective To investigate the spatial distribution pattern and interspecific relationship of dominant tree species in the tree layer of natural secondary forest communities, and to provide a scientific basis for the restoration, rehabilitation and reforestation management of the secondary forest community in the region. Method This paper set up 1 hm2 (100 m×100 m) sample plot in each type of typical natural secondary forest communities (evergreen braod-leaved secondary forest, mason pine and broad-leaved mixed secondary forest and secondary forest of mason pine) in Jiande, Zhejiang Province. Based on the tally, the Pianka niche overlap index, point pattern analysis method, variance ratio method (VR), χ2-test and Spearman rank correlation coefficient were used to analyze the spatial distribution pattern and interspecific relationship of the dominant tree species in each community. Result (1) The dominant tree species in each type of secondary forest community showed an aggregate distribution on all scales; (2) In the 0−25.0 m scale, the spatial correlation of each community is dominated by insignificant correlations, and the number of species pairs showing negative correlation is more than the number of species pairs showing positive correlation; (3) The overall correlations between the dominant tree species of each community and the interspecific associations obtained by the χ2-test were mainly non-significant positive associations. Spearman rank correlation analysis results showed that the non-significant correlations were mainly among the species pairs in each community. The results of spatial correlation analysis and niche overlap of the dominant tree species in each community are in good agreement. Conclusion The above results show that the dominant tree species of each community are relatively independent in their respective distribution patterns. Although there are similar environmental resource requirements between species, the inter-species linkages are basically loose, and the community succession has not yet entered the mature stage. [Ch, 7 fig. 4 tab. 37 ref.] -
图 1 常绿阔叶林主要树种空间分布格局
Figure 1 Spatial distribution pattern of dominant tree species in evergreen broad-leaved forest
图 2 松阔混交林主要树种空间分布格局
Figure 2 Spatial distribution pattern of dominant tree species in mason pine and broad-leaved mixed forest
图 3 松林主要树种空间分布格局
Figure 3 Spatial distribution pattern of dominant tree species in mason pine forest
图 4 常绿阔叶林主要树种间空间分布格局图
Figure 4 Spatial distribution pattern of dominant tree species in evergreen broad-leaved forest
图 5 松阔混交林主要树种间空间分布格局图
Figure 5 Spatial distribution pattern of dominant tree species in mason pine and broad-leaved mixed forest
图 6 松林主要树种间空间分布格局图
Figure 6 Spatial distribution pattern of dominant tree species in mason pine forest
图 7 不同森林类型种间Spearman秩相关半矩阵图
Figure 7 Semi-matrix of Spearman’s rank correlation coefficients of dominant tree species of different forest types
表 1 样地基本信息
Table 1. Basic information of sample plots
样地类型 海拔/m 纬度(N) 经度(E) 坡度/(°) 坡向 土壤类型 地点 常绿阔叶林 172 29°40′ 119°23′ 44 西 红壤 杨村桥镇徐坑村 松阔混交林 165 29°28′ 119°12′ 38 南 红壤 新安江林场朱家埠林区 松林 90 29°21′ 119°09′ 33 东 红壤 新安江林场朱家埠林区 
下载: 导出CSV
表 2 不同森林类型主要树种生态位重叠数值矩阵
Table 2. Niche overlap of dominant tree species of different forest types
常绿阔叶林 松阔混交林 松林 树种 苦槠 木荷 青冈 树种 檵木 苦槠 马尾松 石栎 树种 枫香 化香树 苦槠 马尾松 木荷 0.377 2 苦槠 0.801 8 化香 0.757 5 青冈 0.615 4 0.518 2 马尾松 0.631 2 0.632 4 苦槠 0.720 1 0.625 8 石栎 0.421 9 0.861 4 0.473 3 石栎 0.451 3 0.458 4 0.753 1 马尾松 0.676 9 0.567 6 0.442 7 杉木 0.393 7 0.521 8 0.646 2 0.340 9 杉木 0.466 2 0.470 7 0.600 1 0.567 5
下载: 导出CSV
表 3 不同森林类型主要树种的总体关联性
Table 3. Overall interspecific associations among dominant tree species of different forest types
样地类型 方差比率 W ${\; \textit{χ}^{2}_{0.95}(N)} $，${ \; \textit{χ}^{2}_{0.05}(N)} $ 结果 常绿阔叶林 1.389 34.722 14.611, 37.652 不显著正关联 松阔混交林 1.397 34.930 14.611, 37.652 不显著正关联 松林 1.199 29.966 14.611, 37.652 不显著正关联
下载: 导出CSV
表 4 不同森林类型的种间联结χ2统计量矩阵
Table 4. Value of χ2 of different forest types
常绿阔叶林 松阔混交林 松林 树种 苦槠 木荷 青冈 树种 檵木 苦槠 马尾松 杉木 树种 枫香 化香 马尾松 杉木 木荷 0.001 苦槠 1.223 化香 0.179 青冈 0.230 0.092 马尾松 1.103 1.103 马尾松 0.230 1.103 石栎 0.039 0.001 0.230 杉木 0.001 0.001 0.010 杉木 0.020 0.179 0.230 石栎 0.089 0.089 0.069 0.110 苦槠 2.214 0.069 0.038 0.368
下载: 导出CSV
-
[1] 王本洋, 余世孝. 种群分布格局的多尺度分析[J]. 植物生态学报, 2005, 29(2): 235 − 241. WANG Benyang, YU Shixiao. Multi-scale analyses of population distribution patterns [J]. Acta Phytoecol Sin, 2005, 29(2): 235 − 241. [2] STERNER R W, RIBIC C A, SCHATZ G E. Testing for life historical changes in spatial patterns of 4 tropical tree species [J]. J Ecol, 1986, 74(3): 621 − 633. [3] 赵艳云, 刘京涛, 陆兆华. 渤海湾贝壳堤湿地芦苇种群与蒙古蒿种群空间分布格局和种间关系[J]. 湿地科学, 2017, 15(2): 187 − 193. ZHAO Yanyun, LIU Jingtao, LU Zhaohua. Spatial pattern and interspecific relationship of Phragmites australis and Artemisia mongolica populations in Chenier Wetlands in Bohai Bay [J]. Wetland Sci, 2017, 15(2): 187 − 193. [4] 史浩伯, 陈亚宁, 李卫红, 等. 塔里木河下游植被种间关系与稳定性分析[J]. 干旱区研究, 2020, 37(1): 220 − 226. SHI Haobo, CHEN Yaning, LI Weihong, et al. Interspecific association and stability of vegetation in the lower reaches of the Tarim River [J]. Arid Zone Res, 2020, 37(1): 220 − 226. [5] 李丘霖, 宗秀虹, 邓洪平, 等. 赤水桫椤群落乔木层优势物种生态位与种间联结性研究[J]. 西北植物学报, 2017, 37(7): 1422 − 1428. LI Qiulin, ZONG Xiuhong, DENG Hongping, et al. Niche and interspecific of dominant species in tree layer of Chishui Alsophila spinulosa community [J]. Acta Bot Boreali-Occident Sin, 2017, 37(7): 1422 − 1428. [6] 涂洪润, 李娇凤, 杨丽婷, 等. 桂林岩溶石山青冈群落主要乔木树种的种间关联[J]. 应用生态学报, 2019, 30(1): 67 − 76. TU Hongrun, LI Jiaofeng, YANG Liting, et al. Interspecific associations of the main tree populations of the Cyclobalanopsis glauca community in karst hills of Guilin, southwest China [J]. Chin J Appl Ecol, 2019, 30(1): 67 − 76. [7] HE Fangliang, DUNCAN R P. Density-dependent effects on tree survival in an old-growth Douglas fir forest [J]. J Ecol, 2000, 88(4): 676 − 688. [8] JOHN R, DALLING J W, HARMS K E, et al. Soil nutrients influence spatial distributions of tropical tree species [J]. Proc Nat Acad Sci USA, 2007, 104(3): 864 − 869. [9] XIANG Wenhua, LI Shaohui, LEI Xiangdong, et al. Secondary forest floristic composition, structure, and spatial pattern in subtropical China [J]. J For Res, 2013, 18: 111 − 120. [10] 朱教君. 次生林经营基础研究进展[J]. 应用生态学报, 2002, 13(12): 1689 − 1694. ZHU Jiaojun. A review on fundamental studies of secondary forest management [J]. Chin J Appl Ecol, 2002, 13(12): 1689 − 1694. [11] 汤孟平. 森林空间经营理论与实践[M]. 北京: 中国林业出版社, 2007. [12] 吴初平, 袁位高, 盛卫星, 等. 浙江省典型天然次生林主要树种空间分布格局及其关联性[J]. 生态学报, 2018, 38(2): 537 − 549. WU Chuping, YUAN Weigao, SHENG Weixing, et al. Spatial distribution patterns and associations of tree species in typical natural secondary forest communities in Zhejiang Province [J]. Acta Ecol Sin, 2018, 38(2): 537 − 549. [13] 罗佳, 张灿明, 牛艳东, 等. 森林生态系统大样地定位研究综述[J]. 湖南林业科技, 2013, 40(4): 79 − 81. LUO Jia, ZHANG Canming, NIU Yandong, et al. The research review on large, long-term plot location of forest ecosystem [J]. Hunan For Sci Technol, 2013, 40(4): 79 − 81. [14] 蔡飞, 陈爱丽, 陈启瑺, 等. 浙江建德青冈常绿阔叶林种群结构和动态的研究[J]. 林业科学研究, 1998, 11(1): 99 − 106. CAI Fei, CHEN Aili, CHEN Qichang, et al. Study on the structure and dynamics of populations of Cyclobalanopsis glauca in Jiande County, Zhejiang Province [J]. For Res, 1998, 11(1): 99 − 106. [15] CONDIT R. Research in large, long-term tropical forest plots [J]. Trends Ecol Evol, 1995, 10(1): 18 − 22. [16] 白雪娇, 邓莉萍, 李露露, 等. 辽东山区次生林木本植物空间分布[J]. 生态学报, 2015, 35(1): 98 − 105. BAI Xuejiao, DENG Liping, LI Lulu, et al. Distribution patterns of woody plants in a secondary forest in the montane region of eastern Liaoning Province, China [J]. Acta Ecol Sin, 2015, 35(1): 98 − 105. [17] 宋永昌. 植被生态学[M]. 上海: 华东师范大学出版社, 2007. [18] PIANKA E R. The structure of lizard communities [J]. Ann Rev Ecol Syst, 1973, 4(1): 53 − 74. [19] 张金屯. 植物种群空间分布的点格局分析[J]. 植物生态学报, 1998, 22(4): 344 − 349. ZHANG Jintun. Analysis of spatial point pattern for plant species [J]. Chin J Plant Ecol, 1998, 22(4): 344 − 349. [20] CONDIT R, ASHTON P S, BAKER P, et al. Spatial patterns in the distribution of tropical tree species [J]. Science, 2000, 288(5470): 1414 − 1418. [21] HE Fangliang, LEGENDRE P, LAFRANKIE J V. Distribution patterns of tree species in a Malaysian tropical rain forest [J]. J Veg Sci, 2010, 8(1): 105 − 114. [22] LAN Guoyu, GETZIN S, WIEGAND T, et al. Spatial distribution and interspecific associations of tree species in a tropical seasonal rain forest of China [J]. PLoS One, 2012, 7(9): e46074. doi: 10.1371/journal.pone.0046074. [23] HIGUCHI P, SILVA A C, LOUZADA J N C, et al. Spatial patterns of a tropical tree species growing under an eucalyptus plantation in South-East Brazil [J]. Brazil J Biol, 2010, 70(2): 271 − 277. [24] 岳永杰, 余新晓, 秦富仓, 等. 北京雾灵山保护区蒙椴林空间点格局分析[J]. 林业资源管理, 2009, 38(2): 49 − 54. YUE Yongjie, YU Xinxiao, QIN Fucang, et al. Spatial-point-pattern analysis of Mongolian linden in Beijing Wulingshan Nature Reserve [J]. For Resour Manage, 2009, 38(2): 49 − 54. [25] 董雪, 杜昕, 孙志虎, 等. 生境梯度影响下的天然红松种群空间格局与种内关联[J]. 生态学报, 2020, 40(15): 5239 − 5246. DONG Xue, DU Xin, SUN Zhihu, et al. Spatial pattern and intraspecific association of natural Korean pine population under the influence of habitat gradient [J]. Acta Ecol Sin, 2020, 40(15): 5239 − 5246. [26] 赵明水, 庞春梅, 杨淑贞, 等. 浙江天目山交让木种群空间点格局分析[J]. 浙江大学学报(理学版), 2015, 42(1): 47 − 53. ZHAO Mingshui, PANG Chunmei, YANG Shuzhen, et al. Spatial patterns of Daphniphyllum macropodum in Tianmu Mountain, Zhejiang Province [J]. J Zhejiang Univ Sci Ed, 2015, 42(1): 47 − 53. [27] SCHULTER D. Avariance test for detecting species association, with some example applications [J]. Ecology, 1984, 65(3): 998 − 1005. [28] 武秀娟. 芦芽山阴坡典型天然次生林群落的种间联结性[J]. 西北林学院学报, 2020, 35(1): 54 − 61. WU Xiujuan. Interspecific association of the plant communities in natural secondary forests on north slope of Luya Mountain [J]. J Northwest For Univ, 2020, 35(1): 54 − 61. [29] 王伯荪, 彭少麟. 南亚热带常绿阔叶林种间联结测定技术研究(Ⅰ)种间联结测式的探讨与修正[J]. 植物生态学报, 1985, 9(4): 274 − 279. WANG Bosun, PENG Shaolin. Studies on the measuring techniques of interspecific association of lower-subtropical evergreen-broadleaved forests (Ⅰ) The exploration and the revision on the measuring formulas of interspecific association [J]. Chin J Plant Ecol, 1985, 9(4): 274 − 279. [30] 黄祥童, 王绍先, 黄炳军, 等. 珍稀植物对开蕨与其伴生物种的联结性及群落稳定性[J]. 生态学报, 2015, 35(1): 80 − 90. HUANG Xiangtong, WANG Shaoxian, HUANG Bingjun, et al. Analyses of community stability and inter-specific associations between the rare plant Phyllitis scolopendrium and its associated species [J]. Acta Ecol Sin, 2015, 35(1): 80 − 90. [31] BISHARA A J, HITTNER J B. Testing the significance of a correlation with nonnormal data: comparison of Pearson, Spearman, transformation, and resampling approaches [J]. Psycholl Methods, 2012, 17(3): 399 − 417. [32] 韩有志, 王政权. 森林更新与空间异质性[J]. 应用生态学报, 2002, 13(5): 615 − 619. HAN Youzhi, WANG Zhengquan. Spatial heterogeneity and forest regeneration [J]. Chin J Appl Ecol, 2002, 13(5): 615 − 619. [33] BROENNIMANN O, FITZPATRICK M C, PEARMAN P B, et al. Measuring ecological niche overlap from occurrence and spatial environmental data [J]. Glob Ecol Biogeogr, 2012, 21(4): 481 − 497. [34] GONZALEZ A, LOREAU M. The causes and consequences of compensatory dynamics in ecological communities [J]. Ann Rev Ecol Evol Syst, 2009, 40(1): 393 − 414. [35] JIA Guodong, YU Xinxiao, FAN Dengxing, et al. Mechanism underlying the spatial pattern formation of dominant tree species in a natural secondary forest [J]. PLoS One, 2016, 11(3): e0152596. doi: 10.1371/journal.pone.0152596. [36] 邓莉萍, 白雪娇, 李露露, 等. 辽东山区次生林优势木本植物种间联结与相关分析[J]. 生态学杂志, 2015, 34(6): 1473 − 1479. DENG Liping, BAI Xuejiao, LI Lulu, et al. Interspecific association and correlation among dominant woody plants of secondary forest in montane region of eastern Liaoning Province, China [J]. Chin J Ecol, 2015, 34(6): 1473 − 1479. [37] 胡楠, 范玉龙, 丁圣彦. 伏牛山森林生态系统灌木植物功能群分类[J]. 生态学报, 2009, 29(8): 4017 − 4025. HU Nan, FAN Yulong, DING Shengyan. Functional group classification of shrub species in the Funiu Mountain forest ecosystem [J]. Acta Ecol Sin, 2009, 29(8): 4017 − 4025. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20200586
点击查看大图
图(7) / 表(4)
计量
- 文章访问数: 1563
- HTML全文浏览量: 292
- PDF下载量: 95
- 被引次数: 0
