下载:
-
立木胸径和树高是衡量立木生长状况的重要因子[1]，立木因子的获取是森林资源调查中最重要的工作之一[2-3]。传统的立木因子测量主要依靠人工或二维图像完成。人工测量方法中，使用皮尺、测距仪等测树工具[4]，工作量大且主观误差较大；电子经纬仪、全站仪等精密设备[5-6]专业性强，但操作复杂。随着计算机视觉技术的发展，基于二维图像的测量方法[7-9]取得了一定的成果，但由于维度的限制，这类方法对于遮挡严重的场景测量精度不高。近几年，三维重建方法被广泛用于植物表形参数的测量[10-11]。其中地面激光扫描技术(terrestrial laser scanning, TLS)[12-13]测量精度高，但地面激光扫描仪价格昂贵，产生点云数据量大，对计算机的运行速度、传输容量等有较高要求，使其在植株表型参数提取与分析方面的应用受到了制约，难以满足社会化的需求。运动恢复结构(structure from motion，SfM)[14]是一种通过特征点匹配建立不同视角的二维图像的关系，从而恢复相机参数与目标三维信息的算法。该算法为植株表型参数测量提供了一种新思路[15]。梁秀英等[16]使用户外小车自动拍摄田间玉米Zea mays植株，基于SfM 算法首先获取玉米植株稀疏三维点云，然后再进一步得到植株稠密点云，通过点云数据测得玉米株高、茎粗和叶面积等参数。HUI等[17]基于SfM算法，利用Visual SFM软件对茄Solanum melongena、辣椒Capsicum annuum和黄瓜Cucumis sativus等3种蔬菜进行了重建和表型解析，获取了植物叶片数、叶长、叶宽和叶面积数据。该方法除用于小型作物表型参数的测量外，在立木因子测量方面也有应用。MILLER等[18]、徐慧丹等[19]围绕单株立木拍摄重叠度约70%的图片，并基于SfM算法获取其三维点云模型，从而估计树高、胸径等参数。孙英伟等[20]在室外围绕单株立木进行拍摄，并基于SfM算法获取立木三维点云，将点云最高和最低的差值作为树高数据，对1.3 m处点云拟合圆提取胸径值。这些方法虽然能够有效替代传统方法和TLS测量立木因子，但均是围绕立木人为控制拍摄间隔获取图像，步骤繁琐且精度难以保障，仅能测量单株立木，效率较低。
本研究提出基于运动恢复结构的多株立木因子测量方法，围绕立木场景拍摄视频，使用关键帧提取算法自动提取三维重建所需的立木图像，减少拍摄的复杂程度；基于SfM算法获取立木三维点云后，进行多株立木点云分割，实现立木单株点云的提取和树高、胸径的自动测量，为多株立木因子的自动测量提供了新思路。
-
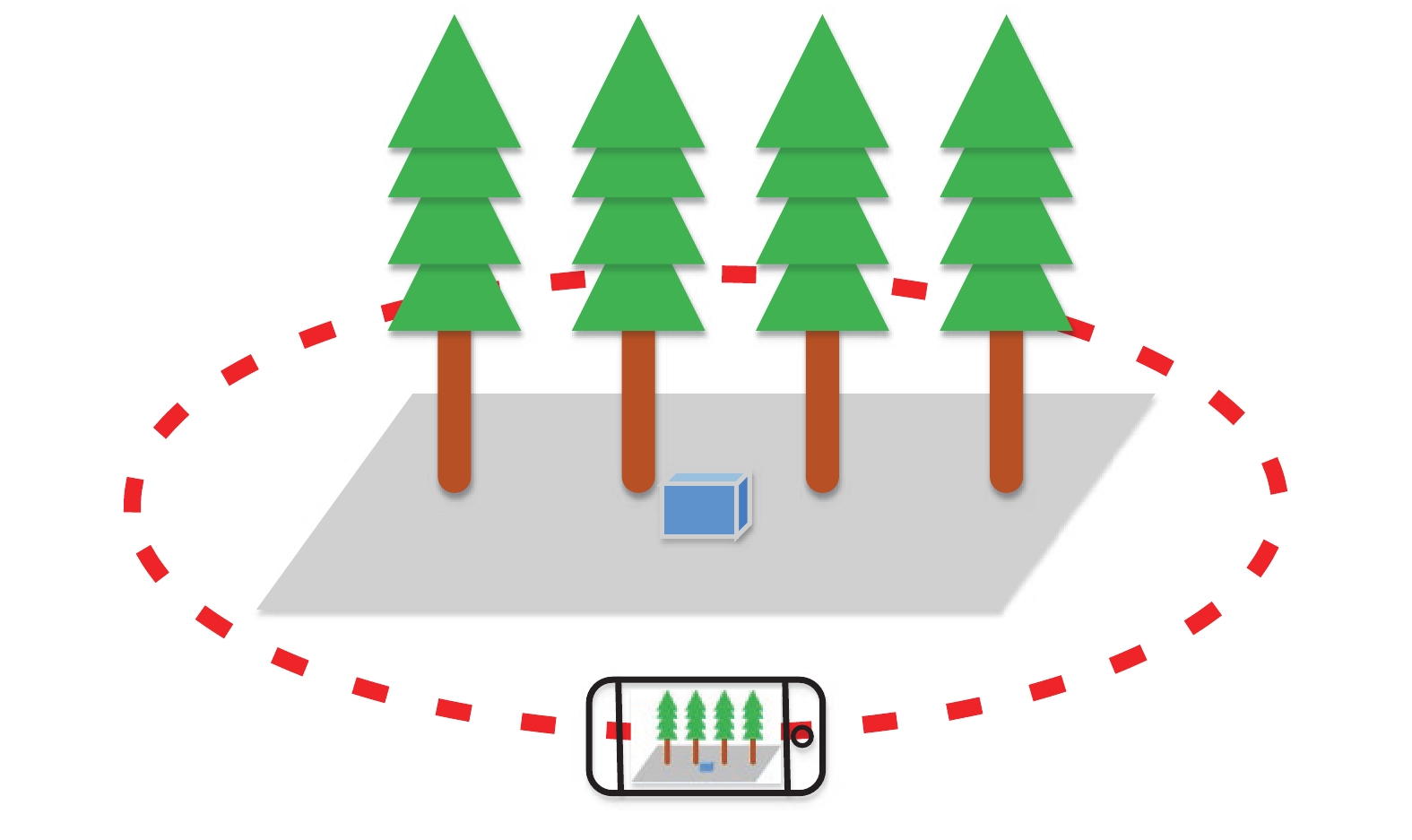
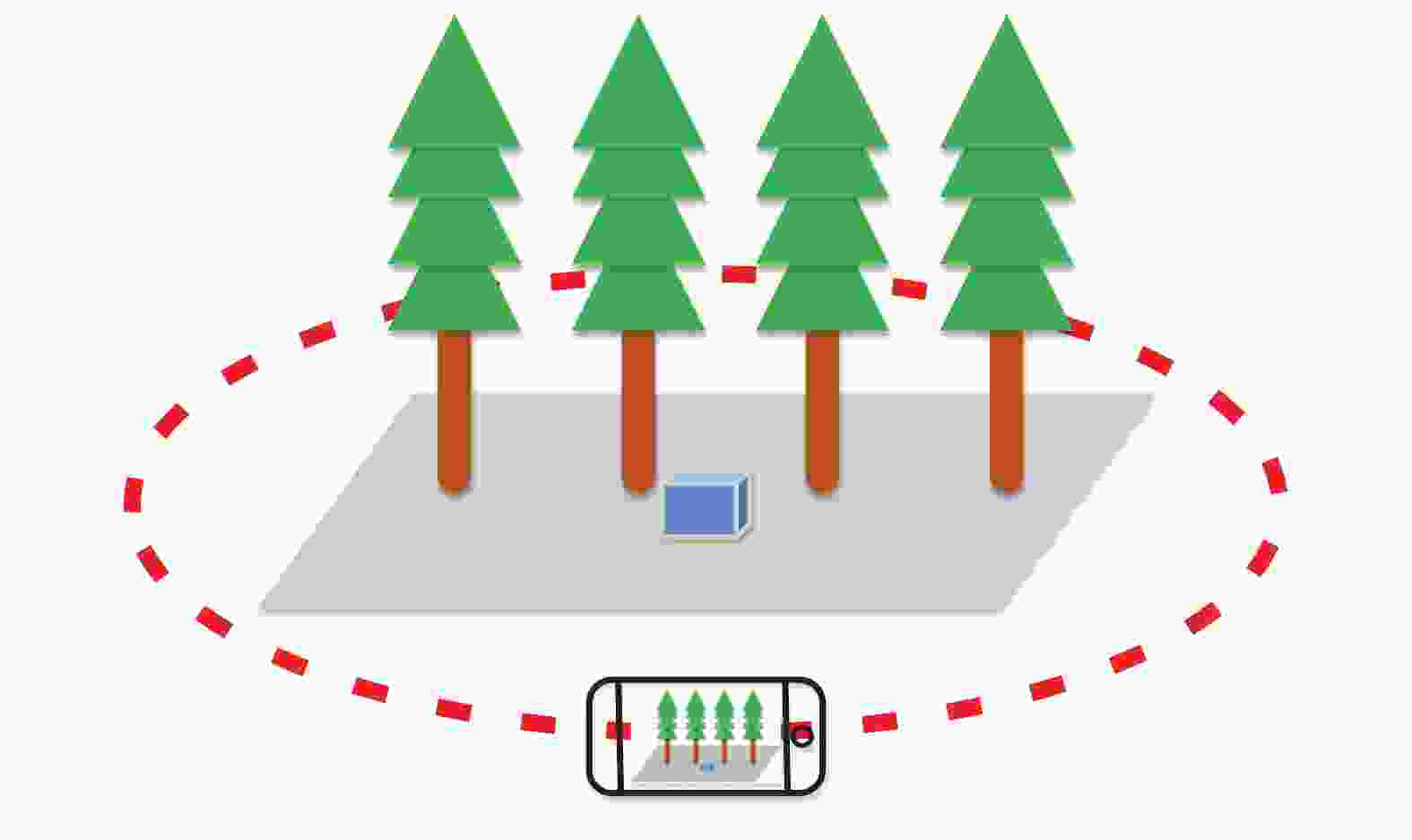
以浙江农林大学校园内的立木为研究对象，在自然条件下使用智能手机环绕包含多株立木的场景拍摄一段视频。拍摄时将手机移动速度尽量保持均匀并减少晃动，尽可能拍到立木的全部，并将相机镜头始终指向场景中心。由于每个场景中的立木数量、高度、间距均不相同，因此拍摄路线也不同。图1为某场景的拍摄路线示意图，场景中放置的蓝色长方体尺寸已知，有助于将立木三维点云的尺度恢复到与实际相同。
图 1 拍摄路线示意图
Figure 1. Schematic diagram of shooting route
-
视频相比图像能够传达更为丰富的信息，但是一个完整的视频序列包含较多冗余数据，关键帧提取算法能够从视频中选择满足特定要求的帧，使得提取的关键帧序列能够在满足后续立木三维点云获取所需基本信息的基础上尽量减少冗余。将固定采样法和相似度度量法相结合，对立木视频进行关键帧提取。先用固定采样法提取视频帧作为候选帧，即以视频的第1帧作为候选帧的开始，使用固定间隔为t帧的采样算法At对包含L帧的视频VL进行候选帧提取，得到候选帧序列Fc，其中
${f_1},{f_{1 + t}}, \cdots ,{f_{1 + nt}}$ 为候选帧序列中的每帧，(1±nt)≤L。$$F_{ {{\rm{c}} }}=\left\{f_{1}, f_{1+t}, \cdots, f_{1+n t}\right\}=A_{t}\left(V_{L}\right)。 $$ (1) 式(1)中，将所有的候选帧提取完成后，以候选帧的第1帧作为关键帧的开始，采用差异值哈希(dHash)算法[21]计算当前关键帧与候选帧之间的相似度。该算法首先将2幅图像分别缩小并灰度化，然后比较每行相邻元素的大小，根据比较结果赋值1或0，得到2幅图像的哈希值，最后利用汉明距离计算2幅图像之间的相似度S。
$$ S=D\left \{ d H\left(I_{i}\right), d H\left(f_{j}\right)\right \} 。 $$ (2) 式(2)中：Ii表示当前关键帧，fj表示候选帧，dH(Ii)和dH(fj)分别表示2幅图像的哈希值，D表示汉明距离。
计算出相似度S之后，设定相似度阈值S1、S2 (分别取值为0.6和0.8)。当S＞0.8时，将筛选出的关键帧序列进行三维重建时立木三维模型的效果并没有明显提升，但是关键帧图像大量增加导致效率降低；当S＞0.6可以较好地排除视频中突然出现的干扰(如车辆)。因此，若0.6≤S≤0.8，则将该候选帧加入到关键帧序列，并将该帧设置为当前关键帧。然后继续计算当前关键帧与下一候选帧的相似度，直至筛选完所有候选帧，得到视频关键帧序列Fe。
-
在立木视频关键帧序列(即有序图像集)提取的基础上，基于运动恢复结构算法生成立木三维点云，基本流程如图2所示。①特征点提取与匹配。通过尺度不变特征变换算法(scale-invariant feature transformation，SIFT)[22]对图像进行特征点提取，并计算每2幅图像特征点描述子之间的欧几里得距离来完成特征点匹配，得到所有图像的特征匹配关系
$M \left\{m_{1,2}, m_{2,3}, \cdots, m_{n-1, n}\right\}$ ，其中n为关键帧图像的数量，m中储存了2幅图像间的特征点匹配对$m\left\{\left(x_{1}, x_{1}^{\prime}\right),\left(x_{2}, x_{2}^{\prime}\right), \cdots,\left(x_{i}, x_{i}^{\prime}\right)\right\}$ ，其中i为特征点匹配对的数量。②使用2幅图像进行重建初始化。首先将第1幅图像与第2幅图像中的匹配点对x和x'代入对极几何约束条件[式(3)]求得基础矩阵F，该矩阵代表了2幅图像匹配点之间的空间几何关系。
图 2 生成立木三维点云流程图
Figure 2. Flow chart of creating 3D point cloud of trees
$$\left(x^{\prime}\right)^{{\rm{T}}} {\boldsymbol{F}} x=0 。 $$ (3) 再通过已知的相机内参K和式(4)求得本质矩阵E和，对E进行奇异值分解后得到第2幅图像相对第1幅图像的相机旋转矩阵R和平移向量T。
$$ {\boldsymbol{E}}=K^{{\rm{T}}} F K。 $$ (4) 在此基础上，可通过式(5)求得2个相机的投影矩阵P1和P2：
$$ \left\{\begin{array}{l}{\boldsymbol{P}}_{1}=K[I, \;0] \\ {\boldsymbol{P}}_{2}=K[{\boldsymbol{R}},\; T]\end{array}\right.。 $$ (5) 通过P1和P2建立二维匹配点x和x'及其对应的三维空间点X的关系：
$$ \left\{\begin{array}{l}x={\boldsymbol{P}}_{1} X \\ x^{\prime}={\boldsymbol{P}}_{2} X\end{array}\right.。 $$ (6) 并将匹配点x和x'的齐次坐标[u, v, 1]T及[u', v', 1]T代入上式，得：
$$ \left[\begin{array}{l}P_{13} u-P_{11} \\ P_{13} v-P_{12} \\ P_{23} u^{\prime}-P_{21} \\ P_{23} v^{\prime}-P_{22}\end{array}\right] X=A X=0 。$$ (7) 式(7)中：Pi1、Pi2、Pi3是Pi的行向量，对A进行奇异值分解后得到二维图像特征点的三维坐标。
③加入新的图像。根据新加入的一幅图像与已重建的上一幅图像上特征点的匹配关系，获得已知的三维点X对应新图像上的二维点x，将对应的二维点和三维点代入式(8)可求得投影矩阵Pi，然后重复使用步骤②中的方法获得新图像上其余未重建的匹配点的三维坐标。
$$ x=P_{i} X。 $$ (8) ④利用光束平差(bundle adjustment，BA)[23]算法进行集束调整，减小相机姿态R、T和重建三维点坐标的误差。将所有三维点通过重新映射的方式到得到其在图像上的二维点坐标，然后计算与其真实二维点之间的距离，并将该距离最小化以完成优化。即：
$$ \min \sum\limits_{i=1}^{n} \sum\limits_{j=1}^{m}\left(x_{i j}-P_{j} \:X_{i}\right)^{2}。 $$ (9) 式(9)中：xij是第i个特征点在第j幅图像上的坐标，Pj为投影矩阵，Xi为第i个特征点的三维坐标。每重建一幅图像进行一次集束调整，当所有图像重建完成后，再次进行集束调整，获得优化后的稀疏三维点云。
⑤三维点云稠密化。采用多视角立体集群算法(cluster multi-view stereo，CMVS)和多视角拼接算法(patch-based multi-view stereo，PMVS)对重建出来的稀疏点云进行稠密化[24]。
-
由于立木场景三维点云数据量大，夹杂了许多噪声点，且点云模型与真实世界三维空间的方向、尺度上也存在不一致，因此需要对点云模型进行下采样、去噪、比例校正、坐标校正、方向校正等预处理，以减少后续算法运行时间。①采用三维体素栅格法对点云进行下采样。首先为输入的点云数据创建由大量指定边长的微小立方体包围的集合，即三维体素栅格；然后在每个体素内计算所有点的重心，利用重心代替该体素内的其余点，这样所有的三维点云最终都由各个体素内的重心表示。②去噪。使用直通滤波器对X、Y、Z阈值范围进行设定，划分出感兴趣的立木范围区域，从而减少背景噪声点。接着采用统计滤波方法去除离群噪声点，计算直通滤波后的每个点pi，计算其与k(取50)个近邻点的平均距离
$\bar{d}\left(p_{i}\right)$ ，假设得到的结果服从高斯分布，得平均距离均值(μ)和标准差(σ)，如果这些点的平均距离$\bar{d}\left(p_{i}\right)$ 大于阈值Cσ(C为常量，取1)，则将被视为离群值去除。③坐标校正。首先进行点云模型与实际的比例校正，由放置物体实际尺寸hr和放置物体的模型尺寸hm得到坐标缩放比例r=hr/hm，在进行立木因子测量时可按比例将其换算到与实际相同的尺度。④方向校正。计算三维点云模型质心点的三维坐标，并基于主成分分析法(principal component analysis，PCA)[25]将点云模型进行质心化，求解点云模型协方差矩阵的特征值和特征向量，特征向量为立木三维点云模型的主方向，根据该主方向创建旋转矩阵M，将原始点云Po以质心点为中心转换到主方向的位置，得到新的三维点云模型Pn=MPo。 -
预处理后的三维点云模型中包含多株目标立木及地面，为此需要进行点云分割，分别提取单株立木三维点云。首先使用RANSAC算法将地面点云拟合成一个平面，然后提取属于该平面内的点云，从而将地面点云与立木点云进行初步分割。
在初步分割后的点云中，同一立木的点云总是紧邻的，而不同立木的点云之间存在间距，因此，根据空间点的欧氏距离采用条件欧几里得聚类算法进行多株立木三维点云的分割。对于三维点云中的某一点P，通过KD树找到三维点云中离点P最近的k个点，这些点与P点的距离若小于阈值d则聚类到集合Q中。然后从集合Q中选取点P以外的点，重复上述过程，直到集合Q中点的数量不再增加，则聚类过程结束。最后将多株立木三维点云分割到不同的点云集合中，从而提取出单株立木三维点云。
-
将立木在z轴方向的最高点与最低点的差值默认为其高度，如图3所示。由于点云坐标校正后单株立木的生长方向均与z轴的正方向一致，且立木底部平面位于oxy平面，所以提取出单株立木点云后，遍历所有点，找到单株立木z轴坐标的最大值与最小值，两者差值的绝对值即为单株立木的高度h (h=|Zmax−Zmin|)。
图 3 立木高度提取示意图
Figure 3. Schematic diagram of tree height extraction
-
将立木位于距地面1.3 m处断面直径的最大值和最小值的平均视为其胸径，如图4所示。在单株立木的三维点云中，利用校正后的比例r求得1.3 m处点云坐标：z=1.3/r。对该处做3 cm厚度的切片，然后再将点云切片投影至oxy平面，利用非线性最小二乘法进行椭圆拟合求解椭圆一般方程式：Ax2+Bxy+Cy2+Dx+Ey+1=0。其中：A、B、C、D、E是待求解参数。求得椭圆一般方程式后，根据式(10)和式(11)求得椭圆的短轴a和长轴b：
图 4 胸径提取示意图
Figure 4. Schematic diagram of tree DBH extraction
$$ \left\{\begin{array}{l}X_{{\rm{C}}}=\dfrac{B E-2 C D}{4 A C-B^{2}} \\ Y_{{\rm{C}}}=\dfrac{B D-2 A E}{4 A C-B^{2}}\end{array}\right.； $$ (10) $$ \left\{\begin{array}{l}a^{2}=\dfrac{2\left(A X_{{\rm{c}}}{ }^{2}+C Y_{{\rm{c}}}{ }^{2}+B X_{{\rm{c}}} Y_{{\rm{c}}}-1\right)}{A+C+\sqrt{(A-C)^{2}+B^{2}}} \\ b^{2}=\dfrac{2\left(A X_{{\rm{c}}}{ }^{2}+C Y_{{\rm{c}}}{ }^{2}+B X_{{\rm{c}}} Y_{{\rm{c}}}-1\right)}{A+C-\sqrt{(A-C)^{2}+B^{2}}}\end{array}\right. 。$$ (11) 然后将椭圆的短轴与长轴的平均值作为立木的胸径(Φ)：Φ=(a+b)/2。
-
基于软件平台Visual Studio 2017和计算机视觉Opencv库提取立木视频关键帧图像并基于运动恢复结构算法获取立木三维点云；基于C++开源点云库(point cloud library，PCL)对点云数据进行预处理及分割操作。
-
立木视频关键帧提取后，基于运动恢复结构算法获取的立木场景三维点云如图5A所示。可以看出该原始三维点云不仅包含了4株立木，还包含了地面、背景及离群噪声点。由图5B所示：进行点云下采样之后点云数据减少了约3倍，这并不影响立木三维点云的整体形状，且经过预处理后的点云成功滤除了背景及大量离群噪声点，点云模型的坐标方向也得到了校正(该场景中种植立木的花坛长度已知，无需在场景中放置用于比例校正的物体)。图5C是将地面点云与立木点云进行初步分割后的结果，图5D是点云通过条件欧几里得聚类算法分割后得到的4株立木。
图 5 立木三维点云处理结果
Figure 5. 3D point cloud processing results of trees
-
由表1可见：经过计算得出树高测量的绝对误差为0.03~0.24 m，测量值与实际值之间的相对误差为0.63%~3.93%，平均相对误差为1.96%。树高测量值总体上比实际值低，主要是因为树冠顶部的枝叶稀少，导致生成的三维点云在树冠顶部较为稀疏，在点云处理阶段被视为噪声点去除，并且在一些枝叶较细或者高度较高的立木上，由于视频拍摄不够清晰导致特征点匹配数量不足，使得立木三维重建时存在点云部分缺失的现象。立木的胸径测量的绝对误差为0.20~0.85 cm，测量值与实际值之间的相对误差为1.45%~6.92%，平均相对误差为3.19%。测量误差主要是由于拍摄时立木之间的遮挡，导致部分立木树干重建效果不佳，并且在使用非线性最小二乘法进行椭圆拟合时，由于利用的点云数量较少且分布不均匀，使得拟合不够准确。
表 1 树高和胸径的测量值与实际值
Table 1. Measured and actual values of tree height and DBH
立木
编号树高 胸径 实际
值/m测量
值/m相对误
差/%实际
值/cm测量
值/cm相对误
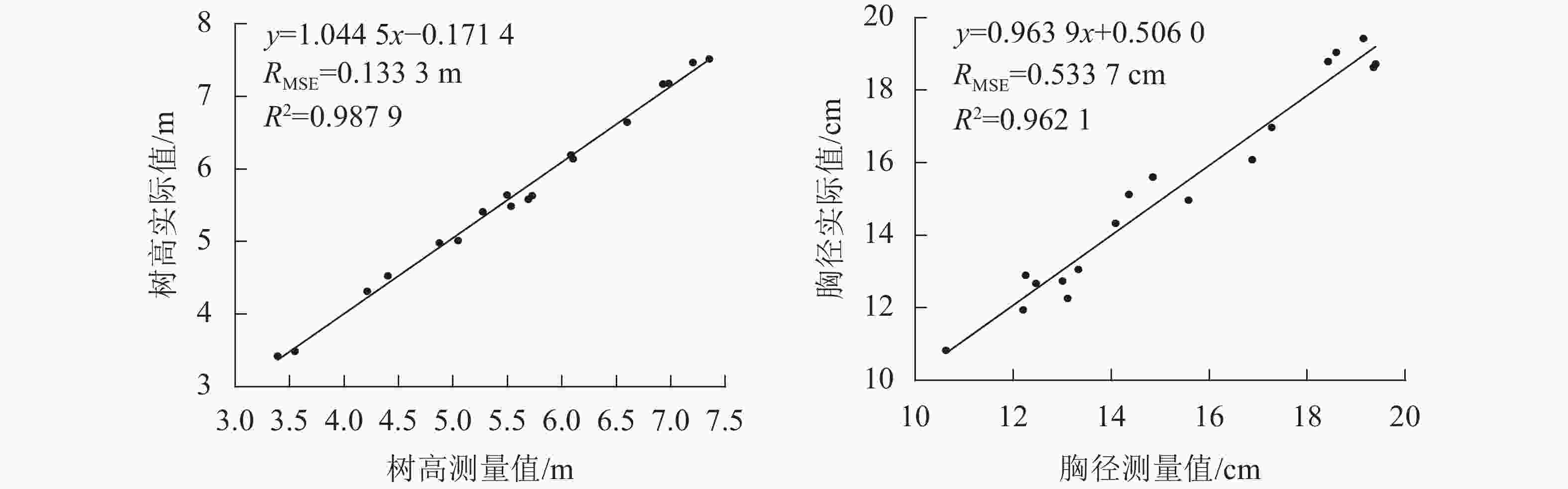
差/%1 6.14 6.10 0.63 15.60 14.85 4.85 2 4.98 4.87 2.15 13.06 13.33 2.07 3 5.49 5.53 0.84 12.74 13.00 2.09 4 5.64 5.49 2.60 14.97 15.58 4.06 5 3.42 3.39 0.93 10.83 10.62 1.87 6 3.49 3.55 1.69 12.26 13.11 6.91 7 4.53 4.40 2.78 12.90 12.25 4.99 8 4.31 4.21 2.39 14.33 14.09 1.70 9 6.65 6.60 0.71 19.43 19.14 1.44 10 6.19 6.08 1.79 18.63 19.35 3.87 11 7.17 6.93 3.40 18.80 18.42 1.94 12 5.63 5.73 1.67 18.72 19.39 3.58 13 7.52 7.35 2.18 16.97 17.27 1.77 14 7.47 7.20 3.56 19.04 18.59 2.37 15 5.58 5.69 1.93 15.13 14.36 5.08 16 5.01 5.05 0.64 11.94 12.20 2.16 17 5.41 5.27 2.57 12.67 12.46 1.68 18 7.18 6.98 2.78 16.08 16.88 4.93 平均值 1.96 3.19 图6为树高和胸径测量值与实际值的线性回归分析图，使用本研究方法测量的立木树高和胸径与实际值之间均存在着显著的线性相关关系，树高相关系数(R2)为0.987 9，均方根误差(RMSE)为0.133 3 m；胸径R2为0.962 1，RMSE为0.533 7 cm。
图 6 树高和胸径的测量值与实际值的回归分析
Figure 6. Regression analysis of measured and actual values of tree height and DBH
-
针对当前基于三维点云的立木因子测量方法效率低或成本高的问题，本研究提出了一种基于运动恢复结构的多株立木因子测量方法，使用普通智能手机实现了自然环境下多株立木树高和胸径的灵活、有效测量。本研究表明：使用本方法测量树高的平均相对误差为1.96%，相关系数为0.987 9，均方根误差为 0.133 3 m；测量胸径的平均相对误差为3.19%，相关系数为0.962 1，均方根误差为0.533 7 cm。本方法测量树高的平均相对误差均低于文献[26-27]，具有更高的树高测量精度；测量胸径的平均相对误差低于文献[26]，略高于文献[27]，但是文献[26-27]分别需要使用三维激光扫描仪和ToF手机，而本方法仅需使用普通智能手机，具有更好的普适性。
本方法具有较高的精度，但是测量胸径和树高仍有一定的误差，可能原因为：①树冠顶部的枝叶稀少，导致生成的三维点云在树冠顶部较为稀疏，在点云处理阶段被视为噪声点去除，导致树高测量值总体上比实际值低。②在一些枝叶较细或者高度较高的立木上，由于视频拍摄不够清晰导致特征点匹配数量不足，使得立木三维重建时点云部分缺失。③采用非线性最小二乘法拟合椭圆时由于树干点云的数量较少或分布不均导致立木胸径计算结果不理想。因此，可尝试采用高分辨率无人机等设备进行树冠顶部视频的拍摄，以获得立木清晰且全面的图像，同时进一步研究立木图像特征点提取与匹配算法，增加树干与树冠顶部枝叶的特征点匹配对数量，以提高重建立木的三维点云质量。
Measuring method of multiple trees attributes based on structure from motion
-
摘要:
目的 提出基于运动恢复结构的多株立木因子测量方法，以解决目前基于三维点云的立木因子测量方法获取立木树高和胸径存在效率低或成本高的问题。 方法 ①使用智能手机环绕包含多株立木的场景拍摄一段视频，并采用固定帧采样法和差异值哈希算法自动提取立木视频中的关键帧图像，然后，基于运动恢复结构(structure from motion，SfM)算法处理立木关键帧图像，从而获取立木场景的原始三维点云；②在对原始三维点云进行预处理及初步分割后，运用条件欧几里得聚类算法对多株立木三维点云进行分割，以提取单株立木三维点云；③对立木三维点云使用最值遍历法和椭圆拟合法实现立木树高和胸径的自动测量。 结果 与真实值相比，本研究方法测得的树高、胸径的平均相对误差分别为1.96%、3.19%，均方根误差分别为0.133 3 m、0.533 7 cm，相关系数分别为0.987 9、0.962 1。 结论 该方法具有较高的树高和胸径测量精度，提供了一种便捷、低成本的多株立木因子三维测量方法。图6表1参27 Abstract:Objective Tree attributes are generally measured by obtaining the tree height and DBH using a method based on three-dimensional point cloud, which is featured with either low efficiency or high cost. To solve this problem, this study is aimed to propose a measuring method of multiple trees attributes based on Structure from Motion. Method Firstly, a smart phone was used to shoot a video of a scene with multiple trees before its key frame images were automatically extracted using the fixed-frame sampling and dHash algorithm; Secondly, such key frame images of the trees were processed on the basis of structure from motion (SfM) algorithm to obtain the original 3D point cloud of the scene; Thirdly, after the pre-procession and initial segmentation of the original 3D point cloud, the conditional European clustering algorithm is used to segment the 3D point cloud of multiple trees to extract the 3D point cloud of a single tree; Finally, the most value traversal method and ellipse fitting method were employed to deal with the tree 3D point cloud to realize the automatic measurement of tree height and DBH. Result Compared with real values, the mean relative errors of tree height and DBH measured using this method are 1.96% and 3.19%, the root mean square errors were 0.1333 m and 0.5337 cm whereas the correlation coefficients were 0.9879 and 0.9621 respectively. Conclusion This method, with high measurement accuracy of tree height and DBH, serves as a convenient and low-cost three-dimensional measurement method for multiple trees attributes. [Ch, 6 fig. 1 tab. 27 ref.] -
物种多样性的形成和维持机制是生物多样性保护的基础，长期以来，生态学家针对植物物种多样性形成和维持的潜在机制先后提出了地质历史过程、水热动态假说、能量假说、寒冷忍耐假说及生境异质性假说等数十项假说[1]。森林群落的物种分布受多种因素影响，主要包括非生物环境因子、群落类型和空间距离等[2]，而林下物种又是人工林森林生态系统的重要组成部分，深入揭示环境因素对林下物种分布的影响，是解读人工林森林生态系统物种多样性的形成和维持的有效途径之一。油松Pinus tabuliformis林是华北地区地带性植被，也是华北地区顶级群落松栎针阔混交林的重要组成部分。但由于人为活动干扰，该区域油松林以人工林为主，相比天然林，人工林存在病虫害严重，生物多样性、生产力、天然更新和生态稳定性下降等问题，森林生态系统健康面临挑战，系统原有的组成和结构被破坏，进而影响到生态过程和生态系统功能[3-4]。所以，开展环境因子对油松人工林下物种分布影响的研究，对于区域人工林生物多样性保护和经营管理具有重要的意义。大量研究[5]表明：地形、海拔、土壤、光照、植被类型等均对林下物种分布产生影响。对太岳山[6]与关帝山[7]油松林下物种分布研究表明：油松林下物种分布主要受非生物因子影响，受生物因子影响较小，且受地形因子的影响大于林分因子和土壤因子。以上2个研究地气候类型为暖温带半干旱气候区，而中条山处于暖温带半湿润气候区[8]，不同的气候和土壤条件势必会影响研究结果，对油松人工林经营管理带来不确定性。基于此，本研究以山西中条山油松人工林为研究对象，基于植物和土壤调查数据，分析环境因子对影响油松人工林下物种分布的影响，为该地区油松人工林生物多样性保护和经营管理提供数据支撑。
1. 材料与方法
1.1 研究区概况
中条山位于山西省南部，是中国黄土高原向华北平原过渡的东南边缘区，在气候区划上属暖温带半湿润季风气候区。油松人工林分布区土壤为山地褐土及淋溶褐土，植被区划上属暖温带落叶阔叶林地带，森林植被垂直分布明显[9]。林下物种主要有连翘Forsythia suspensa、土庄绣线菊Spiraea pubescens、披针薹草Carex lancifolia、早开堇菜Viola prionantha、茜草Rubia cordifolia和金线草R. membranace等。
1.2 样地设置与植被调查
2018年6—8月，在对中条山油松人工林进行全面踏查的基础上，根据海拔、林龄、密度、坡度、坡向、混交等选择具有代表性的12个油松人工林样地(表1)，每个样地3个重复，共计36个乔木样方。除2号样地受条件限制，乔木样方面积为15 m×15 m，其他各样方面积为20 m×20 m，记录样方内出现的全部乔木种，并测定胸径≥5 cm乔木树种的名称、胸径、树高。将2号样地划分为9个、其他样地划分为16个5 m×5 m的灌木样方，并于每个灌木样方中心设置1个1 m×1 m的草本样方，灌木、草本样方数量合计均为555个，分别记录灌木和草本样方内的灌木、草本植物的种类、数量，并记录灌木样方内藤本的种类、数量。共记录178种植物，其中灌木47种，草本112种，藤本19种，分属56科124属，以36个乔木样方的物种多度数据建立物种矩阵(Z47×36、Z112×36、Z19×36)。记录每个样地的经纬度、海拔、坡度、坡向，根据中条山森林二类调查数据获取林龄和间伐时间，采用树冠投影法测定大样方郁闭度。
表 1 样地概况Table 1 Overview of the sample sites样地 林龄/a 坡度/(°) 坡向 海拔/m 密度/(株∙ hm−2) 平均胸径/cm 平均树高/m 1 40 22 西南 1 916 808 24.08 14.89 2 46 34 东南 1 924 1511 17.56 9.31 3 28 19 西 1 880 1600 14.77 12.43 4 38 35 西南 1 750 925 18.66 11.20 5 48 21 东 1 722 508 25.64 15.46 6 48 13 东北 1 933 583 27.84 16.31 7 41 20 西南 1 917 500 27.79 14.74 8 36 26 南 1 509 1383 17.39 11.60 9 39 25 西南 1 997 2475 14.79 9.07 10 32 11 东南 1 872 1250 17.39 12.95 11 48 8 西 1 928 467 29.32 15.94 12 46 23 西南 1 960 558 21.76 10.90 1.3 土壤样品采集与测定
在每个乔木样地内沿对角线随机选择3个点为土壤样品采集点，在每个采样点挖掘1个土壤剖面，按0~10 、10~20、20~40 cm划分土壤层次。在每个土壤层次上，用100 cm3的环刀取样。采用土壤袋采集各层土样200 g，挑出侵入物质，带回实验室自然风干、研磨、过筛后进行化学分析和测定。
测定土壤质量含水量、最大持水量、毛管持水量、田间持水量、毛管孔隙、非毛管孔隙和总孔隙度等土壤物理性质，测定方法按照LY/T 1215—1999《森林土壤水分-物理性质的测定》[10]进行。pH采用pH酸度计法(HANNA pH 211 )测定；土壤有机质采用重铬酸钾氧化-外加热法测定；全氮采用凯氏定氮法测定；速效氮采用碱解扩散法测定；全磷和速效磷采用等离子发射光谱法(IRIS Intrepid Ⅱ XSP)测定。每个样地土壤理化性质以所有测定值的平均值表征。
1.4 物种与环境矩阵建立
生物因子数据选取乔木样方林分平均胸径、平均树高、胸高断面积、油松相对优势度、株树密度、林龄、疏密度、郁闭度、乔木公顷蓄积、乔木公顷生物量、乔木平均蓄积、乔木平均生物量，蓄积量采用一元材积表计算[11]，生物量采用方精云等[12]生物量/材积转换系数计算。非生物因子数据包括土壤理化性质、坡度、坡向、海拔、间伐间隔。其中坡向为无序分类变量，按方位划分为北、东北、东、东南、南、西南、西、西北，分析时按1~8依次赋值。将以上因子构成环境矩阵(Z36×29)。
1.5 数据处理
采用主成分分析(PCA)法对环境数据降维；采用除趋势对应分析(DCA)法去除“弓形效应”；采用典范对应分析(CCA)对物种进行排序。数据整理采用Excel 2016完成；物种多样性分析、作图及环境因子PCA分析均采用R 4.0.3软件中“vegan”程序包完成；DCA和CCA采用Canoco 5软件完成。
2. 结果与分析
2.1 环境因子主成分分析
由于环境因子较多，且因子间存在多重共线性，需降低数据维度。因土壤pH对物种丰富度及空间分布影响较大[13]，故将除土壤pH以外的28个环境因子进行主成分分析(表2)。根据因子载荷矩阵，第1主成分主要反映土壤水分；第2主成分主要反映林分密度；第3主成分主要反映土壤养分；第4主成分主要反映土壤通气性；第5主成分主要反映生物量；第6主成分主要反映林冠郁闭度；第7主成分为海拔。将以上7个主成分与土壤pH共同建立生境矩阵(Z36×8)。将土壤水分、养分、通气性、pH、海拔归为非生物环境因子，将林分密度、生物量、林冠郁闭度归为生物环境因子。基于主成分分析结果构建环境矩阵，分析环境因子对林下物种分布的影响。
表 2 环境因子主成分分析因子旋转载荷矩阵Table 2 Rotated component matrix for principal component analysis of environmental factors环境因子 主成分 1 2 3 4 5 6 7 土壤毛管持水量 0.93 0.05 0.23 0.18 0.06 −0.04 −0.06 田间持水量 0.93 0.12 0.18 −0.03 0.07 0.14 0.08 土壤毛管孔隙度 0.91 0.13 0.21 −0.19 0.01 −0.01 0.07 土壤总孔隙度 0.87 0.08 0.21 0.37 −0.08 0.05 −0.01 土壤最大持水量 0.81 −0.01 0.20 0.49 0.02 0.00 −0.10 土壤质量含水量 0.80 0.09 0.22 −0.34 0.16 0.00 0.32 株树密度 −0.10 −0.92 0.15 0.03 0.17 0.08 0.10 平均胸径 0.15 0.90 −0.02 −0.23 0.24 0.06 0.02 乔木平均蓄积 0.10 0.88 0.08 −0.19 0.31 −0.02 0.12 疏密度 −0.05 0.80 −0.06 −0.33 0.31 −0.11 0.03 平均树高 0.06 0.73 −0.23 −0.46 0.30 −0.05 −0.05 林龄 0.47 0.61 −0.01 0.34 0.06 0.37 0.14 土壤有机质 0.18 0.02 0.95 0.12 −0.03 −0.13 −0.03 土壤全氮 0.22 −0.11 0.92 0.20 −0.03 −0.16 0.06 土壤速效氮 0.21 −0.11 0.90 −0.05 0.11 −0.02 0.12 土壤全磷 0.41 0.09 0.67 −0.30 −0.06 0.06 0.26 土壤有效磷 0.29 −0.21 0.61 −0.03 0.04 0.01 −0.44 土壤非毛管孔隙度 0.13 −0.06 0.05 0.86 −0.14 0.10 −0.12 坡度 −0.06 −0.31 0.10 0.81 −0.28 −0.15 −0.19 油松相对优势度 0.05 0.21 0.11 −0.77 0.04 −0.26 −0.19 乔木平均生物量 0.40 −0.20 0.02 0.62 0.22 −0.09 −0.03 乔木公顷蓄积 0.04 0.29 0.04 −0.08 0.91 0.14 0.09 乔木公顷生物量 0.04 0.29 0.04 −0.08 0.91 0.14 0.09 胸高断面积 0.26 −0.51 −0.11 −0.33 0.63 0.02 −0.25 郁闭度 −0.12 0.00 −0.27 0.26 0.18 0.83 0.04 坡向 −0.30 −0.08 0.17 0.03 −0.03 −0.78 0.29 间伐间隔 −0.05 −0.46 0.27 −0.10 0.16 0.66 0.17 海拔 0.46 −0.02 0.20 −0.14 0.20 −0.13 0.73 贡献率/% 26.91 22.96 12.55 9.65 6.78 4.90 4.00 累计贡献率/% 26.91 49.88 62.43 72.07 78.85 83.75 87.74 说明：表中加粗字体表示指标在该主成分上有较高载荷 2.2 环境因子对林下物种分布影响分析
为排除冗余变量共轭效应对排序结果的影响，在CCA排序前先使用前向选择，并进行蒙特卡罗显著性检验(表3)，综合检验结果确定可以进入CCA排序分析的环境因子。由表3可知：所有环境因子均可以进入CCA排序分析，且环境因子对灌木、草本、藤本物种的解释率(校正解释率)分别为45.7% (34.5%)、37.0% (20.4%)、43.4% (30.6%)，因此分析中很大一部分的物种信息可能会丢失。
表 3 环境因子前向选择结果Table 3 Forward selection results of environmental factors环境因子 灌木 草本 藤本 解释率/% P 解释率/% P 解释率/% P 土壤水分 1.7 0.690 4.2 0.012 5.4 0.034 林分密度 6.6 0.002 5.1 0.002 4.8 0.046 土壤养分 4.6 0.002 3.3 0.112 6.3 0.044 土壤通气性 7.6 0.002 9.9 0.002 6.1 0.004 生物量 5.0 0.002 4.2 0.008 1.9 0.440 林冠郁闭度 5.8 0.002 4.2 0.014 4.6 0.038 海拔 10.7 0.002 3.5 0.068 8.7 0.002 pH 3.7 0.034 2.6 0.322 5.5 0.016 累计解释率/% 45.7 37.0 43.4 校正解释率/% 34.5 20.4 30.6 物种与环境变量CCA分析模型变量的方差膨胀因子分别为8.91、7.98、9.32，均小于10，说明模型可靠。由不同环境要素对油松人工林下物种分布的解释率可知(表4)：油松林下物种分布主要受非生物环境影响。由生境因子与物种分布的相关显著性检验可知(表5)：灌木、草本、藤本分布与环境因子极显著相关(P＜0.001)，前两轴的方差贡献率分别为53.63%、49.12%、63.93%，排序的大部分信息被反映。
表 4 生物与非生物环境因子对物种分布的校正解释率Table 4 Adjusted explanation rates of biotic and abiotic environmental factors for species distribution校正解释率/% 未解释率/% 非生物 生物 交互 灌木 19.6 11.1 3.8 65.5 草本 12.8 6.5 4.8 75.9 藤本 20.6 8.0 7.4 69.4 表 5 油松人工林下物种分布与环境因子在前4排序轴上的相关系数Table 5 Correlation coefficients between distribution of species and environmental factors at the first fourth canonical correspondence analysis ordination axes under P. tabuliformis plantation环境因子 排序轴 R2 P CCA1 CCA2 CCA3 CCA4 灌木 土壤水分 0.25 0.01 0.86 −0.44 0.59 0.001*** 林分密度 −0.37 0.40 0.73 0.41 0.83 0.001*** 土壤养分 0.37 −0.46 0.26 −0.77 0.37 0.051 土壤通气性 −0.85 −0.42 0.13 −0.28 0.48 0.007** 生物量 0.69 −0.13 −0.71 −0.10 0.33 0.099 林冠郁闭度 −0.06 −0.62 −0.01 0.78 0.76 0.001*** 海拔 0.90 −0.07 0.31 0.29 0.61 0.001*** pH −0.02 0.58 −0.81 0.00 0.55 0.004** 特征值 0.57*** 0.26*** 0.23*** 0.17*** 累计解释率/% 36.95 53.63 68.68 79.87 草本 土壤水分 0.38 −0.14 0.11 0.91 0.22 0.124 林分密度 −0.21 0.35 0.89 0.21 0.86 0.001*** 土壤养分 0.37 −0.70 0.42 −0.44 0.30 0.032* 土壤通气性 0.85 0.46 0.16 −0.18 0.88 0.001*** 生物量 −0.50 0.45 −0.39 0.63 0.56 0.001*** 林冠郁闭度 −0.18 0.77 −0.04 −0.60 0.63 0.001*** 海拔 −0.36 −0.19 0.31 −0.86 0.41 0.004** pH 0.56 0.21 −0.72 −0.34 0.37 0.004** 特征值 0.63*** 0.23*** 0.23*** 0.19*** 累计解释率/% 35.72 49.12 62.27 73.35 藤本 土壤水分 −0.39 0.08 0.76 0.51 0.68 0.001*** 林分密度 −0.66 −0.71 −0.26 0.06 0.32 0.053 土壤养分 −0.61 −0.11 0.67 −0.41 0.31 0.052 土壤通气性 0.69 0.42 −0.20 0.55 0.48 0.002** 生物量 −0.54 0.27 −0.79 −0.04 0.24 0.162 林冠郁闭度 0.65 0.19 −0.36 −0.64 0.44 0.005** 海拔 −0.59 0.62 −0.45 −0.25 0.70 0.001*** pH 0.64 0.25 0.72 0.13 0.47 0.006** 特征值 0.48*** 0.26*** 0.19*** 0.14*** 累计解释率/% 41.38 63.90 79.80 91.65 说明：*表示P＜0.05，**表示P＜0.01，***表示P＜0.001 基于油松人工林下灌木、草本、藤本与环境因子的CCA二维排序结果可知(表5和图1)：油松人工林下灌木、藤本分布主要受海拔影响，其次是土壤通气性，而草本分布主要受土壤通气性影响，其次是林冠郁闭度，即随着海拔、土壤通气性的升高油松人工林下物种多样性下降。
图 1 油松人工林下物种分布与环境因子典范对应分析二维排序图Figure 1 Two-dimensional ordination diagram of canonical correspondence analysis between distribution of species and environmental factors under P. tabuliformis plantation林下灌木物种分布除与土壤养分和生物量无显著相关关系外，与其他环境因子均显著相关，且灌木主要分布在海拔相对较低、土壤通气条件较好的油松人工林下，而偶见种黄芦木Berberis amurensis(S19)、美蔷薇Rosa bella (S28)主要分布在海拔较高的区域。林下草本物种分布除与土壤水分无显著相关关系外，与其他环境因子均显著相关，且草本主要分布在土壤条件较好、林内郁闭度较低油松人工林下，而偶见种中华秋海棠Begonia grandis subsp. sinensis (H22)、大油芒Spodiopogon sibiricus (H110)主要分布在土壤通气条件较差的区域，小花灯心草Juncus articulatus (H26)、独活Heracleum hemsleyanum (H96)主要分布在土壤养分较好的区域，羊齿天门冬Asparagus filicinus (H101)主要分布在郁闭度较高的区域。林下藤本物种分布除与林分密度、土壤养分、生物量无显著相关关系外，与其他环境因子均显著相关，且藤本主要分布在低海拔、土壤通气性良好、林分密度相对较低的油松人工林下，而偶见种粉绿铁线莲Clematis glauca (L10)主要分布在土壤通气条件较好的高海拔区域。
3. 讨论与结论
物种分布受多种因素影响。一般认为大尺度下，气候差异是物种多样性变化的最主要原因[1, 14-16]，其中寒冷地区非生物因子对物种分布影响较大，温暖地区生物因子影响相对较大[17-18]；随着纬度升高，物种多样性降低[19]。而在小尺度区域内，地形、土壤、生物等因素是物种多样性变化的主要驱动因素[2, 20-21]。中条山油松人工林下物种主要受非生物环境因子影响，由非生物环境因子(海拔)和土壤理化性质形成的局域尺度上的环境异质性，是影响局域内植物物种分布的关键因子，即非生物因子形成的环境筛(environmental filtering)作用是影响该区域林下物种的扩散和生存[22-24]。
海拔和土壤通气性是影响油松林下物种分布的关键性因子，其中灌木和藤本分布主要受海拔影响，草本分布主要受土壤通气性影响。研究[25]表明：海拔是影响植物物种分布的关键性因子之一，是反映温度、湿度、光照等因素的综合环境因素，对物种多样性的影响较复杂。一般认为海拔升高，水热条件将变差，物种多样性将下降；但在某些特殊环境中，海拔升高后水分条件会有所改善，人为干扰活动下降，物种多样性将升高[26]；当上升到水热条件限制植物生存的海拔，物种多样性又下降[27]；此外，植物物种多样性随海拔升高还呈现其他更复杂变化[28]。本研究发现：中条山物种分布与海拔显著负相关，即海拔升高，林下物种多样性下降。KRAFT等[29]研究发现：生态策略趋同的物种主要受地形环境筛控制，而生态策略趋异的物种主要受生物因素(竞争或密度制约过程)的影响。海拔是中条山油松人工林下灌木和藤本物种分布的重要影响因子之一，说明该地区林下物种生态策略存在趋同性。
在局域范围内，除海拔外，土壤是主导植物物种分布格局的另一个关键非生物环境因子[30-32]。本研究发现：土壤通气性对林下灌木和藤本物种分布的影响仅次于海拔，但对草本物种分布的影响大于海拔，即土壤因素对草本的影响大于地形因素，而对灌木和藤本的影响小于地形因素。该结论与前人研究结果相反，之前研究结果认为，在局域范围内，地形因素是影响植物物种分布最关键的因素，而土壤因素次之[26]，其主要原因是，海拔升高导致温度、土壤肥力、土层厚度下降，辐射增加[33-36]，即海拔是主导环境改变的关键因子。本研究的土壤通气性是土壤非毛管孔隙度、坡度、油松相对优势度、乔木平均生物量等4个环境因子的集合体，且土壤非毛管孔隙度是影响该综合指标的关键环境因子，此外，本研究区域各海拔土壤厚度变化不大，且海拔越高林分密度越大，辐射对林下植物影响较小，所以当土壤通气性增大时，土壤的保水能力下降，甚至消失，土壤孔隙被空气占据，植物根系无法吸收水分与养分，进而导致植物物种无法生存，所以当其值增大时植物分布将受到限制。
光照也是影响物种分布的主要环境因子之一[37]。本研究发现：林冠郁闭度对林下灌草藤物种分布均存在显著影响，说明光照是限制该区域林下物种多样性的另一个关键环境因子。刘浩栋等[38]研究发现：冠层郁闭度坡向是解释海南岛霸王岭陆均松Dacrydium petinatum天然群落物种分布的主要驱动因素。本研究中，林冠郁闭度是郁闭度、坡向、间伐间隔的等3个环境要素的综合体，所以在今后的森林经营活动中，可以通过开林窗的方式改变林下光照环境，增加林下物种多样性。
油松人工林下物种分布主要受非生物环境因子影响，其中地形(海拔)和土壤(土壤通气性)是影响中条山油松人工林下物种分布的关键环境因子。由于山地生态系统的水热主要受海拔影响，海拔对物种的分布的影响占主导地位，因此随着海拔和土壤通气性的升高，林下物种多样性下降，即地形和土壤因子形成的非生物环境筛作用影响区域群落植物物种的扩散和生存，使物种广泛分布于适宜其自身生存的环境中。
本研究校正解释率较低，说明分析中很大一部分的物种信息可能丢失。造成解释率较低的原因可能是未考虑一些生物、非生物环境要素的结果，如非生物因素中的温度、降水量、光照等，生物因素中的植物功能性状、竞争、人类活动等[39]。所以为了增加环境因子对中条山油松人工林下物种多样性的解释率，今后的研究需增加相应的环境因子。
-
图 6 树高和胸径的测量值与实际值的回归分析
Figure 6 Regression analysis of measured and actual values of tree height and DBH
表 1 树高和胸径的测量值与实际值
Table 1. Measured and actual values of tree height and DBH
立木
编号树高 胸径 实际
值/m测量
值/m相对误
差/%实际
值/cm测量
值/cm相对误
差/%1 6.14 6.10 0.63 15.60 14.85 4.85 2 4.98 4.87 2.15 13.06 13.33 2.07 3 5.49 5.53 0.84 12.74 13.00 2.09 4 5.64 5.49 2.60 14.97 15.58 4.06 5 3.42 3.39 0.93 10.83 10.62 1.87 6 3.49 3.55 1.69 12.26 13.11 6.91 7 4.53 4.40 2.78 12.90 12.25 4.99 8 4.31 4.21 2.39 14.33 14.09 1.70 9 6.65 6.60 0.71 19.43 19.14 1.44 10 6.19 6.08 1.79 18.63 19.35 3.87 11 7.17 6.93 3.40 18.80 18.42 1.94 12 5.63 5.73 1.67 18.72 19.39 3.58 13 7.52 7.35 2.18 16.97 17.27 1.77 14 7.47 7.20 3.56 19.04 18.59 2.37 15 5.58 5.69 1.93 15.13 14.36 5.08 16 5.01 5.05 0.64 11.94 12.20 2.16 17 5.41 5.27 2.57 12.67 12.46 1.68 18 7.18 6.98 2.78 16.08 16.88 4.93 平均值 1.96 3.19 
下载: 导出CSV
-
[1] 孟宪宇. 测树学[M]. 北京: 中国林业出版社, 2006: 350. MENG Xianyu. Forest Mensuration[M]. Beijing: China Forestry Publishing House, 2006: 350. [2] MARKUS H, MIKKO V, JUHA H. Outlook for the next generation’s precision forestry in finland [J]. Forests, 2014, 5(7): 1682 − 1694. [3] 程文生, 冯仲科, 黄晓东. 便携式森林资源调查仪研制与试验[J]. 西北林学院学报, 2018, 33(5): 156 − 162. CHENG Wensheng, FENG Zhongke. HUANG Xiaodong. Development and experiment of portable instrument for forest resources inventory [J]. J Northwest For Univ, 2018, 33(5): 156 − 162. [4] 冯仲科, 黄晓东, 刘芳. 森林调查装备与信息化技术发展分析[J]. 农业机械学报, 2015, 46(9): 257 − 265. FENG Zhongke, HUANG Xiaodong, LIU Fang. Forest survey equipment and development of information technology [J]. Trans Chin Soc Agric Mach, 2015, 46(9): 257 − 265. [5] 杜鹏志, 曾伟生, 冯仲科, 等. 利用电子经纬仪测量林木树高和材积的精度分析[J]. 林业资源管理, 2016(2): 45 − 48, 55. DU Pengzhi, ZENG Weisheng, FENG Zhongke, et al. Precision analysis on tree height and stem volume measurements using electronic theodolite [J]. For Resour Manage, 2016(2): 45 − 48, 55. [6] 于东海, 冯仲科, 曹忠, 等. 全站仪测量立木胸径树高及材积的误差分析[J]. 农业工程学报, 2016, 32(17): 160 − 167. YU Donghai, FENG Zhongke, CAO Zhong, et al. Error analysis of measuring diameter at breast height and tree height and volume of standing tree by total station [J]. Trans Chin Soc Agric Eng, 2016, 32(17): 160 − 167. [7] 陈相武, 徐爱俊. 基于智能手机单目视觉的多株立木高度提取方法[J]. 北京林业大学学报, 2020, 42(8): 43 − 52. CHEN Xiangwu, XU Aijun. Height extraction method of multiple standing trees based on monocular vision of smart phones [J]. J Beijing For Univ, 2020, 42(8): 43 − 52. [8] 管昉立, 徐爱俊. 基于智能手机与机器视觉技术的立木胸径测量方法[J]. 浙江农林大学学报, 2018, 35(5): 892 − 899. GUAN Fangli, XU Aijun. Tree DBH measurement method based on smartphone and machine vision technology [J]. J Zhejiang A&F Univ, 2018, 35(5): 892 − 899. [9] 高莉平, 徐爱俊. 应用智能终端的立木高度测量方法[J]. 东北林业大学学报, 2018, 46(11): 28 − 34. GAO Liping, XU Aijun. Tree height measurement method with intelligent terminal [J]. J Northeast For Univ, 2018, 46(11): 28 − 34. [10] VÁZQUEZ-ARELLANO M, GRIEPENTROG H W, REISER D, et al. 3-D imaging systems for agricultural applications: a review [J/OL]. Sensors, 2016, 16 (5): 618. doi: 10.3390/s16050618. [11] 仇瑞承, 张漫, 魏爽, 等. 基于RGB-D相机的玉米茎粗测量方法[J]. 农业工程学报, 2017, 33(增刊 1): 170 − 176. QIU Ruicheng, ZHANG Man, WEI Shuang, et al. Method for measurement of maize stem diameters based on RGB-D camera [J]. Trans Chin Soc Agric Eng, 2017, 33(suppl 1): 170 − 176. [12] NEWNHAM G J, ARMSTON J D, CALDERS K, et al. Terrestrial laser scanning for plot-scale forest measurement [J]. Curr For Rep, 2015, 1(4): 239 − 251. [13] 刘浩, 张峥男, 曹林. 机载激光雷达森林垂直结构剖面参数的沿海平原人工林林分特征反演[J]. 遥感学报, 2018, 22(5): 872 − 888. LIU Hao, ZHANG Zhengnan, CAO Lin. Estimating forest stand characteristics in a coastal plain forest plantation based on vertical structure profile parameters derived from ALS data [J]. J Remote Sensing, 2018, 22(5): 872 − 888. [14] WESTOBY M J, BRASINGTON J, GLASSER N F, et al. ‘Structure-from-Motion’ photogrammetry: a low-cost, effective tool for geoscience applications [J]. Geomorphology, 2012, 179: 300 − 314. [15] 周静静, 郭新宇, 吴升, 等. 基于多视角图像的植物三维重建研究进展[J]. 中国农业科技导报, 2019, 21(2): 9 − 18. ZHOU Jingjing, GUO Xinyu, WU Sheng, et al. Research progress on plant three-dimensional reconstruction based on multi-view image [J]. J Agric Sci Technol, 2019, 21(2): 9 − 18. [16] 梁秀英, 周风燃, 陈欢, 等. 基于运动恢复结构的玉米植株三维重建与性状提取[J]. 农业机械学报, 2020, 51(6): 209 − 219. LIANG Xiuying, ZHOU Fengran, CHEN Huan, et al. Three-dimensional maize plants reconstruction and traits extraction based on structure from motion [J]. Trans Chin Soc Agric Mach, 2020, 51(6): 209 − 219. [17] HUI Fang, ZHU Jinyu, HU Pengcheng, et al. Image-based dynamic quantification and high-accuracy 3D evaluation of canopy structure of plant populations [J]. Ann Bot, 2018, 121(5): 1079 − 1088. [18] MILLER J, MORGENROTH J, GOMEZ C. 3D modelling of individual trees using a handheld camera: accuracy of height, diameter and volume estimates [J]. Urban For Urban Greening, 2015, 14(4): 932 − 940. [19] 徐慧丹, 周小成, 黄洪宇, 等. 移动多视图立体摄影的单木结构参数提取[J]. 测绘科学, 2018, 43(9): 108 − 114. XU Huidan, ZHOU Xiaocheng, HUANG Hongyu, et al. Single tree structure parameter extraction of structure-from-motion with multi-view stereophotogrammetry [J]. Sci Surv Mapp, 2018, 43(9): 108 − 114. [20] 孙英伟, 林文树. 基于SFM算法的单木结构参数提取研究[J]. 西北林学院学报, 2020, 35(5): 180 − 184. SUN Yingwei, LIN Wenshu. Extraction of the parameters of single tree structure based on SFM algorithm [J]. J Northwest For Univ, 2020, 35(5): 180 − 184. [21] 化春键, 马金科, 陈莹. 基于差异哈希算法的改进非局部均值去噪算法[J/OL]. 激光与光电子学进展, 2020, 57(14): 141007. doi: 10.3788/LOP57.141007. HUA Chunjian, MA Jinke, CHEN Yin. Improved non-local mean denoising algorithm based on difference hash algorithm[J/OL]. Laser Optoelectron Prog, 2020, 57(14): 141007. doi: 10.3788/LOP57.141007. [22] LOWE D G. Distinctive image features from scale-invariant keypoints [J]. Int J Comput Vision, 2004, 60(2): 91 − 110. [23] TRIGGS B, MCLAUCHLAN P F, HARTLEY R I, et al. Bundle adjustment-a modern synthesis[C]//[s.l.]. International Workshop on Vision Algorithms. Berlin: Springer, 1999: 298 − 372. [24] 何豫航, 岳俊. 基于CMVS/PMVS多视角密集匹配方法的研究与实现[J]. 测绘地理信息, 2013, 38(3): 20 − 23. HE Yuhang, YUE Jun. Research and implementation based on multi-view dense matching by applying CMVS /PMVS [J]. J Geomatics, 2013, 38(3): 20 − 23. [25] WOLD S, ESBENSEN K, GELADI P. Principal component analysis [J]. Chemometrics Intell Lab Syst, 1987, 2(1/3): 37 − 52. [26] 杨全月, 陈志泊, 孙国栋. 基于点云数据的测树因子自动提取方法[J]. 农业机械学报, 2017, 48(8): 179 − 185. YANG Quanyue, CHEN Zhibo, SUN Guodong. Automatic extraction method of tree measurement factors based on point cloud data [J]. Trans Chin Agric Mach, 2017, 48(8): 179 − 185. [27] 范永祥, 冯仲科, 陈盼盼, 等. 基于RGB-D SLAM手机的森林样地调查系统研究[J]. 农业机械学报, 2019, 50(8): 226 − 234. FAN Yongxiang, FENG Zhongke, CHEN Panpan, et al. Research on forest plot survey system based on RGB-D SLAM mobile phone [J]. Trans Chin Soc Agric Mach, 2019, 50(8): 226 − 234. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20210547
点击查看大图
计量
- 文章访问数: 674
- HTML全文浏览量: 228
- PDF下载量: 23
- 被引次数: 0
