-
森林碳汇量与森林生物量有着密切关系。生物量是森林生态系统最基本的数量特征,是研究森林及其生态问题的基础,直接关系到森林生态系统的碳储量和碳汇功能[1-2]。因研究方法不同及生态系统空间、时间变化的复杂性,生物量估测还存在一定的不确定性,但可以依靠增加建模的样本来降低模型中参数的不确定性[3]。目前,生物量估测方法主要有直接测量法和间接估算法2类。直接测量法估算精度高,但消耗大量人力、物力和时间,对森林也会造成一定的破坏;间接估算法的核心就是生物量建模,是当前最常用的方法[4]。传统生物量模型往往是对树木的枝、干、茎、叶等各分量生物量进行单独估测,容易造成各分量生物量之和不等于总生物量,即出现模型不相容问题[5-6]。为解决这一问题,研究人员多采用非线性回归与极大似然法[7]、比例平差法[8]和线性或非线性联合估计方法[9]等。符利勇等[10]通过对上述3种方法进行综合比较,发现非线性联立方程组法的预测精度与效果最佳,该方法已在青冈栎Cyclobalanopsis glauca、杉木Cunninghamia lanceolata、日本落叶松Larix kaempferi等用材林中进行了应用[11-13]。
杨梅Myrica rubra原产浙江省余姚市,现已成为浙江省最具特色优势、种植经济效益高的优质农产品。2019年全省杨梅种植面积达8.88万 hm2,产量为61.84万 t,面积和产量位居全国首位。当前对于杨梅生态学的研究往往偏重于土壤性质、矿质养分、果实品质等方面[14-17],而对杨梅生物量估测方法的研究未见报道。本研究以浙江省杨梅人工林为研究对象,采用非线性联立方程组法,构建一元相容性单株生物量模型,以期为杨梅人工林可持续经营及生物量精确估测提供理论依据。同时,通过生物量估算可以计算森林的碳汇量[18],帮助农户实现对杨梅林碳汇总量的精准估测,以获取更精确的碳汇收入。
-
研究区位于浙江省仙居县福应街道。仙居是浙江省台州市第一杨梅主产区,是“中国杨梅之乡”。研究区的杨梅人工林具有广泛的代表性,地理位置为28°25′~28°52′N, 120°23′~120°42′E,海拔为140~230 m,属中亚热带季风气候,年平均气温为18.3 ℃,最热的7月平均气温为28.5 ℃,最冷的1月平均气温为5.6 ℃,无霜期为240 d左右,历年平均降水量为2 000 mm,年日照时数为1 786.2 h。母岩为花岗岩,土壤为红壤。
-
2017年8月,选择不同龄级(幼苗期、产前期、初产期、盛产期)的杨梅林(中心位置28°46′09″N, 120°31′18″E),分别建立20 m×10 m的标准地各4个,共16个。杨梅林均由马尾松Pinus massoniana林改造而来。土壤成土母岩为花岗岩,海拔140~230 m,西北坡。
对标准地内杨梅林的地径、树高、冠幅进行全面调查,计算平均地径、树高、冠幅(表1),并在每个标准地内选取标准木(地径和株高均约为平均值)各3株,共48株。采用全收获法,野外分离叶片、枝干和根系,并分别实测鲜质量。同时均匀选取不同器官样品500~1 000 g(准确称量)于样品袋中,带回实验室。样品带回室内在105 ℃烘箱内烘干至恒量,计算各组分生物量和总生物量。48株杨梅生物量数据分成2组,32株用于生物量建模,剩余16株用于模型检验。
表 1 不同龄级杨梅人工林的基本情况
Table 1. Basic conditions of M. rubra plantations at different stand ages
龄级 平均地径/
cm平均树高/
m平均冠幅/
m2平均密度/
(株·hm−2)幼苗期 2.0±0.2 0.6±0.1 0.1±0.0 600±30 产前期 7.3±0.8 2.0±0.3 3.2±0.6 525±30 初产期 10.3±1.2 2.7±0.3 12.2±2.2 375±15 盛果期 13.9±1.5 3.5±0.4 20.6±3.2 375±15 说明:数值为平均值±标准差 -
使用建模的32株杨梅的地径、树高、冠幅与各组分生物量及总生物量(不含果实)进行相关分析(表2),结果均呈极显著正相关(P<0.01),因此采用3个因子作为自变量构建杨梅各组分生物量及总生物量模型。
表 2 杨梅自变量因子与各组分生物量及总生物量相关性
Table 2. Correlation of independent variables and all biomasses
因子 叶生物量 枝干生物量 根系生物量 总生物量 地径 0.927** 0.926** 0.929** 0.933** 树高 0.743** 0.735** 0.720** 0.736** 冠幅 0.899** 0.913** 0.911** 0.914** 说明:**表示在0.01水平(双侧)上显著相关 -
采用常见的线性方程y=a+bx、对数函数y=a+blnx、指数函数y=abx、幂函数y=axb、二次多项式函数y=a+bx+cx2等方程构建杨梅树独立单株生物量模型。用决定系数(R2)来评价模型优劣。R2越接近1表示回归效果越好。选出拟合度最好、相关最密切的数学模型。
-
一元、二元相容性生物量模型都能较好地解决总生物量与各组分生物量的相容性问题,但从模型构造和应用性考虑,一元相容性生物量模型在大尺度范围估测森林生物量的效果要优于二元相容性生物量,且模型数据较易获取,准确性较高,模型形式也较简单[19-20]。因此,本研究参照唐守正等[21]提出的非线性误差变量模型法,建立总生物量与各组分生物量非线性联立一元方程组模型。
$$ \left\{\begin{array}{l} y_1= a_1x^{b_1}\\ y_2=a_2x^{b_2}\\ y_3=a_3x^{b_3}\\ y_0=c_0x^{b_0} \end{array}\right. 。 $$ 其中:y0为总生物量,y1为叶生物量,y2为枝干生物量(枝条和树干生物量之和),y3为根系生物量,y0= y1+y2+y3,x为建立单株生物量模型时选取的变量,a1、a2、a3、b0、b1、b2、b3、c0为模型参数。使用未建模的16株杨梅数据,计算总相对误差(SR)、平均相对误差(EE)和预估精度(P0)。
$$ S_{\rm{R}}=\frac{\displaystyle \sum\limits_{i=1}^N ({y}_{i}-\widehat{{y}_{i}})}{\displaystyle \sum\limits_{i = 1}^N \widehat{{y}_{i}}}\times 100{\%} ; $$ $$ {E}_{{\rm{E}}}=\frac{1}{N}\sum\limits_{i = 1}^N \frac{({y}_{i}-\widehat{{y}_{i}})}{\widehat{{y}_{i}}}\times 100{\%} ;$$ $$ {P}_{0}=\left(1-\frac{{t}_{\alpha }\sqrt{\displaystyle \sum\limits_{i = 1}^N {\left({y}_{i}-\widehat{{y}_{i}}\right)}^{2}}}{{\bar{y}_{i}}\sqrt{N\left(N-T\right)}}\right)\times 100{\%} 。$$ $ {\mathrm{其}\mathrm{中}:y}_{i} $ 和$ \widehat{{y}_{i}} $ 分别为第i株杨梅样木的生物量实测值和估计值,${\bar{y}_{i}} $ 为全部杨梅样木实测值的平均值,N为杨梅样木的总数,T为模型参数个数,tα为自由度 (N−T) 置信水平 α=0.05。对建立的杨梅生物量方程进行预测精度验证和效果检验。非线性误差变量模型法估计要求模型参数不能有冗余,因此,上述模型经简化改写,得到如下相容性生物量模型。$$ \left\{ \begin{array}{l} {y_1} = {c_0}{x^{b_0}}/\left( {1 + {r_1}{x^{r_3}} + {r_2}{x^{r_4}}} \right)\\ {y_2} = {c_0}{r_1}{x}^{r_3 + b_0}/\left( {1 + {r_1}{x^{r_3}} + {r_2}{x^{r_4}}} \right)\\ {y_3} = {c_0}{r_2}{x}^{r_4 + b_0}/\left( {1 + {r_1}{x^{r_3}} + {r_2}{x^{r_4}}} \right)\\ {y_0} = {c_0}{x^{b_0}} \end{array} \right.。$$ 其中:r1、r2、r3、r4为模型参数。
-
分别以地径、树高和冠幅为自变量,用指数函数、线性函数、对数函数、多项式函数和幂函数拟合杨梅叶生物量、枝干生物量、根系生物量及总生物量模型(表3)。可见,采用幂函数拟合的决定系数均最大。叶生物量(y1)与地径(x1)、树高(x2)和冠幅(x3)的幂函数模型分别为y1=0.004x12.795、 y1=0.150x23.142、 y1=0.239x31.041,决定系数分别为0.951、0.841和0.864;枝干生物量(y1)与地径、树高和冠幅的幂函数模型分别为y2=0.003x13.048、y2=0.150x23.444、y2=0.249x31.143,决定系数分别为0.942、0.859和0.885;根系生物量(y3)与地径、树高和冠幅的幂函数模型分别为y3=0.002x13.141、y3=0.128x23.470、y3=0.206x31.169,决定系数分别为0.964、0.832、0.884;总生物量(y0)与地径、树高和冠幅的幂函数模型分别为y0=0.010x12.995、y0=0.433x23.351、y0=1.137x31.000, 决定系数分别为0.959、0.849、0.822。可见,与树高、冠幅相比,以地径为自变量拟合的幂函数模型决定系数均最大,为最优模型。
表 3 各组分生物量及总生物量模型决定系数
Table 3. R2 values of all biomass models
模型 叶生物量 枝干生物量 根系生物量 总生物量 地径 树高 冠幅 地径 树高 冠幅 地径 树高 冠幅 地径 树高 冠幅 指数函数 0.442 0.316 0.539 0.469 0.364 0.581 0.438 0.324 0.562 0.705 0.578 0.723 线性函数 0.690 0.407 0.786 0.693 0.410 0.822 0.674 0.385 0.810 0.697 0.409 0.802 对数函数 0.657 0.380 0.503 0.665 0.385 0.521 0.648 0.362 0.494 0.668 0.384 0.517 多项式函数 0.894 0.628 0.791 0.889 0.818 0.870 0.935 0.624 0.820 0.933 0.639 0.781 幂函数 0.951 0.841 0.864 0.942 0.859 0.885 0.964 0.832 0.884 0.959 0.849 0.822 -
在ForStat 2.1 软件支持下,建立杨梅非线性误差变量一元联立方程组,求解模型各参数值,得到杨梅相容性各单株生物量模型。用决定系数、总相对误差、平均相对误差、预估精度对模型进行综合评价与检验(表4)。以地径为自变量的相容性单株生物量模型:
表 4 各相容性单株生物量模型参数与评价指标值
Table 4. Parameters and evaluation index values of the compatible individual-tree biomass models
自变量 生物量 c0 b0 r1 r2 r3 r4 决定系数 总相对误差 /% 平均相对误差/% 预估精度/% 地径 y1 0.084 0 2.162 7 0.780 0 0.779 9 0.224 3 0.204 5 0.881 8 3.097 8 2.577 8 91.63 y2 0.084 0 2.162 7 0.780 0 0.779 9 0.224 3 0.204 5 0.883 4 1.337 1 0.748 1 91.63 y3 0.084 0 2.162 7 0.780 0 0.779 9 0.224 3 0.204 5 0.912 4 1.351 5 4.185 9 92.03 y0 0.084 0 2.162 7 0.904 2 1.090 2 2.417 6 92.22 树高 y1 0.645 4 3.155 8 1.095 3 1.095 2 0.219 6 0.162 0 0.631 8 4.584 6 1.477 9 84.88 y2 0.645 4 3.155 8 1.095 3 1.095 2 0.219 6 0.162 0 0.636 8 4.584 6 1.411 9 85.50 y3 0.645 4 3.155 8 1.095 3 1.095 2 0.219 6 0.162 0 0.623 7 4.584 6 0.483 4 85.00 y0 0.645 4 3.155 8 0.615 9 4.584 6 2.646 4 83.56 冠幅 y1 0.589 5 1.219 5 0.897 9 0.897 8 0.149 1 0.130 0 0.838 3 1.243 8 0.961 4 90.03 y2 0.589 5 1.219 5 0.897 9 0.897 8 0.149 1 0.130 0 0.808 3 1.775 3 0.948 9 89.51 y3 0.589 5 1.219 5 0.897 9 0.897 8 0.149 1 0.130 0 0.834 8 2.937 0 0.343 4 90.14 y0 0.589 5 1.219 5 0.836 9 1.201 4 2.444 0 89.31 $$ \left\{ \begin{array}{l} {y_1} = 0.084\;0{x_1}^{2.162\;7}/(1 + 0.780\;0{x_1}^{0.224\;3} + 0.779\;9{x_1}^{0.204\;5})\\ {y_2} = 0.065\;5{x_1}^{2.387\;0}/(1 + 0.780\;0{x_1}^{0.224\;3} + 0.779\;9{x_1}^{0.204\;5})\\ {y_3} = 0.065\;5{x_1}^{2.367\;2}/(1 + 0.780\;0{x_1}^{0.224\;3} + 0.779\;9{x_1}^{0.204\;5})\\ {y_0} = 0.084\;0{x^{2.162\;7}} \end{array} \right.。$$ 以树高为自变量的相容性单株生物量模型:
$$ \left\{ \begin{array}{l} {y_1} = 0.645\;4{x_2}^{3.155\;8}/(1 + 1.095\;3{x_2}^{0.219\;6} + 1.095\;2{x_2}^{0.162\;0})\\ {y_2} = 0.707\;0{x_2}^{3.375\;4}/(1 + 1.095\;3{x_2}^{0.219\;6} + 1.095\;2{x_2}^{0.162\;0})\\ {y_3} = 0.706\;9{x_2}^{3.317\;8}/(1 + 1.095\;3{x_2}^{0.219\;6} + 1.095\;2{x_2}^{0.162\;0})\\ {y_0} = 0.645\;4{x_2}^{3.155\;8} \end{array} \right.。$$ 以冠幅为自变量的相容性单株生物量模型:
$$ \left\{ {\begin{array}{*{20}{l}} {{y_1} = 0.589\;5{x_3}^{1.219\;5}/(1 + 0.897\;9{x_3}^{0.149\;1} + 0.897\;8{x_3}^{0.130\;0})}\\ {{y_2} = 0.529\;3{x_3}^{1.368\;5}/(1 + 0.897\;9{x_3}^{0.149\;1} + 0.897\;8{x_3}^{0.130\;0})}\\ {{y_3} = 0.529\;2{x_3}^{1.349\;5}/(1 + 0.897\;9{x_3}^{0.149\;1} + 0.897\;8{x_3}^{0.130\;0})}\\ {{y_0} = 0.589\;5{x_3}^{1.219\;5}} \end{array}} \right.。$$ 可以看出:杨梅相容性单株生物量模型R2均较高,都在0.600 0以上,说明模型代表性较强,拟合优度较高;平均相对误差均在±4.6%范围内,小于±5%,相对误差较小;总相对误差小于5.0%,说明模型系统偏差较小,拟合效果较好;预估精度均达85%以上,估测精度较高。总体看,本研究建立的杨梅相容性单株生物量模型精度较高,拟合效果较好,满足研究区对杨梅生物量的估测要求。其中,以地径为自变量的相容性单株生物量模型,决定系数和预估精度值最大,分别为0.881 8~0.912 4和91.63%~92.22%,为最优相容性单株生物量模型。
-
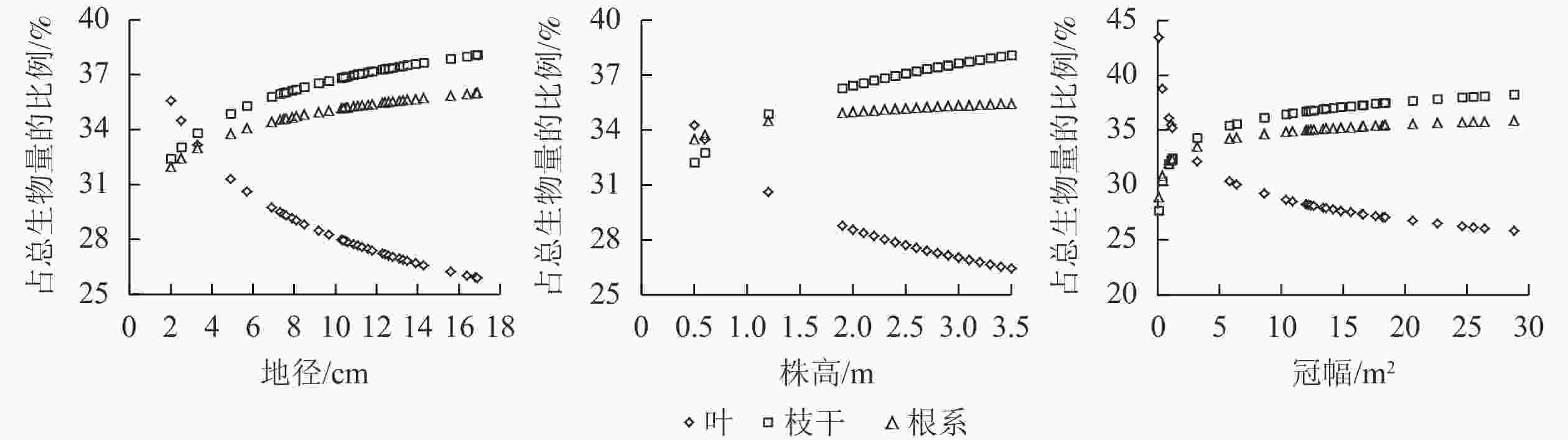
利用建立的各相容性单株生物量模型,对杨梅各组分生物量占总生物量比例随地径、株高、冠幅的变化进行分析。从图1可见:枝干、根系生物量占杨梅总生物量的比例随地径增大而逐渐升高,增速逐渐趋缓,从地径为2 cm的32.4%、31.9%分别提高到17 cm的38.1%、36.0%;叶生物量占杨梅总生物量的比例则随地径增大呈明显快速下降趋势,从地径为2 cm的35.6%下降到17 cm的25.9%。枝干、根系生物量随树高增长而缓慢升高,从树高为0.5 m的32.2%、33.5%分别提高到3.5 m的38.1%、35.5%;叶生物量则随树高增长呈明显快速下降趋势,从树高为0.5 m的34.3%下降到3.5 m的26.4%。枝干、根系生物量随冠幅扩展缓慢升高并趋于平缓,从冠幅为0.1 m2的27.7%、28.9%分别提高到30.0 m2的38.4%、35.9%;叶生物量随冠幅扩展而逐渐下降,但降幅趋缓,从冠幅为0.1 m2的43.4%下降到30.0 m2的25.7%。
-
分别以地径、树高和冠幅为自变量,对比不同函数拟合出的模型,采用幂函数拟合的杨梅叶生物量、枝干生物量、根系生物量及总生物量模型的决定系数均为最大,为0.822~0.964,统计学意义显著。格日乐图等[22]在研究广宁茶秆竹Pseudosasa amabilis地上生物量分布特征时,选定幂函数模型作为最优模型;尹惠妍等[23]在对中国主要乔木树种生物量方程研究中,收集了1996—2012年间在国内外发表的66篇文献中的乔木生物量模型,其中包括44个乔木树种模型和612个分量模型,以幂函数的形式最多。对比地径(x1)、树高(x2)和冠幅(x3)拟合的幂函数模型,又以地径的决定系数为最大,叶生物量、枝干生物量、根系生物量及总生物量模型决定系数分别为0.951、0.942、0.964和0.959,所对应幂函数分别为y1=0.004 x12.795、y2=0.003 x13.048、y3=0.002 x13.141和y0=0.010 x12.995。
为解决生物量模型的相容性问题,本研究采用非线性联立方程组法,构建以地径、树高和冠幅为自变量的各相容性单株生物量模型,充分考虑了各组分生物量与总生物量之间的内在相关性问题,确保了各组分生物量预测值之和等于总生物量。从研究结果来看,3个模型拟合效果均较好,预估精度都在85%以上,模型平均相对误差较小。其中以地径为自变量的相容性单株生物量模型预估精度最大,达91.63%~92.22%,模型为最优,模型参数c0、b0、r1、r2、r3和r4分别为0.084 0、2.162 7、0.780 0、0.779 9、0.224 3和0.204 5。研究区杨梅标准木数量有限,加之生物量估测影响因素较多,因此,若要提高生物量估测精确度,还要从提高样本数量、减少抽样误差、控制采样条件等多方面加以提升改进[24-25]。
随地径增大、树高增长和冠幅扩展,各组分生物量占总生物量的比例基本呈相似的变化规律,其中枝干生物量、根系生物量占比均呈升高趋势,叶生物量呈下降趋势。随着杨梅生长(林龄增大),各组分生物量从高到低快速演变为枝干、根系、叶片。孙拥康等[13]构建的鄂西山区日本落叶松相容性单株生物量模型显示,树干生物量占总生物量的比例随胸径增大而升高,树冠生物量呈明显下降趋势,而树根生物量呈先增后减趋势,但整体变化较平缓;曹磊等[26]构建的广东省樟树Cinnamomum camphora相容性生物量模型显示,樟树各组分生物量占地上部分比例随胸径增大而呈现出不同的规律,树干生物量比例先增大然后基本维持不变最后逐渐下降,树叶生物量和干皮生物量比例逐渐降低,而树枝生物量比例逐渐提高。与本研究结果相反,这可能因树种不同造成的。
需要对杨梅人工林采取一定的技术措施来提高果实产量和品质。采取大枝修剪可以改善果园中的通风透光,提高果实的品质和产量,但为避免主枝被日光灼伤,大枝修剪应选在冬季最为合适;疏果是提高果实品质的一项重要管理措施,疏枝疏果可以显著提高果实品质及其商品果率;不合理的施肥会导致杨梅不结果或果实畸形等问题,配方施肥对提升杨梅品质也是极为重要的一项举措。浙江大部分土壤为酸性土,土壤中缺乏钾、钙等元素,需有针对性地施用肥料,提高果实品质,并防止采前落果、果实腐烂病的发生[27];农户有足够经济条件时也可搭建设施大棚,以此提前杨梅的上市时间,延长杨梅的采收时段,并且可以提升杨梅的单果质量,提高果实中可溶性固形物、维生素C、糖等含量[28]。
杨梅生物量模型在碳中和、碳达峰目标下具有更强的可用性和推广性。常规森林的固碳量一般都会随着林分年龄的增大而增多[29],相同年龄下的地径、树高、冠幅存在一定的差异,年龄的增大仅仅呈现出生物量不断增长的趋势,而通过测量杨梅的单一变量如地径、树高、冠幅即可准确估算出树木的生物量,可以减少在实际测量中所需投入的人力、物力等资源。同时,利用生物量模型可以准确估算森林碳储量的生态效益,对发展碳汇经济有着极为深远的意义[30],也是衡量森林固碳能力的关键[31]。下一步的研究中,还应探索研究其他生物量估测方法,加大样本采集数量,以期建立更加科学的杨梅通用性生物量模型。
Construction of compatible individual tree biomass model of Myrica rubra plantation
-
摘要:
目的 构建杨梅Myrica rubra一元相容性单株生物量模型,为杨梅人工林可持续经营及生物量精确估测提供理论依据。 方法 基于48株杨梅标准木实测数据,在以地径、树高、冠幅为自变量建立独立单株生物量模型基础上,运用非线性误差变量模型法,对浙江仙居县杨梅人工林相容性单株生物量模型进行研究。 结果 拟合出的独立单株生物量模型中,以地径(x1)为自变量的幂函数模型决定系数为最大,叶片生物量(y1)、枝干生物量(y2)、根系生物量(y3)及总生物量(y0)模型分别为y1=0.004x12.795、y2=0.003x13.048、y3=0.002x13.141和y0=0.010x12.995。以地径、树高、冠幅构建的3个相容性单株生物量模型拟合效果均较好,其中又以地径为自变量的模型决定系数和预估精度最大,模型最优,相关参数c0、b0、r1、r2、r3和r4分别为0.084 0、2.162 7、0.780 0、0.779 9、0.224 3和0.204 5。随地径、树高和冠幅增大,叶片、枝干、根系生物量的分配规律基本相似,枝干、根系生物量占总生物量的比例呈上升趋势,叶片生物量则逐渐下降。各组分生物量随杨梅林龄增大从大到小快速演变为枝干、根系、叶片。 结论 在运用杨梅一元相容性单株生物量模型进行估算时,以地径为自变量的幂函数模型决定系数最大,且模型决定系数和预估精度最大。地径是最适合用于估算杨梅生物量的变量。 图1表4参31 Abstract:Objective The purpose is to construct an individual tree biomass model of Myrica rubra, so as to provide a theoretical basis for sustainable management and accurate biomass estimation of M. rubra plantation. Method Based on the data of 48 M. rubra samples and the independent individual tree biomass model established with ground diameter, tree height and crown breadth as independent variables, the compatible individual tree biomass model of M. rubra plantation in Xianju County of Zhejiang Province was studied by using the nonlinear error variable model. Result The power function model with ground diameter (x1) as independent variable had the maximal R2, and the models of leaf biomass (y1), branch biomass (y2), root biomass (y3) and total biomass (y0) were y1=0.004x12.795, y2=0.003x13.048, y3=0.002x13.141 and y0=0.010x12.995 respectively. The model with ground diameter as independent variable had the maximal R2 and accuracy, and the relevant parameters of c0, b0, r1, r2, r3 and r4 were 0.084 0, 2.162 7, 0.780 0, 0.779 9, 0.224 3 and 0.204 5 respectively. The distribution law of leaf, branch and root biomass was basically similar with the increase of ground diameter, tree height and crown width. The proportion of branch and root biomass in the total biomass was increasing, while the leaf biomass was gradually decreasing. With the increase of stand ages, the biomass of each component evolved rapidly to branches, roots, and leaves in descending order. Conclusion When using the individual tree biomass model of M. rubra with unitary compatibility for estimation, the power function model with ground diameter as independent variable has the largest determination coefficient and estimation accuracy. Ground diameter is the most suitable variable for estimating M. rubra biomass. [Ch, 1 fig. 4 tab. ref. 31] -
Key words:
- Myrica rubra /
- ground diameter /
- power function /
- compatible /
- biomass model
-
表 1 不同龄级杨梅人工林的基本情况
Table 1. Basic conditions of M. rubra plantations at different stand ages
龄级 平均地径/
cm平均树高/
m平均冠幅/
m2平均密度/
(株·hm−2)幼苗期 2.0±0.2 0.6±0.1 0.1±0.0 600±30 产前期 7.3±0.8 2.0±0.3 3.2±0.6 525±30 初产期 10.3±1.2 2.7±0.3 12.2±2.2 375±15 盛果期 13.9±1.5 3.5±0.4 20.6±3.2 375±15 说明:数值为平均值±标准差 表 2 杨梅自变量因子与各组分生物量及总生物量相关性
Table 2. Correlation of independent variables and all biomasses
因子 叶生物量 枝干生物量 根系生物量 总生物量 地径 0.927** 0.926** 0.929** 0.933** 树高 0.743** 0.735** 0.720** 0.736** 冠幅 0.899** 0.913** 0.911** 0.914** 说明:**表示在0.01水平(双侧)上显著相关 表 3 各组分生物量及总生物量模型决定系数
Table 3. R2 values of all biomass models
模型 叶生物量 枝干生物量 根系生物量 总生物量 地径 树高 冠幅 地径 树高 冠幅 地径 树高 冠幅 地径 树高 冠幅 指数函数 0.442 0.316 0.539 0.469 0.364 0.581 0.438 0.324 0.562 0.705 0.578 0.723 线性函数 0.690 0.407 0.786 0.693 0.410 0.822 0.674 0.385 0.810 0.697 0.409 0.802 对数函数 0.657 0.380 0.503 0.665 0.385 0.521 0.648 0.362 0.494 0.668 0.384 0.517 多项式函数 0.894 0.628 0.791 0.889 0.818 0.870 0.935 0.624 0.820 0.933 0.639 0.781 幂函数 0.951 0.841 0.864 0.942 0.859 0.885 0.964 0.832 0.884 0.959 0.849 0.822 表 4 各相容性单株生物量模型参数与评价指标值
Table 4. Parameters and evaluation index values of the compatible individual-tree biomass models
自变量 生物量 c0 b0 r1 r2 r3 r4 决定系数 总相对误差 /% 平均相对误差/% 预估精度/% 地径 y1 0.084 0 2.162 7 0.780 0 0.779 9 0.224 3 0.204 5 0.881 8 3.097 8 2.577 8 91.63 y2 0.084 0 2.162 7 0.780 0 0.779 9 0.224 3 0.204 5 0.883 4 1.337 1 0.748 1 91.63 y3 0.084 0 2.162 7 0.780 0 0.779 9 0.224 3 0.204 5 0.912 4 1.351 5 4.185 9 92.03 y0 0.084 0 2.162 7 0.904 2 1.090 2 2.417 6 92.22 树高 y1 0.645 4 3.155 8 1.095 3 1.095 2 0.219 6 0.162 0 0.631 8 4.584 6 1.477 9 84.88 y2 0.645 4 3.155 8 1.095 3 1.095 2 0.219 6 0.162 0 0.636 8 4.584 6 1.411 9 85.50 y3 0.645 4 3.155 8 1.095 3 1.095 2 0.219 6 0.162 0 0.623 7 4.584 6 0.483 4 85.00 y0 0.645 4 3.155 8 0.615 9 4.584 6 2.646 4 83.56 冠幅 y1 0.589 5 1.219 5 0.897 9 0.897 8 0.149 1 0.130 0 0.838 3 1.243 8 0.961 4 90.03 y2 0.589 5 1.219 5 0.897 9 0.897 8 0.149 1 0.130 0 0.808 3 1.775 3 0.948 9 89.51 y3 0.589 5 1.219 5 0.897 9 0.897 8 0.149 1 0.130 0 0.834 8 2.937 0 0.343 4 90.14 y0 0.589 5 1.219 5 0.836 9 1.201 4 2.444 0 89.31 -
[1] 陶玉华. 森林生态系统碳储量研究的意义及国内外研究进展[J]. 现代农业科技, 2012(9): 205 − 212. TAO Yuhua. Research significance of carbon storage of forest ecosystem and research progress at home and abroad [J]. Modern Agric Sci Technol, 2012(9): 205 − 212. [2] 王棣, 佘雕, 张帆, 等. 森林生态系统碳储量研究进展[J]. 西北林学院学报, 2014, 29(2): 85 − 91. WANG Di, SHE Diao, ZHANG Fan, et al. Advances in the researches of carbon storage of forest ecosystems [J]. J Northwest For Univ, 2014, 29(2): 85 − 91. [3] 秦立厚, 张茂震, 钟世红, 等. 森林生物量估算中模型不确定性分析[J]. 生态学报, 2017, 37(23): 7912 − 7919. QIN Lihou, ZHANG Maozhen, ZHONG Shihong, et al. Model uncertainty in forest biomass estimation [J]. Acta Ecol Sin, 2017, 37(23): 7912 − 7919. [4] 符利勇, 雷渊才, 孙伟, 等. 不同林分起源的相容性生物量模型构建[J]. 生态学报, 2014, 34(6): 1461 − 1470. FU Liyong, LEI Yuancai, SUN Wei, et al. Development of compatible biomass models for trees from different stand origin [J]. Acta Ecol Sin, 2014, 34(6): 1461 − 1470. [5] 范文义, 张海玉, 于颖, 等. 3种森林生物量估测模型的比较分析[J]. 植物生态学报, 2011, 35(4): 402 − 410. FAN Wenyi, ZHANG Haiyu, YU Yin, et al. Comparison of three models of forest biomass estimation [J]. Chin J Plant Ecol, 2011, 35(4): 402 − 410. [6] 陈振雄, 贺东北, 肖前辉, 等. 西藏冷杉立木生物量和材积模型研建[J]. 中南林业科技大学报, 2018, 38(1): 16 − 21. CHEN Zhenxiong, HE Dongbei, XIAO Qianhui, et al. Establishment of biomass and tree volume equations for Abies in Tibet [J]. J Central South Univ For Technol, 2018, 38(1): 16 − 21. [7] BASUKI T M, van LAAKE P E, SKIDMORE A K, et al. Allometric equations for estimating the above-ground biomass in tropical lowland dipterocarp forests [J]. For Ecol Manage, 2009, 257(8): 1684 − 1694. [8] 唐守正, 张会儒, 胥辉. 相容性生物量模型的建立及其估计方法研究[J]. 林业科学, 2000, 36(增刊 1): 19 − 27. TANG Shouzheng, ZHANG Huiru, XU Hui. Study on establish and estimate method of compatible biomass model [J]. Sci Silv Sin, 2000, 36(suppl 1): 19 − 27. [9] 董利虎, 张连军, 李凤日. 立木生物量模型的误差结构和可加性[J]. 林业科学, 2015, 51(2): 28 − 36. DONG Lihu, ZHANG Lianjun, LI Fengri. Error structure and additivity of individual tree biomass model [J]. Sci Silv Sin, 2015, 51(2): 28 − 36. [10] 符利勇, 雷渊才, 曾伟生. 几种相容性生物量模型及估计方法的比较[J]. 林业科学, 2014, 50(6): 42 − 54. FU Liyong, LEI Yuancai, ZENG Weisheng. Comparison of several compatible biomass models and estimation approaches [J]. Sci Silv Sin, 2014, 50(6): 42 − 54. [11] 刘秀红, 姜春前, 徐睿, 等. 相容性单木生物量模型估计方法的比较: 以青冈栎为例[J]. 林业科学, 2020, 56(9): 164 − 73. LIU Xiuhong, JIANG Chunqian, XU Rui, et al. Comparison of methods to construct compatible individual tree biomass models: a case study of Cyclobalanopsis glauca [J]. Sci Silv Sin, 2020, 56(9): 164 − 73. [12] 蔡兆炜, 孙玉军, 施鹏程. 基于非线性度量误差的杉木相容性生物量模型[J]. 东北林业大学学报, 2014, 42(9): 28 − 32. CAI Zhaowei, SUN Yujun, SHI Pengcheng. Compatible tree biomass models for Chinese fir plantations based on nonlinear measurement error [J]. J Northeast For Univ, 2014, 42(9): 28 − 32. [13] 孙拥康, 汤景明, 臧颢. 鄂西山区日本落叶松林相容性单株生物量模型研究[J]. 西部林业科学, 2019, 48(5): 125 − 130. SUN Yongkang, TANG Jingming, ZANG Hao. Compatible individual-tree biomass model of Larix kaempferi plantation in western Hubei mountainous area [J]. J West China For Sci, 2019, 48(5): 125 − 130. [14] 梁森苗, 王耀锋, 刘玉学, 等. 我国杨梅主产地土壤养分状况的分析[J]. 果树学报, 2015, 32(4): 658 − 665. LIANG Senmiao, WANG Yaofeng, LIU Yuxue, et al. Present situation of soil nutrients in bayberry orchard of China [J]. J Fruit Sci, 2015, 32(4): 658 − 665. [15] 颜晓捷, 黄坚钦, 邱智敏, 等. 生草栽培对杨梅果园土壤理化性质和果实品质的影响[J]. 浙江农林大学学报, 2011, 28(6): 850 − 854. YAN Xiaojie, HUANG Jianqin, QIU Zhimin, et al. Soil physical and chemical properties and fruit quality with grass cover in a Myrica rubra orchard [J]. J Zhejiang A&F Univ, 2011, 28(6): 850 − 854. [16] 叶柳欣, 张勇, 蒋仲龙, 等. 不同林龄杨梅叶片与土壤的碳、氮、磷生态化学计量特征[J]. 安徽农业大学学报, 2019, 46(3): 454 − 459. YE Liuxin, ZHANG Yong, JIANG Zhonglong, et al. The stoichiometric characteristics of carbon, nitrogen and phosphorus in soil and leaves of different ages of Myrica rubra [J]. J Anhui Agric Univ, 2019, 46(3): 454 − 459. [17] 吴家森, 蒋仲龙, 吕爱华, 等. 不同年龄杨梅各器官氮、磷、钾化学计量特征[J]. 江西农业大学学报, 2019, 41(3): 447 − 453. WU Jiasen, JIANG Zhonglong, LÜ Aihua, et al. The ecological stoichiometry of N, P and K in organs of Myrica rubra of different ages [J]. Acta Agric Univ Jiangxi, 2019, 41(3): 447 − 453. [18] 简盖元, 冯亮明, 王文烂, 等. 森林碳汇价值与农户林业收入增长的分析[J]. 林业经济问题, 2010, 30(4): 304 − 308. JIAN Gaiyuan, FENG Liangming, WANG Wenlan, et al. The analysis of forest carbon sequestration value and peasant household forestry income growth [J]. Issues For Econ, 2010, 30(4): 304 − 308. [19] 曾伟生, 唐守正. 利用度量误差模型方法建立相容性立木生物量方程系统[J]. 林业科学研究, 2010, 23(6): 797 − 802. ZENG Weisheng, TANG Shouzheng. Using measurement error modeling method to establish compatible single-tree biomass equations system [J]. For Res, 2010, 23(6): 797 − 802. [20] 董利虎, 李凤日, 贾炜玮. 东北林区天然白桦相容性生物量模型[J]. 林业科学, 2013, 49(7): 75 − 85. DONG Lihu, LI Fengri, JIA Weiwei. Compatible tree biomass models for natural white birch (Betula platyphylla) in northeast China forest area [J]. Sci Silv Sin, 2013, 49(7): 75 − 85. [21] 唐守正, 郎奎建, 李海奎. 统计和生物数学模型计算( ForStat教程)[M]. 北京: 科学出版社, 2009: 275 − 279. TANG Shouzheng, LANG Kuijian, LI Haikui. Calculation for Statistics and Biomathematics Mode [M]. Beijing: Science Press, 2009: 275 − 279. [22] 格日乐图, 吴志民, 杨校生, 等. 广宁茶秆竹地上生物量分布特征研究[J]. 林业科学研究, 2011, 24(1): 127 − 131. Geriletu, WU Zhimin, YANG Xiaosheng, et al. Study on above-ground biomass allocation characteristics of Pseudosasa amabilis [J]. For Res, 2011, 24(1): 127 − 131. [23] 尹惠妍, 张志伟, 李海奎. 中国主要乔木树种生物量方程[J]. 中南林业科技大学学报, 2019, 39(5): 63 − 69. YIN Huiyan, ZHANG Zhiwei, LI Haikui. Biomass equations of primary arbor tree species in China [J]. J Cent South Univ For Technol, 2019, 39(5): 63 − 69. [24] POUDEL K P, TEMESGEN H. Methods for estimating above ground biomass and its components for Douglas-fir and Lodgepole pine trees [J]. Can J For Res, 2016, 46(1): 77 − 87. [25] 付甜, 朱建华, 肖文发, 等. 8种亚热带森林类型乔木层地上生物量分配模型[J]. 林业科学, 2014, 50(9): 1 − 9. FU Tian, ZHU Jianhua, XIAO Wenfa, et al. Above-ground biomass distribution models for arbor layer of eight subtropical forest types [J]. Sci Silv Sin, 2014, 50(9): 1 − 9. [26] 曹磊, 李海奎. 广东省樟树相容性生物量模型的构建[J]. 森林与环境学报, 2018, 38(4): 458 − 465. CAO Lei, LI Haikui. Establishment and analysis of compatible biomass model for Cinnamomum camphora in Guangdong Province [J]. J For Environ, 2018, 38(4): 458 − 465. [27] 方海涛, 黄雄峰, 周丕考, 等. 3种栽培管理措施对东魁杨梅果实品质的影响[J]. 江西农业学报, 2014, 26(3): 8 − 11. FANG Haitao, HUANG Xiongfeng, ZHOU Pikao, et al. Effects of three cultivation and management measures on fruit quality of Dongkui red bayberry [J]. Acta Agric Jiangxi, 2014, 26(3): 8 − 11. [28] 黄士文, 戴智慧, 倪穗. 大棚内地温和光照强度对荸荠种杨梅果实品质的影响[J]. 中国野生植物资源, 2016, 35(4): 9 − 13. HUANG Shiwen, DAI Zhihui, NI Sui. Effect of ground-temperature and light intensity in greenhouse to fruit quality of Myrica rubra ‘Biqizhong’ [J]. Chin Wild Plant Resour, 2016, 35(4): 9 − 13. [29] 刘恩斌, 施拥军, 李永夫, 等. 基于非空间结构的浙江省毛竹林固碳潜力[J]. 林业科学, 2012, 48(11): 9 − 14. LIU Enbin, SHI Yongjun, LI Yongfu, et al. Carbon sequestration potential of moso bamboo forest in Zhejiang Province based on the non-spatial structure [J]. Sci Silv Sin, 2012, 48(11): 9 − 14. [30] 孙成明, 孙政国, 穆少杰, 等. 基于MODIS的植被指数模型及其在草地生态系统中的应用[J]. 中国农学通报, 2011, 27(22): 84 − 88. SUN Chengming, SUN Zhengguo, MU Shaojie, et al. Vegetation index models based on MODIS and their application in grassland ecosystem [J]. Chin Agric Sci Bull, 2011, 27(22): 84 − 88. [31] 钱逸凡, 伊力塔, 张超, 等. 浙江省中部地区公益林生物量与碳储量[J]. 林业科学, 2013, 49(5): 17 − 23. QIAN Yifan, YI Lita, ZHANG Chao, et al. Biomass and carbon storage of public service forests in the central area of Zhejiang Province [J]. Sci Silv Sin, 2013, 49(5): 17 − 23. -

-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20210272






 下载:
下载:













