-
林木树高是基本测树因子之一,能够反映林木生长状况,是森林资源经营管理和林木生长收获研究所必需。树高生长模型是描述树高生长过程的统计模型,也是林木生长收获模型系统中一个重要的组成部分,同时林分优势木树高的预测为适地适树、森林经营活动和林分生长收获预测提供重要的基础数据[1]。因此,树高生长模型的研究对于建立林分生长模型系统及评价立地质量具有重要意义。模型的建立方法很多,混合效应模型是近代发展起来的新统计方法,混合效应模型由固定效应和随机效应两部分组成,既可以反映总体变化趋势,又可以提供方差、协方差等多种信息来反映个体之间的差异[2]。国外开展了大量树高生长的混合效应模型研究[3-12],国内对混合效应模型的拟合方法也进行了系统的研究[13-15],但是目前国内林业上对混合效应模型的应用基本限于与传统模型拟合效果上的比较,对预测的研究还很少。祖笑锋等[16]基于混合效应模型及经验线性无偏最优预测法(EBLUP)预测美国黄松Pinus ponderosa林分优势木树高生长过程,很好地解释了EBLUP,并且深入地分析了EBLUP的特点。EBLUP最早用于动物育种学中,与地统计学的Kriging,时间序列的卡尔曼滤波及小域估计法的数学原理一致[16]。本研究以福建将乐林场杉木Cunninghamia lanceolata人工林为研究对象,基于30株解析木数据,建立拟合最优的非线性混合效应树高生长模型,研究如何利用EBLUP预测树高生长过程,并通过设置不同的观测次数、观测间隔研究与预测精度之间的关系,并探究提高预测精度的方法。
-
研究区位于福建省将乐县国有林场,26°26′~27°04′N,117°05′~117°40′E。将乐县位于福建省西北部,地处武夷山脉东南部,以中、低山为主,最高峰海拔为1 640.2 m。属亚热带季风气候,具有海洋性和大陆性气候特点,年平均气温为19.8 ℃,年平均降水量为2 027.0 mm。境内气温较高,夏季时间长,冬季较温暖,霜冻较少,生长期长。土壤以红壤为主,并分布有黄红壤,土层深厚,土质较好的一般为沙壤土或轻壤土,水分充足,土壤肥沃。植被以亚热带植物区系为主,植被种类非常丰富。其中人工次生林的乔木主要有杉木、马尾松Pinus massoniana等;灌木主要有粗叶榕Ficus hirta,黄毛楤木Aralia decaisneana,檵木Loropetalum chinensis等;草本主要有乌毛蕨Blechnum orientale,乌蕨Stenoloma chusanum,铁线蕨Adiantum capillus-veneris等。
-
2010-2012年,根据林分不同年龄和密度,以典型抽样原则设置了15块20 m × 30 m标准地。对标准地内的林木进行每木检尺,选取标准木2株·标准地-1,共30株,伐倒并进行树干解析,解析木编号为F01~F30。根据解析木内业表内插法获得各年龄对应的树高值。随机选择20株进行拟合,10株进行预测(表 1)。
表 1 建模数据和检验数据概况
Table 1. Summary statistics of the fitting and calibration data
项目 拟合数据(20) 验证数据(10) 树高/m 年龄/a 树高/m 年龄/a 平均值 14.3 23 15.1 24 最大值 25.0 33 22.3 38 最小值 6.6 6 4.1 7 标准差 5.4 7.7 7.5 12.5 说明:表头括号中为随机选择的株数。 -
选择Richards方程、Weibull方程、Korf方程以及Logistic方程的2种变化形式等5个方程作为基础模型,对树高生长进行模拟(表 2)。运用非线性最小二乘法对5个树高生长方程进行拟合,选出拟合效果最好的模型作为基础模型,构建非线性混合效应模型[17]。
表 2 树高生长方程
Table 2. The equations of height growth
编号 模型 方程 1 Richards $H = {\beta _1}{\left[ {1 - {\text{exp}}\left( {{\beta _2}t} \right)} \right]^{{\beta _3}}}$ 2 Weibull $H = {\beta _1}\left[ {1 - {\text{exp}}\left( {{\beta _2}{t^{{\beta _3}}}} \right)} \right]$ 3 Korf $H = {\beta _1}{\text{exp}}\left( {\frac{{ - {\beta ^2}}}{{{t^{{\beta _3}}}}}} \right)$ 4 Logistic $H = \frac{{{\beta _1}}}{{1 + {\text{exp}}\left( {{\beta ^2} - {\beta _3}t} \right)}}$ 5 Logistic2 $H = \frac{{{\beta _1}}}{{{\text{exp}}\left( {{\beta ^2} + {\beta _3}{\text{lg}}\left( t \right)} \right)}}$ -
非线性混合效应模型主要特点是参数分为固定效应和随机效应,固定效应可以反映研究对象的总体变化规律,随机效应随个体的不同而变化,反映总体中不同个体的变化规律,从而获得较好的拟合效果。笔者主要研究利用EBLUP预测树高生长过程,并探究提高预测精度的方法。因此将样木作为随机效应,建立混合效应模型后,通过选取生长过程与总体平均生长过程差异较大的样木进行预测分析。非线性混合模型的一般表达式为:
$${y_i} = f\left( {{A_i}\beta + {B_i}{b_i},{X_i}} \right) + {e_i}。$$ (1) 式(1)中:β为p×1维的固定效应向量;p为固定参数个数,bi为q×1维的随机效应向量;q为随机参数个数;Ai和Bi为具有相应维度的设计矩阵,其元素通常为0,1或与固定效应和随机效应相关的协方差值;ei为随机误差项向量;f为非线性函数;Xi为年龄;yi为树高。其中随机向量bi:N(0, D),ei:N(1, Ri),并且相互独立;ei和bi协方差矩阵分别为Ri和D,且为ni维和q维的对称矩阵。
构建非线性混合效应模型还要确定以下3种结构:① 混合效应参数。依据PINHEIRO等[18]的研究,将基础模型中参数进行组合作为混合参数进行模拟,选择收敛的模型,通过比较其赤池信息量准则(AIC),贝叶斯信息准则(BIC)以及对数似然函数(Loglik)模型评价指标。AIC,BIC值越小,Loglik值越大,模型拟合效果越好。② 随机效应内的方差协方差矩阵。为了确定随机效应内的方差协方差矩阵,需要解决异方差和自相关性结构。以指数函数(Exp),幂函数(Power)和常数加幂函数(ConstPower)3种结构形式,消除数据间的异方差。表达式为:
$${R_i}\left( {\beta ,{b_i},p} \right) = {\sigma ^2}G_i^{0.5}{I_{ni}}G_i^{0.5};$$ (2) $${\text{VarExp}}\left( {{e_i}} \right) = {\sigma ^2}{\text{exp}}\left( {\beta t} \right);$$ (3) $${\text{VarPower}}\left( {{e_i}} \right) = {\sigma ^2}{t^\beta };$$ (4) $${\text{VarConstPower}}\left( {{e_i}} \right) = {\sigma ^2}\left( {{\beta _1} + {t^{{\beta _2}}}} \right)。$$ (5) 式(2)~式(5)中:σ2为误差方差值,由模型残差方差值给出;Gi为ni×ni维对角矩阵来解释方差异质性,对角元素为相应误差项的标准差;由于本研究数据间不存在自相关性,因此,Ini为ni×ni维的单位矩阵。β,β1,β2为参数,t为年龄[19-22]。从自变量为年龄的3种函数中,根据AIC,BIC,Loglik值以及似然比检验,确定残差方差模型。③ 随机效应间的协方差矩阵。随机效应间的协方差矩阵反映了随机效应之间的变化性。本研究包含3个随机参数,因此,矩阵为3 × 3维的方差协方差矩阵,结构例如下:
$$D = \left[ {\begin{array}{*{20}{l}} u \\ v \\ w \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\sigma _u^2}&{{\sigma _{uv}}}&{{\sigma _{uw}}} \\ {{\sigma _{vu}}}&{\sigma _v^2}&{{\sigma _{vw}}} \\ {{\sigma _{wu}}}&{{\sigma _{wv}}}&{\sigma _w^2} \end{array}} \right]。$$ (6) 式(6)中:σu2,σv2,σw2分别为随机参数u,v,w的方差,σuv=σvu为随机参数u和v的协方差,σuw=σwu为随机参数u和w的协方差,σvw=σwv为随机参数w和v的协方差。
-
推导方法基于多元正态分布理论,以bi=0为基点,用一阶泰勒公式将非线性混合效应模型式(1)近似地表达为:
$${y_i} \approx f\left( {{A_i}\beta ,{X_i}} \right) + {Z_i}{b_i} + {e_i}。$$ (7) 式(7)中:矩阵Zi为q × ni维矩阵,其元素可以通过对混合效应模型式(1)分别求关于随机效应bi的偏导数,随后令所有bi取0即可求出。前文提到bi:N(0, D),ei:N(1, Ri),且相互独立,因此对式(7)求yi的方差矩阵为:
$${\text{Var}}\left( {{y_i}} \right) = {Z_i}DZ_i^T + {R_i}。$$ bi和yi间协方差矩阵为:
$$\begin{gathered} {\text{Cov}}\left( {{b_i},{y_i}} \right) = {\text{Cov}}\left[ {{b_i},f\left( {{A_i}\beta ,{X_i}} \right) + {Z_i}{b_i} + {e_i}} \right] \hfill \\ = {\text{Cov}}\left( {{b_i},{Z_i}{b_i}} \right) = DZ_i^T。 \hfill \\ \end{gathered} $$ bi和yi的联合分布为:
$$\left( {\begin{array}{*{20}{l}} {{b_i}} \\ {{y_i}} \end{array}} \right) \sim {\text{N}}\left[ {\left( {\begin{array}{*{20}{c}} 0 \\ {f\left( {{A_i}\beta ,{X_i}} \right)} \end{array}} \right),\left( {\begin{array}{*{20}{c}} D&{DZ_i^T} \\ {{Z_i}{D^T}}&{{Z_i}DZ_i^T + {R_i}} \end{array}} \right)} \right]。$$ 根据多元正态分布理论,当 ${y_i} = {{\tilde y}_i}$ ( ${{\tilde y}_i}$ 为观测值)时,bi的条件分布数学期望为:
$$E\left( {{b_i}|{y_i} = {{\tilde y}_i}} \right) = E\left( {{b_i}} \right) + DZ_i^T{\left( {{Z_i}DZ_i^T + {R_i}} \right)^{ - 1}}\left[ {{{\tilde y}_i} - f\left( {{A_i}\beta ,{X_i}} \right)} \right]。$$ 对于随机变量取值最优预测值是其数学期望值,所以随机变量bi在yi取观测值时可以用bi的条件分布数学期望表示:
$${{\hat b}_i} = DZ_i^T{\left( {{Z_i}DZ_i^T + {R_i}} \right)^{ - 1}}\left[ {{{\tilde y}_i} - f\left( {{A_i}\beta ,{X_i}} \right)} \right]。$$ 将式中β,D,R,Zi及f(Ai β, Xi)用相应的估计值取代后则:
$${{\hat b}_i} = \hat D\hat Z_i^T{\left( {{{\hat Z}_i}\hat D\hat Z_i^T + {{\hat R}_i}} \right)^{ - 1}}\left[ {{{\tilde y}_i} - f\left( {{A_i}\hat \beta ,{X_i}} \right)} \right]。$$ (8) 式(8)称为经验线性无偏最优预测法(EBLUP)[16]。
设定 ${y_i} = \left( {\begin{array}{*{20}{l}} {{y_{i,1}}} \\ {{y_{i,2}}} \end{array}} \right)$ ,yi, 1为观测值,yi, 2为预测值。则yi, 1和yi, 2的联合分布为:
$${y_i} = \left( {\begin{array}{*{20}{l}} {{y_{i,1}}} \\ {{y_{i,2}}} \end{array}} \right) \sim N\left[ {\left( {\begin{array}{*{20}{c}} {f\left( {{A_i}\beta ,{X_{i,2}}} \right)} \\ {f\left( {{A_i}\beta ,{X_{i,1}}} \right)} \end{array}} \right),\left( {\begin{array}{*{20}{c}} {{W_{22}}}&{{W_{21}}} \\ {{W_{12}}}&{{W_{11}}} \end{array}} \right)} \right]。$$ 其中:W21=Cov(yi, 2, yi, 1)=Zi, 2DZi, 1T+Cov(ei, 1T, ei, 2),W11=Var(yi)=Zi, 1DZTi, 1+Ri, 1,则yi, 2的条件分布数学期望:
$${{\tilde y}_{i,2}} = f\left( {{A_i}\tilde \beta ,{X_{i,2}}} \right) + {{\tilde W}_{21}}\tilde W_{11}^{ - 1}\left[ {{y_{i,1}} - f\left( {{A_i}\tilde \beta ,{X_{i,1}}} \right)} \right]。$$ 将各项参数用相应估计值带入的:
$${{\tilde y}_{i,2}} = f\left( {{A_i}\tilde \beta ,{X_{i,2}}} \right) + {{\hat Z}_{i,2}}\underbrace {\hat D\hat Z_{i,1}^T{{\left( {{{\hat Z}_{i,1}}\hat D\hat Z_{i,1}^T} \right)}^{ - 1}}\left[ {{y_{i,1}} - f\left( {{A_i}\hat \beta ,{X_{i,1}}} \right)} \right]}_{{{\hat b}_i}}。$$ 简化为:
$${{\tilde y}_{i,2}} = f\left( {{A_i}\hat \beta ,{X_{i,2}}} \right) + {{\hat Z}_{i,2}}{{\hat b}_i}。$$ (9) 结合公式(8)和公式(9)即可利用混合效应模型进行EBLUP预测。详细推导过程参考文献[23]。
根据EBLUP预测原理,式(9)中Zi, k可通过求关于随机效应bi的偏导数,求出偏导数后令所有bi取0即可。本模型有3个随机效应,故k取1,2,3。Zi, k的估计值为:
$${{\hat Z}_{i,1}} = 1 - {{\text{e}}^{ - {{\tilde \beta }_2}{t_i}^{{{\tilde \beta }_3}}}};$$ (10) $${{\hat Z}_{i,2}} = {{\hat \beta }_1}{{\text{e}}^{ - {{\tilde \beta }_2}{t_i}^{{{\tilde \beta }_3}}}}{t_i}^{{{\tilde \beta }_3}};$$ (11) $${{\hat Z}_{i,3}} = {{\hat \beta }_1}{{\text{e}}^{ - {{\tilde \beta }_2}{t_i}^{{{\tilde \beta }_3}}}}{{\tilde \beta }_2}{t_i}^{{{\tilde \beta }_3}}{\text{lg}}{t_i}。$$ (12) 列向量 $f\left( {{A_i}\hat \beta ,{X_i}} \right)$ 表达式为:
$$f\left( {{A_i}\hat \beta ,{X_i}} \right) = {{\hat \beta }_1}\left( {1 - {{\text{e}}^{ - {{\tilde \beta }_2}{t_i}^{{{\tilde \beta }_3}}}}} \right)。$$ (13) 式(11)~式(14)中: ${{\hat \beta }_{i,1}},{{\hat \beta }_{i,2}},{{\hat \beta }_{i,3}}$ 为βi, 1,βi, 2,βi, 3的估计值,通过R语言软件得出。随机效应参数的预测值 ${{\hat b}_{i,1}},{{\hat b}_{i,2}},{{\hat b}_{i,3}}$ 根据式(8),利用SAS 9.3的IML过程计算获得。将各参数估计值代入式(9)进行预测。
-
利用R语言软件基于表 1中拟合数据,对表 2中6个树高生长方程进行拟合,拟合结果见表 3。根据决定系数R2越接近于1,均方根差Rmse以及平均绝对残差|E|越接近于0,其拟合效果越好的原则,选取方程1,方程2,方程3作为基础模型。
表 3 各树高生长方程拟合结果
Table 3. Simulant result of height growth
方程 参数 确定系数R2 均方根差(Rmse 平均绝对残差|E| β1 β2 β3 1 45.517 7 0.024 1 1.192 1 0.819 9 2.698 8 0.042 7 2 41.994 9 0.013 2 1.157 9 0.819 9 2.699 1 0.076 2 3 2 647.267 0 8.858 0 0.177 1 0.820 1 2.697 2 0.002 7 4 20.734 9 2.434 6 0.169 2 0.808 3 2.784 4 2.976 8 5 65.986 0 4.821 0 -2.730 0 0.819 9 2.986 0 0.042 1 -
基于基础模型,将单木考虑作为随机效应,利用R语言软件中的nlme函数对模型进行估计,改变随机参数个数比较拟合效果。基于不同随机参数组合的混合模型的拟合效果见表 4。从表中拟合情况可以看出模型2.5的AIC,BIC最小且Loglik值最大,即当模型2以β1,β2和β3同时作为混合效应参数时,模型拟合效果最佳。因此,选择模型2.5(Weibull方程)进一步构建混合效应模型。
表 4 基于不同随机效应参数组合的树高生长模型拟合精度比较
Table 4. Comparison of models' fitting precisions with different combinations of random effects parameters
模型编号 随机效应参数 AIC BIC Loglik 1.1 β1 1 516.717 0 1 537.274 -753.358 4 1.2 β2 1 461.503 0 1 482.060 -725.751 3 1.3 β3 1 600.736 0 1 621.293 -795.368 1 1.4 β1, β3 1 207.652 0 1 236.432 -596.826 0 1.5 β2, β3 1 147.023 0 1 175.803 -566.511 4 2.1 β1 1 516.378 5 1 536.936 -753.189 3 2.2 β2 1 455.967 7 1 476.525 -722.983 8 2.3 β3 1 382.081 0 1 402.638 -686.040 5 2.4 β2, β3 1 158.258 6 1 187.039 -572.129 3 2.5 β1, β2, β3 973.412 2 1 014.527 -476.706 1 3.1 β2 1 513.753 0 1 534.311 -751.876 7 3.2 β3 1 484.579 0 1 505.136 -737.289 6 3.3 β1, β2 1 253.315 0 1 282.096 -619.657 7 3.4 β2, β3 1 241.380 0 1 270.160 -613.690 0 其他情况 不收敛 -
加权残差方差模型的评价指标见表 5。考虑残差加权的3种模型中幂函数的AIC和BIC最小且Loglik值最大,故选它作为模型的残差方差模型。
表 5 各残差方差模型的模拟结果
Table 5. Simulation results for each residual variance model
残差方差模型 AIC BIC Loglik 指数函数 975.447 1 1 020.673 -476.723 5 幂函数 975.070 0 1 020.296 -476.535 0 常数加幂函数 977.447 0 1 026.785 -476.723 5 -
利用R语言软件拟合模型的各参数列于表 6,基于非线性混合效应模型的杉木树高生长方程表达式为:
表 6 模型拟合结果
Table 6. Statistical results of the model fitting
固定效应参数 随机效应参数协方差矩阵 参数 估计值 参数 bi, 1 bi, 2 bi, 3 β1 1.954 00 bi, 1 5.936 4 0.016 6 0.473 7 β2 0.018 96 bi, 2 0.016 6 -0.302 0 -0.251 0 β3 1.631 90 bi, 3 0.473 7 -0.251 0 -0.655 0 $$\begin{gathered} H = 1.954\;0\left( {1 - {{\text{e}}^{ - 0.018\;96{t^{1.6319}}}}} \right); \hfill \\ {b_i} = \left[ {\begin{array}{*{20}{c}} {{u_i}} \\ {{v_i}} \\ {{w_i}} \end{array}} \right] \sim N\left( {0,D} \right){e_i} \sim N\left[ {0,{R_i}} \right]; \hfill \\ R = 0.535\;2G_i^{0.05}{\text{Var}}\left( {{e_i}} \right) = 0.535\;2{t^{ - 0.004\;446}}。 \hfill \\ \end{gathered} $$ (14) -
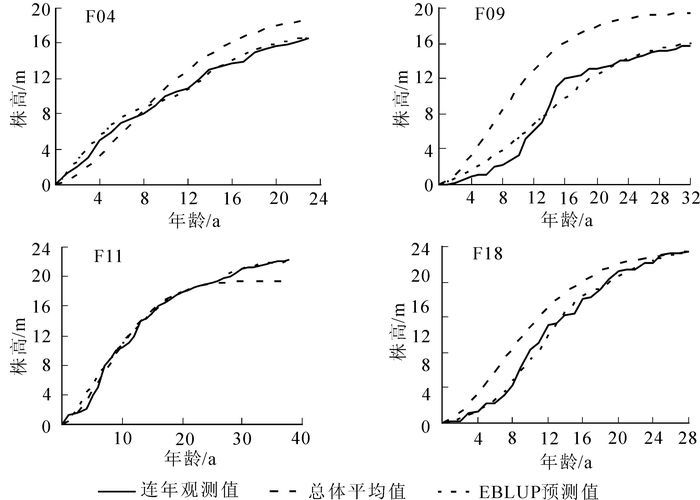
由于EBLUP算法的原因,本研究利用式(9)预测,具体原因参考NI等[23]。从验证数据中选取F04解析木作为预测数据,选3对观测值用于预测bi,结果统计于表 7。表中 ${{\tilde y}_i}$ 为样木在Xi时树高观测值, $f\left( {{A_i}\hat \beta ,{X_i}} \right)$ 通过式(13)计算得出, ${{\tilde Z}_i}$ 通过式(10)~式(12)计算得出, ${{\tilde b}_i}$ 是通过SAS 9.3的IML过程获得。利用表 7的 ${{\tilde b}_i}$ 预测F18样木19~22 a间的树高值,并与观测值比较列于表 8。总体估计值通过式(13)计算得到,预测值通过式(9)计算获得,校正值为预测值减总体估计值的差。可见根据3对观测值获得的对样木进行EBLUP预测树高,能较准确地反映样木生长过程。在验证数据中选择样木生长过程与总体平均生长过程有差异的F04,F09,F11,F18解析木,进行EBLUP预测,将预测生长曲线、解析木树高曲线和总体平均生长过程进行比较(图 1)。通过图 1可看出:当单木生长过程和总体估计值差距较大时,基于Weibull混合效应模型的EBLUP预测能充分地预测单木生长过程。本研究依据EBLUP预测的算法,利用样木的3组观测值,基于混合效应模型使每个样木获得对应的随机效应参数,进而充分地预测样木的生长过程。
表 7 预测的向量和矩阵
Table 7. The matrices and vectors used for prediction
${{\tilde y}_i}/{\text{m}}$ ${X_i}/{\text{a}}$ $f\left( {{A_i}\hat \beta ,{X_i}} \right)/{\text{m}}$ ${{\hat Z}_{i,1}}$ ${{\hat Z}_{i,2}}$ ${{\hat Z}_{i,3}}$ ${{\hat b}_i}$ 16.60 23 18.713 9 0.957 7 137.837 1 8.196 0 -2.412 3 15.00 18 17.195 6 0.880 0 262.154 1 14.369 5 -0.016 4 12.00 13 13.923 5 0.712 6 369.254 3 17.961 2 0.312 6 表 8 F18样木树高观测值、总体估计值、EBLUP预测值比较
Table 8. Comparison of observations of height, population mean, and EBLUP predicted for F18
年龄/a 树高观测值/m 总体估计值/m EBLUP预测值 校正值 22 16.28 18.509 2 16.533 9 -1.975 3 21 15.96 18.261 8 16.312 6 -1.949 2 20 15.64 17.965 1 16.0342 -1.930 9 19 15.32 17.612 1 15.689 3 -1.922 8 -
在进行单木树高生长预测时发现,观测值的选择方式对预测精度高低有较大的影响,因此本研究通过设置不同的观测值间隔、观测值选取次数以及预测时长,比较预测结果的精度高低。评价预测精度的指标为均方误差(EMS):
$${E_{{\text{MS}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} 。$$ 以解析木F04,F18,F15和F11为例(由于这几株样木生长过程与总体平均生长过程差距较大,通过不同处理方式能较明显反应预测精度的提高),通过不同的选择观测值方式来研究对EMS的影响,其中观测间隔指每隔多少年对树高进行一次观测。本研究分别选取间隔1,3,5 a;观测次数是指观测多少个树高值,由于本研究基于具有3个随机效应参数的混合模型,预测随机效应参数至少需要3对观测值,故分别选取3,6,9次观测次数;相应地,因为每3对观测值会求得1组随机效应参数,故观测次数为6,9次时,需要分别取2,3组数据,分别按照1/2,1/3将解析木数据分段,年龄向上取整,每年龄段从最大值开始向下取观测值。以样木F15(35年生)为例,观测间隔5 a观测3次时,使用的是35,30,25年生的树高观测值;观测间隔为3 a观测6次时,分别使用35,32,29年生以及18,15,12年生这2组共6个树高观测值;观测间隔为1 a观测9次时,分别使用35,34,33年生,24,23,22年生以及12,11,10年生这3组共9个树高观测值。由于F04,F18年龄较小,故没有进行间隔5 a 9次的观测。以树高观测值为基础,根据式(8)预测bi值,再对树高逐年预测最后求总均方误差。结果列于表 9。
表 9 验证数据统计分析
Table 9. The statistical analysis of data verification
观测间隔/a 观测次数/次 均方误差 F04(23年生) F18(28年生) F15(35年生) F11(38年生) 1 3 5.546 0 4.178 7 12.396 0 22.533 3 3 3 2.866 1 1.092 4 3.388 9 2.310 8 5 3 2.746 0 0.391 7 2.704 3 0.941 7 1 6 5.218 6 3.982 9 5.238 3 3.607 2 3 6 0.332 1 0.2145 2.212 0 0E925 9 5 6 0.271 6 0.195 6 0.284 0 0E707 1 1 9 4.256 1 2.401 7 2.631 7 1E020 8 3 9 0.1670 0.189 4 0.200 3 0.379 7 5 9 0.094 6 0E247 0 观测次数相同时,随着观测间隔的增大,均方误差降低。观测次数均为3,观测间隔取1,3,5 a,各解析木的均方误差随着观测间隔的增大而明显降低。观测间隔相同时,随着观测次数的增加,均方误差降低。观测间隔均为3 a时,随着观测次数从3次增加到9次,各组的均方误差均相应降低,观测间隔为1或5 a按同样方式比较,也可以得出相同的结论。以F15为例,观测间隔均为1 a时,随着观测次数从3次增加到9次,均方误差从12.396 0降低到2.631 7。
从图 2中可以看出:“1 a 3次”在其观测值28,27,26年生附近均方误差较低,远离观测值时,均方误差开始变大。同样,“3 a 3次”在远离20年生时均方误差开始变大,而“5 a 3次”的观测值为28,23,18年生,故在图 2中均方误差较低。所以在EBLUP预测时,随着预测远离用来预测bi的观测值,均方误差逐渐变大。
-
本研究选用5个生长方程,选取3个拟合效果较好的方程作为基础模型,进一步改变不同的随机效应组合,最终以式(2)为基础的Weibull方程中,3个参数都作为混合模型的模型精度最高,拟合效果最好。通过EBLUP预测表明:本研究建立的非线性混合效应模型在考虑样木随机效应时,预测效果明显优于固定模型,能更好地反映树高生长过程。将随机效应考虑到样木水平,就相当于为每株样木建立树高生长模型,可以充分预测样木的生长过程,能够为将乐林场的杉木林经营决策提供一定的依据。进行预测时,观测次数相同,增加观测间隔能够降低预测误差,提高预测精度。由于增加观测值间年龄间隔,可以更充分提供树高生长过程信息,因此可以显著降低预测误差。观测次数不同,预测精度变化较大。观测间隔相同时,增加观测次数,预测精度会提高。因此在预测杉木树高生长过程时,要根据其年龄选择适当的观测间隔和观测次数。EBLUP可以充分利用观测值所涵盖的生长过程信息降低预测误差,随着预测远离用来预测bi的观测值,均方误差逐渐变大。
通过本次研究得到的数据不能明确观测间隔和观测次数对预测准确度影响,有关研究还需要进一步进行。
Based on mixed-effects model and empirical best linear unbiased predictor predicting growth profile of height for Chinese fir
-
摘要: 基于福建省将乐县国有林场15块标准地的30株杉木Cunninghamia lanceolata标准木的解析数据,首先对5个生长方程运用非线性最小二乘法进行拟合,选出拟合效果最好的模型作为基础模型,利用解析木数据构建非线性混合效应树高生长模型。以单株树木作为随机效应,通过变换混合效应参数个数,利用R软件选择赤池信息准则(AIC),贝叶斯信息准则(BIC)最小,对数似然函数(Loglik)值最大的混合效应模型作为最优模型,基于混合效应模型研究经验线性无偏最优预测法(EBLUP)预测树高生长过程的特点。结果表明:Weibull方程中,β1,β2和β3等3个参数都作为混合效应参数的模型模拟精度最高。观测次数相同时,延长观测间隔能够降低预测误差,提高预测精度;观测间隔相同时,增加观测次数,预测精度会提高。
-
关键词:
- 森林测计学 /
- 树高生长模型 /
- 混合效应模型 /
- 经验线性无偏最优预测法 /
- 杉木
Abstract: Based on the data of 30 sample trees from 15 permanent plots of Chinese fir in the national forest farm of Jiangle, at first we study the best function as the base model with the least square method among five growth profile equations. The nonlinear mixed model was constructed based on the base model and modeling data. We use the R for model fitting. Select the mixed model with the minimum value of AIC, BIC and the maximum value of Loglik as the best model by changing the number of mixed parameters in fitting progress. Using mixed model to predict growth profile of height and studying the characteristics of Empirical Best Linear Unbiased Predictor (EBLUP). Fitting results showed the simulation's precision of Weibull's including three random effect parameters(β1, β2 and β3) was maximal. In the analysis of prediction, prediction accuracy decreased as age interval of observations extended with the same number of previous observations. MSE decreased as the number of previous observations increased. EBLUP prediction could fully predict individual growth process, given that there were multiple previous observations with long-enough age intervals.-
Key words:
- forest measuration /
- height growth model /
- mixed-effects model /
- EBLUP /
- Chinese fir
-
表 1 建模数据和检验数据概况
Table 1. Summary statistics of the fitting and calibration data
项目 拟合数据(20) 验证数据(10) 树高/m 年龄/a 树高/m 年龄/a 平均值 14.3 23 15.1 24 最大值 25.0 33 22.3 38 最小值 6.6 6 4.1 7 标准差 5.4 7.7 7.5 12.5 说明:表头括号中为随机选择的株数。 表 2 树高生长方程
Table 2. The equations of height growth
编号 模型 方程 1 Richards $H = {\beta _1}{\left[ {1 - {\text{exp}}\left( {{\beta _2}t} \right)} \right]^{{\beta _3}}}$ 2 Weibull $H = {\beta _1}\left[ {1 - {\text{exp}}\left( {{\beta _2}{t^{{\beta _3}}}} \right)} \right]$ 3 Korf $H = {\beta _1}{\text{exp}}\left( {\frac{{ - {\beta ^2}}}{{{t^{{\beta _3}}}}}} \right)$ 4 Logistic $H = \frac{{{\beta _1}}}{{1 + {\text{exp}}\left( {{\beta ^2} - {\beta _3}t} \right)}}$ 5 Logistic2 $H = \frac{{{\beta _1}}}{{{\text{exp}}\left( {{\beta ^2} + {\beta _3}{\text{lg}}\left( t \right)} \right)}}$ 表 3 各树高生长方程拟合结果
Table 3. Simulant result of height growth
方程 参数 确定系数R2 均方根差(Rmse 平均绝对残差|E| β1 β2 β3 1 45.517 7 0.024 1 1.192 1 0.819 9 2.698 8 0.042 7 2 41.994 9 0.013 2 1.157 9 0.819 9 2.699 1 0.076 2 3 2 647.267 0 8.858 0 0.177 1 0.820 1 2.697 2 0.002 7 4 20.734 9 2.434 6 0.169 2 0.808 3 2.784 4 2.976 8 5 65.986 0 4.821 0 -2.730 0 0.819 9 2.986 0 0.042 1 表 4 基于不同随机效应参数组合的树高生长模型拟合精度比较
Table 4. Comparison of models' fitting precisions with different combinations of random effects parameters
模型编号 随机效应参数 AIC BIC Loglik 1.1 β1 1 516.717 0 1 537.274 -753.358 4 1.2 β2 1 461.503 0 1 482.060 -725.751 3 1.3 β3 1 600.736 0 1 621.293 -795.368 1 1.4 β1, β3 1 207.652 0 1 236.432 -596.826 0 1.5 β2, β3 1 147.023 0 1 175.803 -566.511 4 2.1 β1 1 516.378 5 1 536.936 -753.189 3 2.2 β2 1 455.967 7 1 476.525 -722.983 8 2.3 β3 1 382.081 0 1 402.638 -686.040 5 2.4 β2, β3 1 158.258 6 1 187.039 -572.129 3 2.5 β1, β2, β3 973.412 2 1 014.527 -476.706 1 3.1 β2 1 513.753 0 1 534.311 -751.876 7 3.2 β3 1 484.579 0 1 505.136 -737.289 6 3.3 β1, β2 1 253.315 0 1 282.096 -619.657 7 3.4 β2, β3 1 241.380 0 1 270.160 -613.690 0 其他情况 不收敛 表 5 各残差方差模型的模拟结果
Table 5. Simulation results for each residual variance model
残差方差模型 AIC BIC Loglik 指数函数 975.447 1 1 020.673 -476.723 5 幂函数 975.070 0 1 020.296 -476.535 0 常数加幂函数 977.447 0 1 026.785 -476.723 5 表 6 模型拟合结果
Table 6. Statistical results of the model fitting
固定效应参数 随机效应参数协方差矩阵 参数 估计值 参数 bi, 1 bi, 2 bi, 3 β1 1.954 00 bi, 1 5.936 4 0.016 6 0.473 7 β2 0.018 96 bi, 2 0.016 6 -0.302 0 -0.251 0 β3 1.631 90 bi, 3 0.473 7 -0.251 0 -0.655 0 表 7 预测的向量和矩阵
Table 7. The matrices and vectors used for prediction
${{\tilde y}_i}/{\text{m}}$ ${X_i}/{\text{a}}$ $f\left( {{A_i}\hat \beta ,{X_i}} \right)/{\text{m}}$ ${{\hat Z}_{i,1}}$ ${{\hat Z}_{i,2}}$ ${{\hat Z}_{i,3}}$ ${{\hat b}_i}$ 16.60 23 18.713 9 0.957 7 137.837 1 8.196 0 -2.412 3 15.00 18 17.195 6 0.880 0 262.154 1 14.369 5 -0.016 4 12.00 13 13.923 5 0.712 6 369.254 3 17.961 2 0.312 6 表 8 F18样木树高观测值、总体估计值、EBLUP预测值比较
Table 8. Comparison of observations of height, population mean, and EBLUP predicted for F18
年龄/a 树高观测值/m 总体估计值/m EBLUP预测值 校正值 22 16.28 18.509 2 16.533 9 -1.975 3 21 15.96 18.261 8 16.312 6 -1.949 2 20 15.64 17.965 1 16.0342 -1.930 9 19 15.32 17.612 1 15.689 3 -1.922 8 表 9 验证数据统计分析
Table 9. The statistical analysis of data verification
观测间隔/a 观测次数/次 均方误差 F04(23年生) F18(28年生) F15(35年生) F11(38年生) 1 3 5.546 0 4.178 7 12.396 0 22.533 3 3 3 2.866 1 1.092 4 3.388 9 2.310 8 5 3 2.746 0 0.391 7 2.704 3 0.941 7 1 6 5.218 6 3.982 9 5.238 3 3.607 2 3 6 0.332 1 0.2145 2.212 0 0E925 9 5 6 0.271 6 0.195 6 0.284 0 0E707 1 1 9 4.256 1 2.401 7 2.631 7 1E020 8 3 9 0.1670 0.189 4 0.200 3 0.379 7 5 9 0.094 6 0E247 0 -
[1] 孟宪宇.测树学[M].北京:中国林业出版社, 2006. [2] LITTLE R C, MILLIKEN G A, STROUP W W, et al. SAS System for Mixed Models [M]. Cary North Carolina: SAS Institute Inc., 1996. [3] NANOS N, CALAMA R, MONTERO G, et al. Geostatistical prediction of height/diameter models [J]. For Ecol Manage, 2004, 195(1/2): 221-235. [4] CALAMA R, MONTERO G. Interregional nonlinear height-diameter model with random coefficients for stone pine in Spain [J]. Can J For Res, 2004, 34(1): 150-163. [5] MEHTÄTALO L. A longitudinal height-diameter model for Norway spruce in Finland [J]. Can J For Res, 2004, 34(1): 131-140. [6] BUDHATHOKI C B, LYNCH T B, GULDIN J M. Individual tree growth models for natural even-aged shortleaf pine[C]//CONNER K F. Proceedings of the 13th Biennial Southern Silvicultural Conference. Asheville, NC: U.S. Department of Agriculture, Forest Service, Southern Research Station, 2006: 359-361. [7] CASTEDO D F, DIEGUEZARANDA U, BARRIO A M, et al. A generalized height-diameter model including random components for radiata pine plantations in northwestern Spain [J]. For Ecol Manage, 2006, 229(1/3): 202-213. [8] LYNCH T B, HOLLEY A G, STEVENSON D J. A random-parameter height-dbh model for cherrybark oak [J]. South J Appl For, 2005, 29(1): 22-26. [9] LAPPI J, BAILEY R L. A height prediction model with random stand and tree parameters: an alternative to traditional site index methods [J]. For Sci, 1988, 34(4): 907-927. [10] HALL D B, BAILEY R L. Modeling and prediction of forest growth variables based on multilevel nonlinear mixed models [J]. For Sci, 2001, 47(3): 311-321. [11] FANG Z, BAILEY R L. Nonlinear mixed effects modeling for slash pine dominant height growth following intensive silvicultural treatments [J]. For Sci, 2001, 47(3): 287-300. [12] CALEGARIO N, DANIELS R F, MAESTRI R, et al. Modeling dominant height growth based on nonlinear mixed-effects model: a clonal Eucalyptus plantation case study [J]. For Ecol Manage, 2005, 204(1): 11-21. [13] TANG Shenglan, MENG Fanrui, BOURQUE C P A. Analyzing parameters of growth and yield models for Chinese fir provenances with a linear mixed model approach [J]. Silv Genet, 2001, 50(3/4): 140-145. [14] 李永慈, 唐守正.用Mixed和Nlmixed过程建立混合生长模型[J].林业科学研究, 2014, 17(3):279-283. LI Yongci, TANG Shouzheng. Establishment of tree height growth model based on Mixed and Nlmixed of SAS [J]. For Res, 2004, 17(3): 279-283. [15] 李春明, 张会儒.利用非线性混合模型模拟杉木林优势木平均高[J].林业科学, 2010, 46(3):89-95. LI Chunming, ZHANG Huiru. Modeling dominant height for Chinese fir plantation using a nonlinear mixed-effects modeling approach [J]. Sci Silv Sin, 2010, 46(3): 89-95. [16] 祖笑锋, 倪成才, NIGH G, 等.基于混合效应模型及EBLUP预测美国黄松林分优势木树高生长过程[J].林业科学, 2015, 51(3):25-33. ZU Xiaofeng, NI Chengcai, NIGH G, et al. Based on mixed-effects model and empirical best linear unbiased predictor to predict growth profile of dominant height [J]. Sci Silv Sin, 2015, 51(3): 25-33. [17] 董云飞, 孙玉军, 许昊, 等.基于非线性混合模型的杉木标准树高曲线[J].东北林业大学学报, 2014, 42(11):72-76, 81. DONG Yunfei, SUN Yujun, XU Hao, et al. Generalized height-diameter model for Chinese fir based on nonlinear mixed effects model [J]. J North For Univ, 2014, 42(11): 72-76, 81. [18] PINHEIRO J C, BALES D M. Mixed-Effects Models in S and S-PLUS [M]. New York: Springer Verlag, 2000. [19] 董灵波, 刘兆刚, 李凤日, 等.基于线性混合模型的红松人工林一级枝条大小预测模拟[J].应用生态学报, 2013, 24(9):2447-2456. DONG Lingbo, LIU Zhaogang, LI Fengri, et al. Primary branch size of Pinus koraiensis plantation: a prediction based on linear mixed effect model [J]. Chin J Appl Ecol, 2013, 24(9): 2447-2456. [20] 姜立春, 李凤日, 张锐.基于线性混合模型的落叶松枝条基径模型[J].林业科学研究, 2012, 25(4):464-469. JIANG Lichun, LI Fengri, ZHANG Rui. Modeling branch diameter with linear mixed effects for Dahurian larch [J]. For Res, 2012, 25(4): 464-469. [21] 姜立春, 蒋雨航.利用混合模型模拟树冠特征对兴安落叶松树干干形的影响[J].北京林业大学学报, 2014, 36(2):10-14. JIANG Lichun, JIANG Yuhang. Modeling effects of crown characteristics on stem taper of Dahurian larch using mixed model [J]. J Beijing For Univ, 2014, 36(2): 10-14. [22] 曾伟生, 唐守正.非线性模型对数回归的偏差校正及与加权回归的对比分析[J].林业科学研究, 2011, 24(2):137-143. ZENG Weisheng, TANG Shouzheng. Bias correction in logarithmic regression and comparison with weighted regression for non-linear models [J]. For Res, 2011, 24(2): 137-143. [23] NI Chengcai, NIGH G D. An analysis and comparison of predictors of random parameters demonstrated on planted loblolly pine diameter growth prediction [J]. Forestry, 2011, 85(2): 271-280. -

-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.2017.05.003







 下载:
下载: