Construction of diversity index of tree species composition

林分树种组成多样性指数构建既要遵循生物多样性表征的基本规律和要求，又要充分体现林分树种组成的具体特征和经营管理要求。满足树种丰富度越大，树种分布越均匀，指数值就越高这一基本思想。

树种组成多样性指数的构建首先应满足生物多样性意义，指数值应分别与树种丰富度、分布均匀度呈相应的正向等比关系。其次，应以科学合理的方式结合丰富度、均匀度等多方面信息。最后构建的指数值体现相应的树种组成特征，反映树种总数、树种密度以及树种蓄积(生物量)比例和分布等多方面的内在相关信息。

构建指数选用指标时应兼顾科学性和可操作性2条重要原则^[10]。科学性主要从指标的构建方法考虑，涉及构建的指标参数应当准确客观，具有指征性、代表性和可比性。参数之间应相互补充、相对独立，尽可能全面而不重复地反映树种组成特征。可操作性体现在计算指标的原始数据要容易收集，指标计算方法不宜太复杂，要容易被理解接受并易于推广使用等。

基于树种组成多样性指数构建的基本理论和要求，对体现树种丰富度的信息与各树种均匀度的信息进行分解使其相对独立，并通过和式进行综合。用树种数体现树种丰富度的信息，用现实林分各个树种的实际株数、蓄积比例与理想林分中完全均匀分布时的树种株数、蓄积所占比例值(1/s，s为树种数)进行较差，并赋予树种株数均匀度、蓄积均匀度相同的权重关系，用平方消除正负值偏差，以体现各树种均匀度的信息，并使之与丰富度信息之间不产生交互和干扰作用。构建的林分树种组成多样性指数(I_SCD)计算模型为：

式(1)中：I_SCD为树种组成多样性指数；s为树种数；v为森林总蓄积量；v_i为森林中树种i的蓄积量；n为森林总株数；n_i为森林中树种i的株数。

I_SCD与树种数、树种株数和树种蓄积比例分布均匀性呈正相关。作为正向指标，I_SCD直接体现林分树种组成多样性的特征，并具有以下意义：①I_SCD表达了林分中树种数这一重要特征。绝对纯林时，树种数s为1，I_SCD为1。非绝对纯林时，树种数s≥2，I_SCD为(s−1，s]，林分的丰富度或树种数可由I_SCD向上取整得到，即可以根据数值所处范围直接确定树种数。当林分中树种数相等时，树种混交程度越高，各树种的株树、蓄积分布越均匀，其比例越接近于1/s，则I_SCD越大；当林分中所有树种在株数和蓄积2个方面都呈均匀分布时，I_SCD达到最大值s。②I_SCD表达了林分中各树种的株数、蓄积比例及分布均匀性，体现出混交程度。林分树种均匀度、混交度由I_SCD值的小数部分体现。当林分中树种间均匀度、混交度越小，I_SCD值的小数部分就越小；反之就越大。小数部分与数值1的差值体现在一定树种数下，实际林分与分布最均匀、混交度最高时的理想林分之间的差异程度。由于同时考虑了不同树种的株数占比和蓄积占比，I_SCD更能全面反映树种的分布及混交情况。

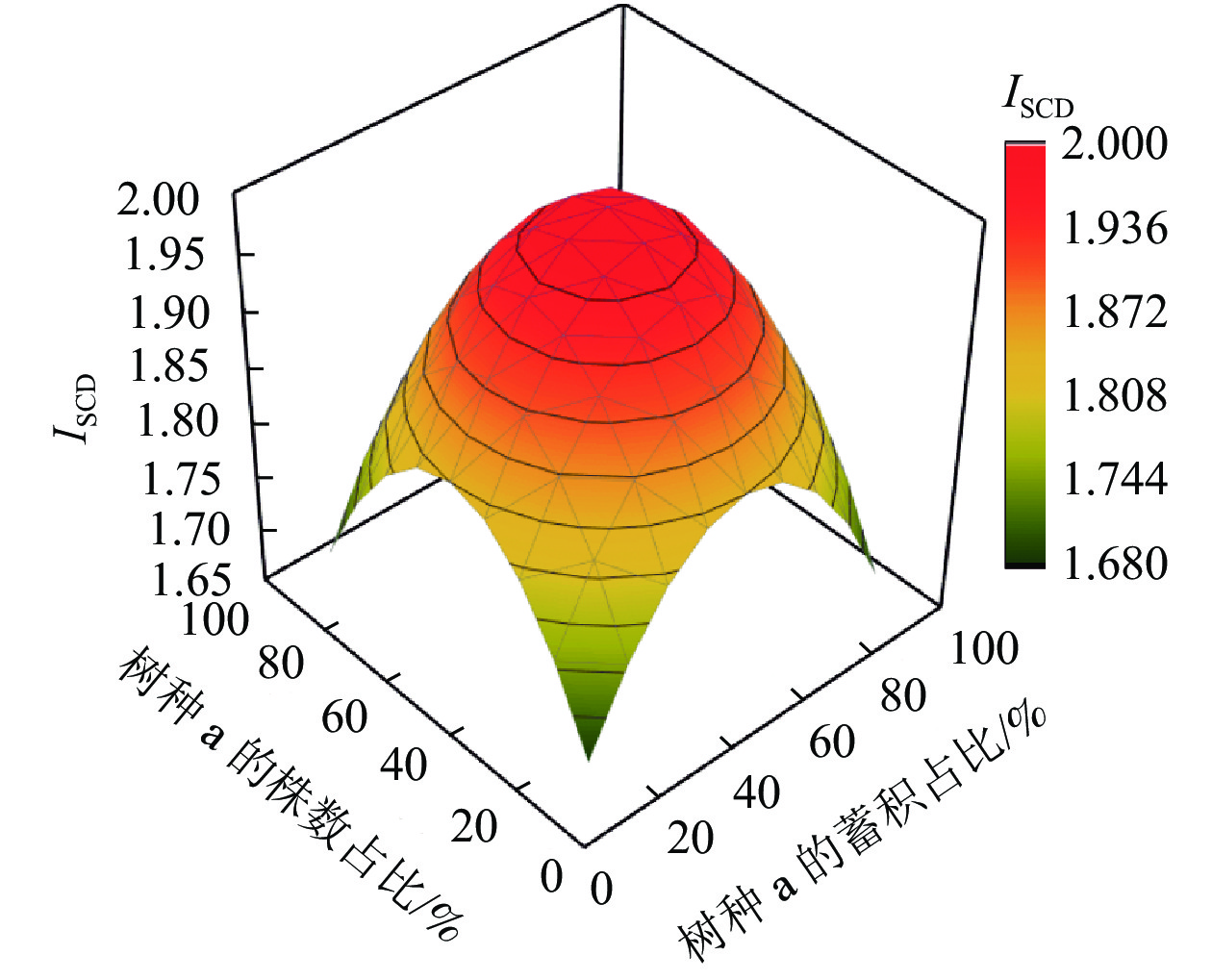
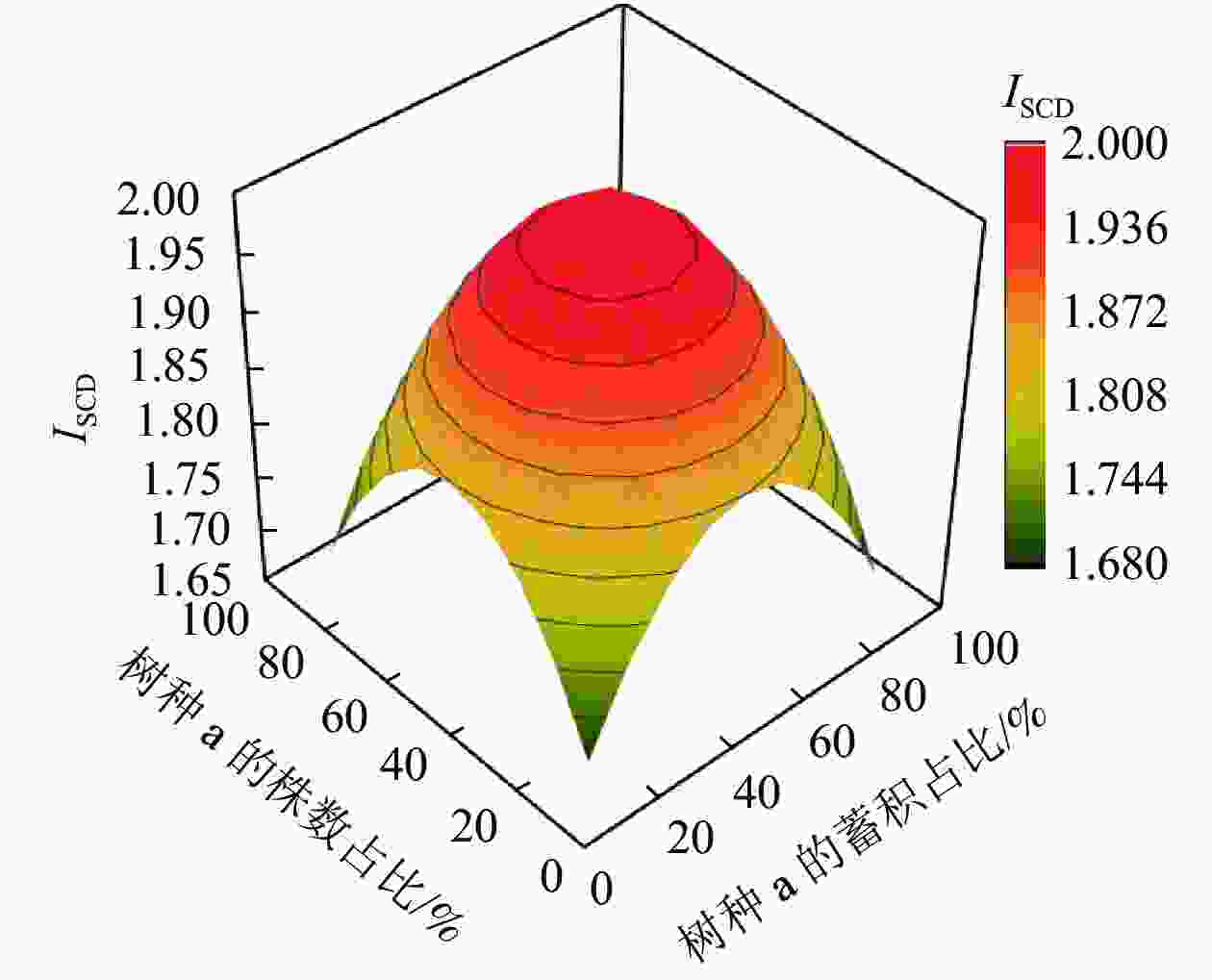
从图1可以看出：当2个树种的株数、蓄积比例分布越不均匀，即某个树种的株数、蓄积占比越接近100%，另一个树种的株数、蓄积占比越接近0时，I_SCD就越小，其值就越接近于s−1；当2个树种的株数、蓄积分布越平均，即占比各自越接近50%时，树种结构多样性指数就越趋近最大值2。

Figure 1.  Trend of diversity index of tree species composition (I_SCD) for two species

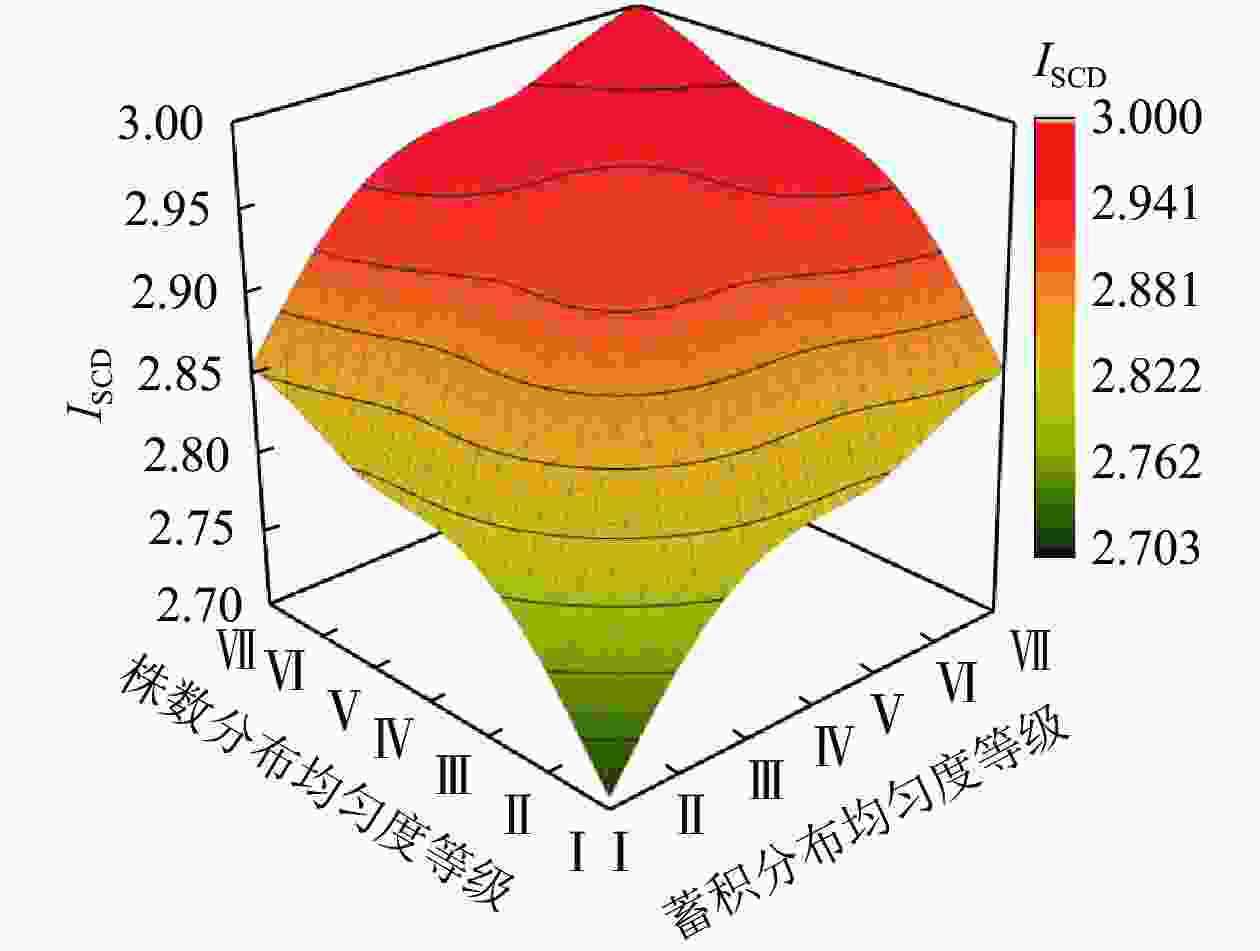
当树种数大于2个时，将各树种的株数和蓄积比例按照其分布均匀程度，进行相应的等级(状态)划分，并以此作为x轴、y轴和z轴数据。设当树种数为3个时，对树种a、b、c存在的株数(或蓄积)分布等级按“3等份”进行划分，并根据Simpson均匀度指数进行分级，株数(或蓄积)分布等级见表1。其中，均匀度等级越大，表明株数(或蓄积)分布的均匀程度越高，Ⅶ为最理想的完全均匀状态。根据表1，对树种的均匀性分布类型组合进行汇总，得到表2。对现实林分中不同均匀度等级之间还存在的连续过渡类型，拟合I_SCD变化趋势曲面图(图2)表明：森林中各树种的株数与蓄积的分布均匀度等级越高，I_SCD越大，越接近最大值3。与树种数为2个时的规律一致，株数和蓄积分布不均都会导致最终的指数值远小于最大值，I_SCD越接近于s−1。

Figure 2.  Trend of diversity index of tree species composition (I_SCD) for three species

对树种数10个以内的I_SCD的变化规律，可以采用“十分法”的分级方法进行均匀度等级划分，即将各树种的株数或蓄积比例的范围划分为10个等份，每变化10%作为一级进行组合。对树种数处于[1，10]的森林，计算其各自不同分布情况下的I_SCD值(表3)。

当森林具有a、b 2个树种时，“十分法”下2个树种株数(或蓄积)的比例可以分为9∶1、8∶2、7∶3、6∶4、5∶5这5种中任意一种，即树种组成形式^[6]数为5。此外，每种类型还需考虑蓄积(或株数)比例，则又各自有5种可能性，故理论上所有可能的树种混交组合形式应为25种。但由于I_SCD赋予树种株数均匀度、蓄积均匀度相同的权重关系，且在考量株数、蓄积均匀度时都是基于树种占比与1/s较差取平方的计算方式，故a树种株数占比为x、蓄积占比为y的森林与株数占比为y、蓄积占比为x的森林拥有相同的I_SCD指数值，可认为两者属于同一均匀度分布水平，可进行合并。故25个类型又最终归并为15个，即树种组成类型数为15。

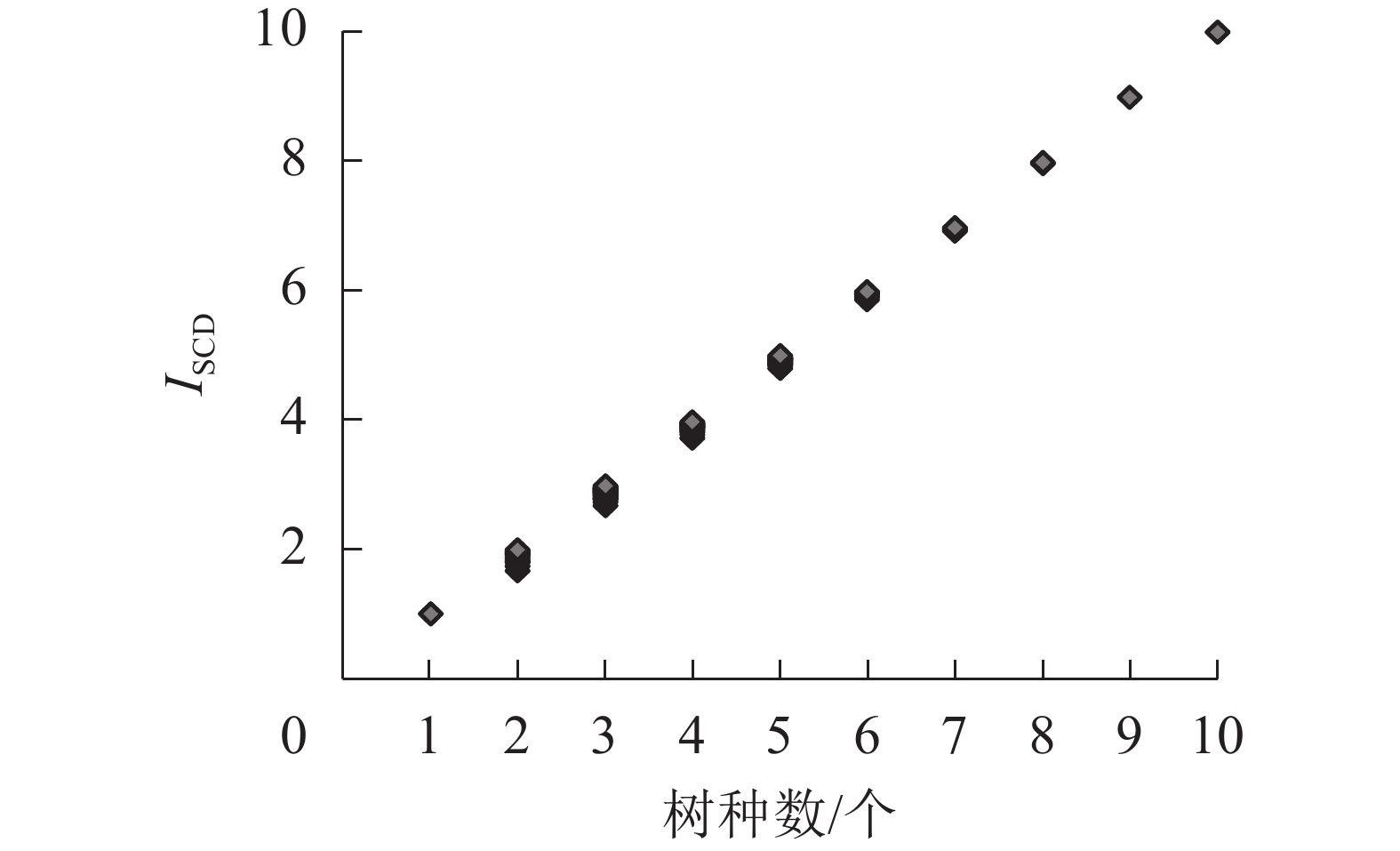
由图3可见：142个树种混交组合中，I_SCD随树种数增加呈线性增长趋势，且不同树种数之间I_SCD互不重叠。

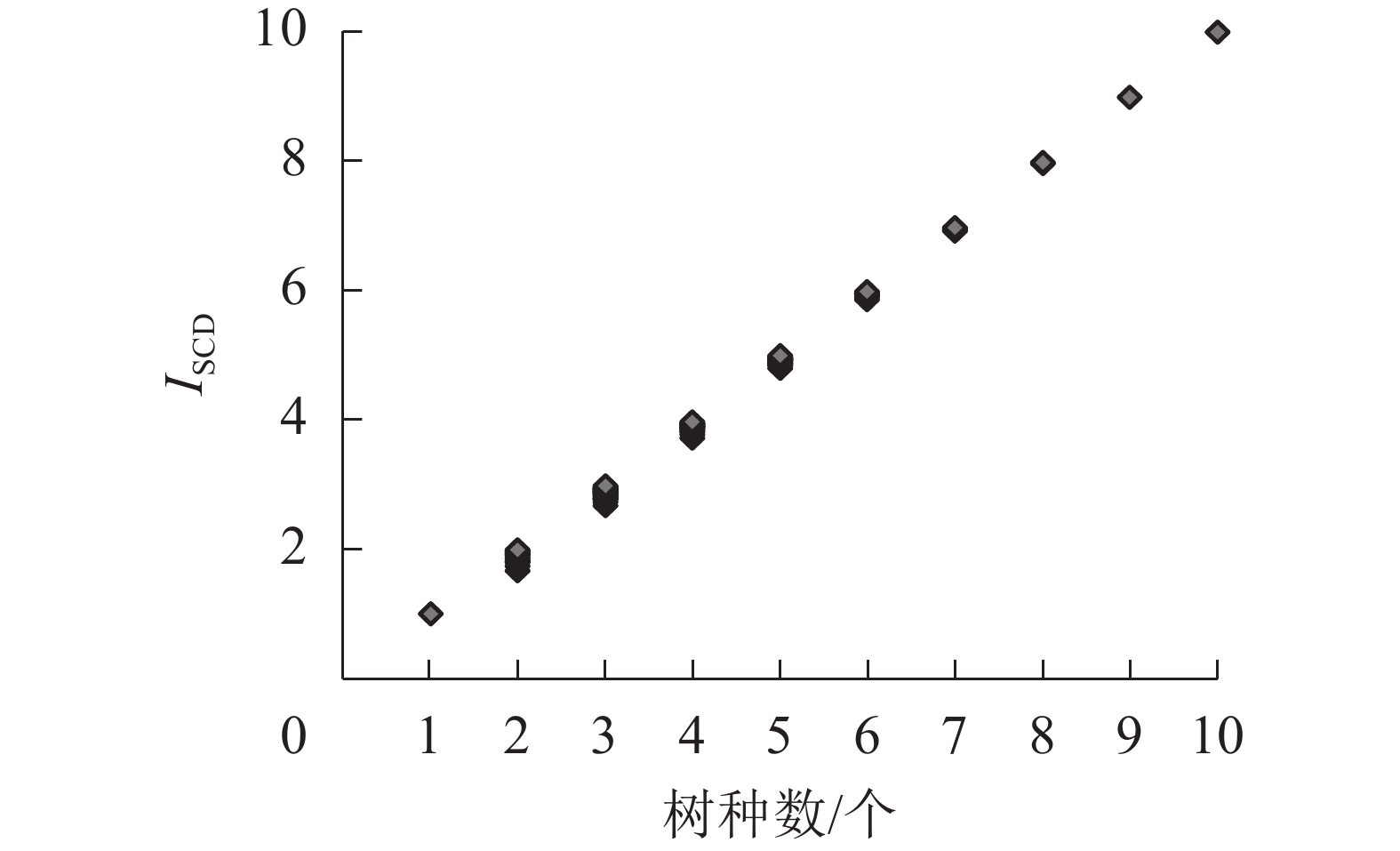
Figure 3.  Relationship between diversity index of tree species composition (I_SCD) and the number of tree species

综上所述，I_SCD随树种数增加呈明显增大趋势。当树种数不变时，I_SCD能随树种株数及蓄积(生物量)比例和分布的均匀度、混交度变化而有相应的同向变化。同理，对树种数10个以上的I_SCD值，经推论也有相同的规律和特性。

以浙江省2009年森林资源连续清查数据中322个针阔混交林样地为材料，计算分析I_SCD模型的实际应用情况，并比较I_SCD与其他多样性指数在反映林分树种组成中树种丰富度、均匀度及多样性等方面的实用表现。

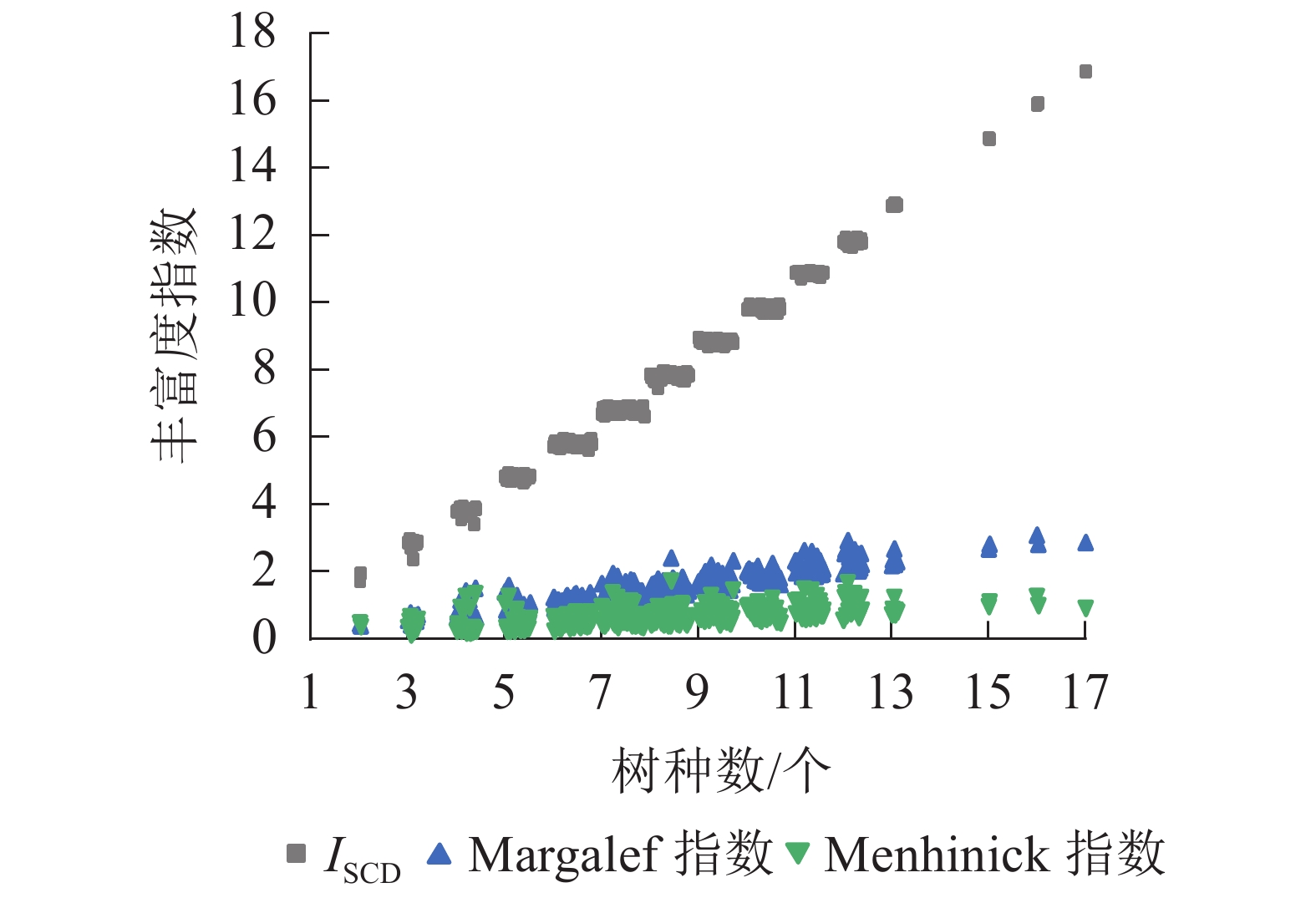
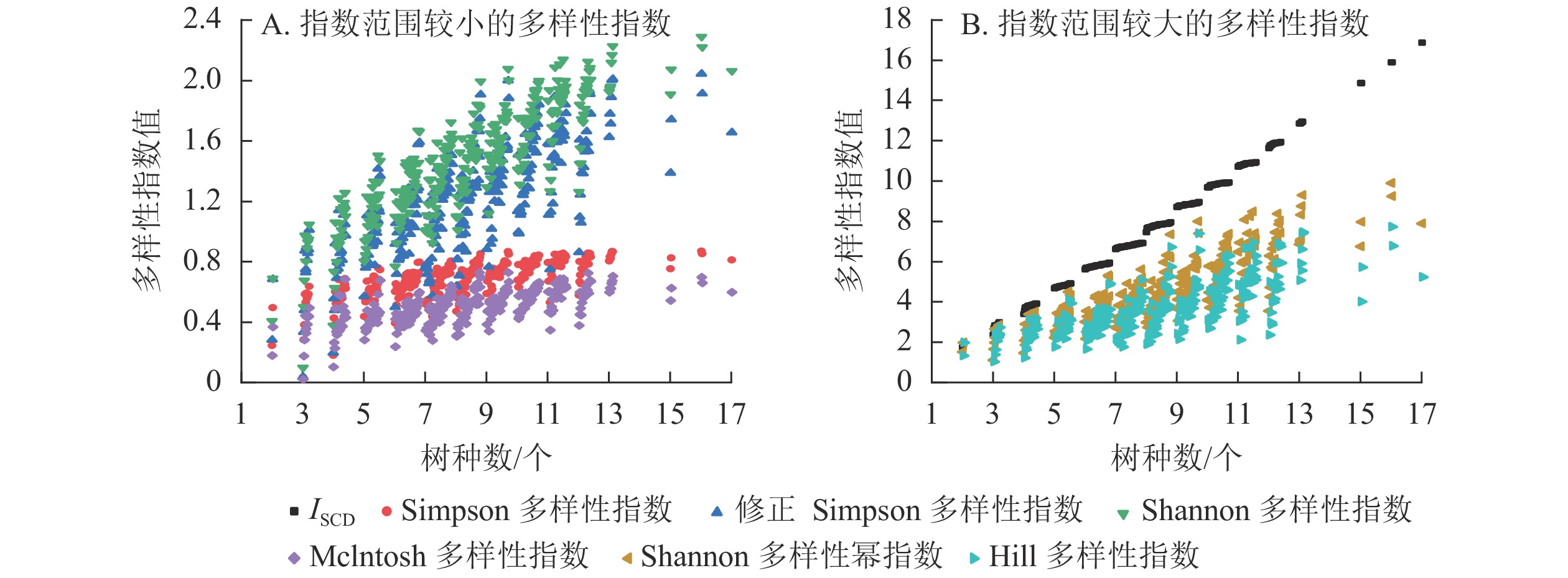
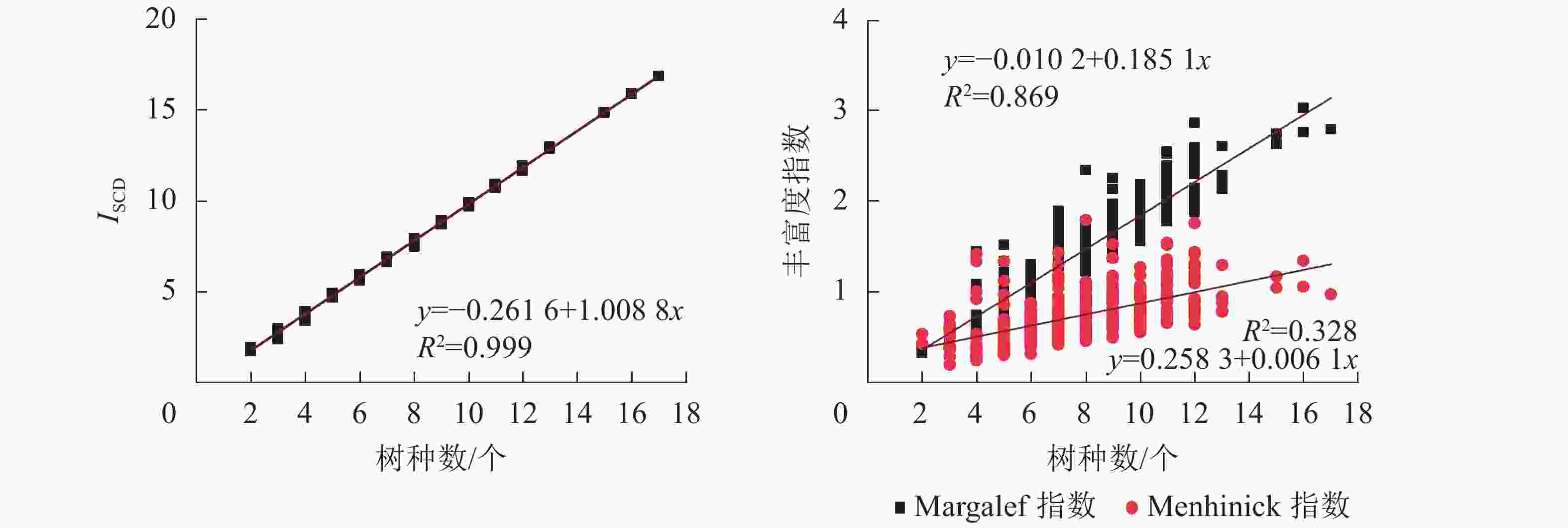
选取Margalef指数^[11]、Menhinick指数^[11]与I_SCD对样地林分丰富度进行计算和对比分析。从图4可见：I_SCD随树种数的增多呈上升趋势，具有明显的“分段”现象，表明I_SCD对树种数的分异性能强；Margalef指数与Menhinick指数值聚集在较小范围内，随树种数增多呈上升趋势，但变化幅度不大。

Figure 4.  Species richness of sample plots

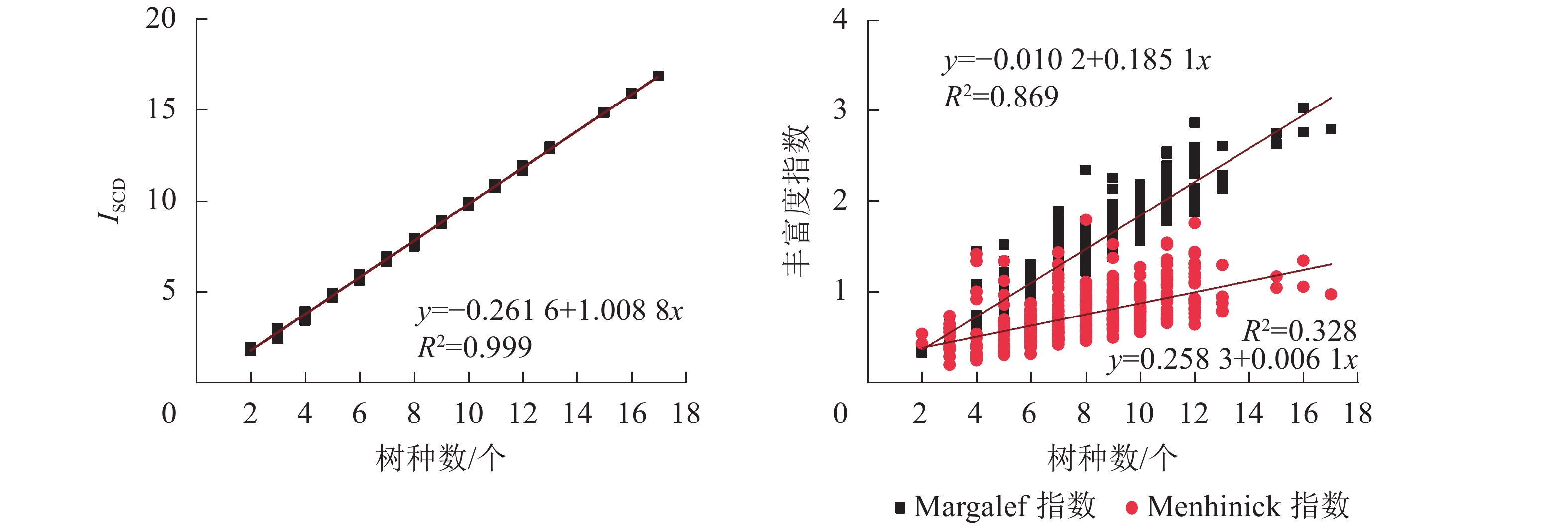
根据不同树种数时各指数的分布形态(图5)，对其进行指数函数、线性函数、对数函数、多项式函数以及幂函数等多种函数拟合，并选择最优拟合模型。结果显示：I_SCD、Margalef指数以及Menhinick指数与树种数均呈正相关。I_SCD的线性拟合决定系数(R²)达0.999，斜率接近于1，与树种丰富度相关性十分紧密，可信度高。Margalef指数的线性拟合R²为0.869，斜率为0.185 1，与树种丰富度相关性较为紧密，可信度较高。Menhinick指数与树种数的拟合模型R²均未超过0.4，线性斜率为0.006 1，与树种丰富度相关性不明显。表明I_SCD比Margalef指数和Menhinick指数对树种丰富度变化的反映更敏感，更具有一致性。

Figure 5.  Relationship between each diversity indices and the number of tree species

基于I_SCD指数的构造特性，其值中的小数部分(I_SCD-U)仅反映树种分布的均匀度，故可单独提取用于比较分析，以消除树种丰富度的影响。I_SCD-U指标计算公式为：

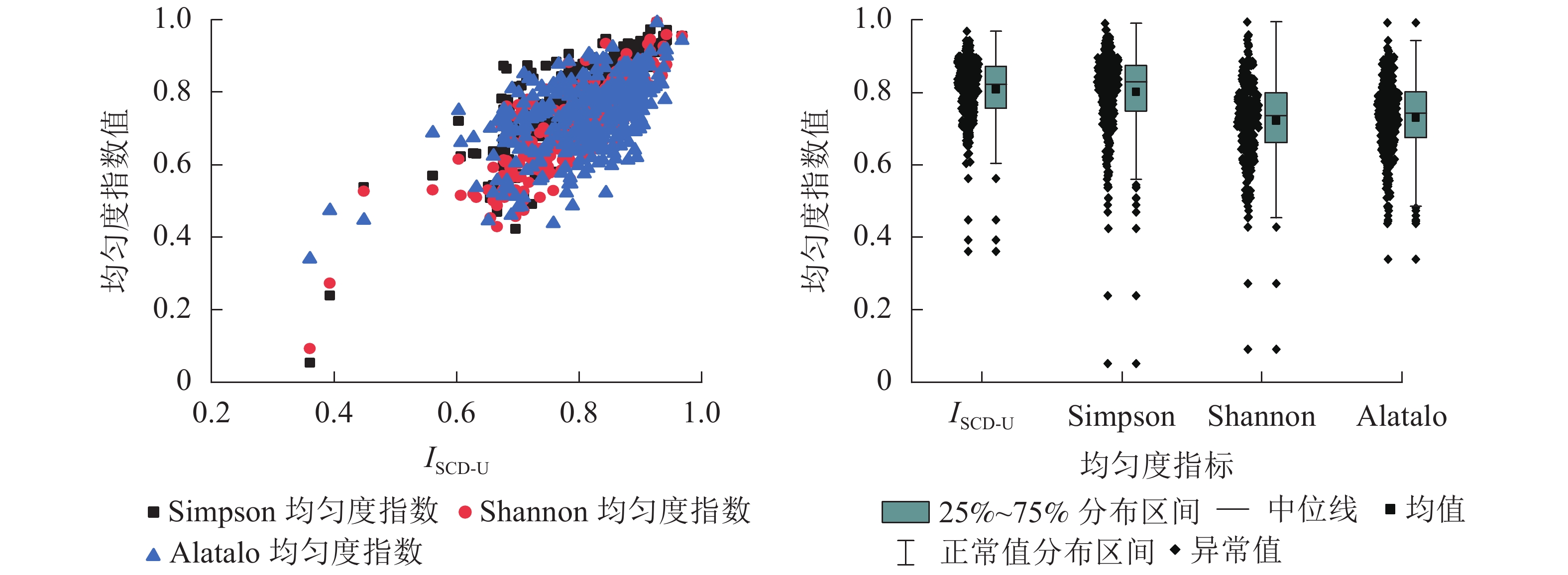
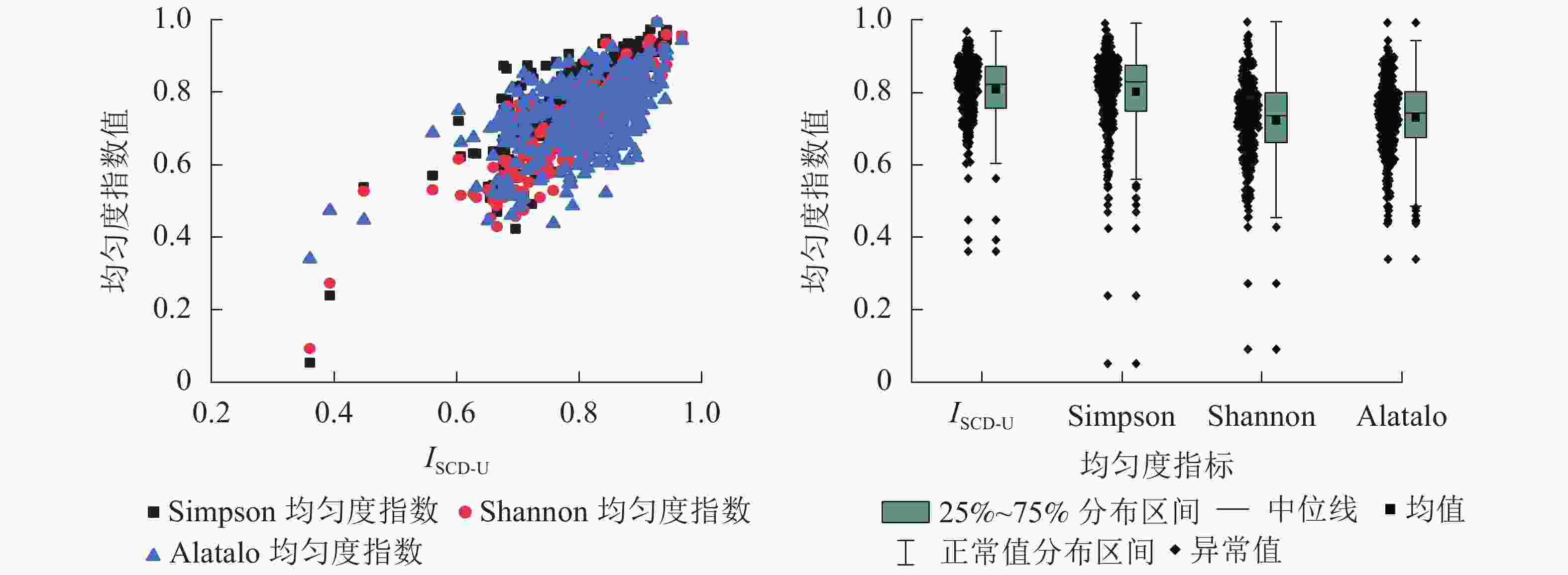
选取α多样性指数中的Shannon均匀度指数^[12]、Simpson均匀度指数^[12]、Alatalo均匀度指数^[13]等与I_SCD-U进行均匀度计算和对比分析。各均匀度指数统计结果见表4，依I_SCD-U进行升序排列结果见图6。

Figure 6.  Evenness of tree species in the sample plot

由表4和图6可知：I_SCD-U与Simpson均匀度指数、Shannon均匀度指数以及Alatalo均匀度指数具有较强一致性，且I_SCD-U与Simpson均匀度指数分布较为接近，两者均值分别为0.808、0.801，中位数分别为0.824、0.829，最大值和最小值有所差异，且I_SCD-U的变动幅度小于Simpson均匀度指数。此外，I_SCD-U、Simpson均匀度指数的均值、中位数明显大于Shannon均匀度指数、Alatalo均匀度指数。从分布范围来看，I_SCD-U的分布最为集中，对树种均匀程度的评价最为严密。

对I_SCD-U、Shannon均匀度指数、Simpson均匀度指数及Alatalo均匀度指数进行Pearson相关分析(表5)表明：I_SCD-U与Simpson均匀度指数相关系数为0.840，与Shannon均匀度指数相关系数为0.825，与Alatalo均匀度指数相关系数为0.555。4个指数两两之间相关性均达到极显著水平(P＜0.01)。Simpson均匀度指数与Shannon均匀度指数相关性最高，其次是I_SCD-U与Simpson均匀度指数、I_SCD-U与Shannon均匀度指数。相关性最低的为I_SCD-U与Alatalo均匀度指数。I_SCD-U与Shannon均匀度指数、Simpson均匀度指数在反映林分树种组成均匀度方面具有比较一致的灵敏性和分异性。

选取具有代表性的Simpson多样性指数^[12]、修正Simpson多样性指数^[14]、Shannon多样性指数^[12]、Shannon多样性幂指数^[14]、Hill多样性指数^[15]、Mclntosh指数^[16]等与I_SCD进行多样性的对比分析。

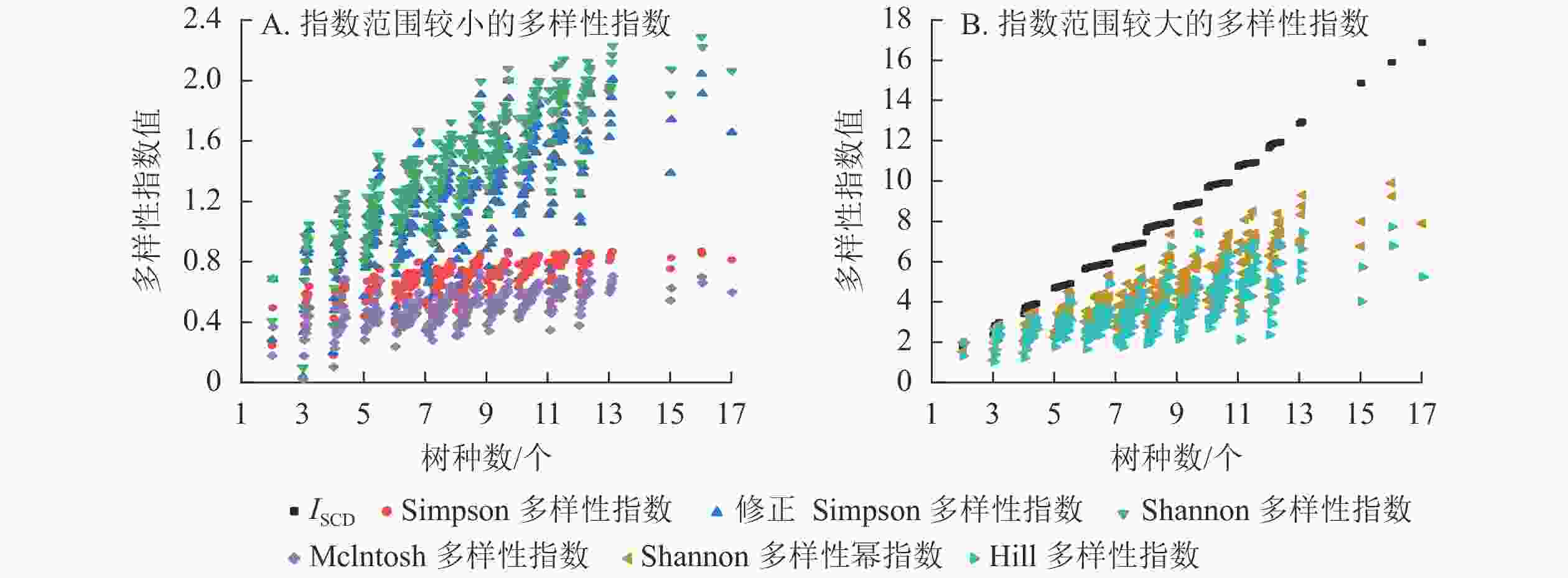
由表6和图7可知：多样性指数按指数范围从大到小依次为I_SCD、Shannon多样性幂指数、Hill多样性指数、Shannon多样性指数、修正Simpson多样性指数、Simpson多样性指数、Mclntosh多样性指数，7个指数的均值、中位数、最大值、最小值等都有明显差异。分布形态上，I_SCD呈分段聚集，与其他6个指数的分布形态明显不同。Shannon多样性幂指数与Hill多样性指数分布较为接近，Shannon多样性指数与修正Simpson多样性指数分布较为接近，Simpson多样性指数与Mclntosh多样性指数分布较为接近。

Figure 7.  Species diversity of the sample plots

由表7可知：7个指数间相关性都达到极显著水平(P＜0.01)。I_SCD与其他多样性指数具有极显著的相关性(P＜0.01)，与Shannon多样性幂指数的相关系数最大，为0.840，其次是Shannon多样性指数、修正Simpson指数、Hill多样性指数、Simpson多样性指数以及Mclntosh多样性指数。α多样性指数中，各指数之间普遍具有显著相关性(P＜0.01)，对多样性的评价具有一致性。

由图7可知：同一树种数时，I_SCD、Simpson多样性指数、修正Simpson多样性指数、Shannon多样性指数、Shannon多样性幂指数、Mclntosh多样性指数以及Hill多样性指数均对样地林分多样性水平具有较为一致的评价；由于对稀有种的不同看法，一旦树种数增加，就会产生2种截然不同的变化：I_SCD重视树种数的重要性，强调树种的“存在价值”，认为树种数多，多样性便高，指数就呈不断上升趋势，稀有树种与富集树种的差异更多反映在小数部分。而其余指数则倾向于对树种多度分布均匀的样地赋予更大的指数值。稀有树种的出现并不一定直接提高林分多样性。

在多样性指数中，普遍存在1个指数值对应多种树种数的现象，即存在指标难以区分低丰富度高均匀度群落与高丰富度低均匀度群落的问题，指数的大小并不能有效反映具体的多样性信息，只在相对比较中具有意义。I_SCD在反映树种组成多样性上弥补了现有多样性指数的缺陷，更有利于实现对林分树种组成的定量化表征。

在对树种组成的定量化描述上，不论是Margalef指数、Menhinick指数，还是Shannon指数、Simpson指数，亦或是Hill指数，都各有其优势与不足。Margalef指数和Menhinick指数等试图权衡丰富度与总丰度的关系，却缺少考虑物种内个体的同质性(均匀性)；在测度树种的丰富度时，以树种数和林分总株数的关系为基础，虽然肯定了稀疏树种与富集树种对群落林分中树种多度的贡献，但对于描述林分树种组成而言仍显不足，其数值具有较大不确定性，即只能判断相对抽象的树种丰富性程度，却无法给出具体丰富度信息等(如林分树种数)。

基于丰度的多样性指数(如Shannon指数和Simpson指数)在物种丰富度的基础上增加了个体数量的信息，考虑了异质性，却依旧无法代表一个群落的真正“多样性”。对于均匀性的度量方案似乎是无穷无尽的，有许多方法可以根据“均匀性”的不同定义来估计，这使得对均匀性的概念并不十分清晰^[17]。目前常用的Simpson均匀度指数与Shannon均匀度指数将均匀度定义为群落的实测多样性与理论最大多样性的比率。

Shannon指数和Simpson指数及变体往往被认为可以将物种丰富度和均匀度巧妙地整合成全方位的衡量标准而广泛使用。然而，这些复合指数对多样性的度量依旧有限：①Shannon指数植根于信息理论，是一种熵，量化的是随机挑选得到的某个个体物种身份的不确定性强弱(不确定性强，多样性高)。Simpson指数也是广义的熵^[18]，量化的是从数据集中随机挑选的2个个体不代表同一物种的概率。指数作为熵，反映的是物种集合体与多样性有关的不同特性，衡量的是不确定性，并不是真正的多样性^[19]。虽然熵的变化在数学上与物种丰富度相关，但在很大程度上它们与丰富度的关系已被证明是不一致的^[20-21]。此外，熵及其变化因其可能掩盖多样性各组成部分之间的差异而显得不足，致使有学者认为复合指数在很大程度上是没有意义^[22]。②物种丰富度和均匀度之间可能存在反向关系，在复合指数中会相互抵消，并不能得到与直观感觉一致的结果^[23]。③复合指数对多样性和均匀性的权重高于丰富性，且对稀有物种与丰富物种赋予不同的权重，这掩盖了物种丰富度的重要性。

HILL^[24]提出希尔数(hill numbers)，即有效物种数，用以量化多样性。有效物种数借助参数实现对丰富物种与稀有物种的权重控制，并能服从生物学家多样性概念中隐含的复制原则或加倍性质，被认为是物种多样性丰度的最佳选择^[25]。然而同样有学者提出，有效物种数的使用存在一定局限性^[17]。

I_SCD以树种数量直接作为多样性丰富度，指数值接近实际树种数显得更加简洁、直观、有效，可根据指数值快速反推单个样地树种数。这是其他α多样性指数无法实现的。

I_SCD对均匀度的评价方法以林分中树种的个数及各树种的属性比例作为变量，从树种的株数分布和蓄积分布2个方面衡量森林中树种分配的均匀性。通过各树种株数以及蓄积比例的不同，对两者的作用有了明确区分。此外，I_SCD-U指标以现有林分与同一树种数下的理想林分(树种完全均匀分布)之间存在的差距进行均匀性评价，是一种新视角下的均匀性度量方式。

从指数构造角度而言，I_SCD也具有科学性。物种丰富度和均匀度之间存在一定关系^[26]。许多学者倾向于认为物种丰富度与均匀度应该是相对独立的^{[20, 27]}，但实际发现均匀度总是不可避免地受到丰富度的制约，两者依旧存在相关关系。I_SCD将指数丰富度信息与均匀度信息进行了明确分离，使其各自独立而不再相互作用。

从指数表现来看，I_SCD对林分树种丰富度反映灵敏，有着很好的区分性，弥补了现有指数对林分树种数反映表征模糊、指数范围重叠、区分不灵敏等不足。在反映树种组成多样性综合效应时，比其他指数有更好的区分性，同时与其他指数存在显著相关性，表明I_SCD具有与其他多样性指数相同的理论基础，其本质相同但形式与侧重点不同。

对于α多样性指数而言，当用直径、树高或其他结构分类变量来代替物种时，它就可以反映林分结构多样性，体现对应林分组成结构属性特征^[9]，例如Simpson大小多样性指数、Shannon大小多样性指数、Simpson大小分化度指数、Shannon大小分化度指数等林木大小多样性指数^[28]以及树高多样性指数等。同理，I_SCD在后续应用时，亦可衍生类似指数，例如以胸高断面积、生物量、生产力替代蓄积使用，I_SCD指数同样具有一定的可拓展性。但对于描述复杂树种结构而言，依旧存在不足。如何体现树种结构的空间分布，如何对不同树种属性进行合理的权重设置，仍是I_SCD未来需要攻克的难点。

I_SCD在数量化表达林分树种组成多样性时，有效地将树种丰富度与树种株数、蓄积均匀性既分离又融合在一起，是一个较全面反映树种组成多样性信息的综合指标。它对林分树种组成的丰富度反映比其他多样性指数更加灵敏，分异性更强，对林分树种组成的均匀度有着与其他多样性指数一致的灵敏度和区分度，其数值大小还体现出现有林分与理想林分的差距，这也为评价林分树种组成均匀程度提供了一种新思路。相互独立的丰富度、均匀性信息使得指数值本身具有意义，解决了对低丰富度高均匀度、高丰富度低均匀度等不同林分树种组成类型难以有效区分这一难题，有利于准确描述树种组成多样性。