Construction of compatible individual tree biomass model of Myrica rubra plantation

研究区位于浙江省仙居县福应街道。仙居是浙江省台州市第一杨梅主产区，是“中国杨梅之乡”。研究区的杨梅人工林具有广泛的代表性，地理位置为28°25′~28°52′N， 120°23′~120°42′E，海拔为140~230 m，属中亚热带季风气候，年平均气温为18.3 ℃，最热的7月平均气温为28.5 ℃，最冷的1月平均气温为5.6 ℃，无霜期为240 d左右，历年平均降水量为2 000 mm，年日照时数为1 786.2 h。母岩为花岗岩，土壤为红壤。

2017年8月，选择不同龄级(幼苗期、产前期、初产期、盛产期)的杨梅林(中心位置28°46′09″N， 120°31′18″E)，分别建立20 m×10 m的标准地各4个，共16个。杨梅林均由马尾松Pinus massoniana林改造而来。土壤成土母岩为花岗岩，海拔140~230 m，西北坡。

对标准地内杨梅林的地径、树高、冠幅进行全面调查，计算平均地径、树高、冠幅(表1)，并在每个标准地内选取标准木(地径和株高均约为平均值)各3株，共48株。采用全收获法，野外分离叶片、枝干和根系，并分别实测鲜质量。同时均匀选取不同器官样品500~1 000 g(准确称量)于样品袋中，带回实验室。样品带回室内在105 ℃烘箱内烘干至恒量，计算各组分生物量和总生物量。48株杨梅生物量数据分成2组，32株用于生物量建模，剩余16株用于模型检验。

使用建模的32株杨梅的地径、树高、冠幅与各组分生物量及总生物量(不含果实)进行相关分析(表2)，结果均呈极显著正相关(P＜0.01)，因此采用3个因子作为自变量构建杨梅各组分生物量及总生物量模型。

采用常见的线性方程y=a+bx、对数函数y=a+blnx、指数函数y=ab^x、幂函数y=ax^b、二次多项式函数y=a+bx+cx²等方程构建杨梅树独立单株生物量模型。用决定系数(R²)来评价模型优劣。R²越接近1表示回归效果越好。选出拟合度最好、相关最密切的数学模型。

一元、二元相容性生物量模型都能较好地解决总生物量与各组分生物量的相容性问题，但从模型构造和应用性考虑，一元相容性生物量模型在大尺度范围估测森林生物量的效果要优于二元相容性生物量，且模型数据较易获取，准确性较高，模型形式也较简单^[19-20]。因此，本研究参照唐守正等^[21]提出的非线性误差变量模型法，建立总生物量与各组分生物量非线性联立一元方程组模型。

其中：y₀为总生物量，y₁为叶生物量，y₂为枝干生物量(枝条和树干生物量之和)，y₃为根系生物量，y₀= y₁+y₂+y₃，x为建立单株生物量模型时选取的变量，a₁、a₂、a₃、b₀、b₁、b₂、b₃、c₀为模型参数。使用未建模的16株杨梅数据，计算总相对误差(S_R)、平均相对误差(E_E)和预估精度(P₀)。

$ {\mathrm{其}\mathrm{中}：y}_{i} $和$ \widehat{{y}_{i}} $分别为第i株杨梅样木的生物量实测值和估计值，${\bar{y}_{i}} $为全部杨梅样木实测值的平均值，N为杨梅样木的总数，T为模型参数个数，t_α为自由度 (N−T) 置信水平 α=0.05。对建立的杨梅生物量方程进行预测精度验证和效果检验。非线性误差变量模型法估计要求模型参数不能有冗余，因此，上述模型经简化改写，得到如下相容性生物量模型。

其中：r₁、r₂、r₃、r₄为模型参数。

分别以地径、树高和冠幅为自变量，用指数函数、线性函数、对数函数、多项式函数和幂函数拟合杨梅叶生物量、枝干生物量、根系生物量及总生物量模型(表3)。可见，采用幂函数拟合的决定系数均最大。叶生物量(y₁)与地径(x₁)、树高(x₂)和冠幅(x₃)的幂函数模型分别为y₁=0.004x₁^2.795、 y₁=0.150x₂^3.142、 y₁=0.239x₃^1.041，决定系数分别为0.951、0.841和0.864；枝干生物量(y₁)与地径、树高和冠幅的幂函数模型分别为y₂=0.003x₁^3.048、y₂=0.150x₂^3.444、y₂=0.249x₃^1.143，决定系数分别为0.942、0.859和0.885；根系生物量(y₃)与地径、树高和冠幅的幂函数模型分别为y₃=0.002x₁^3.141、y₃=0.128x₂^3.470、y₃=0.206x₃^1.169，决定系数分别为0.964、0.832、0.884；总生物量(y₀)与地径、树高和冠幅的幂函数模型分别为y₀=0.010x₁^2.995、y₀=0.433x₂^3.351、y₀=1.137x₃^1.000， 决定系数分别为0.959、0.849、0.822。可见，与树高、冠幅相比，以地径为自变量拟合的幂函数模型决定系数均最大，为最优模型。

在ForStat 2.1 软件支持下，建立杨梅非线性误差变量一元联立方程组，求解模型各参数值，得到杨梅相容性各单株生物量模型。用决定系数、总相对误差、平均相对误差、预估精度对模型进行综合评价与检验(表4)。以地径为自变量的相容性单株生物量模型：

以树高为自变量的相容性单株生物量模型：

以冠幅为自变量的相容性单株生物量模型：

可以看出：杨梅相容性单株生物量模型R²均较高，都在0.600 0以上，说明模型代表性较强，拟合优度较高；平均相对误差均在±4.6%范围内，小于±5%，相对误差较小；总相对误差小于5.0%，说明模型系统偏差较小，拟合效果较好；预估精度均达85%以上，估测精度较高。总体看，本研究建立的杨梅相容性单株生物量模型精度较高，拟合效果较好，满足研究区对杨梅生物量的估测要求。其中，以地径为自变量的相容性单株生物量模型，决定系数和预估精度值最大，分别为0.881 8~0.912 4和91.63%~92.22%，为最优相容性单株生物量模型。

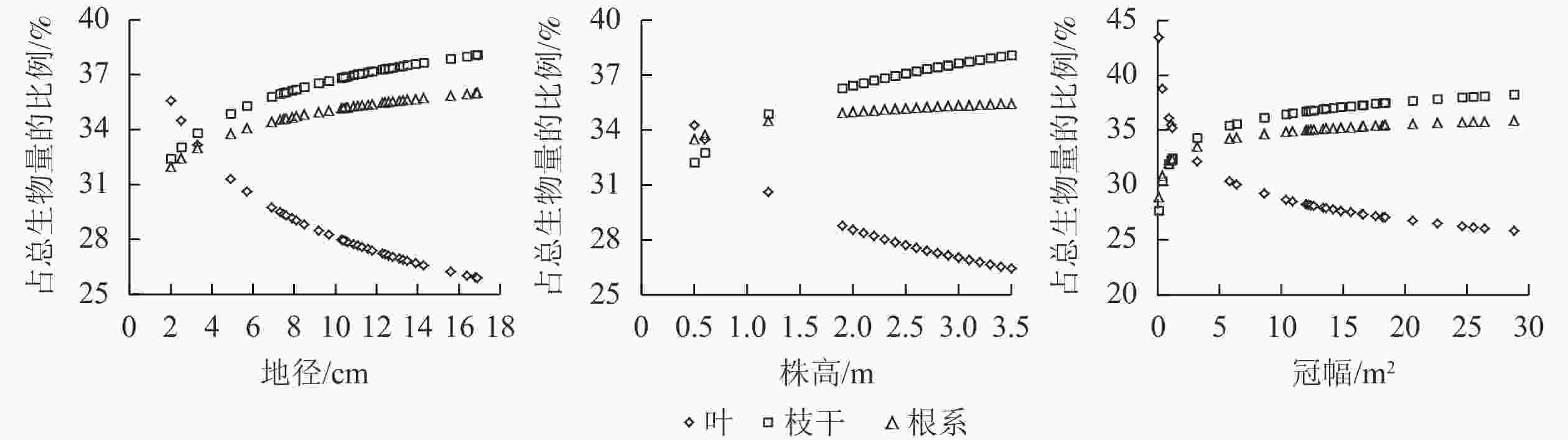
利用建立的各相容性单株生物量模型，对杨梅各组分生物量占总生物量比例随地径、株高、冠幅的变化进行分析。从图1可见：枝干、根系生物量占杨梅总生物量的比例随地径增大而逐渐升高，增速逐渐趋缓，从地径为2 cm的32.4%、31.9%分别提高到17 cm的38.1%、36.0%；叶生物量占杨梅总生物量的比例则随地径增大呈明显快速下降趋势，从地径为2 cm的35.6%下降到17 cm的25.9%。枝干、根系生物量随树高增长而缓慢升高，从树高为0.5 m的32.2%、33.5%分别提高到3.5 m的38.1%、35.5%；叶生物量则随树高增长呈明显快速下降趋势，从树高为0.5 m的34.3%下降到3.5 m的26.4%。枝干、根系生物量随冠幅扩展缓慢升高并趋于平缓，从冠幅为0.1 m²的27.7%、28.9%分别提高到30.0 m²的38.4%、35.9%；叶生物量随冠幅扩展而逐渐下降，但降幅趋缓，从冠幅为0.1 m²的43.4%下降到30.0 m²的25.7%。

Figure 1.  Proportions of component biomasses to total biomass with ground diameter, tree height and crown breadth increasing

分别以地径、树高和冠幅为自变量，对比不同函数拟合出的模型，采用幂函数拟合的杨梅叶生物量、枝干生物量、根系生物量及总生物量模型的决定系数均为最大，为0.822~0.964，统计学意义显著。格日乐图等^[22]在研究广宁茶秆竹Pseudosasa amabilis地上生物量分布特征时，选定幂函数模型作为最优模型；尹惠妍等^[23]在对中国主要乔木树种生物量方程研究中，收集了1996—2012年间在国内外发表的66篇文献中的乔木生物量模型，其中包括44个乔木树种模型和612个分量模型，以幂函数的形式最多。对比地径(x₁)、树高(x₂)和冠幅(x₃)拟合的幂函数模型，又以地径的决定系数为最大，叶生物量、枝干生物量、根系生物量及总生物量模型决定系数分别为0.951、0.942、0.964和0.959，所对应幂函数分别为y₁=0.004 x₁^2.795、y₂=0.003 x₁^3.048、y₃=0.002 x₁^3.141和y₀=0.010 x₁^2.995。

为解决生物量模型的相容性问题，本研究采用非线性联立方程组法，构建以地径、树高和冠幅为自变量的各相容性单株生物量模型，充分考虑了各组分生物量与总生物量之间的内在相关性问题，确保了各组分生物量预测值之和等于总生物量。从研究结果来看，3个模型拟合效果均较好，预估精度都在85%以上，模型平均相对误差较小。其中以地径为自变量的相容性单株生物量模型预估精度最大，达91.63%~92.22%，模型为最优，模型参数c₀、b₀、r₁、r₂、r₃和r₄分别为0.084 0、2.162 7、0.780 0、0.779 9、0.224 3和0.204 5。研究区杨梅标准木数量有限，加之生物量估测影响因素较多，因此，若要提高生物量估测精确度，还要从提高样本数量、减少抽样误差、控制采样条件等多方面加以提升改进^[24-25]。

随地径增大、树高增长和冠幅扩展，各组分生物量占总生物量的比例基本呈相似的变化规律，其中枝干生物量、根系生物量占比均呈升高趋势，叶生物量呈下降趋势。随着杨梅生长(林龄增大)，各组分生物量从高到低快速演变为枝干、根系、叶片。孙拥康等^[13]构建的鄂西山区日本落叶松相容性单株生物量模型显示，树干生物量占总生物量的比例随胸径增大而升高，树冠生物量呈明显下降趋势，而树根生物量呈先增后减趋势，但整体变化较平缓；曹磊等^[26]构建的广东省樟树Cinnamomum camphora相容性生物量模型显示，樟树各组分生物量占地上部分比例随胸径增大而呈现出不同的规律，树干生物量比例先增大然后基本维持不变最后逐渐下降，树叶生物量和干皮生物量比例逐渐降低，而树枝生物量比例逐渐提高。与本研究结果相反，这可能因树种不同造成的。

需要对杨梅人工林采取一定的技术措施来提高果实产量和品质。采取大枝修剪可以改善果园中的通风透光，提高果实的品质和产量，但为避免主枝被日光灼伤，大枝修剪应选在冬季最为合适；疏果是提高果实品质的一项重要管理措施，疏枝疏果可以显著提高果实品质及其商品果率；不合理的施肥会导致杨梅不结果或果实畸形等问题，配方施肥对提升杨梅品质也是极为重要的一项举措。浙江大部分土壤为酸性土，土壤中缺乏钾、钙等元素，需有针对性地施用肥料，提高果实品质，并防止采前落果、果实腐烂病的发生^[27]；农户有足够经济条件时也可搭建设施大棚，以此提前杨梅的上市时间，延长杨梅的采收时段，并且可以提升杨梅的单果质量，提高果实中可溶性固形物、维生素C、糖等含量^[28]。

杨梅生物量模型在碳中和、碳达峰目标下具有更强的可用性和推广性。常规森林的固碳量一般都会随着林分年龄的增大而增多^[29]，相同年龄下的地径、树高、冠幅存在一定的差异，年龄的增大仅仅呈现出生物量不断增长的趋势，而通过测量杨梅的单一变量如地径、树高、冠幅即可准确估算出树木的生物量，可以减少在实际测量中所需投入的人力、物力等资源。同时，利用生物量模型可以准确估算森林碳储量的生态效益，对发展碳汇经济有着极为深远的意义^[30]，也是衡量森林固碳能力的关键^[31]。下一步的研究中，还应探索研究其他生物量估测方法，加大样本采集数量，以期建立更加科学的杨梅通用性生物量模型。