下载:
-
森林生物量是森林碳储量的主要载体，约占陆地碳库的45%和全球碳库的31%，在维系陆地碳循环和稳定全球气候方面发挥着主导作用，因此准确估算乔木和林分生物量对于评估森林生态系统碳储量、碳汇及生态系统服务功能至关重要[1]。异速生长方程是将林木的胸径(DBH)和树高(H)等易测因子转换为林分生物量的常用方法[2−3]。该方法结构简单、精确度高并且可以获得树木各器官生物量的分配规律，已被广泛应用于树木生物量的估算[4−5]。树木的异速生长关系受树种、林龄、竞争关系、立地条件以及气候等因素的综合影响[6−7]，如何研发高精度的异速生长方程一直是国内外学者研究的重点。
以往的研究大多采用幂函数且多利用DBH作为预测变量，建立异速生长方程估算树木生物量[3, 8−11]。有研究认为：树木的高径比更能反映树木的形状，因此将H作为额外的预测变量来建立异速生长方程，这比仅基于DBH建立的异速生长方程的预测精度要高[12]。还有研究发现：树冠直径可以作为树木生物量的预测变量，且树冠直径的加入可改善生物量的预测精度[13−14]。此外，树木的异速生长关系并非静态。随着林分的生长，微立地条件(如光照和土壤养分)以及单株树木之间相互作用关系都会发生巨大变化，这将导致树木的树形、树冠结构和根系特征发生变化，进而导致各组分生物量分配比例及其异速生长关系发生变化[7]。因此，采用没有考虑林龄的特定异速生长方程参数估算各组分生物量时可能出现较大误差[15−16]。总之，在异速生长关系的众多影响因素中，选择最优参数组合作为预测变量来建立异速生长方程，是提高异速生长方程预测精度的核心。
桉树Eucalyptus是中国南方重要的速生丰产林树种之一，种植面积已达546万hm2[17]，其巨大的林分生产力和碳汇功能，关系着中国的木材供给安全和碳收支平衡，因此对桉树人工林生物量的精确估算意义重大。以往很多研究已对中国桉树人工林建立了异速生长方程，如杨忠等[18]对元谋干热河谷桉树人工林的研究发现：幂函数可较真实地反映桉树生物量随DBH及H的变化趋势；张利丽等[19]建立了仅使用DBH的雷州半岛尾巨桉Eucalyptus urophylla×E. grandis人工林生物量各器官的异速生长模型；揭凡等[20]基于已发布文献数据，建立了桉树人工林地上部分和地下部分生物量异速生长模型。这些异速生长方程的研究大部分未加入林龄因素，也不清楚桉树的哪些生长指标受到林龄的显著影响，这限制了对中国桉树人工林碳储量及其固碳潜力的精确估算。为此，本研究以中国种植面积最大的尾巨桉为研究对象，采用整株收获法，测定1、2、3、6、10年生的57株尾巨桉各器官的生物量，分析其生物量分配格局随林龄的变化特征，并基于H、DBH和林龄建立了各器官不同的异速生长模型，探讨不同异速生长模型的预测精度差异，确定加入林龄后预测精度显著提高的异速生长模型。研究结果可为桉树异速生长模型的优化提供参考，并为中国桉树产业碳储量及碳汇精准评估提供理论依据和数据支持。
-
试验地设置于广东湛江桉树人工林生态系统国家定位观测研究站内(21°16′N，110°05′E)。海拔为80~220 m。根据1980—2020年的长期气象记录，该地属南亚热带海洋性季风气候，年平均降水量为1 760.9 mm，其中77%~85%出现在雨季(5—10月)。年平均气温为23.1 ℃。最低气温为1.4 ℃，出现在1月；最高气温为38.1 ℃，出现在7月，年相对湿度为80.4%[21]。根据世界土壤资源参考基准，该地区土壤属于由玄武岩风化沉积物发育的暗红湿润铁铝土，土壤呈酸性，0~80 cm土层土壤的平均pH为4.9[22]。
-
本研究选取的5个林龄(1、2、3、6和 10 a)的尾巨桉人工林均为平地造林，造林无性系为 DH32-29，造林方式均为挖穴造林，造林密度均为1 666株·hm−2。任意2块林分间直线距离均小于1 km，立地差异小，且经营方式完全相同。在每个林龄的尾巨桉人工林中分别建立3个20 m×20 m的正方形样地。对每个样地进行每木检尺，记录胸径(DBH)和树高(H)，按径阶选取样树，其中1、2年生采用1 cm整化，3年生采用2 cm整化，6、10年生采用3 cm整化 (表1)。整株收割，测量其生物量。
表 1 样木的基本信息
Table 1. Basic informations of sample woods
林分年
龄/a平均胸
径/cm平均树
高/m径阶范
围/cm样本
数量活立木密度/
(株·hm−2)林分年
龄/a平均胸
径/cm平均树
高/m径阶范
围/cm样本
数量活立木密度/
(株·hm−2)1 4.92±0.92 5.27±0.90 3.00~4.00 3 1 666 3 10.95±1.79 12.51±0.87 7.00~9.00 3 1 616 4.00~5.00 3 9.00~11.00 3 5.00~6.00 3 11.00~13.00 3 6.00~7.00 3 6 12.62±2.80 16.09±1.95 8.00~11.00 3 1 449 2 8.71±1.37 11.81±1.38 5.00~6.00 3 1 616 11.00~14.00 3 6.00~7.00 3 14.00~17.00 3 7.00~8.00 3 10 22.35±2.89 20.71±2.68 18.00~21.00 3 1 366 8.00~9.00 3 21.00~24.00 3 9.00~10.00 3 24.00~27.00 3 10.00~11.00 3 说明：径阶数值采用上限排除法，平均胸径与平均树高的表示形式为平均值±标准差。 -
用油锯砍伐尾巨桉样树，测量树高、冠幅、胸径和枝下高。在测定干全长的同时，将干按照2 m规格分成若干木段(在1.3~2.0 m处额外增加1段)，在每个区分段底直径的位置截取圆盘，所余不足2 m长度的干为梢头木，在梢头木底直径的位置也截取圆盘，称取全部木段与圆盘质量，作为干鲜质量。将枝从每个木段上分离，并将叶从枝上完全分离，在原地分别称取枝及叶鲜质量。在1株树中均匀收集圆盘、叶和枝的样本各50 g，送至实验室。
根生物量的测量采用人工挖掘法。首先挖掘树桩，后挖掘其余的根系，并尽可能挖掘至根尖。清理粘附在根上的泥土，并在原地称其鲜质量。称量后收集树桩与根的样本50 g，送至实验室。
将干、枝、叶、树桩和根的样本在恒温干燥箱中以85 ℃烘烤至恒量，计算各部分的含水量。树木各器官干质量均利用含水量由鲜质量换算。地上生物量为干、枝、叶生物量之和；根生物量为树桩与根生物量之和。将其相加得到单株树木总生物量，并计算出各林龄树木不同器官及整株平均生物量。
-
分别计算每个林龄尾巨桉各器官生物量的平均值、各器官生物量占总生物量的百分比，及根生物量与地上部分生物量、叶生物量与干生物量、枝生物量与干生物量的比值，并研究其变化与林龄变化之间关系。绘制树木各器官生物量与地上部分生物量的关系。
本研究参考XIANG等[23]的异速生长模型，将所有变量经过自然对数转换后(确保各变量之间的线性关系并使其满足异方差的要求)，采用单独的胸径 (DBH)、单独的树高(H)、胸径和树高的组合(DBH 2 H)，以及胸径(DBH)和树高(H)同时作为预测变量4种模型形式来建立不包含林龄的各器官异速生长模型1~24。另外，又将林龄作为补充变量引入上述4种模型形式，同时考虑林龄的个体效应及其与其他预测变量(即DBH、H和DBH 2 H)间的交互效应，建立包含林龄的各器官异速生长模型25~48，以验证引入林龄是否可以提升模型对生物量预测的准确性。
在以前的研究中，只有使用最广泛的2个方程，即DBH模型和DBH 2 H模型有加入林龄的拟合研究。在本研究中则对上述所有方程均加入了林龄作为拟合变量，且同时选取每个树木器官的包含了林龄的最佳拟合方程。另外，由于对生物量进行对数转换会对回归估计带来偏差，因此，将用于预测的模型反向转换时需要计算矫正因子(FC)进行偏差矫正[11]。
本研究采用R-3.6.3的nlme包对模型进行拟合，并估计截距、斜率和树木各器官生物量与预测变量的固定效应之间的关系。
-
对于拟合的结果，计算赤池信息准则(CAI)[24]和残差标准误(ERS)，以确定模型的适用性。同时，为了比较各模型的拟合优度，随机选取70%的数据进行模型拟合，另外30%用于验证模型拟合能力。将验证集中使用模型计算的预测值与树木生物量的实测值进行对比，利用调整决定系数($ {{R}}_{\text{adj}}^{\text{2}} $)和平均预测误差(EMP)估计模型拟合优度。
本研究利用R-3.6.3进行数据分析，利用Origin 2022绘图。
-
由图1A可知：尾巨桉各器官平均单株生物量随林龄增长而增加，其中干生物量由1年生的2.62 kg·株−1增长至10年生的206.67 kg·株−1；枝生物量由1年生的1.13 kg·株−1增长至10年生的31.81 kg·株−1；叶生物量由1年生的0.95 kg·株−1增加至10年生的8.81 kg·株−1；根生物量由1年生的1.10 kg·株−1增加至10年生的55.52 kg·株−1。在所有林龄中，干生物量均最大，其在总生物量中的占比随林龄增加而增加，从1年生的45.21%增加至10年生的68.25%，叶生物量及枝生物量均随林龄的增加而呈下降趋势，其中叶生物量占比由1年生的16.31%下降至10年生的2.91%，枝生物量占比由1年生的19.43%下降至10年生的10.51%。根生物量随年龄的变化则呈相对稳定趋势，自19.05%上升至25.21%后，又回落至18.33%(图1B)。
图 1 不同林龄尾巨桉生物量分配格局
Figure 1. Patterns of biomass allocation in E. urophylla×E. grandis at different stand ages
各器官生物量与地上生物量呈现出显著的线性关系(图2)，其中干生物量的回归斜率最高，为0.849，决定系数(R2)为0.998；叶生物量的回归斜率最低，为0.030，R2为0.900；枝和根生物量的回归斜率分别为0.121和0.208，R2分别为0.923和0.884。这说明随着地上生物量的增加，各器官生物量的增长率不同，从大到小依次为干、根、枝、叶。由表2可见：根生物量与地上生物量的比值(根冠比)在各林龄间的平均值由0.235增加至0.337，后下降至0.225，总体趋势平稳。多重比较后发现：1、2、6、10年生林龄间根冠比数值无显著差异，所有林龄根冠比平均值为0.26。枝生物量与干生物量的比在2年生之前下降，此后维持在0.14左右。叶生物量与干生物量比在1~2年生时急剧下降，由0.361降至0.107，在3~10年生时略微下降(0.043~0.068)。
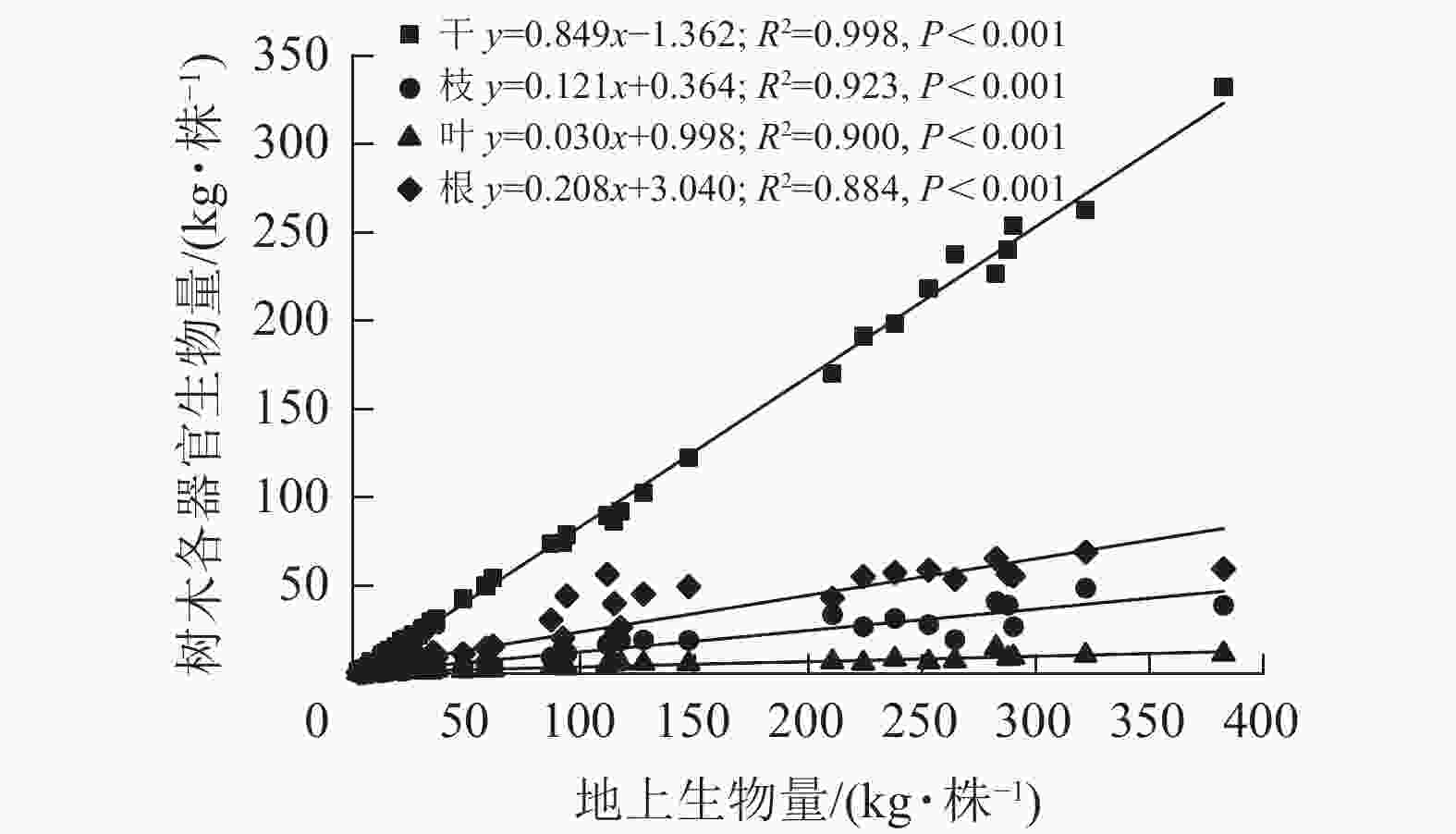
图 2 尾巨桉各器官单株生物量与地上生物量拟合
Figure 2. Fitting of individual tree biomass of various organs of E. urophylla×E. grandis with aboveground biomass
表 2 尾巨桉各器官间单株生物量比率随林龄的变化
Table 2. Changes in single-tree biomass ratios among various organs of E. urophylla×E. grandis with stand age
林龄/a 根生物量/
地上生物量枝生物量/
干生物量叶生物量/
干生物量林龄/a 根生物量/
地上生物量枝生物量/
干生物量叶生物量/
干生物量1 0.235 0.430 0.361 6 0.251 0.144 0.052 2 0.263 0.143 0.107 10 0.225 0.154 0.043 3 0.337 0.144 0.068 -
对尾巨桉各器官(根、枝、干、叶)，地上生物量及总生物量进行回归分析，共建立24个不含林龄的尾巨桉生物量异速生长模型(表3)。依据$ {{R}}_{\text{adj}}^{\text{2}} $、EMP和CAI对模型拟合效果进行评价。评价结果表明：干生物量最优模型为模型4 (DBH和H模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.992， EMP=6.532%；枝生物量最优模型为模型8 (DBH和H模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.880， EMP=4.654%；叶生物量最佳模型为模型12 (DBH和H模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.684， EMP=3.131%；根生物量最优模型为模型13 (DBH模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.961， EMP=5.702%。对地上生物量和总生物量的拟合发现，无最大$ {{R}}_{\text{adj}}^{\text{2}} $和最小EMP的组合，因此引入CAI作为辅助评价指标。选取地上生物量各模型中具有最大${{R}}_{\text{adj}}^{\text{2}} $的模型17和具有最小EMP的模型20，并选取CAI最小的模型。对总生物量各模型采用相同选择方式，在模型21和模型24中，选取CAI最小的模型，即地上生物量最优拟合模型为模型17 (DBH模型)，总生物量最优拟合模型为模型21 (DBH模型)。
表 3 桉树人工林各器官不含林龄的生物量估测模型
Table 3. Models for estimating biomass of eucalyptus plantation forests by organ without stand age
模型编号 因变量 预测变量 βi0 βi1 βi2 ERS FC CAI $ {{R}}_{\text{adj}}^{\text{2}} $ EMP/% 1 lnBst lnDBH −3.390*** 2.819*** 0.198 1.020 −2.796 0.988 15.329 2 lnH −4.294*** 2.992*** 0.379 1.074 45.139 0.760 31.771 3 ln(DBH 2 H) −3.839*** 0.981*** 0.127 1.008 −35.879 0.991 6.594 4 lnDBH+lnH −3.819*** 2.008*** 0.931*** 0.126 1.008 −28.036 0.992 6.532 5 lnBbr lnDBH −3.900*** 2.266*** 0.411 1.088 51.183 0.779 8.105 6 lnH −3.980*** 2.139*** 0.738 1.313 94.521 0.337 12.947 7 ln(DBH 2 H) −4.073*** 0.761*** 0.509 1.138 67.036 0.660 9.651 8 lnDBH+lnH −3.078*** 3.820*** −1.783*** 0.289 1.043 33.141 0.880 4.654 9 lnBlf lnDBH −2.752*** 1.443*** 0.309 1.049 30.082 0.615 4.669 10 lnH −2.635*** 1.367*** 0.494 1.130 64.880 0.294 6.724 11 ln(DBH 2 H) −2.685*** 0.485*** 0.362 1.068 41.757 0.529 5.378 12 lnDBH+lnH −2.070*** 2.392*** −1.089*** 0.252 1.032 23.012 0.684 3.131 13 lnBrt lnDBH −3.878*** 2.546*** 0.296 1.045 26.836 0.961 5.702 14 lnH −4.529*** 2.634*** 0.515 1.142 67.830 0.583 16.449 15 lnDBH 2 H −4.235*** 0.879*** 0.315 1.051 31.470 0.891 8.424 16 lnDBH+lnH −3.968*** 2.375*** 0.195 0.294 1.044 34.402 0.944 5.982 17 lnBab lnDBH −2.520*** 2.563*** 0.151 1.011 −23.122 0.984 15.244 18 lnH −3.179*** 2.653*** 0.448 1.105 57.539 0.662 51.487 19 ln(DBH 2 H) −2.881*** 0.885*** 0.184 1.017 −8.271 0.942 18.871 20 lnDBH+lnH −2.616*** 2.380*** 0.210 0.147 1.011 −17.100 0.977 13.434 21 lnBtt lnDBH −2.284*** 2.558*** 0.161 1.013 −18.204 0.988 17.691 22 lnH −2.940*** 2.648*** 0.451 1.107 58.157 0.655 67.534 23 ln(DBH 2 H) −2.644*** 0.883*** 0.193 1.019 −4.695 0.940 25.156 24 lnDBH+lnH −2.378*** 2.380*** 0.204 0.157 1.012 −11.837 0.980 16.482 说明：Bst. 干生物量；Bbr. 枝生物量；Blf. 叶生物量；Brt. 根生物量；Bab. 地上生物量；Btt. 总生物量。ERS. 残差标准误；FC. 矫正因子；CAI. 赤池信息准则；EMP. 平均预测误差。***表示P＜0.001水平上有显著性；βi0、βi1、βi2为回归系数。 -
将林龄作为自变量加入后再次进行回归分析，建立了加入林龄自变量的生物量异速生长模型共24个(表4)，其中树干生物量最优模型为模型27(DBH和H+林龄模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.993，EMP=7.167%；枝生物量最优模型为模型32 (DBH和H+林龄模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.894，EMP=3.931%；根生物量最优模型为模型37 (DBH+林龄模型)，$ {{R}}_{\text{adj}}^{\text{2}} $=0.959，EMP=7.164%；叶生物量、地上生物量及总生物量无最大$ {{R}}_{\text{adj}}^{\text{2}} $和最小EMP的组合。对于叶生物量，仅有模型35的$ {{R}}_{\text{adj}}^{\text{2}} $在0.9以上，因此可认为模型35为最佳模型(DBH 2 H+林龄模型)。对于地上生物量和总生物量，和不含林龄的异速生长模型选取的方式相同，于模型43、模型44和模型47、模型48中分别选取CAI最低拟合方程，得出地上生物量最优模型为模型43 (DBH 2 H+林龄模型)，总生物量最优模型为模型47 (DBH 2 H+林龄模型)。
表 4 桉树人工林各器官加入林龄的生物量估测模型
Table 4. Models for estimating the biomass of eucalyptus plantation forests by adding organs to stand age
模型
编号因变量 预测变量 βi0 βi1 βi2 βi3 βi4 βi5 ERS FC CAI $ {{R}}_{\text{adj}}^{\text{2}} $ EMP/% 25 lnBst lnDBH+a −3.617*** 2.829*** 0.291*** −0.089** 0.171 1.015 4.399 0.963 14.593 26 lnH +a −2.721*** 2.156*** −0.151 0.097 0.225 1.026 38.563 0.973 20.152 27 ln(DBH 2 H)+a −3.516*** 0.908*** 0.084 −0.005 0.115 1.007 −0.947 0.993 7.167 28 lnDBH+lnH+a −3.552*** 1.378*** 1.318** 0.140 0.066 −0.094 0.111 1.006 22.208 0.988 7.957 29 lnBbr lnDBH+a −2.619*** 1.671*** −0.399* 0.155** 0.368 1.070 71.897 0.872 6.345 30 lnH+a −1.004 0.683* −0.720 0.312* 0.519 1.144 93.797 0.787 7.458 31 ln(DBH 2 H)+a −2.154*** 0.464*** −0.591* 0.077** 0.415 1.090 83.892 0.822 6.935 32 lnDBH+lnH+a −2.495*** 4.076*** −2.258*** −0.408 −0.178 0.319 0.299 1.046 83.620 0.894 3.931 33 lnBlf lnDBH+a −1.938*** 1.282*** −0.507*** 0.163*** 0.264 1.036 50.066 0.686 3.955 34 lnH+a −0.751 0.548* −0.805* 0.300** 0.388 1.078 74.726 0.598 5.271 35 ln(DBH 2 H)+a −1.620*** 0.364*** −0.638*** 0.077*** 0.295 1.044 61.371 0.969 4.151 36 lnDB+lnH+a −1.992*** 2.235*** −0.862 −0.395 0.065 0.054 0.254 1.033 73.541 0.670 3.160 37 lnBrt lnDBH+a −4.083*** 2.544*** 0.290 −0.088 0.295 1.044 57.307 0.959 7.164 38 lnH+a −3.141*** 1.788*** 0.233 −0.022 0.421 1.093 80.024 0.906 13.746 39 ln(DBH 2 H)+a −3.873*** 0.788*** 0.170 −0.012 0.320 1.052 66.739 0.953 8.777 40 lnDBH+lnH+a −4.358*** 2.484*** 0.143 0.597* 0.010 −0.200 0.297 1.045 83.276 0.942 7.110 41 lnBab lnDBH+a −2.218*** 2.333*** 0.114 −0.022 0.133 1.009 −14.121 0.976 14.261 42 lnH+a −1.236*** 1.650*** −0.290 0.150* 0.257 1.033 47.385 0.950 31.455 43 ln(DBH 2 H)+a −2.050*** 0.734*** −0.079 0.017* 0.131 1.009 7.631 0.994 13.088 44 lnDBH+lnH+a −2.131*** 1.775*** 0.486* −0.016 0.017 0.008 0.130 1.009 32.134 0.985 13.055 45 lnBtt lnDBH+a −2.076*** 2.373*** 0.146 −0.034 0.155 1.012 14.686 0.960 20.894 46 lnH+a −1.106** 1.675*** −0.187 0.116 0.282 1.041 53.588 0.943 44.784 47 ln(DBH 2 H)+a −1.903*** 0.744*** −0.032 0.011 0.157 1.012 19.870 0.987 19.751 48 lnDBH+lnH+a −2.069*** 1.905*** 0.428 0.109 0.019 −0.037 0.152 1.012 41.869 0.986 18.834 说明：a. 林龄。Bst. 干生物量；Bbr. 枝生物量；Blf. 叶生物量；Brt. 根生物量；Bab. 地上生物量；Btt. 总生物量；ERS. 残差标准误；FC. 矫正因子；CAI. 赤池信息准则；EMP. 平均预测误差。***表示P＜0.001水平上有显著性；**表示P＜0.01；*表示P＜0.05。βi0、βi1、βi2、βi3、βi4、βi5为回归系数。 -
将不含林龄的各器官异速生长方程和加入林龄的各器官异速生长方程对比。在干水平上，不含林龄的异速生长方程最优模型为模型4，加入林龄后的异速生长方程最优模型为模型27。将两者进行比较，模型4的$ {{R}}_{\text{adj}}^{\text{2}} $小于模型27，模型27的EMP大于模型4，且两者$ {{R}}_{\text{adj}}^{\text{2}} $均大于0.99，将两者的预测值进行t检验，结果无显著差异(P=0.978)。由此可知：在干生物量预测方面，模型4与模型27均可视为最佳预测模型。在枝水平上，不含林龄的异速生长方程最优模型为模型8，加入林龄的最优异速生长模型为模型32，比较发现模型32的$ {{R}}_{\text{adj}}^{\text{2}} $大于模型8，且EMP小于模型8。由此可知：在枝水平上，加入林龄的模型32为最优预测模型。在叶生物量的8个模型中，仅有加入林龄的模型35的$ {{R}}_{\text{adj}}^{\text{2}} $＞0.9，因此选择模型35为叶生物量预测的最佳模型。在根水平上，不含林龄的最优模型(模型13)拥有比加入林龄的最优模型(模型37)更大的$ {{R}}_{\text{adj}}^{\text{2}} $与更小的EMP。由此可知：根生物量的最佳预测模型为不含林龄的模型13。在地上生物量水平上，比较不含林龄的最佳模型(模型17)与加入林龄的最佳模型(模型43)，发现模型43为两者中具有较的大$ {{R}}_{\text{adj}}^{\text{2}} $和较小的EMP，因此模型43为地上生物量的最佳预测模型。在全株生物量水平上进行比较，不含林龄最优模型21的EMP=17.691%，小于加入林龄最优模型47 (EMP=19.751%)。由此可知：在全株生物量预测中，不含林龄的模型21为最优模型。
-
林龄对树木生物量分配格局的影响既是树木自身生长的结果，同时也是树木为保证各个器官的生理活动和功能而进行资源分配平衡的结果[25−26]。以前的研究表明：植株的地上生物量在总生物量中的占比为79.00%[27−28]。本研究发现：尾巨桉人工林的地上生物量占总生物量的比例为74.79%~81.67%。地上生物量随林龄变化的分配模式为随着林龄的增长，干生物量占比逐渐增加，而枝生物量与叶生物量的占比逐渐减小。这与很多研究的结论相似[29−33]。在幼龄期，较高的枝和叶生物量占比，可以保证更多的生物量被分配用于光合作用[21]，这对于幼树的存活极为重要[30, 34]。随着林龄的增长，树木为了保证自身的物理稳定性[30]，会将更多的生物量分配给干的生长，因此叶和枝生物量增加的比例小于干生物量增加的比例[25]，进而导致干生物量占比随林龄逐渐增大，而枝和叶生物量占比随林龄的增大逐渐减小。根生物量在总生物量中的占比随林龄变化无一定规律。在本研究中，根生物量占比先增加，后逐渐下降，直至稳定，为18.33%~25.21%。这与其他研究得出的根生物量占比在林分建立后即大幅下降，最终稳定在一个数值的结论并不一致[30, 35]。这可能是由于人工林的人为抚育措施，尤其是施肥，对根系发育有着重要的影响，施肥时间的不固定性同样会导致根系生物量所占比例发生起伏[19]。
本研究发现：与对其他树种的研究结果一致[7, 36−40]，尾巨桉各器官生物量均符合异速关系理论；加入树高变量后，除根生物量、地上生物量及总生物量以外，其余各器官生物量的异速生长方程拟合效果均有提升。有许多研究也讨论了树高作为第2变量加入后对树木生物量异速生长方程的影响[41−43]，如WANGER等[41]对白松Pinus armandii进行研究，发现树高的加入改善了叶生物量异速生长方程的预测精度，XIANG等[23]对杉木Cunninghamia lanceolata的研究表明：加入树高变量后，提高了干、枝及叶生物量模型的预测精度；CIENCALA等[43]研究认为：赤松Pinus densiflora树高的加入轻微改善了各器官生物量方程的拟合效果。但JENKINS等[44]在对美国主要树种进行异速生长方程研究后认为：树高并不是一个有效变量，仅小部分改善预测效果。
林龄的加入对树木不同器官生物量的预测模型的改善程度并不相同。当将林龄加入异速生长方程后，枝、叶和地上生物量的异速生长方程的拟合效果均有改善，其中叶生物量方程的拟合效果改善最为明显，但对干生物量、根生物量和总生物量的拟合效果改善不大。这与PEICHL等[30]对白松的年龄序列下各器官生物量异速生长方程的研究结果一致。他们的研究表明：林龄变量的加入可改善枝和叶生物量的估算。XIANG等[23]对杉木的研究也表明：枝、叶生物量在不同林龄中有较高的变异。SAINT-ANDRÉ等[29]对杂交桉E. hybrid的研究也发现：林龄的加入改善了干、枝、叶和地上生物量的预测效果，但未改善根生物量的预测效果。同时他们也指出：加入林龄后，预测结果的变异不是林龄单一作用的结果，而是林龄和竞争共同作用的结果。BOND-LAMBERTY等[45]在研究6种北方树种的地上和地下生物量异速生长模型时引入了林龄，但发现引入林龄后对预测效果的改善并不总是具有显著性，具体取决于立地条件和树种。因此，在建立异速生长模型时，除考虑常规测树因子(树高、胸径、林龄等)以外，还需考虑竞争关系和立地条件等因素。
-
尾巨桉人工林各器官的生物量分配格局存在明显的林龄效应。随着尾巨桉林林龄的增加，枝、叶生物量占总生物量的比例逐渐下降，而干生物量占总生物量的比例逐渐增加，根生物量的比例先增加后下降，整体呈稳定趋势。在异速生长模型拟合效果对比中，加入树高因素后，干生物量、枝生物量及叶生物量模型的预测效果明显改善，但对根生物量、地上生物量及整株生物量预测效果的影响较小。将林龄作为变量加入异速生长方程后，枝生物量、叶生物量和地上生物量方程的预测结果明显改善，而对根生物量、干生物量及整株生物量影响较小。在各器官生物量最优模型选择上，以单独的DBH为自变量的模型对根生物量和总生物量的预测要优于其他模型；以DBH 2 H+林龄为自变量的模型对叶生物量和地上生物量的预测最佳；以DBH和H+林龄为自变量的模型对枝生物量的预测最佳；在对干生物量的预测精度对比中，以DBH和H与以DBH 2 H+林龄为自变量的预测模型之间无显著差异，均能较好的预测干生物量。
Age effect on biomass distribution pattern and optimization of allometric growth equation in Eucalyptus urophylla×E. grandis plantations
-
摘要:
目的 分析桉树Eucalyptus spp.人工林生物量分配格局随林龄的变化特征，为精准评估中国桉树产业碳储量及碳汇提供理论依据和数据支持。 方法 以雷州半岛尾巨桉E. urophylla×E. grandis人工林为研究对象，采用整株收获法测定1、2、3、6、10 年生的57株尾巨桉各器官的生物量，并利用胸径(DBH)、树高(H)和胸径-树高(DBH 2 H和DBHH)作为自变量分别建立不加入林龄变量与加入林龄变量的各器官生物量、地上生物量和总生物量的异速生长模型，进而筛选最优模型。 结果 尾巨桉各器官的生物量均随林龄增大而增大，但各器官生物量占总生物量的比例随林龄变化的特征并不相同，其中干生物量占比随林龄的增大而增大，由1年生的45.21%增长至10年生的68.25%；枝和叶的生物量占比则随林龄的增大而减小，分别由1年生的19.43%和16.31%减少至10年生的10.51%和2.91%；根生物量占比随林龄先增大后减小，由1年生的19.05%增长至3年生的25.21%后，逐渐下降到10年生的18.33%。尾巨桉的根冠比为0.16~0.39。在各器官生物量最优模型选择上，以DBH为自变量且未加入林龄变量的模型对根生物量和总生物量的预测优于其他模型；以DBH 2 H为自变量且加入林龄变量的模型对叶生物量和地上生物量的预测最佳；以DBH、H和林龄3个变量为自变量的模型对枝生物量的预测最佳；在对干生物量的预测精度对比中，以DBHH与以DBH 2 H+林龄为自变量的预测模型之间无显著差异，均能较好地预测干生物量。 结论 林龄对尾巨桉人工林各器官生物量分配比例影响较大，加入了林龄的异速生长模型对桉树人工林枝、叶和地上生物量的预测精度显著改善。图2表4参45 Abstract:Objective This study aims to analyze the biomass distribution pattern of Eucalyptus plantations at different ages, so as to provide theoretical basis and data support for accurate assessment of carbon storage and carbon sink in China’s Eucalyptus industry. Method Eucalyptus urophylla×E. grandis plantation in Leizhou Peninsula was taken as the research object. The whole-plant harvesting method was used to measure the biomass of various organs in 57 trees aged 1, 2, 3, 6 and 10. Using diameter at breast height (DBH), height (H), and diameter at breast height-tree height (DBH 2 H and DBHH) as independent variables, allometric growth models for organ biomass, aboveground biomass, and total biomass without and with age variables were established, respectively, to screen for the optimal model. Result The biomass of different parts of E. urophylla×E. grandis increased with age, but the proportion of each organ to the total biomass varied with age. The proportion of stem biomass increased with age, from 45.21% at 1 year old to 68.25% at 10 years old, whereas the proportion of branch and leaf biomass decreased with forest age, from 19.43% and 16.31% at 1 year old to 10.51% and 2.91% at 10 years old , respectively. The proportion of root biomass first increased from 19.05% at 1 year old to 25.21% at 3 years old, and then gradually decreased to 18.33% at 10 years old. The root to shoot ratio of E. urophylla×E. grandis ranged from 0.16 to 0.39. In selecting the optimal model for biomass of various organs, the model with DBH as the independent variable (without age variable) had better predictions for root biomass and total biomass than other models. The model with DBH 2 H plus age as independent variables had the best predictions for leaf biomass and aboveground biomass. The model with DBH, H, and age as independent variables had the best predictions for branch biomass. Regarding the prediction accuracy for stem biomass, there was no significant difference between the prediction models with DBHH and DBH 2 H plus age as independent variables, and both models could predict stem biomass well. Conclusion Forest age has significant impacts on the biomass allocation ratio of various organs in E. urophylla×E. grandis plantations. The prediction accuracy of branch, leaf, and aboveground biomass in E. urophylla×E. grandis plantations significantly improves if forest age is included in the allometric growth model. [Ch, 2 fig. 4 tab. 45 ref.] -
Key words:
- Eucalyptus urophylla×E. grandis /
- forest age /
- biomass /
- distribution pattern /
- allometric growth model
-
森林生态系统是陆地生态系统的主体，在减缓全球变暖方面具有不可替代的作用[1]。净生态系统生产力(net ecosystem productivity, NEP)作为净初级生产力和异养呼吸的差值，是表征生态系统碳收支的重要指标，被广泛应用于定量描述森林生态系统碳源/汇的能力。然而，大气温室气体浓度的增加使大气持水能力不断增强，显著增加了暴雨发生的频率和强度[2−3]，已成为影响森林NEP最大的因子之一[4]。中国位于北半球中高纬度地区，跨越不同的气候带，不同地区气候条件、植被生长异质[5]，使得中国极端降水及森林碳汇具有明显的区域特征，并且NEP对极端降水的响应也不同。因此，开展区域碳源/汇分布及其对极端降水响应研究，对气候灾害预防和生态保护具有重要意义。
准确估算极端降水时空格局是研究森林NEP响应极端降水的前提。相对阈值法是评判极端降水的常用方法，充分考虑了降水的地区间差异和季节因素[6]，具有极端性弱、噪声低、显著性强等优点，可以更客观地分析极端降水的气候特征和变化趋势[7]。遥感观测协同生态过程模型不仅能估算森林NEP时空动态，更能帮助分析NEP对气候的响应机制，在区域NEP时空动态研究中具有显著优势[8]。InTEC模型是CHEN等[9]开发的融入森林年龄及干扰影响的生态系统模型，能更准确地模拟长期森林碳循环动态变化，在省域[10]和全国[11]尺度均得到了广泛应用。结构方程模型综合了方差、回归、路径和因子等统计分析方法，能模拟多因子的内在逻辑关系，综合评估因果联系和潜变量关系，已被广泛应用于生态学领域[12]。本研究以浙江省丽水市为研究区域，通过百分位阈值法分析1979—2079年极端降水时空演变特征，采用InTEC模型模拟不同情景下丽水市森林NEP时空格局，并构建结构方程定量分析丽水市森林NEP对极端降水的响应。研究结果将为丽水森林生态系统响应与适应全球气候变化提供理论支持，为维持和提升其植被碳汇功能提供依据。
1. 材料与方法
1.1 研究区域
丽水市位于浙江省西南部(27°25′~28°57′N，118°41′~120°26′E)，森林面积为142.14 万hm2，森林覆盖率达82.27%，蓄积量为0.96 亿m 3，森林类型主要为亚热带针叶林、阔叶林和竹林等。林地的净初级生产力年总量与浙江省平均相比，所占比例较高[13]。丽水市地势西南高东北低，西南部以中山为主，东部以低山为主，中间有中山以及河谷盆地。全市主要气候类型为亚热带湿润季风气候，光照充足、四季分明、雨量丰沛。年均降水量为1 598.9 mm，多集中在3—9月，6月最多，是降水较为丰富的地区，也是极端气候事件多发的地区[14]。
1.2 丽水市极端降水时空格局估算
本研究利用百分位法描述极端降水时空特征，将月尺度的降水量从小到大排序，取其第95百分位值作为极端降水量阈值(mm·月−1)[15]。如果某月降水量超过这一阈值，则称该月发生了极端降水事件，累积该月降水量即为年极端降水量(mm·a−1)，并定义该年发生极端降水月数为极端降水频度(次·a−1)。最后，将极端降水量除以极端降水频度为极端降水强度(I)。
1.3 丽水市森林生态系统NEP时空分布估算
本研究使用InTEC模型模拟丽水市1979—2079年森林生态系统NEP，主要包括气象、土壤、森林年龄、参考年净初级生产力、氮沉降、二氧化碳(CO2)浓度及森林分布信息等时空分布数据。
1.3.1 气象数据
1979—2015年丽水市气象数据来源于中国气象局国家气象中心丽水市地面日值气象数据(
https://data.cma.cn )，包括最高气温、最低气温、降水量、太阳辐射及相对湿度。通过反距离加权插值法获得空间分辨率为1 km的日尺度栅格气象数据，然后通过累计获得月尺度气象数据。2016—2079年气象数据则采用第5次国际耦合比较计划(Coupled Model Intercomparison Project Phase 5, CMIP5)的3种气候情景RCP 2.6、RCP 4.5和RCP 8.5获得，并通过最近邻法重采样到1 km分辨率。1.3.2 森林分布数据
利用最大似然法从Landsat5 TM数据中提取2004年丽水市针叶林、阔叶林、竹林等30 m分辨率森林分布信息。为了保持数据空间分辨率的一致性，采用局部平均法获取1 km森林丰度信息。具体步骤见文献[16]。
1.3.3 土壤数据
土壤数据包括土壤粉粒百分比、砂粒百分比、黏粒百分比、土壤深度、土壤有效持水力、土壤容重以及土壤萎蔫点。其中前3个数据来源于联合国粮食和农业组织及国际应用分析学会共同开发的全球土壤数据库(HWSD 1.2，
https://iiasa.acat/Research/LUC/luc07/External-World-soil-database )。土壤容重使用Saxton改进的Brooks-Corey模型，结合土壤粉粒、砂粒、黏粒百分比来计算，土壤萎蔫点也根据粉粒、砂粒、黏粒百分比计算所得[17]。1.3.4 森林年龄数据
根据浙江省森林资源清查小班数据提供的森林年龄信息，在对2004年浙江省森林资源样地清查年龄信息统计的基础上，利用克里金插值法得到2004年浙江省丽水市1 km分辨率的森林年龄空间分布数据。
1.3.5 CO2浓度数据
1979—1999年的CO2浓度数据来源于全球监测地球系统研究实验室(
https://www.esrl.noaa.gov/gmd/ccgg/trends )；2000—2079年RCP 2.6、RCP 4.5和RCP 8.5等3种情景下模拟的CO2浓度数据来自典型浓度路径(representative concentration pathways，RCPs)数据库(https://tntcat.iiasa.ac.at/RcpDb )，使用线性插值将10 a尺度的CO2浓度数据插值成年尺度。1.3.6 氮沉降数据
氮沉降数据来源于全球格点大气总估计的无机氮、氮氢化合物和氮氧化物沉降量。1860、1993和2050年的氮沉降数据利用全球三维化传输模型(TM 3)模拟得到(
https://doi.org/10.3334/ORNLDAAC/830 )。本研究采用线性插值得到丽水市1979—2079年1 km空间分辨率的氮沉降数据。1.3.7 参考年净初级生力
本研究将2004年作为参考年校正初始的净初级生力值，使用BEPS模型模拟丽水市1 km分辨率净初级生力。具体模拟过程参考文献[18]。
1.4 极端降水和NEP时空演变分析
本研究利用最小二乘法计算线性回归模型的斜率来分析变量的时空演变特征(θ)。计算公式为：
$$ \theta = \frac{{n\displaystyle \sum\limits_{i = 1}^n {{x_i}{y_i} - \displaystyle \sum\limits_{i = 1}^n {{x_i}\displaystyle \sum\limits_{i = 1}^n {{y_i}} } } }}{{n\displaystyle \sum\limits_{i = 1}^n {{x_i}^2 - {{\left(\displaystyle \sum\limits_{i = 1}^n {{x_i}} \right)}^2}} }} 。 $$ (1) 式(1)中：n为年的总数；xi为年($ i $=1，2，…，50)；yi为第i年的变量值。θ＞0表示上升趋势，＜0表示下降趋势。
1.5 极端降水对NEP变化的影响
偏最小二乘(partial least square, PLS)通径分析是结构方程模型估计方法，可用以分析多变量之间的线性统计关系，可以有效解决多变量复共线问题，适用于变量多重相关或样本容量较小的情况，能克服变量数据分布复杂和变量之间相关的问题[12]。本研究采用该方法定量分析气候因子对NEP影响的相对重要程度及NEP驱动因子的直接作用和间接作用，在SmartPLS 3.3.9软件中进行。
2. 结果与分析
2.1 丽水市极端降水事件时空分布特征
通过百分位阈值法计算月尺度的极端降水和阈值的空间分布结果，以及极端降水强度的空间分布结果如图1所示。总体上，未来丽水市极端降水量及强度除RCP 2.6情景外，其他2种情景下均呈上升趋势，并且RCP 4.5情景下2个指标上升趋势面积达90%以上，但上升趋势不显著。丽水市历史极端降水阈值为(313.32±18.77) mm·月−1，随着辐射胁迫增加极端降水阈值逐步增加，最大达(364.28±11.87) mm·月−1，在空间上呈现由西南向东北递减的趋势。2016年之前丽水市所有地区极端降水量及强度均呈上升趋势，极端降水量平均值为481.73 mm·a−1。RCP 8.5情景下未来变化最明显，极端降水量均值达638.19 mm·a−1，比历史的年均极端降水量增加了156.46 mm·a−1，强度是历史的1.28倍。
图 1 历史(1979—2015年)及不同气候情景下未来(2016—2079年)丽水市极端降水的空间分布Figure 1 Spatial distribution of extreme precipitation in Lishui City under historical (1979－2015) and future (2016－2079) climate scenarios1979—2079年丽水市年极端降水累计次数的年际变化如图2所示。总体上，历史和未来极端降水增加趋势相近，分别为0.55与0.60，历史年极端降水次数增加量为20次·a−1，未来气候情景下年极端降水次数随辐射胁迫的增加而增加，至2079年累计发生次数分别较2016年增加33、35和36次·a−1，分别比历史次数增加了165%、175%、180%。
图 2 历史(1979—2019年)及不同气候情景下未来(2019—2079年)丽水市年极端降水累计次数的年际变化Figure 2 Interannual changes of the cumulative number of extreme precipitation in Lishui City under historical (1979－2019) and different climate scenarios (2019－2079)2.2 丽水市森林生态系统NEP时空演变特征
1979—2079年丽水市森林NEP的年际变化如图3所示。由图3A可见：1979—2015年丽水市森林NEP整体呈显著增长趋势。1979—1988年表现为碳源，1986年NEP值历史最低，为−439.24 g·m−2·a−1，1989年开始从碳源转为碳汇，累计NEP增至2015年的6.8 Pg。由图3B~C可见：3种情景下2016—2079年丽水市森林NEP碳汇量呈下降趋势，RCP 8.5气候情景对比最不明显，RCP 2.6和RCP 4.5情景下森林碳汇从2064年开始已经表现为碳源。碳汇累积量在2064年之前一直处于增加状态，之后除了RCP 8.5情景继续增加外，其他2种情景已经停止增加甚至有下降的现象。3种情景下的NEP累积量相对于2015年分别增加了8.51、9.32、10.97 Pg。总体来说，1979—2079年间丽水市森林NEP呈先增加再减少的趋势，并且在RCP 8.5情景下减少最慢。
图 3 历史(1979—2015年)及不同气候情景下未来(2016—2079年)丽水市森林NEP的年际变化Figure 3 Historical (1979－2015) and future (2016－2079) interannual changes of forest NEP in Lishui City under different climate scenarios图4为1979—2079年丽水市NEP以及时空演变特征的空间分布结果。从历史来看，1988—1996年碳汇能力增强，NEP＜0的区域减少到9.74%，2015年时NEP＞0的区域已达100%，丽水所有区域在历史上森林碳汇上升趋势都比较高。3种气候情景下，2016—2031年丽水市整体表现为碳汇，超过50%的区域为300＜NEP＜500 g·m−2·a−1，主要分布在北部区域；2032—2047年森林全市碳汇能力下降，超过80%的区域为100＜NEP＜300 g·m−2·a−1；2048—2063年森林碳汇能力持续下降，RCP 2.6下降最明显，主要在西部区域；2064—2079年，依旧持续下降。RCP 8.5气候情景77.01%的区域集中在0＜NEP＜100 g·m−2·a−1，RCP 2.6和RCP 4.5情景下NEP＜0的区域增加到66.49%和65.46%，积累量有下降的现象，且下降趋势高值区主要分布在东部和北部。
图 4 1979—2015基准年以及不同气候情景下2016—2079年丽水市NEP的空间分布和时空演变特征Figure 4 Spatial distribution of NEP and linear trend in Lishui City during 1979－2015 base year and 2016－2079 under different climate scenarios2.3 气候变化对森林生态系统NEP的影响
分析图5可知：1979—2079年丽水市气候因子对NEP的通径系数绝对值最大的均为降水，可见降水是森林生态系统NEP变化的重要驱动因子。由图5A得出：气候变化对NEP变化的直接影响为0.64，对极端降水的直接影响为0.30，气候变化通过影响极端降水进而影响NEP的间接影响为0.11 (0.30×0.37=0.11)，极端降水对NEP的直接影响为0.37，因此1979—2015年丽水市极端降水对NEP产生积极影响。由图5B可知：在RCP 2.6情景下，2016—2079年丽水市气候变化对NEP变化的直接影响为0.66，对极端降水的直接影响为0.62，气候变化通过影响极端降水进而影响NEP的间接影响为0.01 (0.62×0.02=0.01)，极端降水对NEP的直接影响不显著。由图5C可知：在RCP 4.5情景下，2016—2079年丽水市气候变化对NEP变化的直接影响为0.93，对极端降水的直接影响为0.53，气候变化通过极端降水对NEP产生的间接影响为0.20 (0.53×0.37=0.20)，极端降水对NEP的直接影响为0.37，并且对NEP产生消极影响。由图5D可知：在RCP 8.5情景下，2016—2079年丽水市气候变化对NEP变化的直接影响为0.93，对极端降水的直接影响为0.62，气候变化通过影响极端降水进而影响NEP的间接影响为0.07 (0.62×0.12=0.07)，极端降水对NEP的直接影响为0.12，对NEP变化产生消极影响。
图 5 历史(1979—2015年)及不同气候情景下未来(2016—2079年)下极端降水对NEP的影响Figure 5 Effects of extreme precipitation on NEP under historical (1979－2015) and different climate scenarios (2016－2079)3. 讨论
3.1 丽水市极端降水时空演变特征
本研究通过百分位阈值法研究了浙江省丽水市近百年的极端降水状况，结果表明：1979—2015年丽水市极端降水事件呈上升趋势，在丽水市东南部地区的上升趋势较大。RCP 2.6情景下，2016—2079年极端降水大部分呈下降趋势，RCP 4.5及RCP 8.5情景下，极端降水主要呈上升趋势，RCP 4.5情景相对于RCP 8.5情景的极端降水量、频数及强度增加更为明显。这与前人研究结果一致[19]。人类活动的加剧及地形影响，使浙江省温室气体增加，气温上升从而导致极端降水事件更容易发生[2−3]。极端降水在浙江西部及南部等地上升趋势较大的原因主要是由于南部及西部地区多丘陵山地，湿润气流遇到山脉等阻挡时被迫抬升，气温降低，容易形成地形雨。丽水位于浙江省西南部，全市多山地，比浙江的中部盆地和东北部冲积平原更容易发生极端降水事件，因此丽水市未来应加强洪涝灾害的预防。
长江流域及以南地区极端降水增多主要是由极端降水频数增加导致的[20]。本研究采用偏最小二乘法分析得知：1979—2079年极端降水频数对极端降水事件的通径系数大于极端降水强度对极端降水事件的通径系数，说明丽水市极端降水量的增加亦主要受极端降水频数的影响。另外，本研究是以年尺度分析极端降水事件变化。极端降水与季节有较强的相关性，并且极端降水的开始时间及持续时间都将直接或间接影响[7]丽水市气候的变化，因此，未来应将这些指标纳入丽水市极端降水变化特征的研究。
3.2 NEP时空模拟的不确定性
本研究发现：1979—2015年期间，丽水市森林NEP从1989年由碳源逐渐转为碳汇，这主要是由于1989年前人为干扰严重，导致森林质量下降，1989年以后，随着退耕还林政策的实施，全省森林质量得到改善，森林面积、年龄逐渐增加，使得碳汇能力增强[21]。2016—2079年3种气候情景下，丽水市森林碳汇均呈下降趋势，主要是受到森林年龄继续增加及气候变化的影响[10]，其中随着未来极端降水事件的增加，森林NEP也呈下降趋势。
本研究通过InTEC模型模拟丽水市森林NEP的时空分布，虽然总体上精度较好，但仍然存在一些误差。首先，森林年龄对InTEC模型的模拟结果影响较大[10]。丽水市森林多属异龄林，森林资源清查的年龄数据为森林平均年龄，与森林实际情况有差别，通过空间插值后的数据也会存在误差。其次，本研究采用的3种气候情景的气象数据空间分辨率较低，通过线性插值生成的1 km分辨率气象数据对森林碳通量和极端降水空间解析不够细致，导致结果存在误差，但对长时间(百年尺度)碳通量演变和极端降水变化趋势仍具有一定参考价值。另外，本研究假设丽水市森林区域未来保持不变，然而实际上随着社会经济的发展，森林区域会发生改变，给模型模拟结果带来不确定性。因此，未来应进一步提高丽水森林空间分布、土壤、地形、气象等数据分辨率，更精确地模拟丽水市森林碳通量时空格局。
3.3 极端降水对NEP的影响
偏最小二乘通径模型分析结果表明：降水是影响NEP变化的重要因子。1979—2015年极端降水对NEP产生了积极影响。这与WANG等[5]的研究结果一致，可能得益于植被对降水有一定程度的适应和抵抗能力，当极端降水超过阈值时，会对生态系统造成消极影响[4]。一方面可能导致植被根系严重缺氧、呼吸减慢，最终引起植被死亡；另一方面极端降水频次和强度会加剧土壤侵蚀，导致地表水土流失，造成颗粒和有机碳从陆地生态系统流向河流生态系统，从而改变生态系统碳源汇的大小和空间分布。可见，气候变化强度的增加对生态系统消极影响的也会变得严重[22]。虽然偏最小二乘通径分析因子间存在直接和间接影响，但受模型算法限制无法得到超过生态系统抵抗力和恢复力的阈值，未来可以通过极端降水和气候综合敏感性分析、多情景模拟比较，进一步揭示极端降水对NEP影响的阈值，阐明极端降水影响森林NEP的关键。
4. 结论
浙江省丽水市历史、RCP 4.5及RCP 8.5情景下极端降水量、频数及强度均呈增加趋势，RCP 2.6呈下降趋势。极端降水事件上升趋势较高的地区主要位于丽水市南部和东南部地区。
1979—2015年丽水市森林NEP以18.44 g·m−2·a−1的速度增加，在1989年由碳源转变为碳汇。2016—2079年，3种气候情景下丽水市森林NEP均呈下降趋势，但碳汇总量呈上升趋势，说明在未来气候情景下，丽水市森林生态系统依然具有较高的碳汇潜力。
降水是影响NEP变化的重要驱动因子。虽然历史模拟显示极端降水对丽水NEP的影响为0.37，但未来气候变化情景下，除RCP 2.6情景不显著外，其余2种情景均对NEP产生显著消极影响，说明随着气候变化强度加剧，极端降水将对丽水市森林生态系统碳汇能力产生负面作用，应当积极采取森林经营措施，提高森林对极端气候事件抵抗力，使森林更好地服务实现“双碳”目标。
-
图 1 不同林龄尾巨桉生物量分配格局
Figure 1 Patterns of biomass allocation in E. urophylla×E. grandis at different stand ages
图 2 尾巨桉各器官单株生物量与地上生物量拟合
Figure 2 Fitting of individual tree biomass of various organs of E. urophylla×E. grandis with aboveground biomass
表 1 样木的基本信息
Table 1. Basic informations of sample woods
林分年
龄/a平均胸
径/cm平均树
高/m径阶范
围/cm样本
数量活立木密度/
(株·hm−2)林分年
龄/a平均胸
径/cm平均树
高/m径阶范
围/cm样本
数量活立木密度/
(株·hm−2)1 4.92±0.92 5.27±0.90 3.00~4.00 3 1 666 3 10.95±1.79 12.51±0.87 7.00~9.00 3 1 616 4.00~5.00 3 9.00~11.00 3 5.00~6.00 3 11.00~13.00 3 6.00~7.00 3 6 12.62±2.80 16.09±1.95 8.00~11.00 3 1 449 2 8.71±1.37 11.81±1.38 5.00~6.00 3 1 616 11.00~14.00 3 6.00~7.00 3 14.00~17.00 3 7.00~8.00 3 10 22.35±2.89 20.71±2.68 18.00~21.00 3 1 366 8.00~9.00 3 21.00~24.00 3 9.00~10.00 3 24.00~27.00 3 10.00~11.00 3 说明：径阶数值采用上限排除法，平均胸径与平均树高的表示形式为平均值±标准差。 
下载: 导出CSV
表 2 尾巨桉各器官间单株生物量比率随林龄的变化
Table 2. Changes in single-tree biomass ratios among various organs of E. urophylla×E. grandis with stand age
林龄/a 根生物量/
地上生物量枝生物量/
干生物量叶生物量/
干生物量林龄/a 根生物量/
地上生物量枝生物量/
干生物量叶生物量/
干生物量1 0.235 0.430 0.361 6 0.251 0.144 0.052 2 0.263 0.143 0.107 10 0.225 0.154 0.043 3 0.337 0.144 0.068
下载: 导出CSV
表 3 桉树人工林各器官不含林龄的生物量估测模型
Table 3. Models for estimating biomass of eucalyptus plantation forests by organ without stand age
模型编号 因变量 预测变量 βi0 βi1 βi2 ERS FC CAI $ {{R}}_{\text{adj}}^{\text{2}} $ EMP/% 1 lnBst lnDBH −3.390*** 2.819*** 0.198 1.020 −2.796 0.988 15.329 2 lnH −4.294*** 2.992*** 0.379 1.074 45.139 0.760 31.771 3 ln(DBH 2 H) −3.839*** 0.981*** 0.127 1.008 −35.879 0.991 6.594 4 lnDBH+lnH −3.819*** 2.008*** 0.931*** 0.126 1.008 −28.036 0.992 6.532 5 lnBbr lnDBH −3.900*** 2.266*** 0.411 1.088 51.183 0.779 8.105 6 lnH −3.980*** 2.139*** 0.738 1.313 94.521 0.337 12.947 7 ln(DBH 2 H) −4.073*** 0.761*** 0.509 1.138 67.036 0.660 9.651 8 lnDBH+lnH −3.078*** 3.820*** −1.783*** 0.289 1.043 33.141 0.880 4.654 9 lnBlf lnDBH −2.752*** 1.443*** 0.309 1.049 30.082 0.615 4.669 10 lnH −2.635*** 1.367*** 0.494 1.130 64.880 0.294 6.724 11 ln(DBH 2 H) −2.685*** 0.485*** 0.362 1.068 41.757 0.529 5.378 12 lnDBH+lnH −2.070*** 2.392*** −1.089*** 0.252 1.032 23.012 0.684 3.131 13 lnBrt lnDBH −3.878*** 2.546*** 0.296 1.045 26.836 0.961 5.702 14 lnH −4.529*** 2.634*** 0.515 1.142 67.830 0.583 16.449 15 lnDBH 2 H −4.235*** 0.879*** 0.315 1.051 31.470 0.891 8.424 16 lnDBH+lnH −3.968*** 2.375*** 0.195 0.294 1.044 34.402 0.944 5.982 17 lnBab lnDBH −2.520*** 2.563*** 0.151 1.011 −23.122 0.984 15.244 18 lnH −3.179*** 2.653*** 0.448 1.105 57.539 0.662 51.487 19 ln(DBH 2 H) −2.881*** 0.885*** 0.184 1.017 −8.271 0.942 18.871 20 lnDBH+lnH −2.616*** 2.380*** 0.210 0.147 1.011 −17.100 0.977 13.434 21 lnBtt lnDBH −2.284*** 2.558*** 0.161 1.013 −18.204 0.988 17.691 22 lnH −2.940*** 2.648*** 0.451 1.107 58.157 0.655 67.534 23 ln(DBH 2 H) −2.644*** 0.883*** 0.193 1.019 −4.695 0.940 25.156 24 lnDBH+lnH −2.378*** 2.380*** 0.204 0.157 1.012 −11.837 0.980 16.482 说明：Bst. 干生物量；Bbr. 枝生物量；Blf. 叶生物量；Brt. 根生物量；Bab. 地上生物量；Btt. 总生物量。ERS. 残差标准误；FC. 矫正因子；CAI. 赤池信息准则；EMP. 平均预测误差。***表示P＜0.001水平上有显著性；βi0、βi1、βi2为回归系数。
下载: 导出CSV
表 4 桉树人工林各器官加入林龄的生物量估测模型
Table 4. Models for estimating the biomass of eucalyptus plantation forests by adding organs to stand age
模型
编号因变量 预测变量 βi0 βi1 βi2 βi3 βi4 βi5 ERS FC CAI $ {{R}}_{\text{adj}}^{\text{2}} $ EMP/% 25 lnBst lnDBH+a −3.617*** 2.829*** 0.291*** −0.089** 0.171 1.015 4.399 0.963 14.593 26 lnH +a −2.721*** 2.156*** −0.151 0.097 0.225 1.026 38.563 0.973 20.152 27 ln(DBH 2 H)+a −3.516*** 0.908*** 0.084 −0.005 0.115 1.007 −0.947 0.993 7.167 28 lnDBH+lnH+a −3.552*** 1.378*** 1.318** 0.140 0.066 −0.094 0.111 1.006 22.208 0.988 7.957 29 lnBbr lnDBH+a −2.619*** 1.671*** −0.399* 0.155** 0.368 1.070 71.897 0.872 6.345 30 lnH+a −1.004 0.683* −0.720 0.312* 0.519 1.144 93.797 0.787 7.458 31 ln(DBH 2 H)+a −2.154*** 0.464*** −0.591* 0.077** 0.415 1.090 83.892 0.822 6.935 32 lnDBH+lnH+a −2.495*** 4.076*** −2.258*** −0.408 −0.178 0.319 0.299 1.046 83.620 0.894 3.931 33 lnBlf lnDBH+a −1.938*** 1.282*** −0.507*** 0.163*** 0.264 1.036 50.066 0.686 3.955 34 lnH+a −0.751 0.548* −0.805* 0.300** 0.388 1.078 74.726 0.598 5.271 35 ln(DBH 2 H)+a −1.620*** 0.364*** −0.638*** 0.077*** 0.295 1.044 61.371 0.969 4.151 36 lnDB+lnH+a −1.992*** 2.235*** −0.862 −0.395 0.065 0.054 0.254 1.033 73.541 0.670 3.160 37 lnBrt lnDBH+a −4.083*** 2.544*** 0.290 −0.088 0.295 1.044 57.307 0.959 7.164 38 lnH+a −3.141*** 1.788*** 0.233 −0.022 0.421 1.093 80.024 0.906 13.746 39 ln(DBH 2 H)+a −3.873*** 0.788*** 0.170 −0.012 0.320 1.052 66.739 0.953 8.777 40 lnDBH+lnH+a −4.358*** 2.484*** 0.143 0.597* 0.010 −0.200 0.297 1.045 83.276 0.942 7.110 41 lnBab lnDBH+a −2.218*** 2.333*** 0.114 −0.022 0.133 1.009 −14.121 0.976 14.261 42 lnH+a −1.236*** 1.650*** −0.290 0.150* 0.257 1.033 47.385 0.950 31.455 43 ln(DBH 2 H)+a −2.050*** 0.734*** −0.079 0.017* 0.131 1.009 7.631 0.994 13.088 44 lnDBH+lnH+a −2.131*** 1.775*** 0.486* −0.016 0.017 0.008 0.130 1.009 32.134 0.985 13.055 45 lnBtt lnDBH+a −2.076*** 2.373*** 0.146 −0.034 0.155 1.012 14.686 0.960 20.894 46 lnH+a −1.106** 1.675*** −0.187 0.116 0.282 1.041 53.588 0.943 44.784 47 ln(DBH 2 H)+a −1.903*** 0.744*** −0.032 0.011 0.157 1.012 19.870 0.987 19.751 48 lnDBH+lnH+a −2.069*** 1.905*** 0.428 0.109 0.019 −0.037 0.152 1.012 41.869 0.986 18.834 说明：a. 林龄。Bst. 干生物量；Bbr. 枝生物量；Blf. 叶生物量；Brt. 根生物量；Bab. 地上生物量；Btt. 总生物量；ERS. 残差标准误；FC. 矫正因子；CAI. 赤池信息准则；EMP. 平均预测误差。***表示P＜0.001水平上有显著性；**表示P＜0.01；*表示P＜0.05。βi0、βi1、βi2、βi3、βi4、βi5为回归系数。
下载: 导出CSV
-
[1] 郭泽鑫, 曹聪, 刘萍. 基于连清数据的广东杉木人工林生物量模型构建[J]. 中南林业科技大学学报, 2022, 42(8): 78 − 89. GUO Zexin, CAO Cong, LIU Ping. Construction of biomass models of Cunninghamia lanceolata plantation based on continuous forest inventory in Guangdong [J]. Journal of Central South University of Forestry &Technology, 2022, 42(8): 78 − 89. [2] 周昊, 叶尔江•拜克吐尔汉, 何怀江, 等. 东北地区主要造林树种幼苗期生物量分配特征与异速生长模型[J]. 林业科学, 2023, 59(11): 23 − 32. ZHOU Hao, Yeerjiang Baiketuerhan, HE Huaijiang, et al. Biomass distribution characteristics and species-specific allometric equations for afforestation species in Northeast China [J]. Scientia Silvae Sinicae, 2023, 59(11): 23 − 32. [3] 王海军, 李峰, 肖楠. 黑龙江省主要碳汇树种生物量异速生长方程研究[J]. 防护林科技, 2016(5): 21 − 22. WANG Haijun, LI Feng, XIAO Nan. Allomteric equation fog biomass of the main carbon sink species in Heilongjiang Province [J]. Protection Forest Science and Technology, 2016(5): 21 − 22. [4] SOLTANI A. Mathematical Modeling in Field Crops [M]. Mashhad: JMD Press, 2009. [5] NIKLAS K J. Plant Allometry: the Scaling of Form and Process [M]. Chicago: University of Chicago Press, 1994. [6] SUN Han, WANG Xiaoping, FAN Dayong. Effects of climate, biotic factors, and phylogeny on allometric relationships: testing the metabolic scaling theory in plantations and natural forests across China [J/OL]. Forest Ecosystems, 2020, 7: 51[2024-01-14]. doi: 10.1186/s40663-020-00263-y. [7] 陈东升, 孙晓梅, 金英博, 等. 林龄和竞争对日本落叶松各组分生物量异速关系的影响[J]. 生态学报, 2020, 40(3): 843 − 853. CHEN Dongsheng, SUN Xiaomei, JIN Yingbo, et al. Effects of stand age and competition on allometric relationships for biomass partitioning in Larix kaempferi plantation [J]. Acta Ecologica Sinica, 2020, 40(3): 843 − 853. [8] 董点, 林天喜, 唐景毅, 等. 紫椴生物量分配格局及异速生长方程[J]. 北京林业大学学报, 2014, 36(4): 54 − 63. DONG Dian, LIN Tianxi, TANG Jingyi, et al. Biomass allocation patterns and allometric models of Tilia amurensis [J]. Journal of Beijing Forestry University, 2014, 36(4): 54 − 63. [9] 薛春泉, 徐期瑚, 林丽平, 等. 基于异速生长和理论生长方程的广东省木荷生物量动态预测[J]. 林业科学, 2019, 55(7): 86 − 94. XUE Chunquan, XU Qihu, LIN Liping, et al. Biomass dynamic predicting for Schima superba in Guangdong based on allometric and theoretical growth equation [J]. Scientia Silvae Sinicae, 2019, 55(7): 86 − 94. [10] 兰洁, 肖中琪, 李吉玫, 等. 天山雪岭云杉生物量分配格局及异速生长模型[J]. 浙江农林大学学报, 2020, 37(3): 416 − 423. LAN Jie, XIAO Zhongqi, LI Jimei, et al. Biomass allocation and allometric growth of Picea schrenkiana in Tianshan Mountains [J]. Journal of Zhejiang A&F University, 2020, 37(3): 416 − 423. [11] 刘坤, 曹林, 汪贵斌, 等. 银杏生物量分配格局及异速生长模型[J]. 北京林业大学学报, 2017, 39(4): 12 − 20. LIU Kun, CAO Lin, WANG Guibin, et al. Biomass allocation patterns and allometric models of Ginkgo biloba [J]. Journal of Beijing Forestry University, 2017, 39(4): 12 − 20. [12] PICARD N, RUTISHAUSER E, PLOTON P, et al. Should tree biomass allometry be restricted to power models? [J]. Forest Ecology and Management, 2015, 353: 156 − 163. [13] DJOMO A N, CHIMI C D. Tree allometric equations for estimation of above, below and total biomass in a tropical moist forest: case study with application to remote sensing [J]. Forest Ecology and Management, 2017, 391: 184 − 193. [14] GOODMAN R C, PHILLIPS O L, BAKER T R. The importance of crown dimensions to improve tropical tree biomass estimates [J]. Ecological Applications, 2014, 24(4): 680 − 698. [15] SATOO T, MADGWICK H A I. Forest Biomass [M]. Boston: Martinus Nijhoff /Dr. W. Junk Publishers, 1982: 152. [16] HELMISAARI H, MAKKONEN K, KELLOMÄKI S, et al. Below- and above-ground biomass, production and nitrogen use in scots pine stands in eastern Finland [J]. Forest Ecology and Management, 2002, 165(1/3): 317 − 326. [17] 国家林业和草原局. 中国森林资源报告(2014—2018)[M]. 北京: 中国林业出版社, 2019. National Forestry and Grassland Administration. China Forest Resources Report (2014−2018) [M]. Beijing: China Forestry Publishing House, 2019. [18] 杨忠, 张建平, 王道杰, 等. 元谋干热河谷桉树人工林生物量初步研究[J]. 山地学报, 2001, 19(6): 503 − 510. YANG Zhong, ZHANG Jianping, WANG Daojie, et al. Preliminary study on the biomass of artificial Eucalyptus camaldulensis Dehnl forests in Arid-Hot Valleys, Yuanmou [J]. Journal of Mountain Science, 2001, 19(6): 503 − 510. [19] 张利丽, 王志超, 陈少雄, 等. 不同林龄尾巨桉人工林的生物量分配格局[J]. 西北农林科技大学学报(自然科学版), 2017, 45(6): 61 − 68. ZHANG Lili, WANG Zhichao, CHEN Shaoxiong, et al. Biomass allocation pattern of Eucalyptus urophylla×Eucalyptus grandis plantation at different ages [J]. Journal of Northwest A&F University (Natural Science Edition), 2017, 45(6): 61 − 68. [20] 揭凡, 杜阿朋, 竹万宽. 桉树生物量估算模型及与IPCC法的对比分析[J]. 桉树科技, 2019, 36(1): 1 − 8. JIE Fan, DU Apeng, ZHU Wankuan. Allometry equations for estimating Eucalyptus tree biomass and comparison with IPCC method [J]. Eucalypt Science &Technology, 2019, 36(1): 1 − 8. [21] XU Yuxing, DU Apeng, WANG Zhichao, et al. Effects of different rotation periods of eucalyptus plantations on soil physiochemical properties, enzyme activities, microbial biomass and microbial community structure and diversity [J/OL]. Forest Ecology and Management, 2020, 456: 117683[2024-01-14]. doi: 10.1016/j.foreco.2019.117683. [22] WANG Zhichao, LIU Siru, XU Yuxing, et al. Differences in transpiration characteristics among Eucalyptus plantations of three species on the Leizhou Peninsula, Southern China [J/OL]. Forests, 2022, 13(10): 1544[2024-01-14]. doi: 10.3390/f13101544. [23] XIANG Wenhua, LI Linhua, OUYANG Shuai, et al. Effects of stand age on tree biomass partitioning and allometric equations in Chinese fir (Cunninghamia lanceolata) plantations [J]. European Journal of Forest Research, 2021, 140(2): 317 − 332. [24] AKAIKE H. A new look at the statistical model identification [J]. IEEE Transactions on Automatic Control, 1974, 19(6): 716 − 723. [25] MENSAH S, KAKAÏ R G, SEIFERT T. Patterns of biomass allocation between foliage and woody structure: the effects of tree size and specific functional traits [J]. Annals of Frest Research, 2016, 59(1): 49 − 60. [26] 刘宣, 肖洒, 朱鹏, 等. 亚热带同质园不同人工林的生物量和林下植被多样性差异[J]. 浙江农林大学学报, 2022, 39(4): 717 − 726. LIU Xuan, XIAO Sa, ZHU Peng, et al. Difference of biomass and understory vegetation diversity among different subtropical plantations in common gardens [J]. Journal of Zhejiang A&F University, 2022, 39(4): 717 − 726. [27] HOUGHTON R A, LAWRENCE K T, HACKLER J L, et al. The spatial distribution of forest biomass in the Brazilian Amazon: a comparison of estimates [J]. Golbal Change Biology, 2001, 7(7): 731 − 746. [28] SAATCHI S S, HOUGHTON R A, ALVALÁ R C D S, et al. Distribution of aboveground live biomass in the Amazon Basin [J]. Global Change Biology, 2007, 13(4): 816 − 837. [29] SAINT-ANDRÉ L, M BOU A T, MABIALA A, et al. Age-related equations for above- and below-ground biomass of a eucalyptus hybrid in Congo [J]. Forest Ecology and Management, 2005, 205(1): 199 − 214. [30] PEICHL M, ARAIN M A. Allometry and partitioning of above- and belowground tree biomass in an age-sequence of white pine forests [J]. Forest Ecology and Management, 2007, 253(1/3): 68 − 80. [31] SEO Y O, LEE Y J, LUMBRES R I C, et al. Influence of stand age class on biomass expansion factor and allometric equations for Pinus rigida plantations in South Korea [J]. Scandinavian Journal of Forest Research, 2013, 28(6): 566 − 573. [32] LIM H W, LEE K H, LEE K H, et al. Biomass expansion factors and allometric equations in an age sequence for Japanese cedar (Cryptomeria japonica) in Southern Korea [J]. Journal of Forest Research, 2013, 18(4): 316 − 322. [33] LI Hui, LI Chunyi, ZHA Tianshan, et al. Patterns of biomass allocation in an age-sequence of secondary Pinus bungeana forests in China [J]. The Forestry Chronicle, 2014, 90(2): 169 − 176. [34] FATEMI F R, YANAI R D, HAMBURG S P, et al. Allometric equations for young northern hardwoods: the importance of age-specific equations for estimating aboveground biomass [J]. Canadian Journal of Forest Research, 2011, 41(4): 881 − 891. [35] TOBIN B, NIEUWENHUIS M. Biomass expansion factors for Sitka spruce (Picea sitchensis (Bong. ) Carr. ) in Ireland [J]. European Journal of Forest Research, 2007, 126(2): 189 − 196. [36] ZIANIS D, MENCUCCINI M. On simplifying allometric analyses of forest biomass [J]. Forest Ecology and Management, 2004, 187(2/3): 311 − 332. [37] PILLI R, ANFODILLO T, CARRER M. Towards a functional and simplified allometry for estimating forest biomass [J]. Forest Ecology and Management, 2006, 237(1/3): 583 − 593. [38] VERÓNICA G, LUIS P P, GERARDO R. Allometric relations for biomass partitioning of Nothofagus antarctica trees of different crown classes over a site quality gradient [J]. Forest Ecology and Management, 2010, 259(6): 1118 − 1126. [39] MOROTE F A G, SERRANO F R L, ANDRÉS M, et al. Allometries, biomass stocks and biomass allocation in the thermophilic Spanish juniper woodlands of Southern Spain [J]. Forest Ecology and Management, 2012, 270: 85 − 93. [40] SINGNAR P, DAS M C, SILESHI G W, et al. Allometric scaling, biomass accumulation and carbon stocks in different aged stands of thin-walled bamboos Schizostachyum dullooa, Pseudostachyum polymorphum and Melocanna baccifera [J]. Forest Ecology and Management, 2017, 395: 81 − 91. [41] WAGNER R G, TER-MIKAELIAN M T. Comparison of biomass component equations for four species of northern coniferous tree seedlings [J]. Annals of Forest Science, 1999, 56(3): 193 − 199. [42] XIAO Chunwang, CEULEMANS R. Allometric relationships for below- and aboveground biomass of young scots pines [J]. Forest Ecology and Management, 2004, 203(1/3): 177 − 186. [43] CIENCIALA E, ČERNÝ M, TATARINOV F, et al. Biomass functions applicable to scots pine [J]. Trees, 2006, 20(4): 483 − 495. [44] JENKINS J C, CHOJNACKY D C, HEALTH L S, et al. National scale biomass estimators for United States tree species [J]. Forest Science, 2003, 49(1): 12 − 35. [45] BOND-LAMBERTY B, WANG C, GOWER S T. Aboveground and belowground biomass and sapwood area allometric equations for six boreal tree species of northern Manitoba [J]. Canadian Journal of Forest Research, 2002, 32(8): 1441 − 1450. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20240180
点击查看大图
计量
- 文章访问数: 542
- HTML全文浏览量: 122
- PDF下载量: 34
- 被引次数: 0
