-
由断裂力学原理可知，构件中的孔洞会导致出现应力集中的现象，从而削弱构件的承载能力[1]。然而，不同材料对于孔洞损伤的容受程度有明显区别：脆性材料对于孔洞的容受能力差，塑性材料对于孔洞损伤的容受能力虽然强于脆性材料，但普通塑性材料构件中的孔洞损伤仍会导致构件承载能力明显下降[2]。已有研究表明：生物在进化过程中需不断对抗外载荷及意外破坏，相比于非生物质材料所制成的承载构件，由生物质材料制成的承载构件往往具有更优良的孔洞容受特性[3−5]，对其机制的深入研究有助于开发具有优良损伤容受特性的新型工程材料[6−7]。木材是重要的生物质材料，木构件对于孔洞损伤的容受特性及其“孔洞相容”的力学机制值得深入研究。
孔洞损伤[8−9]在承载木构件中具有普遍性，在许多使用情形下都需要木构件与孔洞共存。如木构件中存在虫洞[10]或结疤[11]，因结构连接的需要对木构件打孔[12]，因装修中管线布设的需要对木构件钻孔，木构件被意外破坏且难以更换(如应县木塔中带有弹孔但难以更换的木梁[13])等。
木梁作为极其重要的承载构件，研究孔洞对其力学性能的影响至关重要。含孔洞木梁在脆性较强时，承载破坏时的断裂现象往往是突然发生的，因此需要通过模拟实验预估断裂的风险，避免断裂事故发生。目前已有研究尝试评估孔洞对承载木梁的影响。温宇鑫等[14]分析了 3 种不同的孔洞位置(中心、受压区和受拉区)对核桃楸Juglans mandshurica木梁弯曲应变分布的影响，探讨了中性轴位置的偏移规律；OKAMOTO等[15]针对带有圆孔的胶合木梁的承重能力问题开展了研究，结合实验测试和数值模拟，考察了3种不同尺寸的孔洞对木梁整体承载能力的影响；DANIELSSON等[16]利用一种基于概率断裂力学(PFM)的方法，分析了带有孔洞的胶合木梁的强度；BUKSNOWITZ等[17]通过电子散斑干涉术和有限元仿真(FEA)研究了树木节疤作为树干上的自然孔洞对于树干整体应力分布的影响；PARRACHA等[18]研究了含微小虫洞松木承载构件的剩余强度问题。上述研究对于木梁孔洞周围的应变场变化规律和木梁中性轴的偏移规律给出了较为精准的描述，对木梁承重性能受到孔洞影响的规律进行了初步的分析。
本研究在上述研究的基础上，提出孔洞相容的力学概念，并给出孔洞相容系数的计算公式用以评估孔洞对木梁承载能力的影响，探讨木梁孔洞相容力学现象的形成机制。本研究能为含孔木梁的安全评估与合理设计提供参考依据，并对新型纤维增强复合材料[19]、含孔洞轻量化承载结构[20]的设计，以及微孔洞结构材料[21]的制备研究等有所启发。
-
根据密度从低到高的原则，选取了10种具有代表性的木材(表1)。表1中所列数据参考了《中国木材志》[22]中提供的数据，并通过测量数据进行了修正。
表 1 实验考察木材的名称、气干密度及分类特征
Table 1. Names, air dry density and classification characteristics of experimental wood
序号 木材名称 气干密度/
(kg·m−3)分类特性 序号 木材名称 气干密度/
(kg·m−3)分类特性 1 轻木Ochroma lagopus 150 阔叶材 6 水曲柳Fraxinus mandshurica木 686 阔叶材 2 泡桐Paulownia fargesii木 280 阔叶材 7 黑胡桃Juglans nigra木 720 阔叶材 3 杉木Cunninghamia lanceolata 320 针叶材 8 榉Zelkova schneideriana木 790 阔叶材 4 樟子松Pinus sylvestris var. mongolica木 477 针叶材 9 黄檀Dalbergia hupeana木 923 阔叶材 5 白桦Betula platyphylla木 615 阔叶材 10 紫光檀Dalbergia melanoxylon木 1290 阔叶材 -
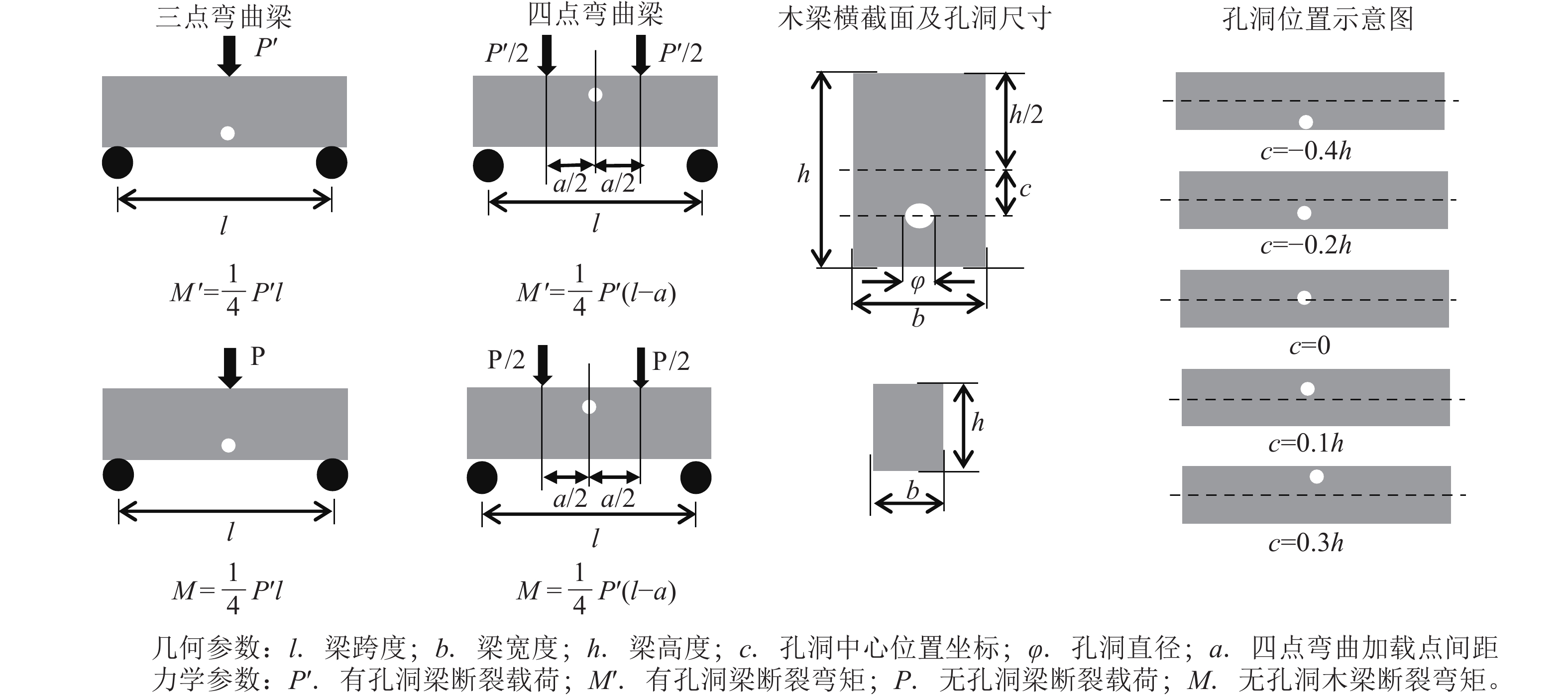
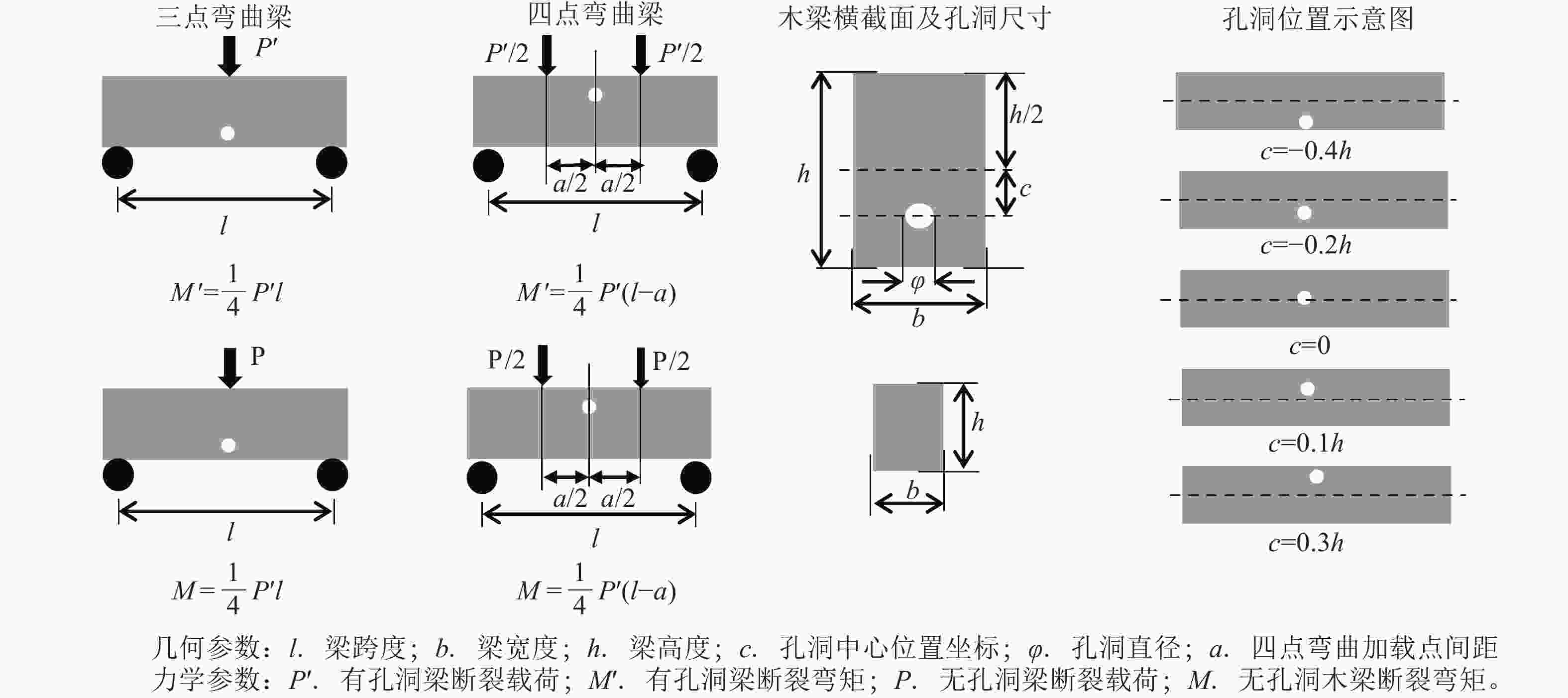
考虑到梁的中跨截面通常是危险截面，重点分析了中跨截面处孔洞对木梁承载能力的影响。中木梁的加载方式、几何参数及断裂弯矩计算方法如图1所示。
图 1 实验梁模型
Figure 1. Experimental beam model
因样本总量大，为减少工作量，先对比分析三点弯曲与四点弯曲加载方式所得的数据，择优选择其中一种加载方式完成后续实验。
为方便对比不同木梁的测量结果，本研究中限定木梁跨度(l)与高度(h)的关系为l = 10h，采用统一尺寸试件(l=150 mm，h=15 mm，b=10 mm)及统一的四点弯曲加载点间距(a = 40 mm)进行测试。测试之前，准备好无孔洞木梁，以及具有不同中心位置坐标(c)和直径(φ)孔洞的木梁。通过万能力学试验机(型号PY980，最大载荷20 kN，载荷测量分辨率0.01 N)配合特制的三点弯曲、四点弯曲专用压头及金属支架对木梁进行断裂破坏加载，并通过图1中的公式将所测得的断裂载荷值换算成断裂弯矩值。实验结束后，将木梁的几何参数及断裂弯矩值代入公式(详见1.3)，计算不同c和φ木梁的剩余承载力系数Φ，剩余抗弯刚度系数(ζ)以及孔洞相容系数(ψ)。基于上述3个系数的计算结果，分别绘制剩余承载力曲线(该曲线描述木梁承载力下降程度与孔洞参数之间的关系)、剩余抗弯刚度曲线(该曲线描述木梁横截面削弱程度与孔洞参数之间的关系)和孔洞相容系数曲线(该曲线描述木梁的孔洞相容系数随孔洞参数变化的规律)，并进行分析。
本研究先完成对樟子松木梁3条曲线的分析，总结3个系数与孔洞位置、大小之间的关系和规律；随后完成10种木材孔洞相容系数的对比分析，总结孔洞相容系数与木材密度之间的关系和规律；进一步选取塑性金属铝和脆性亚克力材料制成与木梁尺寸相同的样品，测量和计算孔洞相容系数，与木梁相对比从而验证木梁具有高于常见塑性及脆性材料的孔洞相容力学性能。完成上述对比分析后，进一步通过有限元分析、计算机断层扫描(CT)检测及分析等技术手段，探讨木梁孔洞相容的力学机制。
考虑到木梁力学性能个体差异较大，为排除随机因素干扰，对精度要求较高或离散性较大的参数组合测试较大数量(n=60)的样品；为减小工作量，对于数据离散性相对较小或精度要求相对较低的参数组合则适当减少样本数量。
-
为衡量孔洞对梁承载能力的影响，首先定义归一化的系数ψ，即孔洞相容系数，其物理意义是梁被孔洞削弱后，等效抗弯强度与原有抗弯强度的比值。计算公式为：
$$ \psi =\frac{\mathit{\Phi }}{\zeta } 。 $$ (1) 式(1)中：Φ与ζ均为归一化的系数，分别为梁的剩余承载力系数与剩余抗弯刚度系数。Φ的物理意义是梁被孔洞削弱后的断裂弯矩与原有断裂弯矩的比值。计算公式为：
$$ \mathit{\Phi }=\frac{M{'}_{\max }}{{M}_{\mathrm{m}\mathrm{a}\mathrm{x}}} 。 $$ (2) 式(2)中：M'max为有孔洞梁的平均断裂弯矩值，Mmax为无孔洞梁的平均断裂弯矩值。数据处理时断裂弯矩的具体计算方法见图1。
ζ的物理意义是梁的横截面被孔洞削弱后，截面惯性矩与原有横截面惯性矩的比值。计算公式为：
$$ \zeta =1-\frac{I'}{{I}_{0}} 。 $$ (3) 式(3)中：I'为梁被孔洞削弱后其横截面的惯性矩，I0为未被孔洞削弱的横截面的惯性矩。对于图1中所给出的矩形截面梁，ζ的计算公式可改写为：
$$ \zeta =1-\frac{{\varphi }^{3}+12\varphi {c}^{2}}{{h}^{3}} 。 $$ (4) 式(4)中：φ为孔洞的直径，c为孔洞中心的位置坐标，h为梁的高度。
将式(1)、式(2)和式(4)结合后可得式(5)，将数据代入后可直接计算得到孔洞相容系数：
$$ \psi=\frac{M'_{\max}h^3}{M_{\mathrm{m}\mathrm{a}\mathrm{x}}(h^3-\varphi^3-12\varphi c^2)}。 $$ (5) -
采用 Excel 2019 对实验测得的断裂载荷、断裂弯矩及计算的孔洞相容系数进行整理、统计与初步计算。采用 SPSS统计软件对不同孔洞位置、不同孔径木梁的断裂弯矩进行单因素方差分析(one-way ANOVA)，并使用 Tukey HSD 算法进行多重比较，以检验组间差异的显著性。利用 Origin 2024 绘制剩余承载力系数、剩余抗弯刚度系数、孔洞相容系数与孔洞位置及孔径的关系曲线。
-
表2为孔洞直径φ=2h/15情况下，不同孔洞位置樟子松木梁断裂弯矩的测量数据。经对比分析，所有孔洞位置三点弯曲与四点弯曲加载工况下的断裂弯矩差别不大(均未超过5%)。为减小工作量，并且考虑到三点弯曲数据的总体变异系数相对较小，之后的分析对所有木材样品均采用三点弯曲的方式加载。
表 2 不同孔洞位置樟子松木梁断裂弯矩对比
Table 2. Comparison of fracture moments of P. sylvestris var. mongolica wooden beams with holes at different positions
孔洞位置 三点弯曲加载 四点弯曲加载 样本量 断裂弯矩/(N·m) 变异系数/% 样本量 断裂弯矩/(N·m) 变异系数/% 均值 最大值 最小值 均值 最大值 最小值 −0.4 h 40 18.9 23.7 13.4 13.2 20 19.3 25.9 9.0 22.1 −0.3h 60 25.8 36.5 17.4 17.7 20 25.2 36.8 16.7 22.0 −0.2 h 60 27.4 36.8 16.9 16.0 40 27.9 35.6 21.1 15.8 −0.1 h 60 27.7 35.9 20.2 13.7 40 28.0 40.6 14.4 21.9 0 60 28.0 37.2 20.0 15.8 40 28.9 35.6 12.1 15.2 0.1 h 40 27.3 39.3 15.9 17.3 40 27.6 38.8 17.6 17.5 0.2 h 40 25.9 36.9 16.6 20.8 20 26.0 33.0 18.9 15.4 0.3 h 40 25.1 34.6 14.9 17.7 20 26.2 32.2 19.8 15.8 0.4 h 40 24.4 32.9 11.6 19.5 20 25.5 34.2 16.5 20.2 说明：h为梁的高度。 木材因其纤维结构导致了抗拉弹性模量略高于抗压弹性模量，从而使木梁的中性层不再与其中轴线相重合，而是略高于其中轴线位置[23]，并且孔洞的存在也会导致中性层位置发生微小改变[24]。本研究考虑到因上述原因所导致的中性层偏移量较小，同时考虑到中性层的偏移问题会使理论分析过于复杂，故在分析中仍假设木梁中性层位置与其中轴线相重合，即c=0。可认为木梁中c＜0处位于纤维拉伸区，c＞0处位于纤维压缩区。
从表2可以看出：无论是在拉伸区还是压缩区，孔洞中心位置越远离中性层，则木梁的断裂弯矩越小，符合材料力学理论的预期。然而，在拉伸区域孔洞位置对木梁断裂弯矩的影响较大，在压缩区域孔洞位置对木梁断裂弯矩的影响则相对较小，此现象则是因为木材纤维断裂发生在拉伸区，因而当孔洞位于木材纤维拉伸区时，对木梁的承载能力影响更大。考虑到孔洞位于c=－h/5处时，其位置处于木材纤维拉伸区，且试件加工和测试都相对方便。
从表3可以看出：当φ＜h/5时，因孔洞而导致的木梁断裂弯矩下降率不超过10%；继续增大孔洞直径，则随着孔洞直径的增大，木梁断裂弯矩的下降率明显增加。为定量评估不同孔洞直径对木梁断裂弯矩影响的显著性，对表3中的数据进行了单因素方差分析(one-way ANOVA)。分析结果表明：不同孔径木梁的断裂弯矩存在极显著差异[F(9, 430) = 61.39, P＜0.001]，随后进行Tukey HSD事后检验进一步明确了各组间的具体差异。表3所列出的统计结果表明：当孔洞直径φ≤h/5 时，木梁的断裂弯矩与无孔洞木梁(φ = 0)相比，无统计学意义上的显著下降。然而，当孔洞直径φ＞h/5 时，所有孔径组的断裂弯矩均极显著低于无孔洞组(P＜0.001)。根据上述分析结果，可将φ = h/5视为樟子松木梁承载力是否会出现明显下降的临界孔径值。
表 3 不同孔洞直径樟子松木梁断裂弯矩对比
Table 3. Comparison of fracture moments of P. sylvestris var. mongolica wooden beams with holes with different diameters
孔洞直径 样品量 断裂弯矩/(N·m) 变异系数/% P 均值 均值差异 最大值 最小值 0 60 28.2 0 38.7 18.7 15.1 h/15 40 27.7 −0.5 35.7 15.1 16.2 0.999 h/10 40 27.5 −0.7 39.6 13.7 15.4 0.998 2h/15 60 27.4 −0.8 36.8 16.9 16.0 0.995 h/6 40 27.2 −1.0 33.5 14.1 15.8 0.980 h/5 60 26.1 −2.1 35.0 17.6 14.9 0.650 4h/15 40 23.5 −4.7 34.0 13.9 21.0 ＜0.001 h/3 40 20.5 −7.7 30.2 11.6 22.1 ＜0.001 2h/5 40 17.5 −10.7 26.1 11.1 19.9 ＜0.001 h/2 20 9.3 −18.9 11.5 3.9 23.7 ＜0.001 说明：均值差异 = 有孔梁均值−无孔梁均值。h为梁的高度。 -
图2给出了φ为2h/15情况下3条与圆孔位置相关的归一化曲线：分别为剩余承载力曲线、剩余抗弯刚度曲线和孔洞相容系数曲线。其中，剩余承载力系数曲线与剩余抗弯刚度曲线的最大值点均出现在孔洞位于木梁中心位置的c=0处，然而随着孔洞中心位置的偏移，剩余承载力曲线在大多数情况下都高于剩余抗弯刚度曲线(孔洞中心位于木梁下表面附近时除外)。剩余承载力与剩余抗弯刚度的上述关系导致了当孔洞位置从木梁中轴线上下偏移后，孔洞相容系数呈现“不降反升”的现象，但当孔洞接近木梁下表面时，孔洞相容系数又会急剧下降。进一步由孔洞相容系数曲线可以看出：当孔洞位于木梁下表面附近时，木梁的孔洞相容系数最小；当孔洞位于木梁的上表面附近时，木梁的孔洞相容系数最大。考虑到上表面的孔洞处于木梁的压缩区域，木梁在孔洞被压溃后仍能承受载荷，所以当孔洞位于木梁压缩区域时，所计算出的孔洞相容系数并不能描述木材的真实孔洞相容力学性能。因此，木梁孔洞相容系数的计算应以中性轴以下的孔洞为准。为了实验、观察和统计的方便，后续统一选取c=－h/5位置的孔洞，并计算木梁样品的孔洞相容系数。
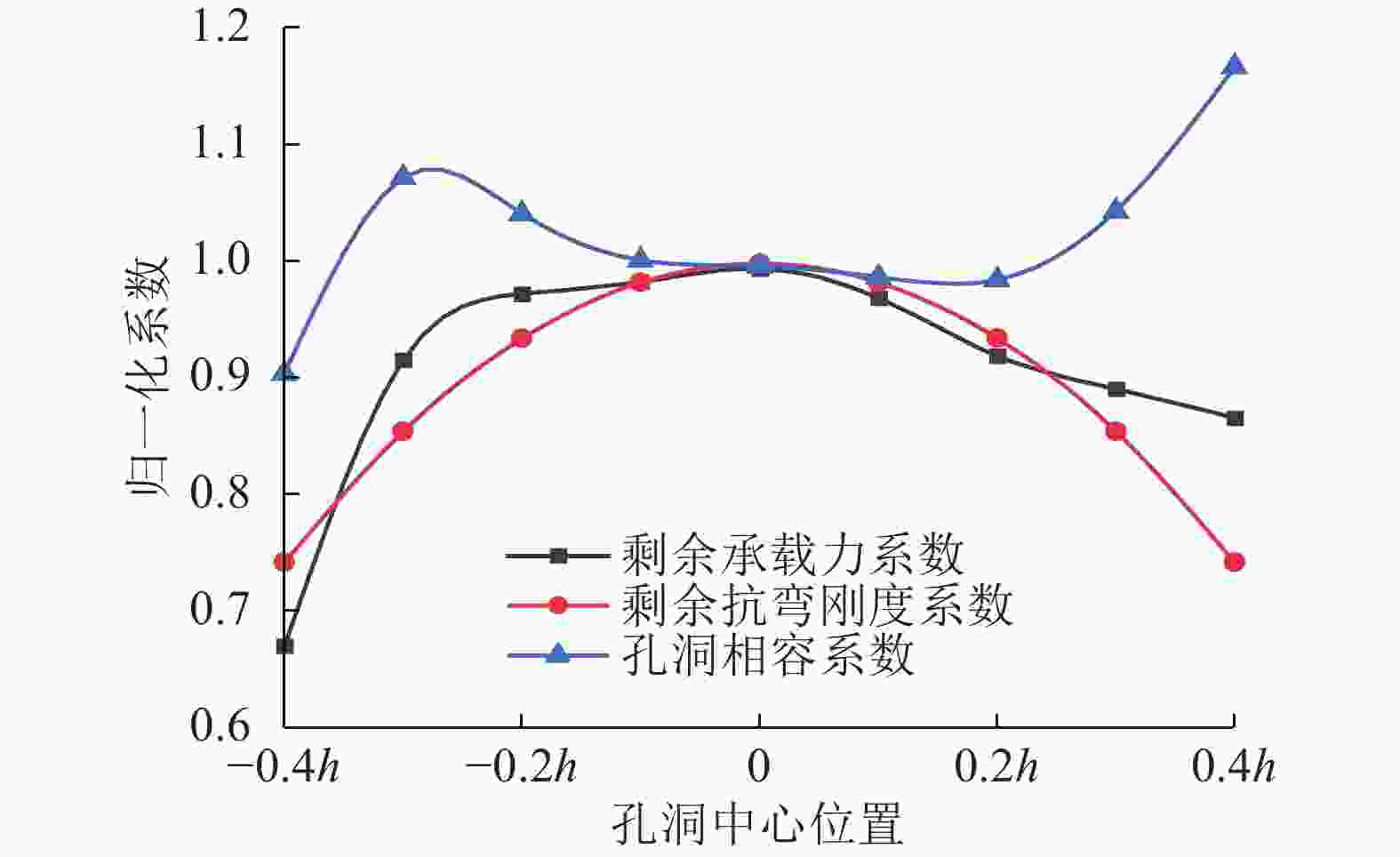
图 2 剩余承载力系数、剩余抗弯刚度系数、孔洞相容系数与孔洞位置的关系
Figure 2. Relationship between residual bearing capacity, residual bending stiffness, hole compatibility coefficients and the position of circular holes
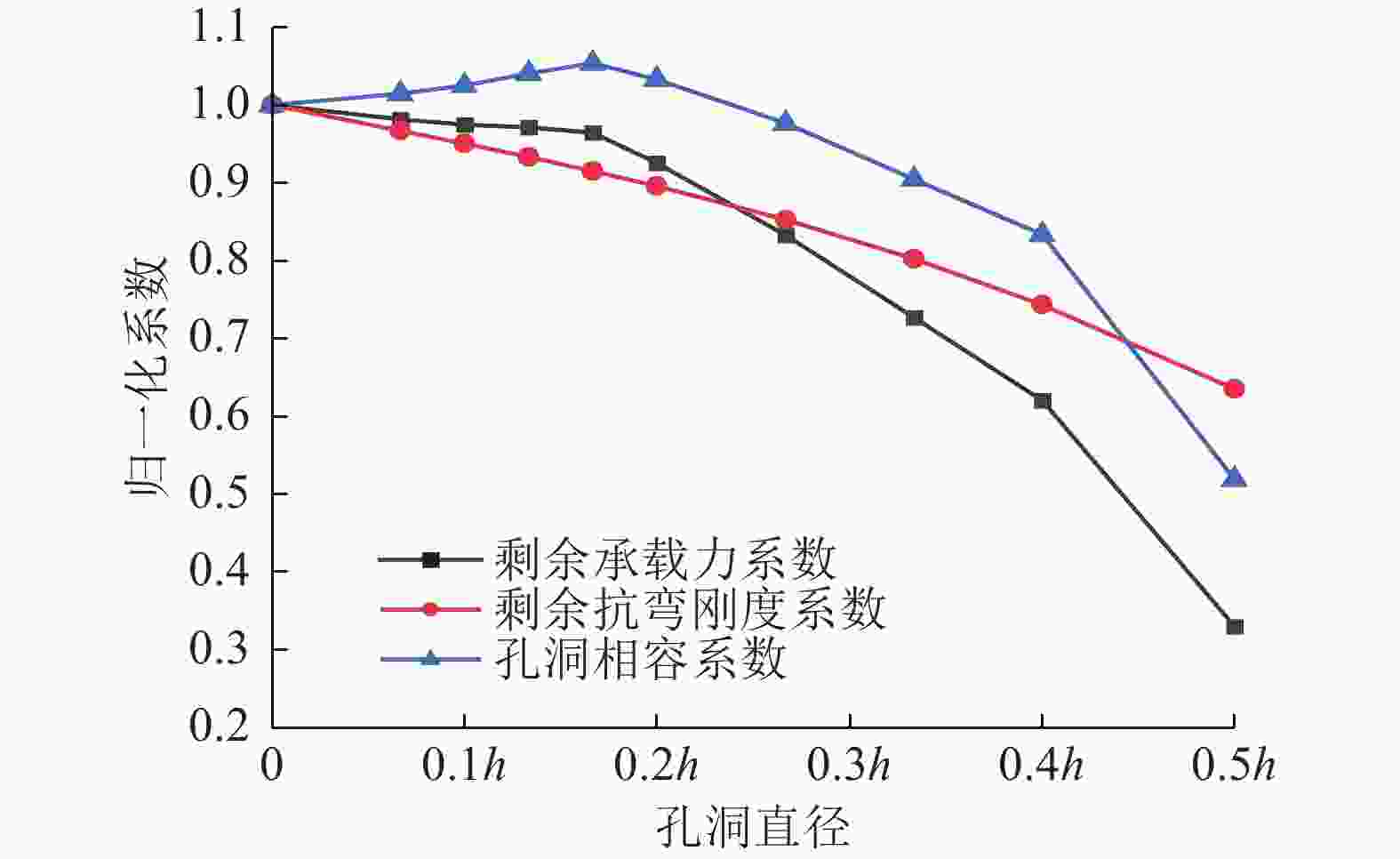
图3给出了不同孔径木梁的剩余承载力曲线、剩余抗弯刚度曲线和孔洞相容系数曲线。对比剩余承载力曲线与剩余抗弯刚度曲线可以看出，随着孔洞直径的增大，木梁的剩余承载力与剩余抗弯刚度均不断下降。然而，剩余抗弯刚度曲线上没有明显拐点，剩余承载力曲线则在当孔洞直径接近h/5时出现拐点。该拐点表明当孔洞直径接近h/5时，继续增大孔洞直径木梁的承载能力下降趋势将加剧。由孔洞相容系数曲线可以看出：当孔洞直径从最小值开始不断增大，则随着孔洞直径的增大，木梁孔洞相容系数先是缓慢增大，随后开始缓慢减小；继续增大孔径，木梁孔洞相容系数加剧减小。不同木材品种的木梁孔洞相容系数达到最大值时所对应的孔洞直径也可能有所不同，因此很难统一选定孔洞相容系数达到最大值时的孔径进行实验；为了测量、观察的方便以及减少样本数量，后续统一选取φ=2h/15的孔洞直径测量和计算孔洞相容系数。
图 3 剩余承载力系数、抗弯刚度系数以及孔洞相容系数与孔洞直径的关系
Figure 3. Relationship between the residual bearing capacity, residual bending stiffness, hole compatibility coefficients and hole diameter
-
为考察木材密度对孔洞相容系数的影响，本研究对比测量了由表1中10种木材所制成木梁的孔洞相容系数。由表4可以看出：随着木梁密度的增大，其断裂弯矩值总体也呈现增大的趋势。密度相近的木材，如黑胡桃木与水曲柳木，虽然黑胡桃木的密度略高于水曲柳木，但其木梁的断裂弯矩却略低于水曲柳木，说明密度不是唯一影响因素，木材的纤维结构、纹理等对木梁的断裂弯矩也有影响。在所考察的木材品种中，有洞木梁的断裂弯矩平均值均略低于无洞木梁，但相差不大。轻木断裂弯矩的变异系数较大，说明其力学性能波动大，这是因为轻木的密度过小，其细胞壁过薄且细胞腔相对更大，增加了其力学性能的不确定性。由图4可以看出：除了密度极低和密度极高的木材所制成木梁的孔洞相容系数相对较小外，其余密度区间的木材所制成的木梁孔洞相容系数均在1.0左右。
表 4 不同密度木材制成木梁的断裂弯矩
Table 4. Fracture bending moment of wooden beams made of wood with different densities
木材名称 气干密度/
(kg·m−3)无洞木梁 有洞木梁 样本量 断裂弯矩/(N·m) 变异系数/% 样本量 断裂弯矩/(N·m) 变异系数/% 均值 最大值 最小值 均值 最大值 最小值 轻木 150 60 6.4 9.4 3.3 33.5 60 5.7 11.7 2.4 31.6 泡桐木 280 60 18.5 23.8 13.9 23.5 60 18.0 24.4 10.3 15.5 杉木 320 60 26.4 38.1 16.3 16.3 60 25.8 34.7 12.5 20.3 樟子松木 477 60 28.2 38.7 18.7 15.1 60 27.5 36.8 16.9 15.6 白桦木 615 60 37.3 50.7 18.0 22.9 60 36.0 54.8 19.7 23.7 水曲柳木 686 60 43.2 57.6 29.3 15.9 60 41.0 58.7 27.3 12.7 黑胡桃木 720 40 41.4 57.3 19.3 17.8 40 39.9 49.4 25.1 19.8 榉木 790 60 48.2 55.5 36.0 14.9 60 45.8 58.2 29.9 9.3 黄檀木 923 40 77.0 101.3 25.3 22.7 40 70.9 94.6 28.4 25.7 紫光檀木 1 290 40 87.3 107.5 55.5 26.2 40 73.1 113.4 32.2 15.9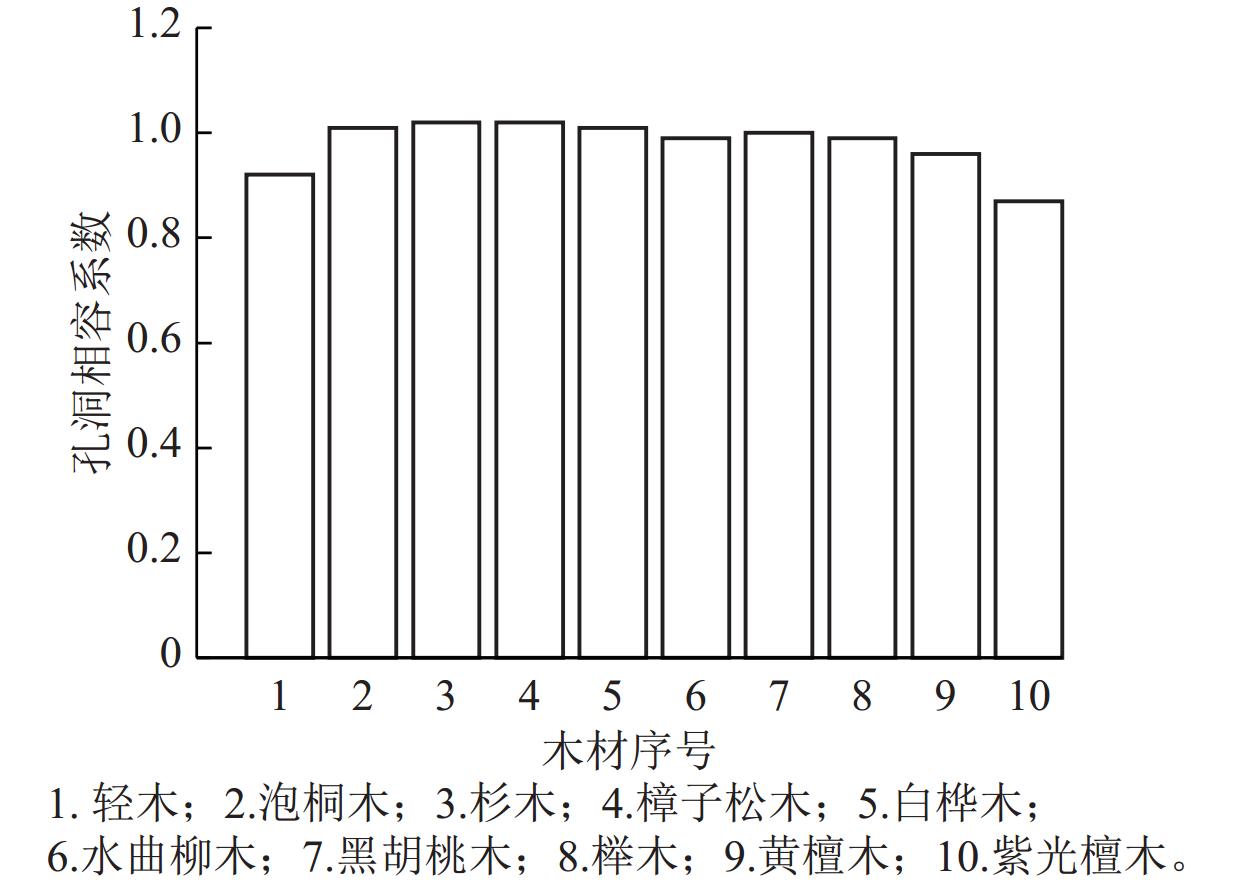 
图 4 不同密度木材所制成木梁的孔洞相容系数对比
Figure 4. Comparison of pore compatibility coefficients of wood beam with different densities
除测试10种木材所制成的木梁外，还测试了塑性金属铝和脆性亚克力材料制成的梁(表5)。考虑到不同金属铝梁和不同亚克力梁之间的个体差异远小于木梁，采用的样本数量也相应减少。与木梁的断裂载荷即为极限载荷不同的是，金属铝梁与无洞的亚克力梁在变形较大时也不会发生断裂，因此取其加载曲线中的最大载荷值计算孔洞相容系数。由表5数据可见金属铝制成的梁孔洞相容系数为0.81，脆性亚克力制成的梁孔洞相容系数为0.46，均低于木梁的孔洞相容系数。此外，测试结果表明金属铝及亚克力无孔洞梁断裂弯矩的变异系数较低，而有孔洞梁断裂弯矩的变异系数则相对较高；与之相反的是，有孔洞木梁与无孔洞木梁之间并不存在此差异。这也从另一个角度反映塑性金属铝与脆性亚克力材料所制成梁的孔洞相容力学性能低于木梁。
表 5 对照材料梁的极限弯矩及孔洞相容系数
Table 5. Ultimate bending moment and hole compatibility coefficient of the reference material beam
材料名 无洞梁 有洞梁 孔洞相
容系数样本量 断裂弯矩/(N·m) 变异系数/% 样本量 断裂弯矩/(N·m) 变异系数/% 均值 最大值 最小值 均值 最大值 最小值 金属铝 10 244.6 250.1 237.3 1.9 10 191.0 211.7 173.1 6.3 0.81 亚克力 20 61.2 65.6 56.3 4.4 20 27.2 41.7 19.7 20.3 0.46 -
木梁具有较高的孔洞相容系数，其与木材的微观结构有较大关系。进一步通过拍摄断裂木梁的照片及CT图片(图5)，对比研究了有孔洞与无孔洞木梁的表面及内部破坏形貌，发现有孔洞木梁断裂时，裂纹往往从这些孔洞处开始萌生和扩展。相比于无孔洞的木梁，有孔洞木梁的断裂面往往更为平整，尤其是孔洞下方的木材纤维往往能够形成平整的断裂面。而无孔洞的木梁从表面形貌照片中可见木刺较多，CT图片中同样可以看到“之”字形断裂面。断面不平整的现象说明木纤维的承载能力并未协同发挥，而是存在不同位置纤维先后断裂的现象。
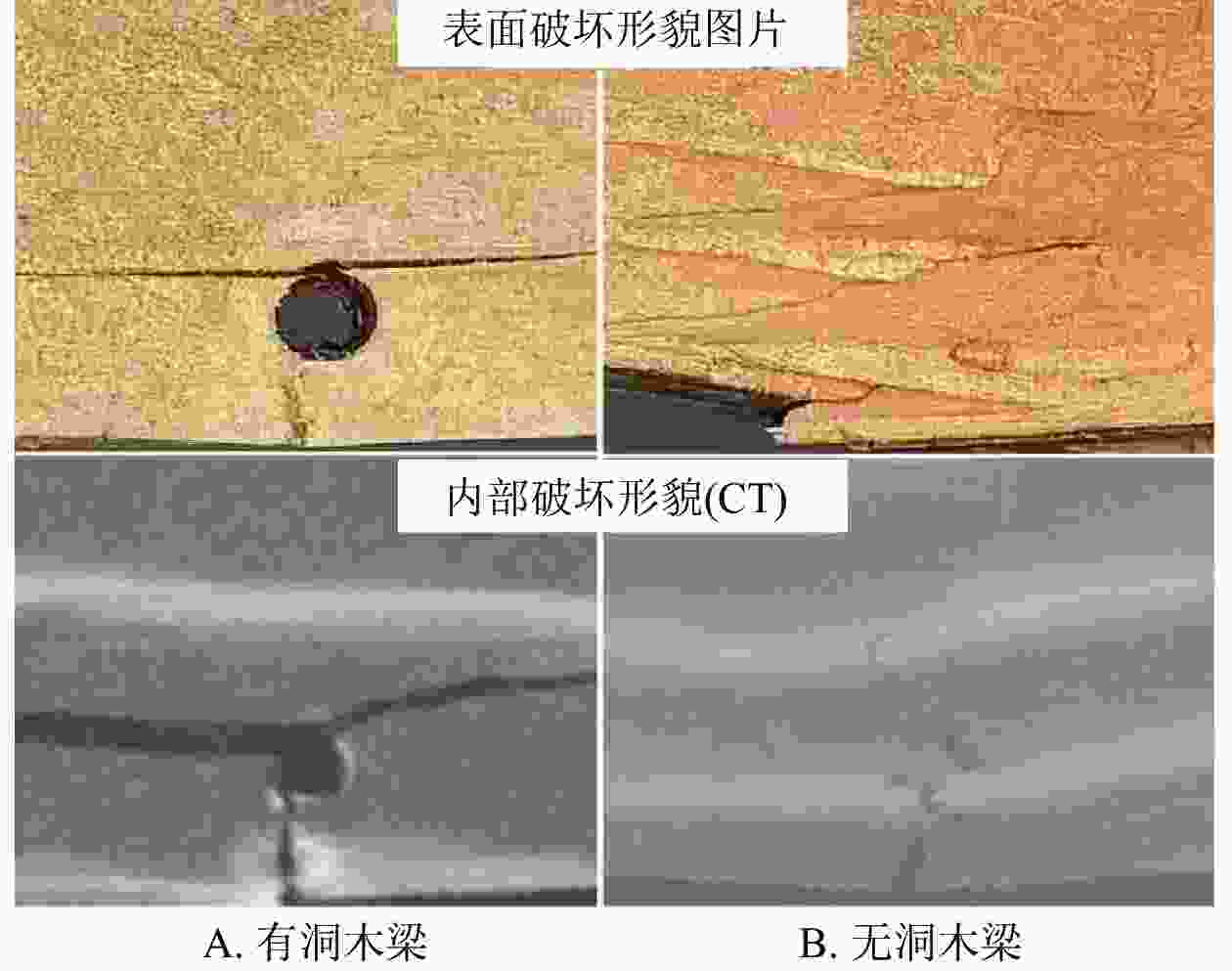
图 5 有孔洞与无孔洞松木梁断裂后的表面与内部形貌
Figure 5. Surface and internal morphology of pine beams with and without holes after fracture
通过有限元仿真，可研究孔洞对于木梁应力分布的影响。本研究在Abaqus软件中分别建立了有孔洞木梁与无孔洞木梁的有限元仿真模型(采用4节点平面应力CPS4单元，具体网格尺寸及数量见图6)，并参照樟子松木弹性常数测量数据[25]设置了具有各向异性材料特性的木材结构参数(表6)，对2种模型进行了仿真和对比分析。由表6中数据可以看出，樟子松木在沿纤维方向上的力学性能远高于径向和弦向，这种极强的各向异性特性是导致木梁具有孔洞相容力学性能的重要原因。
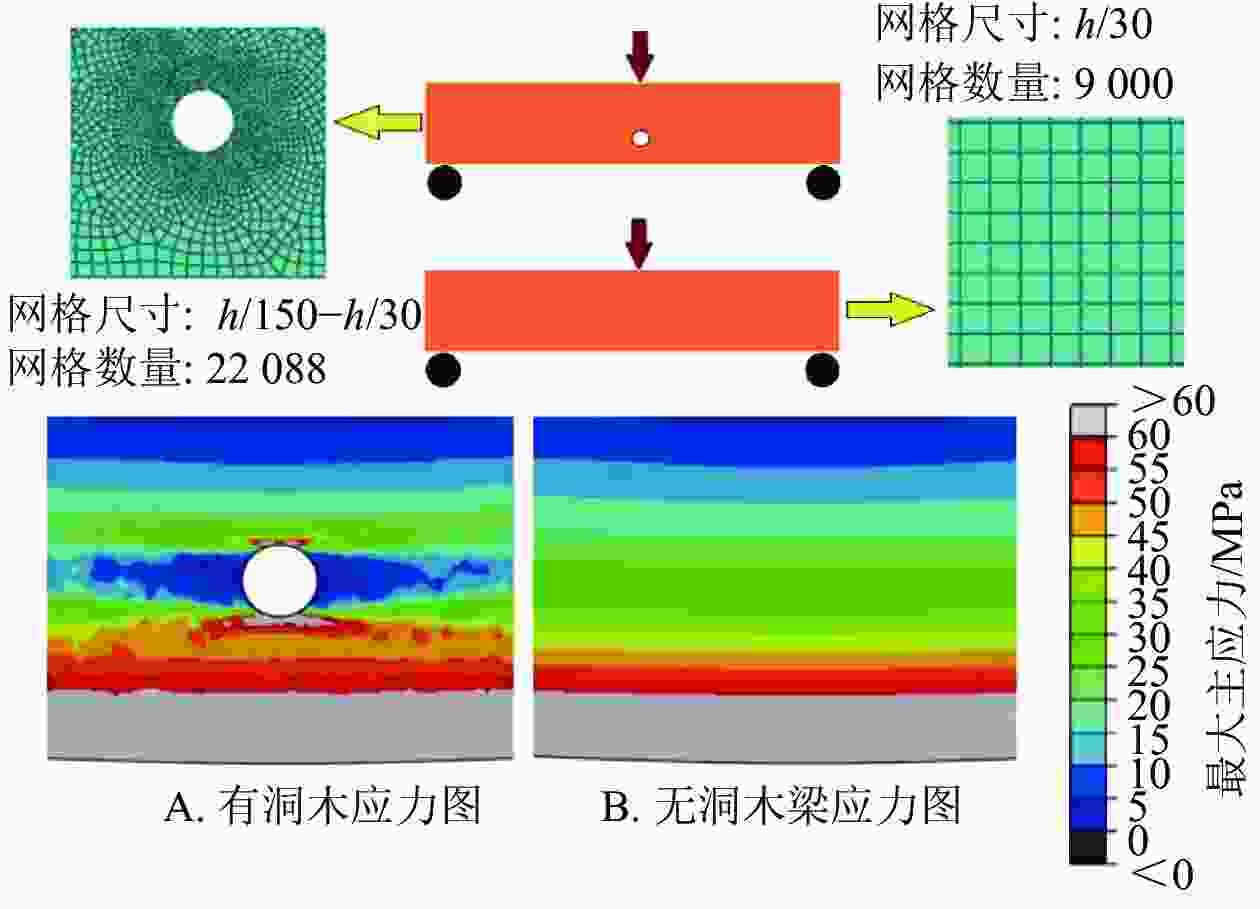
图 6 有孔洞与无孔洞木梁拉应力区的有限元仿真结果
Figure 6. Finite element simulation results of tensile stress zones in wooden beams with and without hole
表 6 有限元仿真模型中设定的樟子松木弹性常数数据
Table 6. Elastic constant data of P. sylvestris var. mongolica used in the finite element simulation model
EL/MPa ER/MPa ET/MPa GLR/MPa GLT/MPa GRT/MPa vLR vLT vRT 10000 800 400 620 540 70 0.46 0.62 0.73 说明：EL、ER、ET分别为轴向、径向、弦向的弹性模量值；GLR、GLT、GRT为剪切弹性模量值；vLR、vLT、vRT为泊松比。 从有限元仿真结果图中可以看出：木梁孔洞下方的应力集中区使拉应力有所增大，而无孔洞木梁在拉应力区的应力分布规律为应力由下而上逐渐减小、形成应力梯度。木梁中孔洞的存在减缓了孔洞底部与梁底面之间区域的应力变化趋势，减小了应力的梯度，这样就使得孔洞下方区域的应力分布比无孔洞木梁更为均匀。更为均匀的应力分布也意味着此区域的木材纤维更易协同发挥承载能力，并且这些纤维的破坏也更为同步，这就能够解释断裂形貌照片中看到的木梁孔洞下方的断裂面更为平整的现象。孔洞下方纤维的协同承载效应在一定程度上弥补孔洞对木梁横截面削弱而引起的承载能力下降。
-
本研究探讨了孔洞对木梁承载能力的影响和木梁孔洞相容力学现象的形成机制，提出了剩余承载力系数、剩余抗弯刚度系数和孔洞相容系数的概念，通过大量的测量及数据对比验证木梁具有孔洞相容的力学性能，并分析孔洞参数对木梁承载能力的影响。孔洞中心位置越远离中性层，木梁的断裂载荷越小；位于木梁拉伸区的孔洞对木梁承载能力的影响比位于木梁压缩区的孔洞更为显著。当孔洞直径小于临界直径时，木梁的断裂载荷不会出现明显下降。密度极低和极高的木材所制成木梁的孔洞相容系数相对较小，其余密度区间的木材所制成的木梁孔洞相容系数均在1.0左右。木梁的孔洞相容系数明显高于塑性金属铝和脆性亚克力材料制成的梁，说明木梁具有较强的孔洞相容力学性能。
木梁具有较强的孔洞相容力学性能与其具有各向异性力学特性及纤维结构有关。有孔洞木梁断裂时，孔洞下方的木材纤维往往在相同水平位置发生断裂，断裂面平整。无孔洞木梁的断裂面往往呈现“之”字形，不如有孔洞木梁的断裂面平整。孔洞的存在减小了孔洞底部与木梁底面之间区域的应力梯度，使得该区域的应力分布比无孔洞木梁更为均匀，这使得孔洞下方的木材纤维更易协同发挥承载功能，在一定程度上弥补了因孔洞存在而引起的木梁横截面削弱效应。
此外，本研究结果表明孔洞的直径存在临界值，当孔洞直径小于该值时木梁承载能力下降轻微；孔洞直径达到该值时若继续增大孔洞直径，则木梁的承载能力迅速劣化。工程中可将孔洞直径是否超过临界值作为能否继续使用的重要判定依据。
综上所述，本研究从木梁的宏观力学性能及纤维断裂机制出发，通过实验与仿真相结合，阐释了木梁具备良好孔洞相容力学特性的机理，为含孔洞构件的安全评估与设计应用提供参考依据。
Influence of circular holes on the bearing capacity of wooden beams
-
摘要:
目的 考察木梁中不同位置和尺寸的圆形孔洞对其承载能力的影响规律，探究木梁对孔洞损伤具有一定容受能力的力学机制，启发高孔洞耐受性能材料或轻量化结构的设计。 方法 提出孔洞相容的力学概念，给出孔洞相容系数的计算公式。通过对木梁进行弯曲断裂实验，测量具有不同位置、不同直径孔洞的木梁的断裂弯矩值，绘制相应的关系曲线，计算木梁的孔洞相容系数。通过对代表性木梁进行仿真分析和断口形貌分析，阐明其具有孔洞相容力学特性的机制。 结果 中性层下方孔洞对木梁承载能力的影响大于中性层上方孔洞的影响。当孔洞直径小于梁高的1/5时，木梁承载力的下降不超过10%。除密度极高和密度极低的木梁外，大部分木梁的孔洞相容系数均接近1.0，高于塑性的金属铝梁和脆性的亚克力梁。有限元分析表明：孔洞下方的应力分布比孔洞上方的应力分布更为均匀。断口形貌分析则发现：孔洞下方断裂面更为平整。 结论 当孔洞直径小于临界直径时，木梁的整体承载力下降轻微，并且当这样的孔洞位于木梁拉伸区域时，孔洞下部区域木纤维的承载能力得到更均匀发挥，木梁在整体上表现出孔洞相容的力学现象。木梁具有优于塑性金属铝梁和脆性亚克力梁的孔洞相容力学性能，其孔洞相容的力学机制能够启发新型纤维增强复合材料、含孔洞轻量化承载结构，以及微孔洞结构材料的设计。图6表6参25 Abstract:Objective This study aims to examine the influence of circular holes of different positions and sizes on the load-bearing capacity of wooden beams, explore the mechanical mechanism by which wooden beams have a certain tolerance for hole damage, and inspire the design of materials with high hole tolerance or lightweight structures. Method The mechanical concept of hole compatibility was proposed, and the calculation formula for hole compatibility coefficient was provided. By conducting bending and fracture experiments on wooden beams, the fracture bending moment values of wooden beams with holes of different positions and diameters were measured, corresponding relationship curves were drawn, and the hole compatibility coefficient of wooden beams was calculated. By conducting simulation analysis and fracture morphology analysis on representative wooden beams, the mechanism of their hole compatibility mechanical properties was clarified. Result The impact of holes below the neutral layer on the load-bearing capacity of wooden beams was greater than that of holes located above the neutral layer. When the diameter of the hole was less than 1/5 of the beam height, the bearing capacity of the wooden beam did not exceed 10%. Except for wooden beams with extremely high and low densities, the compatibility coefficient of most wooden beams was close to 1.0, which was higher than that of plastic metal aluminum beams and brittle acrylic beams. Finite element analysis showed that the stress distribution below the hole was more uniform than that above the hole, and the fracture morphology analysis revealed that the fracture surface below the hole was smoother. Conclusion When the diameter of the hole is smaller than the critical value, the overall bearing capacity of the wooden beam decreases slightly. When such holes are located in the stretching area of the wooden beam, the bearing capacity of the wood fibers in the lower area of the hole is more evenly exerted, and the wooden beam exhibits a mechanical phenomenon of hole compatibility as a whole. Wooden beams have better hole compatibility mechanical properties than plastic metal aluminum beams and brittle acrylic beams. The mechanical mechanism of hole compatibility can inspire the design of new fiber-reinforced composite materials, lightweight load-bearing structures with holes, and micro porous structural materials. [Ch, 6 fig. 6 tab. 25 ref.] -
Key words:
- wood beam /
- circular hole /
- bearing capacity /
- hole compatibility /
- lightweight
-
图 2 剩余承载力系数、剩余抗弯刚度系数、孔洞相容系数与孔洞位置的关系
Figure 2 Relationship between residual bearing capacity, residual bending stiffness, hole compatibility coefficients and the position of circular holes
图 3 剩余承载力系数、抗弯刚度系数以及孔洞相容系数与孔洞直径的关系
Figure 3 Relationship between the residual bearing capacity, residual bending stiffness, hole compatibility coefficients and hole diameter
图 4 不同密度木材所制成木梁的孔洞相容系数对比
Figure 4 Comparison of pore compatibility coefficients of wood beam with different densities
图 5 有孔洞与无孔洞松木梁断裂后的表面与内部形貌
Figure 5 Surface and internal morphology of pine beams with and without holes after fracture
图 6 有孔洞与无孔洞木梁拉应力区的有限元仿真结果
Figure 6 Finite element simulation results of tensile stress zones in wooden beams with and without hole
表 1 实验考察木材的名称、气干密度及分类特征
Table 1. Names, air dry density and classification characteristics of experimental wood
序号 木材名称 气干密度/
(kg·m−3)分类特性 序号 木材名称 气干密度/
(kg·m−3)分类特性 1 轻木Ochroma lagopus 150 阔叶材 6 水曲柳Fraxinus mandshurica木 686 阔叶材 2 泡桐Paulownia fargesii木 280 阔叶材 7 黑胡桃Juglans nigra木 720 阔叶材 3 杉木Cunninghamia lanceolata 320 针叶材 8 榉Zelkova schneideriana木 790 阔叶材 4 樟子松Pinus sylvestris var. mongolica木 477 针叶材 9 黄檀Dalbergia hupeana木 923 阔叶材 5 白桦Betula platyphylla木 615 阔叶材 10 紫光檀Dalbergia melanoxylon木 1290 阔叶材 
下载: 导出CSV
表 2 不同孔洞位置樟子松木梁断裂弯矩对比
Table 2. Comparison of fracture moments of P. sylvestris var. mongolica wooden beams with holes at different positions
孔洞位置 三点弯曲加载 四点弯曲加载 样本量 断裂弯矩/(N·m) 变异系数/% 样本量 断裂弯矩/(N·m) 变异系数/% 均值 最大值 最小值 均值 最大值 最小值 −0.4 h 40 18.9 23.7 13.4 13.2 20 19.3 25.9 9.0 22.1 −0.3h 60 25.8 36.5 17.4 17.7 20 25.2 36.8 16.7 22.0 −0.2 h 60 27.4 36.8 16.9 16.0 40 27.9 35.6 21.1 15.8 −0.1 h 60 27.7 35.9 20.2 13.7 40 28.0 40.6 14.4 21.9 0 60 28.0 37.2 20.0 15.8 40 28.9 35.6 12.1 15.2 0.1 h 40 27.3 39.3 15.9 17.3 40 27.6 38.8 17.6 17.5 0.2 h 40 25.9 36.9 16.6 20.8 20 26.0 33.0 18.9 15.4 0.3 h 40 25.1 34.6 14.9 17.7 20 26.2 32.2 19.8 15.8 0.4 h 40 24.4 32.9 11.6 19.5 20 25.5 34.2 16.5 20.2 说明：h为梁的高度。
下载: 导出CSV
表 3 不同孔洞直径樟子松木梁断裂弯矩对比
Table 3. Comparison of fracture moments of P. sylvestris var. mongolica wooden beams with holes with different diameters
孔洞直径 样品量 断裂弯矩/(N·m) 变异系数/% P 均值 均值差异 最大值 最小值 0 60 28.2 0 38.7 18.7 15.1 h/15 40 27.7 −0.5 35.7 15.1 16.2 0.999 h/10 40 27.5 −0.7 39.6 13.7 15.4 0.998 2h/15 60 27.4 −0.8 36.8 16.9 16.0 0.995 h/6 40 27.2 −1.0 33.5 14.1 15.8 0.980 h/5 60 26.1 −2.1 35.0 17.6 14.9 0.650 4h/15 40 23.5 −4.7 34.0 13.9 21.0 ＜0.001 h/3 40 20.5 −7.7 30.2 11.6 22.1 ＜0.001 2h/5 40 17.5 −10.7 26.1 11.1 19.9 ＜0.001 h/2 20 9.3 −18.9 11.5 3.9 23.7 ＜0.001 说明：均值差异 = 有孔梁均值−无孔梁均值。h为梁的高度。
下载: 导出CSV
表 4 不同密度木材制成木梁的断裂弯矩
Table 4. Fracture bending moment of wooden beams made of wood with different densities
木材名称 气干密度/
(kg·m−3)无洞木梁 有洞木梁 样本量 断裂弯矩/(N·m) 变异系数/% 样本量 断裂弯矩/(N·m) 变异系数/% 均值 最大值 最小值 均值 最大值 最小值 轻木 150 60 6.4 9.4 3.3 33.5 60 5.7 11.7 2.4 31.6 泡桐木 280 60 18.5 23.8 13.9 23.5 60 18.0 24.4 10.3 15.5 杉木 320 60 26.4 38.1 16.3 16.3 60 25.8 34.7 12.5 20.3 樟子松木 477 60 28.2 38.7 18.7 15.1 60 27.5 36.8 16.9 15.6 白桦木 615 60 37.3 50.7 18.0 22.9 60 36.0 54.8 19.7 23.7 水曲柳木 686 60 43.2 57.6 29.3 15.9 60 41.0 58.7 27.3 12.7 黑胡桃木 720 40 41.4 57.3 19.3 17.8 40 39.9 49.4 25.1 19.8 榉木 790 60 48.2 55.5 36.0 14.9 60 45.8 58.2 29.9 9.3 黄檀木 923 40 77.0 101.3 25.3 22.7 40 70.9 94.6 28.4 25.7 紫光檀木 1 290 40 87.3 107.5 55.5 26.2 40 73.1 113.4 32.2 15.9
下载: 导出CSV
表 5 对照材料梁的极限弯矩及孔洞相容系数
Table 5. Ultimate bending moment and hole compatibility coefficient of the reference material beam
材料名 无洞梁 有洞梁 孔洞相
容系数样本量 断裂弯矩/(N·m) 变异系数/% 样本量 断裂弯矩/(N·m) 变异系数/% 均值 最大值 最小值 均值 最大值 最小值 金属铝 10 244.6 250.1 237.3 1.9 10 191.0 211.7 173.1 6.3 0.81 亚克力 20 61.2 65.6 56.3 4.4 20 27.2 41.7 19.7 20.3 0.46
下载: 导出CSV
表 6 有限元仿真模型中设定的樟子松木弹性常数数据
Table 6. Elastic constant data of P. sylvestris var. mongolica used in the finite element simulation model
EL/MPa ER/MPa ET/MPa GLR/MPa GLT/MPa GRT/MPa vLR vLT vRT 10000 800 400 620 540 70 0.46 0.62 0.73 说明：EL、ER、ET分别为轴向、径向、弦向的弹性模量值；GLR、GLT、GRT为剪切弹性模量值；vLR、vLT、vRT为泊松比。
下载: 导出CSV
-
[1] 郑文涛, 陈晶华, 李田. 孔洞对疲劳裂纹扩展路径的影响[J]. 沈阳工业大学学报, 2024, 46(2): 177−183. ZHENG Wentao, CHEN Jinghua, LI Tian. Influence of holes on fatigue crack propagation path[J]. Journal of Shenyang University of Technology, 2024, 46(2): 177−183. DOI: 10.7688/j.issn.1000-1646.2024.02.10. ZHENG Wentao, CHEN Jinghua, LI Tian. Influence of holes on fatigue crack propagation path[J]. Journal of Shenyang University of Technology, 2024, 46(2): 177−183. DOI: 10.7688/j.issn.1000-1646.2024.02.10 .[2] 寇佩佩, 冯瑞成, 李海燕, 等. 孔洞对含Nb单晶β-TiAl合金力学性能的影响[J]. 材料导报, 2020, 34(14): 14140−14146. KOU Peipei, FENG Ruicheng, LI Haiyan, et al. Effect of voids on mechanical properties of single crystal β-TiAl alloy containing Nb[J]. Materials Review, 2020, 34(14): 14140−14146. DOI: 10.11896/cldb.19070089. KOU Peipei, FENG Ruicheng, LI Haiyan, et al. Effect of voids on mechanical properties of single crystal β-TiAl alloy containing Nb[J]. Materials Review, 2020, 34(14): 14140−14146. DOI: 10.11896/cldb.19070089 .[3] LEE E, JIA Zian, YANG Ting, et al. Multiscale mechanical design of the lightweight, stiff, and damage-tolerant cuttlebone: a computational study[J]. Acta Biomaterialia, 2022, 154: 312−323. DOI: 10.1016/j.actbio.2022.09.057. [4] MA Chunyang, DU Tianming, NIU Xufeng, et al. Biomechanics and mechanobiology of the bone matrix[J]. Bone Research, 2022, 10: 59. DOI:10.1038/s41413-022-00223-y. [5] NIKNEJAD E, JAFARI R, VALIPOUR MOTLAGH N. Mechanical properties of biodegradable fibers and fibrous mats: a comprehensive review[J]. Molecules, 2025, 30(15): 3276. DOI:10.3390/molecules30153276. [6] ZHANG Xiaofang, YUAN Yanan. Synergistic enhancement of strength and toughness through meta-biomimetic design: integrating crossed-lamellar and bouligand microstructures[J]. Composites Science and Technology, 2024, 254: 110668. DOI:10.1016/j.compscitech.2024.110668. [7] OLHAN S, ANTIL B, KHATKAR V, et al. Mechanical, thermal, and viscoelastic behavior of sisal fibre-based structural composites for automotive applications: experimental and FEM analysis[J]. Composite Structures, 2023, 322: 117427. DOI:10.1016/j.compstruct.2023.117427. [8] 陈勇平, 郭文静, 唐启恒. 基于雷达检测的木材内部孔洞面积测算与修正[J]. 浙江农林大学学报, 2020, 37(6): 1193−1199. CHEN Yongping, GUO Wenjing, TANG Qiheng. Calculation and correction of wood internal cavity area based on radar detection[J]. Journal of Zhejiang A&F University, 2020, 37(6): 1193−1199. DOI: 10.11833/j.issn.2095-0756.20190709. CHEN Yongping, GUO Wenjing, TANG Qiheng. Calculation and correction of wood internal cavity area based on radar detection[J]. Journal of Zhejiang A&F University, 2020, 37(6): 1193−1199. DOI: 10.11833/j.issn.2095-0756.20190709 .[9] XU Ning, LI Ming, FANG Saiyin, et al. Research on the detection of the hole in wood based on acoustic emission frequency sweeping[J]. Construction and Building Materials, 2023, 400: 132761. DOI: 10.1016/j.conbuildmat.2023.132761. [10] 钟慧娴, 袁霄, 陈勇平. 木结构古建筑常见虫害特征及防治分析[J]. 木材科学与技术, 2022, 36(3): 96−100. ZHONG Huixian, YUAN Xiao, CHEN Yongping. Characteristics and prevention of common pests in ancient wooden buildings[J]. Chinese Journal of Wood Science and Technology, 2022, 36(3): 96−100. DOI: 10.12326/j.2096-9694.2021131. ZHONG Huixian, YUAN Xiao, CHEN Yongping. Characteristics and prevention of common pests in ancient wooden buildings[J]. Chinese Journal of Wood Science and Technology, 2022, 36(3): 96−100. DOI: 10.12326/j.2096-9694.2021131 .[11] 李明月, 陈东升, 王雪玉, 等. 节子的性质及其对木材材性的影响[J]. 西北林学院学报, 2020, 35(4): 197−204. LI Mingyue, CHEN Dongsheng, WANG Xueyu, et al. Properties of knots and their effects on wood properties[J]. Journal of Northwest Forestry University, 2020, 35(4): 197−204. DOI: 10.3969/j.issn.1001-7461.2020.04.31. LI Mingyue, CHEN Dongsheng, WANG Xueyu, et al. Properties of knots and their effects on wood properties[J]. Journal of Northwest Forestry University, 2020, 35(4): 197−204. DOI: 10.3969/j.issn.1001-7461.2020.04.31 .[12] 唐践扬, 宋晓滨, 郭宇, 等. 钻孔导致孔边木材残余变形和弹塑性损伤研究[J]. 建筑结构学报, 2023, 44(10): 114−122. TANG Jianyang, SONG Xiaobin, GUO Yu, et al. Study on residual deformation and elastic-plastic damage of wood near hole caused by drilling[J]. Journal of Building Structures, 2023, 44(10): 114−122. DOI: 10.14006/j.jzjgxb.2022.0178. TANG Jianyang, SONG Xiaobin, GUO Yu, et al. Study on residual deformation and elastic-plastic damage of wood near hole caused by drilling[J]. Journal of Building Structures, 2023, 44(10): 114−122. DOI: 10.14006/j.jzjgxb.2022.0178 .[13] 刘勇. 品读应县木塔[J]. 中国测绘, 2019(8): 76−80. LIU Yong. Reading Yingxian wooden pagoda[J]. China Surveying and Mapping, 2019(8): 76−80. LIU Yong. Reading Yingxian wooden pagoda[J]. China Surveying and Mapping, 2019(8): 76−80. [14] 温宇鑫, 赵健, 赵东. 孔洞对木梁弯曲应变分布影响的试验研究[J]. 北京林业大学学报, 2017, 39(11): 106−113. WEN Yuxin, ZHAO Jian, ZHAO Dong. Experimental study on the effects of holes on bending strain distribution of wood beams[J]. Journal of Beijing Forestry University, 2017, 39(11): 106−113. DOI: 10.13332/j.1000-1522.20170221. WEN Yuxin, ZHAO Jian, ZHAO Dong. Experimental study on the effects of holes on bending strain distribution of wood beams[J]. Journal of Beijing Forestry University, 2017, 39(11): 106−113. [15] OKAMOTO S, AKIYAMA N, ARAKI Y, et al. Study on the strength of glued laminated timber beams with round holes: difference in structural performance between homogeneous-grade and heterogeneous-grade timber[J]. Journal of Wood Science, 2021, 67(1): 8. DOI:10.1186/s10086-021-01941-3. [16] DANIELSSON H, GUSTAFSSON P J. A probabilistic fracture mechanics method and strength analysis of glulam beams with holes[J]. European Journal of Wood and Wood Products, 2011, 69(3): 407−419. DOI: 10.1007/s00107-010-0475-1. [17] BUKSNOWITZ C, HACKSPIEL C, HOFSTETTER K, et al. Knots in trees: strain distribution in a naturally optimised structure[J]. Wood Science and Technology, 2010, 44(3): 389−398. DOI: 10.1007/s00226-010-0352-4. [18] PARRACHA J L, PEREIRA M F C, MAURÍCIO A, et al. A semi-destructive assessment method to estimate the residual strength of maritime pine structural elements degraded by anobiids[J]. Materials and Structures, 2019, 52(3): 54. DOI:10.1617/s11527-019-1354-9. [19] 刘海笑, 张楚汉, 周锡礽. 冲击作用下含孔洞纤维增强复合材料平板的动力学实验与数值研究[J]. 爆炸与冲击, 2000, 20(4): 313−318. LIU Haixiao, ZHANG Chuhan, ZHOU Xireng. Experimental and numerical study on fiber reinforced comp osite plate with cavity under impact loading[J]. Explosion and Shock Waves, 2000, 20(4): 313−318. DOI: 10.3321/j.issn:1001-1455.2000.04.004. LIU Haixiao, ZHANG Chuhan, ZHOU Xireng. Experimental and numerical study on fiber reinforced comp osite plate with cavity under impact loading[J]. Explosion and Shock Waves, 2000, 20(4): 313−318. DOI: 10.3321/j.issn:1001-1455.2000.04.004 .[20] 陈斌, 王崇恩. 多孔砖孔型及孔洞率有限元优化研究[J]. 新型建筑材料, 2019, 46(9): 141−144. CHEN Bin, WANG Chongen. Finite element optimization of pore patterns and pore rate of porous bricks[J]. New Building Materials, 2019, 46(9): 141−144. DOI: 10.3969/j.issn.1001-702X.2019.09.034. CHEN Bin, WANG Chongen. Finite element optimization of pore patterns and pore rate of porous bricks[J]. New Building Materials, 2019, 46(9): 141−144. DOI: 10.3969/j.issn.1001-702X.2019.09.034 .[21] CHEN Jiaji, XIE Hui, LIU Lingzhi, et al. Strengthening gold with dispersed nanovods [J]. Science, 2024, 385(6709): 629−633. DOI: 10.1126/science.abo7579. [22] 成俊卿, 杨家驹, 刘鹏. 中国木材志[M]. 北京: 中国林业出版社, 1992: 67−694. CHENG Junqing, YANG Jiaju, LIU Peng. Wood Records of China[M]. Beijing: China Forestry Publishing House, 1992: 67−694. CHENG Junqing, YANG Jiaju, LIU Peng. Wood Records of China[M]. Beijing: China Forestry Publishing House, 1992: 67−694. [23] RICARDO SANTOS COIMBRA P, DE SOUZA ALMEIDA A, HENDRIGO DE ALMEIDA T, et al. Stress distribution in tauari wood beam[J]. International Journal of Materials Engineering, 2018, 8(1): 5−11. DOI: 10.5923/j.ijme.20180801.02. [24] WEN Yuxin, YANG Ping, ZHAO Jian, et al. Theoretical and experimental considerations on the neutral axis of wood beams with a hole in different locations[J]. Holzforschung, 2018, 72(9): 769−777. DOI: 10.1515/hf-2017-0174. [25] 何盛. 樟子松指接材有限元模型分析研究[D]. 南京: 南京林业大学, 2011. HE Sheng. Study of Finite Element Modeling Analysis for Pinus sylvestris L. var. mongolica Litv. Finger-jointed Lumber[D]. NanJing: Nanjing Forestry University, 2011. HE Sheng. Study of Finite Element Modeling Analysis for Pinus sylvestris L. var. mongolica Litv. Finger-jointed Lumber[D]. NanJing: Nanjing Forestry University, 2011. -
-
链接本文:
https://zlxb.zafu.edu.cn/article/doi/10.11833/j.issn.2095-0756.20250389
点击查看大图
图(6) / 表(6)
计量
- 文章访问数: 37
- HTML全文浏览量: 16
- PDF下载量: 11
- 被引次数: 0
